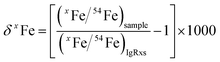Assessment of matrix effects associated with Fe isotope analysis using 266 nm femtosecond and 193 nm nanosecond laser ablation multi-collector inductively coupled plasma mass spectrometry†
Xin-Yuan
Zheng
 *ab,
Brian L.
Beard
ab and
Clark M.
Johnson
ab
*ab,
Brian L.
Beard
ab and
Clark M.
Johnson
ab
aDepartment of Geoscience, University of Wisconsin – Madison, 1215 W. Dayton Street, Madison, WI 53706, USA. E-mail: xzheng75@wisc.edu
bNASA Astrobiology Institute, USA
First published on 2nd November 2017
Abstract
This study evaluated matrix effects during Fe isotope analysis using a 266 nm femtosecond (fs) laser and a 193 nm nanosecond (ns) laser coupled to a multi-collector ICP-MS. During 150 second spot analysis on pyrite, Fe isotope fractionation was not observed for fs-laser ablation (fs-LA), but was evident for ns-LA. The observed downhole Fe isotope fractionation during ns-LA is caused by multiple processes comprising ablation, transport, and ionization in the ICP. Contrary to the common perception of “matrix-free” analysis, matrix effects clearly exist during fs-LA analysis; small deviations of up to ∼0.2‰ in the measured 56Fe/54Fe ratios from the true value of magnetite grains with ≥∼8 wt% impurities were resolved using a nearly pure magnetite as the bracketing standard. Moreover, inaccurate and imprecise 56Fe/54Fe results were obtained when magnetite and pyrrhotite was measured against a non-matrix-matched standard (pyrite or Fe metal). The observed matrix effects during fs-LA cannot be explained by formation of a large heat-affected zone during ablation, but result from the influence of different chemical compositions of samples and standards on space-charge effects in the ICP-MS. Such matrix effects can be largely suppressed by water addition during analysis at a price of reduced sensitivity, so that precise and accurate Fe isotope analysis to a ∼0.1‰ level can be routinely achieved under “wet” conditions without matrix-matching between sample and standard. These results may reconcile dramatically different precisions previously reported for Fe isotope analysis by fs-lasers, and also highlight fs-LA-MC-ICP-MS as an appealing option for in situ Fe isotope analysis on samples with complex matrices and high-symmetry minerals, both of which encounter significant analytical difficulties using secondary ion mass spectrometry (SIMS). For ns-LA, in addition to similar composition-related matrix effects experienced by fs-LA in the ICP, matrix effects also originate from ablation-related processes that produce sample particles with matrix-dependent size distributions and, often, larger aerodynamic sizes, resulting in highly inaccurate 56Fe/54Fe results during non-matrix-matched analysis under “dry” conditions. The collective matrix effects during Fe isotope analysis by ns-LA cannot be fully suppressed by water addition, therefore, matrix matching is required for accurate Fe isotope analysis by ns-LA.
1. Introduction
Metal and metalloid stable isotopes have proven extremely useful for a broad spectrum of biogeochemical studies.1,2 These so-called “non-traditional” stable isotopes (e.g., Fe, Mg, Si, Cu) are now routinely analyzed using solution nebulization multi-collector inductively coupled plasma mass spectrometry (MC-ICP-MS) to high precision (e.g., ≤0.1‰, 2σ),3 but they are not routinely analyzed by in situ methods that resolve μm-scale isotopic variations associated with textural and chemical zonation in a sample. Such in situ measurements can provide critical information on a wide range of geological processes.4–6Laser ablation (LA) coupled to MC-ICP-MS (LA-MC-ICP-MS) has emerged as an attractive tool for in situ metal and metalloid stable isotope analysis,4–8 due to its ease of use and low cost as compared to alternatives such as secondary ion mass spectrometry (SIMS). SIMS analysis typically offers better spatial resolution, but it suffers from more complicated instrumental mass bias,9 including crystal orientation effects during analysis of some high-symmetry minerals,10,11 such as Fe isotope analysis on magnetite (Fe3O4).12 In contrast, crystal orientation effects do not affect LA-MC-ICP-MS analysis.
Reliable LA-MC-ICP-MS analysis requires a thorough understanding of matrix effects, because (1) matrix effects have a major impact on instrumental mass bias; (2) correction of instrumental mass bias that preserves natural isotopic variations generally requires a sample–standard bracketing method that assumes identical mass bias between the sample and standard during analysis by MC-ICP-MS; and (3) a high precision of ∼0.1‰ in stable isotope ratios is often required to resolve the limited natural variations of a few per mil (‰) for many metal and metalloid stable isotopes (e.g., Fe, Mg, Si, Cu). Such precisions are more than an order of magnitude more stringent than the typical percent-level precision attained during LA analyses of elemental abundances.13–15
Laser ablation-induced elemental fractionations, typically matrix-dependent, can occur due to differential volatilization or condensation of elements during ablation, differential transport of chemically- and size-fractionated sample particles, or incomplete ionization of particles on the ICP.16 LA-induced isotopic fractionations have also been observed,7,17,18 posing a primary obstacle for precise and accurate LA measurements, but the origin of isotopic fractionation is not well studied.
Lasers with ultra-short pulse widths in the femtosecond (fs; 10−15 s) regime have been adopted in hopes of overcoming matrix effects during LA analysis. The technique relies on the unique physical processes underlying the fs-LA, where transfer of the pulsed photon energy to the sample is faster than conventional heat diffusion that occurs in the picosecond (ps; 10−12 s) timescale. This is in marked contrast to the more commonly-used nanosecond (ns; 10−9 s) LA, where significant heating and melting of samples can occur due to the longer laser–matter interaction time relative to heat diffusion time.19,20 Consequently, fs-LA minimizes the heat-affected zone that is thought to be a major source of LA-induced fractionations.21 This technique is advantageous in potentially eliminating the need for well-characterized standards with matrices matching those of samples, because such standards do not exist for many materials.
Detailed discussions of LA-induced isotopic fractionation prior to the ICP have been highlighted in recent studies that used a cascade aerosol impactor.8,22,23 These studies showed that, depending on the Fe mineral ablated, particle-size dependent Fe isotope fractionation of up to several per mil in 56Fe/54Fe ratios can occur during both fs- and ns-LA, contrary to the common assumption of no isotopic fractionation at the ablation site or smaller isotopic fractionation during fs-LA as compared to ns-LA.17,24 The fs-LA, however, is superior to ns-LA in terms of always providing a stoichiometric aerosol for Fe isotope analysis,8,22,23 where non-stoichiometric sampling can occur under certain conditions during ns-LA.22 In addition, fs-LA produces largely similar particle size distributions regardless of the substrate mineralogy or ablation conditions, in contrast to ns-LA, which creates mineral-dependent particle size distributions, where more Fe mass often resides in particles with larger aerodynamic sizes as compared to fs-LA.22
It, however, remains unclear if the superiority of fs-LA can directly translate into better isotopic analysis in practice. Using a non-matrix-matched sample–standard bracketing protocol, one group is able to routinely achieve accurate 56Fe/54Fe analysis with a precision of ∼0.1‰ (2σ) for samples ranging from conductive Fe metals to insulating silicates,6,17,25 but another group, using a matrix-matched protocol, only yielded a precision of ∼0.3–0.5‰,24,26 lying in the range of that produced by ns-LA-MC-ICP-MS.27 Distinct operating conditions may contribute to these different results. The non-matrix-matched Fe isotope analyses with better precision were conducted under “wet” LA conditions,6,17,25 where aqueous solution was introduced via a spray chamber before the ICP torch. In contrast, the matrix-matched analyses with less precise results were conducted under “dry” LA conditions.24,26 The difference in precision is broadly consistent with observations of suppression or stabilization of matrix effects under wet plasma conditions during solution and LA analysis,28–30 contradicting the common perception that fs-LA analysis is “matrix-free”. These studies indicate further assessment of matrix effects during fs-LA-MC-ICP-MS is needed to fully apply this approach to stable isotope analysis of complex natural samples.
In this contribution, we evaluated and compared matrix effects during Fe isotope analysis using fs- and ns-LA under both dry and wet conditions via matrix-matched and non-matrix matched measurements of a suite of chemically and isotopically well-characterized Fe minerals. A previous study suggested that fs-LA does not always offer better analytical performance compared to ns-LA during elemental analysis,31 but whether the same conclusion applies to stable isotope analysis is unknown. Our results help answer the question “is it worth it to have the more costly and complex fs-LA” for high-precision stable isotope analysis.32
2. Experimental
2.1 Instruments
A Nd:YLF-pumped Ti:sapphire femtosecond laser (Analyte-fs, Teledyne-Photon Machines) was used in this study. The system is equipped with a chirped pulse amplification device, and produces 266 nm ultraviolet (UV) laser at the third harmonic with a pulse-width of ∼150 fs. Laser energy is adjustable using the built-in attenuator, and follows a Gaussian profile. Repetition rate can vary between 1 and 250 Hz. Laser spot size (i.e., diameter) at sample surface was controlled by adjusting the distance between sample and laser objective lens, but always keeping the laser focus below the sample surface. Smaller spot sizes were achieved by moving the objective further from the sample (i.e., laser focus closer to the sample surface), whereas larger spot sizes were obtained by moving the objective closer to the sample surface. For comparison, a 193 nm ArF excimer laser (Teledyne-Photon Machines) with a pulse-width of ∼4 ns was used. Laser energy is adjustable via the built-in attenuator, and follows a uniform profile due to a built-in beam homogenizer. Repetition rate can vary between 1 and 300 Hz. Laser spot size was controlled using a series of selectable apertures with pre-defined sizes. The same type of two-volume HelEx ablation cell (CETAC) was equipped on both laser ablation systems.A Nu Plasma II MC-ICP-MS with the Enhanced Sensitivity (ES) interface was used in this study. The instrument is capable of resolving argide interferences from Fe isotopes (e.g., 40Ar14N+ on 54Fe+, 40Ar16O+ on 56Fe+, 40Ar16OH+ on 57Fe+) by using a 0.05 mm source defining slit combined with narrowing alpha slits under (pseudo-) high mass resolution mode. These settings typically yielded mass resolving power of ∼6000–7000 following a “5–95%” definition,33 and ∼8% of the ion beam transmission at low mass resolution mode using a 0.3 mm defining slit without using the alpha slits. Hydride formation, such as 55MnH+ on 56Fe+, and 56FeH+ on 57Fe+, had negligible influence on the measured Fe isotope ratios, although some hydride interferences (e.g., 56FeH+) cannot be fully resolved during analysis (Appendix).
2.2 Coupling of laser ablation systems to the MC-ICP-MS
The same MC-ICP-MS was coupled to the 266 nm fs-laser or 193 nm ns-laser during the LA tests, and delivery of the LA-produced aerosols to the MC-ICP-MS was done in the same fashion for both lasers, where aerosols were carried by He gas, and mixed with make-up Ar gas at the HelEx cell output. The Teflon tubing that carried sample aerosols was attached to the ICP torch either directly, or through a T-connection where a peltier-cooled cyclonic spray chamber (glass expansion) was joined, using a commercial quartz tee connector, or by a homemade tubing assembly (Fig. 1). No difference in the measured Fe isotope compositions was found using either T-connection setup. When the T-connection was used during analysis, the spray chamber was always cooled to 7 °C. A nebulizer was attached to the spray chamber, so that water or Ar gas could be introduced to mix with sample aerosols immediately before the ICP torch via the T-connection during LA analysis. The nebulizer uptake rate was controlled by adjusting the flow rate of nebulization Ar gas using a mass flow controller on the MC-ICP-MS. The actual uptake rates were determined at each session by measuring the mass loss of pure water after aspiration for a known duration. Because the nebulizer was typically operated at an uptake rate lower than the designated rate during our LA analyses, two nebulizers (MicroMIST) with manufacture-designated uptake rates of 50 and 100 μL min−1 were tested. Each nebulizer was fitted to sample tubes with different inner diameters (0.18 and 0.25 mm) during our tests, giving a total of 4 combinations of nebulizer assembly. No difference in the measured Fe isotope compositions was observed using either nebulizer assembly; the most important factor that controlled Fe isotope measurements was the water uptake rate.During dry LA conditions, the tubing that carries sample aerosols was connected to the ICP torch either directly, or via the T-connection. When the T-connection was used, the nebulizer was either configured not to aspirate by setting the nebulization Ar gas flow rate to 0, or to aspirate Ar gas from an additional Ar source at variable rates. Aspiration of Ar gas via the nebulizer was intended to prevent potential split and loss of sample aerosols through the spray chamber of the T-connection during LA analysis. During wet LA conditions, the sample-carrying tubing was attached to the ICP torch through the T-connection, and ultra-pure (i.e., 18.2 MΩ cm) water was introduced at controlled rates via the nebulizer and spray chamber.
2.3 Laser ablation substrates
In-house Fe standards, including a suite of magnetites (Fe3O4) with varied amount of impurity cations (mainly Mn, Mg, Zn, and Ti), a pyrite (FeS2), a pyrrhotite (Fe4S5), a siderite (FeCO3), and a pure Fe metal were used in this study. Chemical compositions of Fe mineral standards were characterized using an electron microprobe (Appendix Tables A1 and A2†). Iron isotopic compositions of each standard, analyzed by multiple analyses using solution nebulization MC-ICP-MS after ion-exchange chromatographic purification, are homogenous within 0.1‰ in 56Fe/54Fe ratios (Appendix Table A3†).2.4 Experimental details
A series of experiments were conducted using the fs- and ns-laser to evaluate downhole Fe isotope fractionation, matrix effects, and analytical limits of spatial resolution. Typical operating conditions of laser and MC-ICP-MS were summarized in Table 1. Nominal fluences, defined by the pulse energy at sample surface divided by the crater area,22,34 were used in this study for the fs-laser that has a Gaussian beam profile. Iron isotopes were measured using the time-resolved analysis (TRA) with 0.2 s integration time.| Laser ablation system | ||
| Laser type | Analyte-fs Ti:sapphire laser (Teledyne-Photon Machines) | Excite.193 ArF excimer laser (Teledyne-Photon Machines) |
| Wavelength | 266 nm | 193 nm |
| Pulse-width | ∼150 fs | ∼4 ns |
| Beam profile | Gaussian | Uniform |
| Ablation cell | Two-volume HelEX (CETAC) | |
| He gas flow | ∼0.6 L min−1 | |
| Ar make-up gas flow | ∼1 L min−1 (dry LA) | |
| ∼0.3–1 L min−1 (wet LA) | ||
| Fluence on sample | 0.5–1.1 J cm−2 (typically ∼1.1 J cm−2) | ∼2 J cm−2 |
| Repetition rate | 12–21 Hz (typically 17 Hz) | 7–34 Hz (typically 17 Hz) |
| Spot size on sample | 20–42 μm circle (typically 25 μm) | 25 μm circle |
| Ablation mode | Raster (typical); spot | Raster |
| Raster scan speed | 1 μm s−1 | |
| Raster iteration | 1 pass (typical); 2 passes | 1 pass |
| H2O addition rate during wet LA | ∼3–40 μL min−1 | ∼7–17 μL min−1 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||
| MC-ICP-MS:Nu plasma II with the Enhanced Sensitivity (ES) interface | ||
| Mass resolution | Pseudo-high mass resolution (∼10% ion transmission) | |
| Optimization | Tuning when connected to Aridus before switching connection to LA | |
| Data collection mode | Time-resolved analysis (TRA) with an integration time of 0.2 s | |
| RF power | 1300 W | |
| Coolant Ar gas flow | 13.2 L min−1 | |
| Auxiliary Ar gas flow | 0.8 L min−1 | |
| Total Fe ion intensity | Typically 5–15 V | |
| On-peak gas blank | ∼60 s | |
| Data acquisition time | ∼20–110 s (typically 110 s) | ∼110 s |
Two types of in situ Fe isotope analyses were conducted during multiple analytical sessions spanning a duration of ∼2 years. The first type of test was mineral-phase-matched analysis on a suite of 5 magnetite standards containing <1 to ∼15 wt% impurities, using the purest magnetite standard as the bracketing standard for instrumental mass bias correction. The second type of test was non-mineral-phase-matched analysis of a magnetite and pyrrhotite standard, using pyrite or pure Fe metal as the bracketing standard. Pyrite was chosen as the bracketing standard, because there is negligible particle-size dependent Fe isotope fractionation during raster ablation of pyrite using fs-LA.8 Pure Fe metal was also used during a few experiments, because non-matrix-matched Fe isotope analysis using pure Fe metal as the bracketing standard has been shown to achieve a high precision of ∼0.1‰ (2SD) by fs-LA.17,25
All Fe isotope ratios were measured by the sample–standard bracketing protocol using raster ablation with a scan speed of 1 μm s−1 and only one scan pass (Table 1). Typically, each measurement comprised ∼60 s data acquisition of the gas blank (i.e., laser not firing) and ∼110 s acquisition on the analyte, leaving a raster area of 60 × 50 μm2 and mineral-dependent crater depths of several to up to ∼38 μm. A fluence of ∼1 J cm−2 was commonly used during fs-LA, and a lower fluence of ∼0.56 J cm−2 was used during a few analyses to explore the impact of fluence on matrix effects. A fluence of ∼2 J cm−2 was used during ns-LA, because it has been demonstrated that this fluence provides stoichiometric sampling of Fe isotope compositions for all Fe minerals used in this study.22 Plasma conditions were optimized at the beginning of analysis under both wet and dry conditions.
3. Results
3.1 Spot analysis
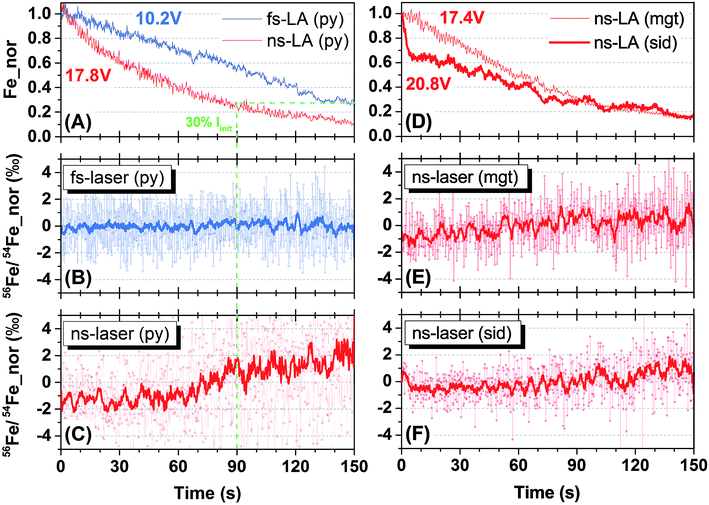
Representative spot analyses of different Fe minerals conducted by fs- and ns-LA are shown in Fig. 2. All plots display individual 56Fe/54Fe ratio (0.2 s integration) measurements normalized to the average value of all measurements taken during the 150 s analysis. Changes in Fe ion intensity normalized to the initial intensity at the onset of analysis are also shown in Fig. 2.Iron intensities during fs- and ns-LA showed monotonic decreases that are typical of spot analysis, probably largely reflecting decreased efficiency in extracting laser ablation produced particles with increasing crater depth. For fs-LA of pyrite, Fe ion intensity decreased from 10.2 to 2.9 volts, representing a ∼70% drop (Fig. 2A), but the measured 56Fe/54Fe ratios remained constant over the whole 150 s of ablation (Fig. 2B). For ns-LA of pyrite, Fe ion intensity decreased from 17.8 to 2.1 volts, representing a ∼90% drop (Fig. 2A). In contrast to fs-LA, the measured 56Fe/54Fe ratios were relatively stable within the first 60 s, and then showed a gradual increase (>3‰ in the 10-point average) in the subsequent 90 s (Fig. 2C).
The crater aspect ratio (i.e., depth/diameter on sample surface) for pyrite, produced by a 150 s spot ablation, is different for fs- and ns-LA. The crater depth for fs-LA is ∼38 μm, giving an aspect ratio of ∼1, whereas for ns-LA the crater depth is ∼54 μm, giving an aspect ratio of ∼1.5. The different crater aspect ratios may have partially contributed to different rates in Fe ion intensity changes during fs- and ns-LA (Fig. 2A), but these differences cannot explain the different trends in the measured 56Fe/54Fe ratios during spot ablation by the two lasers. The measured 56Fe/54Fe ratios remained constant over a ∼70% drop in Fe ion intensity during a duration of 150 s for fs-LA (Fig. 2A and B). For ns-LA, the 70% drop in Fe ion intensity occurred after ∼90 s of ablation (Fig. 2A), but the measured 56Fe/54Fe ratios started to increase after only ∼60 s of ablation (Fig. 2C).
Additional spot analysis was conducted on siderite and magnetite using the ns-laser. Iron ion intensity dropped by ∼85% (decreasing from 20.8 to 3.2 volts) over 150 s during ns-LA of siderite, and decreased by ∼85% (decreasing from 17.4 to 2.6 volts) over the same duration during ns-LA of magnetite (Fig. 2D). Similar to the increase in the measured 56Fe/54Fe ratios during ns-laser ablation on pyrite, the measured 56Fe/54Fe ratios for siderite and magnetite all shifted to heavier values, but by a smaller magnitude (i.e., ∼2‰), during the 150 s spot analysis (Fig. 2E and F).
3.2 Mineral-phase-matched and non-phase-matched Fe isotope analysis by raster ablation
For both fs and ns-LA, all Fe isotope results reported were corrected for instrumental mass bias using the sample–standard bracketing method. Depending on the tests, pure magnetite, pyrite, or pure Fe metal was used as the bracketing standard (Appendix Tables A4 and A5†). True Fe isotope compositions of these standards were established using conventional solution nebulization MC-ICP-MS and an in-house high-purity Fe solution as the bracketing standard, and then referenced to the igneous rock scale.35 All δ-values reported here for Fe isotope compositions were defined by:where x indicates 56 or 57, and IgRxs implies that data are referenced to the igneous rock scale. Under this scale, the commonly used Fe isotope standard, IRMM-014, has a δ56Fe value of −0.09‰, giving a conversion relation of δ56FeIRMM-014 = δ56FeIgRxs + 0.09 between the two reference frames. All measured 56Fe/54Fe and 57Fe/54Fe ratios had an expected mass-dependent relationship (δ57Fe = ∼1.49 × δ56Fe for both fs- and ns-LA data; Appendix Tables A4 and A5†), indicating the absence of isobaric and polyatomic interferences during analyses. To test for possible biases in Fe isotope measurements as a function of ion intensity, analyses were conducted at the beginning of every analytical session with mismatched Fe intensities between sample and standard over an approximate ±40% range by adjusting laser repetition rates. Within the level of analytical precision, the results typically did not show biased δ56Fe results associated with the intensity mismatch (Fig. 3). Nonetheless, total Fe intensities between sample and bracketing standard were typically matched within ∼10% by changing repetition rates as a precaution to avoid any matrix effect associated with ion intensities.
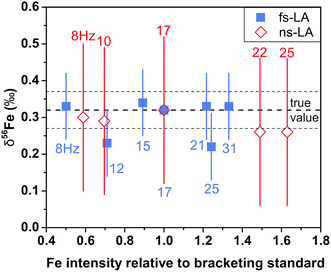
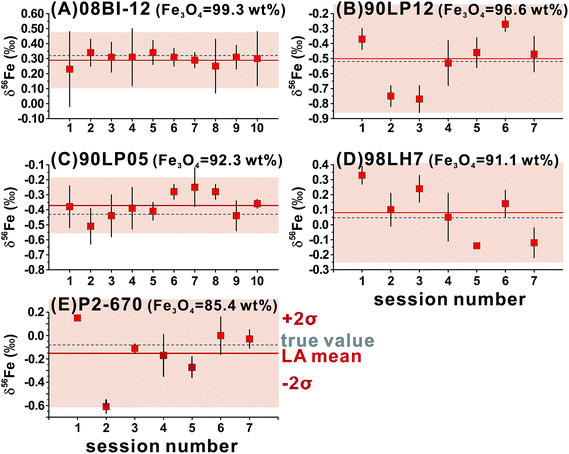
For fs-LA, mineral-phase-matched analyses under dry LA conditions yielded accurate and precise (∼0.1‰) δ56Fe values only on “sample” magnetite grains that contain less than ∼8 wt% impurities (Fig. 4B). When impurities in the “sample” magnetite are higher than ∼8 wt%, the average values of the δ56Fe results show small, but resolvable, deviations of ∼0.2‰ from the true values determined by conventional solution nebulization analysis, although δ56Fe results remain precise to a level of ∼0.1‰ (2SD).
The same analyses were also conducted under wet fs-LA conditions, often during the same analytical session or next day. Ultra-pure water was introduced at rates of ∼11–28 μL min−1via spray chamber at the T-connection during analysis. Addition of water caused a ∼20% decrease in the measured Fe intensities relative to those measured under dry LA conditions during the same analytical session (Fig. 4A). This is consistent with common observations that wet plasma condition gives lower sensitivity compared to dry plasma condition during solution nebulization ICP-MS analysis due to the influence of water on ionization and ion-extraction on ICP-MS. Water addition, however, led to improved accuracy. The δ56Fe values obtained under wet fs-LA conditions are accurate within 0.1‰ for all magnetite standards analyzed, including the ones that contain >8 wt% impurities (Fig. 4B).
For ns-LA, mineral-phase-matched analyses under dry conditions yielded average δ56Fe values that were accurate within ∼0.1‰ for all ablated magnetite grains (Fig. 4C). The δ56Fe values, however, are imprecise, with precisions ranging from 0.18‰ to 0.46‰ (2SD). The worst precision was obtained on the magnetite containing the highest percentage of impurities. When the same magnetite standard was analyzed, precision by ns-LA was typically more than 2-times worse than that achieved by fs-LA. A closer examination of the ns-LA data reveals that δ56Fe results can sometimes be precise and accurate at a ∼0.1‰ level during an individual session, but they show large session-to-session variations (Fig. 5), leading to poor long-term external precision.
Phase-matched analysis of magnetite grains was also conducted under wet ns-LA conditions where ∼7–17 μL min−1 of water was introduced during analysis (Fig. 4C). Similar to fs-LA, water addition also led to decreased Fe ion intensity relative to dry conditions during ns-LA (Fig. 4A). In contrast to water addition during fs-LA, which clearly improved the accuracy of δ56Fe values, water addition during ns-LA did not result in a clear improvement in accuracy. The long-term average δ56Fe values obtained under wet ns-LA conditions seemingly deviate further from the true values of magnetite grains with >∼8 wt% impurities, but it is not possible to confidently determine if wet or dry conditions yielded more accurate results within the obtained precisions of ns-LA analysis (Fig. 4C). The precisions achieved for wet ns-LA analysis, ranging from ∼0.2‰ to ∼0.6‰ (2SD) for δ56Fe, are worse than those achieved under dry plasma conditions, suggesting a detrimental impact of water addition on analytical precision of isotope analysis by ns-LA.
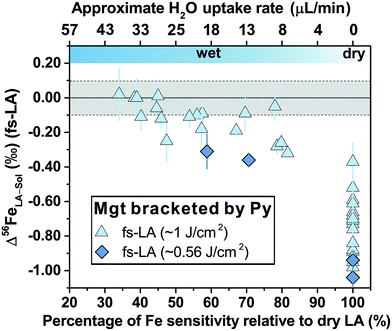
For fs-LA under dry conditions, analyses of pyrrhotite and magnetite using pyrite as the bracketing standard to correct for instrumental mass bias always yielded inaccurate δ56Fe values, although data were commonly precise to a level of 0.1‰ or better (2SD) for individual analytical sessions (Fig. 6). When the laser was connected to the ICP torch via the T-connection during dry ablation analysis (Fig. 1), additional measurements were conducted with introduction of Ar gas at varied rates through the nebulizer fitted to the spray chamber. These tests had two purposes: (1) ruling out the possibility that imprecise and inaccurate δ56Fe values were caused by potential leak of aerosols through the spray chamber at the T-connection; and (2) testing whether addition of Ar gas can lead to accurate δ56Fe values. Introduction of Ar gas through the nebulizer resulted in decreases in the Ar makeup gas by a similar amount to result in maximum Fe sensitivity on the MC-ICP-MS, and the similar antiphase relation between the nebulization Ar gas flow and Ar makeup gas flow was also observed during introduction of water. Introduction of varied amount of Ar gas through the nebulizer resulted in similarly inaccurate, or sometimes even more inaccurate, δ56Fe values, compared to those measured under dry LA conditions without introduction of Ar gas. Consequently, we do not further distinguish data collected with or without addition of Ar gas via the nebulizer used to introduce water under dry conditions. As shown in Fig. 6, the measured δ56Fe values of pyrrhotite by dry fs-LA are ∼0.2‰ to up to ∼0.6‰ lower than the true value during different analytical sessions, and the pooled δ56Fe results yielded a long-term precision of 0.29‰ (2SD). The δ56Fe values for magnetite by dry fs-LA are ∼0.4‰ to up to ∼1‰ lower than the true value during different sessions, yielding a long-term precision of 0.4‰ (2SD).
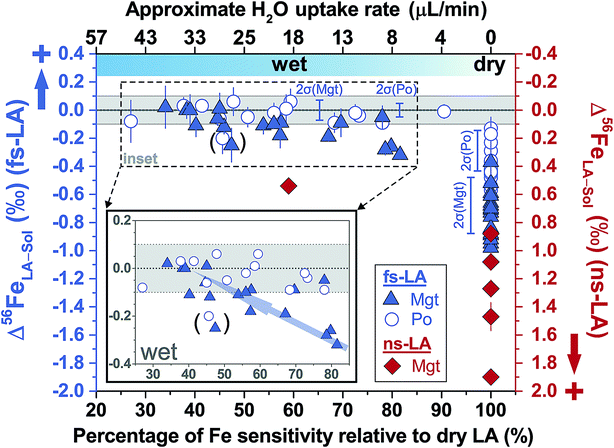 | ||
| Fig. 6 Deviations of δ56Fe results from non-mineral-phase-matched la analyses of magnetite (fs-LA: filled blue triangles; ns-LA: filled red diamonds) and pyrrhotite (fs-LA: blue open circles), using pyrite as the bracketing standard, from the true values at varied water addition rates. The percentage of Fe intensity relative to dry LA conditions in the same analytical session (bottom x-axis) was directly measured, and the water addition rate (top x-axis) was estimates based on the equation in Fig. 7. Note that the directions of y-axis for the fs- and ns-LA are opposite. Each symbol represents the mean value of ≥3 LA analyses with the propagated 2 standard errors that combined uncertainties from both LA and solution nebulization results. The blue thick-line error bars indicate 2 standard deviations of the pooled δ56Fe results obtained by fs-LA under dry- and wet-plasma conditions for pyrrhotite and magnetite. For wet-plasma results, the 2 standard deviations were based on all individual analyses collected at water addition rates between ∼4–50 μL min−1 for pyrrhotite, and ∼13–40 μL min−1 for magnetite. | ||
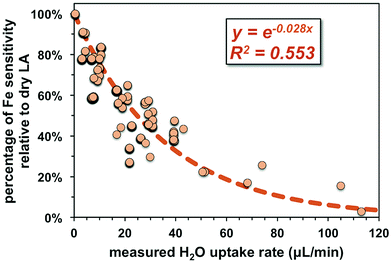
Non-phase-matched analyses were also conducted for fs-LA under wet conditions, where pure water was introduced during analysis via the spray chamber at rates ranging from ∼4 to 50 μL min−1. Consistent with lower ion intensity during phase-matched analysis under wet LA conditions (Fig. 4A), the wider range of water addition rates used during non-phase-matched analysis clearly showed that higher water addition rates led to lower Fe sensitivity on the MC-ICP-MS during analysis (Fig. 7). No data were collected at water addition rates >50 μL min−1, because total Fe intensities typically decreased to <4 volts (loss of >70% intensities relative to dry LA conditions). Under such low ion intensity conditions, the internal precision of an Fe isotope measurement is decreased due to Johnson noise and counting statistics, making evaluation of matrix effects more difficult.
Similar to the results from phase-matched analysis under wet fs-LA conditions (Fig. 4B), addition of water during fs-LA clearly improved the accuracy of non-phase-matched analyses (Fig. 6). Despite the lower Fe intensities during wet fs-LA analysis, ion intensities were still sufficiently high to overcome the influence of Johnson noise and counting statistics, so that the analytical precision of wet fs-LA analysis did not degrade. Analyses of pyrrhotite at water addition rates of ∼4 to ∼50 μL min−1, corresponding to a loss of ∼10–70% ion intensity relative to dry LA conditions, yielded δ56Fe values accurate to within 0.1‰ relative to the true value, and, collectively, gave a long-term precision of 0.14‰ (2SD). For analyses of magnetite, a general trend of improved accuracy with higher water addition rates was observed (Fig. 6). Analyses conducted at water addition rates between ∼13 and 40 μL min−1, corresponding to a loss of 30–65% ion intensity relative to dry LA conditions, almost always yielded δ56Fe results accurate to within 0.1‰ relative to the true value, giving a long-term precision of 0.16‰ (2SD). The long-term precision was 0.1‰ for pyrrhotite and 0.14‰ for magnetite (Fig. 6), if data from one particular session were excluded as outliers. For no apparent reason, δ56Fe values of pyrrhotite and magnetite that were measured at a water addition rate of ∼30 μL min−1 (loss of ∼55% ion intensities) during the same session were less accurate than those measured at lower water addition rates (Fig. 6).
Non-phase-matched analyses of magnetite by fs-LA were also conducted under both dry and wet conditions at a lower fluence (∼0.6 J cm−2), using pyrite as the bracketing standard (Fig. 8). Similarly, δ56Fe values were ∼1‰ lower than the true value under dry fs-LA conditions, and were improved in terms of accuracy under wet LA conditions.
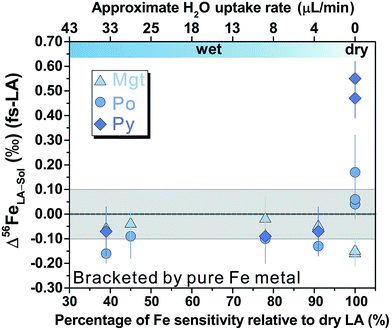
Analyses of magnetite, pyrrhotite, and pyrite against pure Fe metal as the bracketing standard also generally yielded inaccurate δ56Fe values under dry fs-LA conditions (Fig. 9). The offsets of the measured δ56Fe values from true values were up to ∼0.2‰ for magnetite and pyrrhotite, and up to ∼0.6‰ for pyrite under dry fs-LA conditions. Accurate δ56Fe values within ∼0.1‰ of true values were achieved with water addition during analysis.
For ns-LA under dry conditions, non-phased-matched analysis of magnetite, using a pyrite as the bracketing standard, also yielded imprecise and inaccurate δ56Fe values (Fig. 6). Deviations of ∼0.9‰ to 1.9‰ of the measured δ56Fe values from the true value for ns-LA analysis were larger than those measured by fs-LA under the same analytical conditions. Interestingly, the measured δ56Fe values by ns-LA were constantly higher than the true value of substrate, but were constantly lower than the true values of substrates by fs-LA when pyrite was used as the bracketing standard (Fig. 6). The cause of this is unknown, but this phenomenon is similar to our previous results that Fe isotope fractionation often occurs in opposite directions in particles of similar aerodynamic sizes produced by ns- and fs-LA.22
Limited analyses where minerals were not phase-matched were conducted under wet ns-LA conditions, based on the fact that water addition did not improve accuracy and precision for phase-matched analyses that should be less analytically challenging (Fig. 4C). Also, particle size distributions produced by ablation using a 193 nm ns-laser under conditions identical to those used for Fe isotope analysis in our experiments have been shown to be dramatically different for magnetite and pyrite,22 so it is unlikely that water addition can lead to better performance of ns-LA than that of fs-LA. This was supported by our results; water addition clearly improved accuracy compared to dry plasma conditions for ns-LA analysis, but the measured δ56Fe values still showed a significant offset of ∼0.5‰ from the true value (Fig. 6). In contrast, at similar water addition rates, non-phase-matched fs-LA analysis was able to yield δ56Fe values that were accurate to a level of ∼0.1‰ or better.
3.3 Spatial resolution of Fe isotope analysis by fs-LA-MC-ICP-MS
Reduction in sample consumption during fs-LA analysis using raster ablation was achieved via shortening of data acquisition time (i.e., smaller raster sizes), and, in several tests, combined with decreased laser repetition rates. A precision of ∼0.1‰ in δ56Fe values can be maintained during matrix-matched analysis using ∼3 × 103 to 10 × 103 μm3 pyrite (Fig. 10), which was only ∼15–50% of the typical volume consumed during the analyses intended to evaluate matrix effects. The higher sample consumption during the analyses designed to evaluate matrix effects was due to the intentional use of long data acquisition time (∼110 s) to minimize any potential effect of counting statistics. Precise Fe isotope analysis by fs-LA to a precision of ∼0.1‰ is also possible using spot ablation (Fig. 10). There was some variability in precision from different analytical sessions, but, overall, the precision decreased with decreasing data acquisition time or ion intensities (Fig. 10), suggesting that Johnson noise and counting statistics gradually becomes a limiting factor.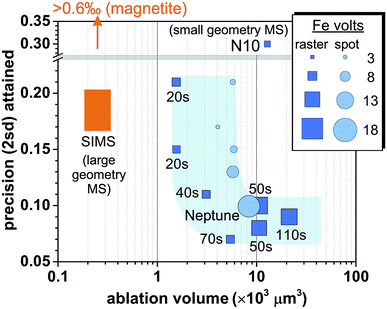 | ||
| Fig. 10 Comparison of spatial resolution for Fe isotope analysis of pyrite and the associated analytical precisions by fs-LA-MC-ICP-MS and SIMS. Iron intensity for spot analysis by fs-LA in the figure is a simple arithmetic average of initial and ending intensity of analysis. The numbers labeled for raster analyses indicate data acquisition time. “N10” indicates the result from the literature,24 and “Neptune” denotes the result obtained using a Neptune instrument from the literature.6,17 Results of SIMS analysis on pyrite were taken from the literature,61,62 and the magnetite result was reported in the literature.12 | ||
4. Discussion
4.1 Iron isotope fractionation during spot analysis
Extensive investigations have evaluated downhole elemental fractionation because of the strong desire to use laser ablation for depth profiling.16,31,36 In contrast, few studies have evaluated stable isotope fractionation during depth profiling. Below we discuss our observations regarding Fe isotope fractionation during spot analysis by ns- and fs-LA in conjunction with our past studies that have measured the Fe isotope composition of aerodynamically size-sorted particles using the same substrates and lasers.Existing studies have suggested that isotopic fractionation is caused by laser–matter interactions at the ablation site,42 or differential transport of isotopically-fractionated particles, or incomplete ionization of particles in the ICP.7,17,27,30,38 Our new results, combined with previous studies on pre-ICP, LA-induced isotopic fractionations,22 suggest that the observed downhole Fe isotope fractionation cannot be fully explained by any single process, but reflects collective processes comprising ablation, particle transport, and ionization in the ICP.
Ablation includes removal of mass from the substrate and formation of particles. Nanosecond laser ablation can stoichiometrically sample Fe minerals in most cases under the raster ablation.22 For ablation alone to change the measured Fe isotope ratios, a transition from stoichiometric to non-stoichiometric sampling during spot ablation should occur. Different from the raster ablation, as the crater deepens during spot ablation, the effective fluence may decrease due to absorption of laser energy by the wall of the ablation crater (i.e., increased crater interior surface area),39,40 causing non-stoichiometric sampling at the late stage of spot analysis. Such a mechanism, however, cannot be dominant, because it does not explain the direction of change in the measured 56Fe/54Fe ratios. The δ56Fe value of the total aerosol produced by ns-LA of magnetite at low fluence is lower than the true composition of substrate,22 interpreted to reflect non-quantitative evaporation of substrate that kinetically favors an isotopically light total aerosol. A transition from stoichiometric to non-stoichiometric sampling, therefore, is expected to result in a decrease in 56Fe/54Fe ratios, which is opposite to our results that showed an increase (Fig. 2C, E and F).
A combination of ablation and transport processes provide another possible mechanism. Laser ablation produced particles with different sizes can possess heterogeneous isotope compositions.22,27,38 Transported particles during spot ablation have been found to gradually shift towards smaller mean sizes, because of the increased difficulty in extracting large particles with increasing crater depth.38,41 Loss of large particles with fractionated isotope compositions should shift the measured isotope ratios towards those of small particles. This predicted trend is qualitatively consistent with increases in measured 56Fe/54Fe ratios for pyrite and magnetite (Fig. 2C and E), because ns-LA produced particles of the smallest aerodynamic diameters have been determined to have higher δ56Fe values than those of the largest particles collected by an aerosol impactor.22 Previously observed isotopic contrasts of <1.5‰ between the aerodynamically smallest and largest particles produced during ns-LA of the two minerals,22 however, are too small to quantitatively explain the observed ∼2–3‰ shift during spot analyses. Moreover, this mechanism alone is not consistent with the increase in measured 56Fe/54Fe ratios for siderite (Fig. 2F), because particles with the smallest aerodynamic sizes have 56Fe/54Fe values lower than those of the largest particles. A key uncertainty is whether the magnitude and direction of isotopic contrasts between small and large particles would change during spot ablation, given that interactions between the incoming ns-laser pulse and ablation-induced plasma plume are expected to vary due to the increased restrictions on plasma plume expansion and on large particle extraction with the increasing crater depth. Košler et al. (2005) reported a larger (i.e., ∼4‰), and opposite, 56Fe/54Fe contrast between small and large particles produced during spot ablation of Fe sulfide using a 213 nm ns-laser,27 as compared to our previous study,22 but Horn et al. (2006) argued that the observed contrast reflected changes in instrumental mass bias, rather than true isotopic differences in particles of different sizes.42
Another source of fractionation is incomplete ionization of large particles in the ICP, coupled with the decreased transport of large particles with time. Particle ionization in the ICP has been hypothesized to be a kinetic process where light isotopes are preferentially diffused to particle surface, and then ionized.17,38 Incomplete ionization of large particles causes the ionized material to be isotopically light, and this ionization-related isotope fractionation is then gradually erased by more complete particle ionization due to decreased transport of large particles with progression of spot ablation. This process has been previously proposed to explain isotopic fractionations of Fe and Cu isotopes during spot ablation using ns-lasers,17,38 and is broadly consistent with the increases in the measured 56Fe/54Fe ratios during ns-LA (Fig. 2C, E and F).
Our results corroborate that, similar to the conclusions of extensive studies on elemental fractionations, LA-induced isotopic fractionations also have complicated origins. The understanding of elemental fractionations, however, might not be directly applicable to isotopic fractionations. For example, significant elemental fractionations are typically considered to occur only when the crater aspect ratio is >6,36 but a ∼3‰ shift in 56Fe/54Fe ratios, which is significantly large as compared to a ∼5‰ spread of Fe isotopes in nature, can occur during ns-LA at an aspect ratio of <2, as demonstrated by our results. The much higher precision required for stable isotope ratio analysis warrants further studies that are specifically focused on LA-induced isotopic fractionation.
4.2 Matrix effects during Fe isotope analysis by fs-LA
A major finding of our work is that inaccurate δ56Fe values can be produced from mineral-phase-matched and non-phase-matched analyses by fs-LA under dry conditions (Fig. 4, 6, 8, and 9). Such effects are neither caused by spectral interferences, nor by ion intensity mismatch. Matrix effects dependent on laser ablation fluence have been previously reported during Cu isotope analysis using a 193 nm fs-laser, and the observed gradual deterioration in accuracy of the measured δ65Cu with increasing fluence was interpreted to reflect formation of a larger heat-affected zone at the higher fluences.18 This fluence-dependent matrix effect, if universal, would predict more accurate isotope ratio measurements at low fluence. This effect, however, was not observed in our study; results from non-mineral-phase-matched Fe isotope analysis at a low fluence of ∼0.56 J cm−2 did not result in any perceptible improvement in accuracy of the measured δ56Fe values as compared to that obtained at a higher fluence of ∼1 J cm−2 (Fig. 8).The observed matrix effects were not related to LA processes. Firstly, it has been demonstrated that particle size distributions produced by ablation of various Fe minerals, including identical ones used in this study, by the 266 nm fs-laser are similar.22 Secondly, effective suppression of matrix effects by water addition, as demonstrated by more accurate δ56Fe results under wet fs-LA conditions (Fig. 4, 6, 8, and 9), implies that the observed matrix effects originated in the ICP.
The observed matrix effects are most likely to result from changes in space-charge effects in the MC-ICP-MS due to differences in chemical compositions between sample and standard. Space-charge effects are considered to develop largely in the region of the skimmer cone during ion extraction into analyzers.43–48 In response to the drop in gas pressure, preferential loss of electrons to a negatively charged electron sheath at the inner wall of the skimmer cone occurs, creating a positively charged ion beam. The repulsion within the charge-imbalanced ion beam defocuses ions with lower kinetic energy more strongly than those with higher kinetic energy, low-mass ions, therefore, typically have lower transmission than that of high-mass ions during extraction into the analyzers.
From an isotopic perspective, space-charge effects probably generate an ion beam that is isotopically-zoned in cross section (Fig. 11). Differences in matrix compositions between sample and bracketing standard during LA analysis are expected to cause different ionization and extraction of ions in the plasma, ultimately resulting in different extents of space-charge effects between sample and standard, and hence erroneous δ56Fe measurements. The (pseudo-) high mass resolution mode used for Fe isotope analysis may be particularly susceptible to this composition-related matrix effect, because only part of the ion beam is sampled through the source defining slits (Fig. 11). This hypothesis is testable by isotope analysis under both low- and high-mass resolution modes for an element that is free from interferences under both modes, such as Mg isotopes. Our unpublished solution-nebulization results of Mg isotope analysis, indeed, typically show a larger instrumental mass bias in the measured 26Mg/24Mg ratios under the high-mass resolution relative to the low-mass resolution mode. The nature of matrix effects during fs-LA is considered to be similar to that commonly demonstrated in matrix-doping tests during solution nebulization analysis of stable isotope ratios.3,49
It is important to stress that the matrix effects observed during fs-LA can be almost completely suppressed by introduction of water during analysis, allowing attainment of a precision and accuracy level of ∼0.1‰ for Fe isotope analysis without matrix matching between the sample and bracketing standard. This agrees with previous work that has shown that wet plasma conditions are often found more tolerant to matrix effects as compared to dry plasma during elemental and isotopic analysis by solution nebulization or laser ablation.28–30
The presence of water changes some fundamental characteristics of the plasma, such as temperature and electron density, although the exact role of water during matrix suppression is not well understood because introduction of water into the plasma is associated with a series of complex physicochemical processes. One possible role of water in matrix suppression is through changing plasma electron density. Absorption of plasma energy during vaporization and dissociation of water is expected to reduce temperature and ionization of the plasma, but this is counterbalanced by supply of electrons from dissociated water, and of hydrogen that promotes ionization due to the better thermal conductivity of hydrogen compared to Ar.50,51 Although there were contradictory observations on the changes in electron density in response to water addition,51–53 the different results may be reconciled by the fact that the influence of water on plasma properties is spatially heterogeneous within the plasma, as demonstrated by spatially-resolved measurements that have shown localized changes in electron density during water addition.54 This is not surprising because matter–plasma interactions are known to be kinetic processes, controlled by physical characteristics of the matter (e.g., aerosol vs. vapor, droplet size), including water, and of its movement through the plasma (e.g., introduction rate).52,55,56 Because only part of the ion beam generated by the plasma is sampled though the small orifices of sampler and skimmer cones in the ICP-MS, even local changes in plasma properties may alter extraction of the ion beam into mass analyzers. Studies based on Langmuir probe measurements have shown that changes in electron density during extraction of the ion beam across the skimmer cone, the key region in generating space-charge effects, exhibit subtle differences under dry and wet plasma conditions,57,58 but it is not clear whether these differences can be quantitatively linked the observed matrix effects during isotope ratio measurements.
Regardless of the exact suppression mechanism, our results independently confirm the feasibility of accurate non-matrix-matched stable isotope analysis by fs-LA with high precision. This analytical capability was first demonstrated by Horn et al. (2006), using a 196 nm fs-laser and Neptune MC-ICP-MS. Our study demonstrates that similar performance can also be achieved using different LA-MC-ICP-MS instruments (a 266 nm fs-laser and Nu Plasma II MC-ICP-MS), highlighting the universal applicability of the fs-LA technique for metal and metalloid stable isotope analysis.
Precise and accurate fs-LA analysis of a range of stable isotopes (e.g., Mg, Fe, Si, Cu and V isotopes) has been shown to be possible without matrix matching under wet plasma conditions.18,25,34,59 Although some of these previous applications have emphasized introduction of elemental solutions, such as Ni solution during Fe isotope analysis,25 as a mean to monitor mass bias, addition of elemental solution via a spray chamber during analysis also effectively creates a wet LA condition. The same Fe isotope data, measured by fs-LA with introduction of Ni solution during analysis, were processed using both Ni-based mass-bias corrections and simple sample–standard bracketing corrections, and the results showed that Ni-based corrections only led to a subtle improvement (<0.1‰) in data accuracy and precision compared to that obtained without Ni-based corrections.25 Our results on the significance of water clearly suggest that the role of elemental solutions as mass bias monitor or simply a suppressor of matrix effects needs to be carefully reconsidered.
4.3 Matrix effects during Fe isotope analysis by ns-LA
Compared to fs-LA, the results of non-mineral-phase-matched analysis by ns-LA suggest more severe matrix effects (Fig. 6). We interpret the matrix effects during ns-LA to originate from both LA-related processes and space-charge effects in the ICP. Improved accuracy of the measured δ56Fe values by ns-LA under wet plasma conditions during non-phase-matched analysis suggests suppression of the matrix effects associated with space-charge effects in the ICP (Fig. 6). A significant offset of ∼0.5‰ between the measured δ56Fe and the true value, however, still existed at a water addition rate that was sufficient to completely suppress the matrix effects during fs-LA (Fig. 6), suggesting the presence of matrix effects associated with ns-LA processes, most likely related to dramatically different particle-size distributions produced by ns-LA of magnetite and pyrite.22 Such differences in particle sizes associated with ns-LA cannot be effectively suppressed by water addition.4.4 A comparison of fs-LA-MC-ICP-MS to SIMS
SIMS is an alternative for in situ stable isotope analysis, including Fe isotopes, and a comparison of this method to fs-LA-MC-ICP-MS provides a useful choice guide for individual applications. Iron isotope analysis on Fe oxide minerals is of considerable geological interests, but SIMS analysis of some high-symmetry oxide minerals, such as magnetite, suffers from crystal orientation effects, resulting in imprecise Fe isotope analysis. For example, measurement of multiple magnetite grains with identical Fe isotope compositions yielded a precision of >0.6‰ in δ56Fe values, even though measurements on a single magnetite grain can yield better precision.12 Methods have been developed to alleviate the influence of crystal orientation effects on δ18O isotope analysis,12 but these methods are often accompanied by a decrease in spatial resolution, and it is not clear if they work for Fe isotope analysis. Large Fe isotope variations and extreme δ56Fe values reported for magnetite grains in Precambrian cherts and Banded Iron Formations (BIFs) by SIMS, prior to the discovery of crystal orientation effects for such analysis, are unlikely to be correct.60,61 The fidelity of these data has significant implications for our understanding of biogeochemical processes in the early Earth. Laser ablation MC-ICP-MS analysis is not affected by crystal orientation effects, and can routinely achieve a precision of ∼0.1‰ for Fe isotopes in magnetite by fs-LA, as demonstrated in this work as well as other studies.6,17,25 Therefore, fs-LA-MC-ICP-MS is the preferred method for in situ Fe isotope analysis of high-symmetry oxide minerals.If crystal orientation effects are set aside, a comparison of SIMS and fs-LA in situ isotope analysis is usefully discussed using Fe isotope analysis of pyrite, which is feasible by both SIMS and fs-LA analysis. The results show that SIMS is advantageous in spatial resolution as compared to fs-LA-MC-ICP-MS (Fig. 10). To achieve a similar precision of ∼0.2‰ in δ56Fe, SIMS analysis consumes ∼6-time less material than that consumed during fs-LA-MC-ICP-MS analysis. The reported spot size of ion beam used for Fe analysis by SIMS is similar to what can be achieved by laser ablation (∼15–20 μm),61,62 and the difference in sample consumption mostly results from the depth of material that is removed during analysis. Crater depth is typically ≤∼1 μm for SIMS analysis of Fe isotopes, but can be up to tens of μm for LA analysis.
Differences in mass spectrometers used by fs-LA and SIMS analysis should be taken into consideration to understand the observed differences in sample consumption by the two techniques. The fs-LA systems used in this study and reported in the literature are all coupled to small-geometry mass spectrometers (e.g., Nu Plasma II or Neptune).6,17 These instruments typically need to sacrifice ∼90% ion transmission when running at high-mass resolution mode to resolve argide interferences from Fe peaks. In contrast, the reported SIMS analysis of Fe isotopes was done on large-geometry mass spectrometers (CAMECA 1270 or 1280), which has intrinsically higher mass resolving powder than the ones used by fs-LA analysis. Because counting statistics appears to be the major obstacle that prevents better spatial resolution for the fs-LA-MC-ICP-MS (Fig. 10), a commercially available, large-geometry mass spectrometer (e.g., Nu Plasma 1700), or a mass spectrometer with a collision cell (e.g., Nu Plasma Sapphire, or Thermo Proteus), should alleviate this limitation by improving ion transmission at high mass resolution. Coupling of these mass spectrometers to fs-LA systems, consequently, should significantly narrow the gap in spatial resolution between fs-LA-MC-ICP-MS and SIMS. In an instrument cost comparison basis, SIMS will be significantly more expensive.
An outstanding advantage of fs-LA-MC-ICP-MS over SIMS is its ability for non-matrix-matched analysis. Matrix matching appears to be extremely important for SIMS analysis. Studies of δ18O and δ13C analysis on carbonate minerals by SIMS have demonstrated that chemical compositions of samples can cause significant non-linear changes in instrumental mass bias.63,64 Complex responses of mass bias to chemical compositions of analyte have also been reported for Mg, Si, and Ca isotope analysis by SIMS.9,65 Corrections of such mass biases on SIMS require precise knowledge on chemical compositions of samples and development of a series of standards with a wide range of compositions that allow for full characterization of the complex, matrix-dependent instrumental mass bias.63,64 Such corrections are in addition to the extremely careful preparation of samples that is required by SIMS analysis to avoid analytical artifacts associated with sample surface topography effects.12,66 Such issues need to be balanced with the potential of SIMS analysis for higher spatial resolution as compared to fs-LA analysis.
5. Conclusions
Downhole Fe isotope fractionation was not observed during 150 s spot analysis of pyrite by fs-LA, but was evident during ns-LA. Downhole isotopic fractionation during ns-LA results from a combination of ablation, transport, and ionization processes. This work clarifies that matrix effects exist during fs-LA analysis, but such effects originate from changes in space-charge effects in the ICP-MS due to different chemical compositions of samples and standards, rather than from LA processes. Matrix effects during fs-LA analysis can be almost completely suppressed by introduction of water. Consequently, accurate non-matrix-matched analysis of Fe isotopes can be routinely achieved by fs-LA with a high precision (∼0.1‰, 2SD). In contrast, matrix effects during Fe isotope analysis by ns-LA result from both LA processes and composition-related space-charge effects in the ICP-MS. Although the later effects can be suppressed by water addition during analysis, matrix effects resulting from ablation processes cannot be effectively suppressed by water. As a result, matrix-matching is essential during in situ Fe isotope analysis by ns-LA.Compared to fs-LA-MC-ICP-MS, SIMS is advantageous in its ability for a range of light stable isotope analysis (e.g., δ18O, δ13C) that cannot be analyzed by LA-MC-ICP-MS, and in spatial resolution. The gap in spatial resolution between fs-LA-MC-ICP-MS and SIMS, however, is expected to significantly narrow or disappear if large-geometry, or collision-cell equipped, mass spectrometers are coupled to LA systems. The ability of non-matrix-matched analysis by fs-LA-MC-ICP-MS poses as one of the most outstanding strengths of this technique over SIMS for metal and metalloid stable isotope analysis.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NSF grant EAR-1347056 and NASA grant NNA13AA94A. We thank Prof. Ingo Horn for providing details on the LA-MC-ICP-MS setup in his lab, and Prof. Martin Whitehouse for providing details on the spatial resolution of Fe isotope analysis by SIMS in his lab, and Miss Thiruchelvi Reddy for help with data collection, and two anonymous reviewers for their helpful comments.References
- Geochemistry of non-traditional stable isotopes, ed. C. M. Johnson, B. L. Beard and F. Albarède, Mineralogical Society of America, Washington, D.C., 2004 Search PubMed.
- Non-traditional stable isotopes, ed. F.-Z. Teng, J. Watkins and N. Dauphas, Mineralogical Society of America, Washington, D.C., 2017 Search PubMed.
- F. Albarède and B. Beard, Rev. Mineral. Geochem., 2004, 55, 113–152 CrossRef.
- C. K. I. Sio, N. Dauphas, F.-Z. Teng, M. Chaussidon, R. T. Helz and M. Roskosz, Geochim. Cosmochim. Acta, 2013, 123, 302–321 CrossRef CAS.
- W. Li, B. L. Beard and C. M. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 8193–8198 CrossRef CAS PubMed.
- I. Horn, F. von Blanckenburg, R. Schoenberg, G. Steinhoefel and G. Markl, Geochim. Cosmochim. Acta, 2006, 70, 3677–3688 CrossRef CAS.
- M. D. Norman, M. T. McCulloch, H. S. C. O'Neill and G. M. Yaxley, J. Anal. At. Spectrom., 2006, 21, 50–54 RSC.
- F.-X. d'Abzac, B. L. Beard, A. D. Czaja, H. Konishi, J. J. Schauer and C. M. Johnson, Anal. Chem., 2013, 85, 11885–11892 CrossRef PubMed.
- M. Chaussidon, Z. Deng, J. Villeneuve, J. Moureau, B. Watson, F. Richter and F. Moynier, Rev. Mineral. Geochem., 2017, 82, 127–163 CrossRef.
- J. M. Huberty, N. T. Kita, R. Kozdon, P. R. Heck, J. H. Fournelle, M. J. Spicuzza, H. Xu and J. W. Valley, Chem. Geol., 2010, 276, 269–283 CrossRef CAS.
- I. C. Lyon, J. M. Saxton and S. J. Cornah, Int. J. Mass Spectrom. Ion Processes, 1998, 172, 115–122 CrossRef CAS.
- N. T. Kita, J. M. Huberty, R. Kozdon, B. L. Beard and J. W. Valley, Surf. Interface Anal., 2011, 43, 427–431 CrossRef CAS.
- S. E. Jackson, N. J. Pearson, W. L. Griffin and E. A. Belousova, Chem. Geol., 2004, 211, 47–69 CrossRef CAS.
- K. P. Jochum, B. Stoll, U. Weis, D. E. Jacob, R. Mertz-Kraus and M. O. Andreae, Geostand. Geoanal. Res., 2014, 38, 265–292 CrossRef CAS.
- Z. Li, Z. Hu, Y. Liu, S. Gao, M. Li, K. Zong, H. Chen and S. Hu, Chem. Geol., 2015, 400, 11–23 CrossRef CAS.
- S. Zhang, M. He, Z. Yin, E. Zhu, W. Hang and B. Huang, J. Anal. At. Spectrom., 2016, 31, 358–382 RSC.
- I. Horn and F. von Blanckenburg, Spectrochim. Acta, Part B, 2007, 62, 410–422 CrossRef.
- M. Lazarov and I. Horn, Spectrochim. Acta, Part B, 2015, 111, 64–73 CrossRef CAS.
- R. E. Russo, X. Mao, J. J. Gonzalez, V. Zorba and J. Yoo, Anal. Chem., 2013, 85, 6162–6177 CrossRef CAS PubMed.
- B. N. Chichkov, C. Momma, S. Nolte, F. von Alvensleben and A. Tünnermann, Appl. Phys. A: Mater. Sci. Process., 1996, 63, 109–115 CrossRef.
- R. E. Russo, X. Mao, J. J. Gonzalez and J. Yoo, Spectroscopy, 2013, 28, 24–39 CAS.
- X.-Y. Zheng, B. L. Beard, S. Lee, T. R. Reddy, H. Xu and C. M. Johnson, Chem. Geol., 2017, 450, 235–247 CrossRef CAS.
- F.-X. d'Abzac, A. D. Czaja, B. L. Beard, J. J. Schauer and C. M. Johnson, Geostand. Geoanal. Res., 2014, 38, 293–309 CrossRef.
- M. Nishizawa, H. Yamamoto, Y. Ueno, S. Tsuruoka, T. Shibuya, Y. Sawaki, S. Yamamoto, Y. Kon, K. Kitajima, T. Komiya, S. Maruyama and T. Hirata, Geochim. Cosmochim. Acta, 2010, 74, 2760–2778 CrossRef CAS.
- M. Oeser, S. Weyer, I. Horn and S. Schuth, Geostand. Geoanal. Res., 2014, 38, 311–328 CrossRef CAS.
- T. Hirata and Y. Kon, Anal. Sci., 2008, 24, 345–354 CrossRef CAS PubMed.
- J. Košler, R. B. Pedersen, C. Kruber and P. J. Sylvester, J. Anal. At. Spectrom., 2005, 20, 192–199 RSC.
- F.-Z. Teng, W.-Y. Li, S. Ke, B. Marty, N. Dauphas, S. Huang, F.-Y. Wu and A. Pourmand, Geochim. Cosmochim. Acta, 2010, 74, 4150–4166 CrossRef CAS.
- C. O'Connor, B. L. Sharp and P. Evans, J. Anal. At. Spectrom., 2006, 21, 556–565 RSC.
- P. E. Janney, F. M. Richter, R. A. Mendybaev, M. Wadhwa, R. B. Georg, E. B. Watson and R. R. Hines, Chem. Geol., 2011, 281, 26–40 CrossRef CAS.
- M. Ohata, D. Tabersky, R. Glaus, J. Koch, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2014, 29, 1345–1353 RSC.
- F. Poitrasson and F.-X. d'Abzac, J. Anal. At. Spectrom., 2017, 32, 1075–1091 RSC.
- S. Weyer and J. B. Schwieters, Int. J. Mass Spectrom., 2003, 226, 355–368 CrossRef CAS.
- J. A. Schuessler and F. von Blanckenburg, Spectrochim. Acta, Part B, 2014, 98, 1–18 CrossRef CAS.
- C. M. Johnson, B. L. Beard and E. E. Roden, Annu. Rev. Earth Planet. Sci., 2008, 36, 457–493 CrossRef CAS.
- A. J. G. Mank and P. R. D. Mason, J. Anal. At. Spectrom., 1999, 14, 1143–1153 RSC.
- C. Liu, X. L. Mao, S. S. Mao, X. Zeng, R. Greif and R. E. Russo, Anal. Chem., 2004, 76, 379–383 CrossRef CAS PubMed.
- S. E. Jackson and D. Günther, J. Anal. At. Spectrom., 2003, 18, 205–212 RSC.
- O. V. Borisov, X. Mao and R. E. Russo, Spectrochim. Acta, Part B, 2000, 55, 1693–1704 CrossRef.
- R. E. Russo, X. Mao, H. Liu, J. Gonzalez and S. S. Mao, Talanta, 2002, 57, 425–451 CrossRef CAS PubMed.
- M. Guillong and D. Günther, J. Anal. At. Spectrom., 2002, 17, 831–837 RSC.
- I. Horn, R. Schoenberg and F. von Blanckenburg, J. Anal. At. Spectrom., 2006, 21, 211–213 RSC.
- H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1996, 51, 779–815 CrossRef.
- S. D. Tanner, Spectrochim. Acta, Part B, 1992, 47, 809–823 CrossRef.
- N. Praphairaksit and R. S. Houk, Anal. Chem., 2000, 72, 2356–2361 CrossRef CAS PubMed.
- C. Agatemor and D. Beauchemin, Anal. Chim. Acta, 2011, 706, 66–83 CrossRef CAS PubMed.
- G. R. Gillson, D. J. Douglas, J. E. Fulford, K. W. Halligan and S. D. Tanner, Anal. Chem., 1988, 60, 1472–1474 CrossRef CAS.
- G. Li, Y. Duan and G. M. Hieftje, J. Mass Spectrom., 1995, 30, 841–848 CrossRef CAS.
- F.-Z. Teng and W. Yang, Rapid Commun. Mass Spectrom., 2014, 28, 19–24 CrossRef CAS PubMed.
- Y. Q. Tang and C. Trassy, Spectrochim. Acta, Part B, 1986, 41, 143–150 CrossRef.
- J. F. Alder, R. M. Bombelka and G. F. Kirkbright, Spectrochim. Acta, Part B, 1980, 35, 163–175 CrossRef.
- S. E. Long and R. F. Browner, Spectrochim. Acta, Part B, 1988, 43, 1461–1471 CrossRef.
- G. Zhu and R. F. Browner, J. Anal. At. Spectrom., 1988, 3, 781–789 RSC.
- B. L. Caughlin and M. W. Blades, Spectrochim. Acta, Part B, 1987, 42, 353–360 CrossRef.
- R. S. Houk, R. K. Winge and X. Chen, J. Anal. At. Spectrom., 1997, 12, 1139–1148 RSC.
- J. W. Olesik, Appl. Spectrosc., 1997, 51, 158A–175A CrossRef CAS.
- H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1994, 49, 1283–1303 CrossRef.
- H. S. Niu, K. Hu and R. S. Houk, Spectrochim. Acta, Part B, 1991, 46, 805–817 CrossRef.
- S. Schuth, I. Horn, A. Brüske, P. E. Wolff and S. Weyer, Ore Geol. Rev., 2017, 81(4), 1271–1286 CrossRef.
- J. Marin-Carbonne, C. Rollion-Bard and B. Luais, Chem. Geol., 2011, 285, 50–61 CrossRef CAS.
- M. J. Whitehouse and C. M. Fedo, Geology, 2007, 35, 719–722 CrossRef CAS.
- A. Galić, P. R. D. Mason, J. M. Mogollón, M. Wolthers, P. Z. Vroon and M. J. Whitehouse, Chem. Geol., 2017, 449, 135–146 CrossRef.
- M. G. Śliwiński, K. Kitajima, R. Kozdon, M. J. Spicuzza, J. H. Fournelle, A. Denny and J. W. Valley, Geostand. Geoanal. Res., 2016, 40, 173–184 CrossRef.
- M. G. Śliwiński, K. Kitajima, R. Kozdon, M. J. Spicuzza, J. H. Fournelle, A. Denny and J. W. Valley, Geostand. Geoanal. Res., 2016, 40, 157–172 CrossRef.
- L. Tissandier and C. Rollion-Bard, Rapid Commun. Mass Spectrom., 2017, 31, 351–361 CrossRef CAS PubMed.
- N. T. Kita, T. Ushikubo, B. Fu and J. W. Valley, Chem. Geol., 2009, 264, 43–57 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ja00272f |
| This journal is © The Royal Society of Chemistry 2018 |