 Open Access Article
Open Access ArticleThe effect of thermal expansion on photoisomerisation in the crystals of [Co(NH3)5NO2]Cl(NO3): different strain origins – different outcomes†
A. A.
Sidelnikov
*a,
S. A.
Chizhik
a,
B. A.
Zakharov
ab,
A. P.
Chupakhin
b and
E. V.
Boldyreva
a
aInstitute of Solid State Chemistry and Mechanochemistry SB RAS, Kutateladze Street 18, Novosibirsk, 630128, Russian Federation. E-mail: eboldyreva@yahoo.com
bNovosibirsk State University, Pirogova Street 2, Novosibirsk, 630090, Russian Federation
First published on 20th May 2016
Abstract
The effect of anisotropic structural strain resulting from thermal expansion on linkage photoisomerisation in crystals of [Co(NH3)5NO2]Cl(NO3) was studied. The quantum yield of the photoisomerisation was qualitatively correlated with the bending of needle-shaped crystals across a series of temperatures from 80–363 K. The thermal evolution of the crystal structure was also studied across the same temperature range by single-crystal X-ray diffraction. A qualitative correlation was found between the photo-reaction rate and both the cell volume and the volume of void space around the nitro groups. However, this correlation was found to be non-linear. The effect of the anisotropic structural strain resulting from temperature variations on the rate of photoisomerisation is qualitatively different from the effect of strain that is generated by elastic external loading. If strain is induced by external load, the reaction rate correlates linearly with compression along the crystallographic b direction. In contrast, if strain results from temperature variations, then the reaction rate correlates linearly with changes along the crystallographic a direction. This effect is measured quantitatively and its rationalisation is attempted.
Introduction
Photomechanical effects in molecular crystals have been studied since the 1980s,1–3 and interest in these phenomena increases every year.4–10 One of the most spectacular manifestations of photomechanical effects is the bending of crystals on irradiation, which was first reported in the 1980s (ref. 1–3) and has since been reproduced many times for a variety of compounds (see recent reviews4–10).Crystals of [Co(NH3)5NO2]Cl(NO3) belong to the most extensively studied compounds that exhibit photomechanical effects, namely bend or jump on homogeneous nitro–nitrito intramolecular linkage isomerisation (the nitro-ligand changes its coordination to the Co(III)-atom from nitrogen in the nitro-form to oxygen in the nitrito-isomer):2,11–16
They can be grown as long thin needles, making it possible to monitor the photoisomerisation quantitatively by precise measurements of crystal bending.2,9,13,17,18 Photochemical transformation is directly related to macroscopic crystal deformation, making it possible to study the microscopic mechanism of the photo-transformation from the macroscopic mechanical response.9 Measuring crystal bending has been used to study the effect of the elastic compression of crystals along axis b induced by external load on the quantum yield of the photoisomerisation; in this way the activation volume has been estimated.11,13,17,18 Although a change in the molar volume over the course of the nitro–nitrito photoisomerisation is negative (the volume is reduced),19 the activation volume is positive, i.e. the reaction quantum yield is reduced if the crystals are elastically compressed along crystallographic axis b.13,18 This unexpected effect is explained by the anisotropy of lattice strain, when the total relatively small negative volume change during the reaction (−0.7%) results from a large (+3.9%) expansion along crystallographic axis b and a large compression along axes a (−2.7%) and c (−1.8%) (Fig. 1).19
 | ||
| Fig. 1 The fragments of the crystal structure of [Co(NH3)5NO2]Cl(NO3) in different orientations. Chlorine anions are green, Co atoms dark blue, N atoms light blue, and oxygen atoms red. The complex hydrogen bond network (Fig. S3 and Table S2 in the ESI†) is not shown for clarity. | ||
An important parameter that can effect a reaction is temperature. The effect of temperature on the photoisomerisation can be related to both “microscopic” intramolecular processes (dissipation of the excitation energy resulting from a series of radiation-less transitions from the higher to lower energy level in a complex cation), and “macroscopic” phenomena related to the anisotropic strain induced in the crystal on temperature variations (expansion on heating, compression on cooling). The “microscopic” and “macroscopic” phenomena are interrelated as the lattice strain on temperature variation results from changes in the anharmonicities of vibrations. Further, structural distortion can have a pronounced effect on the intramolecular transitions between energy states. The problem is very general and is of interest for any photochemical reactions in crystals that are accompanied by structural strain and photomechanical effects.
The rate of photoisomerisation characterises the transition of a compound from the initial state to the final state. Generally, this rate is determined by the transition to the excited state, and the relaxation of the excitation through one or several channels. Temperature can affect any of these stages. If transition to the excited state and radiationless relaxation do not depend on temperature directly, then the effect of temperature on the photoisomerisation is related to the micro- and macro-strain resulting from thermal expansion.
The rate of photoisomerisation of [Co(NH3)5NO2]X2 (X = Cl−, Br−, I−) complexes in the solid state has been reported not to change significantly even at liquid nitrogen20 and liquid helium21 temperatures, the activation energy estimated to be 100 cal mol−1.21 This suggests that the transition to the excited state itself is in fact not thermally activated. It therefore becomes possible to consider the effect of temperature on the photoisomerisation in the crystalline state, focusing on the relation between the rate of photoisomerisation and the anisotropy of lattice strain resulting from temperature variation (thermal expansion on heating or contraction on cooling). It is of particular interest to compare the effect of thermally induced strain with the previously studied effect of strain induced by elastic bending.11,13,17,18 The values of linear strain in the two cases are comparable, but the anisotropy is different.15,22,23 Another important difference is that uniform thermal strain does not create any macroscopic stresses in the crystal, in contrast to bending by external loading. A comparison of the effects of the two types of strain on the reaction may give better insight into the role of the crystalline environment in intramolecular photoisomerisation.
The aim of this study was to monitor the kinetics of the photoisomerisation in the crystals of [Co(NH3)5NO2]Cl(NO3) at multiple temperatures across the range 80–363 K by measuring crystal bending, and to search for correlations between the observed effects and the anisotropic lattice strain induced in the crystals by temperature variations, as measured by single-crystal X-ray diffraction. A study of the temperature dependence of the rate of nitro–nitrito linkage photoisomerisation in [Co(NH3)5NO2]Cl(NO3) is complicated by the existence of reverse thermal nitrito–nitro isomerisation. In order to overcome this difficulty, we limited the study of the kinetics of photoisomerisation to the initial stage of the transformation where the contribution of the reverse process is negligible.
Experimental
Crystals were synthesized and grown as described in ref. 24. To study the kinetics of the photoisomerisation, the experimental set-up described in earlier publications11,13,17,18 was used. This set-up was modified in such a way so as to enable variable-temperature measurements using a home-made cryo-thermostat (Fig. 2). The crystal was fixed on a copper holder and located in a chamber swept by a stream of dry nitrogen to avoid icing; the temperature of the copper holder was held with a precision better than 1 K over the range 80–373 K. A blue LED (λ = 465 nm, 1 W) was used as the source of excitation radiation. The shift of the free crystal end, resulting from its bending, was monitored by measuring the position of a spot from a laser beam reflected by a mirror (a polished silicon plate) to a point 5 meters away.The orientation of the crystal with respect to the light source is plotted in Fig. 3. The crystal was irradiated normal to its broad face. Crystal faces were indexed using CrysAlisPro software25 and 191 reflections were collected with an Oxford Diffraction Gemini R Ultra diffractometer (2D CCD detector, MoKα radiation).
 | ||
| Fig. 3 Orientation of a crystal with respect to the light source. Face indices and directions of crystallographic axes are shown. | ||
The method requires crystals with a certain thickness. A crystal must be thick enough to enable pasting a mirror to its free end (Fig. 2). At the same time, the crystal must be thin enough so as to not suppress its sensitivity to irradiation. The limit of crystal bending is defined by its breaking point; thicker crystals break significantly earlier than thinner ones on bending.
The range of optimum sizes for this compound is given in Table 1, which sums up the data on the crystals used in this work. The most sensitive measurement could be done for crystal 3. Its thickness was still significantly larger than the characteristic light absorption distance, which is 20 μm.17,18 This greatly simplified data analysis: all light reaching the crystal surface can be considered to be absorbed by the surface layer.
| Crystal | Length, μm | Thickness, μm |
|---|---|---|
| 1 | 3230 | 460 |
| 2 | 5140 | 730 |
| 3 | 6060 | 280 |
The bending of a crystal over multiple irradiation/heating (photoisomerisation/reverse thermoisomerisation) cycles was highly reproducible (Fig. 4). This indicates that no irreversible chemical or structural changes (defects) are accumulated in the crystal during these cycles, and there is no fatigue. This makes it possible to use the same crystal for multiple measurements under different conditions (in particular, at different temperatures). This allows one to increase the reliability of the measurements, since data scattering (which would be unavoidable if different crystals were used for the measurements at different temperatures) is eliminated.
Variable-temperature single-crystal X-ray diffraction over the temperature range 100–393 K was carried out using a STOE IPDS-2 diffractometer (MoKα radiation) equipped with an image-plate detector, a graphite monochromator, and an Oxford Cryostream device for temperature control with dry nitrogen flow. At the beginning of the experiment, the sample was heated from 293 K to 393 K in 10 K steps. Subsequently, the sample was cooled directly to 293 K and then X-ray data were collected on cooling to 213 K in 20 K steps, at which point the crystal was covered by ice. The experiment was stopped at 213 K and the sample was heated to evaporate the ice.
After the sample was clear, the temperature was decreased to 193 K and data collection was resumed, obtaining data down to temperatures of 100 K. X-ray data were collected at each temperature point. Cooling and heating rates were ∼60 K per hour.
X-AREA and X-RED32 (ref. 26) were used for cell refinement, data collection and data reduction. Crystal structures were solved by direct methods and refined on F2 using X-STEP32 (ref. 27) and SHELX-2014 (ref. 28) software. All hydrogen atoms were located in the difference Fourier maps; H-atom parameters were treated using HFIX 137 to refine torsion angles in idealized NH3 groups allowing them to rotate but not to tip. Data characterising data collection and crystal parameters are summarized in Table S1.† All crystallographic data have been deposited with the Cambridge Crystallographic Data Centre.29–31 Mercury32 was used for structure visualisation and analysis, including the calculation of voids using the contact surface with a probe radius of 0.9 Å and a grid spacing of 0.2 Å.
Results and discussion
Typical dependences of the shift of the reflected laser beam vs. time at different temperatures are plotted in Fig. 5. The full dataset measured at all temperatures is deposited as ESI† (Fig. S1). As the temperature increases, the deviation of the curves from linearity also increases. The non-linearity of crystal bending is a consequence of two main effects: i) the amount of the non-transformed nitro-isomer decreases, and ii) the rate of the reverse nitrito–nitro thermoisomerisation increases as the concentration of the product of the photoisomerisation (nitrito-isomer) increases. One can approximate the time dependence of the photoisomerisation as a function of depth from the surface according to an equation derived in ref. 9: | ||
| Fig. 5 The displacement of the laser beam during the bending of crystal #3 at variable temperatures: a) 81 K, b) 299 K, c) 360 K (data for other temperatures are available as ESI,† Fig. S1). | ||
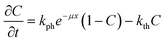
| (1) |
The value of kph can be determined from the rate of photoisomerisation at the initial moment, when C = 0 in the whole crystal bulk. This corresponds to the calculation of the initial rate of displacement of the reflected laser beam by interpolation of the curves plotted in Fig. 5 to t = 0 s. The beam displacement can be related to the geometric parameters of the crystal and experimental set-up (Fig. 2), according to eqn (2):
 | (2) |
 | (3) |
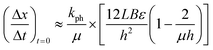 | (4) |
Eqn (4) takes into account that the crystal thickness is much more than the characteristic radiation absorption depth μ−1. This makes it possible to directly calculate the value of kph. This constant is present in eqn (4)via the relation kph/μ = I0αv. This means that the only value that can contribute significantly to the temperature dependence of the measured rate of crystal bending is the quantum yield of the photo-transformation, α.
The temperature dependence of the rate of photoisomerisation kph is plotted in Fig. 6a. It is apparent that a less than two-fold change in the quantum yield, corresponding to a temperature change of almost 300 K, cannot correspond to a thermally activated process. As suggested initially, this can only be related to the effect of thermally induced lattice strain. Relative changes in the rate of photoisomerisation on temperature variation are comparable in value to that on elastic bending by external loading, if the corresponding lattice strain is of the same order of magnitude. This fact additionally supports the hypothesis that lattice strain makes the largest contribution to the temperature dependence of the photoisomerisation rate in a crystal. In the case of external loading, it was logical to seek a correlation between the quantum yield and lattice strain in one selected direction, namely, along the long axis of the crystal. In contrast, in the case of thermal strain, the choice of a selected direction is not so obvious a priori. Uniform thermal strain does not cause any macroscopic stress and is anisotropic. Generally, all components of the strain tensor and their possible combinations should be considered as potentially correlating with the rate of photoreaction.
 | ||
| Fig. 6 The temperature dependences of: a) the rate constant of photoisomerisation kph; b–e) unit cell parameters a, b, c and volume V; f) the distance between the anions Cl and NO3, surrounding a nitro-ligand NO2 (see Fig. 1). | ||
Since the dependence of quantum yield on strain in experiments with external loading of the crystal was linear,11,13,17,18 it also seemed logical to look for the strain tensor components that linearly correlate with the rate of photoreaction in the case of thermally induced strain. The temperature dependences of the unit cell parameters and volume are plotted in Fig. 6b–e. It is clear that only the shape of the a(T) curve resembles that of the temperature dependence of the photoisomerisation rate constant.
Although there is a qualitative correlation between the direction of change of the reaction rate, on the one hand, and the cell volume or the volume of the “voids” around the nitro group, on the other hand, their quantitative changes are not linearly correlated (Fig. 1 and 7). The dependences of the cell volume and void volume on temperature are practically linear (Fig. 6e and 7), whereas the magnitude of the gradient of kph(T) decreases at lower temperatures (Fig. 6f).
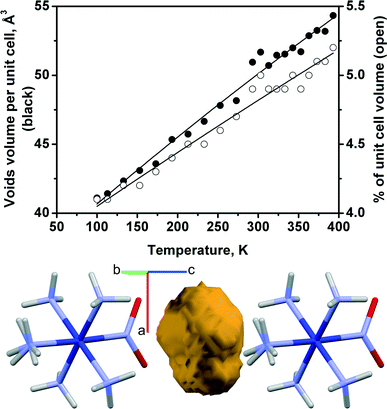 | ||
| Fig. 7 Volume of voids surrounding the nitro-ligand in the structure of [Co(NH3)5NO2]Cl(NO3) vs. temperature. Void shape (yellow) and its position between ligands are shown. | ||
The existence of a formal correlation between the reaction rate constant and lattice strain can be rationalised using the concept of a reaction cavity.13,33–35 A reaction cavity is defined as the free space in the crystalline environment that immediately surrounds a reacting molecule or molecular fragment. The simplest approximation is to consider the reaction cavity as being rigid (i.e. constant over the course of the reaction) and to seek correlations between the size of a reaction cavity and the reaction rate. Such an approach is often helpful when a series of related compounds are compared.13,14,33 Qualitatively, the free volume that is available in the starting crystal correlates with the rate of photoisomerisation in Co(III) compounds: the larger the reaction cavity, the larger the reaction rate constant.13,14 However, further analysis of the anisotropic lattice strain resulting from the reaction itself (when considering a “flexible” reaction cavity34,35) reveals finer details that are not obvious a priori.
If strain is induced by external load, the reaction rate correlates quantitatively with compression along the crystallographic b direction.11,13,14,17 This can be rationalised if one considers the anisotropy of lattice strain resulting from the reaction. As a result of photoisomerisation the structure expands along b, and thus compression along this direction by an external load is not favourable for the reaction.11,13,14
If strain results from temperature variations (as in this work), then the reaction rate correlates with changes along the crystallographic a direction. This effect can be rationalised if one considers the crystal packing. It is logical to start the analysis by considering NH⋯O hydrogen bonds between the nitro-group that is directly involved in the photoisomerisation, and the amino-groups of the neighboring complex cations (Fig. S2†). The change in distance between a select NO2-group and its nearest NH3-ligands (Fig. 1 and Fig. S2†) is qualitatively similar to a(T) and can be correlated with the rate of photoreaction.
Correlating more closely with the rate of photoreaction is the temperature-dependent interatomic distance between the two anions that surround each nitro-ligand, namely Cl− and NO3− (Fig. 1, 6f and 8). The correlation can be approximated by eqn (5):
 | ||
| Fig. 8 The correlation between the rate of photoisomerisation and the distance between the anions Cl and NO3, surrounding a nitro-ligand NO2 (see Fig. 1). | ||

| (5) |
Remarkably, in neither the case of external elastic compression nor thermally induced strain does the reaction rate correlate with lattice strain along the crystallographic c direction (Fig. 1 and 7). Instead, lattice expansion along c that takes place on both cooling (in this work) and on elastic compression of the b axis23 corresponds to a decrease in the reaction rate.
One can suppose that the apparently different effects of macroscopic strain on the photoisomerisation rate in the two cases – external elastic compression and thermal strain – are in fact rooted in identical phenomena. This becomes evident if the microscopic stress experienced by the excited state of the complex cation on irradiation is considered. The macroscopic thermal strain can be suggested to subject the excited state to microscopic stress mainly along the a axis. In contrast, direct external loading of the crystal appears to result in microscopic stress mainly along the b axis. No significant microscopic stress arises along c, presumably, since enough free space is present in this direction in the starting crystal structure, and is preserved over the course of isomerisation. Further investigation into the lattice dynamics of this system may shed more light on the microscopic stresses that arise over the course of the reaction at various temperatures and on elastic compression.
Conclusions
The phenomenon of bending a crystal on irradiation (a photomechanical effect, or photobending) is more than a curious observation. These effects have considerable practical applications in supramolecular devices, e.g. sensors and actuators. Macroscopic strain can be measured quantitatively with high precision and reproducibility. These data can be used to obtain an insight into the microscopic mechanism of the transformation and the effect of crystalline environment on the intramolecular photorearrangement.The rate of photoisomerisation in [Co(NH3)5NO2]ClNO3 correlates clearly with lattice strain, be this strain induced by external elastic loading or by thermal expansion/contraction. At the same time, in the case of external loading the rate of the photoreaction correlates with strain along the long crystal axis (b), whereas in the case of thermal strain the correlation is with changes normal to the long crystal axis, i.e. within the irradiated plane (parameter a). This can be rationalised by assuming that selected lattice vibrations are coupled with photoexcitation. Intramolecular motions are important when strain results from heating/cooling and is not associated with any macroscopic mechanical stresses.
A very interesting fact is that the value of the q parameter, characterising the dependence of the photoisomerisation rate on lattice strain, is high both in the case of external elastic loading and on temperature-induced strain (40 (ref. 17 and 18) and 50 (this work), respectively). This means that the yield of the intramolecular photoisomerisation is highly sensitive to even relatively small distortions of the crystalline environment. This is a manifestation of the large role of feed-back phenomena in solid-state photochemical reactions, which are similar in this respect with other types of solid-state transformations.13,36
Acknowledgements
This work was supported by RFBR, project 14-03-00902. The authors thank Adam Michalchuk for language polishing and helpful discussions.Notes and references
- G. A. Abakumov and V. I. Nevodchikov, Dokl. Akad. Nauk SSSR, 1982, 266, 1407 CAS.
- E. V. Boldyreva, A. A. Sidelnikov, A. P. Chupakhin, N. Z. Lyakhov and V. V. Boldyrev, Dokl. Akad. Nauk SSSR, 1984, 277, 893 CAS.
- F. I. Ivanov and N. A. Urban, React. Solids, 1986, 1, 165 CrossRef.
- M. Irie, Chem. Rev., 2000, 100, 1685 CrossRef CAS PubMed.
- H. J. Shepherd, I. A. Gural'skiy, C. M. Quintero, S. Tricard, L. Salmon, G. Molnár and A. Bousseksou, Nat. Commun., 2013, 4, 2607, DOI:10.1038/ncomms3607.
- N. K. Nath, M. K. Panda, S. C. Sahoo and P. Naumov, CrystEngComm, 2014, 16, 1850 RSC.
- M. Irie, T. Fukaminato, K. Matsuda and S. Kobatake, Chem. Rev., 2014, 114, 12174 CrossRef CAS PubMed.
- T. Kim, L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, ChemPhysChem, 2014, 15, 400 CrossRef CAS PubMed.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440 CrossRef CAS PubMed.
- M. D. Manrique-Juárez, S. Rat, L. Salmon, G. Molnár, C. M. Quintero, L. Nicu and H. J. Shepherd, Coord. Chem. Rev., 2016, 308, 395 CrossRef.
- E. V. Boldyreva, Mol. Cryst. Liq. Cryst. Inc. Nonlinear Opt., 1994, 242, 17 CrossRef.
- N. Masciocchi, A. N. Kolyshev, V. E. Dulepov, E. V. Boldyreva and A. Sironi, Inorg. Chem., 1994, 33, 2579 CrossRef CAS.
- Reactivity of Molecular Solids, Molecular Solid State Series, ed. E. V. Boldyreva and V. V. Boldyrev, Wiley, 1999, vol. 3, p. 328 Search PubMed.
- E. V. Boldyreva, Russ. J. Coord. Chem., 2001, 27, 297 CrossRef CAS.
- P. Naumov, S. C. Sahoo, B. A. Zakharov and E. V. Boldyreva, Angew. Chem., 2013, 252, 9990 CrossRef PubMed.
- B. A. Zakharov, A. S. Marchuk and E. V. Boldyreva, CrystEngComm, 2015, 17, 8812 RSC.
- E. V. Boldyreva and A. A. Sidelnikov, Izv. Sib. Otd. Akad. Nauk SSR, Ser. Khim. Nauk, 1987, 5, 139 Search PubMed.
- B. I. Yakobson, E. V. Boldyreva and A. A. Sidelnikov, Izv. Sib. Otd. Akad. Nauk SSR, Ser. Khim. Nauk, 1989, 1, 6 Search PubMed.
- E. V. Boldyreva, A. V. Virovets, L. P. Burleva, V. E. Dulepov and N. V. Podberezskaya, Zh. Strukt. Khim., 1993, 34, 128 CAS.
- D. A. Johnson and K. A. Pashman, Inorg. Nucl. Chem. Lett., 1975, 11, 23 CrossRef CAS.
- E. J. Rose and D. S. McClure, J. Photochem., 1981, 17, 171 CrossRef.
- E. V. Boldyreva, J. Kivikoski and J. A. K. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 394 CrossRef.
- E. V. Boldyreva, H. Ahsbahs and H. Uchtmann, Ber. Bunsen-Ges., 1994, 98, 738 CrossRef CAS.
- E. V. Boldyreva, J. Kivikoski and J. A. K. Howard, Acta Crystallogr., Sect. B: Struct. Sci., 1997, 53, 394 CrossRef.
- Oxford Diffraction. CrysAlisPro, Oxford Diffraction Ltd, Abington, England, 2010 Search PubMed.
- Stoe & Cie. X-AREA and X-RED32, Stoe & Cie, Darmstadt, Germany, 2006 Search PubMed.
- X-STEP, Stoe&Cie, Darmstadt, Germany, 2000 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380 CrossRef.
- C. H. Görbitz, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 167 CrossRef PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- C. F. Macrae, P. R. Edgington, P. McCabe, E. Pidcock, G. P. Shields, R. Taylor, M. Towler and J. van de Streek, J. Appl. Crystallogr., 2006, 39, 453 CrossRef CAS.
- Y. Ohashi, Crystalline State Photoreactions, Springer, 2014, p. 208 Search PubMed.
- T. Luty and C. J. Eckhardt, J. Am. Chem. Soc., 1995, 117, 2441 CrossRef CAS.
- E. V. Boldyreva, Solid State Ionics, 1997, 101–103, 843 CrossRef CAS.
- A. P. Chupakhin, A. A. Sidel'nikov and V. V. Boldyrev, React. Solids, 1987, 3, 1 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Data characterising diffraction data collection and crystal parameters (Table S1), dependences of the shift of the reflected laser beam vs. time at different temperatures (Fig. S1), the change in the distances between the closest NH3-ligands of the neighboring complex cations surrounding a selected NO2-group (Fig. S2), the fragments of the crystal structure with hydrogen bonds (Fig. S3) and the geometries of hydrogen bonds at different temperatures (Table S2). CCDC 1470414–1470434. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ce00840b |
| This journal is © The Royal Society of Chemistry 2016 |



