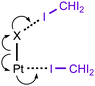Open Access Article
Open Access ArticleHalogen bonding between metal centers and halocarbons†
Daniil M.
Ivanov
a,
Alexander S.
Novikov
a,
Ivan V.
Ananyev
b,
Yulia V.
Kirina
a and
Vadim Yu.
Kukushkin
*a
aInstitute of Chemistry, Saint Petersburg State University, Universitetskaya Nab., 7/9, 199034, Saint Petersburg, Russian Federation. E-mail: v.kukushkin@spbu.ru
bA. N. Nesmeyanov Institute of Organoelement Compounds, Russian Academy of Sciences, Vavilova St., 28, 119991, Moscow, Russian Federation
First published on 16th March 2016
Abstract
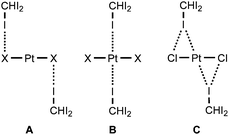
Metal-involving halogen bonding was detected in a series of associates of CHI3 with trans-[PtX2(NCNAlk2)2] (X = Cl, Br). The HI2C–I⋯η1(Pt) halogen bonding and the bifurcated HI2C–I⋯η2(Pt–Cl) halogen bonding – the latter undergoes the thermally induced reversible HI2C–I⋯η2(Pt–Cl) ⇄ HI2C–I⋯η1(Pt) transformation – were observed and confirmed theoretically.
Halogen bonding (XB), among various non-covalent weak interactions, is one of the most intensively studied systems in modern science. Together with hydrogen bonding, π–π-, and metallophilic interactions, it is successfully applied in crystal engineering1,2 and design of compounds exhibiting pharmacological significance.3–5 Recent applications of XB include stabilization of explosives6 and molecular design of materials with tunable photophysical properties.7,8
In accord with the IUPAC definition, XB9 is the real R–X⋯Y (X = halogen) contact, when, firstly, the interatomic distance between X and an appropriate nucleophilic atom of Y (Y = F, O, N, Cl, etc.) is less than the sum of their van der Waals radii and, secondly, the ∠(R–X⋯Y) angle is close to 180° (exceptions from the linearity have been reviewed10). These geometrical parameters are usually easily obtained using single-crystal X-ray diffraction (XRD), which is the most common method for the detection of XB. When application of the two criteria in XRD data fails, some other criteria (lengthening of R–X covalent bonds due to XB and also changes in the appropriate spectroscopic parameters9), or application of some other indirect methods, e.g. UV-vis, IR and Raman spectroscopy,11,12 differential anomalous X-ray scattering studies,13 NMR,14,15 and phosphorescence7 spectroscopy, were also applied for XB recognition.
In the majority of the reported cases when XB was reliably identified, only typical Lewis basic non-metal atoms bearing lone pairs (viz. O, N, S, halogens etc.) behave as XB acceptors, whereas possible XBs with metal centers was found only for I2.16–19 Our inspection of the relevant literature indicates few experimental studies describing X⋯M short contacts, which were either not considered as halogen bonds, or their geometrical parameters fulfill only one of the two aforementioned structural IUPAC criteria. Therefore definitive attribution of these weak interactions to XB was not provided and the other IUPAC criteria should be applied for their identification. Indeed, Chen et al.,20 Wölper et al.,21 and Laguna et al.22 observed X⋯AuI and X⋯AgI contacts, which fulfilled only the “van der Waals criterion”, but in all the three cases the corresponding R–X⋯M angles strongly deviate from 180° (by 30–90°,20 60–70°,21 and 85°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22) thus contrasting with the second structural IUPAC criterion. Yamamoto et al.23 and Liau et al.24 reported, respectively, the I⋯AuI and Cl⋯AuI contacts, which can be interpreted as X⋯AuI halogen bonds, but the nature of these contacts was not verified. Finally, Blakey et al.25 observed contacts between the typical XB donors such as iodoperfluorobenzenes and gold nanoparticles in water solutions, but these halogen bonds were confirmed only by indirect methods such as UV-vis difference spectroscopy, SERS, and XPS and the geometrical parameters were not obtained.
22) thus contrasting with the second structural IUPAC criterion. Yamamoto et al.23 and Liau et al.24 reported, respectively, the I⋯AuI and Cl⋯AuI contacts, which can be interpreted as X⋯AuI halogen bonds, but the nature of these contacts was not verified. Finally, Blakey et al.25 observed contacts between the typical XB donors such as iodoperfluorobenzenes and gold nanoparticles in water solutions, but these halogen bonds were confirmed only by indirect methods such as UV-vis difference spectroscopy, SERS, and XPS and the geometrical parameters were not obtained.
It is important that a metal atom can be an XB acceptor if it contains at least one lone pair, which could interact with empty σ*-orbitals of an XB donor. In particular, some d8-PtII and d8-RhI centers may behave similarly to d10-AuI ones as these centers feature lone pairs on 4dz2 or 5dz2 orbitals. In particular, weak contacts were observed between some d8-PtII and d8-RhI species and iodine.16–19 These two were the only reports on unambiguous recognition of metal-involving XB.
Taking into account that no data for XB between metal centers and halocarbons were published, we focused our efforts on the search of metal-involving XB and we applied platinum(II) species as potential XB donors and iodoform as an XB acceptor.
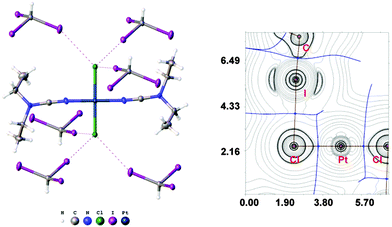
In the current work, we report that the dialkylcyanamide d8-PtII complexes trans-[PtX2(NCNR2)2] (R2 = Me2, X = Cl 1a, Br 1b; Et22, (CH2)43, (CH2)54) easily co-crystallize with iodoform taken as the XB donor. We observed that CHI3 tends to co-crystallize with 1a–b and 4 forming HI2C–I⋯Pt metal-involving halogen bonds (Chart 1, B) that fulfill both structural IUPAC criteria for halogen bonding. The existence of metal-involving halogen bonding has also been confirmed theoretically by the combination of DFT and AIM26 methods. Within the AIM theory, the (3, −1) critical points (bond critical points, BCPs) on the surface of the theoretical electron density function ρ(r) unambiguously reveal all bonding intermolecular interactions, including non-covalent interactions. Energies for the corresponding contacts Eint can be determined using semi-empirical correlations between local energy densities in BCPs and interaction strength.27,28 Moreover, we found and confirmed theoretically by combination of DFT and AIM methods the unique bifurcated HI2C–I⋯η2(Pt–Cl) (C) XB that undergoes thermally induced reversible HI2C–I⋯η2(Pt–Cl) ⇄ HI2C–I⋯η1(Pt) transformation.
Complexes 1a and 1b form isostructural associates 1a·½CHCl3·1½CHI3, 1a·2CHI3, and 1b·2CHI3 upon crystallization from 1a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHI3 = 1
CHI3 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (molar ratio) solutions in chloroform or dichloromethane, or from 1b
2 (molar ratio) solutions in chloroform or dichloromethane, or from 1b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CHI3 = 1
CHI3 = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
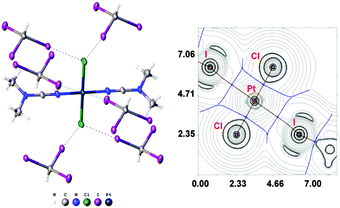
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (molar ratio) solution in dichloromethane, respectively. Apart from numerous HI2C–I⋯X–Pt halogen bonds (Chart 1, A), they exhibit the HI2C–I⋯Pt short contacts, which can be interpreted as metal-involving XB accordingly to both structural IUPAC criteria as the distances I⋯Pt (3.4276(5) Å, 3.4389(5) Å, and 3.4023(5) Å) are less than sums of Bondi's29 vdW radii (RvdW(Pt) + RvdW(I) = 3.73 Å) and the corresponding angles (164.84(17)°, 169.8(3)°, and 172.7(2)°) are close to 180° (for more details see Section XR2 of the ESI†). We also confirmed the formation of the I⋯Pt non-covalent interaction in 1a·½CHCl3·1½CHI3 and 1b·2CHI3 systems theoretically for the 1a·(CHI3)6 and 1b·(CHI3)6 model structures by using Bader's AIM analysis (Fig. 1 and 2; for details see Section TH1 in the ESI†). The estimated energies (Eint) of these contacts are in the ranges of 2.4–2.8 kcal mol−1 and 2.7–3.1 kcal mol−1, respectively. The strength of these weak interactions has been defined according to the procedures proposed by Espinosa et al.27 and Vener et al.,28 these approaches considered explore linear relationships between the local electronic potential V(r) and kinetic G(r) densities at the bond critical points and energies of appropriate contacts.
2 (molar ratio) solution in dichloromethane, respectively. Apart from numerous HI2C–I⋯X–Pt halogen bonds (Chart 1, A), they exhibit the HI2C–I⋯Pt short contacts, which can be interpreted as metal-involving XB accordingly to both structural IUPAC criteria as the distances I⋯Pt (3.4276(5) Å, 3.4389(5) Å, and 3.4023(5) Å) are less than sums of Bondi's29 vdW radii (RvdW(Pt) + RvdW(I) = 3.73 Å) and the corresponding angles (164.84(17)°, 169.8(3)°, and 172.7(2)°) are close to 180° (for more details see Section XR2 of the ESI†). We also confirmed the formation of the I⋯Pt non-covalent interaction in 1a·½CHCl3·1½CHI3 and 1b·2CHI3 systems theoretically for the 1a·(CHI3)6 and 1b·(CHI3)6 model structures by using Bader's AIM analysis (Fig. 1 and 2; for details see Section TH1 in the ESI†). The estimated energies (Eint) of these contacts are in the ranges of 2.4–2.8 kcal mol−1 and 2.7–3.1 kcal mol−1, respectively. The strength of these weak interactions has been defined according to the procedures proposed by Espinosa et al.27 and Vener et al.,28 these approaches considered explore linear relationships between the local electronic potential V(r) and kinetic G(r) densities at the bond critical points and energies of appropriate contacts.
Complex 4 was co-crystallized with CHI3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
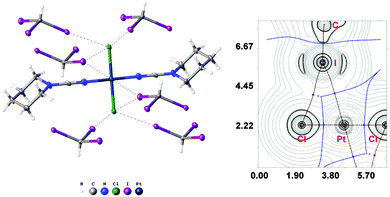
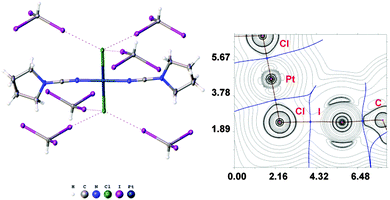
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio from chloroform solution forming 4·2CHI3. Apart from two types of HI2C–I⋯Cl–Pt XB (Chart 1, A), this solid also contains the bifurcated HI2C–I⋯η2(Pt–Cl) metal-involving XB (C). Both distances (d(I⋯Pt) = 3.7060(7) Å and d(I⋯Cl) = 3.6974(19) Å) are slightly less than the corresponding sums of Bondi's29 vdW radii (RvdW(Pt) + RvdW(I) = 3.73 Å; RvdW(Cl) + RvdW(I) = 3.73 Å) and both contact angles are not much different from 160° (∠(C–I⋯Pt) = 158.4(2)°, ∠(C–I⋯Cl) = 163.4(2)°) (see Section XR2 of the ESI†). The formation of the I⋯Pt and I⋯Cl non-covalent interactions was confirmed theoretically for the 4·(CHI3)6 model structure by using Bader's AIM analysis (Fig. 3, see also TH1 of the ESI†). The estimated energies Eint of these contacts are in good agreement with the energy range for XB (1.3–1.4 kcal mol−1 for HI2C–I⋯Cl and 1.6 kcal mol−1 for HI2C–I⋯Pt). To the best of our knowledge, these weak interactions are the first example of metal-involving bifurcated XB. It is noteworthy that examples of metal-free bifurcated XB6 and metal-involving bifurcated hydrogen bonding30 are known. Taking into account that the observed distances within the HI2C–I⋯η2(Pt–Cl) moiety are only slightly less than their van der Waals separations, more examples of metal-involving bifurcates are needed to exclude completely the packing effects on the bonding.
2 molar ratio from chloroform solution forming 4·2CHI3. Apart from two types of HI2C–I⋯Cl–Pt XB (Chart 1, A), this solid also contains the bifurcated HI2C–I⋯η2(Pt–Cl) metal-involving XB (C). Both distances (d(I⋯Pt) = 3.7060(7) Å and d(I⋯Cl) = 3.6974(19) Å) are slightly less than the corresponding sums of Bondi's29 vdW radii (RvdW(Pt) + RvdW(I) = 3.73 Å; RvdW(Cl) + RvdW(I) = 3.73 Å) and both contact angles are not much different from 160° (∠(C–I⋯Pt) = 158.4(2)°, ∠(C–I⋯Cl) = 163.4(2)°) (see Section XR2 of the ESI†). The formation of the I⋯Pt and I⋯Cl non-covalent interactions was confirmed theoretically for the 4·(CHI3)6 model structure by using Bader's AIM analysis (Fig. 3, see also TH1 of the ESI†). The estimated energies Eint of these contacts are in good agreement with the energy range for XB (1.3–1.4 kcal mol−1 for HI2C–I⋯Cl and 1.6 kcal mol−1 for HI2C–I⋯Pt). To the best of our knowledge, these weak interactions are the first example of metal-involving bifurcated XB. It is noteworthy that examples of metal-free bifurcated XB6 and metal-involving bifurcated hydrogen bonding30 are known. Taking into account that the observed distances within the HI2C–I⋯η2(Pt–Cl) moiety are only slightly less than their van der Waals separations, more examples of metal-involving bifurcates are needed to exclude completely the packing effects on the bonding.
Variable temperature XRD experiments for the same single-crystal of 4·2CHI3 were performed at 100, 150, 200, 250, and 300 K. An inspection of the obtained data indicates that the heating leads only to the elongation of the intermolecular distances, whereas the covalent bond lengths remain almost the same. The most significant changes were detected for the bifurcated HI2C–I⋯η2(Pt–Cl) contacts (by 0.08 Å upon an increase in temperature from 100 to 300 K), whereas the HI2C–I⋯Cl–Pt halogen bonds were lengthened by only 0.05 and 0.03 Å, correspondingly (see also XR3 of the ESI†). Bader's AIM analysis (TH2 of ESI†) for the 4·(CHI3)6 model systems at each temperature indicated above showed the gradual reduction of the estimated energies of all halogen bonds. Apart from that one of the bond critical points (between Cl and I) in the bifurcated XB disappeared on going from 250 to 300 K. The reversibility of the thermal transformation was proved by three consecutive XRD experiments for the same single-crystal at 100 K, 300 K, and again at 100 K. This experiment gives evidence supporting the thermally induced reversible HI2C–I⋯η2(Pt–Cl) ⇄ HI2C–I⋯η1(Pt) transformation.
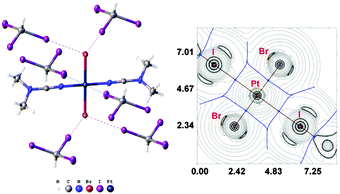
Complexes 2 and 3 were co-crystallized with CHI3 in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio from chloroform solutions forming 2·2CHI3 and 3·2CHI3, respectively. These associates were found to form only three types of HI2C–I⋯Cl–Pt XB in each case (Fig. 4 and 5). In all cases (1a·½CHCl3·1½CHI3, 1b·2CHI3, 2·2CHI3, 3·2CHI3, and 4·2CHI3), the formation of halogen bonds with the halide ligands was confirmed theoretically by using Bader's AIM analysis (XR2 and TH1 of the ESI†). The estimated energies (Eint) of this type of weak interaction are in the range of 1.9–3.5 kcal mol−1. Only the HI2C–I⋯Cl− and the HI2C–I⋯Br− weak interactions were previously described,31 but no single example of the XB between metal-coordinated chloride or bromide and CHI3 has been previously reported.
2 molar ratio from chloroform solutions forming 2·2CHI3 and 3·2CHI3, respectively. These associates were found to form only three types of HI2C–I⋯Cl–Pt XB in each case (Fig. 4 and 5). In all cases (1a·½CHCl3·1½CHI3, 1b·2CHI3, 2·2CHI3, 3·2CHI3, and 4·2CHI3), the formation of halogen bonds with the halide ligands was confirmed theoretically by using Bader's AIM analysis (XR2 and TH1 of the ESI†). The estimated energies (Eint) of this type of weak interaction are in the range of 1.9–3.5 kcal mol−1. Only the HI2C–I⋯Cl− and the HI2C–I⋯Br− weak interactions were previously described,31 but no single example of the XB between metal-coordinated chloride or bromide and CHI3 has been previously reported.
The elongation of the Pt–X (X = Cl, Br) bonds in the CHI3-associates was detected when XRD data of the associates were compared with those of CHI3-free 1a,321b, and 433 (see XR1 in the ESI†). The Pt–Cl distances in 2·2CHI3 and 3·2CHI3 are longer than in CHI3-free complexes 1a and 4. Although these differences are not too large (0.01–0.03 Å), the observed elongation indirectly point out (Chart 2) to the presence of the HI2C–I⋯X–Pt and HI2C–I⋯Pt contacts (see XR2 and TH1 in the ESI†) additionally supporting our conclusions.
In this communication, we reported the first examples of definite and unambiguous identification of metal-involving XB with halocarbons, viz. between PtII and CHI3. Various PtII centers are known to participate in donor–acceptor interactions with Lewis acids (BIII and SIV compounds34,35), but in all cases these donor–acceptor bonds are too strong to be treated as non-covalent bonds. The most relevant example of XB is weak contacts between the PtII and RhI centers and iodine.16–19 Examples of the X⋯M short contacts given in the Introduction have not been clearly identified as metal-involving XB. We plan to continue our studies in the area of metal-involving XB and to expand the range of studied systems to other X's and X-containing species (e.g. Br) and metal centers (e.g. PdII) and studies in these directions are underway in our group.
The authors express their gratitude to the Russian Science Foundation for grant (14-13-00060) supporting their synthetic and structural studies. ASN thanks the Russian Foundation for Basic Research for grant (16-33-60063) focused on theoretical calculations of XB. IVA is grateful to the Russian Foundation for Basic Research for financial support of variable temperature XRD studies (grant 16-33-60133). Physicochemical studies were performed at the Center for X-ray Diffraction Studies, Magnetic Resonance Research Center, and Center for Chemical Analysis and Materials Research (all belong to Saint Petersburg State University).
References
- R. Bertani, P. Sgarbossa, A. Venzo, F. Lelj, M. Amati, G. Resnati, T. Pilati, P. Metrangolo and G. Terraneo, Coord. Chem. Rev., 2010, 254, 677–695 CrossRef CAS.
- G. Cavallo, P. Metrangolo, T. Pilati, G. Resnati, M. Sansotera and G. Terraneo, Chem. Soc. Rev., 2010, 39, 3772–3783 RSC.
- E. Persch, O. Dumele and F. Diederich, Angew. Chem., Int. Ed., 2015, 54, 3290–3327 CrossRef CAS PubMed.
- P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794 CrossRef CAS PubMed.
- P. S. Ho, Halogen Bonding I: Impact on Materials Chemistry and Life Sciences, Springer-Verlag Berlin, Berlin, 2015, vol. 358, pp. 241–276 Search PubMed.
- K. B. Landenberger, O. Bolton and A. J. Matzger, J. Am. Chem. Soc., 2015, 137, 5074–5079 CrossRef CAS PubMed.
- H. Wang, R. X. Hu, X. Pang, H. Y. Gao and W. J. Jin, CrystEngComm, 2014, 16, 7942–7948 RSC.
- V. V. Sivchik, A. I. Solomatina, Y.-T. Chen, A. J. Karttunen, S. P. Tunik, P.-T. Chou and I. O. Koshevoy, Angew. Chem., Int. Ed., 2015, 54, 14057–14060 CrossRef CAS PubMed.
- G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713 CrossRef CAS.
- K. Rissanen, CrystEngComm, 2008, 10, 1107–1113 RSC.
- S. V. Rosokha, C. L. Stern and J. T. Ritzert, Chem. – Eur. J., 2013, 19, 8774–8788 CrossRef CAS PubMed.
- D. A. Bahnick, W. E. Bennett and W. B. Person, J. Phys. Chem., 1969, 73, 2309–2316 CrossRef CAS.
- T. Mager, H. Bertagnolli, D. Degenhardt and R. Frahm, Mol. Phys., 1991, 73, 587–601 CrossRef CAS.
- H. G. Lohr, A. Engel, H. P. Josel, F. Vogtle, W. Schuh and H. Puff, J. Org. Chem., 1984, 49, 1621–1627 CrossRef.
- J. Viger-Gravel, S. Leclerc, I. Korobkov and D. L. Bryce, J. Am. Chem. Soc., 2014, 136, 6929–6942 CrossRef CAS PubMed.
- J. A. M. van Beek, G. van Koten, G. Dekker, E. Wissing, M. C. Zoutberg and C. H. Stam, J. Organomet. Chem., 1990, 394, 659–678 CrossRef CAS.
- J. A. M. van Beek, G. van Koten, W. J. J. Smeets and A. L. Spek, J. Am. Chem. Soc., 1986, 108, 5010–5011 CrossRef CAS.
- R. A. Gossage, A. D. Ryabov, A. L. Spek, D. J. Stufkens, J. A. M. van Beek, R. van Eldik and G. van Koten, J. Am. Chem. Soc., 1999, 121, 2488–2497 CrossRef CAS.
- D. W. Shaffer, S. A. Ryken, R. A. Zarkesh and A. F. Heyduk, Inorg. Chem., 2012, 51, 12122–12131 CrossRef CAS PubMed.
- J. H. Chen, Y. M. Liu, J. X. Zhang, Y. Y. Zhu, M. S. Tang, S. W. Ng and G. Yang, CrystEngComm, 2014, 16, 4987–4998 RSC.
- C. Wölper, S. R. Piñol, S. D. Ibáñez, M. Freytag, P. G. Jones and A. Blaschette, Z. Anorg. Allg. Chem., 2008, 634, 1506–1516 CrossRef.
- A. Laguna, T. Lasanta, J. M. Lopez-de-Luzuriaga, M. Monge, P. Naumov and M. E. Olmos, J. Am. Chem. Soc., 2010, 132, 456–457 CrossRef CAS PubMed.
- H. M. Yamamoto, J. I. Yamaura and R. Kato, J. Am. Chem. Soc., 1998, 120, 5905–5913 CrossRef CAS.
- R. Y. Liau, H. Ehlich, A. Schier and H. Schmidbaur, Z. Naturforsch., B: J. Chem. Sci., 2002, 57, 1085–1089 CAS.
- I. Blakey, Z. Merican, L. Rintoul, Y. M. Chuang, K. S. Jack and A. S. Micallef, Phys. Chem. Chem. Phys., 2012, 14, 3604–3611 RSC.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1990 Search PubMed.
- E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173 CrossRef CAS.
- M. V. Vener, A. N. Egorova, A. V. Churakov and V. G. Tsirelson, J. Comput. Chem., 2012, 33, 2303–2309 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- D. Braga, F. Grepioni, E. Tedesco, K. Biradha and G. R. Desiraju, Organometallics, 1997, 16, 1846–1856 CrossRef CAS.
- H. Bock and S. Holl, Z. Naturforsch., B: J. Chem. Sci., 2001, 56, 152–163 CAS.
- N. A. Bokach, T. B. Pakhomova, V. Y. Kukushkin, M. Haukka and A. J. L. Pombeiro, Inorg. Chem., 2003, 42, 7560–7568 CrossRef CAS PubMed.
- P. V. Gushchin, N. A. Bokach, M. Haukka, E. S. Dmitrieva and V. Y. Kukushkin, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m244–m246 CAS.
- S. Bontemps, M. Sircoglou, G. Bouhadir, H. Puschmann, J. A. K. Howard, P. W. Dyer, K. Miqueu and D. Bourissou, Chem. – Eur. J., 2008, 14, 731–740 CrossRef CAS PubMed.
- P. Steenwinkel, H. Kooijman, W. J. J. Smeets, A. L. Spek, D. M. Grove and G. van Koten, Organometallics, 1998, 17, 5411–5426 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Synthesis of complexes (Section EX1), their co-crystallization with iodoform, full description of XRD experiments, crystallographic data and refinement parameters (Section EX2), full description of the geometrical parameters of covalent bonds and non-covalent interactions (Sections XR1–XR3), and full description of the results of theoretical calculations and computational details (Sections TH1–TH3). CCDC 1446656–1446670. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6cc01107a |
| This journal is © The Royal Society of Chemistry 2016 |