Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational study on the intramolecular self-organization of the macrorings of some ‘giant’ cyclodextrins (CDn, n = 40, 70, 85, 100)†
Petko M.
Ivanov
*a,
Emanouil J.
Atanassov
b and
Carlos
Jaime
c
aInstitute of Organic Chemistry with Centre of Phytochemistry, Bulgarian Academy of Sciences, ul. Acad. G. Bonchev, bloc 9, 1113 Sofia, Bulgaria. E-mail: ivanov@bas.bg
bInstitute of Information and Communication Technologies, Bulgarian Academy of Sciences, ul. Acad. G. Bonchev, bloc 25A, 1113 Sofia, Bulgaria
cUniversitat Autònoma de Barcelona, Departament de Química, Facultat de Ciències, E-08193 Bellaterra (Cerdanyola del Vallès), Spain
First published on 7th November 2014
Abstract
The conformations of some ‘giant’ cyclodextrins (CDn, n = 40, 70, 85, 100) were examined by molecular dynamic simulations using the Glycam06 force field. CD14 and CD26, the largest cyclodextrins, for which crystallographic data are available, were also studied as reference structures. Principal component analysis was used for the analyses of the simulation trajectories. In cases where band-flips were not present in the starting geometry (e.g. CD40), flips appeared later during the conformational search. The results for CDn (n = 14, 26, 40) confirmed an interesting observation for the distribution of band-flips along the perimeters of the macrorings, namely, band-flips separate portions of lengths of about six or twelve glucoses. This allows the formation of energetically favorable small loops of six–seven glucoses or the creation of short two-turns single helices that further enhance the stability of the structures. It was found that flip dihedrals define distributions of fragment lengths 12–6, 12–12, and 12–12–6 residues in the larger CDs (CD70, CD85, CD100). Contributions from 77% (CD40) to 88% (CD26) are from the first three highest-eigenvalue principal components, i.e., a limited number of modes determine the overall deformations of the macrorings. The flexibility of the macrorings increases, going from CD40 to the CDs, with higher degrees of polymerization. CD14 and CD26 present interesting cases – CD26 manifests domination of one deformation mode (ca. 72%), whereas CD14 demonstrates significantly higher flexibility. These results confirm our earlier conclusion, namely, LR-CDs may have more than one cavity. Thus they have the potential to accommodate more than one substrate molecule, as well as larger species by an ‘induced fit’ mechanism.
Introduction
The large-ring cyclodextrins (LR-CDs; CDs with a degree of polymerization (DP) higher than eight),1–5 have attracted attention in recent years, and advances were marked in the study of their physicochemical properties,6–15 in spite of existing difficulties in their synthesis, isolation and purification. The existence of LR-CDs has been proven by the isolation of these products from the action of 4-α-glucanotransferases on amylose and amylopectin,2 almost a century after the first evidence for the existence of cyclodextrins.16 The small cyclodextrins provide a heterogeneous microenvironment to molecules, accommodated in their cavities that acquire significantly modified properties compared to the free forms. Therefore, numerous well-known properties useful for the practical applications of small cyclodextrins were determined. The expectations were that some of the LR-CDs may have new, specific properties.It took about twenty years after the first report of the existence of LR-CDs (DP = 9–14)17 for the preparation method for LR-CDs mixtures to be worked out and δ-CD (DP = 9)18 to be isolated and its crystal structure characterized.19 This opened renewed interest in LR-CDs; within a very short time the crystal determinations of CD10 (ε-CD),14,20–22 CD14 (ι-CD),20,21 and CD26 (ν-CD)23–25 were reported. Important steps related to the development of an effective purification method for LR-CDs4 were the chemical synthesis of a LR-CD – CD9,26 as well as the synthesis of the first chemically modified LR–CD (CD9).27
Experimental information about the conformations of LR-CDs is rare. Crystal structure determinations have been till date successful only for four of them.28 The thermal and structural characterization of the small cyclodextrins have been carried out29 and references to CDs with more than 6030 and several hundred31 glucose units have been made. An advantage of the LR-CDs in comparison with the small CDs, particularly with α-CD and β-CD, is that they are without any significant toxicity and that nutritionally they can be regarded as starch.2 Commercially available CD-mixtures containing LR-CDs with a degree of polymerization from 9 to 21 were examined as additives for food (retrogradation retardant in breads, for freeze resistant jellies and for production of non-sticky rice) and drink products (high energy additive to soft drinks) for improving their texture, mouth feeling, flavor, taste, and palatability.6,11 Others were studied for the stabilization and solubilization of drugs.32 LR-CDs mixtures with a degree of polymerization from 22 to 45 and greater than 50 exhibited an efficient artificial chaperone effect for protein refolding (a protein refolding kit containing a mixture of LR-CDs as one of the active components is in the market3 – the first practical application of LR-CDs in biotechnology33). Such LR-CDs mixtures were able to strip detergent molecules of unfolded protein-detergent complexes, thus allowing the protein molecules to refold to their proper, folded, active state.2 LR-CDs have been suggested for applications in the paper industry as an improved paper coating material and as starch substitutes in adhesives and biodegradable plastics.11 Because the large CDs are able to present a variety of cavity sizes, compared to the small CDs, they may be useful for special applications. δ-CD, for example, has demonstrated to form a stable complex with C70 buckminsterfullerene that allows its solubilization in water.34 It has been proven that η-CD (12 glucoses) is effective in the partial separation of carbon nanotubes.35 Increased interest is evident from the previous studies on developing techniques for isolation of LR-CDs36,37 and for examining the properties of these macromolecules as new polysaccharide-based biomaterials.38
The conformations of some LR-CDs were systematically examined using molecular dynamics simulations as a conformational search protocol.39–51 We started our studies by performing 5.0 ns simulations on several LR-CDs with degrees of polymerization in the range from 40 to 100.39 The results were indicative for a variety of geometries with more than one small cavity. Now we can execute an order of magnitude longer simulations, attempting to arrive at more grounded conclusions about the intramolecular self-organization of the macrorings of such ‘giant’ cyclodextrins. CD14 and CD26 were also studied as reference structures using crystallographic coordinates for the input.
Computational details
The conformational search based on molecular dynamics simulations
The MD simulation trajectories were obtained with the AMBER program (versions 1052 and 1153) using the parameterization for carbohydrates, Glycam06.54 The same starting geometries as in our earlier study were adopted for CDn (n = 40, 70, 85, 100) (Fig. S1†),39 whereas crystal coordinates were used for CD1420 and CD26.23 The molecular dynamics simulations were run in a simulated aqueous solution (a box with TIP4P55 water molecules) using the particle mesh Ewald (PME) method56–59 for the treatment of the long-range electrostatics. A 9.0 Å distance cutoff was used for direct space nonbonded calculations and a 1.0 × 10−5 Ewald convergence tolerance for the inclusion of long-range electrostatic contributions. The ‘solvateBox’ command of LEaP was used to create a cubic solvent box around the CD with buffer distances of 15.0 Å between the walls of the box and the closest atoms of the solute. The dimensions of the periodic TIP4P cubic boxes and the number of water molecules were as follows: CD14 (56.8 Å; 5440), CD26 (60.2 Å; 6364), CD40 (75.9 Å; 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094), CD70 (93.9 Å; 24
094), CD70 (93.9 Å; 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 982), CD85 (98.5 Å; 28
982), CD85 (98.5 Å; 28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 846), CD100 (107.1 Å; 37
846), CD100 (107.1 Å; 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459). The SHAKE option (tolerance 5.0 × 10−5 Å) was used for constraining bonds involving hydrogen atoms. The same protocol from our previous studies was used for the preparation of the systems for the simulation, as well as for the principal component analyses:50,51 (i) 5000 steps steepest descent and 200 steps conjugate gradient minimization of the LR-CD in the gas phase, followed by 5000 steps steepest descent and 400 steps conjugate gradient minimization of the entire (LR-CD plus water molecules) completely unrestrained system; (ii) 50
459). The SHAKE option (tolerance 5.0 × 10−5 Å) was used for constraining bonds involving hydrogen atoms. The same protocol from our previous studies was used for the preparation of the systems for the simulation, as well as for the principal component analyses:50,51 (i) 5000 steps steepest descent and 200 steps conjugate gradient minimization of the LR-CD in the gas phase, followed by 5000 steps steepest descent and 400 steps conjugate gradient minimization of the entire (LR-CD plus water molecules) completely unrestrained system; (ii) 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps steepest descent minimization with holding the solute fixed with positional restraints; (iii) 25.0 ps unrestrained MD were run at 100 K on the water alone with holding the LR-CD constrained (this is the stage of the equilibration process where the bulk of the water relaxation takes place); (iv) gradual release of the restraints on the LR-CD in a series of minimizations and MD steps: 1000 steps minimization and 3.0 ps MD with 25.0 kcal mol−1 Å position restraints, followed by five rounds of 600 steps minimization, reducing the positional restraints by 5.0 kcal mol−1 Å each run; (v) The process was completed with a short MD simulation (NVT) after heating the system gradually to 300 K. An additional 500.0 ps simulation (NPT) was executed before starting the productive runs. The productive runs were performed with the recommended maximum time-step of 2.0 fs when SHAKE is used, at 300 K, using Berendsen weak coupling algorithm for temperature regulation60 and an average pressure of 1.0 bar with isotropic position scaling, using the Berendsen weak coupling algorithm for pressure regulations.60 Samplings were taken every 2.0 ps. The duration of the MD conformational searches was 100.0 ns, except for CD14, in which case it was 50.0 ns. When examining the modes of conformational interconversions and the dynamics of the intramolecular self-organization, monitoring the appearance and the disappearance of band-flips is of particular importance (variation with the simulation time of the flip angle, O3(n)⋯C4(n)⋯C1(n + 1)⋯O2(n + 1) – the dihedral flip between secondary hydroxyls of adjacent glucoses).
000 steps steepest descent minimization with holding the solute fixed with positional restraints; (iii) 25.0 ps unrestrained MD were run at 100 K on the water alone with holding the LR-CD constrained (this is the stage of the equilibration process where the bulk of the water relaxation takes place); (iv) gradual release of the restraints on the LR-CD in a series of minimizations and MD steps: 1000 steps minimization and 3.0 ps MD with 25.0 kcal mol−1 Å position restraints, followed by five rounds of 600 steps minimization, reducing the positional restraints by 5.0 kcal mol−1 Å each run; (v) The process was completed with a short MD simulation (NVT) after heating the system gradually to 300 K. An additional 500.0 ps simulation (NPT) was executed before starting the productive runs. The productive runs were performed with the recommended maximum time-step of 2.0 fs when SHAKE is used, at 300 K, using Berendsen weak coupling algorithm for temperature regulation60 and an average pressure of 1.0 bar with isotropic position scaling, using the Berendsen weak coupling algorithm for pressure regulations.60 Samplings were taken every 2.0 ps. The duration of the MD conformational searches was 100.0 ns, except for CD14, in which case it was 50.0 ns. When examining the modes of conformational interconversions and the dynamics of the intramolecular self-organization, monitoring the appearance and the disappearance of band-flips is of particular importance (variation with the simulation time of the flip angle, O3(n)⋯C4(n)⋯C1(n + 1)⋯O2(n + 1) – the dihedral flip between secondary hydroxyls of adjacent glucoses).
Principal component analysis
Principal component analysis (PCA), also called quasiharmonic analysis or essential dynamics method,61–63 is a very useful analysis tool for MD trajectories.64–73 This statistical method allows trajectories obtained from MD simulations to be analyzed by reducing the degrees of freedom of the system to lower dimensions.67 In large complex systems this approach provides a useful method to extract the most important information pertaining to the essential physics of a biomolecular process such as protein folding or molecular recognition. As a result we can monitor the concerted motions of the atoms of the molecule in a few dimensions, making it easier to visualize and investigate these motions.67,68PCA is a linear transformation applied to the fluctuations in the Cartesian coordinates, represented as a matrix – positional covariance matrix, C, derived from the Cartesian snapshots collected along the MD simulation trajectory. C = (3N)−1TTT, where the 3N rows of matrix T are the coordinates of the N atoms and the columns of T hold the data for the successive time points (snapshots) in the trajectory. T is processed in order to remove the global translation and rotation of the structure, and then the average structure is subtracted. A dihedral angle representation of the method has been also devised.74,75 Diagonalization of C, to solve Λ = VTCV for an N atom system, provides a set of 3N orthogonal eigenvectors, vn, as columns of matrix V, as well as the corresponding eigenvalues, λn, the diagonal elements of Λ.65,73 The eigenvectors provide a vectorial representation of each mode of structural deformation, and the eigenvalue for a mode indicates the relative contribution that this mode has made to motion within the trajectory.65 Ordering the eigenvalues of the transformation decreasingly, it can be determined how many principal components (usually only a few) capture the ‘essential dynamics’ of the system (defined as a given variance threshold: typically 90%–95%73). An analysis based on the dominant PCA modes naturally poses the question about the convergence of the first few modes with the length of the simulation.72,76,77 The duration of the simulation had to be long enough in order to extract by PCA longer time-scale motions. By this method, molecular dynamics trajectories can be explained satisfactorily in terms of a small number of variables (essential degrees of freedom). In addition, the residues whose contributions are important in the formation and stability of different structural elements can be identified by PCA.78 The covariance matrix, whose diagonalization gives PCA, is important in describing the pathway of the dynamic process and the relation between the movements of different regions of the molecule during the process.67
Several steps were executed in order to carry out the PCA analysis: (i) processing of the MD simulation trajectory file by removing the coordinates of the water molecules; (ii) preparation of the modified trajectory file for compression of the macroring atomic coordinates by superimposing all trajectory snapshots in a manner to obtain an average structure for the entire trajectory (in this way we effectively removed the overall translational and rotational motions of the cyclodextrin molecule72); (iii) compression of the trajectory file; (iv) preparation of the covariance matrix, in which the atomic coordinates are the variables; (v) diagonalization of the covariance matrix for calculating the eigenvectors and the corresponding eigenvalues. The sum of all eigenvalues presents the total variance of the trajectory, whereas each eigenvalue contributes that part of the total variance, which is explained by the corresponding eigenvector. The predetermined desirable part of the variance of the starting trajectory can be preserved at the compression stage. In our analysis we used the default value, 90%, suggested for the compression quality in the PCAsuite software.79 It means that 90% of the variance of the original trajectory is contained in the compressed trajectory.
Results and discussion
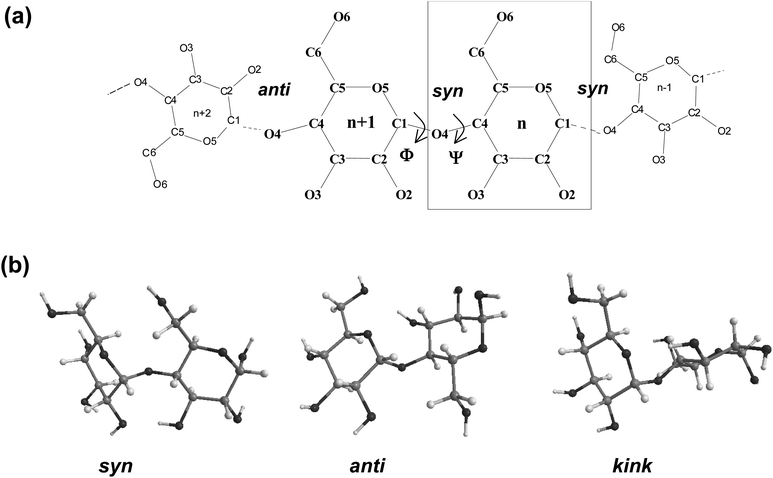
Fig. 1 displays a schematic representation of a fragment of a cyclodextrin macroring with the numbering of the atoms and examples for syn and anti orientations of neighbouring glucose units. Fig. 2 and 3 (also refer Fig. S2–S4, ESI†) present the averaged geometries from the simulation trajectories, decomposed into time intervals of 10.0 ns, and compared with averages over the entire trajectories. More detailed information is presented in Fig. S5–S12, ESI† (animated eigenvectors (Fig. S5–S7), rms curves (Fig. S8†), moments of inertia (Fig. S9†), radius of gyration (Fig. S10†), variation of flip angles (Fig. S11†), fluctuations of atomic coordinates, averaged for each residue (Fig. S12†)).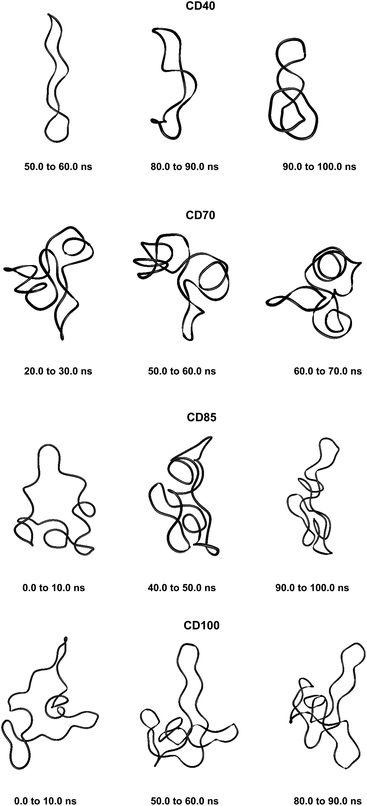 | ||
| Fig. 3 Averaged structures obtained from analyses of the simulation trajectories of CDn (n = 40, 70, 85, 100). | ||
The analysis of the rms deviations from the starting structures registered for each cyclodextrin served to check and confirm the dynamism of the structural variations of the macrorings. The rms curves indeed indicate that conformational changes take place (Fig. S8, ESI†). The following geometrical parameters are used for the structural analysis of large-ring cyclodextrins (Fig. 1 and Table S1, ESI†): O4(n)⋯O4(n − 1) – the distance between the glycosidic oxygen atoms; O2(n)⋯O3(n − 1) – the distance between secondary hydroxyl groups of adjacent glucoses; C1(n)–O4(n − 1)–C4(n − 1) – the angle at the glycosidic oxygen connecting two glucoses; O4(n)⋯O4(n − 1)⋯O4(n − 2) – the angle formed by three neighbor glycosidic oxygen atoms; O5(n)–C1(n)–O4(n − 1)–C4(n − 1) – the dihedral angle ϕ; C1(n)–O4(n − 1)–C4(n − 11)–C3(n − 1) – the dihedral angle ψ (ϕ and ψ describe the orientation of the residues about the α(1→4) glycosidic linkage); O4(n)⋯O4(n − 1)⋯O4(n − 2)⋯O4(n − 3) – the dihedral angle of four consecutive glycosidic oxygen atoms (a measure for the coplanarity of the macrorings); O3(n)⋯C4(n)⋯C1(n + 1)⋯O2(n + 1) – the dihedral flip between secondary hydroxyls of adjacent glucoses.
All computed structural parameters have values in the range of the experimental structural determinations available (Table S1, ESI†). The computed average values for dihedrals ϕ and ψ fall slightly below the minimum values determined for CD26 from crystallographic determinations, whereas the computed values for angle O4(n)⋯O4(n + 1)⋯O4(n + 2) are slightly larger than the maximum values for CD26 determined experimentally. The other computed structural parameters closely resemble the results obtained with the parm99 AMBER parameterization.39
The variations with time of two descriptors of the molecular size were also estimated: the moment of inertia (Fig. S9, ESI†) and the radius of gyration (also provides an absolute measure of compactness) (Fig. S10, ESI†). Both set of curves present similarities for each cyclodextrin. CD40 displays the most pronounced variations with time (also refer Fig. S8† for rms deviations of the atomic coordinates). The macroring of CD40 acquires less compact conformations in the time interval from 20.0 ns to 80.0 ns (Fig. S10, ESI†) and recovers a more compact form at the final stages of the simulation.
Fig. S11, ESI†, presents the variations of the flip angles that undergo significant changes during the simulation. CD14 and CD26 have two band-flips at the opposite sides of the macrorings (flip angles 7 and 14 for CD14 and 13 and 26 for CD26) and they remain unchanged until the end of the simulations. A flip angle of CD14 positioned between the band-flips (angle 10) fluctuates about –60°. Two flip dihedrals of CD26, 7 and 23, deform in an opposite manner acquiring positive and negative values, respectively. Dihedral 7 is cis at the start of the simulation, becomes about 120° after 10.0 ns, and restores the initial cis orientation for a while; it is anti at 17.0 ns and this flipped orientation is preserved until the end of the simulation. Dihedral 23 retains the initial cis orientation during the first 15.0 ns of the simulation; afterwards it fluctuates about −100° to −120°.
Band-flips were not present in the starting geometry of CD40. A flip (dihedral 6) appeared at 5.0 ns, went back to ca. −100° for 3.0 ns at 15.0 ns, and retained the flipped orientation for the remainder of the simulation time. Flip dihedral 19 had a starting value of about −60° and became anti after 85.0 ns. Another flip dihedral, 24, also transformed from cis to anti after 20.0 ns. The results for CDn (n = 14, 26, 40) confirm an interesting observation for the distribution of band-flips along the perimeter of the macrorings,51 namely, band-flips separate portions of lengths about six or twelve glucoses. This allows the formation of energetically favorable small loops of six-seven glucoses or the creation of a short two-turns single helix that further enhances the stability of the structure.50 The appearance of a new band-flip of dihedral angle 19 of CD40 at about 85 ns produces two neighbor fragments of lengths about 6 and 12 glucoses.
The distribution of fragment lengths 12–6 residues defined by the flip dihedrals 67→9→15 is also present along the perimeter of the CD70 macroring. Other six flip dihedral angles undergo significant deviations from the cis orientation. CD85 contains the sequence of fragments 12–12–6 defined by the flip dihedrals 85→14→25→32. Seven other flip dihedral angles, 20, 29, 38, 53, 68, 76, 77, also display significant variations during the simulations. The sequence 12–12 is present in the largest LR-CD, CD100, defined by the flip dihedral angles 10, 22 and 34. Eleven other flip dihedrals vary significantly during the simulation.
The PCA analysis was carried out for each time interval with duration of 10.0 ns (Table 1 and S2, ESI†). The first six eigenvectors (having the highest eigenvalues and the lowest index numbers) describe more than 90% of the total variance in all cases. Contributions from 77% (CD40) to 88% (CD26) are from the first three highest-eigenvalue principal components, i.e., a limited number of modes determine the overall deformation of the macroring. The average percentage contributions are in the ranges from 45% to 72%, from 11% to 24%, and from 6% to 12%, for the first, the second and the third eigenvectors, respectively. If we assume the ratio of percentage contribution for the first animated eigenvector to the second animated eigenvector as an indication of the difference in flexibility of the macrocycles (lower ratio indicates higher flexibility), then the flexibility of the macrorings indeed increases, going from CD40 to the CDs, with higher degrees of polymerization. CD14 and CD26 present interesting cases – CD26 manifests domination of one deformation mode (ca. 72%, ev1), whereas CD14 demonstrates significantly higher flexibility. This is in accord with our conclusions made earlier for CD14.44,48,50
| Eigenvaluesa (weight (%)) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Simulation interval (from ns to ns) | 0.0 to 10.0 | 10.0 to 20.0 | 20.0 to 30.0 | 30.0 to 40.0 | 40.0 to 50.0 | 50.0 to 60.0 | 60.0 to 70.0 | 70.0 to 80.0 | 80.0 to 90.0 | 90.0 to 100 | 0.0 to100.0b |
| a The ratio of the eigenvalues of the first three most significant eigenvectors with the explained variance in percent (weight). b 0.0 ns to 50.0 ns for CD14. | |||||||||||
| Eigenvector | |||||||||||
| CD14 | |||||||||||
| 1 | 56.4 | 63.7 | 49.9 | 45.0 | 52.5 | 47.8 | |||||
| 2 | 15.6 | 17.7 | 19.1 | 25.8 | 18.7 | 24.4 | |||||
| 3 | 10.2 | 5.7 | 14.1 | 8.4 | 11.1 | 9.8 | |||||
| CD26 | |||||||||||
| 1 | 63.4 | 33.9 | 34.3 | 38.8 | 82.7 | 55.4 | 39.8 | 37.3 | 48.6 | 36.9 | 71.9 |
| 2 | 13.3 | 20.2 | 28.1 | 15.9 | 8.2 | 16.8 | 18.4 | 17.8 | 13.1 | 21.7 | 10.8 |
| 3 | 9.2 | 13.1 | 10.8 | 14.8 | 3.1 | 7.2 | 10.1 | 14.7 | 8.4 | 13.7 | 5.6 |
| CD40 | |||||||||||
| 1 | 33.6 | 49.7 | 39.1 | 41.3 | 33.9 | 42.3 | 38.8 | 34.8 | 68.1 | 51.3 | 50.2 |
| 2 | 24.7 | 18.3 | 19.1 | 18.1 | 16.9 | 24.1 | 26.6 | 29.6 | 18.9 | 19.1 | 15.1 |
| 3 | 16.1 | 13.7 | 12.8 | 16.1 | 14.4 | 10.9 | 9.3 | 14.5 | 7.1 | 12.8 | 11.7 |
| CD70 | |||||||||||
| 1 | 40.7 | 48.5 | 46.3 | 40.3 | 41.7 | 47.1 | 39.1 | 66.6 | 52.9 | 39.5 | 51.7 |
| 2 | 23.0 | 17.1 | 21.0 | 23.5 | 24.8 | 25.8 | 21.1 | 10.4 | 13.6 | 21.8 | 19.2 |
| 3 | 11.9 | 7.8 | 9.5 | 10.4 | 9.7 | 9.9 | 12.2 | 6.5 | 9.7 | 13.1 | 10.4 |
| CD85 | |||||||||||
| 1 | 50.6 | 40.0 | 46.3 | 64.9 | 53.6 | 42.2 | 48.0 | 36.5 | 52.6 | 42.4 | 45.0 |
| 2 | 22.1 | 25.6 | 37.6 | 9.7 | 21.1 | 19.2 | 22.0 | 27.9 | 14.3 | 20.5 | 22.3 |
| 3 | 7.7 | 16.5 | 8.5 | 8.2 | 8.4 | 12.2 | 9.3 | 13.6 | 10.1 | 16.8 | 10.9 |
| CD100 | |||||||||||
| 1 | 57.7 | 51.5 | 36.6 | 47.7 | 36.9 | 34.9 | 36.4 | 30.6 | 41.1 | 37.8 | 49.0 |
| 2 | 16.7 | 19.2 | 21.4 | 23.6 | 22.1 | 18.0 | 23.7 | 24.5 | 22.9 | 14.3 | 21.4 |
| 3 | 12.8 | 11.1 | 12.8 | 10.9 | 13.1 | 12.9 | 12.2 | 12.7 | 11.8 | 13.6 | 7.5 |
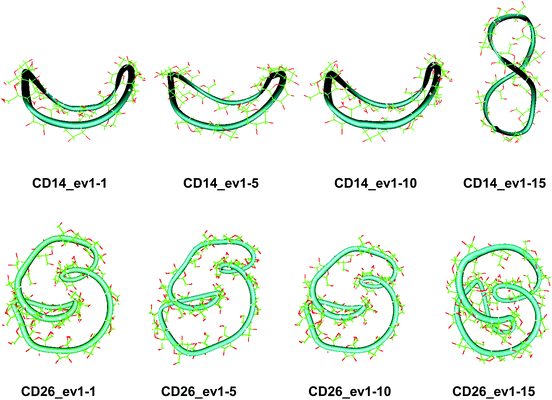
Two loops situated in mutually perpendicular planes were clearly seen in the average structure of CD14 when the Glycam04 parameterization was used.45 The eigenvector explaining the largest part for the variance of the trajectory of CD14 corresponded to a deformation, for which a conformation containing big and small loops, situated in perpendicular planes, assumes an intermediate symmetrical figure-eight-looking geometry.45 The present modeling studies characterize the same cyclodextrin as tending to keep the starting deformed boat-like form to a greater extent (Fig. 2), although figure-eight-like deformations are still visible from the examination of the computed average geometries and the deformation modes (Fig. 2 and 4, and Fig. S2 and S5, ESI†). The glucoses with the maximum fluctuations of atomic coordinates, averaged for each residue, are situated diametrically along the perimeter of the macroring (Fig. S12, ESI†).
The first three animated eigenvectors of CD26, illustrating the most important deformation modes for conformational interconversions of the macroring, are given in Fig. 4 and S6, ESI.† The differences between the results obtained with the two Glycam parameterizations (Glycam0444,46 and Glycam06 (this work)) manifest themselves from the very first stages of the conformational search for CD26 (Fig. S1, ESI,†e.g., the geometry after the first 500.0 ps). Two single helical turns at the opposite sides of the macroring are oriented inwards to the cavity of the macroring in this case (Fig. S3, ESI,† for the first 10.0 ns and the average for the entire trajectory) resulting in more compact optimized geometries. Accordingly, smaller values for the radius of gyration were estimated with Glycam06 (compare Fig. S10, ESI,† in this work with Fig. 3S† in ref. 46). Three glucose residues have the maximum fluctuations of atomic coordinates (i.e., maximum deformations). They define sequences of residues 3→11→22 and 4→15→22 for the first and for the second animated eigenvectors, respectively (Fig. S12, ESI†). The different orientation of the loops is the striking dissimilarity between the representative conformations of CD26, obtained with Glycam-0444,46 and Glycam-06. This observation originates from the differences in the estimates for the relative energies of the flip conformations by the two parameterizations,80 and this also has impact on the energetics of the syn/flip conformational transitions.
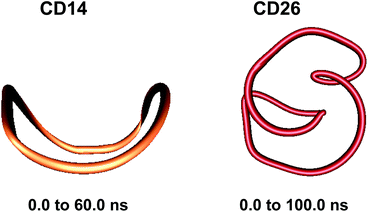
These results confirm our earlier conclusion,39 namely, LR-CDs may have more than one cavity (Fig. 3). Thus, they have the potential to accommodate more than one substrate molecule, as well as larger species, such as nanotubes, by an ‘induced fit’ mechanism.35 The starting geometries of CDn (n = 40, 70, 85, 100) contain spiral portions with different number of turns, big elongated loops and extended portions that close cavities of different sizes. CD40 displays the typical doubly wound extended single helical fragments with a loop of eight to nine glucoses at one of the ends. The first deformation mode (ev1) transforms the extended geometry into a bent structure (Fig. 5 (CD40_ev1–5) and Fig. S7, ESI†). The macrorings of the other LR-CDs present extended helical strands or helices of two or three turns forming several cavities. Three main fragments characterize the overall appearance of CD70: two spirals of two and three turns and an elongated portion of winded helical single chains. The principal deformations comprise stretching/compression of the elongated portion, at the expense of the size of the two short helixes, with concomitant variations of the mutual orientation of the two spiral portions, namely, the axes of the two spirals change from parallel to each other to perpendicular to each other (Fig. S7, ESI†). Two to three elongated portions with loops at the ends are formed along the perimeters of the largest CD85 and CD100 macrorings that may allow the accommodation of larger species in their cavities by an ‘induced fit’ mechanism (Fig. S4 and S7, ESI†). The larger perimeter of the CD85 macroring allows deformations that produce a wider cavity of irregular shape. Two elongated parts of the CD100 macrocycle ‘breath’ between states with these portions parallel or perpendicular to each other (Fig. S7, ESI†).
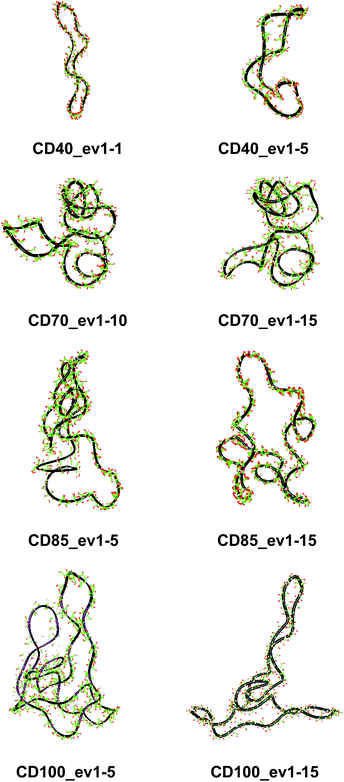 | ||
| Fig. 5 Characteristic deformations of the macrorings of CDn (n = 40, 70, 85, 100) represented by snapshots (with sequential numbers 1, 5, 10 or 15) of the first animated eigenvectors (ev1). | ||
Fluctuations of the atomic coordinate of the LR-CDs (in Å), averaged for each residue, are represented in Fig. S12, ESI.† These graphics contain valuable information about the fragments of the macrorings with the most significant contribution to the conformational deformations. The variations in the shape of these graphics correlate with the appearance and the disappearance of flip dihedral angles between neighbor glucose units (Fig. S11, ESI†). Two glucose residues, diametrically positioned along the perimeter of the CD40 macroring, possess the maximum fluctuations of atomic coordinates for the first animated eigenvector. Four glucoses undergo significant atomic fluctuations within the second and the third modes, and they are evenly distributed along the macroring (sequences 6→15→25→35 and 6→14→24→33 for the second and for the third eigenvectors, respectively (Fig. S12, ESI†)). Six residues of CD70 have the largest fluctuations of atomic coordinates for the first three animated eigenvectors, namely, 12→22→35→47→55→67 (ev1), 16→25→36→47→55→68 (ev2) and 12→25→33→44→53→67 (ev3). Larger numbers of residues may have significant fluctuations of atomic coordinates for the two largest cyclodextrins and they are evenly distributed along the perimeters of the macrorings, e.g., for the first animated eigenvectors, CD85 (3→13→25→35→45→52→63→71) and CD100 (12→28→40→46→56→73→82→90→100). In addition, as it can be deduced from Fig. 3, CD85 changes from a random coil at the beginning of the simulation to a nearly helical arrangement at the mid and finally loses part of the helicity at the end of the simulation. Something similar happens to CD100 that starts off to become a random coil and gradually changes to a more helical conformation.
It may be interesting to compare our computational results for the largest computed CDs (85 and 100 glucose units) with the already known behavior of amylose in aqueous solution, due to the similarity of the systems. Many models have been used to explain the conformational behavior of amylose and they can easily be classified into three different types: (i) a random coil, (ii) an interrupted helix with 10–15 helical turns per region, and (iii) a loosely wound helical chain.81 However, hydrodynamic studies on amylose solutions, even though not totally consistent with one another, have shown that amylose behaves as a random coil. Interestingly, amylose is metastable in neutral aqueous solutions, indicating aggregation of amylose into large particles or changes in conformation to a more crystalline and compact structure. This observation was also found in DMSO as a solvent.82 More recently, measurements of static and dynamic light scattering detected that amylose was structured as a random coil in freshly prepared alkaline and briny aqueous solutions.83 However, after long storage (about 30 days) an increase in the scattered light polarization was observed, a fact which was attributed to a coil-to-helix transition followed by helix amylose crystallization. Spectroscopic studies (13C-NMR)84 on the amylose conformational behavior in binary DMSO–water mixtures indicate that amylose is in a helical conformation below 33% water but from this point on, the helix is progressively lost and when water is over 66% the transition to a random coil is complete. That work also demonstrates that when the water content is over 60%, amylose can form a complex with iodine or butanol, also showing either the capability of modifying the existing “cavities” or the existence of more than one different cavity.
Although our simulations are extremely short when compared with real experiments, in our opinion they already show this capability of amylose (or of very long glucose chains) to adopt different conformations varying from random coils to more organized helical structures (Fig. 3 and 5). In addition, our previous finding (the existence of more than one cavity) is reinforced by the experiment described in the previous paragraph and it is probably very convenient to reformulate it as “LR-CDs are flexible enough as to adopt different conformations, each one presenting a different cavity size”.
Conclusions
The conformations of some ‘giant’ cyclodextrins (CDn, n = 40, 70, 85, 100) were examined by molecular dynamic simulations using the Glycam06 force field. CD14 and CD26 were also studied as reference structures. Principal component analysis was used for the analyses of the simulation trajectories.In cases where band-flips were not present in the starting geometry (e.g., CD40), flips appeared later during the conformational search. The results for CDn (n = 14, 26, 40) confirmed an interesting observation for the distribution of band-flips along the perimeters of the macrorings, namely, band-flips separate portions of lengths about six or twelve glucoses. This allows the formation of energetically favorable small loops of six-seven glucoses, also detected in molecular dynamics simulations of acyclic oligomers,85,86 or the creation of short two-turns single helices that further enhance the stability of the structures. It was found that flip dihedrals define distributions of fragment lengths 12–6, 12–12, and 12–12–6 residues in the larger CDs (CD70, CD85, CD100). The different orientation of the loops is the striking dissimilarity between the representative conformations of CD26, compared with previous results with the Glycam-04 force field. This observation originates from the differences in the estimates for the relative energies of the flip conformations by the two parameterizations that may have impact on the energetics of the syn/flip conformational transitions.
Contributions to the total variance from 77% (CD40) to 88% (CD26) are from the first three highest-eigenvalue principal components, i.e., a limited number of modes determine the overall deformations of the macrorings. The flexibility of the macrorings increases going from CD40 to the CDs with higher degrees of polymerization. CD14 and CD26 present interesting cases – one deformation mode dominates for CD26 (ca. 72%), whereas CD14 demonstrates significantly higher flexibility. These results confirm our earlier conclusion, namely, LR-CDs may have more than one cavity. Thus, they have the potential to accommodate more than one substrate molecule, as well as larger species by an ‘induced fit’ mechanism.
Our expectations are that we will witness advances in the near future in the experimental examination of some of these structures that may open the way for their further practical applications. We consider a further natural step to be the examination of inclusion complexes of LR-CDs. For the first time inclusion complexes of some lower-size LR-CDs were examined computationally, namely, complexes of CDn (n = 13, 14, 26) with adamantane, and they revealed interesting differences in the behavior of the three macrorings when a substrate molecule is included in the cavity.51
Acknowledgements
The financial support is from the National Science Fund within the project TK01/0167. CPU-hours grants from HPC-Europa2 (RII3-CT-2003-506079), RNF01/0110 (NSF-Bulgaria) and HPC-SEE projects, as well as stimulating discussions with partners in the COST action CM1005 are also acknowledged.References
- W. Saenger, J. Jacob, K. Gessler, T. Steiner, D. Hoffmann, H. Sanbe, K. Koizumi, S. M. Smith and T. Takaha, Chem. Rev., 1998, 98, 1787 CrossRef CAS PubMed.
- K. L. Larsen, J. Inclusion Phenom. Macrocyclic Chem., 2002, 43, 1 CrossRef CAS.
- T. Endo and H. Ueda, J. Pharm. Sci., 2004, 29, 27 CAS.
- H. Ueda and T. Endo, in Cyclodextrins and Their Complexes. Chemistry, Analytical Methods, Applications, ed. H. Dodziuk, Wiley-VCH, Weinheim, 2006, pp. 370–380 Search PubMed.
- T. Endo, Trends Glycosci. Glycotechnol., 2011, 23, 79 CrossRef CAS.
- H. Ueda, J. Inclusion Phenom. Macrocyclic Chem., 2002, 44, 53 CrossRef CAS.
- S. Motohama, E. Ishii, T. Endo, H. Nagase, H. Ueda, T. Takaha and S. Okada, Hayastani Kensabanakan Handes, 2001, 53, 27 CAS.
- H. Ueda, M. Wakisaka, H. Nagase, T. Takaha and S. Okada, J. Inclusion Phenom. Macrocyclic Chem., 2002, 44, 403 CrossRef CAS.
- H. Taira, H. Nagase, T. Endo and H. Ueda, J. Inclusion Phenom. Macrocyclic Chem., 2006, 56, 23 CrossRef CAS.
- M. Zheng, T. Endo and W. Zimmermann, J. Inclusion Phenom. Macrocyclic Chem., 2002, 44, 387 CrossRef CAS.
- T. Endo, M. Zheng and W. Zimmermann, Aust. J. Chem., 2002, 55, 39 CrossRef CAS.
- Q. Qi, X. She, T. Endo and W. Zimmermann, Tetrahedron, 2004, 60, 799 CrossRef CAS PubMed.
- T. Endo, H. Ueda, S. Kobayashi and T. Nagai, Carbohydr. Res., 1995, 269, 369 CrossRef CAS.
- H. Ueda, T. Endo, H. Nagase, S. Kobayashi and T. Nagai, J. Inclusion Phenom. Macrocyclic Chem., 1996, 25, 17 CrossRef CAS.
- K. L. Larsen, F. Mathiesen and W. Zimmermann, Carbohydr. Res., 1997, 298, 59 CrossRef CAS.
- M. A. Villiers, C. R. Acad. Sci., 1891, 112, 536 Search PubMed.
- D. French, A. O. Pulley, J. A. Effenberger, M. A. Rougvie and M. Abdullah, Arch. Biochem. Biophys., 1965, 111, 153 CrossRef CAS.
- S. Kobayashi, M. Fukuda, M. Monma, T. Harumi and M. Kubo, Abstracts of Papers, the Annual Meeting of the Agricultural Chemical Society of Japan, Kyoto, April 1986, p. 649 (in Japanese).
- T. Fujiwara, N. Tanaka and S. Kobayashi, Chem. Lett., 1990, 739 CrossRef CAS.
- J. Jacob, K. Gessler, D. Hoffmann, H. Sanbe, K. Koizumi, S. M. Smith, T. Takaha and W. Saenger, Angew. Chem., Int. Ed., 1998, 37, 606 CrossRef CAS.
- J. Jacob, K. Gessler, D. Hoffmann, H. Sanbe, K. Koizumi, S. M. Smith, T. Takaha and W. Saenger, Carbohydr. Res., 1999, 322, 228 CrossRef CAS.
- K. Imamura, O. Nimz, J. Jacob, D. Myles, S. A. Mason, S. Kitamura, T. Aree and W. Saenger, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 833 CAS.
- K. Gessler, I. Uson, T. Takaha, N. Krauss, S. M. Smith, S. Okada, G. M. Sheldrick and W. Saenger, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 4246 CrossRef CAS.
- O. Nimz, K. Gessler, I. Uson and W. Saenger, Carbohydr. Res., 2001, 336, 141 CrossRef CAS.
- O. Nimz, K. Gessler, I. Uson, S. Laettig, H. Welfle, G. M. Sheldrick and W. Saenger, Carbohydr. Res., 2003, 338, 977 CrossRef CAS.
- M. Wakao, K. Fukase and S. Kusumoto, J. Org. Chem., 2002, 67, 8182 CrossRef CAS PubMed.
- K. Teranishi, T. Nishiguchi and H. Ueda, Carbohydr. Res., 2003, 338, 987 CrossRef CAS.
- K. Harata, in Cyclodextrins and Their Complexes. Chemistry, Analytical Methods, Applications, ed. H. Dodziuk, Wiley-VCH, Weinheim, 2006, pp. 147–198 Search PubMed.
- G. Bettinetti and M. Sorrenti, Thermochim. Acta, 2002, 385, 63 CrossRef CAS.
- Y. Terada, M. Yanase, H. Takata, T. Takaha and S. Okada, J. Biol. Chem., 1997, 272, 15729 CrossRef CAS PubMed.
- T. Takaha, M. Yanase, H. Takata, S. Okada and S. M. Smith, J. Biol. Chem., 1996, 271, 2902 CrossRef CAS PubMed.
- K. Tomono, A. Mugishima, T. Suzuki, H. Goto, H. Ueda, T. Nagai and J. Watanabe, J. Inclusion Phenom. Macrocyclic Chem., 2002, 44, 267 CrossRef CAS.
- S. Machida, S. Ogawa, S. Xiaohua, T. Takaha, K. Fujii and K. Hayashi, FEBS Lett., 2000, 486, 131 CrossRef CAS.
- T. Furuishi, T. Endo, H. Nagase, H. Ueda and T. Nagai, Chem. Pharm. Bull., 1998, 46, 1658 CrossRef CAS.
- H. Dodziuk, A. Ejchart, W. Anczewski, H. Ueda, E. Krinichnaya, G. Dolgonos and W. Kutner, Chem. Commun., 2003, 986 RSC.
- F. Ellouze, N. Ben Amar, A. Deratani and W. Zimmermann, Fractionation and separation of cyclodextrins by membrane processes, Results presented at the 15th International Cyclodextrin Symposium, O12, Vienna, Austria, May 9–12, 2010 Search PubMed.
- J. Wang, A. Jiao, Y. Tian, X. Xu, Z. Jin and Y. Li, J. Chromatogr. A, 2011, 1218, 863 CrossRef CAS PubMed.
- S. Toita, N. Morimoto and K. Akiyoshim, Biomacromolecules, 2010, 11, 397 CrossRef CAS PubMed.
- P. M. Ivanov and C. Jaime, J. Phys. Chem. B, 2004, 108, 6261 CrossRef CAS PubMed.
- P. M. Ivanov, M. G. Gotsev and C. Jaime, Bulg. Chem. Commun., 2005, 37, 380 CAS.
- M. G. Gotsev, P. M. Ivanov and C. Jaime, Chirality, 2007, 19, 203 CrossRef CAS PubMed.
- M. G. Gotsev and P. M. Ivanov, Int. J. Quantum Chem., 2007, 107, 1657 CrossRef CAS.
- I. Maestre, I. Bea, P. M. Ivanov and C. Jaime, Theor. Chem. Acc., 2007, 117, 85 CrossRef CAS.
- M. G. Gotsev and P. M. Ivanov, ARKIVOC, 2007,(xiii), 167 CrossRef CAS.
- M. G. Gotsev and P. M. Ivanov, J. Phys. Chem. B, 2009, 113, 5752 CrossRef CAS PubMed.
- P. M. Ivanov, J. Phys. Chem. B, 2010, 114, 2650 CrossRef CAS PubMed.
- P. M. Ivanov, Chirality, 2011, 23, 628 CrossRef CAS PubMed.
- P. M. Ivanov, J. Mol. Struct., 2012, 1009, 3 CrossRef CAS PubMed.
- P. M. Ivanov, Nanoscience&Nanotechnology – Nanostructured materials – Application and Innovation Transfer, ed. E. Balabanova and I. Dragieva, 2011, issue 11, p. 14 Search PubMed.
- P. Ivanov, Curr. Phys. Chem., 2012, 2, 413 CrossRef CAS.
- P. Ivanov, E. Atanassov and C. Jaime, J. Mol. Struct., 2014, 1056–1057, 238 CrossRef CAS PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossvary, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. Brozell, T. Steinbrecher, H. Gohlke, L. Yang, C. Tan, J. Mongan, V. Hornak, G. Cui, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin and P. A. Kollman, AMBER 10. University of California, San Francisco, 2008 Search PubMed.
- D. A. Case, T. A. Darden, T. E. Cheatham III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, M. Crowley, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, B. Wang, S. Hayik, A. Roitberg, G. Seabra, I. Kolossvary, K. F. Wong, F. Paesani, J. Vanicek, X. Wu, S. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollman, AMBER 11, University of California, San Francisco, 2010 Search PubMed.
- K. N. Kirschner, A. B. Yongye, S. M. Tschampel, J. González-Outeiriño, C. R. Daniels, B. L. Foley and R. J. Woods, J. Comput. Chem., 2007, 29, 622 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS PubMed.
- C. Sagui and T. A. Darden, in Simulation and Theory of Electrostatic Interactions in Solution, ed. L. R. Pratt and G. Hummer, American Institute of Physics, Melville NY, 1999, pp. 104–113 Search PubMed.
- A. Toukmaji, C. Sagui, J. Board and T. Darden, J. Chem. Phys., 2000, 113, 10913 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS PubMed.
- A. E. García, Phys. Rev. Lett., 1992, 68, 2696 CrossRef.
- A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Proteins, 1993, 17, 412 CrossRef CAS PubMed.
- A. Amadei, A. B. M. Linssen, B. L. De Groot, D. M. F. van Aalten and H. J. C. Berendsen, J. Biomol. Struct. Dyn., 1996, 13, 615 CAS.
- S. T. Wlodek, T. W. Clark, L. R. Scott and J. A. McCammon, J. Am. Chem. Soc., 1997, 119, 9513 CrossRef CAS.
- E. C. Sherer, S. A. Harris, R. Soliva, M. Orozco and C. A. Laughton, J. Am. Chem. Soc., 1999, 121, 5981 CrossRef CAS.
- K. Tai, Biophys. Chem., 2004, 107, 213 CrossRef CAS PubMed.
- L. I. Smith, A Tutorial on Principal Component Analysis, February 26, 2002, http://www.cs.otago.ac.nz/cosc453/student_tutorials/principal_components.pdf Search PubMed.
- B. Alakent, P. Doruker and M. C. Camurdan, J. Chem. Phys., 2004, 121, 4759 CrossRef CAS PubMed.
- A. Perez, J. R. Blas, M. Rueda, J. M. Lopez-Bes, X. De La Cruz and M. Orozco, J. Chem. Theory Comput., 2005, 1, 790 CrossRef CAS.
- I. Daidone, M. D'Abramo, A. Di Nola and A. Amadei, J. Am. Chem. Soc., 2005, 127, 14825 CrossRef CAS PubMed.
- T. Meyer, C. Ferrer-Costa, A. Perez, M. Rueda, A. Bidon-Chanal, F. J. Luque, C. A. Laughton and M. Orozco, J. Chem. Theor. Comput., 2006, 2, 251 CrossRef CAS.
- H. Lou and R. I. Cukier, J. Phys. Chem. B, 2006, 110, 12796 CrossRef CAS PubMed.
- C. A. Laughton, M. Orozco and W. Vranken, in Science and Supercomputing in Europe – Report 2007, ed. P. Alberigo, G. Erbacci, F. Garofalo and S. Monfardini, CINECA Consorzio Interuniversitario, 2007, p. 753 Search PubMed.
- A. Altis, P. H. Nguyen, R. Hegger and G. Stock, J. Chem. Phys., 2007, 126, 244111 CrossRef PubMed.
- A. Altis, M. Otten, P. H. Nguyen, R. Hegger and G. Stock, J. Chem. Phys., 2008, 128, 245102 CrossRef PubMed.
- M. A. Balsera, W. Wriggers, Y. Oono and K. Schulten, J. Phys. Chem., 1996, 100, 2567 CrossRef CAS.
- O. F. Lange and H. Grubmüller, J. Phys. Chem. B, 2006, 110, 22842 CrossRef CAS PubMed.
- A. Das and C. Mukhopadhyay, J. Chem. Phys., 2007, 127, 165103 CrossRef PubMed.
- F. J. Luque and M. Orozco, PCA Suite: Software Package for Lossy Trajectory Compression Using Principle Component Analysis Techniques, http://mmb.pcb.ub.es/software/pcasuite.html Search PubMed.
- P. M. Ivanov and C. Jaime, Science and Supercomputing in Europe (Research Highlights 2011), HPC-Europa2, Pan-European Research Infrastructure on High-Performance Computing for the 21st century Science, ed. S. Monfardini, CINECA Consorzio Interuniversitario, 2011, p. 16 Search PubMed.
- S. Kitamura and T. Kuge, Food Hydrocolloids, 1989, 3, 313 CrossRef CAS.
- T. Norisuye, Food Hydrocolloids, 1996, 10, 109 CrossRef CAS.
- M. E. Heineck, M. B. Cardoso, F. C. Giacomelli and N. P. Da Silveira, Polymer, 2008, 49, 4386 CrossRef CAS PubMed.
- N. W. H. Cheetham and L. Tao, Starch/Stärke, 1997, 49, 407 CrossRef CAS.
- F. A. Momany and J. L. Willett, Biopolymers, 2002, 63, 99 CrossRef CAS PubMed.
- T. Sakajiri, T. Kikuchi, I. Simon, K. Uchida, T. Yamamura, T. Ishii and H. Yajima, J. Mol. Struct., 2006, 764, 133 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Animated eigenvectors, rms curves, moments of inertia, radius of gyration, variation of flip angles, fluctuations of atomic coordinates, averaged for each residue. See DOI: 10.1039/c4ob02218a |
| This journal is © The Royal Society of Chemistry 2015 |