Highly ordered 2D microgel arrays: compression versus self-assembly

Abstract

Monolayers of micro- and nanoparticles at fluid interfaces are a key component in a variety of applications, ranging from particle lithography to stabilizers in foams or emulsions. In addition to commonly used “hard” colloids, soft polymeric particles like microgels are attracting increasing attention due to their potential in the fabrication of tailored and responsive assemblies. In particular, regular hexagonal arrays of microgels have been previously deposited after assembly at a fluid interface. While the arrangement cannot be easily controlled after adsorption and self-assembly from the bulk phase, specific structures can be achieved by compressing an interfacial microgel monolayer spread in a Langmuir trough and by transferring it onto substrates at distinct compression states. The degree of ordering after compression surpasses the one that is reached after self-assembly from the bulk and is, in general, independent from the presence of charges and different microgel morphologies. As a consequence, by monitoring the surface pressure during compression it is possible to produce highly ordered microgel arrays where the interparticle distance can be systematically and externally controlled.

---

Introduction

Particle-laden fluid interfaces have been used in research and industry since Pickering and Ramsden discovered that solid particles can be used to provide long-term stability against coalescence in emulsions.^1,2 Since then, great effort has been taken to investigate the properties of such particle-covered interfaces, ranging from interfacial rheology to particle arrangement.³

Soft polymeric particles, like microgels, also assemble at oil–water and air–water interfaces and lower significantly the interfacial tension.⁴ Furthermore, compared to hard particles, they have additional properties at the interface due to their soft and deformable nature.^5–9 For instance, it has been observed that microgels deform when adsorbed at the surface of emulsion droplets and that enhanced emulsion stability is a direct consequence of the deformability of the microgels at the interface.¹⁰ However, the degree of deformation after adsorption at flat interfaces is not influenced by the presence of charges in the bulk phase.¹¹ Microgel-coated droplets of opposite charge do not coalesce,¹² and charged microgels are less resistant to compression than uncharged ones.¹³ All these unexpected features highlight the difference between microgels and hard particles and indicate ample possibilities to employ the former for novel materials at interfaces or membranes.^8,9,14

In particular, the high affinity of microgels to accumulate at liquid interfaces and their responsiveness to external stimuli (e.g. temperature or pH) indicate that they have high potential to outperform hard particles in terms of surface patterning through self-assembly at interfaces. Previous studies have in fact shown that solid particles can be assembled into regular close-packed and non-close-packed arrays at liquid–liquid interfaces, which can be subsequently deposited onto solid substrates and used as lithography masks.^15–17

Microgels have also been shown to form very regular patterns on solid substrates when they are assembled from a drying droplet or by spin-coating^18–22 and can also be subsequently patterned into more complex structures by micro-contact printing.²³ Microgel arrays find use in a vast range of applications,²⁴ including microlens arrays,²⁵ interferometers,²⁶ biosensing²⁷ and substrates for cell culture.²⁸ In all of these applications it is very important to be able to tune, in addition to the microgel size, the separation between different microgels on the substrate to achieve complete control on the material structure. Different packing densities of microgels on the surface have been demonstrated using a range of different approaches, e.g. by drying droplets of different concentrations^19,29 or using different drying procedures or substrates.²¹ Extraordinary long range ordering was also achieved by facilitating the spreading of microgels on solid substrates by the addition of alcohol.²⁰ Different spacing between particles could be reached when they were covered with polymer shells of different thicknesses.^16,22,30 Finally, the rotation speed during spin-coating was also found to influence the microgel arrangement.¹⁸

All these methods have the disadvantage that, even though different packing densities can be achieved by concentration variations, one cannot control directly and externally the number of microgels at the interface (i.e. the surface concentration); in these methods the bulk microgel concentration is tuned to control interfacial assembly. Furthermore, adsorption from the bulk and drying can lead to local concentration gradients at the interface and thus affect the final structure. It is therefore desirable to develop a method that enables the possibility to produce monolayers with an externally tunable particle content and separation.

First attempts to achieve the ambitious goal to produce highly ordered interfacial monolayers of soft particles have been made using a Langmuir trough, where surface concentration and pressure can be monitored in situ. The particles can then be transferred to a substrate at a given surface pressure for subsequent production of two-dimensional particle arrays with a desired inter-particle distance. For example, different phases of polymer-covered gold particles could be produced at different surface pressures of a monolayer at the air–water interface³⁰ and the particle distance could be controlled by the surface pressure of the respective particle layer at the fluid interface. In a similar way, soft oxazoline-functionalized poly(methyl methacrylate) microgels have been assembled at the air–water interface and regular arrangement was imaged using Atomic Force Microscopy (AFM).³¹

Here, we report the direct assembly of soft microgel particles in highly ordered arrays. Two methods for producing these arrays from microgel-covered interfaces were used. In a first set of experiments, we examined microgels at the oil–water interface that self-assembled from the aqueous sub-phase without external compression. The local structure of the microgels was investigated by Freeze-Fracture Shadow-Casting cryogenic Scanning Electron Microscopy (FreSCa cryo-SEM).^32,33 Secondly, a defined amount of microgels was spread directly at the oil–water interface to form a monolayer of particles in a Langmuir trough. The particle layer was transferred onto solid substrates using the Langmuir–Blodgett method and the microgel arrangement arising from different degrees of compression was investigated by AFM.

By comparing the microstructure of the deposited microgel arrays with the in situ measurements by FreSCa cryo-SEM we demonstrate that the two methods yield the same results, i.e. clear hexagonal ordering that does not depend on the pH. However, compression and deposition lead to a higher control on the final structure. Finally, we show that the local inter-particle separation depends solely on the local concentration (and thus surface pressure) at the interface, irrespective of the assembly method. Thus, we demonstrate that controlled interfacial microgel assemblies can be produced and deposited from liquid interfaces.

Results

Adsorption and self-assembly from the bulk phase

The microgels contain N-isopropylacrylamide (NiPAm) as the main monomer and methacrylic acid (MAA) as a comonomer, inducing pH-sensitivity. They are uncharged at low pH and charged at high pH due to the deprotonation of the acidic groups. The swelling of the microgels at higher charge density is due to the osmotic pressure and illustrated in the insets in Fig. 1. Additionally, we used a second microgel where a pure PNiPAm shell surrounds the P(NiPAm-co-MAA) core. This leads to restricted swelling of the core even in the charged state. For both particle morphologies, the distribution of the crosslinker is not homogenous but decreases toward the periphery of the microgel.³⁴

Fig. 1 Images of microgel particles at the water–heptane interface (seen from the heptane side) after fracturing. Hexagonal ordering can be observed in all cases: (a) uncharged core microgel at pH 3; (b) charged core microgel at pH 9; (c) uncharged core–shell microgel at pH 3; (d) charged core–shell microgel at pH 9.

Fig. 1 shows an example of FreSCa cryo-SEM images of the two microgel types at the oil–water interface in the uncharged and in the charged state. Local ordering with hexagonal symmetry can be observed for all samples.

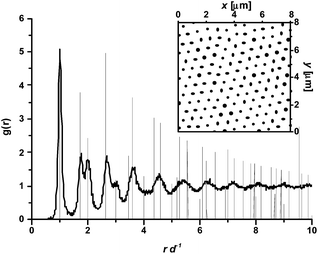
As detailed in the Methods section, the coordinates of each particle's center can be identified in every image and used to measure several structural parameters. In addition to the local surface concentration obtained by counting the number of particles per unit area (N_p μm⁻²), the radial distribution function g(r) can be calculated. g(r) identifies the probability of finding a particle at a distance r from a given particle at the interface; peaks in the distribution indicate preferred distances and are a signature of order in the interface microstructure. An example of a radial distribution function of charged core–shell microgel particles at the water–heptane interface is given in Fig. 2. Several peaks are found, which imply the extension of structural order over several particle diameters. Moreover, the position of the peaks corresponds to the position of the peaks in the g(r) of an ideal hexagonally packed monolayer, identifying the local packing as hexagonal, at least at short range.

Fig. 2 Example of a radial distribution function of charged core–shell microgel particles at the oil–water interface; d is the microgel diameter at the interface. Solid vertical lines indicate the peaks of g(r) of an ideal hexagonally packed monolayer generated numerically. The inset highlights the centers of the particles as found from the automated particle location procedure.

Spontaneous adsorption and self-assembly can therefore produce uniform monolayers with local hexagonal order in the microgel layers. The method is appealing for its extreme simplicity, but as evidenced in the FreSCa cryo-SEM images of Fig. 1, the global structure cannot be controlled and, as a consequence, mostly locally ordered patches are found. Similar to what has been shown for microgel-covered emulsion droplets,³⁵ non-uniform coverage of the oil–water interface can be observed in some images that is due to sample preparation (Fig. S1†). Measurements of the dynamic interfacial tension (Table S1†) show that the surface coverage at the interface is far from the steady state at the time where samples for FreSCa cryo-SEM are vitrified, implying that freezing and thus imaging may take place before microgel assembly reaches the steady state. Larger waiting times between sample loading and freezing may increase the degree of ordering, allowing the microgels to move and rearrange at interface after adsorption.^5,6,36 A further drawback of FreSCa cryo-SEM is that the separation between the microgels at the interface cannot be directly controlled, but depends on external parameters like bulk particle concentration and adsorption time, but also on uncontrolled applied shear or local concentration gradients (refer to the ESI† for more detailed discussion).

Systematic assembly under compression

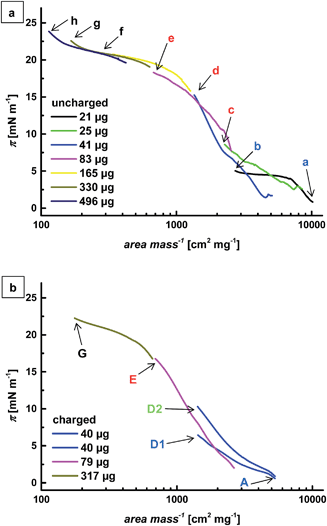
In order to overcome these limitations and produce directly tunable, highly ordered microgel arrays we chose a second route. We have performed Langmuir–Blodgett experiments where the compression of the monolayer was accompanied by deposition of the particles at controlled surface pressures. The microgel layer was transferred onto silicon wafers and the deposited samples were then analyzed by AFM.

We have already shown that charges influence the behavior of a microgel monolayer under compression. The compression isotherms showed the same trend in the uncharged and in the charged state, where counter-intuitively an increase in surface pressure was observed at lower area per particle when charges were present in the microgel.¹³ As this phenomenon is more pronounced for the core microgel, only this particle type was investigated with the Langmuir–Blodgett technique.

The compression isotherms of the core microgel layer in the uncharged and in the charged state are shown in Fig. 3. Given the dimensions of the deposition trough, it was not possible to explore the whole compression isotherm in one single experiment. Different amounts of microgels were thus placed at the interface and the resulting isotherms were normalized to the applied amount. The surface pressure is shown as a function of the specific area and increases with increasing compression (i.e. with decreasing area per microgel). The absence of full overlap between the different segments may be due to variations in the number of microgels actually confined at the interface after spreading (a small percentage of the particles may fall into the bulk during spreading and/or compression). In this context it is worth noticing that similar amounts of nominally spread microgels can lead to varying surface pressures and thus microgel arrangements (Fig. 3b, points D1 and D2).

Fig. 3 Compression isotherms of the (a) uncharged and (b) charged core microgel. The points where the microgel monolayer was transferred to a solid substrate are indicated by arrows. The same letters indicate similar amounts of spread microgels and the differently colored letters mark different particle arrangements. Blue: random. Green: hexagonal packing with voids. Red: hexagonal packing. Black: close hexagonal packing.

Compression of a low amount of particles leads to a small increase in surface pressure. When more microgels are placed at the interface, the surface pressure rises more steeply until a plateau is formed at high interfacial coverage. In the case of the uncharged microgel, a second rise can be anticipated at high concentration, similar to what has been observed earlier in a different setup.¹³

Fig. 4 shows the AFM images of the transferred microgel monolayer in the uncharged state at the points indicated in Fig. 3a. The particle density increases with the amount of microgel at the interface from images 4(a)–(h). The particles are distributed randomly at the interface at low concentrations (Fig. 4a and b), corresponding to a low surface pressure. In any case the underlying presence of repulsive forces can be inferred by the absence of aggregation and the presence of a minimum separation between neighboring particles. The microgels start to interact when the amount of spread microgels is increased. As soon as interactions are present, the formation of local hexagonal microgel arrays is favored over the formation of e.g. clusters or random close packing (Fig. 4c–e). This leads to the conclusion that soft repulsive interactions are present and govern the arrangement. By further increase of the microgel concentration, the packing becomes tighter until the microgels are squeezed together at high loading (Fig. 4f and g). At high concentrations, the interface is fully covered and further squeezing of the microgel particles is not possible. This leads to a monolayer collapse through buckling of the interface or the formation of multilayers. This can be inferred by the long-wavelength height modulations in Fig. 4h.

Fig. 4 AFM images of the transferred microgel monolayer in the uncharged state at the points indicated in Fig. 3a. The particle density increases from a to h. Insets in images f, g and h show higher magnifications of the microgel arrangement.

An analogous behavior is observed for the charged microgels, where the degree of ordering in the particle layer also increases with particle concentration (Fig. 5). The particles are separated at low concentrations (Fig. 5A and D1). With increasing compression, the transition between random and hexagonal ordering can be observed (Fig. 5D2) where areas with close hexagonal packing are separated by voids. The particles are close enough to adopt an ordered structure, but the interface is still not completely covered with microgels. The structure of D1 and D2 is similar to what has been observed for microgels directly deposited on the interface from bulk, where hexagonal packing coexists with random particle arrangement (Fig. S1†). A complete hexagonal array is formed as soon as the whole interface is covered by microgels (Fig. 5E). At high concentration a close packing of the microgels is observed (Fig. 5G).

Fig. 5 AFM images of the transferred microgel monolayer in the charged state at the points indicated in Fig. 3b. The inset in G shows higher magnification of close packed microgels. The increasing ordering is represented by clearer oscillations in the radial distribution functions corresponding to images A and G. Each graph reports radial distribution functions from images at three different spots on the same substrate (red, green and black lines).

The position of particles in the AFM images was also analyzed to calculate the radial distribution functions. Examples are given in Fig. 5, while the remaining functions are shown in Fig. S2 and S3.† The various g(r) at different surface pressures mirror the qualitative trend reported above. At low surface pressure and high area per particle, no clear oscillations can be observed in g(r) (Fig. 5). Only a first peak is clearly visible corresponding to the existence of a well-defined separation between particles. The shape of g(r) is similar to the one obtained by the random deposition of repulsive (charged) particles.³⁷ With increasing surface pressure, particles are pushed together and form regular structures. Correspondingly, the oscillations in g(r) become clearer, indicating a higher degree of ordering. In particular, clear hexagonal ordering (also indicated by the splitting of the second and third peak of g(r), see ESI†) is present at intermediate surface pressures. At the highest surface pressures, where the particles are closely packed, the material is polycrystalline, but retains local hexagonal order. A comparison with microgel deposition from dried droplets (Fig. S4 and S5†) also reveals the increased ordering in the case of the deposition after compression and the relative simplicity and efficiency of producing regular microgel monolayers using the LB-technique.

Discussion

As evident from Fig. 4 and 5, the particle distance at the substrates decreases with increasing compression while the particle arrangement changes from random to highly ordered. We can thus compare different characteristic areas in the isotherms where the particle arrangement changes significantly. This is indicated by the different colors of the letters in Fig. 3.

Blue area

The particles do not show any ordered arrangement but adsorb to the interface randomly. There exists a minimum separation distance between the particles that is much larger than the particle size.

Green area

The particles start to arrange hexagonally, but patches of particles are separated by voids. This arrangement marks the transition between a random and a hexagonal structure. It shows that it is not necessary for the interface to be covered completely with particles to achieve hexagonal arrangement.

Red area

The interface is completely covered with microgels that form a hexagonal pattern. With increasing particle concentration, the distance between the particles decreases. This leads to the conclusion that the interaction causing the particle arrangement can be overcome by compression and higher particle concentration.

Black area

A close arrangement of microgels is reached. The particles are compressed against each other and the particle distance equals their size.

 

Additional quantifiers can be extracted from the images to describe further the structure of the interface. The nearest neighbor distance (D) between particles at the interface is identified by the position of the first peak of g(r).

A plot of the mean nearest neighbor distance against the surface pressure (Fig. 6) reveals that the distance decreases with increasing surface pressure. The higher the surface pressure, the closer the particles are squeezed together. At low surface pressures the particles can move freely within the interface and maintain a high distance to each other. When the surface pressure increases, the particles are squeezed together and the distance between them decreases rapidly. At high compression, a plateau in surface pressure and interparticle distance is reached corresponding to the occurrence of very dense packing and monolayer collapse.

Fig. 6 Mean nearest neighbor distance as a function of the surface pressure. D was determined from the position of the first peak in the g(r) functions corresponding to the AFM images in Fig. 4 and 5. Error bars represent the standard deviation and were calculated from the full width of half maximum of a Gauss fit on the first oscillation of g(r).

Now that we have discussed the arrangement at different surface pressures after transferring the microgel monolayer to solid substrates, we turn to compare these results to the ones obtained from FreSCa cryo-SEM measurements. Fig. 6 shows that there is a direct correlation between the nearest neighbor distance and the surface pressure at which the monolayer was transferred to the substrate. Turning our attention to the FreSCa micrographs and the corresponding g(r) functions, we have already commented on the fact that the adsorption and thus the particle distance cannot be controlled directly while the microgels assemble at the interface from the bulk phase. Nevertheless, the local nearest neighbor distance from the FreSCa images can be analyzed and compared to the nearest neighbor distance from the AFM images.

The results of this comparison as a function of the local particle density are shown in Fig. 7. Additionally, the compression isotherms of Fig. 3 were converted to particles per area (as measured from the corresponding AFM images) and included in the graphic to highlight the different degrees of compression corresponding to the observed inter-particle separation. This plot emphasizes that closer distances are achieved at higher microgel loading. This is valid for both assembly methods, self-assembly (FreSCa) and directed assembly (Langmuir trough and subsequent AFM); in both cases the dependence of the particle distance versus microgel concentration at the interface follows the simple scaling of a soft repulsive hexagonal lattice (x^−1/2).¹⁵ Images with random arrangement were also analyzed and included for comparison (grey rectangle in Fig. 7). It is obvious that those data do not follow this simple scaling rule. Furthermore, there is no clear difference detectable for microgels in the charged and in the uncharged state. This is in contrast to recent results where charges increase the particle distance at the surface of microgel-covered oil droplets, as measured in situ using confocal microscopy.³⁶ This discrepancy to our results further underlines the sensitivity of microgel-covered interfaces and shows that sample preparation and slight changes in the investigated system can influence the outcome of the experiments to a large extent.

Fig. 7 Nearest neighbor distance plotted versus particle density as extracted from FreSCa cryo-SEM (filled squares) and AFM images (open triangles). Green: uncharged core microgels; blue: charged core microgels; black: uncharged core–shell microgels; red: charged core–shell microgels. Compression isotherms of the uncharged (green) and the charged (blue) core microgels are also shown. The grey rectangle marks random particle arrangement and the black line shows the x^−1/2 relation between D and N_p per area.

In contrast to the Langmuir trough deposition followed by AFM measurements, FreSCa images were taken not only of the core but also of the core–shell microgel, and the corresponding interparticle distances are also included in Fig. 7. This allows a comparison of arrangement of the different microgel morphologies after spontaneous adsorption to the interface. A higher number of particles per area is found for the core particles compared to the core–shell microgels that can be attributed to the smaller size of the core particles. However, a normalization of the data to the microgel size at the interface shows that both microgel types reach area fractions close to 1 after spontaneous adsorption (Fig. S6†) and no significant difference in the interfacial coverage of the core and the core–shell microgel can be detected.

Microgels deform at the interface after adsorption and appear in a flattened shape, with the loosely crosslinked corona being spread out at the interface to produce a high interfacial coverage with polymer segments.^10,11 This is reflected in the lower particle density of the interface after self-assembly from the bulk (squares in Fig. 7) compared to the compressed microgels after assembly in a Langmuir trough (triangles in Fig. 7). The interparticle distance is strongly reduced under compression, corresponding to an increasing surface pressure. The surface pressure reaches a plateau when the microgels cannot be compressed further.

Additional evidence of the compressed nature of microgels after deposition on a solid substrate can be gathered by calculating the area fraction φ that is occupied by microgels as reported in Fig. S6.† The area fraction is calculated assuming the size of the uncompressed microgels at a flat oil–water interface as previously determined from FreSCa cryo-SEM micrographs.¹¹ As also evidenced in Fig. 8, which shows the hexagonal order parameter ξ₆ as a function of area fraction, very high values of φ beyond 1 are obtained, implying a strong compression of the microgels at the interface at the highest values of surface pressure. Even though the actual size of the microgels in the AFM images after exposure to the oil phase and drying may not correspond to their hydrated size at the interface (a comparison of the size on the substrate with the hydrodynamic diameter measured in bulk shows that the microgels are indeed collapsed on the substrate – see the Methods section), from the AFM images in Fig. 4 and 5 it can still be noticed that when the microgels come into contact, their size, measured after deposition, decreases as they are compressed against each other.

Fig. 8 Hexagonal order parameter ξ₆ as a function of the area fraction φ for the core and the core–shell microgel after self-assembly (imaging with FreSCa cryo-SEM, squares) and for the core microgel after directed assembly in a Langmuir trough (imaging with AFM, triangles). Uncharged (core: green; core–shell: black) as well as charged microgels (core: blue; core–shell: red) were used for both methods. Note the break in the abscissa.

In a recent paper, the size of microgels at the interface was compared to compression isotherms. Significant shrinking of the microgels was observed after compression as well as after spontaneous adsorption by comparison of the isotherms with measured microgel sizes resulting from cryo-SEM imaging and light scattering.³⁵ This evidence further supports the finding that the microgel size on the substrates in the dried state does not represent the real size at the interface.³⁸

Self-assembly (FreSCa images, Fig. 1) as well as directed assembly under compression (AFM images, Fig. 4 and 5) can produce microgel layers with high local order. The degree of structural order can be quantified by computing the hexagonal order parameter ξ₆ as a function of the area fraction (Fig. 8). Random arrangement results in an absolute value of ξ₆ ≈ 0.4; values of ξ₆ closer to 1 indicate higher ordering.

A higher area fraction (i.e. higher particle density) results in a higher ordering for both assembly methods and no clear difference can be found between the charged and the uncharged state of each microgel type. This leads to the conclusion that the ordering and the particle density do not depend strongly on electrostatic interactions. As mentioned in the Introduction, the behaviour of microgels at interfaces and of microgel-stabilized emulsions exhibits complex dependence on charge effects. For instance, oil droplets covered with oppositely charged microgels do not coalesce when they meet.¹² Moreover, counterintuitively, monolayers of charged microgels are more easily compressed than monolayers of uncharged microgels,¹³ emphasizing the minor role played by electrostatics compared to steric interactions and the interplay between the latter and the deformability and softness of the particles at the interface. Finally, the core–shell microgel produces slightly higher ordering after self-assembly at similar area fractions compared to the core microgel. This suggests that the presence of the PNiPAM shell has an effect on the particle arrangement at the interface.

The self-assembled microgels cover an area fraction between 0.25 and 1 with no preferred order. In contrast to that, the samples taken from the Langmuir trough show a steep increase of ξ₆ at an area fraction around 0.5 that indicates the transition from random to hexagonal order. The microgels assembled directly under compression show a high degree of ordering as soon as hexagonal order appears. Thus, a higher and more specific degree of ordering can be achieved after direct assembly in the Langmuir trough than after self-assembly from the bulk phase.

Interestingly, ξ₆ seems to decrease again when the close packing at high area fractions is reached for samples taken from the Langmuir trough (triangles around φ ≈ 8). This is due to the fact that upon strong compression smaller crystalline domains are formed which give lower values of ξ₆. From the AFM image in Fig. 4h we can assume that buckling occurs at high loading of the interface. This may lead to reduced measured crystalline order of the interfacial microgel layer.

Different groups have shown that the size of the polymeric layer influences the arrangement at interfaces. Polymers stretch at the oil–water interface to cover a maximum area^10,11,39,40 leading to an arrangement where the interparticle distance is influenced by the thickness of the polymeric layer.^16,22,30 Horecha et al. imaged ordered microgel arrays with AFM and could resolve the core-corona structure adopted by microgels at interfaces.⁴¹ It can thus be expected that the presence of a loosely cross-linked shell influences the arrangement at liquid interfaces and subsequently the imaged microgels on solid substrates. In the present study the corona was visible in the FreSCa cryo-SEM micrographs but not in the AFM images. The center-to-center distance is similar to the size of the corona in the former case and it is thus likely that the corona influences the particle distance. In the latter case, the center-to-center distance is not constant but decreases when the particles are compressed. It is therefore expected that the arrangement under compression is not mainly governed by the thickness of the polymeric shell. Otherwise, particle rearrangement, the formation of multilayers or increased presence of defects would be dominant instead of an ordered array with varying particle density. The influence of the corona can in this case be overcome by compression.

Experimental part

Materials

N-Heptane (Merck, 99%) and n-hexane (Sigma-Aldrich, 99%) were used as received. 0.1 M HCl and 0.1 M NaOH were used to adjust the pH and Milli-Q water at pH 3 or pH 9 was used as the subphase in the Langmuir trough measurements. The microgels were placed at the interface in a mixture of aqueous 1 wt% microgel dispersion (pH 3 or pH 9) with isopropyl alcohol (IPA, 99.8%, Merck) in a ratio of 5 : 1 (v/v).

Microgel synthesis and characterization

The microgel synthesis was performed by standard precipitation polymerization with a surfactant and has already been described in detail elsewhere.¹¹ An ALV-5000 instrument with light of 633 nm wavelength was used to determine the hydrodynamic diameter d_w of the microgels in bulk by dynamic light scattering (DLS). Sizes d_w = 276 ± 3 nm and d_w = 362 ± 4 nm were measured for the core microgel at pH 3 and pH 9, and d_w = 378 ± 9 and d_w = 400 ± 4 for the core–shell microgel at pH 3 and pH 9. Electrophoretic mobility was measured with a NANO ZS Zetasizer (Malvern Instruments, UK) to be −0.09 ± 0.01 × 10⁻⁸ m² V⁻¹ s⁻¹ at pH 3 and −0.70 ± 0.03 × 10⁻⁸ m² V⁻¹ s⁻¹ at pH 9 for the core microgel, and −0.05 ± 0.02 10⁻⁸ m² V⁻¹ s⁻¹ at pH 3 and −0.22 ± 0.02 10⁻⁸ m² V⁻¹ s⁻¹ at pH 9 for the core–shell microgel. The content of MAA in the microgels was determined by pH titration to 6.3 ± 0.6 wt% for the core microgel and 2.8 ± 0.5 wt% for the core–shell microgel. The interfacial tension data (reported in the ESI†) were acquired on a DSA100 (Krüss GmbH) with a pendant drop module. A drop of the microgel dispersion of 0.1 wt% was created in a cuvette filled with n-heptane. A video camera recorded the evolution of the drop shape with time. The calculation of the IFT was performed by image analysis with a drop shape analysis program supplied by the manufacturer. The diameter of the microgels at the interface determined from FreSCa cryo-SEM imaging is d_i = 559 ± 49 nm (pH 3) and d_i = 534 ± 14 nm (pH 9) for the core microgel and d_i = 642 ± 66 (pH 3) and d_i = 671 ± 22 nm (pH 9) for the core–shell microgel.¹¹ The area fraction for both assembly methods was calculated from the number of particles per area and the size of the microgels in the FreSCa cryo-SEM images (d_i). The size of the microgels at the AFM substrates was determined using the automatic particle tracking procedure implemented in ImageJ.⁴² The diameter of the core microgel on the substrate at pH 3 corresponding to the images in Fig. 4 is 262 ± 26 nm (a), 334 ± 38 nm (b), 270 ± 34 nm (c), 365 ± 33 nm (d), 254 ± 35 nm (e), 202 ± 9 nm (f), 172 ± 8 nm (g) and 142 ± 6 nm (h). The diameter at pH 9 corresponding to the images in Fig. 5 is 287 ± 42 nm (A), 253 ± 28 nm (D1), 266 ± 32 nm (D2), 222 ± 24 nm (E) and 202 ± 6 nm (G).

FreSCa cryo-SEM

The sample preparation for FreSCA cryo-SEM is described in detail elsewhere.^11,32 In brief, the aqueous microgel suspension (0.1 wt%) was placed inside a custom-made copper holder and a droplet of n-heptane was carefully placed on top to create the liquid–liquid interface. Then the holder was closed with a flat copper plate, vitrified in a liquid propane jet freezer (Bal-Tec/Leica JFD 030, Balzers/Vienna) and mounted under liquid nitrogen onto a double fracture cryo-stage. It was transferred under inert gas in a cryo-high vacuum airlock (<5 × 10⁻⁷ mbar Bal-Tec/Leica VCT010) to a pre-cooled freeze-fracture device at −140 °C (Bal-Tec/Leica BAF060 device) and then the samples were fractured and partially freeze-dried at −100 °C for 1 min. This was followed by unidirectional tungsten deposition at an elevation angle α = 30° to a total thickness δ = 2 nm at −120 °C and by additional 2 nm with a continuously varying angle between 90° and 30°. Freeze-fractured and metal-coated samples were then transferred for imaging under high vacuum (<5 × 10⁻⁷ mbar) at −120 °C to a pre-cooled (−120 °C) cryo-SEM (Zeiss Gemini 1530, Oberkochen) for imaging either with an in-lens or a secondary electron detector.

Image analysis

The center of particles in the FreSCa cryo-SEM and AFM images was located using the well-known Crocker and Grier⁴³ algorithm written in IDL (Exelis Visual Information Solutions), which is publicly available.⁴⁴ The radial distribution function and the order parameter ξ₆ are calculated with custom-written IDL routines. ξ₆ is a commonly used order parameter to detect the presence of hexagonal order in two-dimensional atomic or colloidal structures.^45,46 Its calculation proceeds via the identification of each particle's nearest neighbors using a triangulation algorithm. Once the nearest neighbors are identified, the absolute value of ξ₆ is calculated for each particle as

ξ₆ = 1/6〈∑_j|exp(i6θ_j)|〉, (1)

where θ_j is the angle between the selected particle and the j-th nearest neighbor. For perfect hexagonal ordering ξ₆ is 1 for each particle in the lattice; deviations from hexagonal ordering, including a number of nearest neighbors different from 6, lead to values smaller than one.

Langmuir trough measurements and deposition on substrates

Compression isotherms were recorded at room temperature with a home-made Langmuir trough. The trough is made from Teflon and is equipped with two movable Delrin barriers, a Wilhelmy balance with a Pt-plate and a dipping device. The compressible area between the barriers is 210 cm² and the plate is placed parallel to the barriers. The dipping arm does not disturb the interface during lifting due to the special shape of the trough. In a typical measurement, the lower part of the trough is filled with water at pH 3 or pH 9. A silicon wafer (cleaned by sonication in toluene and ethanol and plasma-hydrophilization) is mounted on the dipping arm and lowered into the subphase. The water–air interface is cleaned with a suction pump and the Wilhelmy plate is placed at the interface. Then n-hexane is added, the Wilhelmy balance is set to zero and the microgel-IPA solution is placed directly at the interface with a Hamilton syringe. The interface is left to equilibrate for 30 min before the compression starts. A velocity of 10 mm min⁻¹ is used for compression. At a trough area of 57 cm² the compression is stopped and the silicon substrate is lifted through the interface with a speed of 8.56 mm min⁻¹. Alterations of the layer during deposition were avoided by using hexane as oil and thus minimizing capillary forces and viscous drag during drying. Additionally, the substrate was moved at a slow speed to reduce flow effects and to ensure that it dries faster than the extraction speed (i.e. the samples dries immediately when pulled out of the hexane). After each measurement, the trough, the barriers and the Pt-plate were cleaned thoroughly with ethanol and large amounts of Milli-Q water.

AFM imaging

AFM height images were obtained by tapping mode AFM (DI Dimension 3000, Olympus AC240 Si tips, k = 48.9–58.8 N m⁻¹, scan size 15 × 15 μm², 512 × 512 pixel² acquired at 0.5 Hz) and the height was converted into a 256 bit grey scale for the particle location analysis.

Conclusions

In this paper we demonstrated that externally controlled microgel monolayers with a high degree of two-dimensional crystalline order can be prepared and deposited in a Langmuir trough. The results have also been compared to in situ inspection of monolayers of the same particles produced by spontaneous adsorption and self-assembly.

In general, we found that the two methods produced similar structures at the interface and that no significant differences in the interface microstructure are obtained using different microgel types and pH. Overall, spreading and compression lead to a much higher degree of control on the monolayer order and inter-particle spacing, with marked advantages from an application perspective. Furthermore, the presence of charges and different particle architecture did also not influence the assembled structures and in all cases the inter-particle separation versus area concentration followed the square-root law for a soft repulsive hexagonal lattice. In this case though, the main driving force for the soft repulsion does not come from electrostatics, but rather from the compressibility of the corona of the polymer surrounding the particles at the interface.¹³

Even though spontaneous adsorption is very attractive due to its simplicity, the interplay between particle mobility and interface microstructure implies that at high surface concentrations crystallization of the monolayer requires extended cooperative rearrangements of the particles.⁴⁷ Consequently, and due to slow relaxation of the interfacial tension and thus microgel arrangement, the structure observed by FreSCa cryo-SEM may not be the steady-state one. This obstacle is overcome by Langmuir–Blodgett deposition of microgel monolayers starting with a defined, uniform packing density that is slowly and uniformly increased by interface compression. Following the second approach, direct and systematic production of microgel arrays of different center-to-center distances is thus possible.

In summary, our results emphasize once more the differences in the preparation of Gibbs monolayers, where particles spontaneously adsorb in the presence of excess in the bulk, to Langmuir monolayers, where a fixed amount of particles is spread at the interface. In the former case, the microstructure of the interface is determined by the competition between the adsorption rate and the timescale for particle rearrangements at the interface; in the latter, it emerges as a balance between the compression rate and the rate of the particle rearrangements. The fact that the microgels are practically irreversibly trapped at the interface indicates that relaxation processes can only take place via particle mobility and interactions within the interface and not through an adsorption/desorption equilibrium. Both routes offer in principle the possibility to tune the microstructure of the interface, either by controlling the adsorption rate and bulk concentration in the Gibbs case, or by controlling the compression rate and the spread amount in the Langmuir case. Our results show that, in practice, the second route is much more effective for the fabrication of two-dimensional ordered microgel arrays, where the interparticle separation can be easily tuned by changing the surface pressure upon compression.

The deposition of controlled, large-area arrays of microgels could therefore pave the way for surface patterning and lithography after assembly at a fluid interface, similar to what has already been shown by using hard colloidal particles,¹⁵ but with far more potential stemming from the flexibility of the design and responsiveness of soft microgel particles.

Acknowledgements

We thank Marco-Philipp Schürings and Alexander Böker for measuring the AFM images of the dried microgel droplets. LI acknowledges the SNSF grants PZ00P2_142532/1 and PP00P2_144646/1 for financial support and the Electron Microscopy Centre of ETH Zurich (EMEZ) for technical support. KG and WR acknowledge financial support of the IDEA League and the Deutsche Forschungsgemeinschaft within the Sonderforschungsbereich SFB 985 “Functional Microgels and Microgel Systems”.

Notes and references

1. S. U. Pickering, J. Chem. Soc., Trans., 1907, 91, 2001–2021.
2. W. Ramsden, Proc. R. Soc. London, 1903, 72, 156–164.
3. R. Aveyard, B. P. Binks and J. H. Clint, Adv. Colloid Interface Sci., 2003, 100–102, 503–546.
4. J. Zhang and R. Pelton, Langmuir, 1999, 15, 8032–8036.
5. Y. Cohin, M. Fisson, K. Jourde, G. G. Fuller, N. Sanson, L. Talini and C. Monteux, Rheol. Acta, 2013, 52, 445–454.
6. Z. Li, K. Geisel, W. Richtering and T. Ngai, Soft Matter, 2013, 9, 9939–9946.
7. C. Monteux, C. Marliere, P. Paris, N. Pantoustier, N. Sanson and P. Perrin, Langmuir, 2010, 26, 13839–13846.
8. W. Richtering, Langmuir, 2012, 28, 17218–17229.
9. V. Schmitt and V. Ravaine, Curr. Opin. Colloid Interface Sci., 2013, 18, 532.
10. M. Destribats, V. Lapeyre, M. Wolfs, E. Sellier, F. Leal-Calderon, V. Ravaine and V. Schmitt, Soft Matter, 2011, 7, 7689–7698.
11. K. Geisel, L. Isa and W. Richtering, Langmuir, 2012, 28, 15770–15776.
12. T. Liu, S. Seiffert, J. Thiele, A. R. Abate, D. A. Weitz and W. Richtering, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 384–389.
13. K. Geisel, L. Isa and W. Richtering, Angew. Chem., Int. Ed., 2014, 126, 5005–5009.
14. D. Menne, F. Pitsch, J. E. Wong, A. Pich and M. Wessling, Angew. Chem., Int. Ed., 2014, 53, 5706–5710.
15. L. Isa, K. Kumar, M. Müller, J. Grolig, M. Textor and E. Reimhult, ACS Nano, 2010, 4, 5665–5670.
16. S. Ullrich, S. P. Scheeler, C. Pacholski, J. P. Spatz and S. Kudera, Part. Part. Syst. Charact., 2013, 30, 102–108.
17. N. Vogel, C. K. Weiss and K. Landfester, Soft Matter, 2012, 8, 4044–4061.
18. A. Burmistrova and R. v. Klitzing, J. Mater. Chem., 2010, 20, 3502–3507.
19. K. Horigome and D. Suzuki, Langmuir, 2012, 28, 12962–12970.
20. S. B. Quint and C. Pacholski, Soft Matter, 2011, 7, 3735.
21. S. Schmidt, T. Hellweg and R. v. Klitzing, Langmuir, 2008, 24, 12595–12602.
22. S. Tsuji and H. Kawaguchi, Langmuir, 2005, 21, 2434–2437.
23. J. Peng, D. Zhao, X. Tang, F. Tong, L. Guan, Y. Wang, M. Zhang and T. Cao, Langmuir, 2013, 29, 11809–11814.
24. G. R. Hendrickson, M. H. Smith, A. B. South and L. A. Lyon, Adv. Funct. Mater., 2010, 20, 1697–1712.
25. J. Kim, M. J. Serpe and L. A. Lyon, J. Am. Chem. Soc., 2004, 126, 9512–9513.
26. L. Hu and M. J. Serpe, ACS Appl. Mater. Interfaces, 2013, 5, 11977–11983.
27. J. Kim, S. Nayak and L. A. Lyon, J. Am. Chem. Soc., 2005, 127, 9588–9592.
28. Y. Xia, X. He, M. Cao, C. Chen, H. Xu, F. Pan and J. R. Lu, Biomacromolecules, 2013, 14, 3615–3625.
29. S. Tsuji and H. Kawaguchi, Langmuir, 2005, 21, 8439–8442.
30. N. Vogel, C. Fernández-López, J. Pérez-Juste, L. M. Liz-Marzán, K. Landfester and C. K. Weiss, Langmuir, 2012, 28, 8985–8993.
31. E. Wolert, S. M. Setz, R. S. Underhill, R. S. Duran, M. Schappacher, A. Deffieux, M. Hölderle and R. Mülhaupt, Langmuir, 2001, 17, 5671–5677.
32. L. Isa, F. Lucas, R. Wepf and E. Reimhult, Nat. Commun., 2011, 2, 438.
33. L. Isa, Chimia, 2013, 67, 231–235.
34. M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206.
35. F. Pinaud, K. Geisel, P. Massé, B. Catargi, L. Isa, W. Richtering, V. Ravaine and V. Schmitt, Soft Matter, 2014 10.1039/c4sm00562g.
36. H. Monteillet, M. Workamp, J. Appel, J. M. Kleijn, F. A. M. Leermakers and J. Sprakel, Adv. Mater. Interfaces, 2014 DOI:10.1002/admi.201300121.
37. L. Isa, K. Kumar, M. Müller, J. Grolig, M. Textor and E. Reimhult, ACS Nano, 2010, 4, 5665–5670.
38. S. Schmidt, H. Motschmann, T. Hellweg and R. v. Klitzing, Polymer, 2008, 49, 749–756.
39. L. Isa, D. C. E. Calzolari, D. Pontoni, T. Gillich, A. Nelson, R. Zirbs, A. Sánchez-Ferrer, R. Mezzenga and E. Reimhult, Soft Matter, 2013, 9, 3789–3797.
40. C. A. Rezende, J. Shan, L.-T. Lee, G. Zalczer and H. Tenhu, J. Phys. Chem. B, 2009, 113, 9786–9794.
41. M. Horecha, V. Senkovskyy, A. Synytska, M. Stamm, A. I. Chervanyov and A. Kiriy, Soft Matter, 2010, 6, 5980–5992.
42. W. S. Rasband, ImageJ, U.S. National Institutes of Health, Bethesda, Maryland, USA, http://imagej.nih.gov/ij/, 1997–2014.
43. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
44. E. R. Weeks and J. C. Crocker, http://www.physics.emory.edu/%7Eweeks/idl/.
45. M. Schmidt and H. Lowen, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 7228–7241.
46. K. G. Ayappa and R. K. Mishra, J. Phys. Chem. B, 2007, 111, 14299–14310.
47. K. Schwenke, L. Isa and E. Del Gado, Langmuir, 2014, 30, 3069–3074.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4sm01166j

---