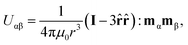Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Directed colloidal self-assembly in toggled magnetic fields
James W.
Swan†
,
Jonathan L.
Bauer
,
Yifei
Liu‡
and
Eric M.
Furst
*
Department of Chemical and Biomolecular Engineering and Center for Molecular and Engineering Thermodynamics, University of Delaware, 150 Academy Street, Newark, Delaware 19716, USA. E-mail: furst@udel.edu; Tel: +1 302 8310102
First published on 29th November 2013
Abstract
Suspensions of paramagnetic colloids are driven to phase separate and self-assemble by a toggled magnetic field. Initially, all suspensions form network structures that span the sample cell. When the magnetic field is toggled, this network structure coarsens diffusively for a time that scales exponentially with frequency. Beyond this break through time, suspensions cease diffusive coarsening and undergo an apparent instability. The magnetic field drives suspensions to condense into dispersed, domains of body-centered tetragonal crystals. Within these domains the crystalline order depends on the pulse frequency. Because the scaling of the break through time with respect to frequency is exponential, the steady state limit corresponding to an infinite pulse frequency is kinetically arrested and the equilibrium state is unreachable. These experiments show that there is an out-of-equilibrium pathway that can be used to escape a kinetically arrested state as well as a diverging time scale for phase separation as the critical frequency for condensation is approached. Rather than fine tuning the strength of the interactions among particles, a simple annealing scheme – toggling of the magnetic field – is used to create a broad envelope for assembly of ordered particle structures.
1. Introduction
The self-assembly of microscopic materials remains a subject of intense scientific investigation.1 The ability to engineer the growth of complex nano-structures will address the need for new materials and devices in areas as diverse as medicine, energy production, energy storage, chemical separations, and catalysis. Ultimately, however, such processes are highly tailored and difficult to translate to new constituents. A deeper understanding of what leads to successful self-assembly and alternative, reliable paths to achieving ordered materials is necessary. The ability for materials processing to circumvent kinetically arrested states is key. However, the same forces that drive materials to condense and order can leave them arrested as a glass or gel far from a desired equilibrium state.Steady and pseudo-steady external fields and fluid flow have long been used to drive colloidal scale materials into ordered phases.2–4 However, these same steady driving forces also produce disordered, arrested phases and exhibit a limited envelope for assembly. A steady driving force or flow is just one pathway to an ordered state. In this article, we demonstrate how time varying external fields can be used create a broad envelope for self-assembly of colloidal materials.
In a steady magnetic field, suspensions of micrometer-sized paramagnetic spheres first form chains parallel to magnetic field lines and then aggregate laterally.6–11 This lateral aggregation gradually arrests the motion of the particles, leaving them entangled in a disordered, system-spanning state.12 These entangled structures are of great utility when applied to mechanical damping since their elastic properties are easily controlled by varying the strength of the magnetic field.8,13 Thermodynamic calculations14 suggest that the dipolar interactions resulting at high field strength would yield well ordered crystalline domains, but because the suspension is kinetically arrested this is not realized.
Promislow and Gast demonstrated in a series of experiments with paramagnetic emulsions,15,16 the kinetically arrested structures of magnetic colloids can be driven to condense by toggling the magnetic field on and off. Recent experiments in microgravity5 demonstrate that pulse frequency is the key parameter for producing a condensed, and as we show here, ordered phases of paramagnetic particles. The toggle period must be sufficiently long to allow rearrangements of the suspension structure. The limit of asymptotically high frequency is essentially equivalent to a steady state with half the applied field strength. This limit is satisfied when the pulse frequency is much larger than the characteristic relaxation rate of the suspension. Thus the suspension remains kinetically arrested.
In these new experiments, we find similar slow coarsening kinetics at high toggle frequency. However, we observe slowing in the low frequency limit as well. This regime is reached when the pulse frequency is much smaller than the rate at which one freely diffusing magnetic dipole captures another. When the frequency is lower than this, the suspension cannot retain memory of its assembled form during the field-off portion of the pulse. The suspension remains disordered. In between the low and high frequency limits and near the capture frequency is an optimum toggle frequency that leads to rapid collapse of the magnetic suspension into crystalline domains.
In this article, we perform experiments with paramagnetic latex particles in pulsed magnetic fields. In Section 2 we describe the materials and methods as well as how we systematically vary the pulse frequency and measure the time required for these suspensions to collapse. The aggregation kinetics are tracked over time scales that are up to least 4 orders of magnitude longer than the characteristic diffusive time scale for the paramagnetic colloids. In Section 3 we present the micrographs of the suspension structure as it evolves in time and measurements of the time needed for a suspension to form a condensed phase. We demonstrate that this break up time grows exponentially in pulse frequency with its distance from the frequency for most rapid self-assembly. Strong, field induced interactions yield effective assembly of crystalline aggregates. However, rather than fine tuning the strength of this interaction, a simple annealing scheme – toggling of the magnetic field – is used to create a broad envelope for assembly. This will be important for future applications of field-directed self-assembly.
2. Materials and methodology
The magnetic suspensions are composed of superparamagnetic polystyrene latex particles (radius a = 525 nm, CV < 3%, Dynabead MyOne, Invitrogen) dispersed in ultra-pure water. A volume fraction of 0.5% is used for all experiments. The latex particles are embedded with iron oxide nanoparticles in such a way that the magnetic moments of the nanoparticles are randomly oriented within the latex. This gives the particles no net magnetic moment while making them highly polarizable. The particles' magnetic susceptibility is characterized with a vibrating sample magnetometer (χ = 1.4). The iron nanodomains are more dense than the polymer matrix in which they are embedded, therefore the density of these particles is much greater than that of water and they sediment due to gravity (ρ = 1.8 mg mL−1).Sample chambers are prepared by placing two pieces of double sided tape on a glass slide approximately 15 mm apart and then adhering a glass coverslip to the exposed tape. Approximately 50 μL of suspension is loaded into the chamber via pipette and capillary action. The chamber is sealed using UV cure optical adhesive. The thickness of the fluid containing space is 100 ± 2 μm. Because the particles sediment so strongly, the characteristic length scale kT/(4πa3Δρg/3) = 0.8 μm where kT is the thermal energy and g is the acceleration due to gravity, indicates that they form a thin layer relative to the particle size on the surface of the glass slide with approximate area fraction 74%. A monolayer of spheres packs as a hexagonal crystal with a maximum area fraction of approximately 91% and has a random close packing area fraction of nearly 84%. Therefore, at the given volume concentration the particles form a concentrated sub-monolayer which is disordered in the absence of applied magnetic field.
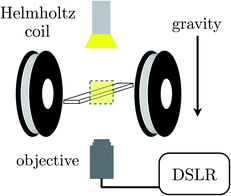
The sample chamber is orientation within a Helmholtz coil mounted on an inverted microscope (Zeiss Axio Observer.A1) is depicted in Fig. 1. The coil generates a magnetic field oriented perpendicular to gravity and parallel to the imaging plane. We operate the coil with a magnetizing field strength of 1500 A m−1. A 4× microscope objective (Zeiss Achroplan) is used to image the sample chamber from below and micrographs are recorded with a DSLR camera (Canon EOS Rebel T2i) every five seconds with a shutter speed of 1/4 s. The magnetic field is made to pulse in amplitude between 1500 A m−1 and 0 A m−1 at a prescribed frequency with a 50/50 duty cycle through use of a function generator (Agilent 33220A). This supplies a square wave voltage signal to a transistor (IRF 840) that in turn gates the current driving the Helmholtz coil. This frequency is far below the response frequencies of any of the electrical equipment employed.
By toggling the magnetic field, the attractive magnetic interactions between colloids are suppressed when the field is off. This allows the particles to relax and reconfigure and enables the suspension as a whole to find its lowest energy state. Cycling the field on and then off can be thought of as equivalent to lowering and then raising the temperature. In a sense, we are cyclically heat treating or annealing the otherwise arrested and system spanning particulate structure. To analyze this process, we image the suspension in bright field under low magnification for up to 5 hours and watch the structural rearrangements that result from different magnetic field pulse frequencies.
3. Results and discussions
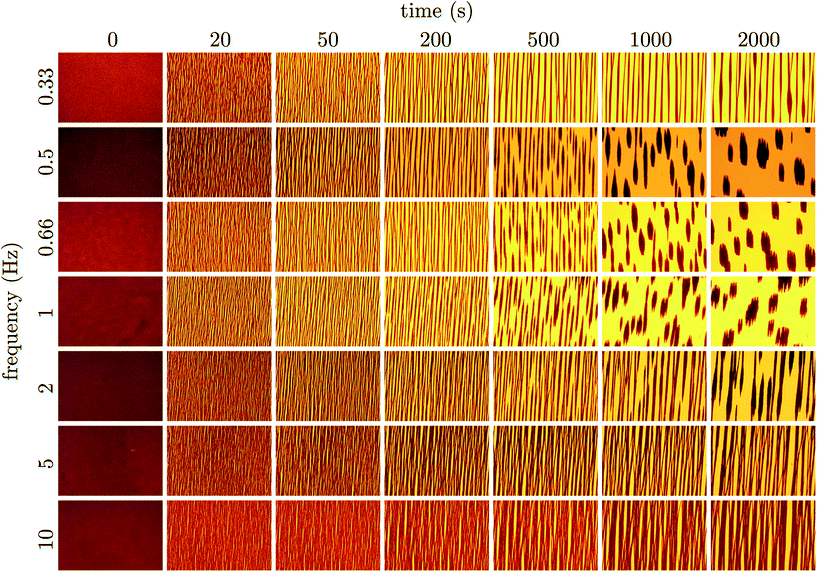
Micrographs of the suspensions during coarsening were taken at logarithmically spaced time intervals. These series begin with application of the pulsed magnetic field, and are shown in Fig. 2. In the micrographs, the dark regions are particle rich. Regardless of the pulse frequency, initially, all suspensions form a system-spanning web of particle chains. As time progresses, these chains merge and the system-spanning structure coarsens. For frequencies below 3 Hz, there is an apparent depercolation of the system-spanning web after more than 500 seconds in the pulsed field. For high frequencies, the system-spanning structure continues to coarsen slowly. In contrast, the depercolated suspensions contract and densify into a dispersion of sub-millimeter sized domains.Collapse of the suspension appears to happen soonest at a pulse frequency of 1 Hz. When pulsing above and below this frequency, coarsening is slower. Similarly, for suspensions that condense, it appears to take longer to reach this dramatic transition. Therefore, a pulse frequency near 1 Hz is optimal for densifying the suspension. Such a pulse frequency gives the particles just enough mobility to rearrange in the field off state, but does not allow them to diffuse too far and redisperse.
We can estimate the length of the field off portion of the pulse required to yield condensation of the suspension by considering the scale of forces acting on the suspended particles. In the far-field, the magnetic interaction potential, Uαβ, between a pair of polarizable particles α and β is
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) is the unit vector connecting the centers of the particles and colon signifies the double-dot-product.17 A magnetic field H, will cause particle α to polarize, acquiring the magnetic moment
is the unit vector connecting the centers of the particles and colon signifies the double-dot-product.17 A magnetic field H, will cause particle α to polarize, acquiring the magnetic moment 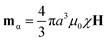 , where χ is the magnetic susceptibility of the particle and a is the particle radius. This potential is most attractive when the particles and their magnetic moments are aligned (i.e.
, where χ is the magnetic susceptibility of the particle and a is the particle radius. This potential is most attractive when the particles and their magnetic moments are aligned (i.e.![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) × mα =
× mα = ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) × mβ = 0). The potential is characterized by its magnitude when particles contact (r = 2a) in this orientation, U* = πμ0a3χ2H2/9. When compared to the Boltzmann energy scale kT, this defines a dimensionless group
× mβ = 0). The potential is characterized by its magnitude when particles contact (r = 2a) in this orientation, U* = πμ0a3χ2H2/9. When compared to the Boltzmann energy scale kT, this defines a dimensionless group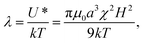 | (1) |
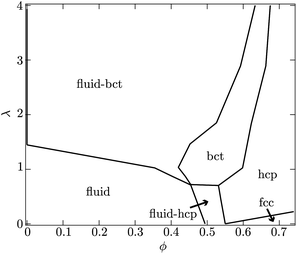 | ||
| Fig. 3 Depicted is the equilibrium phase behavior of dipolar hard-spheres calculated by Hynninen and Dijkstra.14 At low particle volume fractions ϕ, a suspension will display fluid-like structure for dimensionless field strengths λ < 1. For larger values of λ, coexistence of a body-centered-tetragonal (bct) and fluid-like phase is anticipated. At higher particle concentrations, hexagonal-close-packed (hcp) and face-centered-cubic (fcc) crystal structures are possible as well. In the present experiments, λ is more than 60 while the particle volume fraction on the surface is roughly 50%. | ||
The distance, rc, at which a particle pair aligned with the magnetic field experiences a 1 kT attraction is called the magnetic “capture radius” and defined as
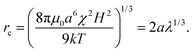 | (2) |
Beyond this distance, Brownian diffusion of the particle pair is stronger than the magnetic interaction force and a particle pair is essentially unbound. If a pair of particles begins at contact the characteristic time it takes them to diffuse to a separation of rc is
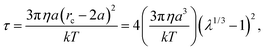 | (3) |
Another view is that rc is the distance a particle must diffuse during the field off portion of the pulse in order to avoid being captured and pulled back into the same configuration as during the field on portion. Thus, τ is characteristic of the time required for the suspension to reconfigure and relax under the magnetic field. At a magnetic field strength of 1500 A m−1 with these latex particles in water, λ = 69 and the capture radius is 3.8 μm. The corresponding relaxation time is τ = 8.7 s or more generally τ ∼ O(1–10) s. This suggests that pulse frequencies on the order of 1 Hz divide the phase space of suspensions that relax to their lowest energy state and those that remain kinetically arrested. We stress that the above expressions for U*, λ, rc and τ are only scaling relations meant to provide a qualitative and physical rationale for the complex relaxation processes (see Fig. 2).
3.1. Depercolation
To quantify our observations, we convert the micrographs from a given experiment, taken once every five seconds, to grey scale and then compute the power spectrum along the direction perpendicular to the magnetic field lines. We find the global maximum in each power spectrum and plot the wave vector at which this peak occurs, qmax, as a function of time (see Fig. 4). As with a scattering experiment, qmax−1 is indicative of a microstructural length scale, in particular how coarsely aggregated the suspension is. This coarsening length scale need not be the same in the parallel and perpendicular directions when the suspension is perturbed anisotropically. The direction perpendicular to the field happens to be most interesting.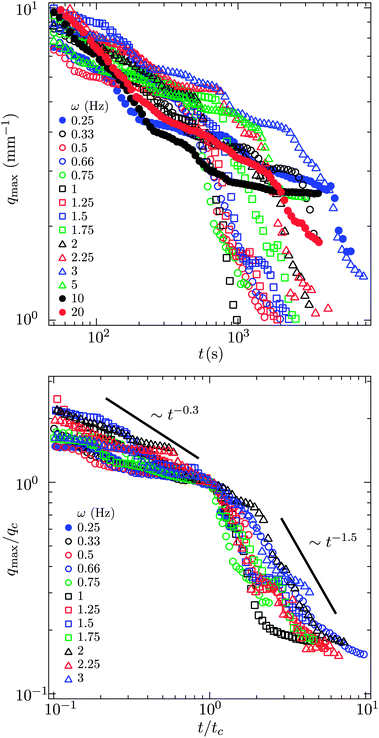 | ||
| Fig. 4 q max, the wave vector at which there is a peak in the power spectrum of the micrographs (see Fig. 2), as a function of time for different pulse frequencies. The value of qmax−1 is characteristic of a structural length scale much as in a scattering experiment. For frequencies below 5 Hz there is an obvious transition in qmax indicative of a change from slow, thermal coarsening to rapid break up and re-coalescence. The field strength is 1500 A m−1. | ||
At short times, all suspensions coarsen with a sub-unity power law, qmax−1 ∼ t0.3. This is characteristic of a diffusion limited process for which coarsening typically scales as t1/4 or t1/3 when surface or bulk diffusion dominates.18 We cannot distinguish between these two power laws. In addition, it seems likely that both surface and bulk diffusion are occurring simultaneously as the suspension coarsens. This thermal coarsening continues unabated to very long times for frequencies 5, 10, 20 Hz.
For pulse frequencies smaller than 5 Hz and at longer times, there is a sharp decrease in qmax as the suspension evolves. This marks the depercolation of the suspension and its coalescence into locally dense domains. In the lower portion of Fig. 4, we plot qmax as a function of time for those suspensions that exhibit this decrease. The value of qmax and the elapsed time are normalized by their values where this transition occurs. We denote these critical values qc and tc.
The power law scaling of the wave vector with respect to time is super-unity during this rapid coarsening, qmax−1 ∼ t1.5, which indicates a ballistic or directed process rather than thermally driven.19 The decrease in qmax eventually halts when the break up of the suspension ceases. In this terminal state, we observe exchange of material between condensed regions, but never coalescence of the entire suspension into a single domain. Apparently in the balance of magnetic energy within the domains, on their surface and between them, a dispersed phase of locally concentrated regions is preferred.
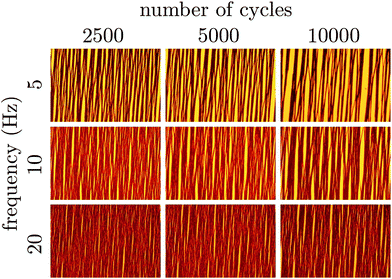
The time at which the suspension is observed to transition from slow thermal coarsening to rapid coalescence, tc, is plotted in Fig. 5 as a function of pulse frequency. For a pulse frequency of approximately ω = 0.5 Hz, we observe a minimum in the break up time. Above 1 Hz, we see the time to break up grows exponentially with increasing frequency. The coefficient of the best fit exponential to these observations is 0.92 s and is commensurate with the characteristic diffusion time scale of the particles. This trend suggests that given enough time, even the suspensions pulsed at 5, 10, 20 Hz would break up. However, extrapolating, we estimate that this would require 4–6 hours for just the 5 Hz pulse. This also suggests that the steady state case, equivalent to ω → ∞, may in fact be kinetically arrested since the time to break up appears to grow as exp[(0.92 s)ω]. For high pulse frequencies, by comparing the micrographs on the basis of number of oscillatory cycles (the product of time and pulse frequency) as in Fig. 6, we conclude that the degree of coarsening at high frequency appears to be super-linear with respect to frequency. That is, the degree of coarsening is not simply linearly dependent on the number of pulse cycles at high frequency. Such an observation is consistent with the exponential scaling of the breakthrough time.
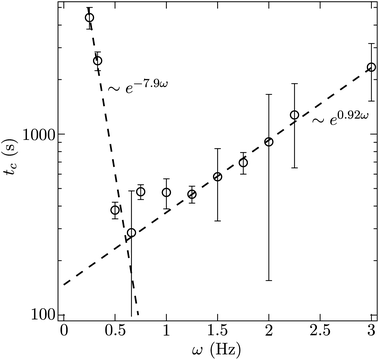 | ||
| Fig. 5 The time at which the transition between thermal and ballistic coarsening occurs plotted as a function of pulse frequency. The field strength is 1500 A m−1. | ||
For a pulse frequency of 0.25 Hz, we observe slow thermal coarsening for over an hour. Beyond this point, qmax drops at a faster rate for another hour. Similar observations were made for a pulse frequency of 0.33 Hz. It is clear from the micrographs and the power spectrum analysis that at lower frequencies, there is still an instability in the coarsening, but the time required to instigate that instability also grows progressively longer with decreasing frequency. This lower barrier can be understood in the following way. When the field is left off for too long, the particles disperse via Brownian motion which acts to make their distribution more homogenous. When the field is turned on again, the progress made in condensing the suspension during the previous cycle is mostly lost. Thus, depercolating the suspension requires more cycles when the field is left off for longer. The time scale characterizing this loss of structure from cycle to cycle is just τ, the time required to diffuse from contact to the capture radius. Indeed, the time scale that results from the exponential fit of the time to break-up (tc ∼ exp[−(7.9s)ω]) is nearly the same as τ.
In a previous paper,5 we observed the same particles self-assembling under a pulsed magnetic field in microgravity. We observed the suspensions for up to six hours with magnetic field strengths ranging from 1000 A m−1 to 2200 A m−1 and at pulse frequencies of 0.66, 1, 5 and 20 Hz. These suspensions were very dilute, less than 1% particles by volume so that formation of the percolated structure and its eventual collapse was significantly slower than in the present terrestrial experiments. In microgravity, we found that there was a frequency beyond which we could no longer observe collapse of the suspension. This critical frequency was seen to scale as H−4/3 and was rationalized by noting that the magnetic field must be off long enough for particles to diffusively rearrange in order for coalescence of the suspension to occur.
Importantly, we identified the time scale τ as the key for describing the kinetics of the self-assembly process. The present experiments suggest that this is still the case. Because we now have access longer time scales and a wider range of experimental conditions, we see that collapse of the system-spanning network will occur at higher frequencies given exponentially long observation times. Any further differences arising from dimensionality – three dimensional assembly in microgravity versus quasi-two dimensional assembly in the present experiments, are not easily quantified.
3.2. Crystallization
Equilibrium thermodynamic calculations suggest that a dilute suspension of polarizable spheres condenses into crystalline domains when exposed to a strong and steady polarizing field. This does not occur, however. Strong polarizing fields (electric and magnetic) tend to leave such suspensions kinetically arrested.6,12 The induced dipole interactions between the particles lead to strong attractions that localize particles. With insufficient mobility, the particles are unable to relax to their lowest energy state over a reasonable observation window. This same localization is also what imparts polarizable suspensions with large viscoelastic moduli. In essence, their is a gel line across the dipolar fluid phase diagram that prevents the suspension from condensing and eventually crystallizing. In our experiments, this gel line is avoided by pulsing the magnetic field.We use a 40× objective (Zeiss Plan-Neofluar) to image the local particle conformation for frequencies 0.33, 0.66, 1, 2, 5, 10 Hz when the suspension is in its terminal state (see Fig. 7). There is a clear onset of crystallinity going from 0.33 to 0.66 Hz. The particles are mobile for too long during the field off portion of the 0.33 Hz pulse to coordinate and crystallize. The quality of the crystal improves for the 1 Hz and 2 Hz pulses. However, for the 2 Hz pulse, the crystal is slightly misaligned relative to the horizontal and vertical of the micrograph. At 2 Hz, the suspension no longer collapses. Instead, the depicted crystalline region is within a system spanning column of particles that is not perfectly aligned with the magnetic field lines. However, the principle axis of the crystal is aligned with the column, hence the apparent skewness. For the 5 Hz and 10 Hz pulse, the suspension does not possess large crystalline regions. Some local, hexagonal ordering is observable, but large inclusions and regions of tangled particle chains dominate the microstructure. These defects cannot anneal and small ordered clusters do not grow significantly. The field off portion of the pulse is now too short for particles to diffuse a significant distance and conjugate with an existing crystal lattice.
We conclude from this that the same mobility that allows the system spanning web of particle chains to condense also gives rise to large, regular, crystalline domains. By pulsing the field, the suspension is allowed to relax periodically and find lower energy states. Because the spatial distribution of particles in response to a pulsed field cannot be described by simple Boltzmann statistics, the terminal state of this out-of-equilibrium process may only approximate the equilibrium thermodynamic state. The optimum pulse frequency for crystallization appears to lie between 1 and 2 Hz in this case (a = 525 nm, χ = 1.4, H = 1500 A m−1, η = 1 cP).
In order to determine the structure of the crystal grown, we view different layers of particles in the condensed domains. In these experiments, after the suspension is exposed for fifty minutes to a pulsed field with frequency 2 Hz, we switch to a quasi-steady, high pulse frequency, field. This has the effect of locking in the condensed structure to enable a layer by layer scan of the structure by adjusting the focal plane of the microscope objective. The structure under the quasi-steady field does not change during the one minute required to perform the scan. Due to the high refractive index of the particles, only the two bottommost layers can be imaged, although we estimate that up to four layers may be present in some aggregates. These two adjacent layers are identified and micrographs recorded. We use typical image processing techniques to identify the particle centers in each micrograph. Fig. 8 depicts the individual layers and a superposition of the two.
With this method, the analysis of two successive layers suggests the assembly of body-centered-tetragonal crystals – the expected equilibrium phase. Each of the layers has hexagonal ordering. It is the stacking of these layers that distinguishes this assembly as BCT. Within hexagonal close-packed and face-centered cubic crystals, sequential layers are shifted so that the particles reside in the interstitices of adjacent layers. However, in Fig. 8 we show that the particles in each layer may be viewed as columns aligned with the magnetic field that stack not top of one another. This suggests that the (110) plane of the BCT structure is parallel to the microscope slide. The columnar stacking of in adjacent layers ensures that the magnetic dipoles are aligned to minimize the suspension's free energy. Growth along (110) plane in BCT crystals has been observed elsewhere.20
4. Conclusions
We show that a uniform pulsed magnetic field can be used to break through the kinetic barriers associated with strong dipolar interactions and self assemble a suspension of paramagnetic colloids into condensed, crystalline domains. Initially in all magnetic fields, pulsed or otherwise, cause the suspension to organize into a tangled chains that are system spanning. However, given time in the pulsed magnetic field, suspensions were observed to break up into condensed droplet like regions. With a field strength of 1500 A m−1, the fastest break up was observed when the pulse frequency was 0.5 Hz. We found that the time required for a suspension of paramagnetic latex particles to form crystalline domains scales exponentially in the difference between the pulse frequency and this optimum. At higher frequencies, the field-off portion of the pulse is too short to allow sufficient relaxation of the kinetically arrested, system-spanning structures so that break up is less rapid. At lower frequencies, the field-off portion of the pulse is too long so that memory of the assembled structure is lost from pulse to pulse. The frequency for optimum assembly resides between the rate at which a pair of particles is brought together in the field-on state and the bare diffusion rate of the suspended particles. In future work, we investigate the crystallization process and the structure of the self-assembled crystals.This is an exciting result for directed-field self-assembly as it enables generation of ordered, condensed phase without careful tuning of the attractive interactions between particles. Rather, the simplest possible toggling of the directing field, anneals the material and produces the desired ordered phase. With such an approach, a broad envelope for effective self-assembly is available.
Acknowledgements
Support from NASA (grant no. NNX07AD02G and NNX10AE44G) is gratefully acknowledged.References
- M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, Directed self-assembly of nanoparticles, ACS Nano, 2010, 4(7), 3591–3605 CrossRef CAS PubMed.
- B. J. Ackerson and P. N. Pusey, Shear-induced order in suspensions of hard spheres, Phys. Rev. Lett., 1988, 61, 1033–1066 CrossRef CAS.
- I. W. Hamley, The effect of shear on ordered block copolymer solutions, Curr. Opin. Colloid Interface Sci., 2000, 5, 342–350 CrossRef CAS.
- O. D. Velev and K. H. Bhatt, On-chip micromanipulation and assembly of colloidal particles by electric fields, Soft Matter, 2006, 2, 738–750 RSC.
- J. W. Swan, et al., Multi-scale kinetics of a field-directed colloidal phase transition, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 16023–16028 CrossRef CAS PubMed.
- T. C. Halsey and W. Toor, Fluctuation-induced couplings between defect lines or particle chains, J. Stat. Phys., 1990, 61, 1257–1281 CrossRef.
- T. C. Halsey and W. Toor, Structure of electrorheological fluids, Phys. Rev. Lett., 1990, 65, 2820–2823 CrossRef CAS.
- T. C. Halsey, Electrorheological fluids, Science, 1992, 258, 761–766 CAS.
- M. Hagenbüchle and J. Liu, Chain formation and chain dynamics in a dilute magnetorheological fluid, Appl. Opt., 1997, 36, 7664–7671 CrossRef.
- E. M. Furst and A. P. Gast, Particle dynamics in magnetorheological suspensions using diffusing-wave spectroscopy, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 3372–3376 CrossRef CAS.
- U. Dassanayake, S. Fraden and A. van Blaaderen, Structure of electrorheological fluids, J. Chem. Phys., 2000, 112, 3851–3859 CrossRef CAS PubMed.
- M. Fermigier and A. P. Gast, Structure evolution in a paramagnetic latex suspension, J. Colloid Interface Sci., 1992, 154, 522–539 CrossRef CAS.
- D. Klingenberg, Magnetorheology: Applications and challenges, AIChE J., 2001, 47, 246–249 CrossRef CAS.
- A.-P. Hynninen and M. Dijkstra, Phase diagram of dipolar hard and soft spheres: Manipulation of colloidal crystal structures by an external field, Phys. Rev. Lett., 2005, 94, 138303 CrossRef.
- J. H. E. Promislow and A. P. Gast, Magnetorheological fluid structure in a pulsed magnetic field, Langmuir, 1996, 12(17), 4095–4102 CrossRef CAS.
- J. H. E. Promislow and A. P. Gast, Low-energy suspension structure of a magnetorheological fluid, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 642–651 CrossRef CAS.
- L. D. Landau, E. M. Lifshitz and L. P. Pitaevskii, Electrodynamics of Continuous Media, 2nd edition, Elsevier Butterworth-Heinemann, Oxford, 1984 Search PubMed.
- J. P. Sethna, Statistical Mechanics: Entropy, Order Parameters and Complexity, Oxford University Press, Oxford, 2006 Search PubMed.
- E. Siggia, Late stages of spinodal decomposition in binary-mixtures, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20(20), 595–605 CrossRef CAS.
- A. Yethiraj, J. H. J. Thijssen, A. Wouterse and A. van Blaaderen, Large-area electric field-induced colloidal single crystals for photonic applications, Adv. Mater., 2004, 16, 596–600 CrossRef CAS.
Footnotes |
| † Current address: Department of Chemical Engineering, Massachusetts Institute of Technology, USA. |
| ‡ Current address: Department of Chemical Engineering, University of Wisconsin, Madison, USA. |
| This journal is © The Royal Society of Chemistry 2014 |