Growth of boronic acid based two-dimensional covalent networks on a metal surface under ultrahigh vacuum

Abstract

The formation of atomically precise covalent networks directly on a surface is a promising approach to produce single layers of two-dimensional organic materials (2D polymers). In the emerging field of on-surface synthesis, there is an urgent need for finding a rationale to new reaction pathways taking place directly on the surface. In this feature article we review and put into perspective recent results on the surface polymerisation of boronic acid based systems under ultrahigh vacuum conditions studied by scanning tunnelling microscopy. By presenting several approaches to control the growth of covalent networks, we aim at providing a comprehensive overview of the complex mechanisms involved.

---

Introduction

The application of the principles of supramolecular chemistry¹ to organic systems on surfaces has led to a rich production of various nanostructures. Self-assembly processes driven by non-covalent intermolecular interactions such as van der Waals forces, hydrogen bonding or metal–ligand coordination are indeed highly efficient for producing extended networks of any desired shape, size, symmetry and functionality after deposition of pre-designed molecular precursors on well-defined surfaces.^2–4 The characterisation of these systems can be achieved with molecular precision by scanning probe microscopy techniques. More recently, an important effort has been made to initiate covalent coupling between adsorbed molecules leading to the emergence of the field of on-surface synthesis.^5–7 Several chemical functions have already been explored to produce in situ new covalent bonds between the precursors, with the ultimate goal being the formation of extended covalent networks. Such an approach is very promising^8–12 because it can potentially deliver single sheets of organic material (two-dimensional polymer), similar to highly popular graphene, but with a tuneable structural motif.¹³ However, the growth of such surface covalent networks is highly complex due to the confinement in the two-dimensional (2D) environment of the surface and to the catalytic activity of the substrate.^14–16 To date, the reactions accessible have been mostly limited locally to a small number of precursors producing macromolecules of reduced size (up to a few tens of nm). Nevertheless, new chemistries that are not possible in solution can emerge using this approach,¹⁷ and there is an urgent need for gaining a higher level of control and understanding in this field and for finding a rationale to the underlying complex mechanisms.

Covalent organic frameworks (COFs) are an emerging class of covalent porous crystalline organic materials with great potential for functional applications.^18,19 In particular, boronic acid based COFs are of special interest due to their ability to form lamellar structures.^20–24 Boronic acids are widely used building blocks in supramolecular self-assembled materials,^25–28 and they can undergo self-condensation reaction to form strongly bonded boroxine rings^29–32 that confer high robustness to such materials. In 2008, we demonstrated that boronic acid self-condensation can take place on a metal surface to form extended covalent networks starting from bi-functional benzene-1,4-diboronic acid (BDBA) molecules,³³ similar to the lamellar structure of COF-1²¹ (see Fig. 1).

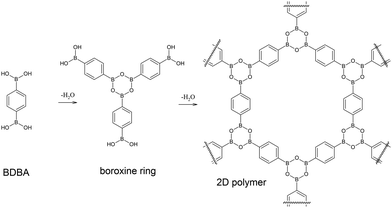Fig. 1 Self-dehydration reaction of benzene-1,4-diboronic acid (BDBA) leads to the formation of boroxine rings and to an extended 2D polymer.

In this feature article we will review the recent literature on the topic of boronic acid based 2D covalent networks on a surface and put it into perspective aiming at providing a comprehensive overview of the complex mechanisms involved in the delicate growth of this new class of materials. The results presented here are, if not otherwise specified, obtained by evaporation of the molecular precursor from a Knudsen-like cell under ultrahigh vacuum conditions (UHV) and characterized by room temperature scanning tunnelling microscopy (RT-STM).

Note that due to the high reactivity of boronic acid, vacuum deposition of large molecular mass compounds is barely feasible because thermal sublimation is competing with prior polymerisation in the crucible. The possibilities for studying boronic acids in UHV are thus probably restricted to the few compounds presented here.

Results and discussion

BDBA hydrogen-bonded phase

The OH groups of the boronic acid moieties are efficient hydrogen bond donors and acceptors.^34,35 In the bulk crystal structure of BDBA,³⁶ primary H-bond association leads to the formation of linear chains that associate via secondary H-bonds to form 2D sheets with a rectangular unit cell. The intrinsic lamellar structure of these compounds is an important issue for promoting efficient supramolecular self-assembly on a surface.³⁷ Pawlak et al. could observe by non-contact atomic force microscopy (nc-AFM) at room temperature the formation of a hydrogen-bonded phase on KCl(001), a weakly interacting substrate (Fig. 2).³⁸ The structure of this phase is very close to the lamellar bulk structure with a rectangular unit cell (a = 5.2 ± 0.2 Å, b = 10.0 ± 0.2 Å) and a compactness of 2 molecules per nm². The rather short intermolecular distance between chains (along a) induces a tilt of the benzene core with respect to the in-plane orientation of the B(OH)₂ groups to prevent steric hindrance. The tilt amounts to ∼38° as derived by calculations compared to ∼35° found experimentally in bulk structure. Nevertheless, the 2D pattern of hydrogen bonds involved in this phase provides a significant cohesion energy of about 1 eV per molecule, as calculated by DFT.³⁸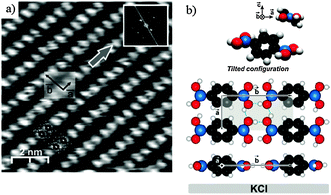

Fig. 2 Deposition of BDBA on KCl(001), a weakly interacting substrate, leads to the formation of a dense hydrogen-bonded phase. (a) nc-AFM image. (b) Corresponding model of the unit cell showing the tilted configuration of the benzene ring. Adapted with permission from ref. 38. Copyright (2010) American Chemical Society.

This phase can similarly form on metal surfaces under specific conditions, although it is always metastable (see below). For the 3 different surfaces Ag(100), Ag(111) and Au(111) on which it has been observed, the unit cell was kept identical within experimental error to that found on KCl(001). The epitaxial growth mode^39,40 was proposed to be incommensurate on Au(111), “point on line” on Ag(111), and commensurate with 2 molecules per unit cell on Ag(100).⁴¹ Remarkably, on all 3 surfaces the extended domains appeared perfectly homogeneous by STM, illustrating the high intermolecular cohesion energy inside the 2D sheet governing the supramolecular growth. The molecule–substrate interaction in this dense phase can be classified following the epitaxial mode, strong on Ag(100), weak on Au(111) and intermediate on Ag(111).

From the supramolecular to the covalent network

On KCl(001), the dehydration reaction of boronic acid could not be observed. Annealing the supramolecular phase led to the mere desorption of the molecules. In contrast, the hydrogen-bonded phase of BDBA formed on a metal surface is metastable at room temperature and evolves slowly into a polymeric phase. On Ag(100), a full monolayer of the supramolecular network is converted into a covalent network within a timeframe of about 2 days.^41,42 In the self-dehydration reaction of boronic acid, the B(OH)₂ moieties couple threefold to form a boroxine ring B₃O₃ and three water molecules as the by-product. In the reaction path, the Lewis acid character of boron allows for the formation of a transition state where an oxygen atom from another acid moiety binds to boron that becomes tetravalent (TS1, see Fig. 3). This transition state relaxes to form a dimer and a water molecule. This mechanism repeats three times until the final boroxine trimer product. The global reaction is endothermic (formation enthalpy of a few tenths of eV per boroxine trimer^31,43–45). In general this reaction is reversible as boron in the boroxine ring pertains its Lewis acid character and can be attacked by oxygen from a water molecule.³⁰ In the case of poly-functional precursors, the reaction can propagate further to form extended covalent networks.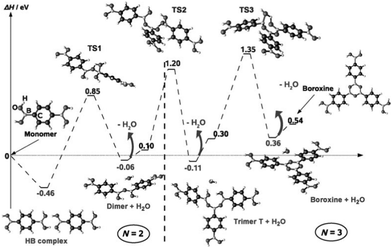

Fig. 3 Boroxine formation reaction mechanism as calculated by DFT. The first step is the formation of a hydrogen-bonded dimer, which represents the only exothermic step. In each transition step, boron becomes tetravalent and relaxes by releasing a water molecule. Reprinted with permission from ref. 44, copyright (2009) Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

In the practical applications described in this article, the solid–vacuum interface represents a highly dilute environment and the availability in water is strongly reduced. Formed as the by-product, water can form hydrogen bonds to the boroxine ring (see Fig. 3) but it is nevertheless easily desorbed and pumped away from the surface at room temperature.⁴⁶ As a consequence, the reverse reaction is prohibited and the dehydration reaction can be considered as irreversible. Introducing a limited partial water pressure in UHV (up to a few Langmuir exposition) is ineffective. Additionally, the mobility of boroxine oligomers is greatly reduced compared to that of the original precursors, which represents a supplemental kinetic blockade for the reverse reaction.

While the solvent based dehydration reaction of BDBA requires thermal activation to form 3D COF,²¹ in the case of adsorbed molecules the underlying metal substrate provides a strong catalytic effect that enables the reaction to occur readily at room temperature. Indeed, the adsorption on the surface induces changes in the molecule conformation and/or electronic configuration⁴⁷ that can considerably modify the reaction path.^14,16 In particular, the activation energy (of the transition state) is greatly reduced and the reaction time is lowered to the order of a few seconds or below. Additionally, the continuous removal (desorption) of water by-product provides an important driving force for the reaction. The upper limit for the reaction time on Ag(100) can be evaluated from STM imaging because the occurrence of a few reactions is observed locally at the border of hydrogen bonded domains between two sequential images (whereby the imaging rate is typically 1 every 2–3 minutes, see Fig. 4). However, this (local) high reaction rate is not compatible with the large global reaction time of 48 h required to convert a full monolayer. In fact, important kinetic quenching effects appear due to the confinement of the system in the two-dimensional environment of the surface. The stable regions of the hydrogen bonded phase are the domain boundaries along the high symmetry directions of the unit cell (a and b) and the domain boundaries directly neighbouring reacted oligomers (see Fig. 4(a)). The reaction rate, calculated from the sequential disappearance of the molecules from the hydrogen-bonded phase, is highly non-linear and presents large variations within the timeframe of STM imaging (Fig. 4(g)).

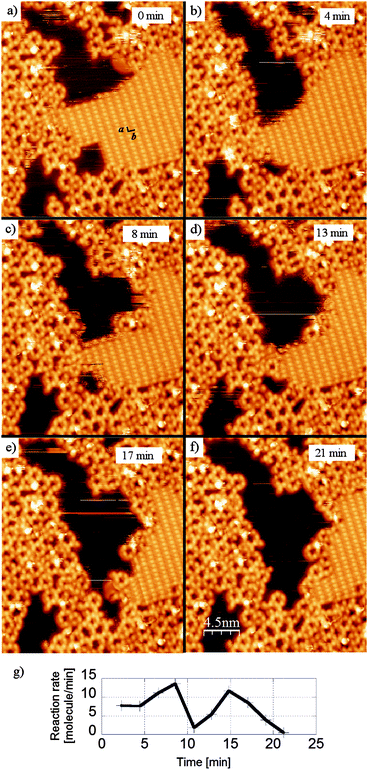Fig. 4 Sequential STM images (28 × 28 nm²) showing the advancement of the polymerisation reaction of BDBA on Ag(100) from the hydrogen bonded phase (a–f). Stable domain boundaries are those along b (long intermolecular distance) or a (short intermolecular distance), or those in direct contact with oligomers. These images were obtained with similar experimental protocol as described in ref. 42. (g) Evolution of the reaction rate calculated from the disappearance of the molecules in the H-bonded phase.

An important parameter producing kinetic quenching is the relative 2D-density of the two phases: the H-bonded supramolecular phase has a packing density of 2 molecules per nm², whereas the ideal honeycomb network of the boroxine polymer has a density of 1.5 molecule (monomer) per nm². As a consequence, the system first needs to create free space on the surface to allow for the reaction product to exist. This is illustrated by the fact that the reaction can only occur at domain boundaries. An additional effect comes from the necessity for the reactants to come into close contact with the correct conformations to be able to follow the reaction path. There may be thus an additional activation step required to release the high cohesion within the supramolecular phase before the reaction can initiate. In particular, along the reaction pathway inter-row H-bonds are broken and the 38° tilt of the benzene ring goes back to 0°.

The kinetic quenching of the polymerisation reaction can be artificially overcome by two different approaches.⁴² In fact, it is sufficient to remove a fraction of the molecules on the surface (inside the H-bonded domains) to immediately release the reaction. This can be done by low-energy electron bombardment, whereby a brief exposure to an e-beam (15 eV, 20 s) can completely convert a full monolayer of the H-bonded supramolecular phase into a polymer layer. Alternately, the tip of the STM can be used as a nanoscale tool to locally promote the polymerisation reaction. This was done by reducing the tip-distance sufficiently and scanning over the H-bonded phase, which resulted in the desorption of part of the molecules over a nanometer scale area. Thanks to the newly made available space, the polymerisation reaction occurred immediately in such a region (Fig. 5).

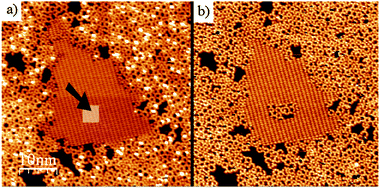Fig. 5 Local initiation of BDBA polymerisation reaction by manipulation with the STM tip. Inside a hydrogen-bonded domain (indicated by the arrow in (a)) the tip-surface distance was reduced to remove some of the molecules. This resulted in immediate reaction in the modified area (b). Adapted from ref. 42.

The global evolution of the supramolecular phase at room temperature is very dependent on the nature of the underlying surface. On Ag(100), a full monolayer of the hydrogen-bonded phase is transformed into a full monolayer of 2D-polymer within a timeframe of about 48 h. On Ag(111), the molecules similarly react but a substantial part directly desorbs before reaction, so that the coverage of the final 2D polymer is lower than a monolayer.^15,41 On Au(111), the adsorption energy of BDBA molecules is lower and they all desorb without apparently reacting.^15,41 Annealing the pre-formed supramolecular 2D network leads in all cases to BDBA polymerisation but only restricted patches stuck to step edges remain on the surface. Indeed, at high temperature the majority of the molecules desorb from the surface.

The initial formation of the hydrogen-bonded phase can be controlled by the deposition conditions.¹⁵ On Ag(100) the supramolecular phase can be obtained readily at room temperature, but to grow it on Au(111) or Ag(111) it is necessary to use a very low deposition flux, as low as about 0.005 ML min⁻¹ (corresponding to 1 ML in about 3 hours). In general, crystal growth is a non-equilibrium process. The nucleation rate and subsequent growth can be modified by two experimental parameters: the substrate temperature (determining the surface diffusivity through an Arrhenius activation term) and the deposition flux.⁴⁸ To approach equilibrium growth conditions the flux of impinging species must be adjusted at values allowing adsorbed precursors to explore all possible sites and thus find the most favourable thermodynamic sites. Such a situation can be obtained at very low deposition fluxes and this is the usual way to grow metals and semiconductors with good crystalline quality. In fact, the formation of hydrogen bonds represents the first step of the reaction pathway of BDBA, as calculated by DFT (Fig. 3). Remarkably, it is also the only exothermic step, so that the formation of the H-bonded phase is well described by thermodynamic equilibrium. Avoiding the initial formation of the supramolecular phase at room temperature can only be done using high deposition flux (of the order of about 0.1 ML min⁻¹). Under such conditions, the system cannot relax to thermodynamic equilibrium, and the polymerisation takes place (kinetic limiting conditions). As expected from the complexity of the multi-step process of the polymerisation, such a mechanism cannot be explained by first order reaction processes only, and higher order kinetics or nucleation effects are necessarily involved. In particular, entropic effects have been proposed for nucleation processes.⁴⁴ Interestingly, with this system it is the thermodynamic phase (low deposition flux) which is metastable, while the kinetic phase (high deposition flux) is stable due to the irreversible character of its formation.

BDBA polymer phase: quantitative characterisation and growth parameters

The polymer phase of BDBA formed in UHV on a metal surface differs from the ideal honeycomb structure of Fig. 1 and presents always a substantial number of defects. Defects can arise from incomplete reaction steps, i.e. from non-reacted boronic acid moieties or non-closed boroxine rings, or from the formation of closed but non-ideal polygonal pores.^41,49 Beside hexagonal pore shape expected from the symmetry of the boroxine ring, pentagonal and heptagonal pores are likewise formed (Fig. 6). Similar geometrical defects were found in other covalently-linked systems of honeycomb symmetry.^50–52 DFT calculations showed that the creation of pentagonal or heptagonal defects can result from only slight geometrical distortions with respect to hexagonal pores, and that the enthalpies of formation for different polygonal pores from BDBA precursors are very close (within 10% difference, see Fig. 6).¹⁵ Other kinds of defects arise when the pores are not exactly closed, due to volume hindrance between molecules when the packing density increases. Because no epitaxial order was observed during polymer growth, the molecules (monomers) can adopt a large number of orientations, and ideal boroxine ring formation and effective polygonal pore closure are difficult to achieve on a larger scale.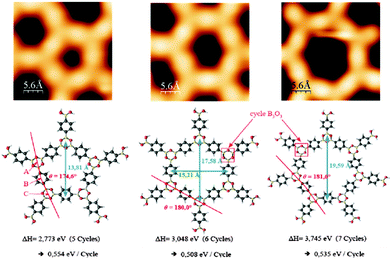

Fig. 6 STM images of closed polygonal pores (pentagons to heptagons, up) and corresponding models from DFT calculations (bottom). The calculated enthalpies of formation per boroxine cycle are reported and vary only within ±10% between the different pore shapes. Adapted from ref. 41 and 15, copyright (2011) American Physical Society.

Due to the large number of defect types encountered in this system, quantitative characterisation of the network quality is a critical issue. In particular, it is important to classify the nature of the underlying metal substrate depending on its ability to promote the 2D-polymerisation in a well-ordered fashion. A degree of reaction advancement τ_R can be defined from STM images by manual counting of the number of intermolecular bonds formed and reporting it to the number of precursors involved. It was thus shown that Ag(111) and Ag(100) surfaces were the most efficient substrates (giving the highest degree of reaction advancement), followed by Au(111), Cu(111) being the less efficient.¹⁵ Note that in all cases τ_R is limited by the non-equilibrium conditions.

Another statistical method based on the minimal spanning tree (MST) approach developed by Dussert et al.⁵³ was introduced to quantify the quality of the networks.¹⁵ The MST is obtained by building a spanning tree connecting the centres of mass of all pores within the network under the conditions that no closed loop appears in the tree, and that the sum of the edge lengths (point-to-point distances) is minimum. The histogram of edge lengths used to build the MST is then computed to extract the average edge length m* and the corresponding standard deviation σ*. After normalization these quantities are plotted in a (m, σ) diagram (Fig. 7). For an ideal hexagonal network σ = 0, m = 1.075. Upon gradual introduction of disorder, the (m, σ) data points plot on a line connecting (1.075, 0) (ideal hexagonal) and (0.662, 0.311) (random disorder, RD).

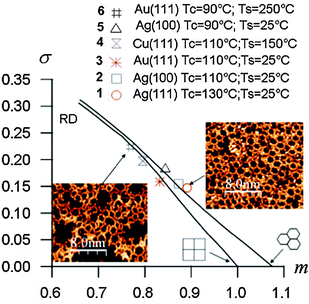Fig. 7 (m, σ) Diagram of the minimal spanning tree (MST) statistical analyses for different BDBA polymer networks. T_c refers to the deposition flux (90 °C = low flux, 110 °C = high flux) and T_s refers to the substrate temperature during deposition. Adapted from ref. 15, copyright (2011) American Physical Society.

Improving the crystalline quality of the polymer phase can be achieved by exploring several parameters governing the growth. Beyond the deposition flux, the substrate temperature can be varied. Elevated substrate temperature favours the diffusion of molecules, the occurrence of contacts and linkages between them, but also favours their desorption from the surface. A temperature window has thus to be found that facilitates the reaction between molecules with minimal desorption. Although strong intermolecular bonds form between BDBA molecules, surface–molecule interactions cannot be ignored. Trials on different coinage metal surfaces showed that the polymerization process is significantly influenced by the underlying metal. Fig. 7 presents MST results obtained using various deposition fluxes and substrate temperatures on different surfaces. It was thus confirmed that BDBA polymer growth on the copper surface is more difficult than on silver or gold surfaces. Indeed, STM images obtained on Cu(111) showed that on that surface the mobility of BDBA molecules is very low and/or their reactivity is very high. The limited diffusion length explains the presence of a large number of nucleation centres on terraces at room temperature. Post-annealing appeared nearly inefficient in pushing the reaction on this surface beyond the formation of individual boroxine trimers.¹⁵ The best polymers were obtained at high fluxes on both silver and gold. On these two surfaces the mobility of BDBA molecules allows frequent and efficient contact between molecules at room temperature, while desorption remains low. Additionally, it is important to avoid prior formation of the supramolecular phase that severely limits the quality of the polymer.

All defects formed during the growth process in UHV cannot be cured by post-annealing because of the irreversible character of the covalent bonding. In fact, the growth of an extended network is strongly limited by the prior formation of small oligomeric species as soon as few precursors start reacting. Their diffusivity is strongly reduced or completely stopped, and this prevents from the possibility of polymer grain ripening. A detailed description of the growth process of a covalent network (porous graphene) was reported by Bieri et al.,¹⁴ where it was shown that the growth is mostly governed by the ratio reactivity/diffusivity, whereby the precise reaction pathway over the metal surface considerably influences the efficiency of the covalent coupling.

In short, optimum polymer growth was obtained when the deposition flux and the substrate temperature—which tunes the energetic terms for adsorption, diffusion, and reaction—can be adjusted to open some favourable window, if any, for the direct polymerization process.

Tuning the reactivity by side functionalisation

As described above (see Fig. 3), the dehydration reaction of boronic acid is governed by the Lewis acid activity of boron through the formation of the first transition state of the reaction mechanism. The reactivity of benzene–boronic acid is therefore strongly influenced by the ability of boron to accept an electron pair, which can be affected by the presence of substituents on the benzene ring. Such a substituent effect is well described and depends on its inductive effect (donor or acceptor) and on its position.^54–56ortho- and para-substituents are directly conjugated with the boronic acid group and possess therefore effective inductive effect, while the substituent in meta position is rather inactive. The inductive effect is outlined in the pK_a value of the boronic acid.⁵⁷ An inductive electron-withdrawing substituent increases the acidity of the acid (decreased pK_a) and stabilises the conjugated base, which is the transition state of the dehydration reaction. Electron-withdrawing inductive effect thus tends to increase the reactivity. Note that such an effect is similarly valid for the reverse reaction (hydrolysis of boroxine). As a consequence, under equilibrium conditions substituent induced reactivity changes are hardly predictable a priori.⁴³ However, under the irreversible (dry) conditions of on-surface reaction in UHV, an electron acceptor substituent can only increase the reactivity of boronic acid towards dehydration reaction. Also, the formation of intramolecular hydrogen bond between the boronic acid moiety and the substituent can further modify the reactivity.

For benzene-1,4-diboronic acid, any substituent will be positioned simultaneously in meta for one boronic moiety and in ortho for the other boronic moiety. The reactivity of a series of substituted precursors was characterised under an inert atmosphere by thermal analysis (thermogravimetric analysis, TGA, and differential scanning calorimetry, DSC).^58,59 For non-substituted BDBA, the boroxine formation is characterised by a mass loss of 36 g mol⁻¹ (corresponding to 2 water molecules per precursor) and a corresponding (endothermic) enthalpy of ∼1 eV occurring at a temperature of 210 °C (see Table 1). The measure of the reaction temperature allowed classifying the effects of the different substituents. The precursors 2,5-dimethyl-1,4-benzenediboronic, 2,5-dihydroxy-1,4-benzenediboronic and 2,3,5,6-tetramethyl-1,4-benzenediboronic could not polymerise as they started to degrade before the reaction could occur. The reactivity of 2-nitro-1,4-benzenediboronic acid and 2,5-dimethoxy-1,4-benzenediboronic acid was enhanced and the temperature of polymerisation was measured at 150 °C and 105 °C, respectively. For 2-methyl-1,4-benzenediboronic acid, the reaction had its temperature lowered to 105 °C but was limited to a mass loss of 18 g mol⁻¹ (1 water molecule per precursor) and to an enthalpy of 0.5 eV, thus indicating that only one of the two boronic acids reacted and formed boroxine trimers. Here the formation of an intramolecular hydrogen bond could be an additional factor modifying the reactivity of the asymmetric boronic groups. Nevertheless, on a metal surface, thanks to a modified reaction mechanism the methyl-BDBA precursor could form extended 2D networks. By contrast, the nitro-BDBA precursor could form only limited size oligomers on the surface due to its too high reactivity. The reactivity was thus found opposite in thermal analyses and in UHV-STM experiments. This discrepancy illustrates the strong catalytic activity of the substrate which modifies the reaction path and the importance of controlling the kinetics to create extended 2D polymers.

Table 1 Results from TGA/DSC thermal analyses for a series of functionalised benzene–diboronic acids (Adapted from ref. 58 and 59)

	Reaction temperature [°C] (TGA)	Reaction enthalpy [eV] (DSC)	Polymerisation on a metal surface
BDBA	210	1.0	Extended
Nitro-BDBA	150	1.2	Limited
Dimethoxy-BDBA	105	1.1	N/A
Methyl-BDBA	105	0.5	Extended
Dihydroxy-/dimethyl-/tetramethyl-BDBA	No reaction observed (degradation)

---

Alternative chemistries

Besides the self-dehydratation reaction described above, alternative reactions involving boronic acids can also be used to create extended two-dimensional polymers.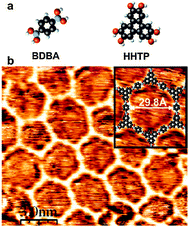

Boronic acid–diol esterification. Boronic acids can react with diols to form a dioxaborole heterocycle. This was demonstrated with the system BDBA-HHTP (hexahydroxy-triphenylene).^21,33,49,60 Here the growth control is delicate because the homopolymerisation of BDBA needs to be prohibited. Copolymerisation was accomplished by first saturating the surface with HHTP followed by co-evaporation of the two molecules on a hot surface. Under such conditions, the bi-molecular esterification reaction was preferred over self-dehydration reaction. The resulting network has a larger pore size (3 nm) as compared to the BDBA-only honeycomb network, as the unit cell comprises 2 HHTP and 3 BDBA (see Fig. 8).

Fig. 8 Covalent network obtained by copolymerisation of diboronic acid (BDBA) and a poly-diol (HHTP). Reprinted with permission from ref. 33. Copyright (2008) American Chemical Society.

Sequential linking. Among the various chemical functions explored to create C–C bonds and covalent coupling on a surface, the Ullmann coupling reaction deserves special attention. It was demonstrated to be highly efficient for the formation of extended 1D polymers^61–63 as well as some 2D-networks.^{14,50,64–66} It consists of the homolytic rupture of an aryl-halogen bond followed by radical coupling to form a new C–C bond.⁶⁷ The underlying metal surface has a decisive catalytic role in this reaction and stabilizes the otherwise highly reactive intermediate radicals.^14,16 The Ullmann coupling reaction is thermally activated on noble metal surfaces at temperatures of 100 to 200 °C. As the self-dehydration of boronic acid occurs at room temperature, a well-designed precursor bearing both a halogen atom and a boronic acid function can thus undergo sequential polymerisation. This was demonstrated with the compound 1-bromobenzene-4-boronic acid (Fig. 9).⁶⁸ The boronic acid groups of the latter precursor deposited on a Au(111) surface at room temperature reacted to form boroxine trimers that self-assembled into an extended dense supramolecular network. Annealing this phase at a temperature of 250 °C resulted in the activation of the radical coupling of the halogenated moieties and in the formation of a 2D nanoporous polymer. Similar to the case of BDBA discussed above, the prior formation of a supramolecular phase was not favourable to the polymerisation reaction mechanism and resulted in incomplete reaction advancement. The number of monomers that effectively reacted through Ullmann coupling was limited to 88% and a large number of defects was observed; the formation of closed polygons represented only 40% of the whole surface covered by the polymer.⁶⁸ To overcome this hurdle, the formation of the supramolecular phase was prevented by depositing the precursors on a surface kept at 200 °C. This resulted in a 2D polymer of high quality (Fig. 9) where the reaction advancement reached 95% and the surface fraction covered by regular closed polymers increased to 75%. The larger network size and the elongated shape of the pore walls (consisting in biphenyl as compared to single phenyl for the BDBA network) allowed larger flexibility in the geometry of the pore. Besides majority of hexagonal, pentagonal and heptagonal pores, tetragonal and octagonal pore shapes were also observed. Interestingly, the pore shape distribution did not depend on the growth parameters as it was very similar for the room temperature deposited, post-annealed sample and for the high temperature deposited sample. In fact such pore shape distribution is very similar to what can be observed in other physical (Bénard–Marangoni convection cells, 2D soap froth), biological (epithelial cells) or even geological (the Giant's Causeway) systems. There, an entropy-maximizing equilibrium model can adequately describe the pore distribution.^69,70

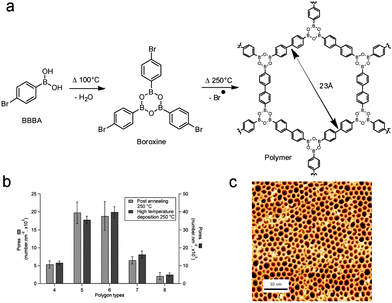Fig. 9 (a) Reaction scheme for the sequential polymerisation of 1-bromobenzene-4-boronic acid (BBBA) through boronic acid self-dehydration followed by Ullmann radical coupling. (b) Distribution of the polygonal pore shape for room temperature post-annealed and hot substrate depositions. (c) STM image of the high quality 2D polymer obtained by hot substrate deposition. Adapted with permission from ref. 68. Copyright (2012) American Chemical Society.

The dual coupling strategy was similarly demonstrated with the molecule 3,5-dibromophenylboronic acid on a Ag(111) surface.⁷¹ In this case, the Ullmann coupling between boroxine trimers is twofold, what increases the reaction possibilities. Nevertheless, well-ordered networks could form, with a domain size limited however to ∼20 nm.

Conclusions and outlook

Diboronic acid is a prototypical system revealing the complex mechanisms governing the growth of a 2D polymer. Important and decisive issues are the irreversibility of the reaction involving 3 reactants and the catalytic effect of the substrate. In the UHV environment, the polymerised phase forms under kinetic conditions (high deposition flux) while thermodynamic conditions (low deposition flux) favour the formation of a metastable supramolecular phase.

The relevance of this class of systems is already largely demonstrated by the achievement of various COFs with well-controlled structure and functionality. Two recent issues described below highlight their high potential for a wide range of applications on a surface.

2D polymer as a tool for nanolithography

An important characteristic of the BDBA polymer is its high thermal stability as it can withstand annealing temperatures of up to 450 °C. In a bottom-up strategy for surface nanostructuring, this 2D-polymer can be combined with a secondary self-assembled system in a hierarchical process to transfer a specific pattern (see Fig. 10).⁷² As a prototypical system, NaCl was deposited on a Ag(100) surface to produce well-defined square islands.⁷³ When deposited on such a surface, BDBA adsorbed preferentially on the free parts of the metal surface, where its self-polymerisation reaction was activated. As a result, the 2D polymer was patterned through precise surrounding of the NaCl islands. Annealing at a temperature of 250 °C selectively removed (desorbed) the NaCl islands while the polymer mask was kept intact. The latter was further used to selectively deposit additional material into the free parts of the patterned surface. This strategy is very similar to the traditional (hybrid) strategies for nanolithography^74–76 but is exclusively based on self-assembly techniques.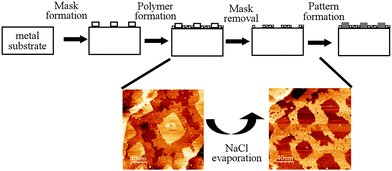

Fig. 10 Schematic of the sequential strategy making use of self-assembly processes and of the high thermal resistance of a boronic acid based 2D polymer in a lithography-mimicking sequence. On a Ag(100) surface, the mask is constituted by square-shaped NaCl islands and the polymer is formed from BDBA precursors. Bottom: STM images of the BDBA polymer surrounding NaCl islands (left) and of the square-patterned BDBA polymer after annealing and NaCl evaporation (right). Adapted with permission from ref. 72, copyright (2012) Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim.

Chemical equilibrium conditions

Due to the highly dilute character of the UHV environment and the strict confinement to the surface, the growth of the boronic acid based covalent network is limited by the irreversible character of the dehydration reaction. As a result, the 2D polymer phase represents the kinetic limiting phase. Recently, two different groups demonstrated the formation of perfectly ordered, extended covalent networks from benzene–diboronic acid or equivalent derivatives (Fig. 11).^77–79 To achieve thermodynamic equilibrium of the dehydration reaction, the boronic acid based system on the surface was annealed in a sealed reactor in the presence of partial water pressure under atmospheric conditions. Water was introduced directly^77,79 or in the form of CuSO₄·5H₂O.⁷⁸ As a result, crystalline networks could form and be imaged by STM under ambient conditions. Note that the ambient moisture degrades the layer in a few days, but the annealing procedure can reversibly heal the network and make it recover its crystallinity.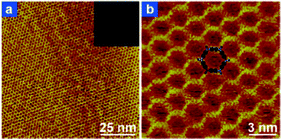

Fig. 11 STM images of the prefect honeycomb network grown from biphenyl-diboronic acid under chemical equilibrium conditions (annealed in the presence of water pressure). Adapted from ref. 78.

In addition, these works demonstrated the flexibility of network formation by use of various precursors where the core unit in-between the two boronic acid moieties were varied using carbon-only groups (bi-, ter- or quarter-phenyl or pyrene).^78,79 In such cases, hexagonal pores of different sizes were formed, depending on the precursor length, while the reactivity and the polymerisation mechanism of the boronic acid were preserved.

Acknowledgements

We thank our co-workers and colleagues for discussions and for their work which is reviewed in this article, in particular Nic Zwaneveld, Rémy Pawlak, Oualid Ourdjini, Thomas Faury, Mathieu Koudia, Daniel Catalin, Laurent Nony, Franck Bocquet, Christian Loppacher, Jean-Marc Themlin, Roland Coratger, Frédéric Dumur, Didier Gigmes, Denis Bertin, Bernard Billia, Liang Chen, Nathalie Bergeon, Michel Sassi, Vincent Oison, Jean-Marc Debierre. This work has been carried out thanks to the support of the A*MIDEX project (no ANR-11-IDEX-0001-02) funded by the “Investissements d'Avenir” French Government program, managed by the French National Research Agency (ANR). Michael Stöger-Pollach is gratefully acknowledged for fruitful discussions.

Notes and references

1. J.-M. Lehn, Supramolecular Chemistry, Concepts and Perspectives, VCH, Weinheim, 1995.
2. J. V. Barth, Annu. Rev. Phys. Chem., 2007, 58, 375–407.
3. T. Kudernac, S. B. Lei, J. Elemans and S. De Feyter, Chem. Soc. Rev., 2009, 38, 402–421.
4. Y. L. Yang and C. Wang, Chem. Soc. Rev., 2009, 38, 2576–2589.
5. J. Björk and F. Hanke, Chem. – Eur. J., 2014, 20, 928–934.
6. J. Mendez, M. F. Lopez and J. A. Martin-Gago, Chem. Soc. Rev., 2011, 40, 4578.
7. X. M. Zhang, Q. D. Zeng and C. Wang, Nanoscale, 2013, 5, 8269–8287.
8. M. El Garah, J. M. MacLeod and F. Rosei, Surf. Sci., 2013, 613, 6–14.
9. M. Lackinger and W. M. Heckl, J. Phys. D: Appl. Phys., 2011, 44, 464011.
10. G. Franc and A. Gourdon, Phys. Chem. Chem. Phys., 2011, 13, 14283.
11. A. Gourdon, Angew. Chem., Int. Ed., 2008, 47, 6950–6953.
12. D. F. Perepichka and F. Rosei, Science, 2009, 323, 216–217.
13. J. Sakamoto, J. van Heijst, O. Lukin and A. D. Schluter, Angew. Chem., Int. Ed., 2009, 48, 1030–1069.
14. M. Bieri, M. T. Nguyen, O. Gröning, J. M. Cai, M. Treier, K. Ait-Mansour, P. Ruffieux, C. A. Pignedoli, D. Passerone, M. Kastler, K. Mullen and R. Fasel, J. Am. Chem. Soc., 2010, 132, 16669–16676.
15. O. Ourdjini, R. Pawlak, M. Abel, S. Clair, L. Chen, N. Bergeon, M. Sassi, V. Oison, J.-M. Debierre, R. Coratger and L. Porte, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125421.
16. J. Björk, F. Hanke and S. Stafstrom, J. Am. Chem. Soc., 2013, 135, 5768–5775.
17. D. Y. Zhong, J. H. Franke, S. K. Podiyanachari, T. Blomker, H. M. Zhang, G. Kehr, G. Erker, H. Fuchs and L. F. Chi, Science, 2011, 334, 213–216.
18. X. Feng, X. S. Ding and D. L. Jiang, Chem. Soc. Rev., 2012, 41, 6010–6022.
19. S. Y. Ding and W. Wang, Chem. Soc. Rev., 2013, 42, 548–568.
20. W. J. Niu, M. D. Smith and J. J. Lavigne, J. Am. Chem. Soc., 2006, 128, 16466–16467.
21. A. P. Cote, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170.
22. E. L. Spitler and W. R. Dichtel, Nat. Chem., 2010, 2, 672–677.
23. A. P. Cote, H. M. El-Kaderi, H. Furukawa, J. R. Hunt and O. M. Yaghi, J. Am. Chem. Soc., 2007, 129, 12914.
24. R. W. Tilford, W. R. Gemmill, H. C. zur Loye and J. J. Lavigne, Chem. Mater., 2006, 18, 5296–5301.
25. N. Fujita, S. Shinkai and T. D. James, Chem. – Asian J., 2008, 3, 1076–1091.
26. K. E. Maly, N. Malek, J. H. Fournier, P. Rodriguez-Cuamatzi, T. Maris and J. D. Wuest, Pure Appl. Chem., 2006, 78, 1305–1321.
27. R. Nishiyabu, Y. Kubo, T. D. James and J. S. Fossey, Chem. Commun., 2011, 47, 1124–1150.
28. S. Varughese, S. B. Sinha and G. R. Desiraju, Sci. China: Chem., 2011, 54, 1909–1919.
29. K. Severin, Dalton Trans., 2009, 5254–5264.
30. A. L. Korich and P. M. Iovine, Dalton Trans., 2010, 39, 1423–1431.
31. K. L. Bhat, G. D. Markham, J. D. Larkin and C. W. Bock, J. Phys. Chem. A, 2011, 115, 7785–7793.
32. Y. Tokunaga, Heterocycles, 2013, 87, 991–1021.
33. N. A. A. Zwaneveld, R. Pawlak, M. Abel, D. Catalin, D. Gigmes, D. Bertin and L. Porte, J. Am. Chem. Soc., 2008, 130, 6678–6679.
34. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76.
35. G. R. Desiraju, Acc. Chem. Res., 2002, 35, 565–573.
36. P. Rodriguez-Cuamatzi, G. Vargas-Diaz, T. Maris, J. D. Wuest and H. Hopfl, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, O1316–O1318.
37. F. Bocquet, L. Nony, S. C. B. Mannsfeld, V. Oison, R. Pawlak, L. Porte and C. Loppacher, Phys. Rev. Lett., 2012, 108, 206103.
38. R. Pawlak, L. Nony, F. Bocquet, V. Olson, M. Sassi, J. M. Debierre, C. Loppacher and L. Porte, J. Phys. Chem. C, 2010, 114, 9290–9295.
39. D. E. Hooks, T. Fritz and M. D. Ward, Adv. Mater., 2001, 13, 227–241.
40. S. C. B. Mannsfeld, K. Leo and T. Fritz, Phys. Rev. Lett., 2005, 94, 056104.
41. O. Ourdjini, PhD thesis, Aix-Marseille Université, 2012.
42. S. Clair, O. Ourdjini, M. Abel and L. Porte, Chem. Commun., 2011, 47, 8028.
43. Y. Tokunaga, H. Ueno, Y. Shimomura and T. Seo, Heterocycles, 2002, 57, 787–790.
44. M. Sassi, V. Oison, J. M. Debierre and S. Humbel, ChemPhysChem, 2009, 10, 2480–2485.
45. J. Kua and C. R. Gyselbrecht, J. Phys. Chem. A, 2007, 111, 4759–4766.
46. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385.
47. T. C. Tseng, C. Urban, Y. Wang, R. Otero, S. L. Tait, M. Alcami, D. Ecija, M. Trelka, J. M. Gallego, N. Lin, M. Konuma, U. Starke, A. Nefedov, A. Langner, C. Woll, M. A. Herranz, F. Martin, N. Martin, K. Kern and R. Miranda, Nat. Chem., 2010, 2, 374–379.
48. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671.
49. R. Pawlak, PhD thesis, Aix-Marseille Université, 2009.
50. M. O. Blunt, J. C. Russell, N. R. Champness and P. H. Beton, Chem. Commun., 2010, 46, 7157–7159.
51. R. Gutzler, H. Walch, G. Eder, S. Kloft, W. M. Heckl and M. Lackinger, Chem. Commun., 2009, 4456–4458.
52. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870–873.
53. C. Dussert, G. Rasigni, M. Rasigni, J. Palmari and A. Llebaria, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 3528–3531.
54. M. K. Cyrański, P. Klimentowska, A. Rydzewska, J. Serwatowski, A. Sporzyński and D. K. Stȩpień, CrystEngComm, 2012, 14, 6282.
55. S. Soundararajan, E. N. Duesler and J. H. Hageman, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1993, 49, 690–693.
56. M. Filthaus, I. M. Oppel and H. F. Bettinger, Org. Biomol. Chem., 2008, 6, 1201–1207.
57. J. Yan, G. Springsteen, S. Deeter and B. H. Wang, Tetrahedron, 2004, 60, 11205–11209.
58. T. Faury, F. Dumur, S. Clair, M. Abel, L. Porte and D. Gigmes, CrystEngComm, 2013, 15, 2067.
59. T. Faury, PhD thesis, Aix-Marseille Université, 2013.
60. R. Coratger, B. Calmettes, M. Abel and L. Porte, Surf. Sci., 2011, 605, 831–837.
61. C. Bombis, F. Ample, L. Lafferentz, H. Yu, S. Hecht, C. Joachim and L. Grill, Angew. Chem., Int. Ed., 2009, 48, 9966–9970.
62. J. M. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Mullen and R. Fasel, Nature, 2010, 466, 470–473.
63. J. A. Lipton-Duffin, J. A. Miwa, M. Kondratenko, F. Cicoira, B. G. Sumpter, V. Meunier, D. F. Perepichka and F. Rosei, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 11200–11204.
64. M. Bieri, S. Blankenburg, M. Kivala, C. A. Pignedoli, P. Ruffieux, K. Mullen and R. Fasel, Chem. Commun., 2011, 47, 10239–10241.
65. L. Grill, M. Dyer, L. Lafferentz, M. Persson, M. V. Peters and S. Hecht, Nat. Nanotechnol., 2007, 2, 687–691.
66. S. A. Krasnikov, C. M. Doyle, N. N. Sergeeva, A. B. Preobrajenski, N. A. Vinogradov, Y. N. Sergeeva, A. A. Zakharov, M. O. Senge and A. A. Cafolla, Nano Res., 2011, 4, 376–384.
67. J. Hassan, M. Sevignon, C. Gozzi, E. Schulz and M. Lemaire, Chem. Rev., 2002, 102, 1359–1469.
68. T. Faury, S. Clair, M. Abel, F. Dumur, D. Gigmes and L. Porte, J. Phys. Chem. C, 2012, 116, 4819.
69. D. Weaire and N. Rivier, Contemp. Phys., 1984, 25, 59–99.
70. A. Hocevar, S. El Shawish and P. Ziherl, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 369–375.
71. S. Schlögl, T. Sirtl, J. Eichhorn, W. M. Heckl and M. Lackinger, Chem. Commun., 2011, 47, 12355–12357.
72. S. Clair, O. Ourdjini, M. Abel and L. Porte, Adv. Mater., 2012, 24, 1252.
73. M. Pivetta, F. Patthey, M. Stengel, A. Baldereschi and W. D. Schneider, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 115404.
74. H. M. Saavedra, T. J. Mullen, P. P. Zhang, D. C. Dewey, S. A. Claridge and P. S. Weiss, Rep. Prog. Phys., 2010, 73, 036501.
75. A. Perl, D. N. Reinhoudt and J. Huskens, Adv. Mater., 2009, 21, 2257–2268.
76. Y. N. Xia and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 551–575.
77. J. F. Dienstmaier, A. M. Gigler, A. J. Goetz, P. Knochel, T. Bein, A. Lyapin, S. Reichlmaier, W. M. Heckl and M. Lackinger, ACS Nano, 2011, 5, 9737–9745.
78. C. Z. Guan, D. Wang and L. J. Wan, Chem. Commun., 2012, 48, 2943–2945.
79. J. F. Dienstmaier, D. D. Medina, M. Dogru, P. Knochel, T. Bein, W. M. Heckl and M. Lackinger, ACS Nano, 2012, 6, 7234–7242.

---