Multimodal optical sensing based on a Sm3+-activated Sr3Sn2O7 phosphor: stress visualization and temperature monitoring
Minyu
Jin†
a,
Wenhao
Li†
a,
Luyue
Niu
a,
Yongshun
Gu
b,
Jiancai
Xie
c,
Shuo
Liu
*a,
Feng
Yan
a,
Jing
Ren
 *a and
Jianzhong
Zhang
a
*a and
Jianzhong
Zhang
a
aKey Laboratory of In-Fiber Integrated Optics of Ministry of Education, College of Physics and Optoelectronic Engineering, Harbin Engineering University, Harbin 150001, China. E-mail: liushuoheu@hrbeu.edu.cn; ren.jing@hrbeu.edu.cn
bCollege of Science, Inner Mongolia University of Technology, Hohhot, 010051, China
cGuang Zhou Rong Fan Technology CO., LTD., China
First published on 31st July 2025
Abstract
Conventional mechanoluminescent (ML) materials are limited to stress sensing, restricting their application in integrated optical sensing. In this study, we develop a multimode-emitting phosphor, Sr2.996(Sn1.75Ge0.25)O7.002:0.004Sm3+, which exhibits simultaneously excellent ML properties through defect engineering of the host matrix and non-contact temperature sensing capability based on the fluorescence intensity ratio (FIR). The incorporation of Li+ boosts the ML intensity by approximately 4-fold, resulting in an ML signal 30 times stronger than its persistent luminescence (PersL). The enhancement drastically suppresses the PersL interference during stress sensing. Furthermore, the phosphor exhibits a high relative temperature sensitivity of 1.48% K−1 at 303 K. Experimental characterization and first-principles calculations elucidate the mechanism behind the ML enhancement. Multifunctional phosphors, capable of simultaneous non-contact stress and temperature sensing, have significant potential for application in advanced optical sensing systems, particularly in high-temperature, high-pressure machinery monitoring, and are expected to find practical applications in industrial monitoring, biomedical devices, aerospace and deep-water exploration.
1. Introduction
Accurate measurement of temperature and stress is essential in fields ranging from biomedicine and materials science to industrial manufacturing and daily life. As technology advances, there is a growing demand for sensors that can operate reliably in complex environments while offering fast and precise detection. Conventional electrical sensors are often limited by their sensitivity to electromagnetic interference and environmental fluctuations, restricting their use and performance.1 They also fall short in aspects such as low energy consumption, miniaturization, and real-time visualization.2 In contrast, optical sensors offer simpler architectures, require no external power, and perform well in challenging settings, including within the human body.3–5 Among these, elastic mechanoluminescent (ML) materials exhibit light emission upon mechanical stress, where the ML intensity typically scales linearly with the applied force, enabling quantitative stress detection. Photoluminescent materials, meanwhile, allow temperature sensing through analysis of emission lifetime, bandwidth, or fluorescence intensity ratio (FIR), with FIR-based techniques providing high accuracy, a wide detection range, and fine resolution.6 However, as application scenarios grow increasingly complex, conventional single-mode sensors often prove insufficient. This limitation has spurred significant demand for multifunctional materials which can concurrently monitor both mechanical stress and temperature variations.In recent years, a large number of studies on stress-temperature dual-mode optical sensors have emerged. In 2021, Chen et al.7 demonstrated visualized dual-mode stress and temperature sensing by utilizing the intensity ratio of two rare-earth ion emission peaks in the ML of SrZnOS:Tb3+,Eu3+. However, the stress-dependent excitation mechanism presents significant implementation challenges for temperature sensing in structurally simplified, miniaturized sensors. Subsequently, in 2023, Li et al.8 developed an alternative dual-mode sensing approach using Sr2MgAl22O36:Mn2+, though their temperature detection relied solely on the absolute intensity of a single emission peak rather than a dual-peak intensity ratio, consequently exhibiting compromised measurement accuracy and inferior interference resistance. Therefore, we should focus on discovering materials for stress-temperature dual-mode sensing that offer simpler sensing mechanisms and higher sensitivity.
The luminescence of Sm3+ originates from the radiative transitions from 4G5/2 to 6H5/2, 6H7/2, 6H9/2, and 6H11/2, resulting in four non-overlapping luminescence peaks. This provides the possibility of FIR testing under single doping of Sm3+ luminescence centers.9 Compared with most reported stress-temperature dual-mode sensing materials based on multi-rare-earth-ion doping,10–12 optical materials doped with single rare-earth ions possess simpler chemical compositions, along with lower fabrication costs and reduced synthesis complexity. There have been numerous reports on the ML properties and temperature-dependent photoluminescence (PL) characteristics of Sm3+-activated phosphors,13–18 research on dual-mode sensing applications based on Sm3+ luminescence remains unexplored to date, and this study presents the first demonstration of a dual-mode sensing platform utilizing Sm3+ ion luminescence, in order to make it capable of coping with increasingly complex application scenarios. Based on above considerations, we adopted the optimal composition of Ge-doped Sr3Sn2O7:Sm3+ (SSS) developed by Li et al.16 Through systematic incorporation of Li as a flux agent into the SSS matrix, we determined that a doping concentration of 30 mol% achieved maximum ML intensity. Comparative analysis revealed that the persistent luminescence (PersL) intensity was negligible relative to the ML signal, demonstrating minimal interference from PersL in stress detection applications. The temperature dependence of 30 mol% Li doped SSS was also investigated across a broad thermal range from 303 K to 583 K. Through experimental data analysis and comparison with recently reported dual-mode sensing materials,10,11,19,20 it was found that our samples show sufficiently high fitting accuracy for linear distribution in stress optical sensing and Boltzmann distribution in temperature optical sensing, while demonstrating obvious advantages in relative sensitivity. The material demonstrated excellent potential for optical thermometry applications via the FIR technique. Combined experimental characterization and first-principles calculations elucidated the underlying mechanism responsible for ML enhancement.
2. Results and discussion
2.1. Crystal phase and microstructure
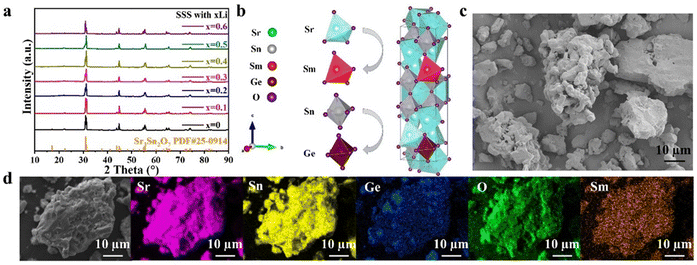
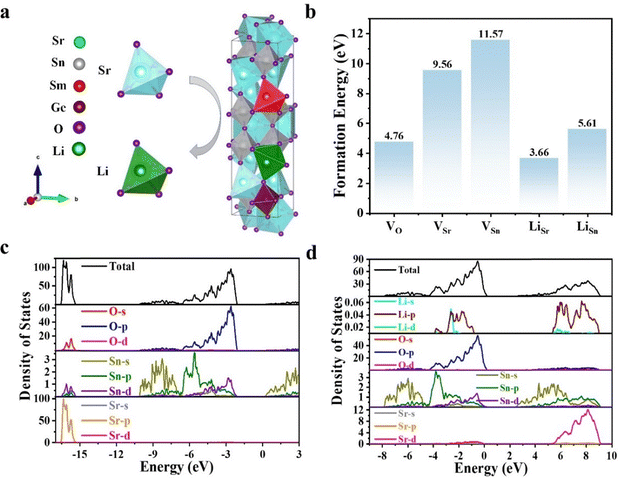
Fig. 1a shows the X-ray diffraction (XRD) patterns of Sr3Sn2O7:Sm3+ samples with varying concentrations of Li doping. All samples exhibit diffraction peaks consistent with the standard orthorhombic phase of Sr3Sn2O7 (PDF #25-0914), confirming that the incorporation of Sm3+, Ge4+, and Li+ does not alter the host crystal structure. The space group remains A21am,21–23 as illustrated in Fig. 1b. After structural optimization, the lattice parameters were determined to be a = 5.77752 Å, b = 5.77312 Å, and c = 20.7151 Å. Each Sr atom is coordinated by six oxygen atoms, forming a distorted octahedron. A scanning electron microscopy (SEM) image of the sample with 30 mol% Li doping is presented in Fig. 1c, showing irregularly shaped particles with an average size of ∼6 μm. Elemental mapping by energy-dispersive X-ray spectroscopy (EDS), shown in Fig. 1d, confirms the uniform distribution of Sr, Sn, Ge, O, and Sm throughout the sample.2.2. ML properties
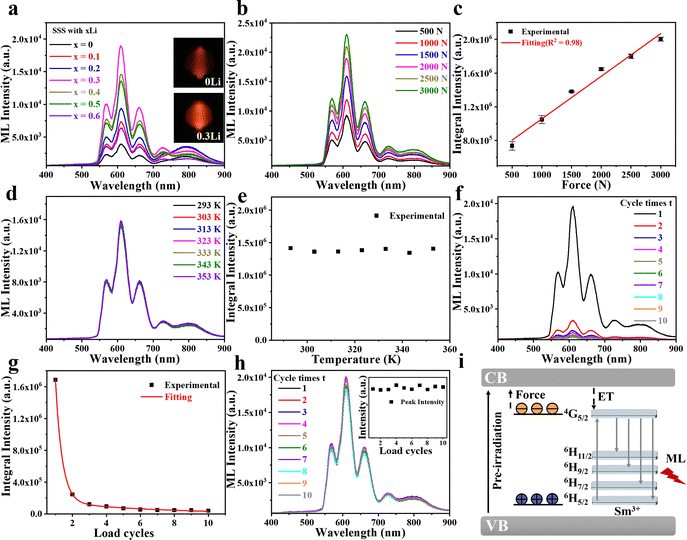
As shown in Fig. 2a, the ML spectra of samples under a compressive force of 2000 N exhibit red emission, with intensity varying with Li doping concentration. The spectra display five distinct emission bands in the ranges of 550–580 nm, 580–640 nm, 640–700 nm, 700–760 nm, and 760–950 nm. The first four bands arise from Sm3+ transitions from the excited state 4G5/2 to the 6H5/2, 6H7/2, 6H9/2, and 6H11/2 levels, respectively.14,24 The broad emission from 760 to 950 nm is attributed to the Sr3Sn2O7 host matrix. The ML intensity of the host peaks at 20 mol% Li doping, while the Sm3+-related emission continues to increase up to 30 mol%, showing a four-fold enhancement before declining at higher concentrations. Thus, 30 mol% Li doping yields the strongest Sm3+ emission. The discrepancy in intensity trends between the host and Sm3+ suggests a possible energy transfer from the matrix to the dopant.25 It is proposed that Li doping facilitates the transfer process, particularly at higher concentrations.As shown in Fig. 2b, the ML spectra of SSS doped with 30 mol% Li (denoted as SSS:0.3Li) were measured under varying compressive loads. The ML intensity increases nearly linearly with the applied force from 500 N to 3000 N (Fig. 2c), suggesting the material's potential for quantitative stress sensing. To assess thermal stability in practical sensing applications, the ML response at temperatures ranging from 293 K to 353 K is investigated (Fig. 2d). The results show minimal variation in ML intensity across this temperature range (Fig. 2e), indicating good thermal stability under small temperature fluctuations. Fig. 2f presents the ML spectra after 10 successive compressive loadings at 2000 N. A sharp decrease in ML intensity occurs after the first cycle, suggesting that most charge carriers trapped in the material are released during initial loading. After ten cycles, the integrated ML intensity drops to 2.40% of its original value (Fig. 2g). To test recoverability, the sample was exposed to 365 nm UV light for one minute before each loading cycle (Fig. 2h). The ML intensity exhibited excellent stability over 10 consecutive cycles, demonstrating that UV irradiation effectively replenishes trapped carriers and confirming the robust, repeatable rechargeability of the ML response.
The mechanism of ML generation in SSS is illustrated in Fig. 2i. Under UV irradiation, electrons are excited from the valence band to the conduction band and are subsequently trapped by electron traps, while holes are captured by hole traps. When a mechanical load is applied, slight displacements of cation and anion centers occur along specific lattice directions, generating an internal piezoelectric field. This field promotes the release of trapped charge carriers. Electrons return to the valence band via the conduction band, and holes are released from the hole traps. The recombination of these carriers transfers energy to Sm3+ ions, which then undergo radiative transitions, producing the observed ML emission.26,27
To distinguish the interference of PersL on ML signals, the luminescence spectra of SSS and SSS:0.3Li were monitored continuously for 10 seconds before applying a compressive load (Fig. 3a and b). Both samples exhibited PersL following UV excitation. After 60 seconds, a compressive load was applied, triggering ML emission. The ML intensity of SSS was 11.88 times greater than its PersL intensity, while that of SSS:0.3Li was 30 times greater (Fig. 3c and d). The significantly stronger ML compared to PersL, particularly in the Li-doped sample, confirms that PersL has minimal interference with the material's optical stress-sensing performance.
2.3. Photoluminescence and temperature sensing properties
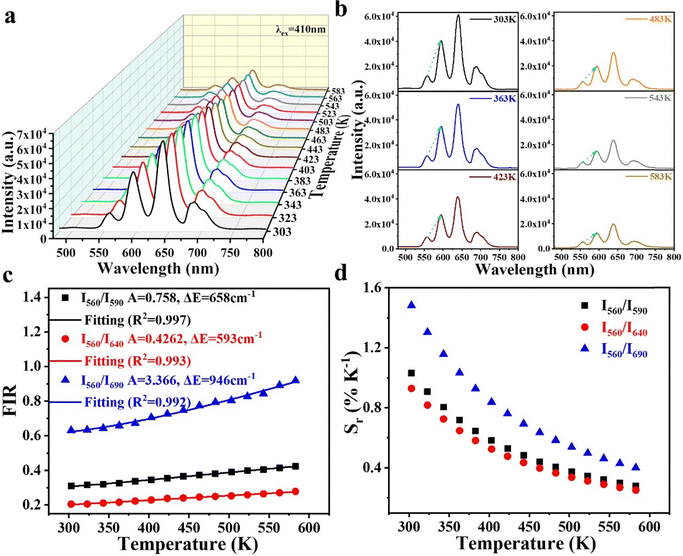
The photoluminescence excitation (PLE) spectra of the SSS phosphor, excited at 405 nm, with PL spectra, monitored at 647 nm, are shown in Fig. 4a and b, respectively. The PLE spectra show distinct absorption peaks corresponding to broad charge transfer spectra (CTS) and Sm3+ in the range of 230–310 nm. The CTS band is attributed to the O2-Sm3+ transition.28–30 Other peaks are ascribed to the transitions of Sm3+ from the 6H5/2 state to the 3H7/2, 4D5/2, 6P7/2, 4K11/2, 6P5/2, 4G9/2, 4F5/2, 4G7/2 and 4F3/2 states.28,31–33 The PL spectra of SSS with 0.3Li under 405 nm excitation exhibit five emission bands in the ranges of 430–550 nm, 550–580 nm, 580–620 nm, 620–680 nm, and 690–740 nm. These bands correspond to radiative transitions of Sm3+ from the excited 4F3/2 state to the 6H5/2 state and from the 4G5/2 state to the 6H5/2 and 6H7/2 states. The photoluminescence mechanism of Sm3+ is illustrated in Fig. 4c. Upon absorbing photon energy at 405 nm, the Sm3+ ion in the 6H5/2 (ground state) is excited to the 4K11/2 state. The Sm3+ ion in the 4K11/2 state then undergoes a non-radiative transition to the 4F3/2 state, where it relaxes to the 6H5/2 state through a radiative process, producing radiation with a peak wavelength of 524 nm. Some ions in the 4F3/2 state are transferred to the 4G5/2 state via a non-radiative process34 and subsequently relax radiatively to the 6H5/2 state, generating four emission bands with peak wavelengths at 563 nm, 600 nm, 647 nm, and 706 nm, respectively.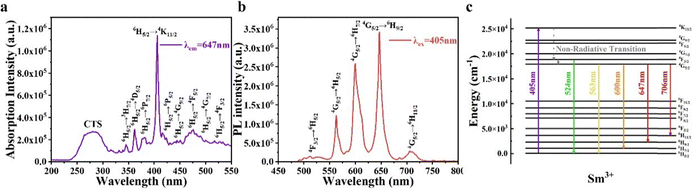 | ||
| Fig. 4 (a) PLE spectra of SSS with 0.3Li. (b) PL spectra of SSS with 0.3Li. (c) Mechanism of the Sm3+ luminescence process. | ||
Fig. 5a demonstrates the variation of PL with temperature. The fluorescence intensity of the leaps 4G5/2–6HJ (J = 5/2, 7/2, 9/2, 11/2) decreases with increasing temperature due to the thermal burst effect. The temperature dependence of the FIR between any two peaks can be expressed by the Boltzmann distribution rule as follows:35
 | (1) |
The monotonic relationship between FIR and temperature, and its relevance for optical temperature sensing, is further illustrated in two ways. Fig. S1b, shows the normalized PL spectra at 600 nm across six temperatures. Notably, the emission intensity at 563 nm increases with temperature, supporting the observed trend of the I560/I590 ratio rising with temperature. Sensitivity is a key parameter for evaluating temperature sensing performance. The relative sensitivity Sr is defined as follows:11
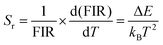 | (2) |
As shown in Fig. 5d, Sr for the three FIR ratios (I560/I590, I560/I640 and I560/I690) decreases monotonically with increasing temperature. Among them, I560/I690 exhibits the highest sensitivity, suggesting that it is most effective for temperature determination. The temperature resolution (δT) can be calculated using the following equation:36
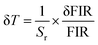 | (3) |
2.4. Traps and bandgaps
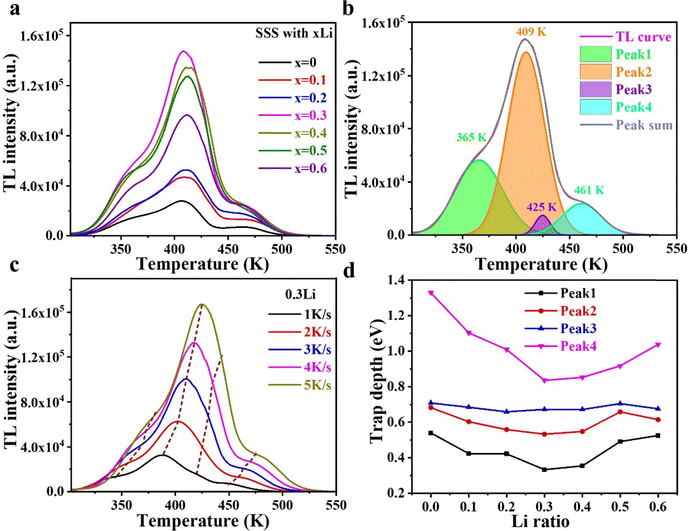
Thermoluminescence (TL) can characterize the concentration and distribution of traps in luminescent materials.37,38 The TL curves of samples with different Li doping concentrations are shown in Fig. 6a. With the increase of Li doping concentration, the TL becomes stronger and reaches the maximum value at a doping concentration of 0.3Li and then decreases. The pattern of change is consistent with that of ML intensity, indicating that the ML of SSS is dominated by traps, and the increase in the trap concentration due to Li doping is an important reason for the enhancement of ML strength. The TL curves of the samples with different Li doping concentrations are similar in shape and have four peaks with peak temperatures of 365 K, 409 K, 425 K and 461 K, corresponding to the four trap centers,24 indicating that the introduction of Li+ only changes the trap concentration but not the trap distribution. The four peaks corresponding to the four trap centers were obtained by TL curve fitting of the peak of SSS with 0.3Li in Fig. 6b.Trap depths at the four trap centers were estimated using the heating rate method.39 The temperature Tm corresponding to the maximum value of the peak of the TL curve is given by the following equation:
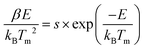 | (4) |
To investigate the effect of Li doping on the bandgap, diffuse reflectance spectra were measured for SSS samples with varying Li concentrations (Fig. S5a). The optical bandgap was estimated using Tauc plots, where [hνF(R∞)]2 was plotted against photon energy hν (Fig. S6). Here, F(R∞) represents the reflectance function derived from the diffuse reflectance data. The experimental bandgap is determined by extrapolating the linear region of the curve to its intersection with the energy axis. As shown in Fig. S5b, the bandgap decreases with increasing Li content. This bandgap narrowing is likely a key factor contributing to the enhancement of ML intensity. A smaller bandgap allows more electrons to be excited into the conduction band under UV excitation, increasing the probability of their subsequent capture by traps.
2.5. Theoretical calculations of the effect of Li doping
As shown in Fig. 7a, Li is most likely to substitute for Sr in the lattice. This conclusion is supported by calculations of defect formation energy (DFE), a key indicator of the thermodynamic stability of doped systems. The DFE of a defect with charge state q is given by the following expression:43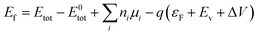 | (5) |
Here, Etot is the total energy of the defect-containing supercell, and E0tot is the total energy of the pristine supercell. ni and μi are the number and chemical potential of atoms of species i, respectively. εF is the Fermi level referenced to the valence band maximum Ev, and ΔV accounts for potential alignment between defective and perfect cells. Applying this theoretical model, we quantitatively evaluated the formation energetics of various defect types: vacancy defects, substitutional dopants, and their complex combinations (Fig. 7b). Before Li doping, the formation energies of vacancies followed the order: VO (4.76 eV) < VSr (9.56 eV) < VSn (11.57 eV). Upon Li doping, the formation energies of the substitutional defects LiSr and LiSn decreased significantly to 5.90 eV and 5.95 eV. These results suggest that Li most favorably replaces Sr. Fig. S7, shows that Li doping narrows the bandgap of Sr3Sn2O7 from 2.51 eV to 0.01 eV. This trend agrees with the experimental results obtained from diffuse reflectance spectra. The electronic density of states (DOS) for undoped Sr3Sn2O7 (Fig. 7c) indicates that the valence band is primarily composed of O p and Sn s, p, and d orbitals, while the conduction band contribution from Sn is limited. After Li doping (Fig. 7d), a significant increase in conduction band states is observed, mainly arising from Sr d, Sn s, p, d, O p, and newly introduced Li s and p orbitals.
3. Conclusions
Li-doped SSS phosphors with an orthorhombic A21am crystal structure were synthesized using a high-temperature solid-state method. By tuning the Li doping concentration, a significant enhancement in ML intensity was achieved. Systematic optimization revealed 30 mol% as the optimal doping concentration, achieving a four-fold enhancement in ML intensity compared to the undoped sample. The ML response exhibited a linear relationship with compressive force in the range of 500–3000 N. Notably, the ML intensity was found to be approximately 30 times stronger than that of PersL. For PL, the FIR between the 4G5/2 → 6H5/2 transition and the 4G5/2 → 6H7/2, 6H9/2, and 6H11/2 transitions of Sm3+ increased with temperature. Based on these findings, a dual-mode sensing platform is established for simultaneous stress and temperature detection: ML intensity correlates linearly with mechanical load, while the FIR-based temperature readout is unaffected by PersL. The maximum temperature sensitivity reached 1.48% K−1 at 303 K, indicating excellent thermal sensing performance. Analysis of TL curves and diffuse reflectance spectra reveals that the enhanced ML performance arises from a combination of bandgap narrowing, reduced trap depths, and increased trap concentrations induced by Li doping. First-principles calculations confirm that Li preferentially substitutes for Sr in the lattice and validate the experimentally observed reduction in bandgap following Li incorporation.4. Experimental
SSS was synthesized using a high-temperature solid-state technique. The chemical raw materials used were SrCO3 (99%, Aladdin), SnO2 (99.95%, Aladdin), Sm2O3 (99. 99%, Aladdin), GeO2 (99.99%, Aladdin) and LiCO3 (99.99%, Aladdin). The powder was then mixed according to the stoichiometric ratio of SSS with xLi (x = 0, 10, 20, 30, 40, 50, and 60 mol%) and thoroughly ground in an agate mortar. The powder was subsequently heated to 1200 °C in a tube furnace under an air atmosphere at a rate of 10 K min−1 for 20 min and then sintered at 1550 °C at a rate of 5 K min−1 for 5 h. The resulting powder was then cooled down to room temperature in the furnace, and the sample obtained from the sintering was ground again to obtain the phosphor. The powder was weighed out and mixed with resin in the ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 to obtain a cylindrical sample with a diameter of about 24 mm and a thickness of 14 mm, which was used for ML testing.
4 to obtain a cylindrical sample with a diameter of about 24 mm and a thickness of 14 mm, which was used for ML testing.
XRD was carried out on an X-ray diffractometer (D/MAX 2550VB/PC, Rigaku Corporation, Japan) with Cu-Kα radiation. The microscopic surface morphology and elemental distribution of the powder samples were analyzed using a scanning electron microscope (ZEISS EVO 18). The ML test was performed by pre-irradiating the samples with a 365 nm UV LED for 1 min, applying a compressive load using a universal testing machine (SUST CMT 1104, China) and measuring the ML spectra using a CCD spectrometer (Ocean Optics fiber spectrometer NIRQuest1.7). Photographs of ML and PersL were taken using a smartphone (NTN-AN20, Honor, China). PLE and PL curves were measured using a PTI Quanta Master™ 8000 spectrofluorometer (Horiba, Canada). TL curves were obtained using a TL dosimeter (SL08, Guangzhou Radiation Science and Technology CO, Ltd, China) at a ramp rate of 5 K s−1. Diffuse reflectance spectra were measured using a Perkin-Elmer Lambda-950 spectrophotometer with an integrating sphere.
5. Computational details
The calculations were set up using the DS-PAW software.44 Projector augmented wave (PAW) pseudopotentials and Perdew–Burke–Ernzerhof (PBE)45 functionals with the generalized gradient approximation (GGA) were employed to investigate electron–ion interactions and electron–electron exchange correlations.46,47 The convergence tolerance of total energy in all self-consistent (SCF) calculations was set at a maximum of 10−4 eV. The k-point meshes of dimensions 11 × 11 × 3 with the Monkhorst–Pack scheme were employed.48,49 All atoms coordinates were relaxed until the magnitude of Hellmann–Feynman forces on each atom was less than 0.05 eV Å−1. The cutoff energy for the basic functions was set at 500 eV.50 The Fermi level is aligned with the valence band maximum (VBM). After determining the band structure, the VBM position EVBM is extracted from the OUTCAR file, and the calibrated Fermi level is obtained by subtracting EVBM from the original Fermi level.Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are available from the corresponding author upon request.Supplementary information is available. See DOI: https://doi.org/10.1039/d5tc02002f
Acknowledgements
We acknowledge the financial support from the National Natural Science Foundation of China (62405074 and 52372003), the Natural Science Foundation of Heilongjiang Province of China (ZD2023E004), and the Fundamental Research Funds for the Central Universities. JingRen thanks Kui Gong, Yibin Hu and Yin Wang (all from HZWTECH) for their help and discussions regarding this study.References
- S. R. Krishnan, C. Su, Z. Xie, M. Patel, S. R. Madhvapathy, Y. Xu, J. Freudman, B. Ng, S. Y. Heo, H. Wang, T. R. Ray, J. Leshock, I. Stankiewicz, X. Feng, Y. Huang, P. Gutruf and J. A. Rogers, Small, 2018, 14, 1803192 CrossRef PubMed.
- J. Heikenfeld, A. Jajack, J. Rogers, P. Gutruf, L. Tian, T. Pan, R. Li, M. Khine, J. Kim, J. Wang and J. Kim, Lab Chip, 2018, 18, 217–248 RSC.
- T. Lyu and P. Dorenbos, Appl. Phys. Rev., 2024, 11, 011415 CAS.
- T. Lyu, P. Dorenbos, P. Xiong and Z. Wei, Adv. Funct. Mater., 2022, 32, 202206024 Search PubMed.
- P. Xiong, B. Huang, D. Peng, B. Viana, M. Peng and Z. Ma, Adv. Funct. Mater., 2021, 31, 2010685 CrossRef CAS.
- J. Xue, H. M. Noh, B. C. Choi, S. H. Park, J. H. Kim, J. H. Jeong and P. Du, Chem. Eng. J., 2020, 382, 122861 CrossRef CAS.
- C. Chen, Y. Zhuang, X. Li, F. Lin, D. Peng, D. Tu, A. Xie and R. Xie, Adv. Funct. Mater., 2021, 31, 2101567 CrossRef CAS.
- N. Li, S. Yu, L. Zhao, P. Zhang, Z. Wang, Z. Wei, W. Chen and X. Xu, Inorg. Chem., 2023, 62, 2024–2032 CrossRef CAS.
- F. Ayachi, K. Saidi and M. Dammak, Mater. Adv., 2024, 5, 6162–6169 RSC.
- P. Zheng, Y. Xiao, P. Xiong, S. Su, A. Yang, X. Wang, S. Xu, P. Shao, Z. Zhou, S. Wu, E. Song, J. Gan and D. Chen, Adv. Funct. Mater., 2025, 2505094 CrossRef.
- C. Chen, Y. Zhuang, X. Li, F. Lin, D. Peng, D. Tu, A. Xie and R. Xie, Adv. Funct. Mater., 2021, 31, 2101567 CrossRef CAS.
- Y. Zhao, G. Bai, Y. Huang, Y. Liu, D. Peng, L. Chen and S. Xu, Nano Energy, 2021, 87, 106177 CrossRef CAS.
- M. Song, W. Zhao, J. Xue, L. Wang and J. Wang, J. Lumin., 2021, 235, 118014 CrossRef CAS.
- S. Kamimura, H. Yamada and C.-N. Xu, Appl. Phys. Lett., 2012, 101, 091113 CrossRef.
- S. Kamimura, H. Yamada and C.-N. Xu, MRS Proc., 2013, 1492, 117–122 CrossRef.
- J. Li, C.-N. Xu, D. Tu, X. Chai, X. Wang, L. Liu and E. Kawasaki, Acta Mater., 2018, 145, 462–469 CrossRef CAS.
- H. Zhao, X. Chai, X. Wang, Y. Li and X. Yao, J. Alloys Compd., 2016, 656, 94–97 CrossRef CAS.
- Y. Chen, Y. Xue, Q. Mao, L. Pei, Y. Ding, Y. Zhu, M. Liu and J. Zhong, J. Mater. Chem. C, 2023, 11, 9974–9983 RSC.
- T. Zheng, M. Runowski, I. R. Martín, K. Soler-Carracedo, L. Peng, M. Skwierczyńska, M. Sójka, J. Barzowska, S. Mahlik, H. Hemmerich, F. Rivera-López, P. Kulpiński, V. Lavín, D. Alonso and D. Peng, Adv. Mater., 2023, 35, 2304140 CrossRef CAS.
- P. Zhang, Z. Guo, Z. Wei, W. Chen, Q. Qiang, B. Liu, T. Lang, L. Peng, W. Wang and L. Zhao, Inorg. Chem. Front., 2025, 12, 2315–2324 RSC.
- D. Tu, C. Xu, S. Kamimura, Y. Horibe, H. Oshiro, L. Zhang, Y. Ishii, K. Hyodo, G. Marriott, N. Ueno and X. Zheng, Adv. Mater., 2020, 32, 1908083 CrossRef CAS.
- Y. Wang, F. Huang, X. Luo, B. Gao and S. Cheong, Adv. Mater., 2017, 29, 1601288 CrossRef PubMed.
- A. T. Mulder, N. A. Benedek, J. M. Rondinelli and C. J. Fennie, Adv. Funct. Mater., 2013, 23, 4810–4820 CrossRef CAS.
- J. Li, C.-N. Xu, D. Tu, X. Chai, X. Wang, L. Liu and E. Kawasaki, Acta Mater., 2018, 145, 462–469 CrossRef CAS.
- P. Xiong, M. Peng, J. Cao and X. Li, J. Am. Ceram. Soc., 2019, 102, 5899–5909 CrossRef CAS.
- W. Li, S. Wu, J. Ren and P. Xiong, Adv. Funct. Mater., 2025, 2506198 CrossRef.
- T. Lyu, P. Dorenbos, P. Xiong and Z. Wei, Adv. Funct. Mater., 2022, 32, 2206024 CrossRef CAS.
- B. Lei, S.-Q. Man, Y. Liu and S. Yue, Mater. Chem. Phys., 2010, 124, 912–915 CrossRef.
- P. Rajput, P. Vashishtha, G. Gupta, P. Singh and K. Pathania, Appl. Phys. A: Mater. Sci. Process., 2020, 126, 593 CrossRef.
- C. N. Xu, T. Watanabe, M. Akiyama and X. G. Zheng, Mater. Res. Bull., 1999, 34, 1491–1500 CrossRef.
- H.-R. Shih and Y.-S. Chang, Materials, 2017, 10, 779 CrossRef.
- D. K. Singh and J. Manam, J. Mater. Sci.: Mater. Electron., 2018, 29, 5579–5588 CrossRef.
- K. Ueda, T. Yamashita, K. Nakayashiki, K. Goto, T. Maeda, K. Furui, K. Ozaki, Y. Nakachi, S. Nakamura, M. Fujisawa and T. Miyazaki, Jpn. J. Appl. Phys., 2006, 45, 6981 CrossRef.
- W. Li, Z. Sui, C. Fan, C. Wang, Y. Zhu, J. Ren and J. Zhang, J. Eur. Ceram. Soc., 2023, 43, 6331–6336 CrossRef.
- E. Saïdi, B. Samson, L. Aigouy, S. Volz, P. Löw, C. Bergaud and M. Mortier, Nanotechnology, 2009, 20, 115703 CrossRef PubMed.
- I. E. Kolesnikov, E. V. Afanaseva, M. A. Kurochkin, E. I. Vaishlia, A. A. Kalinichev, E. Y. Kolesnikov and E. Lähderanta, ACS Appl. Mater. Interfaces, 2022, 14, 1757–1764 CrossRef CAS PubMed.
- Y. Zhuang, Y. Lv, Y. Li, T. Zhou, J. Xu, J. Ueda, S. Tanabe and R.-J. Xie, Inorg. Chem., 2016, 55, 11890–11897 CrossRef CAS PubMed.
- Q. Zhu, J. Xiahou, Y. Guo, H. Li, C. Ding, J. Wang, X. Li, X. Sun and J.-G. Li, ACS Appl. Bio Mater., 2019, 2, 577–587 CrossRef CAS.
- N. Majewska, T. Leśniewski, S. Mahlik, M. Grinberg, A. Chruścińska, D. Michalik and M. Sopicka-Lizer, Phys. Chem. Chem. Phys., 2020, 22, 17152–17159 RSC.
- W. Li, M. Jin, J. Li, C. Wang, H. Shi, J. Nan, Q. Hu, B. Liu, L. Liu, J. Ren and J. Zhang, J. Rare Earths, 2025, 43, 691–700 CrossRef CAS.
- S. Wu, G. Zhou, Y. Wu, P. Xiong, B. Xiao, Z. Zhou, Y. Xiao, P. Shao, S. Wang, Z. Shao, Y. Wang and F. Wang, Adv. Mater., 2024, 36, 2408508 CrossRef CAS.
- H. Yang, Y. Wei, H. Ju, X. Huang, J. Li, W. Wang, D. Peng, D. Tu and G. Li, Adv. Mater., 2024, 36, 2401296 CrossRef CAS.
- H. Xu, D. Lee, J. He, S. B. Sinnott, V. Gopalan, V. Dierolf and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 174103 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Acc. Chem. Res., 2013, 46, 1740–1748 CrossRef CAS PubMed.
- J. Liu, ACS Catal., 2017, 7, 34–59 CrossRef CAS.
- D. J. Chadi, Phys. Rev. B: Solid State, 1977, 16, 1746–1747 CrossRef.
- J. D. Pack and H. J. Monkhorst, Phys. Rev. B: Solid State, 1977, 16, 1748–1749 CrossRef.
- W. Huang, P. Wu and N. Chen, Appl. Surf. Sci., 2025, 693, 162777 CrossRef CAS.
Footnote |
| † Minyu Jin and Wenhao Li are co-first author. |
| This journal is © The Royal Society of Chemistry 2025 |