Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Shaping scintillation and UV-VIS-NIR luminescence properties through synergistic lattice disordered engineering and exciton-mediated energy transfer in Pr3+-doped Lu1.5Y1.5Al5−xScxO12 (x = 0.0–2.0) garnets†
Karol Bartosiewicz *a,
Yevheniia Smortsovab,
Piotr Radmoski
*a,
Yevheniia Smortsovab,
Piotr Radmoski c,
Marcin E. Witkowski
c,
Marcin E. Witkowski d,
Konrad J. Drozdowski
d,
Konrad J. Drozdowski d,
Masao Yoshinoef,
Takahiko Horiaief,
Damian Szymański
d,
Masao Yoshinoef,
Takahiko Horiaief,
Damian Szymański g,
Wioletta Dewoc,
Justyna Zeler
g,
Wioletta Dewoc,
Justyna Zeler h,
Paweł Sochai,
Maksym Buryij,
Andrey Prokhorov
h,
Paweł Sochai,
Maksym Buryij,
Andrey Prokhorov aj,
David John
aj,
David John akl,
Jakub Volfam,
Tomasz Runkac,
Tomasz Pędzińskin,
Karol Hauzan,
Vítězslav Jarýa,
Yasuhiro Shojief,
Kei Kamadaef,
Eugeniusz Zychh,
Winicjusz Drozdowski
akl,
Jakub Volfam,
Tomasz Runkac,
Tomasz Pędzińskin,
Karol Hauzan,
Vítězslav Jarýa,
Yasuhiro Shojief,
Kei Kamadaef,
Eugeniusz Zychh,
Winicjusz Drozdowski d and
Akira Yoshikawaef
d and
Akira Yoshikawaef
aInstitute of Physics, Academy of Sciences of the Czech Republic, Na Slovance 1999/2, 18200, Prague, Czech Republic. E-mail: bartosiewicz@fzu.cz
bDeutsches Elektronen-Synchrotron DESY, Notkestr. 85, Hamburg 22607, Germany
cFaculty of Materials Engineering and Technical Physics, Poznan University of Technology, Piotrowo 3, 60-965, Poznań, Poland
dInstitute of Physics, Faculty of Physics, Astronomy and Informatics, Nicolaus Copernicus University in Toruń, ul. Grudziądzka 5, 87100, Toruń, Poland
eInstitute for Materials Research, Tohoku University, 2-1-1 Katahira Aoba-ku, Sendai, Miyagi 9808577, Japan
fNew Industry Creation Hatchery Center, Tohoku University, Sendai, Miyagi, Japan
gInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, Wrocław, Poland
hFaculty of Chemistry, University of Wrocław, Joliot-Curie Street 14 F, 50383, Wrocław, Poland
iŁukasiewicz Research Network – Institute of Microelectronics and Photonics, Aleja Lotników 32/46, 02-668, Warsaw, Poland
jInstitute of Plasma Physics of the Czech Academy of Sciences, U Slovanky, 2525/1a, Prague, 182 00, Czech Republic
kFaculty of Nuclear Sciences and Physical Engineering, Czech Technical University, Břehová 7, 115019, Prague, Czech Republic
lNuclear Physics Institute of the Czech Academy of Sciences, Na Truhlářce 39/64, 18000, Prague, Czech Republic
mDepartment of Inorganic Chemistry, University of Chemistry and Technology, Technická 5, 166 28, Prague, Czech Republic
nFaculty of Chemistry, Adam Mickiewicz University in Poznań, Uniwersytetu Poznańskiego 8, 61-614 Poznan, Poland
First published on 6th June 2025
Abstract
This study investigated the crystallization behavior, luminescence and scintillation properties of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 (0.0, 0.5, 1.0, 1.5, 2.0) garnets, grown using the micro-pulling-down method, to address challenges associated with the substitution of Sc3+ for Al3+ ions due to their mismatched ionic radii in the same octahedral crystallographic site. A specially engineered crucible with five independent crystallization capillaries was used, which revealed that Sc3+ substitution caused localized melt heterogeneity, resulting in non-uniform melt ejection during crystallization. The threshold of Sc3+ ions concentration (x = 1.5) was identified, beyond which further substitution led to the formation of a garnet/bixbyite-like distorted perovskite hypoeutectic structure. This discovered a novel method for crystallization of hypoeutectic crystal growth by exploiting ionic radii mismatches. Vibrational spectroscopy confirmed that Sc3+ ions incorporation disrupted lattice symmetry, increasing structural disorder around Pr3+ ions. This structural modification significantly enhanced luminescence, particularly in the visible and near-infrared (NIR) ranges, achieving a sixteenfold increase in NIR luminescence intensity. Synchrotron radiation excitation spectra revealed that the band gap energy progressively decreased with increasing Sc3+ ions concentration. This finding provided crucial insights for designing materials based on band gap engineering strategies. A sixfold improvement in scintillation light yield, reaching 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 photons per MeV, was observed in the Lu1.5Y1.5Al3.5Sc1.5O12 crystal (x = 1.5). The enhancement resulted from a Sc3+-mediated energy transfer pathway
200 photons per MeV, was observed in the Lu1.5Y1.5Al3.5Sc1.5O12 crystal (x = 1.5). The enhancement resulted from a Sc3+-mediated energy transfer pathway  , which optimized charge carrier dynamics by reducing deep trapping center density by an order of magnitude while preserving shallow traps. The EPR spectroscopy showed that Sc3+ incorporation reduced concentration of trace impurities, enhancing scintillation light yield. It also confirmed that F+–Pr3+ interactions intensified Pr3+ emission at 370 nm and identified the 410–420 nm band as originating from F+–O− defect pairs. These findings demonstrate that controlled lattice modification through Sc3+ incorporation allows for tuning structural and luminescent properties, offering a new approach for the design of advanced scintillators and luminescent materials with improved performance for targeted applications.
, which optimized charge carrier dynamics by reducing deep trapping center density by an order of magnitude while preserving shallow traps. The EPR spectroscopy showed that Sc3+ incorporation reduced concentration of trace impurities, enhancing scintillation light yield. It also confirmed that F+–Pr3+ interactions intensified Pr3+ emission at 370 nm and identified the 410–420 nm band as originating from F+–O− defect pairs. These findings demonstrate that controlled lattice modification through Sc3+ incorporation allows for tuning structural and luminescent properties, offering a new approach for the design of advanced scintillators and luminescent materials with improved performance for targeted applications.
1. Introduction
Inorganic oxide single crystals represent one of the most important categories of functional materials, encompassing applications such as scintillation, phosphors, laser technologies, and optical sensors. Their prominence over other functional material groups is attributed to their favorable physicochemical properties, including non-hygroscopic nature, high chemical and radiation stability, mechanical hardness, excellent thermal stability, and well-established methodologies for bulk single-crystal growth.1–7 The absence of phase transitions in aluminum garnets distinguishes them from many other materials, such as perovskites, which typically undergo structural changes at varying temperatures. This stability ensures that the material properties of aluminum garnets remain consistent across a broad temperature range. Consequently, the processes of crystal growth from the melt and the sintering of transparent ceramics are significantly simplified.8,9 The invariance of the lattice structure during solidification eliminates phase changes, thereby producing materials that are free of cracks and exhibit excellent mechanical strength. This characteristic makes aluminum garnets particularly advantageous for applications requiring high reliability and durability. These inherent attributes contribute substantially to cost mitigation in the fabrication, operation, and maintenance of devices dedicated to the detection and analysis of ionizing radiation across diverse medical, and industrial applications. The Pr3+-doped Lu3Al5O12 (LuAG:Pr) single crystal deserves special consideration for radiation detection applications. Its physical and chemical merits, including a high density of 6.7 g cm−3, a rapid scintillation decay time of 20 ns, and a theoretical light yield (LY) approaching 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photons per MeV, synergistically contribute to its ability to provide high-resolution imaging and accurate counting measurements.1 A notable advantage of Pr3+ ions in oxide garnets is their exceptional thermal sensitivity across a wide temperature range of 17–700 K.7,10–14 These capabilities are of particular importance in high-energy physics experiments, medical imaging techniques such as positron emission tomography (PET), homeland security applications, radiation monitoring, and highly sensitive and accurate sensor systems.7
000 photons per MeV, synergistically contribute to its ability to provide high-resolution imaging and accurate counting measurements.1 A notable advantage of Pr3+ ions in oxide garnets is their exceptional thermal sensitivity across a wide temperature range of 17–700 K.7,10–14 These capabilities are of particular importance in high-energy physics experiments, medical imaging techniques such as positron emission tomography (PET), homeland security applications, radiation monitoring, and highly sensitive and accurate sensor systems.7
The growing demands for high resolution, efficiency, faster signal processing, and enhanced thermal sensitivity drive the imperative for further development of LuAG:Pr single crystals. A significant structural limitation of the Lu3Al5O12 crystal lattice is the notably constrained ionic radius of Lu3+ ions (rVIII = 0.997 Å; VIII – denotes the coordination number). This characteristic, combined with its high melting point exceeding 2100 K, serves as a driving force for ion displacement processes within the crystal lattice.1,4,15 This process involves the displacement of Lu3+ ions from their preferred dodecahedral coordination to the octahedral coordination sites normally occupied by Al3+ ions, resulting in the formation of LuxAl antisite defects.1 These point defects act as electron trapping centers, significantly complicating the scintillation mechanism by quenching luminescence and slowing down the scintillation response. Consequently, the experimental light yield value was approximately 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 photons per MeV, accompanied by a slow component in the scintillation response over microsecond timescales.16–18 Continuous efforts to enhance the scintillation properties of LuAG:Pr have involved compositional modifications by substituting Al atoms with Ga atoms. However, the incorporation of Ga has a detrimental effect, significantly lowering the energy barrier between the conduction band minimum and the 5d1 excited state of Pr3+ ions. This quenching effect has been demonstrated to inhibit the desired emission originating from the interconfigurational 4f15d11 → 4f2 transition and progressively reduces the light yield value.7,19–21 However, a balanced substitution of Y for Lu atoms in Pr3+-doped (Lu,Y)3Al5O12 crystal resulted in a notable enhancement of the light yield by approximately 50%, accompanied by a significant acceleration of the slow component in the scintillation response.11,13,22
000 photons per MeV, accompanied by a slow component in the scintillation response over microsecond timescales.16–18 Continuous efforts to enhance the scintillation properties of LuAG:Pr have involved compositional modifications by substituting Al atoms with Ga atoms. However, the incorporation of Ga has a detrimental effect, significantly lowering the energy barrier between the conduction band minimum and the 5d1 excited state of Pr3+ ions. This quenching effect has been demonstrated to inhibit the desired emission originating from the interconfigurational 4f15d11 → 4f2 transition and progressively reduces the light yield value.7,19–21 However, a balanced substitution of Y for Lu atoms in Pr3+-doped (Lu,Y)3Al5O12 crystal resulted in a notable enhancement of the light yield by approximately 50%, accompanied by a significant acceleration of the slow component in the scintillation response.11,13,22
Lattice engineering through the manipulation of lattice parameters is a complex process that is constrained by a multitude of physicochemical factors. The incorporation of highly incompatible dopants, such as Pr3+ ions (rVIII = 1.126 Å) into Lu3+ sites (rVIII = 0.977 Å) with an ionic radius mismatch of approximately 15.28%,14,15,23 can significantly increase the strain energy in the lattice around the incompatible dopant. This incompatibility reduces the solubility limit of incompatible atoms and deforms the polyhedral framework that constitutes the unit cell of the lattice.14 Strain relaxation triggers a process of defect formation and local structural rearrangements within the host lattice, eventually leading to the formation of secondary phase inclusions.14,24 The presence of structural defects and charge-trapping centers induces non-uniformities and compromises the functional performance of the material.5,14,24,25 The correlation between cationic substitution, contraction and polyhedral expansion in the  lattice underscores the existence of strong and intricate linkages within the garnet structure. The expansion of REO8 dodecahedra induces compression of M′O6 octahedra and M′′O4 tetrahedra.26–28 This direct relationship between polyhedral deformation highlights the significance of meticulous lattice engineering in garnets by synergistically expanding dodecahedral, octahedral, and tetrahedral units.
lattice underscores the existence of strong and intricate linkages within the garnet structure. The expansion of REO8 dodecahedra induces compression of M′O6 octahedra and M′′O4 tetrahedra.26–28 This direct relationship between polyhedral deformation highlights the significance of meticulous lattice engineering in garnets by synergistically expanding dodecahedral, octahedral, and tetrahedral units.
This comprehensive study meticulously delves into the lattice engineering approach, particularly the simultaneous expansion of dodecahedral coordination (the site where the doping ion Pr3+ is incorporated) and octahedral coordination (where Sc substitutes for Al) and its impact on the microstructure, local structure rearrangement, lattice disorder degree, vibrational modes, luminescence, and scintillation properties and charged trap density. As a research model, a series of the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0, 0.5, 1.0, 1.5, 2.0, was used. This wide range of Sc atom concentrations enables the investigation of the effects of subtle expansion (for x equal to 0.5) to extreme expansion of the ScO6 polyhedral framework, where local structure rearrangement initiates via the formation of secondary phase domains. The simultaneous expansion of dodecahedral and octahedral coordinations paves the way for incorporating higher concentrations of Pr3+ ions, reaching up to 0.15 at%.14 Sc3+ ions not only expand the ScO6 polyhedral framework but also induce locally perturbed potentials, leading to lattice distortions and the formation of localized states that facilitate electron–hole exchange interactions. These interactions promote the formation of bound e−–h+ states (excitons) around Sc3+ ions. The resonant energy state of these excitons with the 5d114f1 energy state of Pr3+ ions enables energy transfer from the Sc3+-bound excitons to Pr3+ ions.29,30 This introduces an additional pathway for energy transfer from the lattice to Pr3+ ions, which can enhance their luminescence efficiency. The incorporation of Sc atoms into the host lattice significantly enhanced the degree of structural disorder, disrupting the local symmetry surrounding Pr3+ ions. This structure disorder led to a pronounced broadening of the excitation and emission bands, reflecting the altered local environment. Notably, this structural disorder resulted in a substantial enhancement of the luminescence intensity of Pr3+ ions. Consequently, Sc-admixed crystals exhibited enhanced emission intensity across a wide spectral range, encompassing the ultraviolet (UV), visible (VIS), and near-infrared (NIR) regions. To the best of our knowledge, this  energy transfer mechanism was experimentally confirmed for the first time through excitation spectroscopy using synchrotron radiation. A key conclusion of this study was the identification of a Sc concentration threshold in the Lu1.5Y1.5Al5−xScxO12 crystals, estimated at x = 1.5. At this critical concentration, the incorporation of Sc resulted in the formation of cubic bixbyite-like distorted perovskite inclusions within the garnet structure. This investigation further reveals that the atomic size mismatch between constituent ions introduces kinetic barriers that drive the co-precipitation of metastable phases. Significantly, the hypoeutectic crystal structure demonstrates a 16-fold enhancement in NIR emission intensity compared to single-phase crystal. These findings open new possibilities for the crystallization of hypoeutectic crystal compositions, offering valuable insights into the design of advanced photonic applications and optical devices, allowing for tailored emission characteristics based on specific spectral range requirements.
energy transfer mechanism was experimentally confirmed for the first time through excitation spectroscopy using synchrotron radiation. A key conclusion of this study was the identification of a Sc concentration threshold in the Lu1.5Y1.5Al5−xScxO12 crystals, estimated at x = 1.5. At this critical concentration, the incorporation of Sc resulted in the formation of cubic bixbyite-like distorted perovskite inclusions within the garnet structure. This investigation further reveals that the atomic size mismatch between constituent ions introduces kinetic barriers that drive the co-precipitation of metastable phases. Significantly, the hypoeutectic crystal structure demonstrates a 16-fold enhancement in NIR emission intensity compared to single-phase crystal. These findings open new possibilities for the crystallization of hypoeutectic crystal compositions, offering valuable insights into the design of advanced photonic applications and optical devices, allowing for tailored emission characteristics based on specific spectral range requirements.
2. Methodology
2.1. Crystallization process
Single crystals were grown from the melt using the micro-pulling down (μ-PD) technique with radiofrequency (RF) inductive heating.31,32 The starting materials were prepared by thoroughly mixing high-purity oxides of Lu2O3, Y2O3, Al2O3, Sc2O3, and Pr6O11 (99.999% purity), obtained from Iwatani Corporation. The powdered mixture was melted under a flowing argon atmosphere via radio-frequency inductive heating within an iridium crucible. This crucible was specifically designed with five crystallization capillaries, each possessing a die diameter of 0.4 mm. Crystal growth was initiated using a LuAG seed oriented along the 〈100〉 crystallographic direction. The pulling rate during crystal growth was maintained at 0.05 mm min−1.2.2. Powder X-ray diffraction, SEM-EDS, and Raman spectroscopy
2.3. Optical, luminescence, scintillation, and thermoluminescence properties
 | (1) |
I represent the luminescence intensity, Ii denotes the intensity at 0 ns, t indicates the time, τi refers to the decay time, and B represents the background intensity. To quantify these parameters, the effective decay time (τeffective) was computed using the following formula:33
 | (2) |
2.4. Electron paramagnetic resonance (EPR)
Electron paramagnetic resonance (EPR) measurements were conducted on a commercial Bruker EMXplus spectrometer operating at the X band (9.4 GHz) and TE011 mode. The measurements were performed at 20 K using an Oxford Instruments ESR900 cryostat. The crystal was placed in a quartz tube for the measurements. X-ray irradiation of samples in the quartz tube was conducted at 20 K using ISO-DEBYEFLEX 3003 highly stabilized X-ray equipment for structural analysis (tungsten X-ray tube, 50 kV, 30 mA). The majority of graphical visualizations were generated utilizing Veusz, an open-source scientific plotting software developed by Sanders.343. Experimental results and interpretation
3.1. Powder X-ray diffraction, SEM-EDS, and Raman spectroscopy
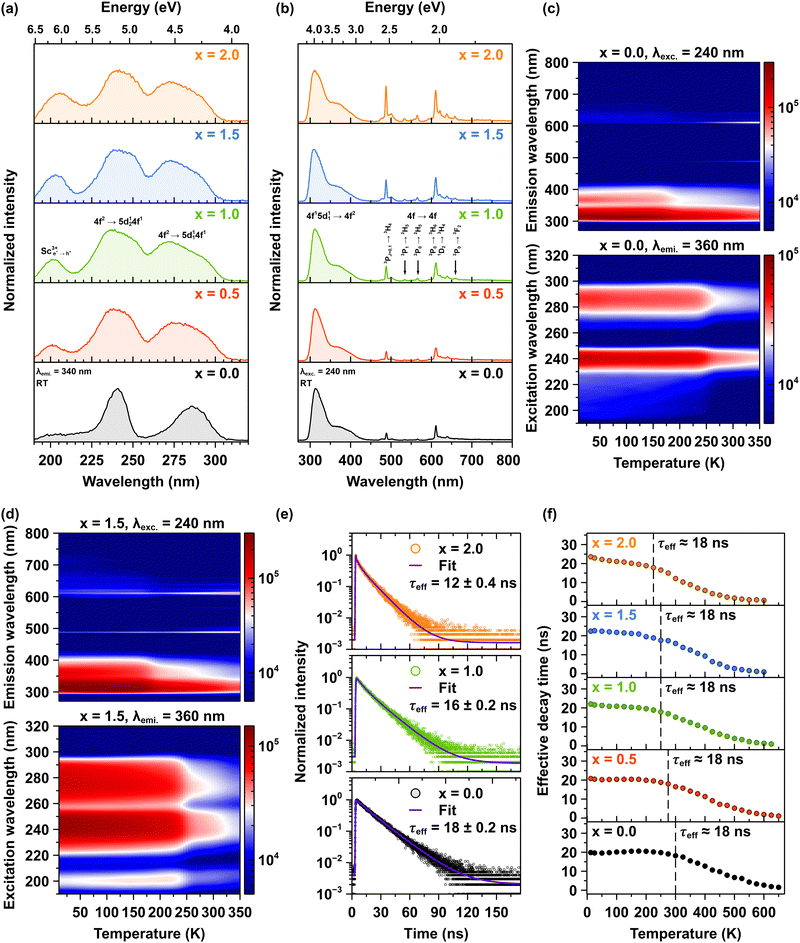
Fig. 1a depicts as-grown crystal rods alongside polished radial plates of Pr3+-doped Lu1.5Y1.5Al5−xScxO12, where x = 0.0, 0.5, 1.0, 1.5, and 2.0. All examined crystals exhibit a crack-free and regular cylindrical morphology. The crystals with scandium concentration up to x = 1.5 demonstrate good optical transparency. However, the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2.0) exhibits significantly reduced transparency. Cross-sectional microscopic analysis of the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal reveals a systematic reduction in optical transparency throughout the entire sample area. This transparency degradation indicates the formation of compositionally heterogeneous inclusions within the crystal lattice, which scatter the incident light.The powder X-ray diffraction patterns depicted in Fig. 1b correspond to Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals with varying concentrations of Sc3+ ions. As the substitution of the Sc atoms for Al proceeds, the crystalline structure maintains its garnet-type phase. The PXRD data confirms that all samples crystallize in the cubic space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d (No. 230) of the garnet crystal system. The exception arises in the case of the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2), wherein additional diffraction peaks are observed (see Fig. 1b). These additional peaks are attributed to the presence of perovskite phase inclusions within the dominant garnet lattice. The presence of perovskite phase inclusions in Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystals (x = 2.0) is a significant factor contributing to the observed reduction in transparency. Fig. 1c presents an analysis between the experimentally estimated and theoretically calculated lattice constants a0 as a function of increasing Sc3+ ions concentration in Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals. The expansion of the host lattice constants correlates well with the calculated values for Sc concentrations up to x = 1.5. Specifically, the lattice constants expand from 11.9594 Å to 12.2114 Å for the Pr3+-doped Lu1.5Y1.5Al5O12 (x = 0.0) and Lu1.5Y1.5Al3.5Sc1.5O12 (x = 1.5) crystals, respectively. However, marginal decrease in the lattice constant is observed for the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2.0), indicating a reversal in the expansion trend. This observation aligns with the experimental PXRD patterns and substantiates that at higher concentrations of the larger Sc3+ cations, there is a decreased propensity for these cations to substitute for Al sites in octahedral coordination. Consequently, it becomes energetically more favorable for the Sc elements to form secondary perovskite phase inclusions rather than integrating into the octahedral sites. This behavior elucidates the noted deviation from Vegard's law observed in the experimental data.35 Deviations from Vegard's law are well-documented, often attributed to factors such as disparities in component sizes and structural incompatibilities.14,35 The observed effect provides compelling evidence regarding the inherent constraints associated with the incorporation of solute species into a solid matrix when the atomic radii of the solute and solvent atoms exhibit significant mismatch.4,14,28 The experimental results reveal a compositional threshold for the saturation of Sc3+ ions in the octahedral sites of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 occurring at x = 1.5. This assertion is corroborated by the substantial deviation between the experimentally estimated lattice constant a0 (12.2049 Å), and the theoretically predicted value for complete saturation (12.3041 Å) in the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2.0). This observation implies an incomplete incorporation of Sc3+ cations into the octahedral sites of the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal when x = 2.0. Consequently, the residual Sc atoms that exceed the substitutional capacity of the octahedral sites precipitate out, leading to the formation of perovskite phase inclusions within the garnet structure.
d (No. 230) of the garnet crystal system. The exception arises in the case of the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2), wherein additional diffraction peaks are observed (see Fig. 1b). These additional peaks are attributed to the presence of perovskite phase inclusions within the dominant garnet lattice. The presence of perovskite phase inclusions in Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystals (x = 2.0) is a significant factor contributing to the observed reduction in transparency. Fig. 1c presents an analysis between the experimentally estimated and theoretically calculated lattice constants a0 as a function of increasing Sc3+ ions concentration in Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals. The expansion of the host lattice constants correlates well with the calculated values for Sc concentrations up to x = 1.5. Specifically, the lattice constants expand from 11.9594 Å to 12.2114 Å for the Pr3+-doped Lu1.5Y1.5Al5O12 (x = 0.0) and Lu1.5Y1.5Al3.5Sc1.5O12 (x = 1.5) crystals, respectively. However, marginal decrease in the lattice constant is observed for the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2.0), indicating a reversal in the expansion trend. This observation aligns with the experimental PXRD patterns and substantiates that at higher concentrations of the larger Sc3+ cations, there is a decreased propensity for these cations to substitute for Al sites in octahedral coordination. Consequently, it becomes energetically more favorable for the Sc elements to form secondary perovskite phase inclusions rather than integrating into the octahedral sites. This behavior elucidates the noted deviation from Vegard's law observed in the experimental data.35 Deviations from Vegard's law are well-documented, often attributed to factors such as disparities in component sizes and structural incompatibilities.14,35 The observed effect provides compelling evidence regarding the inherent constraints associated with the incorporation of solute species into a solid matrix when the atomic radii of the solute and solvent atoms exhibit significant mismatch.4,14,28 The experimental results reveal a compositional threshold for the saturation of Sc3+ ions in the octahedral sites of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 occurring at x = 1.5. This assertion is corroborated by the substantial deviation between the experimentally estimated lattice constant a0 (12.2049 Å), and the theoretically predicted value for complete saturation (12.3041 Å) in the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal (x = 2.0). This observation implies an incomplete incorporation of Sc3+ cations into the octahedral sites of the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal when x = 2.0. Consequently, the residual Sc atoms that exceed the substitutional capacity of the octahedral sites precipitate out, leading to the formation of perovskite phase inclusions within the garnet structure.
The EDS analysis serves as an imaging tool to visualize the distribution of atoms within a crystal structure. Fig. 2 and 3 present the EDS maps and corresponding line profiles for the Lu, Y, Al, Sc, and O elements, respectively. The EDS analysis revealed radial variations in the elemental distributions, exhibiting distinct patterns that depended on the concentration of Sc elements. The elemental variability observed in the crystallization volume is notable for its localized, point-like regions, primarily concentrated in areas where the molten material was ejected through the crystallization capillary. These point-like regions form rounded spots embedded within the main crystal structure. The brighter regions of these spots reflect higher concentrations of certain elements, while the darker regions correlate with lower concentrations of the examined atoms. Additionally, the enrichment of one element within a spot is associated with the concomitant depletion of another element. An illustrative example is the Pr3+-doped Lu1.5Y1.5Al3.5Sc1.5O12 crystal (x = 1.5). In this case, Al elements show enrichment within the rounded spots, indicated by a brighter green color. Conversely, these areas are depleted in Sc atoms, which are represented by a darker cyan color. This pattern highlights the elemental segregation and the intricate interplay between atomic size mismatch and concentrations in the crystal lattice.
It is noteworthy that although the crucible used for crystal growth featured five crystallization capillaries, the EDS maps do not display all five regions with distinct chemical compositions. Furthermore, it has been demonstrated that the number of heterogeneous spots observed in the EDS maps is subject to variation following the Sc3+ ions concentration. This suggests that the molten material was not uniformly ejected from the five capillaries, resulting in compositional differences in the melt ejected from each capillary. If the segregation effect, attributed to the mismatch in ionic radii, were to occur uniformly at the liquid/solid interface, all capillaries would exhibit the same or similar behavior. Specifically, at the liquid/solid interface of each capillary, the same segregation mechanism would manifest, enriching the rim and core with larger ions and with smaller ions, respectively. However, the observed variations in chemical composition and the number of heterogeneous spots imply non-uniform ejection dynamics, indicating that factors beyond ionic radius mismatch may influence the segregation process during crystallization. However, it should be noted that this effect is only observed when the melt contains an incompatible element, i.e. Sc. The observation that the Lu1.5Y1.5Al5O12 crystal, which does not contain Sc, exhibits better homogeneity, lends support to the conclusion. In this sample, the typical behavior of elemental distribution is observed, where ions with larger ionic radii, such as Y3+ ions, show enrichment at the crystal rim and depletion at the crystal center. Conversely, Lu3+ ions, having a smaller ionic radius, exhibit the opposite behavior, with depletion at the crystal rim and enrichment in the central regions.5
The exception to this pattern is observed in the Pr3+-doped Lu1.5Y1.5Al3.0Sc2.0O12 sample (x = 2.0), where the crystal volume, excluding the rim, exhibits the hypoeutectic composition. The secondary phase inclusions display a triangular morphology, with each triangle enriched in Sc and Lu elements. This observation aligns with the PXRD results (see Fig. 1b), which indicate that the triangles predominantly form a perovskite structure, while Al, Y and O elements develop a garnet phase. Furthermore, the formation of this hypoeutectic structure also explains the observed deviation from Vegard's law. For the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals where x > 1.5, it is thermodynamically more favorable for Sc ions to form perovskite phase inclusions rather than incorporating into octahedral coordination within the garnet phase. This mechanism occurs when the concentration of large, incompatible atoms reaches the solubility threshold.4,14,24,36–39
The EDS line profiles provide comprehensive insights into the changes in elemental distribution imposed by Sc admixing. Notably, the EDS line profiles reveal that the smaller Lu elements enrich the central regions, while the larger yttrium Y elements are concentrated at the rim within the Lu1.5Y1.5Al5O12 crystal. In crystals admixed with Sc elements, the areas depleted in Sc (exhibiting lower intensity) and concurrently enriched in Al (higher intensity) are primarily concentrated in areas where the molten material was ejected through the crucible capillary. Furthermore, this observation confirms that the melt ejected from each capillary differed in composition. Interestingly, within these rounded spots, the Lu and Y elements follow the same trend, with the larger Y elements accumulating at the rim of the rounded spot and the smaller Lu elements concentrating within the central part. The spatial distribution analysis reveals a systematic segregation pattern of heterogeneous elements ejected from each capillary: elements with larger atomic radii predominantly migrate toward the peripheral regions of the capillary, whereas elements with smaller atomic radii exhibit preferential concentration within the central domains. This suggests that the crystallization process occurs independently within each capillary.24,40 Another important conclusion is that the melt in the crucible is heterogeneous. Furthermore, the implementation of a 0.1 mm diameter capillary effectively inhibits atomic back-diffusion from the liquid/crystal interface to the crucible reservoir, thereby promoting heterogeneous crystallization processes. This geometric constraint significantly influences the crystallization kinetics and resultant phase formation. The EDS line profile for the Pr3+-doped Lu1.5Y1.5Al3.0Sc2.0O12 crystal (x = 2.0) demonstrates eutectic perovskite-garnet composite structure. The spatial distribution of elements ejected from each capillary demonstrates a spontaneous self-organizing phenomenon, wherein size-dependent elemental segregation occurs as an intrinsic mechanism during the crystallization process, suggesting a thermodynamically driven ordering behavior. This localized crystallization phenomenon represents a significant advancement in hypoeutectic materials engineering, enabling enhanced control over phase self-organization and microstructural evolution. This novel approach enables optimal spatial organization of both phases, leading to materials that display enhanced structural integrity and functional properties. The methodology shows significant promise for the design of next-generation composite materials, allowing for the precise control of microstructures and the customization of performance characteristics to meet specific application demands. To elucidate the impact of Sc incorporation on host lattice disorder and characterize the structural properties of secondary phase inclusions, detailed vibrational spectroscopy analyses were conducted.
The symmetry of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals is described by the cubic Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) d space group. The group theory for such a structure predicts 240 normal vibration modes in the vicinity of the Brillouin zone center:41
d space group. The group theory for such a structure predicts 240 normal vibration modes in the vicinity of the Brillouin zone center:41
| Γ = 3A1g + 5A2g + 8Eg + 14F1g + 5A1u + 5A2u + 10Eu + 18F1u + 16F2u | (3) |
Among them 17 ungerade modes are infrared active (17F1u), 55 are optically inactive, and 25 gerade modes (3A1g + 8Eg + 14F2g) are active in Raman spectroscopy. This theoretical prediction should be considered only as a limit since the observation of modes is often hindered by their accidental degeneracy, weak intensity, or electron transitions.42–44 Generally, the  garnet Raman response is dominated by M′′O4 tetrahedra-related bands. It can be divided into two main regions: (i) low energy one below 500 cm−1, containing RE ions translations, alongside translational, librational, and internal antisymmetric stretching vibrations (v3) of M′O4 tetrahedra, and (ii) high energy range from 500 to roughly 900 cm−1, with breathing (v1), quadrupolar-like (v2), and deformations (v4) of M′O4 units. In an ideal case, all oxygens forming M′′O6 octahedra are equally spaced from the inner M atom, and vibrations of such structure described by the Oh point group are Raman inactive.
garnet Raman response is dominated by M′′O4 tetrahedra-related bands. It can be divided into two main regions: (i) low energy one below 500 cm−1, containing RE ions translations, alongside translational, librational, and internal antisymmetric stretching vibrations (v3) of M′O4 tetrahedra, and (ii) high energy range from 500 to roughly 900 cm−1, with breathing (v1), quadrupolar-like (v2), and deformations (v4) of M′O4 units. In an ideal case, all oxygens forming M′′O6 octahedra are equally spaced from the inner M atom, and vibrations of such structure described by the Oh point group are Raman inactive.
The obtained room temperature and unpolarized Raman spectra are included in Fig. 4a. The positions of modes with assigned symmetries and vibration types are summarized in Table S1 in ESI.† In total, 16, 15, 14, 14, and 14 bands were collected for the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0, 0.5, 1.0, 1.5 and 2.0, respectively. For the Pr3+-doped Lu1.5Y1.5Al5O12 crystal (x = 0.0), the four most intensive peaks located at 260 (F2g), 374 (A1g), 398 (Eg), and 790 cm−1 (F2g). These and most of the other observed bands are separated and relatively narrow, with FWHM below 16 cm−1. The latter indicates a well-developed ordered crystal structure. The overall spectrum resembles that of isomorphous YAG, which, due to its thorough examination by Raman and computational methods, serves as the main reference for interpretation.44–47 With increasing Sc3+ ions concentration in the YAG crystal structure, the A1g and Eg modes become visible in the spectra as a single, greater peak. This accidental degeneracy can be corroborated by considering the height ratio of the resultant and the other two strong F2g modes. The ratio exhibits a positive gradient in the interval 0.5 ≤ x ≤ 1.5, indicating enhanced overlap, followed by a notable decline within the range 1.5 < x ≤ 2.0 (as illustrated in the upper panels of Fig. 4a). This observation may suggest that the A1g and Eg modes have exchanged their order, resulting in the Eg mode being positioned at a lower energy level. The spectral deconvolution of the region spanning 280–440 cm−1, which incorporates the two subsidiary Eg and F2g modes, is depicted by dashed black lines in Fig. 4a. A notable consequence of elevated Sc3+ ions concentration is the manifestation of unexpected broad spectral features within the 570–770 cm−1 spectral region, particularly pronounced in the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.5 and 2.0. The underlying mechanism responsible for these spectral features remains not fully understood. It is possible to propose two potential explanations for this phenomenon. Firstly, in the Pr3+-doped Lu1.5Y1.5Al4.5Sc0.5O12 (x = 0.5) and Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystals, it is conceivable that certain electronic levels of the Pr3+ ions may manifest in this region as a consequence of crystal field splitting. Secondly, these features might arise from structural distortions within the ScO6 octahedra.
The reduction in structural symmetry induces significant modifications in the vibrational spectrum, manifesting as the activation of previously IR-active and silent modes in the Raman spectra. The spectral evolution, illustrated in Fig. 4b, reveals distinctive peak position shifts across the compositional range. The magnitude of these shifts, denoted by Δ, represents the difference between the extrema values estimated for Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0 and 2.0, respectively. A predominant redshift tendency is observed for the majority of vibrational modes, with shifts typically spanning several wavenumbers (cm−1). Notable exceptions to this trend are observed in the A1g and Eg symmetry modes, centered at approximately 375 and 535 cm−1, respectively. While the primary mechanism underlying these spectral modifications can be attributed to the expansion of the lattice parameter, whereby increased interatomic distances generally correlate with decreased vibrational energies (Fig. 1c), the observed peak shifts cannot be fully rationalized by the experimentally determined lattice parameters of the Pr3+-doped Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystal. This discrepancy suggests that additional structural factors, specifically alterations in the internal bond lengths and angular distortions of the AlO4 or ScO4 tetrahedral units, contribute significantly to the observed spectral evolution.
A comprehensive analysis of the crystalline structural quality was conducted through examination of the FWHM parameters for the most prominent Raman bands, as depicted in Fig. 4c. The FWHM exhibits a systematic increase of several wavenumbers across the compositional range from x = 0.0 to x = 1.0, with the Pr3+-doped Lu1.5Y1.5Al5O12 crystal demonstrating excellent structural order. This observation aligns with theoretical predictions, as the absence of Sc3+ ions ensures enhanced crystallographic periodicity and minimizes local structural distortions that would otherwise arise from the larger ionic radius of Sc3+ ions. The correlation between Sc3+ ions concentration and peak broadening offers compelling evidence for the influence of ionic size effects on the increased disorder within the host lattice. For the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 1.5 and 2.0, the observed trend becomes less clear, as some bands exhibit a decrease in width. This phenomenon may suggest that the Sc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Al ratio equal to 1
Al ratio equal to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 leads to saturation of the garnet lattice disorder. The behavior is likely influenced by a combination of factors, such as selective distortions of specific symmetrical units and the activation of modes resulting from reduced symmetry. However, a thorough analysis of these complexities would require theoretical calculations for validation. Additionally, the presence of phase inclusions in the Pr3+-doped Lu1.5Y1.5Al3.0Sc2.0O12 (x = 2.0) crystal, may also contribute to the modifications observed in the vibrational characteristics.
4 leads to saturation of the garnet lattice disorder. The behavior is likely influenced by a combination of factors, such as selective distortions of specific symmetrical units and the activation of modes resulting from reduced symmetry. However, a thorough analysis of these complexities would require theoretical calculations for validation. Additionally, the presence of phase inclusions in the Pr3+-doped Lu1.5Y1.5Al3.0Sc2.0O12 (x = 2.0) crystal, may also contribute to the modifications observed in the vibrational characteristics.
To investigate the nature of the perovskite phase present in the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 crystal, spectra from these specific regions were recorded, as illustrated in Fig. 4d and e. An optical image demonstrating the phases reveals a repetitive triangular morphology, as shown in Fig. 4e. The vibrational spectra obtained from these regions display fundamentally different characteristics from those of the primary garnet phase, indicating a distinct crystallographic structure. A comprehensive comparison with the existing literature48–52 enabled the identification of the structure as a cubic bixbyite-like distorted perovskite, characterized by the space group Ia![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) . The main characteristic proving such assignment is the strong, degenerate band consisting of two modes of Ag and Fg symmetry located at about 398 cm−1. The chemical composition of the inclusions is presumably Lu1−yYyScO3 with y < 1 − y the lack of aluminum and yttrium can be proven by its deficiencies visible in the EDS maps (see Fig. 2 and 3) and also by employing the Goldschmidt tolerance factor53 defined as:
. The main characteristic proving such assignment is the strong, degenerate band consisting of two modes of Ag and Fg symmetry located at about 398 cm−1. The chemical composition of the inclusions is presumably Lu1−yYyScO3 with y < 1 − y the lack of aluminum and yttrium can be proven by its deficiencies visible in the EDS maps (see Fig. 2 and 3) and also by employing the Goldschmidt tolerance factor53 defined as:
 | (4) |
For LuScO3 and YScO3 the parameter roughly equals 0.80, and 0.82, respectively, assuming Lu3+(IX), Y3+(IX), Sc3+(VI), and O−2(VI) oxidation states.15 These fall well within 0.78 < t < 0.83 range appropriate for cubic, bixbyite-like structures.52 On the other hand, YAlO3 and LuAlO3 take values of 0.90, and 0.89, suggesting an orthorhombic crystal system.54 Indeed, such perovskites are well known to crystalize in Pbnm space group and give Raman bands distinctive from those in Fig. 4d.43,55,56 The identification of the bixbyite phase presents significant implications for the structural and physical properties of Pr3+-doped Lu1.5Y1.5Al3Sc2O12, contributing to notable structural coherence within the crystal. The presence of this phase, specifically the Lu1−yYyScO3 structure with its characteristically smaller lattice parameter, provides a plausible explanation for the observed deviation from Vegard's law.51,57 In addition, a local change in the environment of Pr3+ ions can affect their electronic transitions. The ordering of Sc3+, Lu3+, and O2− ions in deformed perovskite phases may also cause their deficiencies in the rest of the material, leading to an increased number of vacancies and explaining the lower optical quality of the Pr3+-doped Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystal in comparison to the other crystals in the series, as evidenced by the broadened Raman bands. The detailed characterization of bixbyite inclusions and their impact on the Lu1.5Y1.5Al3Sc2O12 garnet structure necessitates further investigation. Given the substantial volume of experimental data required and the complexity of this phenomenon, a comprehensive analysis will be presented in subsequent work dedicated exclusively to elucidating these phase relationships.
3.2. Temperature, time, and spatial dependence of Pr3+ photoluminescence properties
The room-temperature photoluminescence excitation spectra for Pr3+ emission are systematically investigated in Lu1.5Y1.5Al5−xScxO12 crystals where x ranging from 0.0 to 2.0, with emission monitored at 340 nm corresponding to the interconfigurational 4f15d11 → 4f2 transitions (see Fig. 5a). The excitation spectra reveal two primary interconfigurational transitions: the 4f2 → 5d124f1 transition centered at 240 nm and the 4f2 → 5d114f1 transition centered at 285 nm.14 Notably, Sc admixing induces significant broadening of these excitation bands. This spectral broadening can be attributed to the increased lattice disorder induced by Sc incorporation. The Sc admixing leads to a higher concentration of Pr3+ ions that experience varied local environments, resulting in reduced symmetry. This phenomenon is corroborated by the vibrational spectra, which reveal distinct variations indicative of these effects.14 A particularly important observation is the appearance of an additional excitation band centered initially at 200 nm in the Pr3+-doped Lu1.5Y1.5Al4.5Sc0.5O12 (x = 0.5) crystal, which progressively shifts to 205 nm for the Pr3+-doped Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystal. This band originates from electron–hole (e+–h−) pairs bound to Sc3+ ions, termed a bounded exciton. Remarkably, the intensity of this excitonic band demonstrates a linear increase with Sc3+ ions concentration, reaching peak intensity in the crystal with x = 2.0 which is approximately twice that observed in the Pr3+-doped Lu1.5Y1.5Al4.5Sc0.5O12 (x = 0.5) crystal. The systematic appearance and intensity progression of the excitonic band provide evidence for an efficient excitation energy transfer mechanism from excitons bound to Sc3+ ions to Pr3+ ions.29,30Fig. 5b compares the room-temperature photoluminescence spectra of Pr3+ emissions, excited via the interconfigurational 4f2→5d124f1 transition at 240 nm in Lu1.5Y1.5Al5−xScxO12 crystals. The emission spectra demonstrate two distinct spectral regions: a dominant interconfigurational 4f15d11 → 4f2 broadband emission spanning 285–450 nm and sharp emission lines between 470–700 nm originating from the intraconfigurational 4f2 → 4f2 transitions of Pr3+ ions. The Sc admixing induces significant modifications to both spectral features. The interconfigurational 4f15d11 → 4f2 broadband demonstrates progressive broadening, while the intensity of the intraconfigurational 4f2 → 4f2 sharp lines exhibits a systematic increase with rising Sc3+ ions concentration. These observations align with the excitation spectra and provide further evidence that Sc admixture introduces significant disorder into the host lattice. This disorder effectively lowers the symmetry around the Pr3+ ions, resulting in enhanced emission intensity. These observations are consistent with the absorption spectra (see Fig. S1 in ESI†).
Fig. 5c and d present 2D temperature-dependent maps of photoluminescence emission (upper panels) and excitation spectra (lower panels) for the Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0 and 1.5, respectively. The upper panels display emission spectra obtained with an excitation wavelength of 240 nm, while the lower panels show excitation spectra monitored at an emission wavelength of 360 nm. The emission map (upper panel) reveals a dominant broadband emission in the ultraviolet-visible range (300–450 nm), which is assigned to the interconfigurational 4f15d11 → 4f2 transitions of Pr3+ ions. The intensity of this band is highest at low temperatures and decreases substantially as the temperature increases, reflecting thermal quenching of the interconfigurational 4f15d11 → 4f2 emission. Simultaneously, the emission map shows a weaker but noticeable increase in intensity in the visible region (above 450 nm) with increasing temperature, indicating an enhancement of intraconfigurational 4f2 → 4f2 transitions within the Pr3+ ions. These intraconfigurational 4f2 → 4f2 transitions are significantly less efficient than the interconfigurational 4f15d11 → 4f2 transition due to parity selection rules. However, with increasing temperature, a thermal population of lower-lying 4f emitting energy states occurs, resulting in increased emission in the visible region. The weaker intensity of the intraconfigurational 4f2 → 4f2 transitions compared to inter-configurational 4f15d11 → 4f2 transitions at low temperatures results from a lower initial population of these lower-lying 4f energy states.
The excitation maps (lower panels), monitored at emission at 360 nm also show a temperature dependence. The intensity of the excitation bands centered around 240 and 280 nm as well as around 200 nm in Sc admixed crystals, decreases as the temperature increases. This confirms the thermal quenching of the 5d1 exited state, consistent with the emission data. The temperature at which the redistribution of emission intensities occurs is strongly influenced by the concentration of Sc3+ ions in the crystals. In the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal, where x = 0.0, the crossover point of the decrease in the interconfigurational 4f15d11 → 4f2 emission and the corresponding increase in intraconfigurational 4f2 → 4f2 emission occurs at approximately 170 K. Conversely, in the Pr3+-doped Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystals, this crossover point is observed at around 130 K. For further details, please refer to Fig. S2a–f in ESI.† A maximum PL intensity is observed for the Pr3+-doped Lu1.5Y1.5Al4Sc1.0O12 (x = 1.0) crystal for both emission regions, indicating an optimal level of Sc admixing that enhances radiative transitions while minimizing detrimental non-radiative decay processes. The high spatial resolution photoluminescence spectra of Pr3+ ions, recorded in the 460–740 nm spectral range, combined with the estimated radial concentration of Pr3+ ions and the degree of host lattice disorder, provide a comprehensive understanding of the influence of Sc3+ ions concentration on host lattice disorder and Pr3+ ion segregation, refers to Fig. S3a–d and Table S2 in ESI.† This integrated analysis reveals the important role of Sc3+ ions admixing in tuning both structural and compositional properties. These findings provide insights into the mechanisms governing the enhancement of emission intensity in luminescent ions, elucidating the relationship between structural modifications and optical properties in doped crystalline systems.
Fig. 5e shows representative decay curves of Pr3+ emission at 320 nm, following excitation at 280 nm, for the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0, 1.0 and 2.0. The emission recorded at 320 nm corresponds to the interconfigurational 4f15d11 → 4f2 transition, which occurs on a nanosecond timescale. The decay curves exhibit multi-exponential behavior due to the complex relaxation dynamics of the Pr3+ ions in the host crystal. Each curve was fitted using a multi-exponential decay model according to eqn (1). To enable quantitative comparisons of the temperature-dependent evolution of the decay behavior, the effective decay time (τeffective) was computed according to eqn (2). The photoluminescence decay kinetics reveals the trend of decreasing τeffective with increasing Sc3+ ions concentration. At room temperature, τeffective decreases systematically from 18 ns to 12 nm, for the Pr3+-doped Lu1.5Y1.5Al5O12 (x = 0.0) and Lu1.5Y1.5Al3Sc2.0O12 (x = 2.0) crystals, respectively (see also Fig. S4 in ESI†). Fig. 5f illustrates the temperature dependence of the effective photoluminescence decay time of Pr3+ ions emission in the Lu1.5Y1.5Al5−xScxO12 crystals, where x ranges from 0.0 to 2.0. The initial effective decay time at low temperatures remains constant at ∼18 ns for all examined crystals, corresponding to the radiative decay of the interconfigurational 4f15d11 → 4f2 transition. However, with increasing temperature, τeffective declines, indicating increasing non-radiative relaxation processes. Importantly, the onset of accelerated decay shifts systematically toward lower temperatures as the concentration of Sc3+ ions increases. The acceleration of decay time and the reduction in photoluminescence emission intensity with increasing temperature suggest the presence of thermally activated processes. The detailed mechanism responsible for the thermally induced decrease in intensity of the interconfigurational 4f15d11 → 4f2 transition, along with the acceleration of decay time values, followed by a systematic increase in emission intensity is observed, originating from the intraconfigurational 4f2 → 4f2 transitions and its correlation with the concentration of Sc3+ ions. This phenomenon is explained further in the text.
3.3. UV-VIS-NIR emission dynamics of Pr3+ ions under synchrotron radiation excitation
The synchrotron radiation excitation spectra, measured at 295 K for Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals and monitored at emission wavelengths of 314 nm and 610 nm, are presented in Fig. 6a and b, respectively. The excitation spectra monitored at 314 nm emission, displayed in Fig. 6a are consistent with photoluminescence excitation spectra shown in Fig. 5a, c and d. For the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal (where x = 0.0), the excitation bands are observed at 4.26 eV and 5.1 eV, which corresponds to the interconfigurational 4f2 → 5d114f1 and 4f2 → 5d124f1 transitions, respectively. The comparatively distinct shape of the bands indicates a relatively ordered crystal lattice environment and a well-defined energy splitting of the 5d energy levels by the crystal field. As the concentration of Sc3+ ions progressively increases, the excitation bands exhibit systematic broadening and intensification, indicating a significant enhancement in excitation efficiency. This phenomenon can be attributed to the improved structural coupling between the host lattice and Pr3+ ions, which facilitates more efficient energy transfer mechanisms within the crystalline lattice. These observations suggest progressive lattice distortions introduced by Sc3+ ions due to their larger ionic radius compared to Al3+ ions, Sc3+ induces strain in the host lattice and alters the local crystal field symmetry surrounding the Pr3+ ions. As a direct consequence, the crystallographic framework exhibits pronounced structural disorder, characterized by significant lattice perturbations. This structural irregularity generates an asymmetric crystal field distribution, ultimately leading to the non-uniform splitting of the 5d1 electronic manifold. The excitation spectra monitored at an emission wavelength of 610 nm, as shown in Fig. 6b, reveal similar characteristics to those observed at 314 nm emission. It is important to emphasize that the excitation spectra for Pr3+ emission further confirm the presence of a band associated with excitons bound to Sc3+ ions. This observation provides additional evidence for the energy transfer mechanism from Sc3+-bound excitons to Pr3+ ions, highlighting the role of these excitonic interactions in facilitating the observed emission dynamics.The host lattice excitation above the 6 eV, corresponding to energy absorption by the host lattice, provides additional insights into the influence of Sc3+ ions concentration. For the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal (where x = 0.0), the absorption edge is sharp and well-defined, indicating the presence of a structurally ordered lattice. As the Sc3+ ions concentration increases, the host absorption edge broadens and shifts slightly to lower energy (see Fig. 6a and b). This effect is pronounced in the excitation spectra for Pr3+ ions emission at 610 nm. In the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal (where x = 0.0), the host lattice absorption edge exhibits very low intensity, whereas in Sc-admixed crystals, it is significantly enhanced. Additionally, the excitonic band associated with Sc3+ ions becomes increasingly pronounced. These features suggest that the intraconfigurational 4f2 → 4f2 transitions of Pr3+ ions are intensified by the presence of Sc3+ ions. This further confirms that Sc3+ ions lower the local symmetry and facilitate the transfer of excitation energy toward Pr3+ ions, thereby enhancing the same time UV, VIS and NIR emissions (see Fig. 6c). Fig. 6d and e present a comparative analysis of the synchrotron radiation excitation–emission maps recorded at 8 K (upper panels) and 295 K (lower panels) for the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, where x = 0.0 and 1.0. The EEMs reveal that both interconfigurational 4f15d11 → 4f2 and intraconfigurational 4f2 → 4f2 emissions are efficiently excited under intraband excitations (with energies exceeding 188 nm) as well as interconfigurational excitations (4f2 → 5d114f1) with energies below 220 nm. Consistent with the observations presented in the photoluminescence emission spectra (refer to Fig. 5b–d), it is evident that the interconfigurational emission bands associated with the transition from 5d114f1 to 4f2 exhibit broadening and a decrease in intensity. Conversely, the intensity of the intraconfigurational 4f2 → 4f2 emission increases with the incorporation of Sc3+ ions (see also Fig. S5a–c, ESI†). A key observation is the presence of antisite defects (LuxAl, YxAl) and F+ center emissions in the 310–450 nm spectral range, which are pronounced at 8 K due to their excitonic character in the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal, where x = 0.0.23,36,58 Conversely, such luminescence is absent in the crystals containing Sc3+ ions. Another notable observation is that the Pr3+ emission is efficiently excited between 190 and 208 nm, but this phenomenon is exclusive to the Sc-admixed crystals. These findings suggest that Sc3+ ions may compete for electronic charge carriers (electrons and holes) with the antisite defects (LuxAl, YxAl) and F+ centers, subsequently channeling the excitation energy towards Pr3+ ions, thereby enhancing their emission efficiency.
Fig. 6f illustrates the dependence of the maximum peak intensity of Pr3+ emission from 305 to 312 nm on the excitation energy, temperature, and Sc3+ ions concentration in the crystal lattice. In the case of Eexc = 6.6 eV (upper panel), the emission intensity increases systematically with Sc3+ ions concentration at both 8 K and 295 K, reaching a maximum value for the Pr3+-doped Lu1.5Y1.5Al4Sc1.0O12 (x = 1.0) crystal. However, across all examined crystals, the emission intensity at 295 K remains considerably lower than at 8 K. Interestingly, for the Pr3+-doped Lu1.5Y1.5Al4.5Sc0.5O12 (x = 2.0) crystal, a deviation from the expected trend is observed, as the emission intensity shows an increase at 8 K. This enhanced intensity is likely linked to the formation of a hypoeutectic structure within the crystal lattice, where the incorporation of a perovskite phase and associated excitonic emissions bounded to Sc3+ ions in the perovskite phase facilitate energy transfer toward Pr3+ ions in the garnet phase.14 This synergistic energy transfer mechanism amplifies the overall Pr3+ emission intensity at 8 K. However, at 295 K, such an enhancement is not observed, as the hypoeutectic structure and the significantly increased lattice disorder notably intensify the intraconfigurational 4f2 → 4f2 emission. This suggests that the structural and thermal effects at this temperature play a dominant role in distributing the emission intensities between inter- and intracofigurational transitions of Pr3+ ions. For the excitation energy equal to 4.35 eV (lower panel), a different trend emerges regarding the dependence of luminescence intensity on Sc concentration and temperature. At both 8 K and 295 K, the maximum peak intensity decreases with increasing Sc3+ ions concentration, except for a notable deviation observed for the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal, where x = 1.0. For this crystal, the maximum intensity is observed at 8 K, while at 295 K, the intensity increases but does not reach the highest value. This suggests that specific structural and electronic conditions of Pr3+ ions in the Lu1.5Y1.5Al4Sc1O12 crystal favor efficient radiative emission. However, as the temperature increases to 295 K, luminescence intensity is substantially reduced. The variation in intensity between the two excitation energies provides further insight into the excitation mechanisms. The significant enhancement of Pr3+ emission intensity under excitation at 6.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV suggests the presence of an efficient Sc3+-to-Pr3+ energy transfer process. This mechanism has not been observed under direct intraconfigurational excitation at 4.35
eV suggests the presence of an efficient Sc3+-to-Pr3+ energy transfer process. This mechanism has not been observed under direct intraconfigurational excitation at 4.35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) eV.
eV.
The reduction of interconfigurational (4f15d11 → 4f2) emission intensity alongside the increase in intraconfigurational (4f2 → 4f2) emission intensity with rising Sc3+ ions concentration and temperature in Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals is primarily due to enhanced non-radiative relaxation processes facilitated by structural disorder and thermal activation (Fig. 5 and 6). Incorporating Sc3+ ions into the crystal lattice substitutes Al3+ ions, causing localized lattice distortions because of differences in ionic radii and bonding characteristics. This substitution increases disorder within the crystal lattice, reduces the local symmetry of luminescent centers, and enhances electron–phonon coupling. The altered electronic environment redistributes the electronic density of the excited 5d1 state of Pr3+ ions. As the temperature rises, thermal energy becomes sufficient to overcome the energy barrier between the excited 5d1 state and lower-lying 4f energy states. The enhanced electron–phonon coupling due to Sc-induced disorder facilitates non-radiative relaxation pathways, notably the phonon-mediated crossover decay from the 5d11 state to the 3PJ states.14,59,60 This process leads to a depopulation of the 5d11 state, resulting in a decreased intensity of the interconfigurational 4f15d11 → 4f2 emissions in the ultraviolet region. Simultaneously, these non-radiative processes populate the lower-energy 4f2 states. The subsequent radiative relaxation within the 4f2 manifold leads to increased emission intensity in the VIS and NIR regions. The presence of Sc3+ ions amplifies this effect by promoting stronger electronic coupling between the 5d11 and 4f2 states and increasing the phonon density, which further enhances the likelihood of non-radiative transitions. The acceleration of photoluminescence decay times (see Fig. 5e, f and Fig. S4, ESI†) is directly associated with the increased non-radiative relaxation mechanisms. The intensified electron–phonon interactions and higher thermal energy expedite the de-excitation of the excited states, resulting in shorter decay times. The distinct Pr3+ emission dynamics emphasize the key role of Sc admixing in tuning the luminescence properties of Pr3+-doped garnet crystals.
3.4. Temperature dependence of radioluminescence, scintillation and thermoluminescence
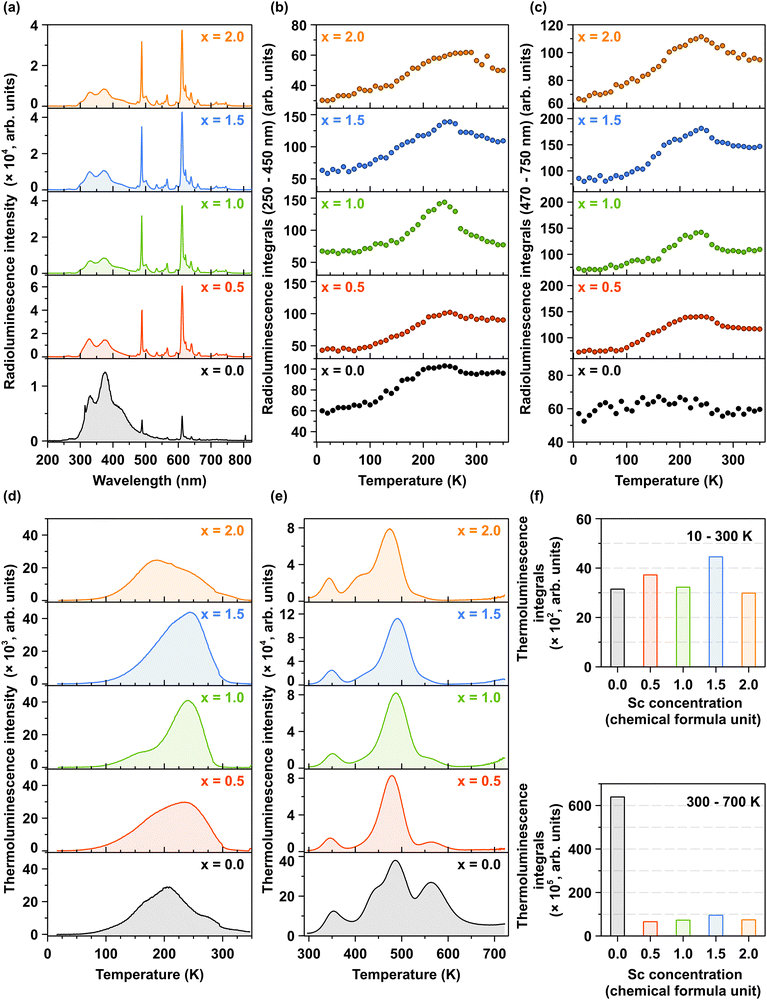
Fig. 7a illustrates the room-temperature X-ray-excited luminescence as a function of increasing Sc3+ ions concentration. The results are consistent with the photoluminescence (PL) spectra under interconfigurational excitation (Fig. 5a) and interband excitation (Fig. 6a). Notably, the increase in the concentration of Sc3+ ions leads to a redistribution of emission intensities between the ultraviolet (UV) and visible (VIS) regions, see also the temperature dependence of 2D RL maps in Fig. S6a–e (ESI†). The underlying mechanism for this redistribution is discussed in detail in Section 3.3. Fig. 7b and c depict the temperature dependence of integrated X-ray-excited luminescence intensities for interconfigurational and intraconfigurational emissions recorded in the 250–450 nm and 470–750 nm spectral regions, respectively. For all Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals, a similar trend is observed: with increasing temperature, the integrated emission intensity for both inter- and intraconfigurational emissions increases up to approximately 260–280 K, depending on the Sc3+ ions concentration. However, the Pr3+-doped Lu1.5Y1.5A5−xScxO12 crystal, where x = 0.0 exhibits a distinct behavior.In this case, an increase in integrated emission intensity is observed exclusively for interconfigurational transitions, while the intraconfigurational transitions remain stable across the 10–350 K temperature range. This observation provides additional evidence that Sc-induced lattice disorder facilitates an increased population of lower-energy 4f states, a process mediated by phonon interactions. The temperature-dependent variation in emission intensity is closely linked to the energy depth of charge trapping centers. At elevated temperatures, shallow traps, such as those associated with LuxAl and YxAl dislocations, become inactive in capturing electrons because the thermal energy exceeds the energy barriers of these traps. Consequently, the excitation energy is efficiently transferred to Pr3+ ions, resulting in a maximized emission intensity. This interplay underscores the role of temperature in modifying the efficiency of energy transfer and emission efficiency. This mechanism is corroborated by the TL glow curves obtained after X-ray excitation at 10 K, as shown in Fig. 7d. The primary TL band is observed between 80 and 300 K, corresponding to the temperature range where the radioluminescence intensity increases. Another significant observation is that Sc admixing does not substantially modify the trap depth distribution and density in the temperature range of 10–300 K. The observed TL glow curves can be attributed to the formation of shallow electron trapping centers in LuxAl and YxAl dislocations.58,61 Similarly, in the high-temperature region (300–700 K), as illustrated in Fig. 7e, the distribution and density of deep trapping centers remains largely unaffected by Sc admixing. These deep trapping centers, responsible for the high-temperature TL glow curves, originate from oxygen vacancies 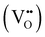 and transition ion impurities.62,63 The incorporation of Sc3+ ions demonstrates minimal impact on the formation of shallow trapping centers, evidenced by the relatively constant trap density across all crystals, as shown in Fig. 7f (upper panel). In contrast, Sc admixing significantly reduces the density of deep trapping centers within the crystal structure, as depicted in Fig. 7f (lower panel). Quantitatively, the integrated TL intensity in Sc-admixed crystals exhibits approximately an order of magnitude reduction compared to Pr3+-doped Lu1.5Y1.5A5−xScxO12 crystal (where x = 0.0), as demonstrated in Fig. 7f (lower panel).
and transition ion impurities.62,63 The incorporation of Sc3+ ions demonstrates minimal impact on the formation of shallow trapping centers, evidenced by the relatively constant trap density across all crystals, as shown in Fig. 7f (upper panel). In contrast, Sc admixing significantly reduces the density of deep trapping centers within the crystal structure, as depicted in Fig. 7f (lower panel). Quantitatively, the integrated TL intensity in Sc-admixed crystals exhibits approximately an order of magnitude reduction compared to Pr3+-doped Lu1.5Y1.5A5−xScxO12 crystal (where x = 0.0), as demonstrated in Fig. 7f (lower panel).
Thermoluminescence is a valuable technique for elucidating the role of charge carriers in the scintillation process. Shallow traps are typically associated with the slow components observed in scintillation decay curves,64 while deep traps, identified through high-temperature thermoluminescence measurements exceeding 300 K, are correlated with a decrease in scintillation light yield.62 The experimental data demonstrate a significant correlation between the reduced density of deep trapping centers and enhanced scintillation parameters in Sc-admixed crystals, as evidenced in Fig. 8a, b and Fig. S7a (ESI†)-as well as Table 1.
| Sc concentration (chemical formula unit) | Scintillation parameters | |||||
|---|---|---|---|---|---|---|
| τ1/err. (ns) | τ2/err. (ns) | τ3/err. (ns) | τeff/err. (ns) | LY/err. (phs/eV, 2 μs) | Energy res. (%) | |
| 0.0 | 10 ± 1.2 | 62 ± 5.4 | 459 ± 16 | 304 ± 8 | 1800 ± 90 | 27 |
| 0.5 | 16 ± 2.4 | 87 ± 1.8 | 613 ± 11 | 534 ± 5 | 9700 ± 480 | 18 |
| 1.0 | 9 ± 0.8 | 106 ± 8.7 | 629 ± 17 | 509 ± 9 | 9500 ± 470 | 14 |
| 1.5 | 7 ± 1.1 | 64 ± 2.6 | 572 ± 14 | 516 ± 7 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 ± 560 200 ± 560 |
15 |
| 2.0 | 5 ± 0.6 | 58 ± 3.1 | 467 ± 10 | 378 ± 6 | 6700 ± 330 | 14 |
Fig. 8a and Fig. S7a in ESI† present the pulse height spectra measured using a 137Cs radioisotope with an amplifier shaping time of 2 μs. Fig. 8b and Fig. S7b (ESI†) compare the scintillation decay times of crystals with increasing Sc concentrations. The key scintillation parameters, including light yield, decay times, and energy resolution, are summarized in Table 1 as a function of Sc3+ ions concentration. As discussed in previous sections, the scintillation properties are also significantly influenced by Sc admixing. Specifically, the light yield value increases approximately sixfold in the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystals for the x ranging from 0.5 to 1.5, reaching a maximum value for the Pr3+-doped Lu1.5Y1.5Al3.5Sc1.5O12 crystal (x = 1.5). Although the Pr3+-doped Lu1.5Y1.5Al3Sc2O12 hypoeutectic crystal (x = 2.0) also exhibits an enhanced light yield, the improvement is less pronounced compared to single-phase crystals. The substantial increase in light yield for Sc-admixed crystals is attributed to the  energy transfer process (Fig. 5 and 6) and reduced density of deep trapping centers, as evidenced by high-temperature TL glow curves (Fig. 7e). Additionally, the effective scintillation decay times are approximately doubled following Sc admixing, indicating significant modifications to the energy transfer dynamics. These strong dependencies of scintillation properties on Sc concentration lead to two key conclusions: (i) the local distortions introduced by Sc3+ ions effectively compete with other trapping centers, such as dislocations, oxygen vacancies, and trace impurities, in capturing charge carriers. (ii) Excitons bound to Sc3+ ions efficiently transfer their energy to Pr3+ ions, thereby enhancing scintillation efficiency.30 Furthermore, Sc admixing significantly improves the energy resolution of the crystals, further demonstrating the beneficial impact of Sc incorporation on scintillation performance.
energy transfer process (Fig. 5 and 6) and reduced density of deep trapping centers, as evidenced by high-temperature TL glow curves (Fig. 7e). Additionally, the effective scintillation decay times are approximately doubled following Sc admixing, indicating significant modifications to the energy transfer dynamics. These strong dependencies of scintillation properties on Sc concentration lead to two key conclusions: (i) the local distortions introduced by Sc3+ ions effectively compete with other trapping centers, such as dislocations, oxygen vacancies, and trace impurities, in capturing charge carriers. (ii) Excitons bound to Sc3+ ions efficiently transfer their energy to Pr3+ ions, thereby enhancing scintillation efficiency.30 Furthermore, Sc admixing significantly improves the energy resolution of the crystals, further demonstrating the beneficial impact of Sc incorporation on scintillation performance.
3.5. Electron paramagnetic resonance
Electron paramagnetic resonance spectra were recorded for all examined crystals. The EPR spectrum of the Pr3+-doped Lu1.5Y1.5A5−xScxO12, where x = 0.0 exhibits a complex multiplet structure, as illustrated in Fig. 1, comprising numerous overlapping resonance signals. These spectral features are tentatively ascribed to paramagnetic centers associated with Mn2+ ions.To validate this observation, the experimental spectrum was approximated using a calculated spectrum based on the following spin-Hamiltonian:
| Ĥ = gβŜzB + AŜzÎz + B04 + O04 | (5) |
 | ||
| Fig. 9 (a) Experimental (Exp.) and calculated (Calc1–3 and Calc_All; Calc_All is the sum of the Calc1–3) EPR spectra of the Pr3+-doped Lu1.5Y1.5A5O12 (x = 0.0). The experimental spectrum is magnified to highlight the details of the weakest spectral components. Three distinct but partially overlapping Mn2+ spectral contributions (Mn1–32+) are presented. The label Fer3+ corresponds to the signal originating from rhombic Fe3+ sites.65 (b) Fer3+ signal in the Pr3+-doped Lu1.5Y1.5A5−xScxO12 crystals with increasing Sc3+ ions concentration, (c) dependence of the double integral intensity of the Fer3+ signal on the Sc concentration. | ||
| Paramagnetic centers | g tensor/factor | A (MHz) | B04 (MHz) | ||
|---|---|---|---|---|---|
| g1 | g2 | g3 | |||
| Mn12+ | 2.00 | 300 | 6.0 | ||
| Mn22+ | 1.99 | 300 | −100 | ||
| Mn32+ | 1.99 | 300 | −170 | ||
| F+ | 1.999 | n/a | n/a | ||
| O− | 2.03 | n/a | |||
| Lu2+ | 1.93 | 1.96 | 1.99 | 300 | |
| Ir4+ | 1.86 | n/a | |||
| O2−OH | 1.93 | 1.96 | 1.99 | 1700 | |
The observed hyperfine constant exhibits values characteristic of Mn2+. The cubic constant demonstrates notable variation among centers: it is relatively small for Mn12+ but approximately two orders of magnitude larger for Mn2,32+. Such large cubic constants, reaching hundreds of MHz, have been previously reported.67 Furthermore, the cubic constant displays opposite signs for Mn2,32+ as compared to the Mn12+. Notably, neither axial (B20) nor (B22) rhombic constants were required to accurately describe the experimental spectrum for any of the three Mn1–32+ centers. These observations collectively suggest that all three centers occupy highly symmetric sites within the LuAG lattice. The centers can only occupy octahedral and tetrahedral alumina positions. The Al–O bond length is larger in the case of octahedral position as compared to the tetrahedrala sites as reported in the isostructural YAG.68 Given that the cubic constant is inversely proportional to the fifth power of the bond length, in can be assumed that the Mn12+ center occupies the octahedral site, while Mn2,32+ are situated at tetrahedral sites. The notably larger cubic constant observed for Mn32+ compared to Mn22+ suggests a reduction in the Mn–O bond length, which may be attributed to the presence of a highly symmetric perturbation in the vicinity of the Mn32+ position within the lattice structure. The incorporation of Sc results in the complete disappearance of the Mn2+ spectrum. This phenomenon can be attributed to Sc substitution at octahedral Al sites, thereby preventing the incorporation of Mn2+ ions (which is considered a trace impurity) into this crystallographic position.
A signal corresponding to a g factor of 4.3 (∼1600 G), identified as Fer3+ in Fig. 9b, is attributed to rhombic Fe3+.65 Notably, this signal is also detected in the Sc admixed samples. To facilitate a more detailed investigation, the Fer3+ signals for all samples are depicted in Fig. 9c. The origin of the rhombic Fer3+ signal is likely associated with the crystal surface, where structural disorder is pronounced, even though EPR inherently measures bulk properties. It is evident that the degree of Sc3+ ions concentration significantly influences the Fer3+ signal. To illustrate this effect, Fig. 9c shows the dependence of the double integral intensity of the Fer3+ signal (which is directly proportional to the concentration of paramagnetic centers69) on the Sc atoms concentration. Specifically, a Sc3+ ions concentration equal to 0.5 leads to an approximately 1.5-fold increase in the Fer3+ signal intensity. Beyond this point, the signal intensity decreases with further increases in Sc3+ ions concentration. This trend suggests that Sc admixing may inhibit the incorporation of trace impurities (e.g. Fe3+ and Mn2+), particularly at the crystal rim, thereby reducing the concentration of Fer3+ paramagnetic centers. Consequently, this leads to an improvement in the scintillation performance. This interpretation is consistent with the scintillation and thermoluminescence characteristics presented in Fig. 7 and 8. Furthermore, the theoretical calculations of the experimentally recorded EPR spectra provide additional validation for the presence of all paramagnetic centers listed in Table 2 and their dependence on Sc concentration (see Fig. S8a–c, in the ESI† and the related discussion). A particularly noteworthy observation is the correlation between the dependence of the double integral intensity on the Sc3+ ions concentration for both the O− defect and the F+ center (Fig. S8a and b, ESI†). These defect-related contributions exhibit a similar trend and comparable double integral intensity, suggesting a possible charge transfer mechanism: O2− + h+ ⇌ V02+ + e−. Additionally, a strong correlation is observed between the dependence of the double integral intensity on the Sc3+ ions concentration for the F+ and O− centers and the variation in luminescence intensity of fits 1–4, as shown in Fig. S9a–d in the ESI.† Notably, the behavior of the F+ and O− centers closely follows that of luminescence fit 4, providing compelling evidence that fit 4 originates from the F+–O− defect pair.
4. Conclusions
The crystallization of materials containing strongly mismatched elements occupying identical crystallographic sites presents significant challenges in achieving good structural homogeneity, particularly when using the micro-pulling-down (μ-PD) method. This investigation addressed these challenges by examining the crystallization process from melts containing highly incompatible elements Sc and Al, which occupy the same octahedral sites within the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 garnet lattice (where x = 0.0, 0.5, 1.0, 1.5, and 2.0). To address the significant issue of radial elemental inhomogeneity, a critical barrier in the μ-PD crystal growth process, a modified crucible design with five independent crystallization capillaries was used. The implementation of five crystallization capillaries revealed the formation of heterogeneous, round-like spots whose occurrence varied randomly with the increasing Sc3+ ions concentration. The random distribution of these heterogeneous spots further indicated non-uniform ejection dynamics, suggesting that the melt within the crucible exhibited localized heterogeneity. This heterogeneity was likely attributable to the ionic radii mismatch between Sc and Al elements, which disrupts the uniformity of the melt composition and influences the crystallization process. This finding highlighted the importance of thoroughly mixing raw materials prior to melting, even in the μ-PD method, where the initial material weight was approximately 1 gram, to achieve improved elemental homogeneity. Another significant observation was the identification of a threshold concentration of Sc3+ ions at x = 1.5. The key finding revealed that at Sc3+ ion concentrations exceeding this threshold, the ionic mismatch induced thermodynamic processes that preferentially facilitated the formation of a garnet/bixbyite-like distorted perovskite hypoeutectic crystal structure, rather than promoting further substitution of Sc3+ for Al3+ ions within the lattice. This discovery provides a novel perspective on exploting ionic radii mismatch as an approach for the controlled crystallization of eutectic and hypoeutectic crystals, potentially advancing materials engineering methodologies. Moreover, the independent crystallization observed in each capillary presented a promising opportunity to enhance the self-organization of non-mixing phases during the crystallization of hypoeutectic crystals, offering valuable insights for optimizing crystal growth processes. Vibrational spectroscopy confirmed that the progressive substitution of Sc3+ for Al3+ ions increased the host lattice disorder, with saturation occurring at Sc3+ ions concentrations of x ≥ 1.0. This enhanced lattice disorder significantly lowered the local symmetry around Pr3+ ions, directly affecting the crystal field strength and tuning the energetic positioning of the 5d11 excited state of Pr3+ ions relative to the conduction band minimum. The incorporation of Sc3+ ions reduced local symmetry around Pr3+ ions, lowering the energy barrier between the 5d11 excited state and the lower-lying 4f energy state. This reduction facilitated non-radiative pathways, enabling the 5d11 to 3PJ crossover of excited electrons. This significantly enhanced the Pr3+ emission intensity within the VIS and NIR spectral ranges, demonstrating its potential for tuning luminescent properties through controlled lattice disorder. For the first time, the energy transfer mechanism was experimentally validated through excitation spectroscopy using synchrotron radiation. This mechanism resulted in a sixfold enhancement of the scintillation light yield, reaching a maximum value of 11
energy transfer mechanism was experimentally validated through excitation spectroscopy using synchrotron radiation. This mechanism resulted in a sixfold enhancement of the scintillation light yield, reaching a maximum value of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 photons per MeV in the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal where x = 1.5. This enhancement was accompanied by an approximate doubling of the scintillation response time. Synchrotron radiation excitation–emission mapping revealed that local lattice distortions induced by Sc3+ ions effectively competed with trapping centers (dislocations, oxygen vacancies, and trace impurities) in charge carrier capture processes. This competitive mechanism enhanced energy transfer efficiency to Pr3+ ions, resulting in significantly improved scintillation properties. The findings demonstrated the crucial role of controlled lattice modification in optimizing energy transfer pathways and enhancing luminescent performance. Thermoluminescence glow curve analysis revealed that trapping centers associated with LuxAl and YxAl dislocations dominated below 200 K, while oxygen vacancies
200 photons per MeV in the Pr3+-doped Lu1.5Y1.5Al5−xScxO12 crystal where x = 1.5. This enhancement was accompanied by an approximate doubling of the scintillation response time. Synchrotron radiation excitation–emission mapping revealed that local lattice distortions induced by Sc3+ ions effectively competed with trapping centers (dislocations, oxygen vacancies, and trace impurities) in charge carrier capture processes. This competitive mechanism enhanced energy transfer efficiency to Pr3+ ions, resulting in significantly improved scintillation properties. The findings demonstrated the crucial role of controlled lattice modification in optimizing energy transfer pathways and enhancing luminescent performance. Thermoluminescence glow curve analysis revealed that trapping centers associated with LuxAl and YxAl dislocations dominated below 200 K, while oxygen vacancies  combined with other trapping centers were prominent above 280 K. Sc admixing had a negligible effect on the formation of shallow trapping centers. However, in the case of deep trapping centers, Sc incorporation significantly reduced their density by approximately an order of magnitude compared to the Sc-free crystal. This significant reduction underscores a key role of Sc admixing in mitigating deep trapping centers, thereby optimizing charge carrier dynamics and enhancing scintillation performance. The incorporation of Sc3+ into the garnet lattice systematically reduced the concentration of Mn2+ and Fe3+ trace impurities, which acted as detrimental trapping centers, thereby improving scintillation light yield. EPR spectroscopy further revealed that synergistic interactions between F+ centers and Pr3+ ions amplified the Pr3+-related emission intensity at 370 nm, corroborating historical assignments from late 20th-century studies. Importantly, the emission band at 410–420 nm, previously misattributed to isolated F+ centers in post-1990s literature, was conclusively linked to F+–O− defect pairs. This discovery resolved long-standing ambiguities in defect-related luminescence mechanisms in garnet materials and highlighted the need for precise spectroscopic characterization to avoid erroneous defect assignments. The findings advocated for revised analytical frameworks in the study of garnet scintillators, emphasizing the critical role of defect pair interactions in governing emission properties. The demonstrated resilience of the Sc-admixed system against shallow trapping centers formation, coupled with its ability to suppress the influence of deep trapping centers and facilitate Sc-mediated energy transfer processes, represents a crucial advancement for the design of next-generation oxide scintillators and phosphors materials. Furthermore, the controlled tuning of host lattice disorder through Sc incorporation enables precise adjustments to structural, scintillation, and luminescence properties. This approach not only enhances the luminescence intensity of rare-earth elements but also significantly improves the material suitability for targeted applications, marking a step forward in the development of advanced scintillators and luminescent materials.
combined with other trapping centers were prominent above 280 K. Sc admixing had a negligible effect on the formation of shallow trapping centers. However, in the case of deep trapping centers, Sc incorporation significantly reduced their density by approximately an order of magnitude compared to the Sc-free crystal. This significant reduction underscores a key role of Sc admixing in mitigating deep trapping centers, thereby optimizing charge carrier dynamics and enhancing scintillation performance. The incorporation of Sc3+ into the garnet lattice systematically reduced the concentration of Mn2+ and Fe3+ trace impurities, which acted as detrimental trapping centers, thereby improving scintillation light yield. EPR spectroscopy further revealed that synergistic interactions between F+ centers and Pr3+ ions amplified the Pr3+-related emission intensity at 370 nm, corroborating historical assignments from late 20th-century studies. Importantly, the emission band at 410–420 nm, previously misattributed to isolated F+ centers in post-1990s literature, was conclusively linked to F+–O− defect pairs. This discovery resolved long-standing ambiguities in defect-related luminescence mechanisms in garnet materials and highlighted the need for precise spectroscopic characterization to avoid erroneous defect assignments. The findings advocated for revised analytical frameworks in the study of garnet scintillators, emphasizing the critical role of defect pair interactions in governing emission properties. The demonstrated resilience of the Sc-admixed system against shallow trapping centers formation, coupled with its ability to suppress the influence of deep trapping centers and facilitate Sc-mediated energy transfer processes, represents a crucial advancement for the design of next-generation oxide scintillators and phosphors materials. Furthermore, the controlled tuning of host lattice disorder through Sc incorporation enables precise adjustments to structural, scintillation, and luminescence properties. This approach not only enhances the luminescence intensity of rare-earth elements but also significantly improves the material suitability for targeted applications, marking a step forward in the development of advanced scintillators and luminescent materials.
Author contributions
Karol Bartosiewicz: conceptualization, methodology, investigation, formal analysis, writing – original draft, writing – review & editing, project administration, supervision, corresponding author. Yevheniia Smortsova: investigation, data curation, formal analysis, writing – review & editing. Piotr Radmoski: investigation, data analysis, writing – review & editing. Marcin E. Witkowski: investigation, data analysis, writing – review & editing. Konrad J. Drozdowski: investigation, data analysis, writing – review & editing. Masao Yoshino: investigation, resources, writing – review & editing. Takahiko Horiai: investigation, validation, writing – review & editing. Damian Szymański: investigation, data analysis, writing – review & editing. Wioletta Dewo: investigation, data analysis, writing – review & editing. Justyna Zeler: investigation, data analysis, writing – review & editing. Paweł Socha: investigation, data analysis, writing – review & editing. Maksym Buryi: investigation, writing – review & editing. Andrey Prokhorov: methodology, writing – review & editing. David John: data analysis, writing – review & editing. Jakub Volf: investigation (Scintillation measurements), writing – review & editing. Tomasz Runka: investigation, data analysis, writing – review & editing. Tomasz Pędziński: investigation, writing – review & editing. Karol Hauza: investigation, writing – review & editing. Vítězslav Jarý: investigation, writing – review & editing. Yasuhiro Shoji: resources, writing – review & editing. Kei Kamada: resources, writing – review & editing. Eugeniusz Zych: writing – review & editing. Winicjusz Drozdowski: writing – review & editing. Akira Yoshikawa: resources, writing – review & editing.Data availability
Upon acceptance of the manuscript for publication, all raw data supporting the findings of this study will be made available in the ASEP repository, provided by the Institute of Physics of the Czech Academy of Sciences, Prague, Czech Republic. Below is the DOI corresponding to the raw data: DOI: https://doi.org/10.57680/asep.0635702, Handle: https://hdl.handle.net/11104/0366734. The repository includes a short description of how to access and interpret the data. The files are organized into separate zipped folders, each containing specific data as presented in the manuscript. For further inquiries regarding data access, please contact the corresponding author, Karol Bartosiewicz, via email at bartosiewicz@fzu.cz. Alternatively, you can refer to the ASEP repository guidelines available at https://asep-portal.lib.cas.cz/ or reach out to the ASEP repository support team via email at arl@lib.cas.cz.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
This project has received funding from the European Union's Horizon Europe research and innovation programme under the Marie Skłodowska-Curie Actions COFUND, Physics for Future, grant agreement No. 101081515, the National Science Centre Poland (NCN) No. 2020/39/D/ST3/02711 as well as the GIMRT program of the Institute for Materials Research, Tohoku University Proposal No. 202306-RDKYA-0533. The financial support of the Leading Agency National Science Centre – Czech Science Foundation Project No. 24-14580L is gratefully acknowledged.References
- M. Nikl, A. Yoshikawa, K. Kamada, K. Nejezchleb, C. R. Stanek, J. A. Mares and K. Blazek, Prog. Cryst. Growth Charact. Mater., 2013, 59, 47–72 CrossRef CAS.
- C. Dujardin, E. Auffray, E. Bourret-Courchesne, P. Dorenbos, P. Lecoq, M. Nikl, A. N. Vasil'ev, A. Yoshikawa and R. Y. Zhu, IEEE Trans. Nucl. Sci., 2018, 65, 1977–1997 CAS.
- G. Bizarri, J. Cryst. Growth, 2010, 312, 1213–1215 CrossRef CAS.
- K. Bartosiewicz, H. Takahiko, Y. Akihiro, A. Yoshikawa, S. Kurosawa, M. Yoshino and Y. Zorenko, Mater. Sci. Eng., B, 2020, 261, 114677 CrossRef CAS.
- K. Bartosiewicz, A. Markovskyi, T. Horiai, D. Szymański, S. Kurosawa, A. Yamaji, A. Yoshikawa and Y. Zorenko, J. Alloys Compd., 2022, 905, 164154 CrossRef CAS.
- I. Carrasco, K. Bartosiewicz, M. Nikl, F. Piccinelli and M. Bettinelli, Opt. Mater., 2015, 48, 252–257 CrossRef CAS.
- P. Bolek, Z. Justyna, J. Trojan-Piegza, L. D. Carlos and E. Zych, Chem. Eng. J., 2021, 421, 129764 CrossRef CAS.
- Y. Kanke and A. Navrotsky, J. Solid State Chem., 1998, 141, 424–436 CrossRef CAS.
- K. Bartosiewicz, A. Szysiak, R. Tomala, P. Gołębiewski, H. Węglarz, V. Nagirnyi, M. Kirm, I. Romet, M. Buryi, V. Jary, R. Kucerkova, M. Wzorek and R. Buczyński, Phys. Rev. Appl., 2023, 20, 014047 CrossRef CAS.
- Z. Hu, X. Chen, H. H. Chen, Y. Shi, X. Liu, T. Xie, H. Kou, Y. Pan, E. Mihóková, M. Nikl and J. Li, J. Lumin., 2019, 210, 14–20 CrossRef CAS.
- W. Drozdowski, K. Brylew, A. J. Wojtowicz, J. Kisielewski, M. Świrkowicz, T. Łukasiewicz, J. T. M. de Haas and P. Dorenbos, Opt. Mater. Express, 2014, 4, 1207 CrossRef.
- M. V. Derdzyan, K. L. Ovanesyan, A. G. Petrosyan, A. Belsky, C. Dujardin, C. Pedrini, E. Auffray, P. Lecoq, M. Lucchini and K. Pauwels, J. Cryst. Growth, 2012, 361, 212–216 CrossRef CAS.
- C. Foster, Y. Wu, L. Stand, M. Koschan and C. L. Melcher, J. Lumin., 2019, 216, 116751 CrossRef CAS.
- K. Bartosiewicz, B. Albini, D. Szymański, P. Socha, T. Horiai, M. Yoshino, A. Yamaji, S. Kurosawa, R. Kucerkova, P. Galinetto and A. Yoshikawa, J. Alloys Compd., 2024, 985, 174078 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- E. Mihóková, V. Babin, K. Bartosiewicz, L. S. Schulman, Č. Václav, K. Miroslav and M. Nikl, Opt. Mater., 2015, 40, 127–131 CrossRef.
- M. Fasoli, A. Vedda, M. Nikl, C. Jiang, B. P. Uberuaga, D. A. Andersson, K. J. McClellan and C. R. Stanek, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 081102(R) CrossRef.
- E. Mihóková, A. Vedda, M. Fasoli, F. Moretti, A.-L. Bulin, M. Nikl, M. Bettinelli, A. Speghini, H. Ogino and A. Yoshikawa, Opt. Mater., 2010, 32, 1298–1301 CrossRef.
- H. Ogino, K. Kamada, A. Yoshikawa, F. Saito, J. Pejchal, J. A. Mares, M. Nikl, A. Vedda, J.-I. Shimoyama and K. Kishio, IEEE Trans. Nucl. Sci., 2008, 55, 1197–1200 CAS.
- K. Kamada, T. Yanagida, J. Pejchal, M. Nikl, T. Endo, T. Kousuke, Y. Fujimoto, F. Akihiro and A. Yoshikawa, IEEE Nuclear Science Symposium Conference Record, 2011 DOI:10.1109/nssmic.2011.6154631.
- K. Kamada, T. Yanagida, J. Pejchal, M. Nikl, T. Endo, T. Kousuke, Y. Fujimoto, F. Akihiro and A. Yoshikawa, IEEE Trans. Nucl. Sci., 2012, 59, 2130–2134 CAS.
- C. Hu, X. Feng, J. Li, A. Vedda, D. Ding, Z. Zhou, H. Kou and Y. Pan, Phys. Rev. Appl., 2016, 6, 064026 CrossRef.
- K. Bartosiewicz, T. Horiai, A. Yamaji, A. Yoshikawa, S. Kurosawa, M. Yoshino and Y. Zorenko, Mater. Sci. Eng., B, 2020, 261, 114677 CrossRef CAS.
- K. Bartosiewicz, K. Bartosiewicz, V. Fritz, V. Fritz, D. V. D. Heggen, D. V. D. Heggen, D. Szymanski, D. Szymanski, J. Zeler, J. Zeler, J. Pejchal, J. Pejchal, A. Yamaji, A. Yamaji, R. Kucerkova, R. Kucerkova, A. Beitlerova, A. Beitlerova, S. Kurosawa, S. Kurosawa, A. Yoshikawa, A. Yoshikawa, P. F. Smet, P. F. Smet, E. Zych, E. Zych, M. Nikl and M. Nikl, J. Mater. Chem. C, 2023, 11, 8850–8865 RSC.
- K. Bartosiewicz, Metals, 2023, 13, 422 CrossRef CAS.
- V. Laguta, M. Buryi, V. Babin, P. Machek, S. Zazubovich, K. Bartosiewicz, S. Kurosawa, A. Yamaji, A. Yoshikawa, K. Ulicná, V. Chlan, H. Štěpánková and M. Nikl, J. Mater. Chem. C, 2023, 11, 1346–1359 RSC.
- Y. O. Zagorodniy, V. Chlan, H. Stepánková, Y. Fomichov, J. Pejchal, V. V. Laguta and M. Nikl, J. Phys. Chem. Solids, 2019, 126, 93–104 CrossRef CAS.
- K. Bartosiewicz, V. Fritz, D. Van, D. Szymański, Z. Justyna, Y. Akihiro, J. Pejchal, R. Kučerková, A. Beitlerová, S. Kurosawa, A. Yoshikawa, P. Smet, E. Zych and M. Nikl, J. Mater. Chem. C, 2023, 11, 8850–8865 RSC.
- K. Miroslav, M. Nikl, P. Průša, J. Mareš, K. Nitsch, M. Hanuš, O. Zuzana and R. Kučerková, J. Cryst. Growth, 2011, 318, 813–819 CrossRef.
- K. Miroslav, P. Průša, J. Mareš, M. Nikl, K. Nitsch, M. Hanuš, O. Zuzana and R. Kučerková, IOP Conf. Ser.:Mater. Sci. Eng., 2010, 15, 012012 Search PubMed.
- P. Veber, K. Bartosiewicz, J. Debray, G. Alombert-Goget, O. Benamara, V. Motto-Ros, T. Mai Pham, A. Borta-Boyon, H. Cabane, L. Kheirréddine, L. Franck, K. Kamada, A. Yoshikawa and M. Maglione, CrystEngComm, 2019, 21, 3844–3853 RSC.
- A. Markovskyi, W. Gieszczyk, P. Bilski, A. Fedorov, K. Bartosiewicz, K. Paprocki, T. Zorenko and Y. Zorenko, J. Alloys Compd., 2020, 849, 155808 CrossRef CAS.
- K. Bartosiewicz, V. Babin, A. Beitlerova, P. Bohacek, K. Jurek and M. Nikl, J. Lumin., 2017, 189, 126–139 CrossRef CAS.
- J. Sanders, Veusz, https://veusz.github.io/, (accessed June 4, 2025).
- M. N. Magomedov, Solid State Commun., 2020, 322, 114060 CrossRef CAS.
- K. Bartosiewicz, T. Horiai, A. Yamaji, A. Yoshikawa, S. Kurosawa, K. J. Kim, V. Vistovskyy, A. Voloshinovskii and Y. Zorenko, J. Lumin., 2021, 235 Search PubMed.
- K. Bartosiewicz, V. Babin, K. Kamada, A. Yoshikawa, A. Beitlerova and M. Nikl, Opt. Mater., 2018, 80, 98–105 CrossRef CAS.
- K. Bartosiewicz, V. Babin, K. Kamada, A. Yoshikawa, J. A. Mares, A. Beitlerova and M. Nikl, Opt. Mater., 2017, 63, 134–142 CrossRef CAS.
- K. Bartosiewicz, A. Markovskyi, T. Zorenko, A. Yoshikawa, S. Kurosawa, A. Yamaji and Y. Zorenko, Phys. Status Solidi RRL, 2020, 14, 2000327 CrossRef CAS.
- K. Bartosiewicz and K. Bartosiewicz, Metals, 2023, 13, 422 CrossRef CAS.
- D. L. Rousseau, R. P. Bauman and S. P. S. Porto, J. Raman Spectrosc., 2005, 10, 253–290 CrossRef.
- K. Papagelis, G. Kanellis, S. Ves and G. A. Kourouklis, Phys. Status Solidi B, 2002, 233, 134–150 CrossRef CAS.
- W. Dewo, K. Luczynska, Y. Zorenko, V. Gorbenko, K. Druzbicki and T. Runka, Spectrochim. Acta, Part A, 2020, 231, 118111 CrossRef CAS PubMed.
- A. Markovskyi, P. Radomski, W. Dewo, V. Gorbenko, A. Fedorov, T. Runka and Y. Zorenko, Mater. Res. Bull., 2025, 182, 113141 CrossRef CAS.
- M. Poulos, S. Giaremis, J. Kioseoglou, J. Arvanitidis, D. Christofilos, S. Ves, M. P. Hehlen, N. L. Allan, C. E. Mohn and K. Papagelis, J. Phys. Chem. Solids, 2022, 162, 110512 CrossRef CAS.
- W. Dewo, V. Gorbenko, A. Markovskyi, Y. Zorenko and T. Runka, J. Lumin., 2023, 254, 119481 CrossRef CAS.
- A. Lukowiak, R. J. Wiglusz, M. Maczka, P. Gluchowski and W. Strek, Chem. Phys. Lett., 2010, 494, 279–283 CrossRef CAS.
- K. Eremeev, P. Loiko, A. Braud, P. Camy, J. Zhang, X. Xu, Y. Zhao, P. Liu, S. Balabanov, E. Dunina, A. Kornienko, L. Fomicheva, X. Mateos, U. Griebner, V. Petrov, L. Wang and W. Chen, Opt. Mater. Express, 2022, 12, 3749–3762 CrossRef CAS.
- J. Li, W. Hou, X. Xu, Y. Xue, Q. Song, J. Liu, F. Wu, P. Luo, F. Wang, H. Yu, Q. Wang and J. Xu, Opt. Mater. Express, 2022, 12, 3071–3080 CrossRef CAS.
- E. Dobretsova, O. Alimov, D. Guryev, V. Voronov, S. Rusanov, V. Kashin, S. Kutovoy, V. Vlasov, L. Badyanova, I. Novikov and V. Tsvetkov, Crystals, 2022, 12, 1745 CrossRef CAS.
- R. N. Maksimov, G. Toci, A. Pirri, V. A. Shitov, E. Sani, A. Santonocito, B. Patrizi, M. Becucci, M. Vannini and V. V. Osipov, Opt. Mater., 2024, 151, 115309 CrossRef CAS.
- O. Alimov, E. Dobretsova, D. Guryev, V. Kashin, G. Kiriukhina, S. Kutovoi, S. Rusanov, S. Simonov, V. Tsvetkov, V. Vlasov, V. Voronov and O. Yakubovich, Cryst. Growth Des., 2020, 20, 4593–4599 CrossRef CAS.
- V. M. Goldschmidt, Die Naturwissenschaften, 1926, 14, 477–485 Search PubMed.
- A. Casu and P. C. Ricci, J. Solid State Chem., 2011, 184, 3028–3033 Search PubMed.
- W. Dewo, V. Gorbenko, Y. Syrotych, Y. Zorenko and T. Runka, J. Phys. Chem. C, 2021, 125, 16279–16288 Search PubMed.
- A. Chopelas, Phys. Chem. Miner., 2011, 38, 709–726 Search PubMed.
- J. L. Wu, J. J. Wang, X. Y. Zhang, F. Liang, D. Z. Lu, S. H. Ma, Z. G. Hu, N. Ye and J. Y. Wang, Infrared Phys. Technol., 2023, 135, 104976 CrossRef CAS.
- A. B. Muñoz-García, Z. Barandiarán and L. Seijo, J. Mater. Chem., 2012, 22, 19888–19897 RSC.
- J. Pejchal, M. Nikl, E. Mihóková, J. A. Mareš, A. Yoshikawa, H. Ogino, K. M. Schillemat, A. Krasnikov, A. Vedda, K. Nejezchleb, V. Múčka, J. Pejchal, M. Nikl, E. Mihóková, J. A. Mareš, A. Yoshikawa, H. Ogino, K. M. Schillemat, A. Krasnikov, A. Vedda, K. Nejezchleb and V. Múčka, J. Phys. D: Appl. Phys., 2009, 42, 055117 CrossRef.
- A. M. Srivastava, J. Lumin., 2016, 169, 445–449 CrossRef CAS.
- W. Guo, B. Jiang, J. Zhu, L. Zhang, W. Guo, B. Jiang, J. Zhu and L. Zhang, Crystals, 2021, 11, 1433 CrossRef CAS.
- R. H. Bartram, D. S. Hamilton, L. A. Kappers and A. Lempicki, J. Lumin., 1997, 75, 183–192 CrossRef CAS.
- V. M. Khanin, I. Venevtsev, K. Chernenko, T. Tukhvatulina, P. A. Rodnyi, S. Spoor, J. Boerekamp, A.-M. van Dongen, D. Buettner, H. Wieczorek, C. R. Ronda, T. Senden and A. Meijerink, Cryst. Growth Des., 2020, 20, 3007–3017 CrossRef CAS.
- M. Nikl, A. Vedda, M. Fasoli, I. Fontana, V. V. Laguta, E. Mihokova, J. Pejchal, J. Rosa and K. Nejezchleb, Phys. Rev. B:Condens. Matter Mater. Phys., 2007, 76, 195121 CrossRef.
- E. McGlynn, Contemp. Phys., 2013, 54, 115–116 CrossRef.
- A. B. Abragam, Electron Paramagnetic Resonance of Transition Ions, Oxford University Press, London, England, 2012 Search PubMed.
- S. K. Misra and L. E. Misiak, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 13579–13587 CrossRef CAS PubMed.
- A. Nakatsuka, A. Yoshiasa and T. Yamanaka, Acta Crystallogr., Sect. B:Struct. Sci., 1999, 55, 266–272 CrossRef PubMed.
- J. R. B. J. E. Wertz, Electron Spin Resonance: Elementary Theory and Practical Applications, Chapman and Hall, New York, 1986 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: NIR-VIS-UV absorption spectra – Fig. S1 Room-temperature unpolarized optical absorption spectra of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 (x = 0.0–2.0) in NIR, VIS, and UV regions. Raman spectroscopy characteristics – Table S1 Experimental Raman bands of Pr3+-doped Lu1.5Y1.5Al5−xScxO12 compared with Y3Al5O12, including symmetry and vibrational modes. Thermal modification of photoluminescence characteristics – Fig. S2 2D temperature-dependent (10–350 K) emission and excitation maps for crystals with varying Sc concentrations. Fig. S3 Radial variation of PL intensity, emission line FWHM, and integrated spectral intensity as a function of Sc3+ content. Photoluminescence decay dynamics – Fig. S4 RT photoluminescence decay time curves and multi-exponential fitting analysis for Sc concentrations x = 0.5 and 1.5. Emission band characteristics – Table S2 Maximum band positions and FWHM of interconfigurational Pr3+ 4f15d11 → 4f2 emission across various garnet matrices and Sc-admixed materials. Luminescence properties under synchrotron radiation – Fig. S5 2D excitation–emission maps at 8 K and 295 K for Sc concentrations of x = 0.5, 1.5, and 2.0, highlighting broadening and intensity trends in emission regions. Radioluminescence and scintillation properties – Fig. S6 Temperature-dependent (10–350 K) radioluminescence spectra for Pr3+-doped Lu1.5Y1.5Al5−xScxO12 with varying Sc concentrations. Fig. S7 (a) Scintillation light yield vs. Sc concentration and (b) decay kinetics under 137Cs (662 keV) γ-ray excitation. Electron paramagnetic resonance (EPR) analysis – Fig. S8 (a) Charge trapping signals (S1–S5) as Sc concentration increases, (b) double integral intensities of signals, and (c) measured vs. calculated EPR spectra interpretation. Emission spectra under controlled excitation – Fig. S9 (a) Emission spectra for x = 0.0 and x = 2.0 at 8 K under 6.52 eV excitation, (b) Gaussian fits illustrating transitions, (c) dependence of fit intensities on Sc3+ ions concentration, (d) spectral evolution with increasing Sc3+ ions concentration. See DOI: https://doi.org/10.1039/d5tc01411e |
| This journal is © The Royal Society of Chemistry 2025 |