Beyond isotropic reorientation: probing anisotropic and internal motions in ionic liquids with fast field cycling NMR relaxometry and MD simulations

Abstract

We investigate the rotational and translational dynamics of ionic liquids (ILs) through a combined approach utilizing fast field cycling nuclear magnetic resonance (FFC NMR) relaxometry and molecular dynamics (MD) simulations. The ILs examined, [TEA][NTf₂] and [C₅Py][NTf₂], were selected to explore differences arising from variations in ion shape and rigidity. FFC NMR relaxometry provides detailed spin–lattice relaxation rate data for both ¹H on cations and ¹⁹F nuclei on anions across broad frequency and temperature ranges, enabling the characterization of ion-specific dynamics. To dissect the total relaxation rates into intramolecular and intermolecular contributions and to accurately interpret these data, advanced relaxation models were employed, accounting for isotropic, anisotropic, and internal rotational motions. The dynamics of the nearly spherical [TEA]⁺ cation were described using the Bloembergen–Purcell–Pound (BPP) model, while the elongated [C₅Py]⁺ cation required a symmetric top model to capture anisotropic rotational behavior. Additionally, the [NTf₂]⁻ anion's rotational dynamics were modeled to include fast internal rotations of the CF₃ groups. For both ILs, self-diffusion coefficients were also obtained in addition to rotational dynamics. Notably, the analysis explicitly considered heteronuclear intermolecular contributions, which were found to play a significant role in accurately capturing the relaxation behavior. Complementary MD simulations provided rotational correlation times and self-diffusion coefficients, which showed excellent agreement with experimental results, thereby validating the employed relaxation models. These findings contribute to a deeper understanding of IL dynamics, emphasizing the role of ion geometry and internal motions in data evaluation. Thereby, this work establishes a comprehensive framework for future studies on complex IL systems.

---

1 Introduction

Fast field cycling nuclear magnetic resonance (FFC NMR) relaxometry has been established as a powerful technique for investigating relaxation processes and molecular dynamics in a wide range of materials, including soils,^1,2 food,^3,4 biological tissues,^5,6 polymers,^7,8 and liquids.^9,10 Among these many applications, FFC NMR has also been frequently employed to study the dynamics of ionic liquids (ILs),^11–31 a fascinating substance class, that consists solely out of ions and is defined by a melting point below 100 °C. ILs are characterized by their broad liquid range and significantly higher viscosities^32–34 compared to a lot of conventional molecular liquids. These properties make them particularly suitable candidates for studying spin–lattice relaxation rates R₁(ω) in dependence on an external magnetic field B₀, enabling the acquisition of so-called nuclear magnetic relaxation dispersion (NMRD) profiles across a wide range of temperatures. Beyond their fundamental scientific interest, ILs offer a wide range of tunable physicochemical properties due to the nearly unlimited combinations of cations and anions. This adaptability makes them valuable as designer solvents for various applications. One of the most promising application areas of ILs is electrochemical devices, including batteries,^35–37 supercapacitors^38,39 and solar cells.^40,41 In such applications, the transport properties of ILs play a crucial role in optimizing performance and, thus, in the further development of energy storage and conversion technologies. Therefore, a better understanding of dynamical parameters such as rotational correlation times and translational diffusion coefficients is essential. FFC NMR relaxometry is uniquely suited for studying these properties, as it provides access to both rotational and translational dynamics within one single experiment. However, analyzing FFC NMR data for ILs also presents challenges, particularly in selecting appropriate relaxation models to extract reliable dynamical information.

A review of the literature reveals various approaches for the evaluation of FFC NMR data collected for ILs. Some studies focus on ILs containing only protons like e.g. [EMIm][SCN]¹¹ and [BMIm][Br],⁴² where data analysis is relatively straightforward as only homonuclear dipole–dipole-relaxation has to be taken into account. However, other investigations focus on ILs where protons are located on the cation and fluorine atoms on the anion. In these cases, relaxation data are sometimes only collected for protons in order to draw conclusions about the dynamics of the cations, while heteronuclear contributions from fluorine atoms located on [BF₄]^− 13 or [NTf₂]^− 24,30 anions are neglected due to the significant differences in spin densities. Other studies measured relaxation rates for both nuclei but analyzed them independently from each other rather than simultaneously.^26,27 A more complex approach involves simultaneously analyzing relaxation rates for both nuclei. The literature also contains several examples for this.^12,15,31,43 Regardless of whether heteronuclear contributions are considered and independent of the specific fitting approach used, another aspect remains subject to variation in the literature. Most studies employ the Bloembergen–Purcell–Pound (BPP) model^{12,26,27,30,31,42,43} for the spectral density to describe rotational motion. This model assumes the isotropic rotation of a rigid, spherical object characterized by a single rotational correlation time. However, these assumptions can be overly restrictive. To address this limitation, alternative studies adopt the Cole–Davidson model,^11,15,24 which introduces an empirical stretching parameter to account for deviations from a purely Lorentzian spectral density. However, to date, only a single study has accounted for an additional anisotropic rotation when interpreting relaxation data from ILs.¹³ All in all, two of the main challenges in analyzing FFC NMR experiments are selecting an appropriate evaluation method and choosing suitable relaxation models. These points can be addressed by combining FFC NMR relaxometry with molecular dynamics (MD) simulations. MD simulations also allow for determining rotational correlation times and self-diffusion coefficients, complementing the experimental data. Moreover, they can contribute to mechanistically verifying the used relaxation models. Several studies^24,44,45 have already demonstrated the benefits of this combined approach, highlighting its potential to enhance the interpretation of FFC NMR relaxometry data. Singer et al. extensively studied NMR relaxation mechanism between viscous polydisperse fluids combining MD simulations with experiments.^46–48 A particular innovative approach that goes beyond traditional motional models has been recently introduced by Asthagiri and co-workers,^49,50 who suggest to expand the spectral density (or, for the time-domain, the corresponding dipole–dipole correlation function) into a continuous distribution of Lorentz-functions (or “modes”) via an inverse Laplace transform. A recent study by Valiya Parambathu et al.⁵¹ on complex viscous liquids such as glycerol and a viscosity standard composed of oligomers of poly-(isobutene) demonstrated the power of their methodology. Their approach is particularly valuable for systems where a meaningful factorization into contributions from translatoric, rotational, and internal motions is not possible. Although it heavily relies on MD simulation results, it can provide unprecedented dynamical insights in terms of the distribution of dynamical modes in complex viscous liquids.⁵¹ However, their approach appears to be less practical for the analysis of experimental data sets, as it requires handling a comparatively large number of variables (modes), which may limit its applicability in routine data interpretation.

In this study, we present two specially synthesized ILs, [TEA][NTf₂] and [C₅Py][NTf₂], as model systems to advance the understanding of IL dynamics. Both substances contain protons on the cation and fluorine on the anion. These two ILs were carefully selected based on differences in ion shape and rigidity. Generally, the effective molecular shape can be categorized as a spherical top, a symmetric top, or a completely asymmetric rotor.^52,53 Here, [TEA]⁺ cations are selected for their overall regular proton distribution and their spherical shape to explore isotropic rotation, while in [NTf₂]⁻ anions all ¹⁹F nuclei are located in fast-rotating CF₃ groups for internal rotation analysis. The elongated shape of [C₅Py]⁺ cations allows for the investigation of anisotropic contributions corresponding to the model of a symmetric top. To the best of our knowledge, this is the first study to employ FFC NMR relaxometry on ILs by simultaneously analyzing ¹H and ¹⁹F data from both cations and anions across all temperatures, while utilizing advanced relaxation models that account for internal rotation or anisotropy, depending on the ion under consideration. Importantly, our experimental results, including rotational correlation times and self-diffusion coefficients, show excellent agreement with MD simulation data. This comprehensive approach improves our understanding of the rotational and translational dynamics of ILs, thereby supporting further advancements in this field.

2 Relaxation theory

Relaxation rates in FFC NMR relaxometry

FFC NMR relaxometry provides valuable insights into the dynamic properties of various materials by measuring the spin–lattice relaxation rate (R₁) as a function of the spectrometer frequency (ω). Unlike conventional NMR methods, FFC NMR enables controlled variation of ω, allowing for the acquisition of dispersion curves (R₁(ω)) that reflect multiple molecular processes occurring on different timescales within a single experiment. The spin–lattice relaxation rate, R₁, is defined as the inverse of the spin–lattice relaxation time, T₁. At the same time, this technique is unable to resolve NMR signals originating from chemical groups containing the same type of nucleus with different chemical shifts. As a result, the measured relaxation rates represent averaged R₁(ω) values for each nuclear type rather than spatially resolved relaxation data. Nonetheless, the simultaneous measurement of different nuclei – such as protons and fluorine – can yield crucial dynamical information about complex systems such as ILs.

In this study, we analyze spin–lattice relaxation profiles for both ¹H and ¹⁹F nuclei. Since both of them are dipolar in nature (I_H = I_F = 1/2, where I is the nuclear spin quantum number), their dominant relaxation mechanism is based on dipole–dipole magnetic interactions. According to relaxation theory,^53,54 the overall proton relaxation rate can be expressed as a sum of intramolecular and intermolecular contributions:

R^H₁(ω_H) = R^HH_1,intra(ω_H) + R^HH_1,inter(ω_H) + R^HF_1,inter(ω_H) (1)

where, ω_H is the proton Larmor frequency. The first term R^HH_1,intra describes intramolecular proton–proton interaction within the same cation, governed primarily by molecular rotation. The second and third terms, R^HH_1,inter and R^HF_1,inter, correspond to intermolecular interactions – proton–proton interactions between different cations and proton–fluorine interactions reflecting cation–anion interactions, respectively. These contributions are caused by translational motion. For clarity, all equations presented here pertain exclusively to proton relaxation. However, the total relaxation rate can be equivalently expressed for fluorine by exchanging the superscripts H and F. All corresponding equations are provided in the ESI.†

Spectral densities and their role in relaxation analysis

The homonuclear dipole–dipole interaction between two nuclei can be expressed as the product of a structural prefactor, A, and a linear combination of spectral densities J. These spectral densities describe single (J(ω_H)) and double quantum (J(2ω_H)) coherences, as applied to intra- and intermolecular proton–proton relaxation:⁵⁴

R^HH_1,intra = A^HH_intra × [J_intra(ω_H) + 4J_intra(2ω_H)] (2)

R^HH_1,inter = A^HH_inter × [J_inter(ω_H) + 4J_inter(2ω_H)] (3)

However, the situation is more complex for heteronuclear dipolar interactions, as in the case of proton–fluorine interactions, where additional spin interaction pathways contribute to relaxation:⁵⁴

R^HF_1,inter = A^HF_inter × [J_inter(|ω_H − ω_F|) + 3J_inter(ω_H) + 6J_inter(ω_H + ω_F)] (4)

A complete set of equations, including fluorine relaxation and all coupling constants, A_i, is provided in the ESI,† Section S1. Selecting an appropriate spectral density model is crucial for accurately extracting dynamical properties from experimentally obtained spin–lattice relaxation rates. This choice depends on both the type of interaction (intra- vs. intermolecular) as well as the molecular structure.

Models for describing rotational motion

In an early work from Bloembergen, Purcell, and Pound⁵⁵ (BPP), it is shown that the spectral density of an isotropic rotational motion can be expressed by one single Lorentzian function:where ω_H is the proton Larmor frequency and τ_rot represents the rotational correlation time. This model is valid under the assumption of isotropic rotation, making it suitable for the nearly spherical [TEA]⁺ cation. However, these assumptions are not justified for the [C₅Py]⁺ cation, since the molecular shape is not spherical, but ellipsoidal. Therefore, a more refined symmetric top^53,56 (ST) model must be used, requiring three different Lorentzian functions including three different correlation times, τ₀, τ₁ and τ₂:Here, α represents the angle formed between two anisotropic rotational axes. Based on eqn (6), two distinct rotational correlation times, τ^S_rot and τ^L_rot, can be determined:

τ^S_rot = τ₀ (7)

These correlation times characterize the slow reorientation of the longest molecular vector and the faster reorientation of an anisotropic rotational axis, respectively. It shall be noted, that eqn (6)–(8) can also be expressed in terms of rotational diffusion coefficients, D_⊥ and D_‖, as shown in the ESI,† Section S1. In contrast to the cations [TEA]⁺ and [C₅Py]⁺, where the analyzed protons are well distributed over the entire ion, the NMR-active ¹⁹F nuclei of the [NTf₂]⁻ anion are exclusively located within two CF₃ groups. In this case, additional internal rotation (IR)^57–59 contributions must be considered due to the rapid rotation of the CF₃ groups. This additional motion modifies the spectral density in a manner analogous to the ST model:

where β is now defined as the angle between the main axis of the rotation and the axis of internal rotation. In other words, it can be understood as a semi-angle of the cone on which the internal motion takes place with respect to the rest of the ion. Consequently, the correlation times τ₀, τ₁ and τ₂ can be used to calculate the slow overall rotational correlation time τ_rot of the whole ion and the rotational correlation time for the faster internal rotation τⁱ_rot:

τ_rot = τ₀ (10)

Eqn (6) and (9) appear very similar. However, the key difference between the ST and IR models lies in their differing perspectives on the nature of the corresponding ion. In the ST model, the ion is treated as a rigid object with an ellipsoidal shape, characterized by two distinct axes of rotation. In contrast, the IR model considers the ion as a spherical object, exhibiting isotropic overall rotation while allowing for additional internal rotation. Depending on the nature of the ion, one of the three presented spectral densities must, therefore, be chosen to describe the rotational dynamics.

Model for describing translational motion

The modeling of intermolecular dipolar interactions has been done using the well-established expression developed by Hwang and Freed.⁶⁰ They assumed that the particles carrying the interacting nuclei diffuse in a force-free manner, behave as hard spheres with a diameter d, and that the interacting nuclei are located at the center of these spheres. The corresponding spectral density function has been proven to provide reliable translational correlation times for a variety of diverse samples:^61–63Here, u represents an integration variable, while τ_trans generally denotes the translational correlation time. In the following, three different translational correlation times can be used to calculate the self-diffusion coefficients of cations D_H and anions D_F in ionic liquids according to eqn (13) and (14). Additionally, relative diffusion coefficients (D_rel(HH), D_rel(FF), and D_rel(HF)) can also be determined as the sum of the self-diffusion coefficients. Regardless of the specific nature of the ions, this model is consistently applied to describe the translational motion of all ions in this study.

In this study, the rotational correlation times and translational self-diffusion coefficients were determined by simultaneously fitting the ¹H and ¹⁹F spin–lattice relaxation rates for both nuclei across all temperatures using the above proposed models. The description of protons and fluorine nuclei is interconnected through the assumptions τ_HF = τ_FH and d_HF = d_FH. A more detailed description of the data fitting procedure based on all of these equations is included in the ESI,† Section S4.

3 Experimental section

Materials and sample preparation

Both ILs, namely triethylammonium bis(trifluoromethanesulfonyl)imide [TEA][NTf₂] and pentylpyridinium bis(trifluoromethanesulfonyl)imide [C₅Py][NTf₂], were synthesized following procedures previously described in the literature.^64,65 After synthesis, the samples were dried under high vacuum (10⁻⁵ mbar) for 48 h to degas and remove any residual water. Finally, 1 ml of the ILs was transferred into standard 10 mm NMR tubes and sealed under vacuum to prevent contamination. The molecular structures of the nearly spherical [TEA]⁺ cation, the elongated [C₅Py]⁺ cation, and the [NTf₂]⁻ anion, including fast rotating CF₃ groups, are shown in Fig. 1.

Fig. 1 Schemes of (a) [TEA]⁺ cation, (b) [C₅Py]⁺ cation, and (c) [NTf₂]⁻ anion being present in the studied ILs [TEA][NTf₂] and [C₅Py][NTf₂].

FFC NMR relaxometry measurements

Measurements of ¹H (cation) and ¹⁹F (anion) frequency-dependent spin–lattice relaxation rates R₁(ω), as the inverse of spin–lattice relaxation times T₁(ω), were conducted using a FFC 2000 Spinmaster relaxometer (Stelar s.r.l., Mede, Italy). For [TEA][NTf₂], we utilized data from our previous work,⁶⁶ comprising 30 data points between 0.01 MHz and 10 MHz, and 20 data points between 10 MHz and 42.6 MHz. For [C₅Py][NTf₂], 30 data points were logarithmically distributed over a frequency range of 0.01 MHz to 38 MHz. Temperature ranges were carefully selected between 263 K and 333 K for [TEA][NTf₂] and from 263 K to 323 K for [C₅Py][NTf₂], each in 10 K increments. Temperature control was achieved using a built-in variable temperature control unit, employing heated compressed air for high temperatures and evaporated liquid nitrogen for low temperatures. An external thermometer was used to monitor the temperature, ensuring an accuracy of ±0.5 K. For the experiments, prepolarized pulse sequences were used at frequencies below 12 MHz, whereas non-prepolarized sequences were employed above 12 MHz The polarization and detection fields were set to be 25 MHz ¹H Larmor frequency and 16.3 MHz ¹H Larmor frequency, respectively. T₁-times were determined by fitting 16 data points of the magnetization built-up and relaxation curves. All resulting magnetization curves exhibited monoexponential behavior. The relative error in T₁ estimation was consistently maintained below 2% across all experiments, ensuring high data reliability.

Determination of rotational correlation times and self-diffusion coefficients using MD simulations

We have performed MD simulations of the [TEA][NTf₂] and [C₅Py][NTf₂] ILs using classical non-polarisable forcefield models outlined in ref. 67–71 employing fixed bond lengths with an integration time-step of 2  fs. Details about the simulation setup can be found in the ESI,† Section S7. Recently, Asthagiri and Beck⁷² and Rosas Jiménez et al.⁷³ reported that long time-steps in MD simulations of rigid water models led to noticeable violations of the equipartition of kinetic energy. We have therefore performed additional simulations with a reduced time-step of 1  fs. Although we did not directly compute the effect on the equipartition of the kinetic energy, we did observe, in the scope of the present work, only a minor influence on the computed dynamical properties shown in Tables S7 and S11 of the ESI.†

Intramolecular contributions to the relaxation rate are dominantly based on the rotational motions of the cations and anions. To characterize the anisotropic rotational dynamics from MD simulations, we compute reorientational correlation functions

C^ij₂(t) = 〈P₂[u⃑_ij(0)·u⃑_ij(t)]〉 (16)

for several selected intramolecular vectors, where u⃑_ij denote unit vectors oriented along the axis connecting two atoms i and j within an ion of a certain type, P₂[…] indicates the second Legendre polynomial, and 〈…〉 denotes both ensemble averaging as well as averaging over equivalent pairs of atoms. Reorientational correlation times τ_ij are computed by numerically integrating the C^ij₂(t) using the trapezoidal rule. Note that since the molecular models used are flexible, the reorientation of the selected vectors is also affected by internal degrees of freedom. Consequently, the reorientational correlation functions of these vectors inherently reflect contributions from internal dynamics.

Intermolecular relaxation depends strongly on the inter-diffusion coefficients. Therefore, self-diffusion coefficients were computed from the slope of the center-of-mass mean square displacement (cms-MSD) of the ions using the Einstein formula⁷⁴ according to

where r⃑(t) represents the position of the center of mass of an ion at time t. Time-intervals for determining D_self were selected to consistently sample displacements of several times the diameter of the ions involved.

4 Results and discussion

Relaxation rate dispersions

In this study, the ILs are carefully selected such that ¹H nuclei are solely located on the cations, while ¹⁹F nuclei are exclusively located on the anions. This fact allows for ion-specific dynamical investigations by selectively probing the individual motions of cations and anions.

The spin–lattice relaxation rates R₁(ω) for ¹H (cations) and ¹⁹F (anions) were measured as a function of the Larmor frequency. Corresponding NMR dispersion profiles are presented in Fig. 2(a) and (b) for [TEA][NTf₂] and in Fig. 2(c) and (d) for [C₅Py][NTf₂]. Two distinct temperature-dependent trends can be observed. First, the relaxations rates decrease in amplitude and dispersion with increasing temperature, and second, the ¹⁹F NMRD profiles display greater dispersion compared to ¹H data at the same temperature.

Fig. 2 Temperature dependent NMRD profiles for ¹ H (a) and (c) plotted as circles and ¹⁹ F (b) and (d) plotted as diamonds in the ionic liquids [TEA][NTf₂] (a) and (b) and [C₅Py][NTf₂] (c) and (d). The solid lines correspond to the model fits according to eqn (1), (5), (9) and (12) for [TEA][NTf₂] as well as to eqn (1), (6), (9) and (12) for [C₅Py][NTf₂].

For further analysis, these total relaxation rates were dissected into homonuclear intramolecular contributions according to eqn (2) as well as homo- and heteronuclear intermolecular contributions according to eqn (3) and (4) or their respective fluorine-based equivalents. A detailed description of the fitting procedure is provided in Section S4 of the ESI.† For each IL the data of ¹H and ¹⁹F were fitted simultaneously across all temperatures, yielding an excellent agreement between experimental and fitted values. A representative example of the dissected total relaxation rates can be found for [C₅Py][NTf₂] at 263 K in Fig. 3. For the [C₅Py]⁺ cation the relaxation process is primarily driven by the intermolecular ¹H–¹H interactions, followed by intramolecular ¹H–¹H contributions, and then by intermolecular ¹H–¹⁹F contributions. For the [NTf₂]⁻ anion, the intermolecular ¹⁹F–¹H interaction is the dominant contribution, followed by the intermolecular ¹⁹F–¹⁹F interaction, and the intramolecular ¹⁹F–¹⁹F interaction. These sequences are consistent with the spin densities of the nuclei. Since the ¹H spin density N_H is higher by a factor of 2.7 compared to the ¹⁹F spin density N_F (see Table S1 of the ESI†), a lower ¹H–¹⁹F heteronuclear contribution compared to the homonuclear ¹H–¹H contribution in cations is reasonable. Conversely, in the [NTf₂]⁻ anion the intermolecular ¹⁹F–¹H contribution is dominant, followed by the intermolecular ¹⁹F–¹⁹F contribution and the intramolecular ¹⁹F–¹⁹F. Due to the reduced spin densities, the homonuclear contribution now contributes less to the overall rate. It is important to emphasize that, in contrast to many studies in the literature, our approach explicitly accounts for heteronuclear interactions. Both intermolecular ¹H–¹⁹F as well as intermolecular ¹⁹F–¹H interactions significantly contribute to the overall spin–lattice relaxation rates. In a previous study,⁶⁶ we highlighted the importance of these heteronuclear interactions for a comprehensive evaluation of IL dynamics. The dissected total relaxation rates of [TEA][NTf₂] and [C₅Py][NTf₂] for both nuclei and all temperatures can be found in Fig. S1–S4 in the ESI.† The trends previously discussed are consistently observed in all the figures. Furthermore, it is evident that the relative contribution of intramolecular relaxation decreases with increasing temperature, independent of the nucleus or the specific IL.

Fig. 3 Dissected NMRD profiles at 263 K for (a) ¹H and (b) ¹⁹F in the IL [C₅Py][NTf₂]. Experimental data are plotted as open symbols, while the total fits are shown as purple solid lines. The contributions from homonuclear intermolecular relaxation R_inter are shown as blue dashed lines, heteronuclear intermolecular contributions R_inter as green dashed dotted lines, and homonuclear intramolecular contributions R_intra are represented as red dotted lines.

Rotational dynamics of ions

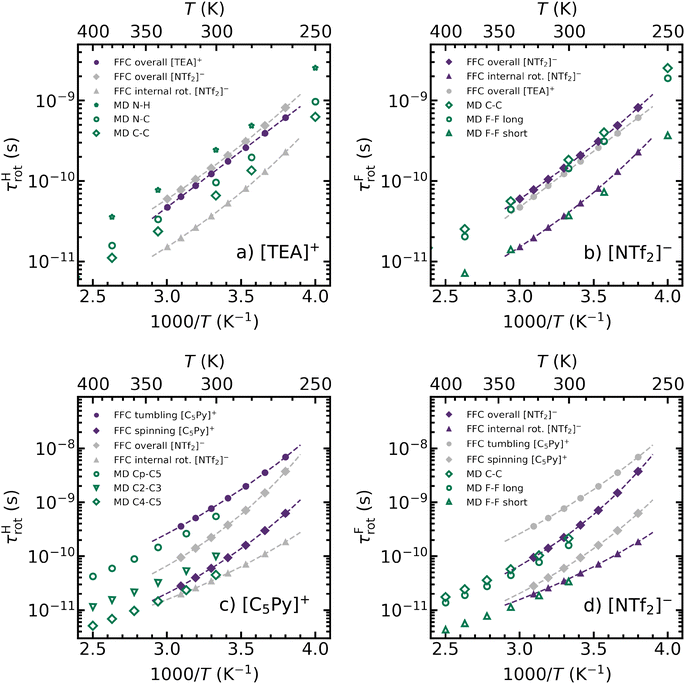
A precise analysis of the intramolecular relaxation rates according to eqn (2) enables a detailed description of the rotational dynamics of the individual ions. The ionic liquids presented here were specifically selected such that the cations and anions differ fundamentally in their rotational dynamics. These differences are explicitly included in the formalism of dipole–dipole relaxation through the spectral density function J. We first consider the [TEA]⁺ cation, which has protons distributed evenly across the ion and can be approximately described as a rigid spherical object. Thus, the spectral density function in eqn (5) is well suited to characterize its rotational dynamics as an isotropic overall tumbling of the whole ion. The corresponding rotational correlation times can be found in Fig. 4(a) as purple filled dots. Here, experimental results indicate an Arrhenius-like temperature behavior, even though the initial fitting parameters were based on a Vogel–Fulcher–Tamman (VFT) approach. In addition to the experimental values, rotational correlation times from MD simulations are shown as open green symbols in Fig. 4(a). The MD simulations offer a key advantage by allowing the calculation of rotational correlation times for any specific vector within the ion. For [TEA]⁺ three different bond vectors were analyzed, namely the N–H vector from the central nitrogen to the acidic proton, the N–C vector from the central nitrogen to the neighboring carbon and the C–C vector between two neighboring carbons within the alkyl chain. Among these, the N–H vector exhibits the longest correlation times, indicating the slowest rotational dynamics within the [TEA]⁺ cation. This observation is in good agreement with the well-documented presence of a hydrogen bond between the N–H group of [TEA]⁺ and the S–O group of [NTf₂]⁻,^75,76 which restricts rotation about this axis. Since FFC NMR relaxometry does not resolve NMR signals from specific ¹H containing chemical groups, the experimentally determined rotational correlation times represent an averaged value of the various motions observed in MD simulations. For comparison, the rotational correlation times of the [NTf₂]⁻ anion are also included in Fig. 4(a) as gray symbols.

Fig. 4 Temperature-dependent rotational correlation times τ_rot of ¹H carrying cations (a) and (c) and ¹⁹F carrying anions (b) and (d) for the ionic liquids [TEA][NTf₂] (a) and (b) and [C₅Py][NTf₂] (c) and (d). Values from FFC NMR relaxometry are shown as purple filled symbols. Values from MD simulations are shown as green open symbols. Subfigures with cation data include anion data as gray symbols and vice versa.

The rotational correlation times of the [NTf₂]⁻ anion of [TEA][NTf₂] are presented separately in Fig. 4(b) as filled purple diamonds and triangles. In contrast to the cation, the ¹⁹F nuclei in [NTf₂]⁻ are not evenly distributed across the whole ion. Instead, they are localized in two CF₃ groups, which undergo fast internal rotation.^77,78 In order to account for this additional motion, the spectral density function in eqn (9) is used instead of eqn (5). Consequently, both an overall tumbling of the whole ion (purple diamonds) and an internal rotation of the CF₃ group (purple triangles) on different timescales can be observed for the [NTf₂]⁻ anion. The latter is faster by a factor of approximately 4. These findings are further supported by MD simulations, where again the reorientation of multiple vectors was analyzed. The slowest reorienting vector within the [NTf₂]⁻ anion is the C–C vector (green open diamonds) between the two carbon atoms of the CF₃ groups. This vector extends across the entire ion, effectively representing the longest molecular axis, which exhibits the slowest reorientation. Another vector, extending from one fluorine atom in one CF₃ group to another fluorine atom in the opposite CF₃ group (green open circles), exhibits only slightly faster reorientation. The experimentally determined rotational correlation times τ_rot are located precisely between the MD values of these two vectors, providing a representative measure of the overall tumbling motion. Furthermore, there is a strong agreement between the experimentally obtained τⁱ_rot values for internal CF₃ group rotation and the reorientation of a vector between two fluorine atoms within the same CF₃ group, shown as open green triangles. This motion corresponds to the fastest reorienting vector identified in MD simulations. Additionally, rotational correlation times for other vectors were determined using MD. These values fall within the range defined by the C–C and the F–F vectors, being slower than the former but faster than the latter. To enhance clarity, the corresponding data points were omitted from Fig. 4(b). However, the complete set of values is provided in Table S7 of the ESI.† The rotational correlation times of the [TEA]⁺ counter-ion are also presented as gray data points in Fig. 4(b). A comparative analysis reveals that the overall tumbling motions of the cation and the anion are nearly identical in [TEA][NTf₂], which can be likely attributed to the presence of a directed hydrogen bond between the N–H group of the [TEA]⁺ cation and the S–O group of the [NTf₂]⁻ anion.

Fig. 4(c) and (d) present the rotational correlation times of the cation and anion in [C₅Py][NTf₂]. Unlike [TEA]⁺, the [C₅Py]⁺ cation is not spherical due to the presence of a long alkyl chain attached to an aromatic ring. Instead, its shape is better approximated as an ellipsoid, with the longest axis extending from the Cp para-carbon in the ring to the terminal C5 carbon in the alkyl chain. In this case, the rotation of this longest axis itself is significantly slower than the rotation around it, making the symmetric top model in eqn (6) more appropriate. The FFC NMR experiment therefore yields two distinct rotational correlation times for the [C₅Py]⁺ cation, that are presented in Fig. 4(c). The slow rotation τ^S_rot of the longest axis corresponds to the tumbling motion of the ion (purple filled circles). Additionally, a faster rotational spinning motion τ^L_rot is depicted by purple filled diamonds. The fitting process determined the angle between these two rotational axes to be 70°. Again, experimental values closely match those from MD simulations, where three different bond vectors were analyzed and shown as open green symbols. The slowest dynamics were observed for the Cp-C5 vector, consistent with its structural role as the longest molecular axis. In contrast, the fastest reorienting vector, as determined by molecular dynamics (MD) simulations, is the C4–C5 bond vector between the terminal methyl group and the nearest methylene group in the alkyl chain. The rotational correlation times of the remaining vectors fall in between these two in terms of magnitude. The complete set of values is provided in Table S8 of the ESI.†

Finally, Fig. 4(d) presents the rotational dynamics of the [NTf₂]⁻ anion in [C₅Py][NTf₂]. Since this anion is identical to that in [TEA][NTf₂], the same spectral density model is applied according to eqn (9). Compared to Fig. 4(b) similar trends according to overall tumbling and internal rotation of the [NTf₂]⁻ anion can be observed. Furthermore, a comparative analysis between the [C₅Py]⁺ cation (gray symbols) and [NTf₂]⁻ anion (purple symbols) dynamics is particularly insightful. Due to the significantly larger size of the cation compared to the anion, their overall tumbling motions are no longer equally fast. Instead, the cation exhibits a noticeably slower overall reorientation. This observation aligns with the prediction of the Stokes–Einstein–Debye equation (eqn (18)), which states that the rotational correlation time is inversely proportional to the hydrodynamic radius. Additionally, the internal rotation of the CF₃ groups occurs faster than the spinning motion of the cation.

A similar argument holds when comparing the overall rotational correlation times of the two different cations. At a given temperature, the correlation times of [C₅Py]⁺ exceed those of [TEA]⁺ by factors ranging from 6 to 11, depending on the temperature. Consequently, [C₅Py]⁺ exhibits slower rotational dynamics in [C₅Py][NTf₂] compared to [TEA]⁺ in [TEA][NTf₂]. This difference can be attributed firstly to its larger hydrodynamic radius, and secondly to the higher viscosity of [C₅Py][NTf₂]. Experimentally determined viscosity values for both ionic liquids are provided in Table S2 of the ESI.†

Translational dynamics of ions

One of the key advantages of FFC NMR relaxometry is its ability to provide both rotational and translational information within one single experiment. Consequently, our analysis not only yields rotational correlation times but also enables the determination of translational self-diffusion coefficients. To describe translational motion, we employ the force-free hard sphere model, whose corresponding spectral density function is given in eqn (12). In case of homo- and heteronuclear contributions this model accounts for four distinct translational correlation times τ^HH_trans, τ^FF_trans, τ^HF_trans and τ^FH_trans, respectively. However, due to the constraint τ^HF_trans =τ^FH_trans, only three of them are independent.

Diffusion coefficients are extracted from ¹H spin–lattice relaxation rates for cations and from ¹⁹F spin–lattice relaxation rates for anions. We emphasize that by simultaneously fitting all data, and by using three different distances of closest approach (d_HH, d_FF, d_HF = d_FH,) for specific ion combinations, our approach yields both relative diffusion coefficients (D_rel (HH), D_rel (FF), D_rel (HF)), as described by eqn (13)–(15), as well as self-diffusion coefficients D_H for cations D_F and anions. The obtained self-diffusion coefficients are presented in Fig. 5(a) for [TEA][NTf₂] and in Fig. 5(b) for [C₅Py][NTf₂]. All data exhibit a Vogel–Fulcher-Tamann dependence, with corresponding data points and fitting parameters being provided in Tables S9 and S10 of the ESI.†

Fig. 5 Temperature-dependent self-diffusion coefficients D_H for cations and D_F for anions in the ionic liquids [TEA][NTf₂] (a) and [C₅Py][NTf₂] (b). Values from FFC NMR relaxometry are shown as purple filled symbols. Values from MD simulations are shown as green open symbols.

For both ILs, the cations consistently exhibit larger self-diffusion coefficients than the anions. This behavior, where cations diffuse faster than anions, is well-documented in the literature across various IL systems.^79–82 For [TEA][NTf₂], the experimentally obtained self-diffusion coefficients across the entire temperature range are in excellent agreement with both MD simulations and literature values derived from Pulsed Field Gradient (PFG) NMR studies.^83,84 In a previous study,⁶⁶ we demonstrated that these diffusion coefficients can also be determined using the low-frequency approach from FFC NMR data. However, this approach is only valid when heteronuclear H–F and F–H interactions are properly accounted for and not neglected. For [C₅Py][NTf₂], a similar trend is observed, with the self-diffusion coefficients of the cation and anion closely matching and showing excellent agreement with values obtained from MD simulations.

A comparison of the self-diffusion coefficients between [TEA][NTf₂] and [C₅Py][NTf₂] reveals that the absolute values for [C₅Py][NTf₂] are approximately two times lower than those for [TEA][NTf₂]. This difference can be attributed to the significantly higher viscosity of [C₅Py][NTf₂], which inversely correlates with diffusion coefficients according to the Stokes–Einstein equation (eqn (19)). The higher viscosity of [C₅Py][NTf₂] results in slower translational dynamics, directly affecting the determined self-diffusion coefficients.

5 Conclusions and outlook

This study provides a comprehensive analysis of the rotational and translational dynamics of the two ILs, [TEA][NTf₂] and [C₅Py][NTf₂], using FFC NMR relaxometry complemented by MD simulations. By simultaneously evaluating ¹H and ¹⁹F spin–lattice relaxation rates across broad frequency and temperature ranges, we have demonstrated the necessity of employing distinct relaxation models including different kinds of spectral densities, tailored to the specific molecular geometry and internal motion of each single cation and anion.

For the nearly spherical [TEA]⁺ cation, the Bloembergen–Purcell–Pound model was found to provide an accurate description of isotropic rotational motion. In contrast, the elongated [C₅Py]⁺ cation exhibits anisotropic rotational dynamics, thus requiring the application of a symmetric top model. Furthermore, the [NTf₂]⁻ anion displays significant internal motion due to two fast rotating CF₃ groups, which required a spectral density especially modified for internal rotation. These results emphasize the importance of considering internal and anisotropic contributions when analyzing ionic liquid rotational dynamics.

In addition, the translational dynamics of the studied ILs were evaluated by extracting self-diffusion coefficients from the FFC NMR data using the force-free hard sphere model. The results showed that cations generally exhibit higher self-diffusion coefficients than anions, a trend consistent with previous studies. Notably, [C₅Py][NTf₂] exhibited slower translational dynamics than [TEA][NTf₂], in accordance with its larger molecular cation size and higher macroscopic viscosity, which was also confirmed by MD simulations.

The consistency between experimentally derived and simulation-based correlation times and self-diffusion coefficients demonstrates the robustness of our approach. Our results not only enhance the current understanding of IL dynamics but also provide a comprehensive framework for future investigations on complex ILs and related soft matter systems. In the future, we plan to extend our analysis by calculating dipolar relaxation from MD simulations. Specifically, we aim to derive dipolar relaxation rates by evaluating all intra- and intermolecular dipole–dipole time correlation functions including finite system-size corrections. This methodology has recently proven successful,^85–87 where we demonstrated the computation of the ¹H dipolar relaxation rate for liquid water within the experimental accuracy. Ultimately, this approach will allow for an even more comprehensive connection between the simulated dynamics and the experimentally observed relaxation behavior. It will enhance our ability to interpret FFC NMR relaxometry results, contributing to a more detailed understanding of the dynamical processes in ILs and related systems.

Author contributions

Lennart Kruse: formal analysis (lead); investigation (lead); visualization (supporting); software (supporting); writing – original draft (equal); writing – review & editing (supporting). Tanja van Alphen: data curation FFC (lead). Johanna Busch: data curation MD (equal); investigation (supporting); software (supporting); writing – review & editing (supporting). Dietmar Paschek: conceptualization (supporting); data curation MD (equal); project administration (supporting), supervision (equal); writing – review & editing (supporting). Ralf Ludwig: conceptualization (supporting); resources (lead); writing – review & editing (supporting). Anne Strate: conceptualization (lead); funding acquisition (lead); project administration (lead); visualisation (lead); software (lead); supervision (equal); writing – original draft (equal); writing – review & editing (lead).

Data availability

The data supporting this article have been included as part of the ESI.† Original spin–lattice relaxation data are available upon request from the authors.

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

A. S. thanks the Deutsche Forschungsgemeinschaft (DFG) under grant STR-1626/2-1 (Project 459405854) for supporting this work. The authors acknowledge Dr. Henning Schröder for his support in developing the Matlab-based evaluation tool CyFi, which we plan to make officially available to the FFC NMR community soon. Additionally, the authors thank Anika Wilhelms for her efforts in performing the density and viscosity measurements.

References

1. S. Haber-Pohlmeier, S. Stapf and A. Pohlmeier, Appl. Magn. Reson., 2014, 45, 1099–1115.
2. P. Conte and P. Lo Meo, Agronomy, 2020, 10, 1040.
3. P. Conte, L. Cinquanta, P. Lo Meo, F. Mazza, A. Micalizzi and O. Corona, Food Res. Int., 2021, 139, 109845.
4. E. Piacenza, D. F. C. Martino, L. Cinquanta, P. Conte and P. L. Meo, Magn. Reson. Chem., 2022, 60, 369–385.
5. L. M. Broche, P. J. Ross, G. R. Davies, M.-J. MacLeod and D. J. Lurie, Sci. Rep., 2019, 9, 1–11.
6. V. Mallikourti, P. J. Ross, O. Maier, K. Hanna, E. Husain, G. R. Davies, D. J. Lurie, G. Lip, H. Lahrech, Y. Masannat and L. M. Broche, Commun. Med., 2024, 4, 1–11.
7. S. Kariyo, A. Brodin, C. Gainaru, A. Herrmann, H. Schick, V. N. Novikov and E. A. Rössler, Macromolecules, 2008, 41, 5313–5321.
8. D. Kruk, A. Herrmann and E. A. Rössler, Prog. Nucl. Magn. Reson. Spectrosc., 2012, 63, 33–64.
9. J. Ward-Williams and L. F. Gladden, Magn. Reson. Imaging, 2019, 56, 57–62.
10. M. Flämig, M. Hofmann, N. Fatkullin and E. A. Rössler, J. Phys. Chem. B, 2020, 124, 1557–1570.
11. D. Kruk, R. Meier, A. Rachocki, A. Korpała, R. K. Singh and E. A. Rössler, J. Chem. Phys., 2014, 140, 244509.
12. A. Ordikhani Seyedlar, S. Stapf and C. Mattea, Phys. Chem. Chem. Phys., 2015, 17, 1653–1659.
13. A. Rachocki, E. Andrzejewska, A. Dembna and J. Tritt-Goc, Eur. Polym. J., 2015, 71, 210–220.
14. D. Kruk, M. Wojciechowski, S. Brym and R. K. Singh, Phys. Chem. Chem. Phys., 2016, 18, 23184–23194.
15. M. Wencka, T. Apih, R. C. Korošec, J. Jenczyk, M. Jarek, K. Szutkowski, S. Jurga and J. Dolinšek, Phys. Chem. Chem. Phys., 2017, 19, 15368–15376.
16. G. W. Driver, Y. Huang, A. Laaksonen, T. Sparrman, Y.-L. Wang and P.-O. Westlund, Phys. Chem. Chem. Phys., 2017, 19, 4975–4988.
17. D. Kruk, M. Wojciechowski, Y. L. Verma, S. K. Chaurasia and R. K. Singh, Phys. Chem. Chem. Phys., 2017, 19, 32605–32616.
18. K. Pilar, A. Rua, S. N. Suarez, C. Mallia, S. Lai, J. R. P. Jayakody, J. L. Hatcher, J. F. Wishart and S. Greenbaum, J. Electrochem. Soc., 2017, 164, H5189.
19. M. Becher, E. Steinrücken and M. Vogel, J. Chem. Phys., 2019, 151, 194503.
20. V. Overbeck, B. Golub, H. Schröder, A. Appelhagen, D. Paschek, K. Neymeyr and R. Ludwig, J. Mol. Liq., 2020, 319, 114207.
21. D. Kruk, E. Masiewicz, S. Lotarska, R. Markiewicz and S. Jurga, Int. J. Mol. Sci., 2021, 22, 9117.
22. M. N. Garaga, N. Jayakody, C. C. Fraenza, B. Itin and S. Greenbaum, J. Mol. Liq., 2021, 329, 115454.
23. V. Overbeck, H. Schröder, A.-M. Bonsa, K. Neymeyr and R. Ludwig, Phys. Chem. Chem. Phys., 2021, 23, 2663–2675.
24. J. B. B. Beckmann, D. Rauber, F. Philippi, K. Goloviznina, J. A. Ward-Williams, A. J. Sederman, M. D. Mantle, A. Pádua, C. W. M. Kay, T. Welton and L. F. Gladden, J. Phys. Chem. B, 2022, 126, 7143–7158.
25. D. Kruk, M. Jancelewicz, A. Klimaszyk, R. Markiewicz, Z. Fojud and S. Jurga, Materials, 2022, 15, 216.
26. D. Kruk, E. Masiewicz, S. Lotarska, R. Markiewicz and S. Jurga, Int. J. Mol. Sci., 2022, 23, 1688.
27. D. Kruk, E. Masiewicz, K. Kołodziejski, R. Markiewicz and S. Jurga, Int. J. Mol. Sci., 2022, 23, 5994.
28. C. C. Fraenza and S. G. Greenbaum, ChemPhysChem, 2023, 24, e202300268.
29. D. Kruk, E. Masiewicz, R. Markiewicz and R. K. Singh, Phys. Chem. Chem. Phys., 2024, 26, 27248–27259.
30. M. Knapkiewicz, I. Jankowska, J. Swiergiel and J. Tritt-Goc, J. Phys. Chem. B, 2024, 128, 6876–6884.
31. T. Pranto, C. C. Fraenza, F. Philippi, D. Rauber, C. W. M. Kay, T. Welton, S. G. Greenbaum and S. Suarez, Phys. Chem. Chem. Phys., 2025, 27, 2462–2472.
32. T. Welton, Biophys. Rev., 2018, 10, 691.
33. S. Jiang, Y. Hu, Y. Wang and X. Wang, J. Phys. Chem. Ref. Data, 2019, 48, 033101.
34. F. Philippi, D. Rauber, K. L. Eliasen, N. Bouscharain, K. Niss, C. W. M. Kay and T. Welton, Chem. Sci., 2022, 13, 2735–2743.
35. S. Pandian, S. G. Raju, K. S. Hariharan, S. M. Kolake, D.-H. Park and M.-J. Lee, J. Power Sources, 2015, 286, 204–209.
36. M. Watanabe, K. Dokko, K. Ueno and M. L. Thomas, Bull. Chem. Soc. Jpn., 2018, 91, 1660–1682.
37. H. Niu, L. Wang, P. Guan, N. Zhang, C. Yan, M. Ding, X. Guo, T. Huang and X. Hu, J. Energy Storage, 2021, 40, 102659.
38. A. Brandt, S. Pohlmann, A. Varzi, A. Balducci and S. Passerini, MRS Bull., 2013, 38, 554–559.
39. A. Ray and B. Saruhan, Materials, 2021, 14, 2942.
40. Y. Zhao and T. Bostrom, Curr. Org. Chem., 2015, 19, 556–566.
41. R. A. Abu Talip, W. Z. N. Yahya and M. A. Bustam, Sustainability, 2020, 12, 7598.
42. A. Ordikhani Seyedlar, S. Stapf and C. Mattea, J. Phys. Chem. B, 2017, 121, 5363–5373.
43. N. K. Jayakody, C. C. Fraenza, S. G. Greenbaum, D. Ashby and B. S. Dunn, J. Phys. Chem. B, 2020, 124, 6843–6856.
44. P. Honegger, V. Overbeck, A. Strate, A. Appelhagen, M. Sappl, E. Heid, C. Schröder, R. Ludwig and O. Steinhauser, J. Phys. Chem. Lett., 2020, 11, 2165–2170.
45. M. Becher, T. Wohlfromm, E. A. Rössler and M. Vogel, J. Chem. Phys., 2021, 154, 124503.
46. P. M. Singer, D. Asthagiri, W. G. Chapman and G. J. Hirasaki, J. Magn. Reson., 2017, 277, 15–24.
47. P. M. Singer, D. Asthagiri, Z. Chen, A. Valiya Parambathu, G. J. Hirasaki and W. G. Chapman, J. Chem. Phys., 2018, 148, 164507.
48. P. M. Singer, A. Valiya Parambathu, X. Wang, D. Asthagiri, W. G. Chapman, G. J. Hirasaki and M. Fleury, J. Phys. Chem. B, 2020, 124, 4222–4233.
49. D. Asthagiri, W. G. Chapman, G. J. Hirasaki and P. M. Singer, J. Phys. Chem. B, 2020, 124, 10802–10810.
50. T. J. Pinheiro dos Santos, B. Orcan-Ekmekci, W. G. Chapman, P. M. Singer and D. Asthagiri, J. Chem. Phys., 2024, 160, 064108.
51. A. Valiya Parambathu, T. J. Pinheiro dos Santos, W. G. Chapman, G. J. Hirasaki and P. M. Singer, J. Phys. Chem. B, 2024, 128, 8017–8028.
52. D. Woessner, Brownian Motion and Correlation Times, John Wiley & Sons, Ltd, 2007.
53. J. Kowalewski, Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, Routledge, New York, USA, 2nd edn, 2019.
54. A. Abragam, The Principles of Nuclear Magnetism, Clarendon Press, Oxford, 1961.
55. N. Bloembergen, E. M. Purcell and R. V. Pound, Phys. Rev., 1948, 73, 679–712.
56. D. E. Woessner, J. Chem. Phys., 1962, 37, 647–654.
57. D. E. Woessner, J. Chem. Phys., 1965, 42, 1855–1859.
58. H. Versmold, J. Chem. Phys., 1980, 73, 5310–5313.
59. H. Versmold, Ber. Bunsenges. Phys. Chem., 1980, 84, 168–173.
60. L.-P. Hwang and J. H. Freed, J. Chem. Phys., 1975, 63, 4017–4025.
61. R. Meier, D. Kruk and E. A. Rössler, ChemPhysChem, 2013, 14, 3071–3081.
62. A. Rachocki and J. Tritt-Goc, Food Chem., 2014, 152, 94–99.
63. E. Carignani, E. Juszyńska-Gałazka, M. Gałazka, C. Forte, M. Geppi and L. Calucci, J. Mol. Liq., 2021, 330, 115597.
64. K. Fumino, V. Fossog, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2013, 52, 2368–2372.
65. J. Busch, T. Niemann, J. Neumann, P. Stange, S. Gärtner, T. Youngs, S. Youngs, D. Paschek and R. Ludwig, ChemPhysChem, 2023, 24, e202300031.
66. L. Kruse, A. Chiramel Tony, D. Paschek, P. Stange, R. Ludwig and A. Strate, J. Phys. Chem. Lett., 2024, 15, 10410–10415.
67. T. Köddermann, D. Paschek and R. Ludwig, ChemPhysChem, 2007, 8, 2464–2470.
68. J. Neumann, B. Golub, L.-M. Odebrecht, R. Ludwig and D. Paschek, J. Chem. Phys., 2018, 148, 193828.
69. D. Paschek, B. Golub and R. Ludwig, Phys. Chem. Chem. Phys., 2015, 17, 8431–8440.
70. B. Golub, D. Ondo, R. Ludwig and D. Paschek, J. Phys. Chem. Lett., 2022, 13, 3556–3561.
71. J. Neumann, D. Paschek, A. Strate and R. Ludwig, J. Phys. Chem. B, 2021, 125, 281–286.
72. D. N. Asthagiri and T. L. Beck, J. Chem. Theory Comput., 2024, 20, 368–374.
73. J. G. Rosas Jiménez, B. Fábián and G. Hummer, J. Chem. Theory Comput., 2024, 20, 11068–11081.
74. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Clarendon, Oxford, 1987.
75. A. E. Khudozhitkov, P. Stange, B. Golub, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2017, 56, 14310–14314.
76. A. E. Khudozhitkov, P. Stange, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Phys. Chem. Chem. Phys., 2022, 24, 6064–6071.
77. P. A. Beckmann, J. Rosenberg, K. Nordstrom, C. W. Mallory and F. B. Mallory, J. Phys. Chem. A, 2006, 110, 3947–3953.
78. N. Kuze, A. Ishikawa, M. Kono, T. Kobayashi, N. Fuchisawa, T. Tsuji and H. Takeuchi, J. Phys. Chem. A, 2015, 119, 1774–1786.
79. H. Tokuda, K. Hayamizu, K. Ishii, Md. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600.
80. H. Tokuda, K. Hayamizu, K. Ishii, Md. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2005, 109, 6103–6110.
81. H. Tokuda, K. Ishii, Md. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833–2839.
82. T.-Y. Wu, S.-G. Su, H. P. Wang, Y.-C. Lin, S.-T. Gung, M.-W. Lin and I.-W. Sun, Electrochim. Acta, 2011, 56, 3209–3218.
83. J. W. Blanchard, J.-P. Belières, T. M. Alam, J. L. Yarger and G. P. Holland, J. Phys. Chem. Lett., 2011, 2, 1077–1081.
84. P. Judeinstein, C. Iojoiu, J.-Y. Sanchez and B. Ancian, J. Phys. Chem. B, 2008, 112, 3680–3683.
85. D. Paschek, J. Busch, E. Mock, R. Ludwig and A. Strate, J. Chem. Phys., 2024, 160, 074102.
86. D. Paschek, J. Busch, E. Mock, R. Ludwig and A. Strate, J. Chem. Phys., 2024, 161, 139902.
87. D. Paschek, J. Busch, A. M. Chiramel Tony, R. Ludwig, A. Strate, N. Stolte, H. Forbert and D. Marx, J. Chem. Phys., 2025, 162, 054501.

---

Footnote

† Electronic supplementary information (ESI) available: Relaxation theory, density information, viscosity information, data fitting procedure, rotational correlation times, self-diffusion coefficients, molecular dynamics simulations, dissected spin–lattice relaxation rates, reorientational correlation functions. See DOI: https://doi.org/10.1039/d5cp00582e

---