QCxMS2 – a program for the calculation of electron ionization mass spectra via automated reaction network discovery†
Johannes
Gorges
 and
Stefan
Grimme
and
Stefan
Grimme
 *
*
Mulliken Center for Theoretical Chemistry, Clausius-Institute for Physical and Theoretical Chemistry, University of Bonn, Beringstr. 4, 53115 Bonn, Germany. E-mail: grimme@thch.uni-bonn.de
First published on 3rd March 2025
Abstract
We present a new fully-automated computational workflow for the calculation of electron ionization mass spectra by automated reaction network discovery, transition state theory and Monte-Carlo simulations. Compared to its predecessor QCxMS [S. Grimme, Angew. Chem., Int. Ed., 52, 6306–6312] based on extensive molecular dynamics (MD) simulations, QCxMS2's more efficient approach of using stationary points on the potential energy surface (PES) enables the usage of accurate quantum chemical methods. Fragment geometries and reaction paths are optimized with fast semi-empirical quantum mechanical (SQM) methods and reaction barriers are refined at the density functional theory (DFT) level. This composite approach using GFN2-xTB geometries in combination with energies at the ωB97X-3c level proved to be an efficient combination. On a small but diverse test set of 16 organic and inorganic molecules, QCxMS2 spectra are more accurate than ones from QCxMS yielding on average a higher mass spectral matching of 0.700 compared to QCxMS with 0.622, and is more robust with a minimal matching of 0.498 versus 0.100. Further improvements were observed when both geometries and energies were computed at the ωB97X-3c level, yielding an average matching score of 0.730 and a minimal score of 0.527. Due to its higher accuracy and robustness while maintaining computational efficiency, we propose QCxMS2 as a complementary, more reliable and systematically improvable successor to QCxMS for elucidating fragmentation pathways and predicting electron ionization mass spectra of unknown chemical substances, e.g., in analytical chemistry applications. If coupled to currently developed improved SQM methods, QCxMS2 opens an efficient route to accurate, and routine mass spectra predictions. The QCxMS2 program suite is freely available on GitHub.
1 Introduction
Mass spectrometry (MS) is due to its high sensitivity and high-throughput capability an indispensable tool for structure elucidation in many areas of chemistry, such as drug discovery,1 metabolomics2 or forensics.3 However, assigning a spectrum to an unknown substance is a challenging task and often proves unsuccessful.2 For example, in recent metabolomics studies approximately 70% of the target metabolites remained unidentified despite extensive efforts.4,5 Despite its great importance, reliable theoretical prediction of mass spectra routinely remains a challenge for chemical theory, and structure annotations in common in silico generated MS libraries are frequently found to be incorrect.6 Data-driven machine-learning approaches, such as NEIMS7 for electron ionization mass spectra (EI-MS), and GrAFF-MS,8 CFM-ID,9 and the recent ICEBERG model10 for electrospray ionization/collision-induced dissociation mass spectra (ESI/CID-MS) show remarkable accuracy but are dependent on known data and are therefore unreliable for the prediction of unknown, unusual fragmentation pathways.11To this end, our group has developed some years ago the QCEIMS program for the automatic calculation of standard 70 eV electron ionization mass spectra. It is based on Born–Oppenheimer molecular dynamics (BO-MD) using efficient quantum mechanical (QM) methods to simulate the fragmentation processes of molecules.12 Due to the computational costs, the BO-MD simulations are mostly restricted to semi-empirical quantum mechanical (SQM) methods. The method was later extended to enable the simulation of electrospray ionization/collision-induced dissociation mass spectrometry (ESI/CID MS) and its name was changed to QCxMS (x = CID, EI) to account for the new functionality of the program.13 For the calculation of CID spectra, other quantum chemistry (QC)-based methods that use MD simulations, such as CIDMD14 and the VENUS program package,15,16 are also available. However, their accuracy has not yet been tested on a broad range of compounds, nor have they been applied to EI-MS.
QCxMS' good accuracy for a large variety of molecules was proven in several studies by our group17,18 and others.19,20 In several applications, it showed great success in elucidating unknown fragmentation pathways, e.g., for environmental pollutants21,22 or chemical warfare agents.23 However, for challenging molecules or if complicated fragmentation pathways are involved, in some cases, significant deviations from the experimentally measured spectra are observed with QCxMS. In a recent study on a large number of diverse organic environmentally relevant molecules, QCxMS spectra at the GFN1-xTB24 level were found to be too inaccurate for the application in spectral matching workflows. In particular, flexible molecules and molecules containing heteroatoms other than H, C, N, and O were found to be difficult for QCxMS.25 Additionally, a separate study found that the spectra of organic oxygen compounds are often inaccurate.20
We concluded that many failures can be attributed to two fundamental limitations of the approach of simulating the fragmentation by MD simulations:
1. To keep computationally feasible, the time scale of the computations (by default 5 ps for a single reaction trajectory) is orders of magnitude shorter than the real time scale of slower fragmentations, which may occur on the ns up to the μs timescale. Consequently, the corresponding peaks can be completely missing in the computed spectra.
2. Already for medium-sized molecules (30–50 atoms), the level of theory for the underlying potential energy surface (PES) in the MD simulations is limited to rather approximate SQM methods. The corresponding errors for reaction energies and barrier heights directly (and in exponentially weighted form) influence the computed reaction probabilities (spectral intensities). Reducing the errors due to the SQM methods by performing the MD simulations at a higher density functional theory (DFT) level is impossible with typical computational resources.
An alternative, completely different route to the BO-MD-based approach is Rice–Ramsperger–Kassel–Marcus26–28 quasi-equilibrium theory29 (RRKM/QET). In this approach, relative intensities are calculated from reaction rates derived from barrier heights in the reaction network and the resulting “master equations”. Drahos and V key expanded this theory to non-equilibrium situations and implemented it in the program “Mass Kinetics”.30 RRKM/QET was applied in several studies concerning EI or CID mass spectrometry.31–35 For more examples, we refer to ref. 36, where an overview of some important applications is given. However, these examples concern only small molecules, where a manual setup of all relevant reaction pathways is feasible. None of these approaches has been used routinely in a black-box type procedure for automated spectra prediction.
key expanded this theory to non-equilibrium situations and implemented it in the program “Mass Kinetics”.30 RRKM/QET was applied in several studies concerning EI or CID mass spectrometry.31–35 For more examples, we refer to ref. 36, where an overview of some important applications is given. However, these examples concern only small molecules, where a manual setup of all relevant reaction pathways is feasible. None of these approaches has been used routinely in a black-box type procedure for automated spectra prediction.
Here, we introduce a new program, QCxMS2, which enables the fully automated computation of mass spectra based on automated reaction network discovery. Herein, a forward open-end exploration approach37 is followed, which focuses exclusively on unimolecular reactions happening in MS experiments, in contrast to more general exploration software, such as Chemoton,38 Nanoreactor39 or AutoMekn2021.40 In QCxMS2, the well-established RRKM/QET approach is integrated with automated fragment/product generation and an efficient workflow utilizing QM methods to calculate reaction barriers. Previously well working parts in QCxMS like the assignment and treatment of fractional charge, the cascading reaction concept or the internal energy distribution model are kept.
This initial work focuses on the calculation of electron-ionization mass spectra (EI-MS) but the approach can be easily extended to CID. We begin by providing a brief overview of the theoretical background of the new approach. Next, we describe the implementation of the workflow and the computational details of the software. To assess the accuracy of the new QCxMS2 method, we apply it to a benchmark set of 16 organic and inorganic main-group molecules with diverse structural motifs and typical fragmentation patterns. We compare the resulting spectra to those computed by QCxMS, which, to the best of our knowledge, is the only comparable first-principles method for the QM-based calculation of EI-MS. After discussing computational timings, we present general conclusions on the accuracy and limitations of QCxMS2 and recommend potential use cases.
2 Theory
The basic assumption of QET is that fragmentation reactions in a mass spectrometer occur from thermally excited but quasi-equilibrated ions.29 According to RRKM theory,26–28 the rate constants of unimolecular decompositions is a function of the internal energy, E of an isolated ion | (1) |
In preliminary studies, we found the advanced treatments mentioned above are impractical to use in an automated workflow as the uncertainty for the depending variables caused by errors of the employed underlying QM method or the overall workflow led to too large errors. Therefore, we decided to employ the Eyring equation from conventional transition state theory50 as a more robust but less exact theoretical description of the reaction rates within the QCxMS2 workflow to avoid inconsistent treatment of the differently occurring reaction types in the generated reaction network. It reads
 | (2) |
 | (3) |
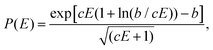 | (4) |
 respectively. The maximum value of the IEE is equal to Eimpact − εHOMO, where Eimpact is an input parameter and represents the kinetic energy of the free electron, before impact. The energy of the HOMO, denoted as εHOMO, is computed by a QM calculation (usually DFT). In this study, Eimpact amounts to 70 eV in analogy to standard EI experiments, and the distribution is set to an average of about 0.8 eV per atom of the input molecule. This energy distribution was determined through extensive testing in the development of QCxMS and showed to be a good approximation for the usually unknown energy distribution in the experiment.12 During the development and evaluation of QCxMS2, we found that the energy distributed uniformly over all atoms overestimates the rate constants for reactions involving hydrogen dissociations. Apart from potential errors related to the chosen QM method, this may suggest an inhomogeneous energy distribution at the timescale of these reactions. To address this systematic error, we applied a simple linear scaling factor to adjust the energy distribution specifically for these reactions (see ESI,† Section S5 for details).
respectively. The maximum value of the IEE is equal to Eimpact − εHOMO, where Eimpact is an input parameter and represents the kinetic energy of the free electron, before impact. The energy of the HOMO, denoted as εHOMO, is computed by a QM calculation (usually DFT). In this study, Eimpact amounts to 70 eV in analogy to standard EI experiments, and the distribution is set to an average of about 0.8 eV per atom of the input molecule. This energy distribution was determined through extensive testing in the development of QCxMS and showed to be a good approximation for the usually unknown energy distribution in the experiment.12 During the development and evaluation of QCxMS2, we found that the energy distributed uniformly over all atoms overestimates the rate constants for reactions involving hydrogen dissociations. Apart from potential errors related to the chosen QM method, this may suggest an inhomogeneous energy distribution at the timescale of these reactions. To address this systematic error, we applied a simple linear scaling factor to adjust the energy distribution specifically for these reactions (see ESI,† Section S5 for details).
For subsequent fragmentations, the internal energy is corrected by the energy loss of a fragment upon dissociation
| E(fragment) = (E0 − KER − ΔH) × nat(frag)/nat(prec), | (5) |
Ion-tracking is conducted as in QCxMS.12 Molecular charges are distributed according to the ionization potential (IP) of the formed fragments, which are determined by self-consistent field (ΔSCF) calculations at a QM level (usually DFT). The statistical weight of each product is then given by
 | (6) |
 | (7) |
Some fundamental limitations of the QCxMS2 approach remain. Direct bond cleavage, also called non-statistical or nonergodic processes, i.e., reactions occurring at a rate faster than the intramolecular vibrational energy redistribution (IVR) cannot be accounted for. Although these are known to happen in a mass spectrometer56 they are assumed here to be less important for the computation of a (for typical applications) sufficiently accurate spectrum, and the assumptions of QET hold for most reactions occurring in a mass spectrometer.29 These reactions can be modeled through dynamical (MD)-based approaches, such as QCxMS, where atomic velocities are scaled non-uniformly to account for the period before the energy is fully equilibrated across the molecule.57 Quantum tunneling through reaction barriers58 may also occur but are also assumed to be less relevant, as they mostly happen for subsequent fragmentation on the ns to μs timescale.56 These effects are expected to cause the largest increase in rate constants for hydrogen dissociations. However, as discussed in Section 2, we tend to overestimate their rates. Therefore, theoretical models to describe this effect, such as those described in ref. 59, are not considered in QCxMS2, but can in principle be applied for critical cases in the future.
Electronically excited states may also affect the reaction barriers. A study using QCxMS reported improved spectra through the application of excited-state dynamics.60 We investigated this for the static approach of QCxMS2 by applying time-dependent DFT for the calculation of the reaction barriers in excited states but no improvement for the spectra was observed, as most excited states were found to be hardly populated at the assumed temperatures (see ESI,† S8 for details).
For a more thorough discussion of the mentioned and other less important physical effects, we refer to the excellent review of Dantus56 of the time-scales of different events in a mass spectrometer observed by time-resolved spectroscopy and Drahos' and Vékey's theoretical work on “Mass Kinetics”.30
3 Implementation and computational details
The theoretical model described above is implemented in the QCxMS2 program available on GitHub.61QCxMS2 is an advanced script that integrates several external QM codes to fully automate the calculation of an electron ionization mass spectrum. The procedure follows a workflow consisting of seven main steps as shown in Fig. 1, which are detailed in the following sections. Additional technical details can be found in the open-source software code.
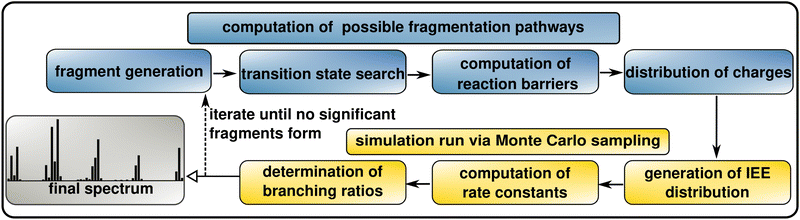 | ||
| Fig. 1 Schematic representation of the workflow of QCxMS2 for the computation of EI-MS. For details on the computational protocol see Section 3. | ||
3.1 Fragment generation
The input is a coordinate file of a molecule. First, possible fragments of the input molecule are generated with the MSREACT mode of CREST.62 The critical aspect of this step is to generate a comprehensive set of possible fragments, which can then be ranked based on their relative barrier heights. Fragments with relative energies exceeding three times the average fragment energy are excluded at this stage to save computation time. Fragments that are not generated at this stage will not appear in the final spectrum (see Section 4.1), whereas incorrectly generated fragments typically do not contribute significantly due to their prohibitively high energy barriers. Furthermore, the desired fragment has to be a local minimum on the PES of the employed level of theory, as its geometry is optimized using the respective method, which can potentially lead to (unintended) atomic rearrangements or artifacts of the method. As the fragment generator is applied to each newly formed fragment with significant relative intensity, QCxMS2 calculations typically involve hundreds to thousands of geometry optimizations, and only efficient SQM methods can be applied here. After removing duplicates (see below), the number of fragments is significantly reduced, allowing for the use of more expensive QM methods, e.g., DFT for reoptimization of the unique fragments.In the fragment (product) generation step with CREST, harmonic repulsive potentials are applied for each atom pair separated by up to three covalent bonds, leading in geometry optimization with GFN2-xTB to typical fragmentation products.63,64 Additionally, further optimizations are conducted with attractive potentials between hydrogen atoms and potential protonation sites within a default cutoff distance of 4 Å to obtain often observed products due to hydrogen rearrangements. Note that these bias potentials are exclusively employed in the generation step and are not utilized in the subsequent energy and barrier calculations. Next, each obtained product is subsequently optimized in a maximum of 15 cycles without constraints to generate reasonable fragments on the GFN2-xTB PES while avoiding the recombination of the dissociation products. Both optimization steps are conducted at a high finite electronic temperature of 5000 K to favor the generation of open-shell (poly)radicals typically occurring in (EI-)MS. Duplicated structures produced are identified with MolBar65 and removed to avoid redundant calculations. Additional (random) shifting of atom positions can be employed to generate a greater number of potential products, however, this option is not activated in the default settings.
For more details on this structure generator, we refer to the original publication in ref. 62.
3.2 Transition state search
For each fragmentation or isomerization reaction, a minimum energy path search is performed with the nudged-elastic band (NEB) method66 as implemented in ORCA 6.0.0.67,68 Loose convergence criteria are chosen (Tol_MaxFP_I = 0.01 and Tol_RMSFP_I = 0.005), otherwise default settings (keyword “NEB”) are used including energy-weighted spring forces. The initial path is generated with the image-dependent pair potential (IDPP) method.69 Not converged NEB runs are restarted with a different guess for the initial path generated by the geodesic interpolation program.70 For the transition state optimization, the Hessian of the structure with the highest energy on the minimum energy path is computed at the GFN2-xTB level and the intrinsic reaction coordinate (IRC) mode is identified by comparing the difference in the root-mean-square deviation (RMSD) of the atoms to start and end structure upon translation along each obtained imaginary frequency mode. The transition state optimization is performed along this mode at “loose” convergence settings in ORCA.3.3 Computation of reaction energies and barriers
Reaction barriers and energies can be refined at a higher level of theory by single-point calculations on the previously optimized geometries. In this work, GFN2-xTB and ωB97X-3c were employed. Thermal corrections are accounted for by the single-point Hessian (SPH)71 approach at the GFN2-xTB level as it is more robust than the conventional approach on not fully optimized structures often exhibiting other small imaginary modes beside the imaginary transition state mode, which may occur in the automated workflow. Low-frequency modes are described with the modified rigid-rotor harmonic oscillator (mRRHO) approximation.72 Due to the high temperatures, the mRRHO rotor cutoff was set to 150 cm−1. To ensure robustness, imaginary modes with an absolute value below 100 cm−1 were inverted. SCF calculations that do not converge with the default settings in ORCA 6.0.0, are restarted with Fermi smearing at elevated electronic temperature to account partially for the potential multireference character of the open-shell radical cations and for the correct dissociation behavior of two-electron bonds. The temperature is chosen according to the HOMO–LUMO gap of the respective QM method as described in ref. 57.3.4 Distribution of charges
The IPs of the fragments are computed at the neutral optimized structures via a ΔSCF approach. By default, a composite level of GFN2-xTB IPs and refinement of close IPs (below 2 eV mol−1) at the ωB97X-3c level of theory is employed.3.5 Generation of IEE distribution
The energy distribution given by eqn (4) is sampled numerically in a Monte Carlo approach, using by default 105 sample points, that lead to sufficient convergence of the relative intensities according to our tests for this quantity. As default, the average energy is set to 0.8 eV times the number of atoms of the input molecule.3.6 Computation of rate constants
For each energy in this distribution, a rate constant is calculated at the corresponding temperature. The thermal contributions to the reaction barriers are determined at each of these temperatures using the previously computed vibrational frequencies. For computational efficiency, these contributions are precomputed across the energy distribution in 200 discrete steps.3.7 Determination of branching ratios
Finally, the branching ratios of the fragmentation reactions are calculated from the relative reaction rates. Relative intensities are determined based on the relative reaction rates and the survival yield of the precursor ion across the energy distribution using a Monte Carlo approach. This calculation is conducted separately for each fragmentation step, as the absolute rate constants for subsequent fragmentations are significantly slower than those of earlier steps due to energy loss upon fragmentation. This simplification is performed, as the branching ratios have to be computed for the entire energy distribution, which would be computationally very expensive to perform for a system of coupled differential equations.The fragment intensities are multiplied by their respective statistical charge computed earlier. Normalization of all computed fragment intensities to the intensity of the largest signal as usual results in the final spectrum.
Note that steps 5–7 are negligible in terms of computational costs compared to steps 1–4, which require QM calculations. This has the advantage that the normally unknown energy distribution can be adapted to the experiment and only any new reaction paths that may arise at higher energies need to be calculated. This is a further advantage over the use of MD trajectories, which have to be completely recalculated for different internal energies.
The natural isotope ratios are introduced in a post-simulation treatment as in QCxMS.12 Steps 1–7 are performed iteratively for each newly formed fragment with a relative intensity above a certain threshold, which is by default 1% of the initial intensity. Thus, subsequent fragmentations via cascade reactions are captured. For a more thorough discussion of the intensity threshold and the reproducibility of the workflow, see ESI,† Section S6.
3.8 Employed programs
The results discussed in Section 4 were computed with QCxMS2 version 1.0.0 with default settings.61 As input, the minimum energy conformer of the radical cation of the molecule at the GFN2-xTB level found by CREST version 3.0.273 was used as a starting point. Fragments were generated with a development version of the CREST MSREACT mode and duplicates were identified with molbar 1.0.3.74 ωB97X-3c calculations, NEB path searches, and transition state optimizations were performed with ORCA version 6.0.0.67 The resolution of identity approximation75 with matching auxiliary basis sets was applied for the Coulomb integrals,76 whereas the exchange integrals were computed analytically, as it is faster than RIJCOSX77 for the small system sizes investigated here. Geometry optimizations of equilibrium structures at the ωB97X-3c level were performed in ORCA with “loose” convergence settings. Initial reaction paths for restarted NEB calculations were generated with geodesic-interpolation 1.0.0.78 GFN2-xTB calculations were conducted with a development version of xTB 6.7.1 with default convergence settings.79 QCxMS spectra for comparison were computed with QCxMS V5.2.113,80,81 with default settings at the GFN2-xTB level. Cosine similarity matching scores82,83 were computed with matchms python package84 and entropy similarity scores85,86 with the msentropy python package.874 Results
In this section, standard 70 eV EI-MS spectra computed with QCxMS2 are shown for a set of 16 organic and inorganic main group molecules listed in Table 1. No system-specific adjustments were made in the calculation of spectra to evaluate QCxMS2's potential for cases with unknown experimental data. Additional investigations for the rotor-cutoff (ESI,† Section S7) and the average internal energy (ESI,† Section S4) parameters were made at the composite level ωB97X-3c//GFN2-xTB (see below) and can be found in the ESI.† For comparison, experimental spectra rounded to integer masses of all compounds are taken from the NIST database,88 except for acibenzolar-S-methyl, for which a high-resolution spectrum was taken from ref. 25. With this selection of molecules we intend to discuss the strengths and weaknesses of the approach. The test set comprises a diverse range of organic and inorganic compounds, including the alkane n-octane, alkene 4-methyl-1-pentene, ether ethyl propyl ether, alcohol 1-butanol, aldehyde butanal, ketone 2-pentanone, carboxylic acid butanoic acid, ester methyl butyrate, amide butanamide, and N-heterocycles uracil, adenine, and caffeine. Additionally, main group inorganic substances such as tabun, tetramethylbiphosphine disulfide, acibenzolar-S-methyl, and dichloroethylaluminum are included. Lewis structures of all compounds can be found in the ESI,† Section S3. In principle, QCxMS2 can also compute molecules containing transition metals without special adjustments. However, due to their often rather special fragmentation patterns and generally more difficult electronic structure compared to the main group elements, they are omitted from this study and are planned for a later study.| Compound | GFN2-xTB | Composite | ωB97X-3c | QCxMS |
|---|---|---|---|---|
| n-Octane | 0.686 | 0.703 | 0.841 | 0.840 |
| 4-Methyl-1-pentene | 0.758 | 0.714 | 0.835 | 0.782 |
| Ethyl propyl ether | 0.762 | 0.869 | 0.813 | 0.697 |
| 1-Butanol | 0.753 | 0.750 | 0.724 | 0.603 |
| Butanal | 0.852 | 0.807 | 0.807 | 0.803 |
| 2-Pentanone | 0.781 | 0.718 | 0.818 | 0.743 |
| Butanoic acid | 0.683 | 0.751 | 0.761 | 0.558 |
| Methyl butyrate | 0.635 | 0.736 | 0.742 | 0.655 |
| Butanamide | 0.494 | 0.673 | 0.674 | 0.620 |
| Uracil | 0.644 | 0.498 | 0.659 | 0.769 |
| Adenine | 0.748 | 0.790 | 0.712 | 0.794 |
| Caffeine | 0.456 | 0.626 | 0.644 | 0.626 |
| Tabun | 0.637 | 0.508 | 0.655 | 0.649 |
| Tetramethylbi-phosphine disulfide | 0.691 | 0.796 | 0.782 | 0.269 |
| Acibenzolar-S-methyl | 0.389 | 0.599 | 0.527 | 0.100 |
| Dichloroethyl-aluminium | 0.752 | 0.667 | 0.679 | 0.438 |
| Average | 0.670 | 0.700 | 0.730 | 0.622 |
| Minimum | 0.389 | 0.599 | 0.527 | 0.100 |
To ease the assessment of the quality spectra, the spectral entropy matching score is used. It captures the presence of relevant peaks, as well as their relevant intensities compared to the experiment, and ranges from 0 (no agreement at all) to 1 (perfect agreement).85 It was recently shown85 that this score is more reliable than the commonly used cosine similarity score82,83 and it is in our opinion a good metric to evaluate the accuracy of the spectra in this work. For comparison, the average values of the cosine score are also given in the discussion below. Herein, a score of at least 0.75 between experimental spectra was found to be a meaningful threshold for reliable structure identification85 and should be aimed for with any theoretical procedure considering the uncertainty of the experiment. However, interpretation of this score is system-specific, e.g., the most important peaks for substance identification may be present despite a comparatively low score.
Spectra were computed with three different combinations of QM methods, given in the short notation “method used for reaction energies and barriers”//“method used for geometry optimizations and reaction path searches”, namely, GFN2-xTB//GFN2-xTB (“GFN2-xTB”), ωB97X-3c//GFN2-xTB (“composite”), and ωB97X-3c//ωB97X-3c (“ωB97X-3c”). IPs were calculated at the GFN2-xTB level and refined at the ωB97X-3c level as described above and for the DFT spectra only with ωB97X-3c calculated throughout. Harmonic vibrational frequencies were always computed with GFN2-xTB. The RSH ωB97X-3c was employed because it yields excellent barriers at low computational costs89 and is considered by us as one of the best yet still affordable methods in our context. For comparison, we computed spectra with QCxMS at the GFN2-xTB level, as the refinement of energies and performing MDs at the ωB97X-3c level is computationally not feasible (see Section 4.3).
4.1 Effect of the level of theory
First, we discuss the effect of the level of theory used for the spectra calculation. Entropy similarity match scores between experimental and theoretical spectra computed with QCxMS and QCxMS2 with the three method combinations described above for all 16 compounds of the test set are given in Table 1.On average, the highest level of theory employed, i.e., ωB97X-3c for geometries and energies, achieves a very good score of 0.73. Seven out of 16 compounds achieve the target accuracy of at least 0.75, while only four compounds, namely butanamide, uracil, tabun, and acibenzolar-S-methyl, exhibit a mediocre score below 0.7. As expected, using GFN2-xTB geometries instead of DFT geometries results in a slight decrease in accuracy with a still good average score of 0.7. When GFN2-xTB reaction barriers are used instead of ωB97X-3c, the accuracy drops to 0.67. The still good accuracy of GFN2-xTB is somewhat unexpected, considering its known limitations in accurately modeling radical cations and reaction barriers.63 Despite some outliers, for which GFN2-xTB or the composite level yields better results than ωB97X-3c presumably due to favorable error compensation, the trend is on average that a more accurate description of the PES leads to better spectra. This is an important observation and supports the underlying theoretical assumptions of the QCxMS2 approach.
For comparison, the commonly used cosine similarity score (see ESI,† S12 for scores for each compound), shows an even more pronounced trend with scores of 0.573 (GFN2-xTB//GFN2-xTB), 0.636 (ωB97X-3c//GFN2-xTB), and 0.711 (ωB97X-3c//ωB97X-3c).
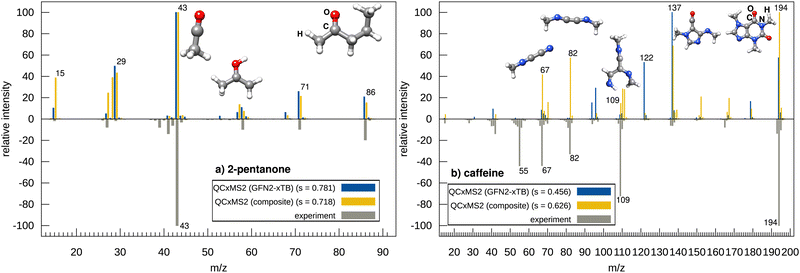
The effect on the spectrum by refining the barriers at the ωB97X-3c level is exemplary shown in two examples. Fig. 2 depicts the spectra computed with QCxMS2 at the GFN2-xTB//GFN2-xTB and ωB97X-3c//GFN2-xTB levels for 2-pentanone and caffeine. For 2-pentanone, only very small differences between the spectra are visible and both show a good agreement with the experiment with matching scores of 0.781 and 0.718, respectively. Here, GFN2-xTB gives already a good description of the PES, and no refinement of the barriers is needed. The ωB97X-3c spectrum, shown in the ESI,† in Section S16, looks slightly better, as the peaks at m/z 57 and 29 are computed much smaller yielding excellent good matching score of 0.818. The spectrum of caffeine computed with GFN2-xTB agrees poorly with experiment. Although many relevant peaks are present, they have incorrect relative intensities which leads to a low matching score of only 0.456. By using ωB97X-3c reaction barriers, a substantial improvement to a score of 0.626 is obtained. However, the peak at m/z 109 has too low relative intensity, while the peaks at m/z 110 and m/z 111 are obtained with too high intensities. Additionally, the peak at m/z 55 is missing. Computing the spectrum using ωB97X-3c also for geometries further improves the agreement with experiment and yields a score of 0.644 (spectrum shown in the ESI,† in Section S16).
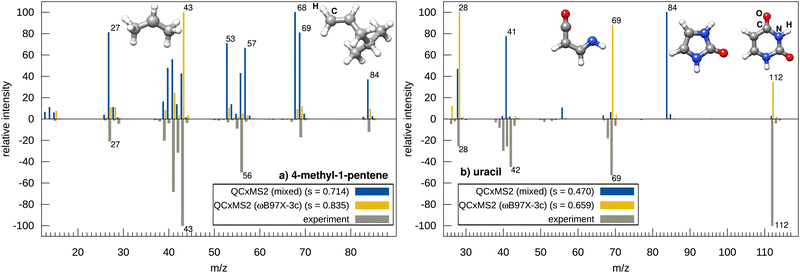
Next, we examine the effect on the spectra using ωB97X-3c geometries instead of GFN2-xTB geometries, as depicted in Fig. 3, with the examples of 4-methyl-1-pentene and uracil. The spectrum of 4-methyl-1-pentene computed with GFN2-xTB geometries generally shows good agreement with the experiment yielding a reasonable score of 0.714. However, several signal intensities are inaccurate, particularly the peaks at m/z 68, 57, and 53. When using ωB97X-3c geometries instead, the spectrum shows almost perfect agreement with the experiment with a matching score of 0.835, and the base peak is also correctly predicted to be at m/z 43. This suggests that the respective transition state geometries optimized at the GFN2-xTB level are insufficient for refinement at the ωB97X-3c level, and accurate relative barrier heights are only achieved when ωB97X-3c is also used for the geometry optimization.
An even more pronounced example for this observation is uracil. Here, the agreement with the experiment with GFN2-xTB optimized geometries is rather bad, as the peak m/z 84 is falsely predicted leading to a match score of only 0.498. This is due to a too “flat” PES of GFN2-xTB for the initial dissociation of CO leading to a wrong transition state structure too late at the reaction path and thus to an underestimated barrier for the peak at m/z 84. The apparently correct peak at m/z 41 stems from further dissociation of this fragment and is therefore predicted here only by chance but via a wrong pathway. As a result, the other correctly predicted peaks are consequently too low in intensity demonstrating the sensitivity of the approach, as one inaccurate barrier can potentially distort the whole spectrum. In contrast, the m/z 84 peak is virtually absent when using ωB97X-3c optimized reaction paths which gives the correct description for the CO dissociation leading to an overall much better agreement with the experimental spectrum (score of 0.659 versus 0.470). Overall, QCxMS2 demonstrates good accuracy, however, certain spectra exhibit low matching scores even at the ωB97X-3c level.
For example, in the ωB97X-3c spectrum of uracil, the signals at m/z 40, and 42 are missing and the peak at m/z 41 has a too low intensity as the competing fragmentation pathway to the peak at m/z 28 has a lower barrier. For m/z 42, we rationalized that the peak most likely stems from a hydrogen rearrangement of the fragment at m/z 69 to a ketene and subsequent loss of HCN. However, this fragmentation reaction is not predicted by the MSREACT fragment generator.
By modeling the reaction path of the H-rearrangement and the HCN loss manually we found a sufficiently low barrier for the fragment to be formed along the fragment at m/z 28.
The fragment with m/z 40 is also not formed by MSREACT and could not be identified manually. It may be not generated as it is very high in energy on the GFN2-xTB PES. The fact that the peak at m/z 40 is completely missing in the GFN2-xTB spectrum of QCxMS (shown in the ESI,† in Section S15) indicates that the fragment is not easily accessible on the GFN2-xTB PES.
To assess if MSREACT has in general problems in predicting the fragments of rigid ring systems, we computed additional spectra with ωB97X-3c//GFN2-xTB for the simplest representatives of this class, namely benzene and naphthalene and found also poor agreement with scores of 0.699 and 0.698, respectively. Notably, many peaks are missing in the computed spectra.
Using ωB97X-3c for geometry optimizations in QCxMS2 does not lead to better results for this class of compounds.
In addition, we computed the spectra at the ωB97X-3c//GFN2-xTB level with additional geometry optimizations after randomly shifting the atomic positions in the fragment generator. By applying these settings, more peaks observed in the experiment are correctly predicted but the overall accuracy of the spectrum does not increase as also more wrong intensities are predicted.
We conclude that the above described problems with conjugated π-ring systens is mainly due to the insufficient description of the PES of the formed fragments by GFN2-xTB. During the constrained optimizations in MSREACT, (unintended) atom rearrangements frequently occur, leading to the generation of numerous artificial structures. Refinement at the DFT level cannot resolve this issue, as the correct fragments are not generated at the GFN2-xTB stage. Employing a higher-level theory, such as ωB97X-3c, in MSREACT is computationally infeasible, as outlined in Section 3.1.
In contrast, QCxMS at the GFN2-xTB level produces reasonably accurate spectra, with scores of 0.895 and 0.826 for benzene and naphthalene. Here, the limited accuracy of GFN2-xTB does not appear to be as critical, as the presumed artifacts coincidentally align with the correct experimental masses. However, substituted benzenes and phenols also prove to be challenging for QCxMS.19,90
Another issue observed in the QCxMS2 spectra is that, for larger or more complex molecules, errors of ±1, m/z may occasionally occur. This indicates that a hydrogen atom is incorrectly assigned to the other fragment of the dissociation products in the respective fragmentation reaction compared to the experimental results. Such cases are observed, for instance, around the peak at m/z 109 for caffeine, as described above, or the missing peak at m/z 181 for acibenzolar-S-methyl (see below). Hydrogen dissociations are generally difficult to describe, as indicated by the scaling factor applied to the internal energy distribution for these reactions.
Another source of error are the ro-vibrational thermal contributions, which are computed only at the GFN2-xTB level, also due to computational costs. We investigated their effect for the spectrum of methyl-butyrate, for which we could achieve an improvement of the spectrum by using ωB97X-3c frequencies instead of GFN2-xTB frequencies (see ESI,† S10 for details).
Despite these problems mainly due to the limited accuracy of the (currently) feasible level of electronic structure theory, QCxMS2 shows overall good robustness, which is also reflected in the minimum score of 0.527 at the ωB97X-3c level for the test set. Taking into account that the set also contains complicated molecules with unusual fragmentation pathways, this is a good result.
4.2 Comparison to QCxMS
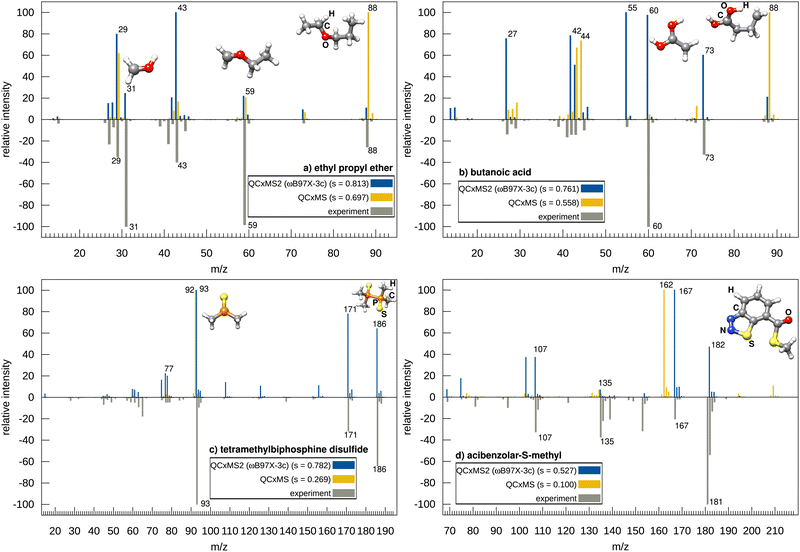
Next, we discuss the accuracy of QCxMS2 in comparison to its predecessor QCxMS. Overall on the test set, QCxMS2 at the ωB97X-3c level yields an average match score of 0.735 compared to 0.622 for the QCxMS spectra computed at the GFN2-xTB level. Employing the cosine similarity score, the difference is even larger with values of 0.755 (QCxMS2) and 0.515 (QCxMS). Notably, the lowest score with QCxMS2 was 0.527 compared to only 0.100 of QCxMS, indicating that QCxMS2 is the more robust approach yielding less outliers, which is important for application in automated structure elucidation workflows. Already at GFN2-xTB//GFN2-xTB level QCxMS2 spectra are more accurate than QCxMS with an average score of 0.673. This indicates that the new “static” approach has intrinsic advantages over MD based QCxMS, which will be investigated in the following for four selected molecules that were identified as problematic for QCxMS.Fig. 4 shows the computed spectra for ethyl propyl ether, butanoic acid, tetramethylbiphosphine disulfide, and acibenzolar-S-methyl using both QCxMS2 and QCxMS. For comparison, we take the best but still affordable level for QCxMS2, i.e., ωB97X-3c. Since computing spectra at this level is unfeasible in the QCxMS (see Section 4.3), we take here the spectra computed with the GFN2-xTB level of theory in the comparison. For ethyl propyl ether, the base peak at m/z 31 is significantly computed only by QCxMS2 and is virtually absent in the QCxMS spectrum, which fails to predict this rearrangement reaction from the fragment with m/z 59. This is a typical reaction occurring for ethers and an important finding that this signal is obtained with QCxMS2. Consequently, the matching score with QCxMS2 is much better (0.813 versus 0.697). A similar cases is butanoic acid, for which the Mclafferty type rearrangement resulting in the peak at m/z 60, which is also the main peak in the experimental spectrum, occurs with a too low probability with QCxMS. Also here, QCxMS2 computed this fragment in good agreement with the intensity from the experiment, yielding also a much better score of 0.761 versus 0.558. Even when using GFN2-xTB with QCxMS2, improved scores compared to QCxMS are achieved for ethyl propyl ether (0.762) and butanoic acid (0.683). These two examples demonstrate, that fragments stemming from rearrangements are underestimated in QCxMS, probably due to the limited MD simulation time.
Examples (c) and (d) in Fig. 4 contain the inorganic main group elements P and S, which were also found to be problematic for QCxMS in a recent study.25 The QCxMS computed spectrum for tetramethylbiphosphine disulfide shows poor agreement (score of 0.269), failing to predict the methyl dissociation to the peak at m/z 171 and the P–P bond breakage leading to the main peak at m/z 93 in the experimental spectrum. Instead, QCxMS predicts an additional H-shift associated with the P–P bond breakage, resulting in an experimentally unobserved peak at m/z 92. Thus, the issue of missing peaks by ±1 m/z unit, as described above for QCxMS2, also occurs with QCxMS. In contrast, QCxMS2 correctly predicts here the bond breakage and achieves a much higher score of 0.782. As the m/z 92 peak is also observed in the GFN2-xTB spectrum of QCxMS2 with a score of 0.691 (spectrum shown in the ESI,† in Section S16), the falsely predicted hydrogen shift in QCxMS is probably due to the MD approach and not due to the inaccuracy of GFN2-xTB.
For acibenzolar-S-methyl, the QCxMS spectrum shows almost no agreement to experiment, with a score of only 0.100. The peak at m/z 182, resulting from the loss of N2, is not found, and instead, a false peak at m/z 162 is computed as the main peak. This peak arises from an α-cleavage, involving an H-shift to the sulfur atom and dissociation of methanethiol at the carbonyl C-atom. Interestingly, this peak is observed in the GFN2-xTB spectrum of QCxMS2 (shown in the ESI,† in Section S16) (however, without hydrogen shift, i.e., resulting in a peak at m/z 163), indicating that the GFN2-xTB PES overestimates the stability of the thiadiazole ring.
Using QCxMS2 in conjunction with ωB97X-3c, the loss of N2 to the peak at m/z 182 is correctly computed. However, the main peak at m/z 181 is also missing here. Due to its high intensity in the experimental spectrum, this stems most probably not from a hydrogen dissociation from the fragment of m/z 182 and has to occur via a different mechanism, as the computed barrier of the hydrogen dissociation is much too high (even without scaling of the IEE applied) compared to the methyl loss to the fragment of m/z 167. The fragment generator does not produce the correct fragment here, probably due to the insufficient accuracy of GFN2-xTB as discussed in Section 4.1. However, apart from the main experimental peak, the relevant signals are obtained and the score of 0.527 is still reasonable compared to QCxMS. Overall, the results for the test set demonstrate that QCxMS2 exhibits improved accuracy and robustness in comparison to QCxMS.
4.3 Computation time
Finally, the computational timings are discussed using the examples of 2-pentanone, a molecule with 16 atoms, and caffeine, a typical metabolite with 24 atoms and the largest molecule in the test set.Fig. 5 shows the computational timings scaled to 16 Intel Xeon “Sapphire Rapids” v4 @ 2.10 GHz CPU cores for the spectra calculation with QCxMS2 with the three different theory levels employed here and timings with QCxMS with GFN2-xTB and ωB97X-3c in comparison.
QCxMS can in principle be perfectly parallelized as every (cascading) trajectory is obtained separately, whereas with QCxMS2 the parallelization efficiency depends on the number of fragments in a fragmentation step and, how long particular calculations, e.g., a specific transition state search takes since some calculations have to be performed in a subsequent manner. The QCxMS2 calculations were performed with 16 CPU cores, with the exception of the expensive ωB97X-3c spectra calculations, which were performed on 96 cores for 2-pentanone and on an 128 AMD EPYC 7763 CPU for caffeine. The respective computational timings are scaled to 16 CPU cores. For the QCxMS calculations, the same number of cores was used as the number of trajectories. However, for a meaningful comparison in terms of the practical use of the program, the timings are scaled to the typical computational resources of 16 CPU cores. A QCxMS2 calculation for 2-pentanone at the GFN2-xTB level takes about an hour. Refining the barriers at the ωB97X-3c level takes only one hour more computation time. Computing the geometries and the reaction path search also at the ωB97X-3c level is very expensive and increases the computational costs massively to 502 hours. For caffeine, the computation time is as expected significantly larger as also more fragments have to be computed. Whereas in the calculation for 2-pentanone 79 isomers and 121 fragment pairs and hence 200 transition state searches and barrier calculations have to be performed, for caffeine 462 isomers and 292 fragment pairs were found, i.e., 754 reaction barriers have to be computed. However, the calculation is still feasible, requiring 3.7 hours for the GFN2-xTB calculation and 15.7 hours if the barriers are refined at the ωB97X-3c level. Computing the geometries at the ωB97X-3c level for caffeine, however, becomes impractically expensive, requiring about 4050 hours.
In comparison, the QCxMS calculation for 2-pentanone at the GFN2-xTB level takes 30 minutes using the default number of 400 trajectories for this molecular size. For caffeine, 600 trajectories have to be computed leading to an overall wall time of about one hour. However, refinement of the geometries at a higher level of theory as in QCxMS2 is not possible in this approach and to reach more accuracy all calculations need to be performed at the higher level of theory too. This is computationally very expensive, as demonstrated by the 2-pentanone calculation, which takes 7664.5 hours at the ωB97X-3c level, which is too expensive to be of practical use. Similarly, the corresponding calculation for caffeine is not feasible with our available resources and was therefore not performed. While QCxMS is computationally cheaper at the GFN2-xTB level, achieving better accuracy using a higher level of theory quickly becomes unfeasible. In contrast, refining barriers via DFT single-point calculations is possible with QCxMS2 and improves the accuracy (see Table 1). Even when using ωB97X-3c also for geometry optimizations, QCxMS2 remains computationally more efficient than QCxMS.
5 Conclusions
Computational tools for predicting mass spectra are of great importance for elucidating the chemical structure of unknown compounds. QCxMS, currently the only fully automated QM-based program for calculating EI-MS spectra, achieves reasonable accuracy but faces limitations in generating accurate spectra with less “outliers” needed for application in structure elucidation workflows. To this end, a new program termed QCxMS2 for the calculation of mass spectra based on automated reaction network discovery using QM methods was developed. In this work, we demonstrate that the approach of computing spectral intensities from relative reaction rate constants in an automated workflow is generally possible. We presented promising results for a diverse test set of 16 organic and inorganic compounds. Here, QCxMS2 yields a good entropy similarity match score compared to experiment of 0.67 and improves upon its predecessor QCxMS with 0.622 at the same GFN2-xTB level of theory. We recommend refining the barriers via single-point calculations with ωB97X-3c on the GFN2-xTB geometries, which yields an improved score of 0.7 at still feasible computational costs. Using ωB97X-3c also for geometries yields even better accuracy and robustness with an average score of 0.73 but at significantly higher computational costs.We attribute the remaining deviations from the experimental data primarily to errors in the methods used to calculate the electronic barriers, the vibrational contributions, and the possible structures appearing in the reaction networks. Due to the large size of these networks, we are limited to using efficient DFT methods for the energy calculations and SQM methods for the frequency calculations.
The CREST MSREACT fragment generator found in most cases all relevant peaks, and only in a few instances, particularly involving complex unsaturated ring rearrangements, missing fragments are suspected as a source of error. This issue is likely due to the limited accuracy of GFN2-xTB used in this step, and we anticipate that employing improved SQM methods will significantly reduce this error. We plan to investigate the issue of missing peaks in more detail in future studies.
For flexible structures, particularly those containing heavy main-group elements, QCxMS2 demonstrated excellent accuracy on average, significantly outperforming QCxMS. Additionally, typical rearrangement reactions of common organic functional groups are better captured by QCxMS2 than with QCxMS.
The QCxMS2 program is open-source and freely available.61 Note that all of the employed programs in the QCxMS2 workflow are open-source or at least free for academic use (ORCA) making QCxMS2 free to use for academia. Furthermore, QCxMS2 is systematically improvable and a more “controlled” approach than the MD-based QCxMS. We expect that QCxMS2 will benefit especially from newly developed QM methods for the computation of reaction pathways and barriers. Currently, efficient tight-binding methods are being developed in our lab and have already shown promising results close to the accuracy of DFT spectra at significantly reduced computation time. Initial tests with the unpublished g-xTB method currently developed in our lab employed for energies and geometries gave on average an excellent matching score of 0.736 close to the ωB97X-3c values at about the same computation time needed for the GFN2-xTB spectra.
Furthermore, an extension of QCxMS2 to describe negatively or multiply charged species, as well as to calculate the experimentally also very relevant ESI/CID-MS, is planned. Since the QCxMS2 approach can be systematically improved with more advanced methods, we view it as a promising pathway toward highly accurate and reliable mass spectrum predictions.
Author contributions
Johannes Gorges: conceptualization (supporting); data curation (lead); methodology (equal); software (lead); writing – original draft (lead); writing – review & editing (equal). Stefan Grimme: conceptualization (lead); methodology (equal); writing – original draft (supporting); writing – review & editing (equal).Data availability
The employed software code is open-source and can be found here: https://github.com/grimmelab/QCxMS2. Geometries in XYZ format for all structures, as well as the computed spectra for the test set including the experimental reference data taken from the literature, can be found here: https://github.com/grimme-lab/QCxMS2-data/. Additional details on the implementation, tests of different technical parameters, and computed spectra not included in the manuscript are provided in the file SI.pdf.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the DFG grant no. 533949111, “Quantum Chemical Calculation of Mass Spectrometry via Automated Transition State Search”. We gratefully acknowledge the access to the Marvin cluster of the University of Bonn. We thank Dr Jeroen Koopman from FACCTs, Thomas Froitzheim, and Julia Kohn for fruitful discussions, and Jasmin Klotz for testing the program. Dr Hagen Neugebauer and Dr Andreas Hansen are thanked for proofreading the manuscript. We further thank Nils van Staalduinen from Aachen for providing a development version of MolBar.Notes and references
- G. L. Glish and R. W. Vachet, Nat. Rev. Drug Discovery, 2003, 2, 140–150 CrossRef CAS PubMed.
- R. R. da Silva, P. C. Dorrestein and R. A. Quinn, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 12549–12550 CrossRef CAS PubMed.
- W. D. Hoffmann and G. P. Jackson, Annu. Rev. Anal. Chem., 2015, 8, 419–440 CrossRef CAS PubMed.
- L. O. Dragsted, Q. Gao, A. Scalbert, G. Vergères, M. Kolehmainen, C. Manach, L. Brennan, L. A. Afman, D. S. Wishart, C. Andres Lacueva, M. Garcia-Aloy, H. Verhagen, E. J. M. Feskens and G. Praticò, Genes Nutr., 2018, 13, 8 CrossRef PubMed.
- X. Zhou, M. M. Ulaszewska, C. Cuparencu, C. De Gobba, N. Vaazquez-Manjarrez, G. Gürdeniz, J. Chen, F. Mattivi and L. O. Dragsted, J. Agric. Food Chem., 2020, 68, 6122–6131 CrossRef CAS PubMed.
- L. van Tetering, S. Spies, Q. D. Wildeman, K. J. Houthuijs, R. E. van Outersterp, J. Martens, R. A. Wevers, D. S. Wishart, G. Berden and J. Oomens, Commun. Chem., 2024, 7, 30 CrossRef PubMed.
- J. N. Wei, D. Belanger, R. P. Adams and D. Sculley, ACS Cent. Sci., 2019, 5, 700–708 CrossRef CAS PubMed.
- M. Murphy, S. Jegelka, E. Fraenkel, T. Kind, D. Healey and T. Butler, arXiv, 2023, preprint, arXiv:2301.11419 DOI:10.48550/arXiv.2301.11419.
- F. Allen, R. Greiner and D. Wishart, Metabolomics, 2015, 11, 98–110 CrossRef CAS.
- S. Goldman, J. Li and C. W. Coley, Anal. Chem., 2024, 96, 3419–3428 CrossRef CAS PubMed.
- P. L. Bremer, A. Vaniya, T. Kind, S. Wang and O. Fiehn, J. Chem. Inf. Model., 2022, 62, 4049–4056 CrossRef CAS PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2013, 52, 6306–6312 CrossRef CAS PubMed.
- J. Koopman and S. Grimme, J. Am. Soc. Mass Spectrom., 2022, 33, 2226–2242 CrossRef CAS PubMed.
- J. Lee, D. J. Tantillo, L.-P. Wang and O. Fiehn, J. Chem. Inf. Model., 2024, 64, 7470–7487 CrossRef CAS PubMed.
- X. Hu, W. L. Hase and T. Pirraglia, J. Comput. Chem., 1991, 12, 1014–1024 CrossRef CAS.
- U. Lourderaj, R. Sun, S. C. Kohale, G. L. Barnes, W. A. de Jong, T. L. Windus and W. L. Hase, Comput. Phys. Commun., 2014, 185, 1074–1080 CrossRef CAS.
- V. Ásgeirsson, C. A. Bauer and S. Grimme, Chem. Sci., 2017, 8, 4879–4895 RSC.
- J. Koopman and S. Grimme, ACS Omega, 2019, 4, 15120–15133 CrossRef CAS PubMed.
- P. R. Spackman, B. Bohman, A. Karton and D. Jayatilaka, Int. J. Quantum Chem., 2018, 118, e25460 CrossRef.
- S. Wang, T. Kind, D. J. Tantillo and O. Fiehn, J. Cheminf., 2020, 12, 63 CAS.
- S. A. Schreckenbach, J. S. Anderson, J. Koopman, S. Grimme, M. J. Simpson and K. J. Jobst, J. Am. Soc. Mass Spectrom., 2021, 32, 1508–1518 CrossRef CAS PubMed.
- R. Schnegotzki, J. Koopman, S. Grimme and R. D. Süssmuth, Chem. – Eur. J., 2022, 28, e202200318 CrossRef CAS PubMed.
- F. C. Chernicharo, L. Modesto-Costa and I. Borges Jr, J. Mass Spectrom., 2020, 55, e4513 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 CrossRef CAS PubMed.
- H. Hecht, W. Y. Rojas, Z. Ahmad, A. Krenek, J. Klánová and E. J. Price, Anal. Chem., 2024, 96, 13652–13662 CrossRef CAS PubMed.
- L. S. Kassel, J. Phys. Chem., 1927, 32, 225–242 CrossRef.
- O. K. Rice and H. C. Ramsperger, J. Am. Chem. Soc., 1927, 49, 1617–1629 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1952, 20, 359–364 CrossRef CAS.
- H. M. Rosenstock, M. B. Wallenstein, A. L. Wahrhaftig and H. Eyring, Proc. Natl. Acad. Sci. U. S. A., 1952, 38, 667–678 CrossRef CAS PubMed.
- L. Drahos and K. Vékey, J. Mass Spectrom., 2001, 36, 237–263 CrossRef CAS PubMed.
- C. Lifshitz, Acc. Chem. Res., 1994, 27, 138–144 CrossRef CAS.
- D. Asakawa, J. Am. Soc. Mass Spectrom., 2023, 34, 435–440 CrossRef CAS PubMed.
- D. Asakawa, K. Todoroki and H. Mizuno, J. Am. Soc. Mass Spectrom., 2022, 33, 1716–1722 CrossRef CAS PubMed.
- D. Lesage, S. Mezzache, Y. Gimbert, H. Dossmann and J.-C. Tabet, J. Am. Soc. Mass Spectrom., 2019, 25, 219–228 CAS.
- C. Chalet, D. Lesage, E. Darii, A. Perret, S. Alves, Y. Gimbert and J.-C. Tabet, J. Am. Soc. Mass Spectrom., 2024, 35, 456–465 CrossRef CAS PubMed.
- C. A. Bauer and S. Grimme, J. Phys. Chem. A, 2016, 120, 3755–3766 CrossRef CAS PubMed.
- J. P. Unsleber and M. Reiher, Annu. Rev. Phys. Chem., 2020, 71, 121–142 CrossRef CAS PubMed.
- J. P. Unsleber, S. A. Grimmel and M. Reiher, J. Chem. Theory Comput., 2022, 18, 5393–5409 CrossRef CAS PubMed.
- L.-P. Wang, A. Titov, R. McGibbon, F. Liu, V. S. Pande and T. J. Martnez, Nat. Chem., 2014, 6, 1044–1048 CrossRef CAS PubMed.
- E. Martnez-Núñez, G. L. Barnes, D. R. Glowacki, S. Kopec, D. Peláez, A. Rodrguez, R. Rodrguez-Fernández, R. J. Shannon, J. J. Stewart and P. G. Tahoces, et al. , J. Comput. Chem., 2021, 42, 2036–2048 CrossRef PubMed.
- T. Baercor and P. M. Mayerfn, J. Am. Soc. Mass Spectrom., 1997, 8, 103–115 CrossRef.
- P. Pechukas and J. C. Light, J. Chem. Phys., 1965, 42, 3281–3291 CrossRef CAS.
- C. E. Klots, Z. Naturforsch., A, 1972, 27, 553 CAS.
- J. I. Steinfeld, J. S. Francisco and W. L. Hase, Chemical kinetics and dynamics, Prentice Hall, Upper Saddle River, NJ, 1999 Search PubMed.
- D. M. Wardlaw and R. Marcus, Chem. Phys. Lett., 1984, 110, 230–234 CrossRef CAS.
- W. L. Hase, Acc. Chem. Res., 1983, 16, 258–264 CrossRef CAS.
- R. G. Gilbert and S. C. Smith, Theory of unimolecular and recombination reactions, 1990 Search PubMed.
- J. L. Bao and D. G. Truhlar, Chem. Soc. Rev., 2017, 46, 7548–7596 RSC.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. Barbatti, J. Chem. Phys., 2022, 156, 204304 CrossRef CAS PubMed.
- M. A. Haney and J. Franklin, J. Chem. Phys., 1968, 48, 4093–4097 CrossRef CAS.
- K. Kim, J. Beynon and R. Cooks, J. Chem. Phys., 1974, 61, 1305–1314 CrossRef CAS.
- V. Ásgeirsson, C. A. Bauer and S. Grimme, Phys. Chem. Chem. Phys., 2016, 18, 31017–31026 RSC.
- J. H. Gross, Mass spectrometry: a textbook, Springer Science & Business Media, 2006 Search PubMed.
- M. Dantus, Acc. Chem. Res., 2024, 033003 Search PubMed.
- S. Grimme, Angew. Chem., Int. Ed., 2013, 52, 6306–6312 CrossRef CAS PubMed.
- J. Meisner and J. Kästner, Angew. Chem., Int. Ed., 2016, 55, 5400–5413 CrossRef CAS PubMed.
- J. Pu, J. Gao and D. G. Truhlar, Chem. Rev., 2006, 106, 3140–3169 CrossRef CAS PubMed.
- S. Wang, T. Kind, P. L. Bremer, D. J. Tantillo and O. Fiehn, J. Chem. Inf. Model., 2022, 62, 4403–4410 CrossRef CAS PubMed.
- Program package for the quantum mechanical calculation of EI mass spectra using automated reaction network exploration qcxms2, https://github.com/grimme-lab/QCxMS2, Accessed: 2025-1-20 Search PubMed.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker and C. Plett, et al. , J. Chem. Phys., 2024, 160, 114110 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- C. Bannwarth, E. Caldeweyher, S. Ehlert, A. Hansen, P. Pracht, J. Seibert, S. Spicher and S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 11, e01493 Search PubMed.
- N. van Staalduinen and C. Bannwarth, Digital Discovery, 2024, 3, 2298–2319 RSC.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- V. Ásgeirsson, B. O. Birgisson, R. Bjornsson, U. Becker, F. Neese, C. Riplinger and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 4929–4945 CrossRef PubMed.
- S. Smidstrup, A. Pedersen, K. Stokbro and H. Jónsson, J. Chem. Phys., 2014, 140, 214106 CrossRef PubMed.
- X. Zhu, K. C. Thompson and T. J. Martnez, J. Chem. Phys., 2019, 150, 164103 CrossRef PubMed.
- S. Spicher and S. Grimme, J. Chem. Theory Comput., 2021, 17, 1701–1714 CrossRef CAS PubMed.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- CREST – A program for the automated exploration of low-energy molecular chemical space, https://github.com/crest-lab/crest, Accessed: 2025-1-16 Search PubMed.
- A Molecular Identifier for Inorganic and Organic Molecules with Full Support of Stereoisomerism, https://git.rwth-aachen.de/bannwarthlab/molbar, Accessed: 2024-10-29 Search PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- Interpolation of molecular geometries through geodesics in redundant internal coordinate hyperspace for complex transformations, https://github.com/virtualzx-nad/geodesic-interpolate, Accessed: 2024-10-29 Search PubMed.
- Semiempirical Extended Tight-Binding Program Package xtb, https://github.com/grimme-lab/xtb, Accessed: 2024-10-29 Search PubMed.
- J. Koopman and S. Grimme, J. Am. Soc. Mass Spectrom., 2021, 32, 1735–1751 CrossRef CAS PubMed.
- Quantum mechanic mass spectrometry calculation program, https://github.com/qcxms, Accessed: 2024-10-29 Search PubMed.
- F. Huber, S. Verhoeven, C. Meijer, H. Spreeuw, E. M. V. Castilla, C. Geng, J. J. J. van der Hooft, S. Rogers, A. Belloum, F. Diblen and J. H. Spaaks, J. Open Source Software, 2020, 5, 2411 CrossRef.
- N. F. de Jonge, H. Hecht, M. Strobel, M. Wang, J. J. van der Hooft and F. Huber, J. Cheminf., 2024, 16, 88 Search PubMed.
- Python program package Matchms, https://github.com/matchms, Accessed: 2024-10-29 Search PubMed.
- Y. Li, T. Kind, J. Folz, A. Vaniya, S. S. Mehta and O. Fiehn, Nat. Methods, 2021, 18, 1524–1531 CrossRef CAS PubMed.
- Y. Li and O. Fiehn, Nat. Methods, 2023, 20, 1475–1478 CrossRef CAS PubMed.
- Spectral entropy for mass spectrometry data, https://github.com/YuanyueLi/MSEntropy, Accessed: 2024-10-29 Search PubMed.
- W. E. Wallace, in Mass Spectra, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, NIST Chemistry WebBook, Gaithersburg, MD, NIST Standard Reference Database Number 69, 2019. https://webbook.nist.gov, Accessed: October 24, 2024 Search PubMed.
- M. Müller, A. Hansen and S. Grimme, J. Chem. Phys., 2023, 158, 014103 CrossRef PubMed.
- S. Devata, H. J. Cleaves, J. Dimandja, C. A. Heist and M. Meringer, J. Am. Soc. Mass Spectrom., 2023, 34, 1584–1592 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: [Geometries in xyz format for all structures, as well as the computed spectra for the test set, can be found here: https://github.com/grimme-lab/QCxMS2-data/]. Additional details on the implementation, tests of different technical parameters, and computed spectra, which are not in the manuscript are provided in the file SI.pdf. See DOI: https://doi.org/10.1039/d5cp00316d |
| This journal is © the Owner Societies 2025 |