Elucidating molecular scale interactions underlying the freezing behavior of salt solutions in silica nanopores

Abstract

Elucidating the influence of nanoscale confinement on the freezing behavior of salt solutions is of fundamental interest to environmental security and materials science and engineering. Specific structural information such as the coordination environment of ions in confined aqueous medium, effects on the extended hexagonal network of water molecules and their mutual non-bonding interactions in confinement are sparse in the literature along with the change in the dynamical characteristics of water in the presence of ions. To address these knowledge gaps, the current study is focused on investigating the influence of reduced dimensionality arising from nanoscale confinement on the structural evolution of salt solutions on freezing and the associated fluid–surface interactions. In this regard, operando wide-angle X-ray scattering (WAXS) measurements and classical molecular dynamics (MD) simulations are conducted with water and 0.5 M CaCl₂, MgCl₂ and KCl solutions confined in 4 nm sized SBA-15 silica pores upon cooling from 300 K to 200 K. The freezing point of the salt solutions is depressed to 235 K which is about 10 K lower than that of confined water. The translational dynamics of confined salt solutions indicates shifts in the fragile-to-strong dynamical crossover to a lower temperature compared to pure water. The strong electrostatic attraction between the cations and the surrounding water molecules contributes to the freezing point depression in confined salt solutions. These insights unlock the molecular-scale basis and mechanisms underlying the freezing behavior of confined salt solutions.

---

1. Introduction

Unlocking fundamental mechanistic insights into the freezing behavior of nanoconfined aqueous solutions helps inform and advance environmental and climate security, thermodynamics and kinetics of unconventional freezing behavior in natural, engineered, and biological environments.^1–8 The bioengineering community leverages this potential for cryopreservation of tissues and organs,⁹ as well as for energy-efficient frozen food storage.¹⁰ Additionally, understanding ice formation below water saturation by airborne porous mineral dust is critical for addressing fundamental climatological questions.⁵ Furthermore, investigating the phase behavior of water in confinement is essential for advancing shale reservoir technologies.^11,12 Prior studies have investigated various approaches to freeze fluids including electrofreezing¹ and pressure-induced freezing,¹³ and have elucidated the freezing behavior of confined water.^5,14,15 However, the freezing behavior of salt solutions in nanoscale confinement remains less understood despite their ubiquitous nature in natural and engineered environments. Unlocking calibrated mechanistic insights into the freezing behavior of confined fluids is now possible due to advances in the synthesis of ordered nanoporous materials with tunable surface functionalities.^16–18 Although unambiguous experimental and computational evidence on the effect of reduced dimensionality on the properties of confined and interfacial water has emerged,^3,19–25 fundamental insights into the organization and dynamics associated with the freezing behavior of salt solutions remain an unaddressed knowledge gap.

It is well-known that water cooled below the freezing point exhibits anomalous physical properties and thermodynamic response functions such as isothermal compressibility²⁶ and heat capacity,²⁷ and the possibility of the existence of two liquids characterized by low and high densities, known as a low-density liquid (LDL) and a high-density liquid (HDL).²⁸ These liquids undergo structural transitions in a time scale of nanoseconds to microseconds and dynamical crossover from fragile to strong (FTS) structures under high pressures and/or low temperatures.^29,30 These unique characteristics have been established for high purity water in bulk and confined environments. However, the influence of dissolved metal ions on the structural and dynamical transitions in salt solutions in nanoscale confinement on freezing is not well understood. Therefore, the aim of this study is to elucidate the molecular scale mechanisms underlying the freezing behavior of salt solutions in nanoscale confinement.

Regarding the confinement effect, clear evidence of the reduced dimensionality-induced alterations in the freezing pathways of confined water has been established.^31,32 In this context, shifts in the freezing points^33–35 and the emergence of novel polymorphs and phases^36–38 are observed in reducing the dimensions of confining space to the range of intermolecular forces.³⁹ Furthermore, dynamical FTS crossover in water hosted in nanoscale confinement has been observed in the temperature range of 180–225 K in pore sizes of 1.4–5.5 nm.^40–43 This crossover is inferred from the relaxation time and diffusion coefficients in which the fragile and strong structures are described by Volger–Fulcher–Tamman (VFT) and Arrhenius behaviors, respectively. In addition, water confined in pores with diameters ∼2 nm exhibits two crossovers at 225 K and 175 K as revealed by ²H NMR measurements.^44,45

It has been shown that salt ions induce depression in the melting point of confined water with the depression magnitude increasing with the increase in salt concentrations.^46,47 Furthermore, confinement-driven heterogeneous crystallization of pore water results in salt enrichment in the remaining confined liquid, leading to local freezing point depression and coexistence of ice water interfaces in the pore space.⁴⁸ Although these findings are significant for elucidating the freezing thermodynamics of confined water, the following knowledge gaps and research questions still exist: (i) How and why do confinement and ions influence the structural evolution of ice polymorphs? (ii) What are the mechanisms underlying the influence of monovalent and divalent ions on the structural and dynamical transitions of supercooled water and ice polymorphs?

To address these knowledge gaps, we resolve the influence of 0.5 M CaCl₂, MgCl₂ and KCl solutions on the glassy to crystalline structural and dynamical crossover transitions of confined water in 4 nm sized SBA-15 silica nanopores on cooling from 300 K to 200 K using operando wide-angle X-ray scattering (WAXS) measurements and classical molecular dynamics (MD) simulations. Wide-angle X-ray scattering (WAXS) provides crucial insights into the structural organization of confined water, capturing long-range order and phase transitions by detecting changes in molecular packing and density fluctuations.^49,50 Complementarily, classical MD simulations offer a molecular-scale perspective, elucidating the underlying mechanisms governing structural and dynamical transformations by resolving hydrogen-bonding networks, translational mobility, phase behavior, and energetics.^51,52 The synergy between WAXS measurements and MD simulations provides mechanistic insights into the freezing behavior of salt solutions confined in nanopores by bridging experimental observations with atomistic interpretations.^53,54

2. Methods

2.1. Wide-angle X-ray scattering (WAXS) measurements

Operando WAXS measurements are performed on powders of porous SBA-15 silica particles with pore diameters of 4 nm loaded with pure water and 0.5 M CaCl₂, MgCl₂ and KCl solutions (see Fig. 1(a and c)). The silica powders are initially dried at 140 °C for 24 hours to remove the adsorbed water and impurities. The dried powder is then immersed in an excess amount of water and salt solutions for 24 hours in an isolated environment, allowing equilibration and the complete filling of the pores embedded in the SBA-15 particles. The particles are then filtered and heated to remove moisture.

Fig. 1 (a) Schematic representing the experimental setup for wide-angle X-ray scattering measurements including the characteristics of the incident beam, the studied sample environments, and the scattered beam detected on a 2D detector and converted to 1D intensity curves as a function of applied temperature. (b) Snapshot showing the initial configurations of confined water and salt solutions in 4 nm sized cylindrical silica nanopores used in molecular dynamics simulations. Silica and salt atoms are shown by the VDW drawing methods, while water molecules are shown in the licorice drawing method implemented in VMD visualization software. (c) Schematic showing the hexagonal structure of SBA-15 particles including the cylindrical pores embedded in the particle and the structure of the pore surface. (d) The temperature profile used in the MD simulations with an equilibration time of 30 ns at the temperatures used to probe the structure of confined liquids in the WAXS measurements.

The materials loaded with the solutions are packed in quartz capillaries with outer and inner diameters of about 1.5 mm and 1.2 mm, respectively. The capillaries are placed in the X-ray beamline instrument's sample environment and equilibrated at 300 K followed by subsequent cooling at 6 K min⁻¹ to 200 K using a liquid N₂ cryo-stream with temperature variations of <1 °C. To capture the temperature-dependent structural changes in the confined solutions, the data are collected at 300 K, 273 K, 265 K, 255 K, 245 K, 235 K, 225 K, 215 K and 200 K. The samples are equilibrated for 5 minutes at each temperature before data acquisition.

WAXS measurements are carried out at beamline 6-ID-D at the Advanced Photon Source (APS) in Argonne National Laboratory (ANL).⁵³ The wavelength of the incident X-ray beam is 0.142692 Å. The scattered X-ray photons are detected on Vartex CT4343 a-Si area detector with an active area of 2880 × 2880 pixels and a pixel size of 200 × 200 μm. The sample to detector distances used to measure the wide angle is about 400 mm. The instrument calibration for the WAXS measurements is performed using cerium dioxide calibrants. The WAXS is reduced using the NIKA⁴⁶ algorithm embedded in Igor software (WaveMetrics) and FIT2D software.⁵⁵ The scattered intensity at each temperature is plotted against the wavevector (Q) (where Q = (4π/λ)sin θ, λ is the X-ray wavelength, and θ is one-half of the scattering angle). Background from the quartz capillary filled with dried SBA-15 powder at each temperature is also acquired and subtracted from the sample-in-capillary intensity. The extracted intensity from FIT2D is used to calculate the pair distribution functions of confined water and emerged ice polymorphs using PDFgetX2 software.^55,56 Standard corrections for self-absorption, oblique incidence and detector efficiency are applied. Following the approach outlined by Egami & Billinge,⁵⁷ the total scattering structure function, S(Q), is Fourier-transformed into the real-space pair distribution function, G(r), according to eqn (1).

This transformation captures both Bragg and diffuse scattering, enabling the identification of emerging crystalline order, as evidenced by the sharpening of peaks in G(r).⁵⁸

2.2. Molecular dynamics simulations

MD simulations are performed on confined water and 0.5 M CaCl₂, MgCl₂ and KCl solutions in 4 nm sized silica nanopores with cylindrical geometry under the experimental temperature range of interest (see Fig. 1(b) and (d)). The nanopore coordinates are frozen in the simulations. The atomic structures of water and silica unit cells are constructed and optimized using density functional theory (DFT) calculations explained in our previous publications.^59,60 The optimized unit cells are replicated in x, y and z directions to create a surface in which pores with a diameter of 4 nm are cleaved. All the nonbridging oxygens on the surfaces of the cleaved pores are terminated with hydrogen and confirmed by reactive forcefields simulations (Fig. S1 and S2, ESI†). The pore is filled with water and salt solutions, to mimic the samples used in the experiments. Silica, water and ions are modeled using ClayFF,⁶¹ TIP5P,⁶² and OPLS/AA⁶³ forcefields, respectively (Table S1, ESI†), and the potentials are accounted for the bonded and nonbonded interactions. TIP5P water model has a melting point of about 274 K at 1 bar, which is consistent with the experimental melting point of water (273.15 K).⁶⁴

The pores loaded with the solutions are optimized using the steepest descent method for 50 000 steps and a force threshold of 100 kJ mol⁻¹ nm⁻¹ is used to eliminate the inappropriate geometries and optimize the positions of the initially randomly distributed water molecules and ions. Periodic simulated annealing with a constant number of atoms, constant volume and constant temperature (NVT) ensemble is performed on the optimized configurations for 290 ns in which 18 annealing points are used to control the applied temperatures on the different groups during the simulations. The temperature algorithm consists of initial equilibration at 300 K for 30 ns followed by systematic cooling to 200 K with 30 ns equilibrating time at 273 K, 265 K, 255 K, 245 K, 235 K, 225 K, 215 K and 200 K. The cooling rate between the equilibrium temperatures is about 6 K ns⁻¹, determined based on the commonly reported range in previous studies.^65–67 The temperature of the simulated systems is controlled using a Nosé–Hoover thermostat with a coupling constant of 0.1 ps.⁶⁸ The short-range interactions are calculated within a cutoff of 1.4 nm, and the long-range electrostatic interactions were treated using the particle mesh Ewald (PME) method.⁶⁹ During the MD simulations, bonded interactions are accounted for bond stretching (only OH bond stretching in silica pores), angle bending and dihedrals, while nonbonded interactions are calculated for van der Waals and electrostatic interactions. van der Waals and electrostatic interactions are modeled by Lennard-Jones and Coulomb interactions, respectively. The MD simulations are performed using the GROMACS 2020.6 code.⁷⁰

3. Results and discussion

3.1. Structural evolution of salt solutions in nanoscale confinement

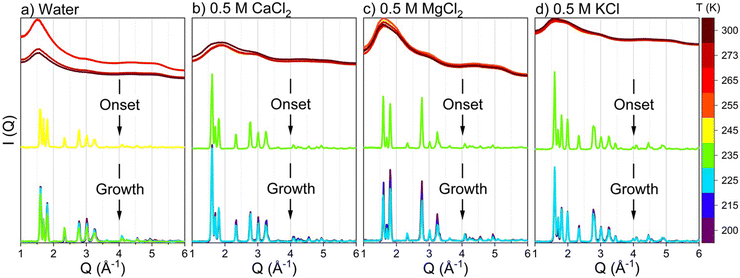
The structural evolution of ice is determined using operando WAXS measurements of confined water as a function of applied temperature which are obtained by converting the scattering pattern on the 2D detectors to intensity curves [I(Q)] plotted on the Q scale (see Fig. 2). At temperatures higher than the freezing point, the intensity curves suggest liquid-like structures of confined water and salt solutions, indicated by the absence of diffraction peaks from crystalline facets on the scattering curve. Diffraction peaks emerge at 245 K in confined pure water and at 235 K in confined salt solutions, indicating the onset of ice polymorphs. The positions of the diffraction peaks on the Q scale suggest that the formed ice phases have a hexagonal orientation.^71,72 Prominent peaks emerge at the positions of 1.60, 1.70, 1.82, 2.33, 2.78, 3.02, 3.25, 3.63, 4.08, 4.55 and 4.94 Å⁻¹. Interestingly, the onset temperature of CaCl₂, MgCl₂, and KCl solutions is similar (occurs at 235 K), suggesting similar effects for the monovalent and divalent ions on lowering the freezing point of confined water.

Fig. 2 The 1D intensity curves of the wide-angle X-ray scattering from (a) water, (b) 0.5 M CaCl₂, (c) 0.5 M MgCl₂ and (d) 0.5 M KCl solutions confined in 4 nm sized SBA-15 nanopores as a function of applied temperature on cooling the samples from 300 K to 200 K.

The crystallization onset of confined water and salt solutions is followed by the continuous growth of the emerged crystals, informed by the continuous increase of the intensities of the emerged peaks. The onset and growth of crystalline ice structures are also evident from the pair distribution function (D(r)), obtained from modeling the intensity curves (see Fig. 3). D(r) consists of O–O and O–H interactions of water molecules. The onset of long-ranged water structures occurs at 245 K in confined water while it shifts to 235 K in CaCl₂, MgCl₂ and KCl solutions. In the long range, multiple oxygen–oxygen coordination shells emerged, indicating the formation of hexagonal ice structures in the nanopores. The formation of hexagonal ice polymorphs in nanoscale confinement and the early onset of freezing in confined salt solutions are the defining features of the freezing behavior of salt solutions in nanoscale confinement.

Fig. 3 The pair distribution function of confined (a) water, (b) 0.5 M CaCl₂, (c) 0.5 M MgCl₂ and (d) 0.5 M KCl in 4 nm sized SBA-15 nanopores as a function of applied temperature, obtained from wide-angle X-ray scattering intensity curves. The scattering from capillaries loaded with dry silica powder is subtracted from the scattering from solution loaded capillaries at each temperature.

The local density profiles of water molecules provide evidence of ice formation. The local density profiles of water molecules along the axes normal to the pore length (z direction) and normal to the pore radius (x direction) obtained from MD simulations trajectories as a function of applied temperature are shown in Fig. 4. The density profile of confined water along the pore length (Fig. 4a–e) shows oscillation-free profiles at temperatures above 245 K for pure water and 235 K for salt solutions. The oscillations emerged in the density profiles followed by continuous growth as the temperature decreased to 200 K. The oscillations in the density profiles indicate the emergence of uniformly distributed crystalline structures in the pore space along the pore length. The onset of crystalline structures occurs at 245 K and 235 K in pure water and salt solutions, respectively, followed by the continuous growth of these oscillations as the temperature decreases to 200 K. The onset temperatures and the continuous oscillations in the density profiles are consistent with the onset and growth of crystalline ice peaks on the WAXS profiles and pair distribution functions (Fig. 2 and 3). The emerged structures at temperatures below the crystallization onset are also evident from the 2D density maps obtained from MD simulations (see Fig. 5). At 200 K, the 2D density maps averaged over the plane perpendicular to the pore length (yz plane) show that the emerged ice structure is dominated by hexagonal orientations. These hexagons are interconnected in confined water. In contrast, discontinuities in the hexagonal structure of water are noted in the presence of Ca²⁺, Mg²⁺ and K⁺ ions since the intermolecular hydrogen bonds between the water molecules are impacted by the ion–dipole interaction between the ions and water molecules.⁷³ Furthermore, the properties and behavior of liquid and adsorbed water, and heterogeneous crystallization of the confined water molecules (see Fig. S3, ESI†) are consistent with the prior studies.^74–79

Fig. 4 (a) A snapshot shows the yz plane (along the pore length) and (b)–(e) the obtained local water density along the pore length. (f) A snapshot shows the xy plane (along the pore diameter) and (g)–(j) the obtained local water density profiles along the pore diameter. The density profiles are calculated as a function of supplied temperature and averaged over the last 5 ns of each temperature segment in the MD simulation trajectory to ensure equilibrated profiles.

Fig. 5 Density maps of (a) water, (b) 0.5 M CaCl₂, (c) 0.5 MgCl₂ and (d) 0.5 M KCl at 200 K, obtained from the MD simulation trajectories. The 2D density maps are averaged over the last 5 ns of the simulation to ensure equilibrated water distribution. The dominant hexagonal structure of confined water is highlighted, and a snapshot of water hexagons and ion-induced discontinuity in the ice structure is added as insets to the density maps. Ca²⁺, Mg²⁺ and K⁺ ions are shown in green, blue and purple colors, respectively, in the embedded insets while oxygen and hydrogen atoms in the surrounding water are shown in red and white, respectively.

Interestingly, the structure of the interfacial water layer as represented by the first layer of water molecules on the pore surface has different structural characteristics compared to the rest of the pore water, indicated by the hydrogen bonding profile and radial distribution function between interfacial water molecules and hydroxyl groups on the pore surface (see Fig. S4 and S5, ESI†). The number of hydrogen bonds between interfacial water molecules and the hydroxyl group increased slightly as the temperature decreased in water and salt solutions. About 20% of the hydroxyl (OH) groups on the silica surface contributed to hydrogen bonding with interfacial water at 200 K (Fig. S4, ESI†). Furthermore, the number of oxygen atoms corresponding to water molecules in the first coordination shells of the OH groups on the silica surface increased slightly in confined water while remaining constant in the presence of salt ions as the temperature decreased (Fig. S5, ESI†). The distinct structure and interactions of interfacial water, informed by the radial distribution function and hydrogen bonding profiles with the surface hydroxyl groups on the pore surface, are consistent with the pre-melted nature of the interfacial water layer.^69,70

3.2. Influence of ions on the crossover transitions associated with the freezing behavior of confined salt solutions

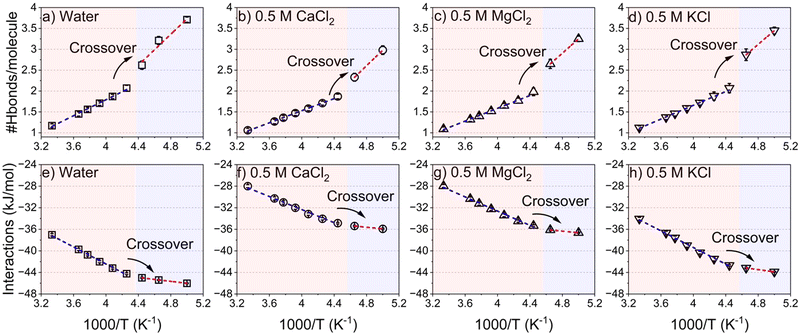
Insights into the freezing behavior of salt solutions in confinement are obtained by probing the translational mobility of water as a function of applied temperature (see Fig. 6).^28,74–76 The fragile to strong transition is characterized by analyzing the temperature dependence of the self-diffusion coefficient (D) of confined water in neat and salt solutions. ‘D’ follows a Vogel–Fulcher–Tammann (VFT) relation at high temperatures (low 1000/T regions) and transitions to Arrhenius-like behavior at low temperatures (high 1000/T regions). This behavior is evident from the translational diffusion of these fluids in confinement as noted in Fig. 6(a–d). The self-diffusion coefficients of confined water are calculated based on the mean square displacement (MSD), along the vector parallel to the pore length (z axis), as the length of the pore diameter is negligible compared to the infinite pore length stemming from the periodic boundary conditions used in the simulations (see Fig. S6, ESI†). The transition from a fragile to strong structure is observed as the log(1/D) values undergo a crossover from the VFT fitted profile to the Arrhenius fitted profile. This transition occurs at 1000/T = 4.3 K⁻¹ in confined pure water while it is depressed to 4.4 K⁻¹ in the presence of salt ions. This behavior is consistent with the evolution of the hydrogen bonding network and intermolecular interactions of the confined water and salt solutions (see Fig. 7). The normalized hydrogen bonds per water molecule increase linearly with the increase of the reciprocal of the temperature (1000/T). However, the slope of the hydrogen bonds profile differs based on the transitions from fragile to strong structures (see Fig. 7(a–d)). The slope of hydrogen bonding in the strong structure region (1000/T > 4.3 K⁻¹) is higher than that in fragile structures (1000/T < 4.3 K⁻¹). The shifts in the linear fitting of hydrogen bonding which increase with higher 1000/T values, align with the observed dynamical crossover (Fig. 6). The maximum number of hydrogen bonds per water molecule, which is about 4 in confined water, is reached at 5 K⁻¹, as also reported in studies on hydrogen bonding networks in confined environments.⁸⁰ In salt solutions, the number of hydrogen bonds per water molecule is lower due to the influence of dissolved ions. This observation can be further confirmed by the chaotropic versus kosmotropic definition of the ions offered by Collins.⁸¹ Chaotropic ions that are large but singly charged (i.e. low charge density) have minor effects on the local hydrogen bonding pattern of water whereas kosmotropic ions that are small but highly charged (i.e. high charge density) exhibit pronounced effects on the local hydrogen bonding in water due to strong electrostatic interactions between water dipoles and the ions.⁸²

Fig. 6 The logarithmic scales of (a)–(d) the reciprocal of the translational diffusion coefficient [log(1/D)] as a function of 1000/T. D is averaged over the last 5 ns of each temperature segment and calculated in the direction along the pore length. The data before and after the crossover regions are fitted using VFT and Arrhenius formula, respectively.

Fig. 7 The number of hydrogen bonds per water molecule in confined (a) water, (b) 0.5 M CaCl₂, (c) 0.5 M MgCl₂ and (d) 0.5 M KCl on the 1000/T scale. (e)–(h) The intermolecular interactions of water are averaged by the number of water molecules obtained from combining the van der Waals and electrostatic interactions on the 1000/T scale. The hydrogen bonds and the intermolecular interactions are averaged over the last 5 ns of each temperature segment to ensure equilibrated profiles.

Furthermore, the absolute values of the intermolecular interactions, combining van der Waals and electrostatic forces normalized per water molecule (Fig. 7(e–h)), increase with 1000/T. This indicates that the attraction between confined water molecules becomes stronger as the temperature decreases. Similar to the hydrogen bonding interactions, the slope of intermolecular interactions is different in the regions of fragile and strong structures, such that the slope in the fragile structure region is higher compared to the strong structure region. The crossover between the two regions shifted to a higher reciprocal of the temperature values in the presence of CaCl₂, MgCl₂ and KCl solutions compared to confined water. Therefore, the underlying dynamical transitions, hydrogen bonding and energetics provide insight into freezing point depression in confined salt solutions.

3.3. Influence of ion and water interactions on the freezing behavior of confined salt solutions

To resolve the origins of the extended depression in the structural and dynamical transitions in confined salt solutions, the interaction between the water molecules and the ions in the first coordination shell of the water molecules, and the intermolecular interactions between the ions and water molecules are analyzed. The number of oxygen atoms in the water molecules, O_water, in the first coordination shell of ions, is determined by integrating the radial distribution function of ions with respect to O_water (see Fig. 8 and Fig. S7, ESI†). Interestingly, the number of water molecules around divalent cations (i.e., Ca²⁺ and Mg²⁺ ions) and the associated Cl⁻ anions remain unchanged as the temperature decreases from 300 K to 200 K. The number of water molecules in the hydration shell of K⁺ is slightly increased by decreasing the temperature to 200 K, associated with a simultaneous decrease in the number of water molecules in the hydration shell of Cl⁻ ions at high temperatures. The number of water molecules in the hydration shells of Ca²⁺, Mg²⁺ and K⁺ ions is about 8, 6 and 5, respectively. The variation is dictated by ion size and charge density, where smaller, highly charged ions (Mg²⁺ and Ca²⁺) attract more tightly bound hydration shells than the larger, monovalent K⁺, consistent with the findings of previous studies.^68,83,84

Fig. 8 The number of water molecules in the first coordination shell of confined (a) cations and (b) anions and the corresponding van der Waals and electrostatic interactions (c) and (d) on the 1000/T scale. The number of water molecules in the first coordination shell of ions is obtained from the ions–O_water radial distribution function and the associated coordination number. The number of water molecules in the hydration shells of ions and the intermolecular interactions are averaged over the last 5 ns of each temperature segment to ensure equilibrated profiles.

The observed structure and density of the hydration shells of divalent ions in the temperature range of 300–200 K stem from the strong attractive electrostatic interactions between the ions and the water that undergo small changes upon cooling (Fig. 8(c) and (d)). As the temperature decreases, the strong electrostatic interactions of Ca²⁺ and Mg²⁺ ions and the associated Cl⁻ ions with the surrounding water molecules are preserved, while the electrostatic interactions of K⁺–water decrease slightly. Furthermore, the electrostatic interactions of divalent ions are 3–5 orders of magnitude higher than the interactions involving potassium or sodium ions and water molecules. The dominant electrostatic interactions between confined ions and the water molecules limit the reordering of the water molecules and result in a lower freezing point of confined salt solutions compared to confined water.

4. Conclusions

Salt-induced effects in the colligative properties of bulk and nanoconfined water encompass an extensively investigated topic of research. However, information on specific non-bonded interactions between water and different ions at varying temperatures is sparse in the literature. The dynamical characteristics of water in the presence of these ions also require in-depth research to facilitate several engineering applications. The current study focuses on filling these knowledge gaps. In this study, the molecular-scale basis underlying the freezing behavior of 0.5 M Mg-, Ca-, and K-chloride solutions confined in 4 nm pores is elucidated. The evolution in the crystallization behavior of the confined salt solutions, the underlying energetic interactions, and the ion–water interactions associated with the freezing point depression of confined salt solutions are discussed in the temperature range of 200–300 K using operando wide-angle X-ray scattering measurements and classical molecular dynamics simulations. Differences in the freezing behavior of interfacial water and water in the center of the pore are noted. Discontinuities in the hexagonal structure of water are noted in the presence of Ca²⁺, Mg²⁺ and K⁺ ions due to the influence of the ion–dipole interactions between the ions and the water molecules on the intermolecular hydrogen bonds. The onset of crystallization in the confined salt solutions decreased to 235 K from 245 K as observed in neat confined water. Less connectivity in the hexagonal structures of ice and hence a smaller number of intermolecular hydrogen bonds is observed in confined salt solutions compared to confined water due to ion induced disruptions to these structures. While the van der Waals interactions between the ions and water remain nearly constant as a function of temperature, a decrease in the electrostatic energy between Cl⁻ ions (KCl) and water is noted.

The overall enthalpy is, however, dominated by the large attractive electrostatic interactions between the cations and water, with small to moderate changes in temperature. The translational dynamics of confined water suggest a depression (1000/T = 4.3 K⁻¹ in confined pure water to 4.4 K⁻¹ in the presence of salt ions) in the temperature of dynamical crossover transition from a fragile to strong structure owing to the structure and dynamics of ion–water interactions in nanoscale confinement. The depression in the freezing point of confined salt solutions arises from the strong electrostatic interactions associated with crystallization. These findings unlock the quantitative molecular scale basis underlying the unconventional freezing behavior of salt solutions in natural, engineered, and biological environments.

Data availability

The data supporting this article have been included in the main manuscript and as part of the ESI.†

Conflicts of interest

There are no conflicts of interest to declare for this work.

Acknowledgements

This work was supported as part of the Multi-Scale Fluid–Solid Interactions in Architected and Natural Materials (MUSE), an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0019285. HEXRD measurements were made on the 6-ID-D beamline at the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by the Argonne National Laboratory under contract no. DE-AC02-06CH11357.

References

1. D. Ehre, E. Lavert, M. Lahav and I. Lubomirsky, Science, 2010, 327, 672–675.
2. L. G. M. Pettersson, R. H. Henchman and A. Nilsson, Chem. Rev., 2016, 116, 7459–7462.
3. A. Haji-Akbari, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3714–3716.
4. J. G. Dash, A. W. Rempel and J. S. Wettlaufer, Rev. Mod. Phys., 2006, 78, 695–741.
5. R. O. David, C. Marcolli, J. Fahrni, Y. Qiu, Y. A. Perez Sirkin, V. Molinero, F. Mahrt, D. Brühwiler, U. Lohmann and Z. A. Kanji, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8184–8189.
6. R. L. Kleinberg and D. D. Griffin, Cold Reg. Sci. Technol., 2005, 42, 63–77.
7. F. M. Etzler and P. J. White, J. Colloid Interface Sci., 1987, 120, 94–99.
8. Y. Fukatsu, K. Morikawa, Y. Ikeda and T. Tsukahara, Anal. Sci., 2017, 33, 903–909.
9. M. J. Taylor, B. P. Weegman, S. C. Baicu and S. E. Giwa, Transfus. Med. Hemother., 2019, 46, 197–215.
10. M. J. Powell-Palm and B. Rubinsky, J. Food Eng., 2019, 251, 1–10.
11. R. O. David, C. Marcolli, J. Fahrni, Y. Qiu, Y. A. Perez Sirkin, V. Molinero, F. Mahrt, D. Brühwiler, U. Lohmann and Z. A. Kanji, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8184–8189.
12. M. J. Powell-Palm, B. Rubinsky and W. Sun, Commun. Phys., 2020, 3, 39.
13. S. Klotz, K. Takemura, T. Strässle and T. Hansen, J. Phys.: Condens. Matter, 2012, 24, 325103.
14. S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Chem. Rev., 2016, 116, 7608–7625.
15. J. Jiang, Y. Gao, W. Zhu, Y. Liu, C. Zhu, J. S. Francisco and X. C. Zeng, J. Am. Chem. Soc., 2021, 143, 8177–8183.
16. M. E. Davis, Nature, 2002, 417, 813–821.
17. M. L. K. Hoa, M. Lu and Y. Zhang, Adv. Colloid Interface Sci., 2006, 121, 9–23.
18. O. D. Velev and A. M. Lenhoff, Curr. Opin. Colloid Interface Sci., 2000, 5, 56–63.
19. H. Weiss, H.-W. Cheng, J. Mars, H. Li, C. Merola, F. U. Renner, V. Honkimäki, M. Valtiner and M. Mezger, Langmuir, 2019, 35, 16679–16692.
20. S. Han, M. Y. Choi, P. Kumar and H. E. Stanley, Nat. Phys., 2010, 6, 685–689.
21. L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342.
22. H. Xue, Y. Fu, Y. Lu, D. Hao, K. Li, G. Bai, Z.-C. Ou-Yang, J. Wang and X. Zhou, J. Am. Chem. Soc., 2021, 143, 13548–13556.
23. S. Hussain and A. Haji-Akbari, J. Am. Chem. Soc., 2021, 143, 2272–2284.
24. A. K. Metya and V. Molinero, J. Am. Chem. Soc., 2021, 143, 4607–4624.
25. D. N. Sibley, P. Llombart, E. G. Noya, A. J. Archer and L. G. MacDowell, Nat. Commun., 2021, 12, 239.
26. R. J. Speedy and C. A. Angell, J. Chem. Phys., 1976, 65, 851–858.
27. C. A. Angell, W. J. Sichina and M. Oguni, J. Phys. Chem., 1982, 86, 998–1002.
28. J. A. Sellberg, C. Huang, T. A. McQueen, N. D. Loh, H. Laksmono, D. Schlesinger, R. G. Sierra, D. Nordlund, C. Y. Hampton, D. Starodub, D. P. DePonte, M. Beye, C. Chen, A. V. Martin, A. Barty, K. T. Wikfeldt, T. M. Weiss, C. Caronna, J. Feldkamp, L. B. Skinner, M. M. Seibert, M. Messerschmidt, G. J. Williams, S. Boutet, L. G. M. Pettersson, M. J. Bogan and A. Nilsson, Nature, 2014, 510, 381–384.
29. K. H. Kim, K. Amann-Winkel, N. Giovambattista, A. Späh, F. Perakis, H. Pathak, M. L. Parada, C. Yang, D. Mariedahl, T. Eklund, T. J. Lane, S. You, S. Jeong, M. Weston, J. H. Lee, I. Eom, M. Kim, J. Park, S. H. Chun, P. H. Poole and A. Nilsson, Science, 2020, 370, 978–982.
30. R. Shi, J. Russo and H. Tanaka, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 9444–9449.
31. S. Mohammed, H. Asgar, C. J. Benmore and G. Gadikota, Phys. Chem. Chem. Phys., 2021, 23, 12706–12717.
32. S. Mohammed, H. Asgar, M. Deo and G. Gadikota, Energy Fuels, 2021, 35, 4687–4710.
33. K. Morishige, J. Phys. Chem. C, 2018, 122, 5013–5019.
34. S. Jähnert, F. Vaca Chávez, G. E. Schaumann, A. Schreiber, M. Schönhoff and G. H. Findenegg, Phys. Chem. Chem. Phys., 2008, 10, 6039.
35. Y. Xia, H. Cho, M. Deo, S. H. Risbud, M. H. Bartl and S. Sen, Sci. Rep., 2020, 10, 5327.
36. W.-H. Zhao, L. Wang, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Acc. Chem. Res., 2014, 47, 2505–2513.
37. M. V. Jyothirmai, B. M. Abraham and J. K. Singh, Phys. Chem. Chem. Phys., 2022, 24, 16647–16654.
38. M. Jazdzewska, M. M. Śliwinska-Bartkowiak, A. I. Beskrovnyy, S. G. Vasilovskiy, S. W. Ting, K.-Y. Chan, L. Huang and K. E. Gubbins, Phys. Chem. Chem. Phys., 2011, 13, 9008.
39. F. G. Alabarse, J. Haines, O. Cambon, C. Levelut, D. Bourgogne, A. Haidoux, D. Granier and B. Coasne, Phys. Rev. Lett., 2012, 109, 035701.
40. A. Faraone, L. Liu, C.-Y. Mou, C.-W. Yen and S.-H. Chen, J. Chem. Phys., 2004, 121, 10843–10846.
41. F. Mallamace, M. Broccio, C. Corsaro, A. Faraone, D. Majolino, V. Venuti, L. Liu, C.-Y. Mou and S.-H. Chen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 424–428.
42. F. Bruni, R. Mancinelli and M. A. Ricci, Phys. Chem. Chem. Phys., 2011, 13, 19773.
43. P. Gallo, M. Rovere and E. Spohr, J. Chem. Phys., 2000, 113, 11324–11335.
44. M. Sattig and M. Vogel, J. Phys. Chem. Lett., 2014, 5, 174–178.
45. M. Sattig, S. Reutter, F. Fujara, M. Werner, G. Buntkowsky and M. Vogel, Phys. Chem. Chem. Phys., 2014, 16, 19229–19240.
46. J. Ilavsky, J. Appl. Crystallogr., 2012, 45, 324–328.
47. E. Jantsch, C. Weinberger, M. Tiemann and T. Koop, J. Phys. Chem. C, 2019, 123, 24566–24574.
48. F. Ginot, T. Lenavetier, D. Dedovets and S. Deville, Appl. Phys. Lett., 2020, 116, 253701.
49. M. Erko, D. Wallacher, A. Hoell, T. Hauss, I. Zizak and O. Paris, Phys. Chem. Chem. Phys., 2012, 14, 3852–3858.
50. M. Cammarata, M. Levantino, A. Cupane, A. Longo, A. Martorana and F. Bruni, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 12, 63–66.
51. S. Chakraborty, H. Kumar, C. Dasgupta and P. K. Maiti, Acc. Chem. Res., 2017, 50, 2139–2146.
52. P. Hirunsit and P. B. Balbuena, J. Phys. Chem. C, 2007, 111, 1709–1715.
53. E. Shalaev and A. K. Soper, J. Phys. Chem. B, 2016, 120, 7289–7296.
54. C. J. Benmore, O. L. G. Alderman, D. Robinson, G. Jennings, A. Tamalonis, J. Ilavsky, E. Clark, E. Soignard, J. L. Yarger and J. K. R. Weber, Nucl. Instrum. Methods Phys. Res., Sect. A, 2020, 955, 163318.
55. D. A. Keen, J. Appl. Crystallogr., 2001, 34, 172–177.
56. X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37, 678.
57. T. Egami and S. J. L. Billinge, Underneath the Bragg Peaks: Structural Analysis of Complex Materials, Elsevier, Amsterdam, 2003, vol. 16.
58. S. J. L. Billinge and M. G. Kanatzidis, Chem. Commun., 2004, 749–760.
59. S. Mohammed, H. Asgar, C. J. Benmore and G. Gadikota, Phys. Chem. Chem. Phys., 2021, 23, 12706–12717.
60. S. Mohammed, M. Liu and G. Gadikota, Environ. Sci.: Nano, 2021, 8, 2006–2018.
61. R. T. Cygan, J.-J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266.
62. M. W. Mahoney and W. L. Jorgensen, J. Chem. Phys., 2000, 112, 8910–8922.
63. W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670.
64. C. Vega, E. Sanz and J. L. F. Abascal, J. Chem. Phys., 2005, 122, 114507.
65. N. Pingua and A. K. Gautam, Mater. Today Commun., 2024, 39, 108777.
66. Z. Wang, Y. Zhou, Y. Feng, J. Zhang, R. Yu and Z. Yu, J. Am. Ceram. Soc., 2024, jace.20047.
67. A. Eltareb, G. E. Lopez and N. Giovambattista, Commun. Chem., 2024, 7, 36.
68. D. J. Evans and B. L. Holian, J. Chem. Phys., 1985, 83, 4069–4074.
69. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092.
70. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25.
71. M. Ladd-Parada, K. Amann-Winkel, K. H. Kim, A. Späh, F. Perakis, H. Pathak, C. Yang, D. Mariedahl, T. Eklund, T. J. Lane, S. You, S. Jeong, M. Weston, J. H. Lee, I. Eom, M. Kim, J. Park, S. H. Chun and A. Nilsson, J. Phys. Chem. B, 2022, 126, 2299–2307.
72. M. Thangswamy, P. Maheshwari, D. Dutta, A. K. Bera, M. N. Singh, A. K. Sinha, S. M. Yusuf and P. K. Pujari, Phys. Chem. Chem. Phys., 2020, 22, 14309–14317.
73. B. Hribar, N. T. Southall, V. Vlachy and K. A. Dill, J. Am. Chem. Soc., 2002, 124, 12302–12311.
74. Q. Zeng, K. Li and T. Fen-Chong, J. Cryst. Growth, 2015, 409, 1–9.
75. Y. Suzuki, M. Steinhart, H.-J. Butt and G. Floudas, J. Phys. Chem. B, 2015, 119, 11960–11966.
76. Y. Bi, B. Cao and T. Li, Nat. Commun., 2017, 8, 15372.
77. C. Li, R. Tao, S. Luo, X. Gao, K. Zhang and Z. Li, J. Phys. Chem. C, 2018, 122, 25992–25998.
78. S. Nakao and T. Nakano, J. Mater. Sci., 2011, 46, 4748–4755.
79. T. Kikuchi, K. Nakajima, S. Ohira-Kawamura, Y. Inamura, O. Yamamuro, M. Kofu, Y. Kawakita, K. Suzuya, M. Nakamura and M. Arai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062314.
80. W.-H. Zhao, J. Bai, L.-F. Yuan, J. Yang and X. C. Zeng, Chem. Sci., 2014, 5, 1757–1764.
81. K. D. Collins, Biophys. J., 1997, 72, 65–76.
82. N. V. Nucci and J. M. Vanderkooi, J. Mol. Liq., 2008, 143, 160–170.
83. M. P. Andersson and S. L. S. Stipp, J. Comput. Chem., 2014, 35, 2070–2075.
84. W. Zhao, Y. Sun, W. Zhu, J. Jiang, X. Zhao, D. Lin, W. Xu, X. Duan, J. S. Francisco and X. C. Zeng, Nat. Commun., 2021, 12, 5602.

---

Footnote

† Electronic supplementary information (ESI) available: A detailed description of the methods (Fig. S1 and S2 and Table S1) and supplementary data supporting the finding of the paper, including the 2D density maps showing heterogeneous water crystallization (Fig. S3), water–OH silica hydrogen bonding along with the total energy and temperature of the system (Fig. S4), radial distribution function of OH on the pore surface with water oxygen (Fig. S5), mean square displacement of water (Fig. S6), and ion–water interactions by radial distribution function profiles (Fig. S7). See DOI: https://doi.org/10.1039/d4cp04622f

---