 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Peculiarities in structural behaviour of graphite during anionic intercalation of PF6−, FSI− and ClO4− at elevated temperature†
Mikhail V.
Gorbunov
 * and
Daria
Mikhailova
* and
Daria
Mikhailova

Leibniz Institute for Solid State and Materials Research (IFW Dresden), Helmholtzstraße 20, 01069, Dresden, Germany. E-mail: m.gorbunov@ifw-dresden.de
First published on 4th March 2025
Abstract
Anionic intercalation into graphite is strongly temperature-dependent. At 333 K, it stops being a sequential process for PF6− and FSI− species, mainly proposed for dual-ion batteries, whereas for ClO4−, no mechanism change is visible from operando XRD. These phenomena might represent one of the critical limitations for dual-graphite systems.
Lithium-ion batteries have been dominating the market of energy solutions for portative electronics since their commercialisation in the 1990's due to their unmatched specific characteristics, negligibly low self-discharge and minimal requirements in terms of maintenance.1 Over the last few decades, rather ambitious steps were made to apply LIBs in hybrid and electric vehicles.2,3 However, certain limitations exist, such as insufficient amount of lithium in the Earth's crust to fulfil all the needs.4 Besides, typical LIB cathodes are usually layered oxides containing 3d elements (LiCoO2, Li(Ni,Mn,Co)O2) or lithium polyanionic compounds (LiFePO4). These mixtures of various chemical elements may be difficult to separate during recycling.5 Many efforts with significant success have been made in the fields of alternative intercalation systems, such as sodium- and potassium-ion batteries. Although inferior in characteristics, they might potentially find their application in large scale electrochemical energy storage, such as the smart-grid concept, where the values of specific capacity, power and energy density are less relevant.4,6 Nevertheless, this topic still has space for improvement.
Another option of reducing the lithium (and 3d elements) usage is to apply graphite, a typical LIB anode material,1 also on the cathode side, benefitting from anionic intercalation, while on the anode, well-known intercalation of cations would occur. The concept is known as a dual-graphite (dual-ion) battery and was proposed in the late 1980's and continuously studied in the 1990's.7–9 The pivoting point for dual-ion systems with lithium salts was the work of Seel and Dahn,10 who demonstrated and explained the reversible electrochemical intercalation of hexafluorophosphate (PF6−) anions into graphite. Since then, various electrochemical systems based on the same principle (Fig. 1a) have been intensively studied, targeting the improvement of their cycling performance.11–15 Such fundamental drawbacks as high potential of anionic intercalation may be avoided by the use of super-concentrated electrolytes. Dramatic increase of the salt concentration would shift the electrochemical potential to lower values, following the well-known Nernst equation.10,11 Many scientific works are focused on the enhancement of specific characteristics delivered by dual-ion cells, also based on other cations like Na or K, in order to make them competitive to currently existing LIBs.11,12 The most impressive specific capacities are reported for PF6− and FSI− anions as well as their mixture, which exceed values of 90 mA h g−1 with an average discharge voltage over 4.5 V vs. alkali metals. However, certain scientific cases are lacking attention. One of them is anionic intercalation beyond room temperature. Low temperatures can be a limiting factor for super-concentrated electrolytes, since they are usually formed on the verge of the solubility limit for the corresponding salts.14,15 Elevated temperatures might also lead to changes in the structural behaviour of graphite during intercalation, as it was shown for cations at low potentials.16 In certain cases, such changes may reduce the performance of the system and limit its practical applicability. Also, solvent decomposition and corrosion of the cathodic current collector at high potentials17 would contribute stronger to battery degradation. The case of elevated temperatures was addressed in our work. We performed a comparative evaluation of bulk structural changes occurring in graphite during intercalation of PF6− and FSI− as the most promising anions in terms of battery-related parameters,14,15 and ClO4−, which was studied in aqueous dual-ion systems.18 Previously, a different temperature behaviour of TFSI− anions was comprehensively studied by Placke et al., as an interesting alternative.19,20 In that case, temperature elevation improved the specific characteristics of the electrochemical cell: 80 mA h g−1 at 293 K vs. almost 120 mA h g−1 at 333 K. As shown by operando XRD, at 293 K, the reversible intercalation of TFSI− into graphite proceeded to stage 3, whereas at 333 K, the process ended at stage 2.20 Note that in our work, we calculate the stage number n differently, using the original equation:10
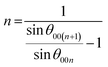 | (1) |
di = d00n·n − (n − 1)d002![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) graphite graphite | (2) |
 | ||
| Fig. 1 (a) Dual-ion battery operation principle,7 (b) a simplified image of intercalation stage 2 in graphite, and (c) typical galvanostatic charge–discharge curves of graphite as a cathode in lithium half-cells with 4 M LiPF6/DMC electrolyte. The applied current density was 40 mA g−1. | ||
Powder X-ray diffractograms obtained operando during anionic intercalation are presented in Fig. 2. All the corresponding parameters calculated from eqn (1) and (2) are listed in Table 1 together with the literature data. At room temperature, PF6− and FSI− species may be reversibly inserted between graphitic layers up to stage 2, in agreement with earlier reports.10,13 Intercalation of ClO4− proceeds only to stage 3; however, we did not evaluate the behaviour of this system at sufficiently high potentials, since beginning from about 4.85 V vs. lithium, pronounced corrosion of the cell cases in the presence of ClO4− occurs,21 causing enormous values of irreversible capacity (Fig. S1e and f, ESI†). Protective covering of the cathodic side of the cells by a nanolayer of titanium (see the ESI†) could not eliminate this issue. Electrochemical insertion of anions at room temperature represents a sequential staging process for all the studied anionic species: only after a certain intercalation stage n is formed, the next, n − 1, appears. Elevation of temperature to 333 K causes a dramatic difference in the structural behaviour of graphite. For PF6− and FSI−, the intercalation process is not sequential anymore. Instead, stage 3 and another one with a lower number are observed simultaneously, with (00n) reflection of the latter continuously growing in intensity, even when the cells are discharging. Intercalation to stage 3, however, remains reversible. If we calculate the stage number for FSI− at the end of charge at 333 K, we will obtain a value of 1.75 and an intercalant gallery height of 4.641 Å. For PF6−, the (00n + 1) reflection in the fully charged state is not observed, and the intercalant gallery height gets even larger: 4.892 Å.
 | ||
| Fig. 2 Part of the X-ray diffractograms obtained operando during electrochemical intercalation of PF6−, FSI−, and ClO4−, respectively, at (a)–(c) room and (d)–(f) elevated temperature. For FSI− at 298 K (b), intercalations to stages 3 and 2 are shown separately due to a beam dump. For ClO4− at 333 K (f), multiple cycles are demonstrated. Corresponding galvanostatic charge–discharge curves are available in the ESI† (Fig. S1). Asterisks in panel e are pointing to irreversible formation of intermediate intercalation stages with high n values. | ||
| Anion | R A, Å | d 00n298, Å | d 00n298, Å (lit.) | d i 298, Å | d 00n333, Å | d 00n333, Å (lit.) | d i333, Å | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n (integer) → | 3 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | 2 | 3 | MIC | |
| PF6− | 2.540 | 3.734 | 3.896 | 3.745 | 3.910 | 4.488 | 4.434 | 3.706 | 4.132 | — | — | 4.376 | 4.892 |
| FSI− | 2.831 | 3.729 | 3.911 | 3.704 | 3.90 | 4.472 | 4.465 | 3.727 | 4.007 | — | — | 4.438 | 4.641 |
| ClO4− | 2.360 | 3.686 | — | — | — | 4.342 | — | 3.655 | — | — | — | 4.222 | — |
| TFSI− | 3.274 | — | — | 3.770 | — | 4.680 | — | — | — | 3.770 | 3.985 | 4.610 | 4.640 |
To our knowledge, there has been no direct confirmation of the impossibility for anionic intercalation to proceed beyond stage 2. In ref. 20, it has been clearly shown that temperature elevation can make the lower stages achievable. A non-integer stage number corresponds to compounds in which filled galleries can be spaced by a varying number of empty galleries.10 For non-integer numbers being the lowest, we may introduce the term of maximal intercalant concentration stage (MIC). Thus, we assume that at 333 K, the MIC stage for FSI− anions is 1.75 (Fig. S2, ESI†), and vanishing (00n + 1) reflection for PF6− might indicate stage 1, with di = d00n. Also noteworthy is that two intercalation mechanisms are generally known for layered host compounds. One is already mentioned staging: a sequential filling of every nth layer, the second is a statistical filling of every interlayer space. Growth of the reflection assigned to MIC can correspond to the latter for PF6− anions.
Certainly, we should analyse other possible reasons that could lead to the increasing average interlayer spacings. The solubilities of LiPF6 and LiFSI in DMC rise with the temperature.23,24 Assuming a rather improbable case with evaporation of electrolyte solvents at elevated temperatures and salt crystallisation would not provide such strong Bragg reflections at the given 2θ angles.25,26 Another possibility could be related to solvent co-intercalation. This case was reported by Read for PF6− species in EMC (ethyl methyl carbonate).27 DMC molecules, used in our experiments, have a smaller size and the same functional group. Thus, they could be inserted into graphite. General chemical considerations are, however, against co-intercalation of DMC: a partial negative charge δ− on the functional group should be repulsed by already intercalated PF6−, which can be represented as octahedra with negative charges on their apices. Additionally, DMC is present in all the electrolytes we used in our experiment, and no changes to the intercalation manner of ClO4− with temperature were observed. Lastly, we conducted the same experiment at 333 K with ethyl methyl sulfone (EMS) serving as a solvent, and evidenced occurrence of the same reflection for PF6− anions (Fig. S3, ESI†). At the end, we assume these constantly growing reflections corresponding to the maximal intercalant concentration in graphite accessible at the given conditions, since they only increase in intensity, but do not shift to higher or lower angles.
The values of interlayer spacing for the corresponding stages of PF6− intercalation at 298 K obtained in the current work are slightly lower than that in the literature, even though the interlayer spacing of KS6L graphite chosen for our study is slightly higher: 3.371 Å vs. 3.35 Å from the articles cited.10,20 This can be explained by the fact that we applied a relatively high current density during cycling, in order to reduce the impact of parasitic electrochemical reactions. Therefore, the stages with integer numbers may have not formed completely. For FSI− species, however, our values are slightly higher. We do not present the reference values for ClO4− intercalation, since according to one of a few reports, it either proceeded only to high stages, or co-intercalation was proposed in the case of γ-butyrolactone used as a solvent.28 Also, in aqueous ClO4− electrolytes,18 the latter would be more probable due to the small size of H2O molecules.
Accumulation of the electrochemically inactive phase with the maximal intercalant concentration seems to be the main reason for the high irreversible capacities of cells with PF6− and FSI− species at 333 K, and this phenomenon in general might be one of the critical limiting factors for dual-ion batteries. Certainly, at elevated temperatures, electrolyte decomposition and corrosion of current collectors should have stronger impacts as well, but if we compare the shapes of the charge curves for LiPF6- and LiFSI-based cells at 298 and 333 K (Fig. 1 and Fig. S1, ESI†), we will not see a big difference. Only the quantity of intercalated anions and cell polarisation decrease, indicating the kinetic effect, which complicates the process at lower temperatures: the activation barrier for anion migration between graphene layers increases at nearly filled stages, similarly to the LiTFSI system20,29 and in agreement with the Daumas–Hérold staging model.30 However, diffusion of PF6− seems to be a much less kinetically hindered process than that of the TFSI− anion: at room temperature, the experimental values of apparent diffusion coefficients are multiple orders of magnitude higher giving a value between 10−12 and 10−11 cm2 s−1 (ref. 31) vs. a value of 3 × 10−15 cm2 s−1.29 This should be directly related to the lower van der Waals radius of PF6−. However, it is important to keep in mind that the correlation between van der Waals radii of anions and their gallery heights is not direct, which can be explained by their chemical nature: while PF6− represents a regular octahedron with no rotational degrees of freedom for chemical bonds, FSI− and TFSI− may be considered as flat, “foldable” anions due to the presence of singular S–N and S–C bonds. Nevertheless, a similar effect to that described in ref. 29 can be assumed: when the amount of PF6− in graphite corresponding to stages 3 and 2 is almost approached, the D(PF6−) value also drops quickly (see Fig. 3). Although in this experiment we used sulfone-based electrolyte, movement of anions between graphene layers can be considered as the limiting stage. Therefore, the apparent diffusion coefficient values should not depend much on the electrolyte solvent. Summarising our operando XRD results and the data for LiPF6-based electrochemical cells, we assume that the anionic intercalation in this system has a lower temperature window of optimal operation than in the LiTFSI-based one. If the temperature is too high, irreversible intercalation occurs, resulting in poor specific characteristics and a low coulombic efficiency. The same can be related to the LiFSI-based system, which behaves similarly. Successful GITT experiments for intercalation of FSI− are not available in the literature, probably due to its high corrosive nature for the current collectors.
 | ||
| Fig. 3 Experimentally obtained values of apparent diffusion coefficient for PF6− intercalation using EMS-based electrolyte. | ||
We should also consider the difference in diffusion paths, proposed by theoretical calculations for intercalation of the discussed anionic species into graphite. Such studies32 propose two main crystallographic directions for the diffusion, namely (100) and (110). It is peculiar that the lowest diffusion barriers calculated for FSI− and PF6− species correspond to the (110) plane, whereas for ClO4− and TFSI−, the preferred direction is (100). Our experiment and ref. 20 show that temperature elevation to 333 K positively influences the latter, whereas the effect is completely opposite for (110) diffusion. However, we cannot establish any correlation between predicted activation barriers for diffusion of the named species in graphite interlayers and uptake ability of the graphite. Evenly complicated is the temperature impact on the structural behaviour of graphite. Thus, the highest barrier is calculated for PF6−, whereas the lowest value is predicted for ClO4−,32 which, however, did not intercalate beyond stage 3 neither in our experiment or in other reports.18,28 Based on the above mentioned, we can presume that diffusion paths for anionic intercalation represent one of the key factors defining the optimal operation temperature of a dual-ion cell with a graphitic cathode. Probably, further temperature elevation would also allow the intercalation of ClO4− to lower stages; however, the corrosion issues must be overcome. For example, the use of gel-polymer electrolytes might be a solution for this case.
Financial support was done by DFG project 448719339 (KIBSS).
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Notes and references
- T. Kim, et al. , J. Mater. Chem. A, 2019, 7, 2942 RSC.
- J. B. Goodenough, et al., J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- A. Bilich, et al. , Environ. Sci. Technol., 2017, 51, 1043–1052 Search PubMed.
- J.-Y. Hwang, et al., Chem. Soc. Rev., 2017, 46, 3529–3614 RSC.
- Z. Dobó, et al., Energy Rep., 2023, 9, 6362–6395 CrossRef.
- X. Min, et al. , Energy Environ. Sci., 2021, 14, 2186 RSC.
- F. P. McCullough, A. Levine and R. V. Snelgrove, US Pat., 4830938, 1989 Search PubMed.
- R. T. Carlin, et al. , J. Electrochem. Soc., 1994, 141, 73 CrossRef.
- R. Santhanam, J. Power Sources, 1998, 76, 147 CrossRef CAS.
- J. A. Seel, J. Electrochem. Soc., 2000, 147, 892–898 CrossRef CAS.
- L. Xiang, et al. , Angew. Chem., Int. Ed., 2020, 59, 17924–17930 CrossRef CAS PubMed.
- M. H. Sheng, et al. , Adv. Energy Mater., 2017, 7, 1601963 CrossRef.
- X. Ding, et al. , ACS Appl. Mater. Interfaces, 2018, 49, 42294–42300 CrossRef PubMed.
- D. Sabaghi, et al. , J. Power Sources, 2023, 588, 233685 CrossRef CAS.
- K. V. Kravchyk, et al. , Nat. Commun., 2018, 9, 4469 CrossRef PubMed.
- C. Schmitt, et al. , ChemElectroChem, 2022, 9, 43–51 Search PubMed.
- P. Meister, et al. , ChemSusChem, 2017, 10, 804–814 CrossRef CAS PubMed.
- Z. A. Zafar, et al. , J. Mater. Chem. A, 2022, 10, 2064 Search PubMed.
- T. Placke, et al. , J. Electrochem. Soc., 2012, 159, A1755–A1765 Search PubMed.
- G. Schmuelling, et al. , J. Power Sources, 2013, 239, 563–571 CrossRef CAS.
- H. Prinz, et al., Corros. Sci., 1998, 40, 1671–1683 CrossRef CAS.
- H.-B. Han, et al. , J. Power Sources, 2011, 196, 3623–3632 CrossRef CAS.
- N. Xin, et al. , Fluid Phase Equilib., 2018, 461, 1–7 CrossRef CAS.
- X. Fang, et al. , J. Chem. Thermodyn., 2024, 191, 107245 CrossRef CAS.
- L. Askelrud, et al. , Mater. Sci. Forum, 1993, 133, 335 Search PubMed.
- M. Beran, et al. , Polyhedron, 2006, 25, 1292–1298 CrossRef CAS.
- J. A. Read, J. Phys. Chem. C, 2015, 119, 8438–8446 CrossRef CAS.
- J. Gao, et al. , El. Acta, 2015, 176, 22–27 CrossRef CAS.
- A. Heckmann, et al. , El. Acta, 2018, 284, 669–680 CrossRef CAS.
- N. Daumas, et al., C. R. Seances Acad. Sci., Ser. A, 1969, 268, 373–380 CAS.
- S. Miyoshi, et al. , J. Phys. Chem. C, 2016, 120, 22887–22894 CrossRef CAS.
- M. Chugh, et al. , Mater. Res. Express, 2021, 8, 085502 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Description of the experimental procedures, galvanostatic charge–discharge curves corresponding to the operando XRD experiment, a few important notes and acknowledgements of the used specific equipment. See DOI: https://doi.org/10.1039/d5cc00366k |
| This journal is © The Royal Society of Chemistry 2025 |
