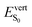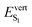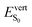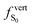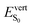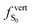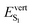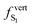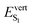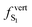Modeling of pressure-induced charge transfer character in piezoluminescent pyridylvinylanthracene crystals

Abstract

Mechanoluminescent (ML) materials show color changes resulting from the application of a mechanical constraint such as an external pressure. In these systems, the applied pressure might alter the structure of the molecular units and their supramolecular packing, which translates into changes in emission wavelength and intensity. In this work, we report a computational study of the ML properties of the recently synthesized 9,10-bis((E)-2-(pyrid-2-yl)vinyl)anthracene (BP2VA) crystal. In a previous experimental report, the BP2VA crystal powder has been shown to undergo drastic changes in photoluminescence color upon exertion of external pressure. The evolution of the piezochromic luminescence upon increasing pressure was rationalized by comparison to the emission behavior of the three BP2VA crystal polymorphs, which are characterized by distinct stacking modes, each exhibiting varying strengths of π–π interactions. Combining periodic calculations based on density functional theory (DFT) and time-dependent DFT within a hybrid QM/MM scheme to account for crystal environment effects, we explored the structural and optical features of the BP2VA polymorphs and examined the changes in supramolecular arrangement and luminescence associated with the application of pressure. Decomposition of the electronic excited states of relevant dimers extracted from the optimized crystal cells on a diabatic basis allowed to characterize the electronic transitions according to their local and charge transfer (CT) nature. The results, which overall compare well to experimental data, provide a new mechanistic picture behind the piezochromic behavior of organic crystals. While intermolecular interactions and structural constraints play a crucial role in the photophysical properties of these materials, we demonstrate that external pressure can alter the nature of the low-lying excited states, notably imparting CT character. The gradual redshift of the fluorescence emission in the three polymorphs under external pressure is attributed to the increasing excimer-like character of the emissive state.

---

1. Introduction

There exists a wide variety of organic luminescent materials that are sensitive to environmental stimuli; among them, mechanoluminescent materials have the ability to emit light upon application of any mechanical action.^1–5 Mechanoluminescence (ML), and in particular piezoluminescence, in which changes in emission color or intensity are triggered by pressure, plays an important role in materials science due to its vast potential in optical, electronic and medical applications. Indeed, ML allows using mechanical energy to generate emission of light without any irradiation or electron excitation source, which is both energy-saving and environmentally protective.^6–10 Pressure-induced alteration of the luminescence properties is generally interpreted as resulting from changes in the structure of the molecular units and their supramolecular packing.^11–14 However, while the luminescent properties of individual organic compounds are now generally well described and controlled by suitable molecular design, the rational development of mechano-responsive systems is currently hampered by the complexity of the ML phenomenon, which can originate from different electronic, structural and aggregation effects that can either lead to fluorescence or phosphorescence emission, or a spectral shift.

In this context, computational chemistry has proven very useful to investigate the structural and electronic origins of ML in organic materials, and different strategies have been used for rationalizing the subtle relationships linking the photophysical properties of individual molecules, their supramolecular arrangement in the solid state, the structural changes induced by mechanical stress and the resulting associated emissive behavior.^15,16 To cite a few examples, Feng et al. combined solid-state and gas-phase density functional theory (DFT) and Becke's virial exciton model to investigate piezochromism in three molecular crystals. They evidenced that the experimentally observed piezochromic redshifts can be rationalized from both the closing of the crystal bandgap upon compression and the increase of the polarizability of the excited units, which stabilizes the excited state.¹⁷ Zheng et al. used hybrid quantum mechanics/molecular mechanics (QM/MM) approaches to elucidate the luminescence properties of dibenzo[b,d]-thiophene 5,5-dioxide (DBTS) and carbazole (Cz) crystalline aggregates under different external pressures. The dramatically different piezochromic behaviors of these two organic fluorophores were shown to be related to a different sensitivity of the molecular structures to compression. Owing to its rigid nature, Cz shows slight changes in its absorption and emission spectra upon compression; in contrast, DBTS is more environment-sensitive and displays redshifted absorption and emission spectra, which is ascribed to an increase of the molecular planarity.¹⁸ Lastly, Crespo-Otero et al. investigated the piezochromism of two 9,10-(bis((E)-2 pyridin-4-yl)vinyl)anthracene (BP4VA) crystal polymorphs by means of DFT and time-dependent (TD) DFT calculations. They concluded that the luminescence properties are driven by the pressure modulation of the intermolecular interactions within the lattice, the red-shifted luminescence being ascribed to a transition from a herringbone to a sheet packing arrangement, and to the subsequent enhancement of π–π and CH–π interactions and restriction of molecular motions.¹⁹

All these studies rationalize the changes in the photophysical properties of extended systems either in terms of structural changes that tune occupied and/or virtual energy levels, i.e., shifting absorption/emission bands, or restricting molecular motion, i.e., hindering non-radiative decay pathways. Additionally, one might hypothesize ML phenomena emerging from changes in the electronic character of low-lying states, but, as far as we are aware of, this mechanism has not been reported or discussed so far. In the present work, we aim to show that, in addition to tuning intermolecular interactions and molecular motion, mechanical pressure can alter the nature of states, representing yet another possible ML mechanism. To that end, we chose to computationally investigate the piezochromic properties of an archetypal anthracene derivative, namely 9,10-bis((E)-2-(pyrid-2-yl)vinyl)anthracene (BP2VA). Tian and coworkers²⁰ reported that the exertion of external pressure on the BP2VA crystals leads to a drastic change in their photoluminescence color. The piezochromic effect was characterized by applying increasing hydrostatic pressures (up to 7.92 GPa) to the powder using a diamond anvil cell, which resulted in a noticeable gradual redshift (from 528 nm to 652 nm) attributed to changes in molecular aggregation state caused by compression. Crystallization of the BP2VA powder gave rise to three polymorphs with different stacking structures (noted C1–C3 hereafter), which were used to rationalize the aforementioned pressure-induced spectral displacement. The evolution in the photoluminescence emission wavelength from C1 to C3 was attributed to their respective different packing modes and associated increasing intermolecular interactions of the anthracene planes. Comparing the piezochromic luminescence behavior of the powder with the fluorescence emission of the three polymorphs, it was hypothesized that the BP2VA powder underwent a transformation between the molecular aggregation states of the three crystals when pressure was exerted.

To rationalize the structural and electronic origins of the ML properties of these systems at the molecular scale, and in particular to explore if indeed external pressure can sensibly modify the nature of electronic transitions, we present here an in-depth computational study of BP2VA crystals. We first characterized the effects of pressure on the structure of the three polymorphs by means of periodic DFT calculations. Then, the low-lying electronic excited states of molecular clusters extracted from the optimized crystal lattices were calculated using a QM/MM scheme accounting for both steric and electrostatic effects of the crystal environment. Finally, the nature of the emissive states was characterized in detail by quantifying the contributions of a localized diabatic model, which enables physical interpretations of these states in terms of local, charge transfer, or multi-excitonic transitions.

2. Computational methods

The computational study was conducted in two steps. First, the C1, C2 and C3 crystal polymorphs were optimized at ambient and high pressures using DFT with periodic boundary conditions. Based on the resulting structures, the S₁ excited state and emission properties in the crystal were modelled at the time-dependent (TD) DFT level on clusters cut from the relaxed crystal structures, using a QM/MM scheme in which the inner QM part contains either a single BP2VA unit or a stacked BP2VA dimer and the peripheral MM region includes the first molecular neighbors. All structures were characterized as real minima of the potential energy surface on the basis of their positive vibrational force constants.

2.1. Periodic DFT calculations

Periodic DFT calculations were performed using the Quantum Espresso (QE) package,^21,22 by employing a plane wave (PW) basis set and the recently developed vdW-DF-c09 exchange–correlation functional (XCF), which was shown to accurately describe dispersion-bound van der Waals complexes.^23–26 The ultra-soft pseudopotential scheme was employed in all calculations, with pseudopotentials obtained from the standard solid-state pseudopotentials (SSSP) library.^27–29 XRD crystal structures were used as starting guess for geometry optimizations carried out by imposing a monoclinic symmetry at zero and with an isotropic pressure of 7.92 GPa, which corresponds to the highest pressure used in the experimental work.²⁰ The BFGS quasi-Newton algorithm was used with a threshold of 10⁻⁴ Ry Bohr⁻¹ on all the atomic forces, and 0.05 GPa (0.3× 10⁻⁵ Ry Bohr⁻¹) on the largest component of stress tensor when cell relaxation was applied. The bulk calculations were conducted using a regular 1 × 2 × 1, 2 × 2 × 1 and 2 × 1 × 2 k-point sampling of the first Brillouin zone for C1, C2 and C3 respectively. After standard testing, kinetic energy cut-offs of 70 Ry for the wavefunctions and 490 Ry for the augmentation charge density were adopted to achieve stable convergence of forces and stress. Self-consistent-field (SCF) convergence was achieved with a threshold of 10⁻⁶ Ry on the total energy. The band structures of the three polymorphs were generated on top of a simple SCF calculation using the same XCF and PW basis set. The QE calculations, including band structures were pre-processed and post-processed using the Atomic Simulation Environment.³⁰

2.2. QM/MM simulations

Starting from the equilibrium structures obtained from periodic DFT, the geometry of the S₁ state was optimized in the molecular crystal environment of the three polymorphs using the hybrid QM/MM “Own N-layered Integrated molecular orbitals and molecular mechanics” (ONIOM) approach.³¹ The QM region, consisting either of the BP2VA molecule or BP2VA molecular pairs, was optimized using the range-separated hybrid XCF CAM-B3LYP³² and the 6-31G(d,p) basis set, including the Grimme's D3 correction to describe dispersion effects.³³ The crystal surrounding, which includes the whole set of closest molecular neighbors, was kept frozen and described classically using the universal force field (UFF). In addition to mechanical embedding (ME), electrostatic embedding (EE) was used in all ONIOM calculations. This technique incorporates the partial charges of the MM region into the QM Hamiltonian to provide a better description of the electrostatic interaction between the QM and MM regions. In line with the experimental hypothesis, the molecular dimers were selected as nearest neighbors along the anthracene core π-stacking direction for each polymorph, allowing to explicitly account for intermolecular interactions, as discussed in the following sections.

2.3. Excited states

Low-lying excited states were computed for monomers and dimers extracted from the periodic DFT optimized crystal structures of the three polymorphs, with and without pressure. Vertical excitation energies and oscillator strengths were computed using time-dependent (TD) DFT within ONIOM calculations at the [CAM-B3LYP-D3/6-31G(d,p):UFF = qeq] = embedcharge level. The Tamm–Dancoff approximation (TDA)³⁴ of TDDFT was also used. The emission behavior of the polymorphs was explored at the same levels of theory considering dimers in the QM region of the QM/MM excited state relaxation calculations. To further assess the effect of intermolecular interactions in the solid state, we also modelled the properties of the BP2VA monomer at its QM/MM geometry (one molecule in the QM region) and considering the isolated molecule in gas phase. For the latter case, the geometry of the ground (S₀) and first singlet excited (S₁) states were optimized in the gas phase at the CAM-B3LYP/6-31G(d,p) level, and used as input for TDDFT (TDA) calculations at the same level of theory.

The local or intermolecular charge transfer character of the TDA adiabatic states of molecular dimers was analyzed using a deconvolution of four adiabatic states in terms of diabatic states (diabats), computed by means of the Boys localization scheme.^35,36 Electronic interactions between diabatic states have been obtained as the off-diagonal elements of the diabatic Hamiltonian. All calculations on molecular monomers and dimers were carried out using the Gaussian 16³⁷ and Q-Chem 5.4.2³⁸ program packages. The Mercury program³⁹ developed by the Cambridge Crystallographic Data Centre (CCDC), as well as the VESTA⁴⁰ program, were used for visualization and exploitation purposes.

3. Results and discussion

3.1. Structural impact of mechanical strain

The crystal lattice parameters and unit cell volume of the three polymorphs optimized in the absence of external pressure (P = 0 GPa) were found to be in good agreement with the experimental ones (Table S1 and Fig. S1, ESI†), pointing at the reliability of the computational approach. Namely, deviations in the unit cell parameters do not exceed −3%, while variations in the volume are comprised between −3% and −5%.

Inter- and intramolecular features are also overall well reproduced. Notably, the packing arrangement of the DFT-optimized crystals (Fig. 1) is in good agreement with the XRD data. In particular, the increased overlap between anthracene cores of neighboring molecules along the C1–C3 series, which is anticipated to impact the observed photoluminescence, is correctly described. In quantitative terms, DFT calculations reproduce well the intermolecular shifts along the short (Δx) and long (Δy) axes of the anthracene core (Table 1), with small discrepancies only for C3, as well as the intermolecular rotation angles (Table S2, ESI†). However, the anthracene interplane distance (Δz) is underestimated by 0.13 Å for C3 (Table 1), which indicates that the vdW-DF-c09 XCF may overestimate van der Waals attraction forces in this case, where Δx and Δy are significantly smaller. Similar issue was reported in the previous study of Crespo-Otero et al., in which the Grimme's D2 approximation was used for parent molecules.¹⁹ The dihedral angles between the anthracene core and the (pyridin-2-yl)vinyl (P2V) moieties (θ_A), and between the pyridine group and vinyl chain (θ_B), are in line with those measured in the experimental crystal structures of C1 and C2, yet they are underestimated for C3 (Table 1). This is likely a consequence of the abovementioned underestimation of the vertical stacking distance, which, in turn, is expected to hinder the out-of-plane intramolecular rotations of the P2V lateral substituents in this polymorph. We also note that, contrary to what is found for C1 and C2 structures, DFT calculations predict a non-symmetric orientation of the P2V branches in C3, with θ_A ≠ θ_A′ and θ_B ≠ θ_B′ (see Fig. 1(a)).

Fig. 1 (a) Scheme of the BP2VA molecule with the definition of dihedral angles (θ_A, θ_B) discussed in the text. (b) Definition of the intermolecular translation parameters along the x (shift), y (slide) and z (rise) molecular axes. (c)–(e) Molecular arrangement in the three single crystals of BP2VA optimized at the periodic DFT level (from left to right: C1, C2, C3), with conventional unit cells shown in (f)–(h).

Table 1 Intermolecular shifts^a along the three molecular axes (Δx, Δy and Δz, Å) and intramolecular torsion angles^a (θ_A and θ_B, degrees) in experimental single crystals, and calculated under zero pressure and at 7.92 GPa. Values in parenthesis reported at P = 0 GPa are deviations with respect to the XRD parameters; those at P = 7.92 GPa are differences with respect to values calculated at P = 0 GPa

		Shift (Δx)	Slide (Δy)	Rise (Δz)	θ A/θA′	θ B/θB′
a See Fig. 1 for the definition of the geometrical parameters. The values of θA′ and θB′ are reported in the case of C3.
C1	Exp	0.43	8.20	3.12	50	15
	P = 0	0.43 (0.00)	8.20 (0.00)	3.12 (0.00)	50 (0)	15 (0)
	P = 7.92	1.00 (+0.57)	7.66 (−0.54)	2.81 (−0.31)	49 (−1)	13 (−2)
C2	Exp	−0.01	4.57	3.48	53	168
	P = 0	−0.01 (0.00)	4.57 (0.00)	3.48 (0.00)	53 (0)	168 (0)
	P = 7.92	0.42 (+0.43)	4.13 (−0.44)	3.11 (−0.37)	52 (−1)	169 (+1)
C3	Exp	1.03	1.22	3.55	−51/53	14/−7
	P = 0	1.09 (+0.06)	1.11 (−0.11)	3.42 (−0.13)	−40/46 (+11/+7)	6/−1 (+8/+6)
	P = 7.92	1.13 (+0.04)	0.87 (−0.24)	2.94 (−0.48)	−18/37 (+22/+9)	−13/1 (+19/−2)

---

In all cases, the 7.92 GPa hydrostatic pressure exerted translates into an anisotropic compression of the crystals and a drastic alteration of their respective cell parameters (Table 1 and Table S1, Fig. S1b, ESI†). Namely, structural change in C1 is dominated by c length reduction (−13%), while for C2 a and c are the most compressible crystal axes (−10% and −12%, respectively). Finally, polymorph C3 shows significant reduction along the a axis (−15%) and noticeable change of the c vector (−7%), while the b lattice parameter remains virtually unaffected (−1%). These pressure-induced structural changes yield a substantial decrease of the unit cell volume, reaching −24% in C1 and C2 and −22% in C3. While relative energies of the optimized crystal structures at ambient condition show little stability difference between the three polymorphs, the application of pressure strongly stabilizes C3, in line with the experimental hypothesis (Table S21, ESI†). Note that geometry optimizations of the three polymorphs under pressure were also performed releasing the symmetry constraints on the α and γ angles. Our calculations are not able to reproduce the hypothesized structural transition between the different polymorphs under application of pressure: not imposing the monoclinic system results in the loss of the crystal space group, but does not yield significant differences in the unit cell parameters. The unit cell compression is similar to that obtained with symmetry constraint, with deviations of up to 15% in the translation vectors and up to 24% in the cell volume (Table S1, ESI†).

For each polymorph, dimers along the stacking direction of the anthracene cores were considered in order to evaluate the effect of crystal cell compression onto the intermolecular structural parameters that are expected to drive the photoluminescence. The exertion of pressure significantly affects the packing arrangement of the three polymorphs (Table 1 and Fig. S3, ESI†). In particular, the interplanar distance Δz is reduced by 0.31 Å and amounts to 2.81 Å in C1, most likely due to the vanishing overlap of the anthracene cores. For C2 and C3, the π–π distance reaches a limit value of 3.11 and 2.94 Å (reduction by 0.37 and 0.48 Å, respectively). This closer packing is accompanied by an overall planarization of the molecules, with a striking reduction of 22° of the θ_A dihedral in C3.

To further characterize the intermolecular interactions at both ambient and high pressure, we resorted to the non-covalent interactions (NCI) method.^41,42 This approach uses the promolecular density ρ(r) for the determination of the reduced density gradient scalar field (RDG, s(ρ)), and the sign of the second eigenvalue of the Hessian density matrix (λ₂) to determine the attractive or repulsive nature of the interactions (Fig. S4, ESI†). Ultimately, non-covalent interactions can be visualised as isosurfaces such as those presented in Fig. 2. As expected, stacked BP2VA molecules display slightly attractive van der Waals interactions, principally arising from interactions between cofacial anthracene backbones. At ambient pressure, the spatial overlap of the molecular cores increases along the C1–C3 series (mainly due to large differences in Δy values, see Table 1), and significantly affects the extent of these interactions, as illustrated by the NCI plots (Fig. 2). Namely, the large long-axis relative shift of anthracene cores in C1 (Δy = 8.20 Å) gives rise to a very small region of weak interactions at the respective extremities of two stacking units. As the molecular xy-superposition increases, this region gets larger in C2 (Δy = 4.57 Å) and ultimately encompasses the whole BP2VA dimer in C3 (Δy = 1.11 Å). The large overlap of adjacent molecules in C3 is associated with a more planar structure of the BP2VA units, which exhibit a reduced dihedral angle between the peripheral P2V substituents and the anthracene core (θ_A = 46° versus 50° and 53° for C1 and C2, respectively). The application of external pressure induces an increase in the molecular overlap in C1 and C2 that can be seen in the larger NCI region but is not as apparent in C3.

Fig. 2 NCI isosurfaces (s(ρ) = 0.5 a.u.) showing the van der Waals interactions (green areas) in dimers extracted from the three optimized polymorphs (a) P = 0 GPa and (b) P = 7.92 GPa (from left to right: C1, C2, C3).

3.2. Impact of mechanical strain on the ground state electronic and vibrational properties

The band structures and corresponding density of states (DOS) diagrams of the C1, C2 and C3 polymorphs, calculated using crystal geometries optimized under P = 0 and P = 7.92 GPa, are reported in Fig. 3. All molecular units exhibit quasi-degenerated band structures. Orbital-projected DOS (pDOS), obtained by decomposing the bands into pseudo-atomic orbital contributions (Fig. S5, ESI†), show that the highest occupied and lowest unoccupied crystalline orbitals (displayed in Fig. S6 (ESI†) at the Γ point of the first Brillouin zone) arise nearly exclusively from contribution of p-orbitals of the carbon and nitrogen atoms, while s-orbitals only contribute to lower energy levels.

Fig. 3 Band structures of C1 (top), C2 (middle) and C3 (bottom) under P = 0 GPa (left) and P = 7.92 GPa (right). The energies are given relative to the Fermi level (dotted line). At P = 0 GPa, the energy of the valence (conduction) band edges for C1, C2 and C3 are 3.272, 3.279, 3.512 eV (1.770, 1.893 and 2.153 eV), respectively. At P = 7.92 GPa, the energy of the valence (conduction) band edges for C1, C2 and C3 are 5.210, 5.192, 5.341 eV (4.037, 4.243 and 4.308 eV), respectively.

At ambient pressure, C1 displays very flat valence and conduction bands all over the first Brillouin zone, as could be expected from the small overlap and weak non-covalent interactions between BP2VA units (Fig. 2). Increasing the intermolecular π–π interactions in C2 and C3 induces a lowering of the band gap (Fig. 3), and a larger dispersion of the frontier energy bands (which can be quantified by the difference between the direct and indirect band gaps in Table S3, ESI†). The decrease of the band gap from C1 to C3 is consistent with the lowering of the measured emission energy, where the position of the maximum emission band evolves as 2.35, 2.14 and 2.01 eV.²⁰

The exertion of pressure has a significant impact on the band structure, the increase of orbital interactions in the compressed unit cell resulting in a decrease of the bandgap in the three polymorphs. However, the effect is more pronounced in C2 (where the bandgap is lowered by 0.4 eV), so that under external pressure of P = 7.92 GPa the bandgaps follow the C2 < C3 < C1 order.

The phonon structure of the three polymorphs was also investigated to gain deeper insights into the possible hindering of non-radiative mechanisms through the restriction of intramolecular motion under pressure, thereby potentially enhancing the luminescence of the crystals. However, due to the large number of atoms per unit cell for C1 and C3 (Z = 4, which corresponds to 200 atoms per cell and thus to 600 phonon modes), it was not possible to calculate the phonon structure for these two polymorphs. The phonon density of states was nevertheless obtained for C2 (Fig. S7, ESI†), which contains only 2 BP2VA molecules. Exertion of pressure leads to a decrease in the density of the low-frequency acoustic modes, which suggests that non-radiative mechanisms may be suppressed by restriction of rotational motions. However, experimental data show a decrease in the fluorescence quantum yield from C1 to C3, pointing at the possible role of exciton coupling instead of the sole structural constraint of a denser packing.

3.3. Impact of structural aggregation constraints on the photophysical properties

To evaluate the effect of intermolecular interactions on the solid-state optical properties at ambient and high pressure, we first characterized the isolated BP2VA molecule in gas phase (Table S5, ESI†). Note that absorption and emission properties of BP2VA were also calculated in THF solvent and compared with experimental data, with the main objective to assess the suitability of the computational level of approximation. Those results are discussed in the ESI† (Section S13).

The vertical S₀ → S₁ excitation of the BP2VA molecule, computed at 3.20 eV, is described by a HOMO → LUMO electronic promotion. The frontier orbitals are centred on the anthracene core with partial delocalization over the lateral P2V branches, which is more pronounced in the LUMO (Fig. 4). Note that this larger delocalization of the LUMO density on the P2V branches is preserved in the crystal, as shown by the crystalline orbitals at the Γ point, plotted in Fig. S6 (ESI†) for the three polymorphs.

Fig. 4 Shape and energy of the frontier molecular orbitals of the BP2VA molecule computed at the S₀ and S₁ equilibrium geometries at the CAM-B3LYP/6-31G(d,p) level in gas phase.

Relaxation on the S₁ potential energy surface induces a distortion of the anthracene plane and a loss in the structural symmetry of the P2V branches. More specifically, one P2V substituent experiences substantial out-of-plane bending with respect to the anthracene core (Table S7, ESI†). The second notable structural change lies in the significant planarization of the molecule (θ_A reduces from 57° at the ground state minimum to 35°/−18° at the first excited state geometry, Table 1 and Table S7, ESI†). The large difference between equilibrium S₁ and S₀ states geometries translates into a large reorganization energy for the S₁ → S₀ transition, to which low frequency modes (intramolecular rotations and out-of-plane bending) contribute the most (Fig. S8, ESI†). The overall planarization of the P2V branches with respect to the anthracene core allows for an increase of the π-electron conjugation within the molecule, as indicated by the smaller bond length alternation (BLA) along the vinylic bridges (BLA = 0.138 Å and 0.082 Å in the S₀ and S₁ geometries, respectively). The larger delocalization of both frontier orbitals over the whole molecule in the S₁ state (Fig. 4) translates into a smaller HOMO–LUMO gap (5.36 eV vs. 4.25 eV), and a vertical de-excitation energy calculated at 2.28 eV, yielding a 0.92 eV decrease with respect to the gap at the ground state geometry, in close agreement with the experimental Stokes shift (0.86 eV) measured in THF (see ESI,† Section S13).

As discussed above, the optical properties of BP2VA are essentially dominated by the degree of overall relative planarity of the P2V arms with respect to the anthracene core (θ_A) and, to a lesser extent, the possibility for their out-of-plane bending distortion (θ_B). These two structural parameters are expected to be the most affected in the solid state both at ambient pressure and under hydrostatic compression. We first assessed the differences in the monomer's optical behavior entailed by the molecular environment in each polymorph. Table 2 reports the Franck–Condon vertical excitation energies (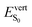) and de-excitation energies from the S₁ state minimum (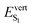) of BP2VA in gas phase, and using geometries optimized within the crystal environment of the three polymorphs. S₁ geometries were optimized using the ONIOM approach at the [CAM-B3LYP-D3/6-31G(d,p):UFF = qeq] = embedcharge level (see Section 2), in which the reference molecule geometry was relaxed within a frozen surrounding constituted of its first neighbors, while crystalline S₀ geometries were directly extracted from the optimized unit cell. In both cases, the optical properties were calculated using ONIOM with electrostatic embedding to include polarization effects of the molecular surrounding.

Table 2 Dihedral angles θ_A/θ_A′ (degrees), vertical excitation energies (in eV) to the S₁ excited state, and de-excitation energies from the S₁ minima with associated oscillator strengths in parenthesis, calculated at the CAM-B3LYP/6-31G(d,p) level for the isolated molecule and at the ONIOM [CAM-B3LYP/6-31G(d,p):UFF = qeq] = embedcharge level in the crystal geometry for the three polymorphs, with D3 correction for S₁ → S₀

Monomer	θ A/θA′ (S0)		θ A/θA′ (S1)
Isolated (opt. geometry)	57	3.20 (0.61)	35/−18	2.28 (0.80)
From C1 (P = 0 GPa)	50	2.92 (0.71)	39/−40	2.49 (0.77)
From C2 (P = 0 GPa)	53	2.97 (0.66)	45/−45	2.55 (0.69)
From C3 (P = 0 GPa)	−40/46	2.81 (0.78)	−31/32	2.42 (0.83)
From C1 (P = 7.92 GPa)	49	2.87 (0.76)	41/−43	2.50 (0.76)
From C2 (P = 7.92 GPa)	52	2.99 (0.67)	56/−56	2.72 (0.55)
From C3 (P = 7.92 GPa)	−37/18	2.65 (0.90)	−38/−3	2.55 (0.82)

---

The vertical S₀ → S₁ excitation energies of BP2VA computed using the crystal S₀ geometries at ambient pressure are significantly smaller than those calculated using the relaxed gas phase geometry. This can be traced back to the overall more planar structure adopted by BP2VA as a result of intermolecular interactions in the solid state (Table 2 and Table S6, ESI†). Reversely, S₁ → S₀ de-excitation energies computed in the crystal environment are all larger than the gas phase value, as steric constraints prevent a complete geometric relaxation of the S₁ state. A similar trend is obtained in THF (see ESI,† Section S13), in line with the experimentally measured blue shift of emission upon aggregation.²⁰

As anticipated, 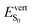values (and the associated oscillator strengths) are directly correlated to the θ_A dihedral angle quantifying deviations from planarity in the S₀ state. From C1 to C2, θ_A slightly increases from 50 to 53° (Table 2 and Table S6, ESI†), leading to a small increase of 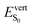from 2.92 to 2.97 eV, while the large redshift of the first absorption band in C3 (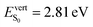) is associated with the significant lowering of θ_A to 40/46°. Similarly, the shifts in the S₁ → S₀ emission band from one polymorph to the other are driven by the θ_A values at the S₁ equilibrium geometry (Table 2 and Table S7, ESI†): the increase of 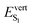from C1 to C2 is linked to the increase of θ_A from 39/40 to 45°, while the low value of 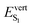in C3 (2.42 eV) is associated with a smaller θ_A angle (−31/32°).

Exertion of external pressure induces non-systematic changes in the 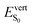values, with a slight increase for C2 (+0.02 eV), a slight decrease for C1 (−0.05 eV) and a more pronounced lowering for C3 (−0.16 eV). Again, the large redshift of the first absorption band of C3 can be understood by considering the large lowering of θ_A from −40/46° to −37/18°. Reversely, the S₁ → S₀ emission band is blue-shifted in the three polymorphs with respect to the isolated molecule when pressure is applied, consistently with the larger hindering of the rotational motion of the lateral P2V branches reflected in the larger θ_A values computed at P = 7.92 GPa for the S₁ geometry (Table S8, ESI†). Note that in the C3 polymorph, the molecule is highly asymmetric, with one branch showing an out-of-plane deviation of 38°, while the other lies in the anthracene plane (θ_A = 3°).

Our results considering single molecular units in crystal environment do not fully reproduce the experimental trends measured on the crystal polymorphs with no external pressure, which show a redshift in both the absorption and emission maxima along the C1–C3 series. In particular, the measured maximum emission energy evolves as 2.35, 2.14, 2.01 eV from C1 to C3, together with a decrease of the fluorescence quantum yields.²⁰ While the 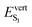value computed for the BP2VA unit extracted from C1 (2.49 eV) is rather close to the experimental value with an overestimation of 0.14 eV, calculations using molecular structures extracted from C2 and C3 show a much larger difference of about 0.4 eV. This is consistent with the fact that, as illustrated in Fig. 2, intermolecular interactions are much weaker in C1 than in the two other polymorphs. Also, photoluminescence spectra of BP2VA powder recorded under increasing external pressure show a progressive redshift of the emission band, and not a blueshift as predicted by TDDFT calculations. These discrepancies between computations and experiments might be attributed to intermolecular cooperative effects, not captured by single molecule calculations, even on a qualitative level. The role of intermolecular interactions on the nature and energy of the electronic excited states is therefore investigated in the next sections.

3.4. Electronic aggregation effects on the photophysical properties

To explicitly explore electronic effects emerging from intermolecular couplings, we expanded our computational model by considering molecular dimers. Concretely, we evaluated vertical transition energies and associated oscillator strengths towards the low-lying excited states of the molecular dimers illustrated in Fig. 2 at the TDDFT level (Table 3) and compared these results to those obtained for single molecular units. All calculations were performed using the ONIOM approach in order to capture the crystal environment effects.

Table 3 Vertical excitation energies (eV) and associated oscillator strengths, calculated at the ONIOM [CAM-B3LYP/6-31G(d,p):UFF = qeq] = embedcharge level for molecular dimers extracted from the three crystal polymorphs

		P = 0 GPa		P = 7.92 GPa
C1 monomer	S1	2.92	0.71	2.87	0.76
C1 dimer	S1	2.89	0.00	2.82	0.00
	S2	2.94	1.30	2.89	1.36
	S3	3.86	0.01	3.62	0.00
	S4	3.86	0.00	3.69	0.22
C2 monomer	S1	2.97	0.66	2.99	0.67
C2 dimer	S1	2.89	0.00	2.71	0.59
	S2	2.94	0.93	2.85	0.00
	S3	3.49	0.00	3.30	0.00
	S4	3.56	0.19	3.59	0.61
C3 monomer	S1	2.81	0.78	2.65	0.90
C3 dimer	S1	2.63	0.00	2.37	0.00
	S2	2.83	1.02	2.57	0.43
	S3	3.02	0.00	2.65	0.00
	S4	3.05	0.26	2.77	1.01

---

Considering crystal dimers with no external pressure, a similar distribution of low-lying excited states is computed for all polymorphs, with a dark S₁ state and a bright S₀ → S₂ transition (with 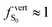) slightly shifted compared to the S₀ → S₁ transition calculated for the monomers in their crystal geometry. In C3, the optically dark S₁ state and the slight blueshift (+0.02 eV) of the first optically allowed transition with respect to the monomer indicates a H-type aggregation, as could be anticipated from the parallel stacking of the two monomers with largely overlapping anthracene cores. Moreover, the energy splitting between S₁ and S₂ in the three dimers (0.05, 0.05 and 0.20 eV for C1, C2 and C3, respectively) suggests stronger excitonic coupling in C3, as qualitatively predicted by the classical approximation of dipole–dipole Coulomb interactions between transition dipoles in parallel orientation⁴³ (see Table S10, ESI†).

In all crystals, applying pressure induces a redshift of the lowest dipole-allowed transition. In C1, in which the molecular units are weakly interacting, this redshift is moderate (0.05 eV) and similar to that calculated for the monomer (Table 2). This result indicates that, despite the large variation of the intermolecular distances (see the changes in the slide and shift parameters, Table 1), applying pressure does not significantly modify excitonic couplings in C1. Therefore, the pressure-induced redshift in the absorption band can be related to the changes in the geometry of the molecular units. In C2, applying pressure induces a substantial redshift (by 0.23 eV) of the lowest optically allowed transition, in contrast to the slight blueshift (+0.02 eV) predicted by the calculations based on single molecules. Consequently, there is an inversion in the ordering of the excited states, with a bright S₁ state and a dark S₂ state. In C3, the isotropic mechanical strain also yields a redshift of 0.25 eV of the first absorption band, which is of larger amplitude than that calculated for the single BP2VA unit (0.16 eV, Table 2). While the changes in the excited state energies and couplings when pressure is applied are driven by the intermolecular compression and subsequent increase in intermolecular electronic interactions for all three polymorphs, these effects are much stronger in C2 and C3 (up to one order of magnitude). These results agree well with the large excitonic coupling predicted by the classical dipole–dipole interaction model for C3 (Table S10, ESI†).

Diabatization of the electronic transitions of the polymorphs allows to characterize electronic transitions according to their intra-monomer (local excitation, LE) and inter-monomer (charge transfer, CT) nature (see ESI,† Section S10). The symmetry of the dimers in the three polymorphs results in doubly-degenerate LE and CT excitations, with relative energies and extent of mixing modulated by the relative disposition of the monomers. Decomposition of electronic transitions in terms of LE and CT contributions (Fig. 5) identifies the optical state of C1 as a pristine combination of LE on each monomer at both ambient and high pressure, in line with the very weak π–π intermolecular interactions (decomposition of other excited singlet states in Table S12, ESI†). The CT involvement in the lowest dipole allowed transition for C2 at ambient pressure is quite important (15%), which results in a decrease of the oscillator strengths as compared to C1 (Table S11, ESI†). Upon application of pressure, the CT diabats are significantly stabilized and the bright state is obtained as a nearly equal mixing of local CT excitations (55% LE and 45% CT). Finally, the role of CT terms in C3 is even more important, as could be anticipated from the strong overlap between π orbitals, with a 74% CT character at ambient conditions and as large as 92% under 7.92 GPa pressure. The larger involvement of CT terms in C3 further decreases the computed oscillator strengths.

Fig. 5 Diabatic decomposition of the lowest optically active excited state into local excited (LE) and charge transfer (CT) contributions, as calculated at the TDA/CAM-B3LYP/6-31G(d,p) level for the dimers of the three polymorphs at P = 0 and P = 7.92 GPa.

3.5. Pressure modulated nature of the emissive state

Finally, we explored the potential impact of intermolecular electronic effects on the excited state relaxation and on the S₁ → S₀ de-excitation energies at ambient and high pressure. For that, we performed excited state optimization calculations for the molecular dimers in their crystal environment by using the ONIOM approach at the [CAM-B3LYP-D3/6-31G(d,p):UFF = qeq] level including electrostatic embedding (Table 4).

Table 4 Vertical de-excitation energies (eV) from the S₁ minima and associated oscillator strengths, calculated at the ONIOM [CAM-B3LYP/6-31G(d,p):UFF = qeq] = embedcharge level for molecular dimers extracted from the three crystal polymorphs

	P = 0 GPa		P = 7.92 GPa
C1	2.49	0.65	2.54	0.60
C2	2.49	0.51	2.39	0.32
C3	2.36	0.45	2.23	0.00

---

In the absence of external pressure, the vertical transition energies at the relaxed S₁ geometry are overall in agreement with the experimental trend, with a reduced oscillator strength along the C1–C3 series and a red-shift from C1 to C3. At the S₁ potential energy minimum (P = 0 GPa), the lowest excited singlet is described as having one electron in the HOMO and one in the LUMO for all polymorphs, these frontier molecular orbitals being (almost exclusively) localized on a single molecule of the C1–C3 dimers (see Fig. 6 and Fig. S9, ESI† for the MO shape at the relaxed S₁ and S₀ geometries, respectively).

Fig. 6 Shape of the frontier molecular orbitals of dimers in their relaxed S₁ geometry, as calculated by using the ONIOM approach at the [CAM-B3LYP-D3/6-31G(d,p):UFF = qeq] = embedcharge level for the three polymorphs.

This local character of the excitation indicates that the three polymorphs have a monomer-like emission at ambient pressure. Besides a slightly lower oscillator strength, emission from S₁ in the dimer of C1 is virtually the same as that of the monomer, in line with the almost unchanged relative arrangement of the constituting BP2VA molecules (only Δx increases by ∼0.2 Å) and associated weak intermolecular interactions. Structural analysis further illustrates the localization of the excitation on one BP2VA exhibiting θ_A value of that of the relaxed S₁ monomer, while the second molecule remains at a geometry similar to that of the ground state (Table S15, ESI†). Relaxation on the S₁ potential energy surface translates into smaller intermolecular distances for polymorphs C2 and C3, reaching an interplanar spacing of about 3.3 Å, with little change in the overall overlap of the anthracene cores with respect to the ground state relative arrangement (Table S15, ESI†). The larger value obtained with respect to the isolated BP2VA can be traced back to the limited possibility for planarization in the crystal environment (in each case, excitation is localized on the monomer with the lowest θ_A values).

The excited state localization breaks the symmetry between the constituting monomers, which lifts the degeneracy of the LE and CT diabats. While the lowest excited singlet of C1 has a purely local character (99%), S₁ gradually holds some CT character as the overlap of the molecules increases within the dimers of C2 and C3 (5% and 7%, respectively). The trend in computed energies can then be rationalized as originating from a combination of effects, namely incomplete structural relaxation and slight change in the nature of the excited state arising from the different relative disposition of the monomers in the three polymorphs. Hence, despite a larger θ_A, C2 shows a value identical to that of C1, while C3 is substantially red shifted. The increase in CT character along the C1–C2–C3 series translates into a decrease in oscillator strength, in line with the decreasing measured fluorescence quantum yield.

The relaxed S₁ geometry of the BP2VA dimer for the three polymorphs is significantly altered at high pressure, with notably the loss of planarity of the anthracene core (Fig. S10, ESI†). Despite this, the pressure induced changes in the intermolecular structural parameters are similar to those obtained when considering the ground state geometries of the crystals (Table S15, ESI†), with yet a slight strengthening of the non-covalent interactions (Fig. S4, ESI†). Emission of C1 remains monomer-like, with the lowest excited state characterized by a HOMO-to-LUMO excitation localized on a single BP2VA molecule, slightly blue-shifted from the emission at ambient pressure likely due to the combined distortion of anthracene plane and small decrease in overall planarity of the P2V arms.

A very different picture is obtained for C2 and C3 polymorphs, for which external pressure enforces excitation delocalization over both BP2VA units. In these structurally symmetric dimers, the frontier molecular orbitals are delocalized over the two molecules, with large intermolecular orbital overlap (Fig. 6). The degenerate CT diabats are substantially stabilized, lying below the LE excitations, and the lowest excited state of C2 and C3 presents excimer characteristic, with significant weight of the CT contributions (58% and 50% for C2 and C3, respectively) and strong CT/LE couplings (see Fig. 7 and diabatization results in ESI,† Section S12). Emission of C2 is red-shifted relative to that of the monomer, with an expectedly decreased oscillator strength. The 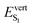transition energy is further lowered in C3, where the S₁ state is found completely dark with zero oscillator strength. This predicted non emissive behavior is however anticipated to be altered to some extent upon accounting for vibrational effects allowing weak emission.

Fig. 7 Diabatic decomposition of S₁ excited state into local excited (LE) and charge transfer (CT) contributions, as calculated at the TDA/CAM-B3LYP/6-31G(d,p) level for the three polymorphs at P = 0 and P = 7.92 GPa.

4. Conclusions

In this work, we propose a new mechanism to rationalize the piezochromic behavior of organic crystals. Through a detailed computational study combining periodic DFT, QM/MM and TDDFT calculations, we carefully characterize the structural, electronic and optical features of three BP2VA polymorphs at ambient conditions and under high pressure. Our results highlight the key role of intermolecular interactions, demonstrating the need to consider a dimer as minimal model for reproducing experimental trends. On this basis, we show that the three polymorphs have a monomer-like emission at ambient pressure, with a decrease of the S₁ → S₀ oscillator strength and a red-shift of the transition energy from C1 to C3. Structural analysis and deconvolution of the excited states on a diabatic basis enable to rationalize the evolution of the transition energies as resulting from the combination of the incomplete structural relaxation due to crystal hindrance, and from the change in the nature of the S₁ state, which holds increasing charge-transfer character as the molecular overlap increases from C1 to C3. While we do not reproduce the pressure-induced structural changes hypothesized experimentally, namely going progressively from C1-like to C3-like dominant supramolecular arrangements, our calculations characterize the associated changes in the molecular aggregation and show that external pressure can overcome excited state localization (as in C1) and induce delocalization of the excitation (C2 and C3).

Data availability

Crystallographic data used in this work have been obtained upon request to Dong et al. (DOI: https://doi.org/10.1002/anie.201204660). The data supporting this article have been included to the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Prof. Bin Xu of Jilin University for kindly providing us with the experimental crystal structures. J. O. acknowledges the Donostia International Physics Center (DIPC) for her PhD grant. This work was supported by the Transnational Common Laboratory QuantumChemPhys (Theoretical Chemistry and Physics at the Quantum Scale, grant number ANR-10-IDEX-03-02) established between the Université de Bordeaux (UB), Euskal Herriko Unibertsitatea (UPV/EHU) and the DIPC. The authors thank the Spanish Ministry of Science and Innovation (projects MICINN/FEDER PID2022-136231NB-I00 and RED2022-134939-T). Calculations were performed using the computing facilities provided by the DIPC and the Mésocentre de Calcul Intensif Aquitain (MCIA) of the University of Bordeaux and of the Université de Pau et des Pays de l’Adour. We also acknowledge the technical and human support provided by DIPC Computer Center.

References

1. Y. Sagara and T. Kato, Nat. Chem., 2009, 1, 605–610.
2. Z. Chi, X. Zhang, B. Xu, X. Zhou, C. Ma, Y. Zhang, S. Liu and J. Xu, Chem. Soc. Rev., 2012, 41, 3878–3896.
3. P. Xue, J. Ding, P. Wang and R. Lu, J. Mater. Chem. C, 2016, 4, 6688–6706.
4. Z. Ma, Z. Wang, M. Teng, Z. Xu and X. Jia, ChemPhysChem, 2015, 16, 1811–1828.
5. Y. Xie and Z. Li, Mater. Chem. Front., 2020, 4, 317–331.
6. X. Qian, Z. Cai, M. Su, F. Li, W. Fang, Y. Li, X. Zhou, Q. Li, X. Feng, W. Li, X. Hu, X. Wang, C. Pan and Y. Song, Adv. Mater., 2018, 30, 1800291.
7. C. Wu, S. Zeng, Z. Wang, F. Wang, H. Zhou, J. Zhang, Z. Ci and L. Sun, Adv. Funct. Mater., 2018, 28, 1803168.
8. C. Wang, Y. Yu, Y. Yuan, C. Ren, Q. Liao, J. Wang, Z. Chai, Q. Li and Z. Li, Matter, 2020, 2, 181–193.
9. L. Tu, Y. Xie and Z. Li, J. Phys. Chem. Lett., 2022, 13, 5605–5617.
10. K. Ariga, T. Mori and J. P. Hill, Adv. Mater., 2012, 24, 158–176.
11. Q. Li and Z. Li, Adv. Sci., 2017, 4, 1600484.
12. N. Li, Y. Gu, Y. Chen, L. Zhang, Q. Zeng, T. Geng, L. Wu, L. Jiang, G. Xiao, K. Wang and B. Zou, J. Phys. Chem. C, 2019, 123, 6763–6767.
13. Y.-B. Gong, P. Zhang, Y. Gu, J.-Q. Wang, M.-M. Han, C. Chen, X.-J. Zhan, Z.-L. Xie, B. Zou, Q. Peng, Z.-G. Chi and Z. Li, Adv. Opt. Mater., 2018, 6, 1800198.
14. Y. Dai, H. Liu, T. Geng, R. Duan, X. Li, Y. Liu, W. Liu, B.-G. He, L. Sui, K. Wang, B. Zou, B. Yang and Y. Qi, J. Mater. Chem. C, 2023, 11, 4892–4898.
15. Y. Gu, N. Li, G. Shao, K. Wang and B. Zou, J. Phys. Chem. Lett., 2020, 11, 678–682.
16. L. Wilbraham, M. Louis, D. Alberga, A. Brosseau, R. Guillot, F. Ito, F. Labat, R. Métivier, C. Allain and I. Ciofini, Adv. Mater., 2018, 30, 1800817.
17. X. Feng, A. D. Becke and E. R. Johnson, J. Chem. Phys., 2020, 152, 234106.
18. J. Zhao, Y. Zeng and X. Zheng, Chem. Mater., 2022, 34, 10711–10720.
19. A. Aziz, A. Sidat, P. Talati and R. Crespo-Otero, Phys. Chem. Chem. Phys., 2022, 24, 2832–2842.
20. Y. Dong, B. Xu, J. Zhang, X. Tan, L. Wang, J. Chen, H. Lv, S. Wen, B. Li, L. Ye, B. Zou and W. Tian, Angew. Chem., Int. Ed., 2012, 51, 10782–10785.
21. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
22. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
23. D. C. Langreth, B. I. Lundqvist, S. D. Chakarova-Käck, V. R. Cooper, M. Dion, P. Hyldgaard, A. Kelkkanen, J. Kleis, L. Kong, S. Li, P. G. Moses, E. Murray, A. Puzder, H. Rydberg, E. Schröder and T. Thonhauser, J. Phys.: Condens. Matter, 2009, 21, 084203.
24. K. Berland, V. R. Cooper, K. Lee, E. Schröder, T. Thonhauser, P. Hyldgaard and B. I. Lundqvist, Rep. Prog. Phys., 2015, 78, 066501.
25. T. Thonhauser, S. Zuluaga, C. A. Arter, K. Berland, E. Schröder and P. Hyldgaard, Phys. Rev. Lett., 2015, 115, 136402.
26. T. Thonhauser, V. R. Cooper, S. Li, A. Puzder, P. Hyldgaard and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125112.
27. G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet, E. Passaro and N. Marzari, A Standard Solid State Pseudopotentials (SSSP) library optimized for precision and efficiency, Materials Cloud Archive 2021.76, 2021 DOI:10.24435/materialscloud:rz-77.
28. G. Prandini, A. Marrazzo, I. E. Castelli, N. Mounet and N. Marzari, npj Comput. Mater., 2018, 4, 72.
29. K. Lejaeghere, G. Bihlmayer, T. Björkman, P. Blaha, S. Blügel, V. Blum, D. Caliste, I. E. Castelli, S. J. Clark, A. Dal Corso, S. de Gironcoli, T. Deutsch, J. K. Dewhurst, I. Di Marco, C. Draxl, M. Dułak, O. Eriksson, J. A. Flores-Livas, K. F. Garrity, L. Genovese, P. Giannozzi, M. Giantomassi, S. Goedecker, X. Gonze, O. Grånäs, E. K. U. Gross, A. Gulans, F. Gygi, D. R. Hamann, P. J. Hasnip, N. A. W. Holzwarth, D. Iuşan, D. B. Jochym, F. Jollet, D. Jones, G. Kresse, K. Koepernik, E. Küçükbenli, Y. O. Kvashnin, I. L. M. Locht, S. Lubeck, M. Marsman, N. Marzari, U. Nitzsche, L. Nordström, T. Ozaki, L. Paulatto, C. J. Pickard, W. Poelmans, M. I. J. Probert, K. Refson, M. Richter, G.-M. Rignanese, S. Saha, M. Scheffler, M. Schlipf, K. Schwarz, S. Sharma, F. Tavazza, P. Thunström, A. Tkatchenko, M. Torrent, D. Vanderbilt, M. J. van Setten, V. Van Speybroeck, J. M. Wills, J. R. Yates, G.-X. Zhang and S. Cottenier, Science, 2016, 351, aad3000.
30. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002.
31. L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H.-B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796.
32. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
33. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
34. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
35. J. E. Subotnik, R. J. Cave, R. P. Steele and N. Shenvi, J. Chem. Phys., 2009, 130, 234102.
36. J. E. Subotnik, S. Yeganeh, R. J. Cave and M. A. Ratner, J. Chem. Phys., 2008, 129, 244101.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
38. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince III, R. A. DiStasio Jr., A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
39. C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
40. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
41. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
42. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
43. F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc02550d

---