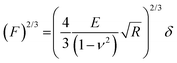Electrochemical modulation of mechanical properties of glycolated polythiophenes

Abstract

Electrochemical doping of organic mixed ionic–electronic conductors is key for modulating their conductivity, charge storage and volume enabling high performing bioelectronic devices such as recording and stimulating electrodes, transistors-based sensors and actuators. However, electrochemical doping has not been explored to the same extent for modulating the mechanical properties of OMIECs on demand. Here, we report a qualitative and quantitative study on how the mechanical properties of a glycolated polythiophene, p(g3T2), change in situ during electrochemical doping and de-doping. The Young's modulus of p(g3T2) changes from 69 MPa in the dry state to less than 10 MPa in the hydrated state and then further decreases down to 0.4 MPa when electrochemically doped. With electrochemical doping–dedoping the Young's modulus of p(g3T2) changes by more than one order of magnitude reversibly, representing the largest modulation reported for an OMIEC. Furthermore, we show that the electrolyte concentration affects the magnitude of the change, demonstrating that in less concentrated electrolytes more water is driven into the film due to osmosis and therefore the film becomes softer. Finally, we find that the oligo ethylene glycol side chain functionality, specifically the length and asymmetry, affects the extent of modulation. Our findings show that glycolated polythiophenes are promising materials for mechanical actuators with a tunable modulus similar to the range of biological tissues, thus opening a pathway for new mechanostimulation devices.

---

Eleni Stavrinidou

We first published in Materials Horizons in 2021 as part of the Emerging Investigators Series. For our work on biohybrid plants with electronic roots, we had the great honor to receive the Materials Horizons Outstanding Article award. In the 10th anniversary collection, we are publishing our second paper in Materials Horizons. This work investigates how the mechanical properties of glycolated polythiophenes are modulated with electrochemistry. Materials Horizons is an excellent journal covering a board range of topics. What I particularly like is that the journal puts emphasis on new concepts. My warmest congratulations and to many more exciting studies.

---

New concepts

The properties of organic mixed ionic–electronic conductors (OMIECs) can be modulated via electrochemical doping. While the changes in conductivity, charge storage and volume during electrochemical doping have been widely studied, how the mechanical properties change is fairly unexplored. This work shows that for a glycolated polythiophene, p(g3T2), the Young's modulus can change more than one order of magnitude with electrochemical doping–dedoping, the largest modulation reported so far. The dynamic range of the Young's modulus of p(g3T2) matches that of biological tissues, opening a pathway for the development of soft actuators for on demand mechanostimulation of biological systems. This work also contributes to furthering our understanding on the fundamental doping process in OMIECs as we show that osmotic phenomena take place during doping and are affected by the molecular design and by the electrolytic environment.

Introduction

Organic mixed ionic electronic conductors (OMIECs) are considered key materials for bioelectronics because of their mixed ionic/electronic transport, biocompatibility, solution processability and electrochemical actuation.^1,2 OMIECs volumetric charging has been exploited for enhanced signal transduction in electrodes³ and electrochemical transistors^4,5 as well as in actuators⁶ due to the voltage-induced volume changes. Furthermore, solution processability enables additive manufacturing for 3D structures as well as material integration into various substrates such as fiber and textiles for tissue engineering, wearables, and soft robotics.^7–9 The soft nature of the OMIECs brings also promise for a better mechanical match with the biological world.¹⁰ However, even though most OMIECs are softer than inorganic semiconductors and metals, they are still much stiffer than tissue, exhibiting Young's modulus from hundreds of MPa to GPa, mostly depending on crystallinity and chain alignment.^11,12

Different strategies have been investigated for modulating the Young's modulus of OMIECs.^13,14 Engineering composites of conducting polymers and hydrogels has been extensively studied, as hydrogels are biocompatible, as soft as tissues and allow flexible fabrication.^15–17 These composites result in an interpenetrating network of conducting polymers within the hydrogel bulk and therefore have improved mechanical properties but at the cost of reduced electronic conductivity.^18–21 Recently, a pure PEDOT:PSS hydrogel was reported, based on an interconnected network of pure polymer fibrils, without the need of any additional cross-linking, resulting in a material with a low Young's modulus and good electrical and electrochemical properties.²² Synthetic design^23,24 and molecular doping have also been explored for modulating the mechanical properties of OMIECs. Stiff polymers with a Young's modulus higher than 100 MPa usually have high crystallinity due to enhanced π–π stacking, and molecular doping only slightly reduces their stiffness.²⁵ Softer polymers on the other hand, have lower crystallinity and more amorphous regions, and in this case, doping results in stiffening due to increase in crystallinity.^25,26 In p(g42T-T), a polythiophene with tetraethylene glycol side chains, doping with F4TCNQ increases the Young's modulus from 8 to 232 MPa while doping with F2TCNQ induces an even higher change reaching Young's modulus values of 377 MPa, the largest modulation reported so far with molecular doping.

While molecular doping is a promising route for tuning the mechanical properties of OMIECs,^19,27 modulation on demand with external stimuli, such as voltage or light, can open new possibilities as mechanostimulation and adaptive interfaces. Electrochemical doping is a dynamic, reversible process where injected charges in the polymer backbone are compensated by ions that migrate from the electrolyte to the polymer matrix together with water molecules, resulting in volume expansion.^28–30 During dedoping, electronic charges are extracted from the backbone and, at the same time, ions and water are expelled from the polymer matrix, resulting in volume contraction. Even though the electrochemical doping processes and volumetric changes have been widely investigated in conducting polymers,^31–38 not many studies have focused on how their mechanical properties are affected per se during doping-induced volume change. Qualitatively such correlation has been evaluated with electrochemical quartz crystal microbalance with dissipation module (eQCM-D) showing that doping and solvent ingress render the polymers more viscoelastic.^28,29 Quantitative studies were performed with AFM coupled to electrochemical module and electrochemical strain microscopy for the model polymers PEDOT:PSS¹² and P3HT,³⁹ respectively. These studies revealed that the ion uptake, accompanied by electrolyte ingress, affects the local order and modulates the electronic conductivity as well as the mechanical properties.

While there is a clear indication that it is possible to tune the mechanical properties of OMIECs through electrochemical doping, this possibility remains largely unexplored. Recently we reported an OMIEC that exhibits a record volume change during electrochemical doping based on a thiophene backbone with triethylene glycol side chains (p(g3T2)).^40–42 We demonstrated that during the first electrochemical oxidation, p(g3T2) expands by more than 1000% undergoing a solid to gel transition resulting in a conducting hydrogel as a single component material. Molecular dynamics revealed that the polymer backbones shift creating a nanoporous matrix while still maintaining percolation pathways and that the ethylene glycol (EG) side chains stabilize water molecules.⁴¹ During subsequent electrochemical cycling, p(g3T2) expands reversibly by 250–300%, which has been exploited for electroactive filters.⁴³

Here, we demonstrate that we can reversibly modulate the mechanical properties of p(g3T2) with electrochemical doping. With electrochemical quartz crystal microbalance with dissipation module (eQCM-D) we qualitatively correlate the changes in mass and volume with changes in the viscoelastic properties and show that p(g3T2) becomes softer when doped and stiffens when dedoped. With in situ electrochemical atomic force microscopy (EC-AFM) we find that the Young's modulus of p(g3T2) in the pristine state is in the order of MPa and decreases by more than one order of magnitude when electrochemically doped. Furthermore, by using aqueous electrolytes with different ionic strengths, we decouple the contribution of ions and water to the volume change and hence to the change in mechanical properties. Finally, we study a series of polythiophenes with varying EG side chain functionalities and show that the change in mechanical properties is highly dependent on side chain functionality.

Results

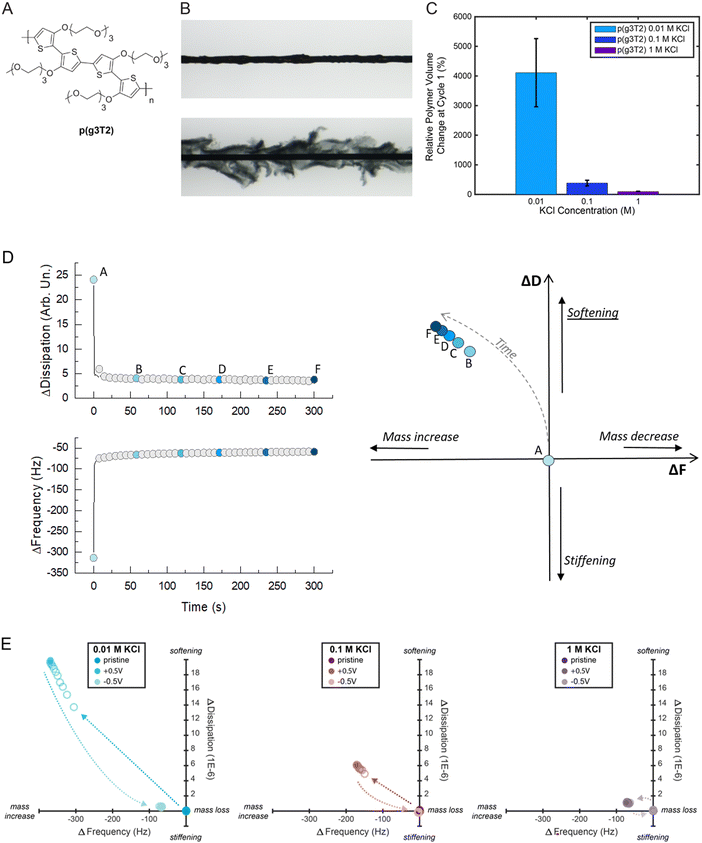
First, we characterized p(g3T2)'s solid to gel conversion, i.e., from pristine to the electrochemically doped state (+0.5 V vs. Ag/AgCl) and back to the electrochemically reduced state (−0.5 V vs. Ag/AgCl) in varying KCl electrolyte concentrations from 0.01 M to 1 M (Fig. 1). A p(g3T2) coated carbon fiber was mounted in an electrochemical cell as the working electrode and the polymer volume change upon electrochemical addressing was recorded by microscopy. The relative polymer expansion [(V_pristine − V_oxidized)/V_pristine)] and contraction [(V_oxidized − V_reduced)/V_oxidized] were then calculated (Fig. 1(C)), as detailed in Methods and Supporting Information S1 (ESI†).

Fig. 1 (A) Chemical structure of EG-polythiophene p(g3T2). (B) Micrograph of a p(g3T2) coated carbon fiber in the pristine state above and the expanded state (oxidized) below. (C) Relative volume change of p(g3T2) in 0.01, 0.1 and 1 M KCl at the 1st switching cycle (4 samples for each concentration, data reported as average ± Standard Deviation). (D) Schematic of the proposed new representation for the dissipation (D) and frequency (F) changes from eQCM-D measurements: left, representative F and D changes over time for p(g3T2) in KCl 0.01 M; right: D(F) plot from the ΔD, ΔF vs. time data. (E) D(F) plots for p(g3T2) at different states (pristine film, expanded (+0.5 V) and contracted (−0.5 V)) in different electrolyte concentrations (0.01, 0.1 and 1 M KCl).

We found that p(g3T2)'s expansion upon doping decreases by one order of magnitude, from 4112 ± 1150% to 384 ± 95% when the electrolyte changes from 0.01 M to 0.1 M KCl. For even higher electrolyte concentration, 1 M KCl, the polymer expansion decreases further to 96 ± 11% (Fig. 1(C)). After the initial couple of cycles, the relative polymer volume change stabilizes for up to 300 cycles. At the 100th cycle p(g3T2)'s relative volume change is 195 ± 6% in 0.01 M KCl, 97 ± 27% in 0.1 M KCl and 59 ± 4% in 1 M KCl following the decreasing trend of the volume change with increasing KCl concentration (Fig. S2, ESI†).

To get a better insight on the associated changes on the polymer properties, we then performed electrochemical-quartz crystal microbalance with dissipation monitoring (eQCM-D) on p(g3T2) thin films coated on Au quartz crystals. eQCM-D gives simultaneous information on the changes in the mass and viscoelastic properties by monitoring the changes in frequency (F) and dissipation (D), respectively.⁴⁴ The F and D changes (ΔF and ΔD) are usually reported as a function of time (Fig. 1(D), left). To have a more straightforward comparison between the different conditions, we propose here a different data visualization for the eQCM-D data. We report the ΔD as a function of ΔF, which will be referred from now on as “D(F) plot”: this allows the visual representation of the correlation between mass increase and softening of the material and the qualitative assessment of the influence of the electrolyte concentration (Fig. 1(D), right). As the increase in frequency represents a mass decrease, and an increase in dissipation represents the softening of the material, if the viscoelastic data are moving towards the first quadrant of the D(F) plot, it means that the material is losing mass and softening at the same time. Hence, we can identify the four quadrants as follows: (I) mass loss and softening; (II) mass loss and stiffening; (III) mass increase and stiffening; (IV) mass increase and softening. For p(g3T2), at each concentration, we record the viscoelastic properties for 30 s in the pristine state, and then we apply the oxidation voltage (expansion, +0.5 V) for 30 s while recording the F and D values; finally, we apply the reduction voltage (contraction, −0.5 V) for 30 s still recording the F and D. We then select one point every 3 s and we report it in the D(F) plot: under each condition (pristine, +0.5 V and −0.5 V), a total of 10 points are reported, which represent the time evolution of the change in viscoelastic properties.

We observe that when p(g3T2) expands, the viscoelastic properties change towards the IV quadrant for all electrolytes; hence, the frequency decreases while the dissipation increases, indicating mass increase and softening of the polymer (Table 1 and Fig. 1(E)). Similarly to the observed volume change, the effect is more pronounced for the 0.01 M electrolyte, while it becomes less strong with increasing electrolyte concentration. When p(g3T2) contracts, we observe mass loss and stiffening of the films as indicated by frequency and dissipation changes towards the values of the pristine state. For 0.01 M and 0.1 M, F and D do not return to the initial values indicating that the more the polymer is expanded, the bigger is the irreversible effect on the polymer structure. This break-in effect can be explained by water and ions that remain in the film after contraction, combined with irreversible changes of the polymer chain conformation and reorganization of the polymer matrix upon expansion.^12,28 Indeed, molecular dynamics calculations have shown that during expansion, the polymer chains slide along each other creating pores while still interacting via the π–π stacking of the backbones.⁴⁰ The hydrophilic EG-side chains possibly stabilize the water and ions in the film. Indeed, water has been shown to contribute to the volumetric expansion of a similar oligothiophene polymer (p(gT2-TT)),²⁸ thus a similar behavior for p(g3T2) is expected. Furthermore, it has been shown that after applying a reducing potential, p(g3T2) recovers its initial absorption spectrum,⁴² indicating that the doping/dedoping process per se is reversible.

Table 1 Frequency and dissipation changes of p(g3T2) in the expanded and contracted states

KCl concentration	0.01 M		0.1 M		1 M
	ΔF (Hz)	ΔD (1 × 10^−6)	ΔF (Hz)	ΔD (1 × 10^−6)	ΔF (Hz)	ΔD (1 × 10^−6)
Expanded state	−364.6 ± 44	30.3 ± 14.7	−181.9 ± 9.4	8.3 ± 2.8	−83.3 ± 9.6	2.9 ± 2.6
Contracted state	−71.2 ± 11.4	2 ± 1.6	−21.6 ± 21.9	0.5 ± 0.6	−6.2 ± 7.8	−0.1 ± 0.3

---

Overall, the observed changes in mass and softness probed by eQCM-D for p(g3T2) in the different electrolytes agree with the trends of the volume changes observed in the fiber geometry. To quantitatively evaluate the changes in the polymer film mechanical properties we performed in situ electrochemical atomic force microscopy (EC-AFM) during electrochemical addressing.

For EC-AFM, the polymer was deposited by spin coating on a gold substrate, acting as working electrode in a three-electrode cell setup. Imaging of the topography and indentations was performed in situ under dry and wet conditions (different electrolyte concentrations) as well as under different applied potentials.

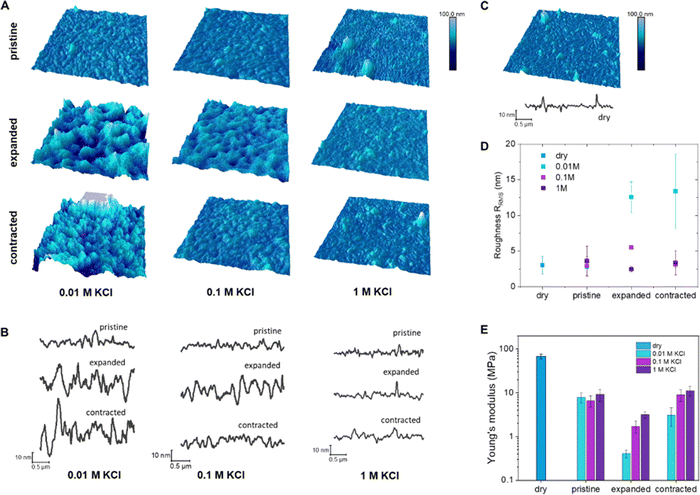
The polymer films in the dry state show a distinct fibrillar morphology with bunches of fibers packed in compact features and holes, 30–50 nm in diameter, were present in between them. When hydrated in a KCl electrolyte solution (without application of bias), this morphology is still clearly visible, but the elongated features appear wider, especially in diluted electrolyte (Fig. 2(B), and (C)) signifying passive swelling. The root mean square roughness, R_RMS, does not change much after hydration, going from 3.02 ± 1.23 nm in the dry state to 2.78 ± 0.22, 2.92 ± 1.36 and 3.60 ± 2.13 nm for KCl 0.01, 0.1 and 1 M, respectively (Fig. 2(D) and Table 2). When the polymer is electrochemically oxidized, a distinct change in the morphology occurs, with wider and taller features as well as larger spaces in between them (Fig. 2(A) and (B)) in agreement with the volume changes observed via microscopy. The R_RMS increases to 12.55 ± 2.14 and 5.51 ± 0.27 for KCl 0.01 and 0.1 M, respectively, while it does not change for KCl 1 M (2.46 ± 0.38 nm). Upon reduction, R_RMS remains high for KCl 0.01M (13.39 ± 5.15 nm), while it decreases to pristine values for KCl 0.1 (3.11 ± 0.41 nm) and 1 M (3.37 ± 1.68 nm).

Fig. 2 (A) Topography and (B) section profiles of p(g3T2)'s pristine, expanded and contracted states in 0.01, 0.1 and 1 M KCl. (C) Topography and section profile of dry p(g3T2) film. (D) Root mean square roughness RRMS of p(g3T2) films in the different states and electrolytes. (E) Young's moduli in the different states and electrolytes.

Table 2 Root mean square roughness of p(g3T2) at different electrolyte concentrations and states

KCl concentration	R RMS pristine (nm)	R RMS oxidation (nm)	R RMS reduction (nm)
Dry	3.02 ± 1.23
0.01 M	2.78 ± 0.22	12.55 ± 2.14	13.39 ± 5.15
0.1 M	2.92 ± 1.36	5.51 ± 0.27	3.11 ± 0.41
1 M	3.60 ± 2.13	2.46 ± 0.38	3.37 ± 1.68

---

When the films are electrochemically reduced (dedoped), the surface topography does not recover to the pristine hydrated state with clear distinct fibrils, but exhibits a more amorphous and slightly swollen surface. The irreversible changes in topography are more pronounced for 0.01 M KCl electrolyte in agreement with the irreversible break-in effects in mass and volume described in the previous section. Indentations at a constant loading force were performed to measure force–displacement curves and extract the Young's modulus of each sample in the different electrolytes and under different applied potentials. The trend in Young's modulus correlates with the trends observed for volume expansion as well as mass and dissipation changes (Fig. 1). In the dry state, the thin films of p(g3T2) have a Young's modulus of 68.04 ± 8.9 MPa (Fig. 2), which decreases up to one order of magnitude once exposed to the electrolytes, with no clear trend between the electrolyte concentrations. In contrast, when p(g3T2) is expanded, the Young's modulus decreases further with increasing electrolyte concentration, with values of 0.41 ± 0.08, 1.71 ± 0.51 and 3.18 ± 0.51 MPa in 0.01, 0.1 and 1 M KCl, respectively (Table 3). Once p(g3T2) is contracted again (−0.2 V), the polymer's Young's moduli are increasing again to values of 3.12 ± 1.4, 9.03 ± 2.64 and 11.14 ± 2.68 MPa in 0.01, 0.1 and 1 M KCl, respectively. In agreement with previous observations, the initial film properties are recovered for 0.1 and 1 M KCl, while in the case of 0.01 M the Young's modulus is only about half as high as for the electrolyte exposed pristine films.

Table 3 Young's modulus of p(g3T2) at different electrolyte concentrations and states

	Pristine (MPa)	Expanded (MPa)	Contracted (MPa)
Dry	68.04 ± 8.97
0.01 M KCl	7.88 ± 2.08	0.41 ± 0.08	3.12 ± 1.40
0.1 M KCl	6.59 ± 1.86	1.71 ± 0.51	9.03 ± 2.64
1 M KCl	9.14 ± 2.75	3.18 ± 0.51	11.14 ± 2.68

---

The electrochemically controllable Young's modulus of p(g3T2) with values between 0.4 MPa and 11 MPa is similar to that of a wide range of tissues,⁴⁵ highlighting the potential of p(g3T2) for biointerface applications.

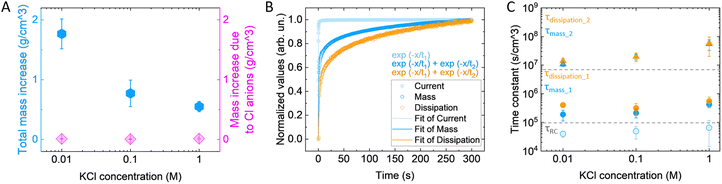
To further elucidate the mechanisms involved during polymer expansion and the role of electrolyte concentration, we attempted to decouple the contribution of ions and water in the volume change. Assuming that during doping each hole is compensated by one anion (1h⁺:1Cl⁻), we calculated the expected mass change due to the anion intake. We found that the anion mass intake is independent of the electrolyte concentration (Fig. 3(A)), indicating that the polymer reaches the same doping level and in agreement with previously reported results for similar polymers.²⁸ In contrast, the mass change recorded by the eQCM-D is concentration dependent, and much bigger than the calculated mass change due to the anion intake (Fig. 3(A)). Even by including the hydration shell of the anions (according to ref. 46, reported in Fig. S3, ESI†), the calculated mass is still lower than the mass recorded with the eQCM-D, indicating that water molecules not associated with the anions still enter the film.

Fig. 3 (A) The total mass increase of p(g3T2) films vs. the calculated one expected from the anion intake at the end of the oxidation cycle, normalized by the volumetric change. (B) Normalized dynamics of current, mass and dissipation during oxidation of the p(g3T2) film in KCl 0.01 M for a representative sample. The dynamics were normalized between 0 (min) and 1 (max). The current normalized dynamics were also reversed for a better comparison. The continuous lines indicate the fitting with single or double phase exponential decay for each case, as in the inset. (C) Extracted time constants as a function of the electrolyte concentration for the current, mass and dissipation. For panels (A) and (C), the results are reported as avg ± SD.

The mass change as a function of time is described by a two-phase exponential decay with a fast and a slow components, with time constants of τ_{mass_1} = 1.13 ± 0.37 s and τ_{mass_2} = 66.1 ± 16.8 s, respectively (Fig. 3(B)). On the other hand, the associated current is described by a single-phase exponential decay with a faster time constant, (τ_RC = 0.24 ± 0.08 s). The charge compensation is the first occurring phenomenon, followed by the mass increase. The charge compensation occurs over time, reaching an equilibrium of almost zero Ampere, like the profile of a charging capacitor. As it is described by an exponential, after a timeframe equivalent to 5τ_RC the current reaches 99% of the final value; hence, it is considered fully charged. Noteworthy, the first time constant of the mass falls within the extinction of the charge compensation (τ_{mass_1} < 5τ_RC), possibly associated with ions moving in the polymer due to the sudden change in the electric field,⁴⁷ while the second one is two orders of magnitude slower (τ_{mass_2} ≫ 5τ_RC). This signifies that extra water is driven in the polymer, as the charge compensation is already completed. We then calculated the time constants related to the viscoelastic properties by fitting the dissipation change. In this case as well, the dissipation change is described with two time constants that are bigger than the ones of mass change, indicating that the viscoelastic properties change as a consequence of the anion and water intake. The time constant of the current, i.e., the charging speed, is not affected by the electrolyte concentration (Fig. 3(C), exact values reported in Table 4), in agreement with previous findings.^28,48,49 Both τ_{mass_1} and τ_{diss_1} are only slightly affected by the electrolyte concentration, indicating that the charge compensation by the anions affects the volumetric change and the elastic properties only to a small extent. On the contrary, the time constants depending on water intake (τ_{mass_2} and τ_{diss_2}) are affected, becoming up to 5 times slower in KCl 1 M compared to 0.01 M.

Table 4 Time constants of current, mass and dissipation for p(g3T2) films upon expansion, normalized by the volume

KCl concentration (M)	Time constant current (s cm^−3)	Time constant mass (τmass_1) (s cm^−3)	Time constant mass (τmass_2) (s cm^−3)	Time constant dissipation (τdiss_1) (s cm^−3)	Time constant dissipation (τdiss_2) (s cm^−3)
0.01	3.9 × 10^4 ± 0.96 × 10^4	1.9 × 10^5 ± 0.76 × 10^5	1.07 × 10^7 ± 0.18 × 10^7	4 × 10^5 ± 0.48 × 10^5	1.39 × 10^7 ± 0.33 × 10^7
0.1	4.8 × 10^4 ± 2.28 × 10^4	2.1 × 10^5 ± 0.70 × 10^5	1.9 × 10^7 ± 0.44 × 10^7	3.1 × 10^5 ± 1.42 × 10^5	1.97 × 10^7 ± 0.64 × 10^7
1	6.4 × 10^4 ± 5.01 × 10^4	4.2 × 10^5 ± 0.99 × 10^5	5.4 × 10^7 ± 2.2 × 10^7	5.5 × 10^5 ± 2.2 × 10^5	5.83 × 10^7 ± 3.8 × 10^7

---

One question that remains is: what drives the extra water to enter the polymer matrix after the anions have compensated the electronic charges? From the time constants of the various processes, we hypothesize that once the hydrated anions enter into the polymer matrix, the latter behaves as a semipermeable membrane.²⁸ In the polymer matrix, the concentration of water molecules and ions is different from the one in the electrolyte, which creates a concentration gradient that drives water molecules into the polymer due to osmotic forces. In agreement with this hypothesis, in the more diluted electrolyte, we recorded the higher volumetric change for a comparable polymer charging (Fig. S4, ESI†), as the concentration gradient of water and ions between polymer and surrounding electrolyte is bigger. By increasing the ionic strength, the concentration gradient decreases, resulting in less water intake, as well as smaller volume change. Indeed, by calculating the anion concentration we found that the concentration of the anions in the expanded polymer is higher than that in the electrolyte (Fig. S5, ESI†).

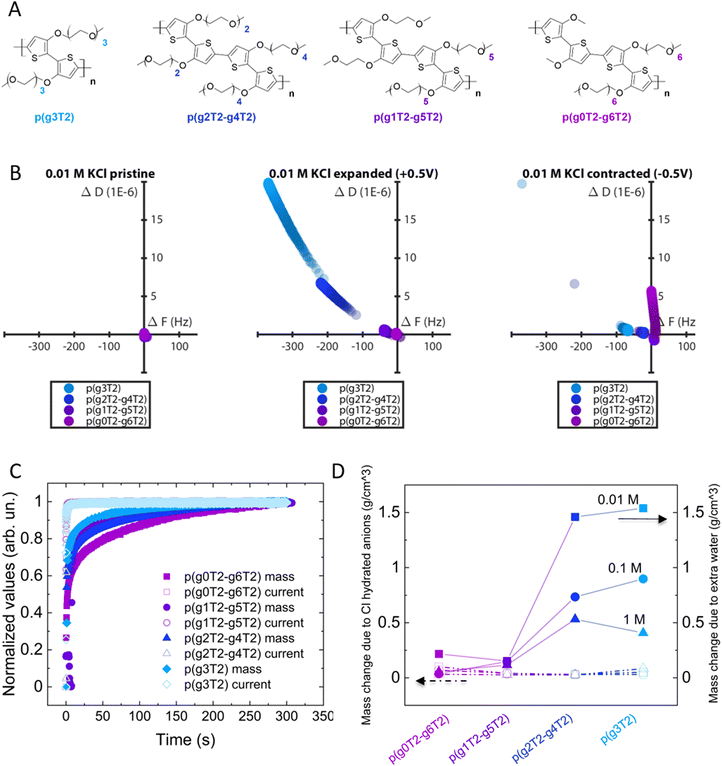
To investigate if the polymer's molecular structure impacts the changes in the volume and viscoelastic properties during electrochemical addressing, we studied using eQCM-D a series of polythiophenes with EG side chains varying in length and asymmetry (Fig. 4(A)) while keeping the total number of EG units constant.⁴²

Fig. 4 (A) Chemical structure of the studied polythiophenes with increasing side chain asymmetry. (B) D(F) plots of the different polymers in KCl 0.01 M for the pristine, expanded and contracted states. (C) Normalized mass and current changes for the different polymers in KCl 0.01 M. The dynamics were normalized between 0 (min) and 1 (max). The current was normalized and reversed for a straightforward comparison with the mass. (D) Comparison of mass change due to Cl intake (calculated from charge) and mass change recorded by eQCM-D. The values are normalized by the volumetric change under each condition.

From D(F) plots of pristine and expanded state we clearly see that by increasing the side chain asymmetry, the changes in mass and viscoelastic properties are less pronounced. When the polymers return to the contracted state, we observe irreversible changes in all polymers, with more irreversibility for p(g3T2) (Fig. 4(B)).

It is noteworthy that p(g0T2–g6T2) shows a strong dissipation drift in the contracted state, indicating that the material cannot be controlled as reliably as the other polymers. Additionally, p(g0T2–g6T2) also shows a positive frequency value in the contracted state, indicating a mass loss with respect to the pristine state exposed to the electrolyte. This indicates an immediate passive swelling of the material when it is exposed to the electrolyte. P(g1T2–g5T2) behaves similarly but to a lower extent. This passive swelling, however, is absent for p(g4T2)–(g2T2) and for p(g3T2), indicating that the passive swelling might be correlated to the longest side chains of p(g0T2–g6T2) and p(g1T2–g5T2). All the polymers charge to a comparable extent (Fig. S4, ESI†) and at the same speed (Fig. 4(C)). Accordingly, the mass change driven by anion intake (calculated by assuming that for each injected hole a Cl anion compensates) is comparable between the different polymers and the different electrolytes. On the contrary, the time constant of the mass change depends both on the side chains and the electrolyte concentration (Fig. 4(C) and (D)). We compared the mass change extracted from the charge compensation with that extracted directly from eQCM-D. Assuming that the mass change is driven only by water and Cl anions, the difference between the mass of eQCM-D and the Cl one gives the extra water loaded in the polymer. For most polymers, the higher the asymmetry of the side chains the lower the amount of loaded water (Fig. 4(D)), despite the longer time required to drive the mass change (Fig. 4(C)). Longer chains possibly need more time to rearrange.⁴² For increasing electrolyte concentration, less water is loaded in the materials, which is reflected in a weaker softening effect (Fig. S6 and S7, ESI†) and a lower volumetric increase (Fig. S8, ESI†).

Conclusions

In conclusion, we demonstrate that with electrochemical doping we can modulate the mechanical properties of OMIECs. We find that p(g3T2) is a soft OMIEC with a Young's Modulus of 68 ± 8.97 MPa and less than 10 MPa in dry and hydrated states, respectively. When electrochemically doped the Young's modulus of p(g3T2) decreases by more than one order of magnitude, and in a reversible manner, reaching a value of 0.4 ± 0.08 MPa. To the best of our knowledge, this is the largest modulation of a OMIEC's Young's modulus with electrochemical doping; however, only a few studies have focused on this topic.¹² We attribute the changes in the mechanical properties of p(g3T2) to the large volume change that occurs upon doping of more than 1000%. The change in mechanical properties depends on the electrolyte concentration used; the more concentrated the electrolyte the less the change in mechanical properties, even if the polymer is doped to the same extent. We argue that this process is driven by osmosis where in a less concentrated electrolyte there is a higher ionic gradient between the charged polymer and the surrounding electrolyte; hence osmosis drives more water molecules into the bulk of the polymer. Furthermore, we propose representing the eQCM-D data in D(F) plots to qualitative assess changes in mass and softness. While eQCM-D is very powerful for monitoring small mass changes, extracting quantitative parameters for the viscoelastic properties is very challenging⁵⁰ due to the multiparameter fitting. Plotting the frequency change as a function of the dissipation change facilitates visual assessment of the changes in mass and viscoelastic properties and comparison of different conditions or materials. In this way, we show that by increasing the EG-side chain asymmetry in a series of polythiophenes, the change in mass and viscoelastic properties is less pronounced. Our study demonstrates that EG-side chain polythiophenes are promising candidates for mechanical actuators, as, depending on the applied voltage, the electrolyte composition, and the side chain functionality, it is possible to deliver different mechanical stimuli on demand. With controllable Young's modulus between 0.4 MPa and 11 MPa, a range that is similar to that of tissues, we expect these materials will be of great interest for biointerfacing applications.

Materials and methods

Synthesis of glycolated polymers

Glycolated polymers were synthesized as presented before.⁴²

Electrochemical characterization

Fibers were coated in a rotating fashion where the carbon fiber was slowly pulled out of the polymer solution in chloroform situated in a glass capillary to reduce the evaporation speed by reducing the exposed surface. The fibers were mounted in an enclosed custom setup with the electrolyte in a 3-electrode configuration with the coated fiber as working, Pt wire as counter and an Ag/AgCl wire as pseudo reference. The custom setup was mounted under a stereo microscope (Nikon SMZ1500, Nikon WD45 lens, Nikon DS-Fi1 camera, Nikon NIS Elements software) and the volume expansion was monitored, following an electrochemical stimulation controlled with Metrohm μAutolab Type III and the Autolab Nova 2 software. The polymer volume was computationally extracted from the micrographs based on a gray value threshold assuming a cylindrical shape (Fig. S1, ESI†). Details can be found in previous publications.⁴⁰

Quartz microbalance characterization

Electrochemical Quartz Crystal Microbalance with Dissipation (eQCM-D) was performed with a QSense Analyzer E4 on gold coated Quartzes (5 MHz, QSX301). The gold surface served as the working electrode in a 3-electrode setup with platinum as the counter electrode, which is part of the eQCM-D chamber, and an Ag/AgCl reference electrode specific to the device (WPI Dri-Ref). The electrochemistry was controlled with a potentiostat of type Metrohm μAutolab Type III and the Autolab Nova 2 software package. For every sample an eQCM-D baseline in air and the respective electrolyte was acquired. Then a polymer film was applied by spin coating (3000 rpm acc., 3000 rpm, 60 s) with a drop of 50 μl of 2.5 mg ml⁻¹ polymer in chloroform. The polymer coated QCM quartz was mounted in eQCM-D and baselines in air and electrolyte were acquired again. Finally, the electrochemical experiment was performed. After the experiment, the individual sections (baselines and experiment) were stitched together and the data were fitted using the QSense DFind software package.

The mass change was extracted using the Sauerbrey equation. Despite the softness of the material, which is also expected to get more hydrated (hence even softer) during electrochemical cycling, the Sauerbrey equation still gives a good estimate of these parameters since the films are thin.

Electrochemical AFM (EC-AFM)

Electrochemical AFM (EC-AFM) experiments were performed on a Dimension Icon XR (Bruker). The polymer films were deposited by spin coating on a gold substrate acting as a working electrode. These samples were then mounted in an electrochemical cell connected to a bipotentiostat and filled with the desired electrolyte. A Pt wire and an Ag wire were used as the counter and reference electrodes, respectively. AFM imaging was performed in the off-resonance mode with silicon nitride probes having a nominal tip radius of 20 nm. The roughness of the films under different conditions was obtained by averaging the R_RMS values measured on different regions (1 μm² area) of an image. During imaging the applied force was controlled so as not to exceed a few nN. For elastic modulus measurements the deflection sensitivity of each probe was calibrated by repeated indentation on a clean sapphire substrate in 1, 0.1 or 0.01 mM KCl, and the spring constant of the cantilever was estimated by the thermal noise method. Indentations were performed by bringing the AFM probe in contact with the sample surface at a controlled load force and recording force–displacement curves during the loading–unloading cycles. Measurements were performed by acquiring 100 force curves per sample, at a maximum load of 2 nN. The elastic modulus was obtained by fitting the force curves through a linearized Hertz model:
where F is the force, d is the sample deformation, E is the Young's modulus, ν is the Poisson ratio, and R is the radius of the indenting probe. A Poisson ratio of 0.3 was considered for all the fittings.

Conflicts of interest

The authors declare that there are no conflicts of interest pertaining to the content of this manuscript.

Acknowledgements

The authors thank Dr. Achilleas Savva (TU Delft) for fruitful discussions on eQCM-D data analysis. The authors acknowledge support from the Swedish Foundation for Strategic Research (Grant Nr. FFL18-0101), the Swedish Research Council (Grant Nr. VR-2020-05045) and the Swedish Government Strategic Research Area in Materials Science on Advanced Functional Materials at Linköping University (Faculty Grant SFO-Mat-LiU No. 2009-00971).

References

1. J. Rivnay, R. M. Owens and G. G. Malliaras, The rise of organic bioelectronics, Chem. Mater., 2014, 26(1), 679–685,  DOI:10.1021/CM4022003/ASSET/IMAGES/MEDIUM/CM-2013-022003_0004.GIF.
2. B. D. Paulsen, K. Tybrandt, E. Stavrinidou and J. Rivnay, Organic mixed ionic–electronic conductors, Nat. Mater., 2019, 19(1), 13–26,  DOI:10.1038/s41563-019-0435-z.
3. D. Khodagholy, et al., NeuroGrid: recording action potentials from the surface of the brain, Nat. Neurosci., 2015, 18(2), 310–315,  DOI:10.1038/nn.3905.
4. D. Khodagholy, et al., In vivo recordings of brain activity using organic transistors, Nat. Commun., 2013, 4(1), 1–7,  DOI:10.1038/ncomms2573.
5. J. Rivnay, et al., High-performance transistors for bioelectronics through tuning of channel thickness, Sci. Adv., 2015, 1, 4,  DOI:10.1126/SCIADV.1400251.
6. D. Cao, J. G. Martinez, E. S. Hara and E. W. H. Jager, Biohybrid Variable-Stiffness Soft Actuators that Self-Create Bone, Adv. Mater., 2022, 34(8), 2107345,  DOI:10.1002/adma.202107345.
7. Z. Lin, et al., Recent Advances in Perceptive Intelligence for Soft Robotics, Adv. Intell. Syst., 2023, 5(5), 2200329,  DOI:10.1002/AISY.202200329.
8. X. Dong, et al., Recent advances in biomimetic soft robotics: fabrication approaches, driven strategies and applications, Soft Matter, 2022, 18(40), 7699–7734,  10.1039/D2SM01067D.
9. M. Criado-Gonzalez, A. Dominguez-Alfaro, N. Lopez-Larrea, N. Alegret and D. Mecerreyes, Additive Manufacturing of Conducting Polymers: Recent Advances, Challenges, and Opportunities, ACS Appl. Polym. Mater., 2021, 3(6), 2865–2883,  DOI:10.1021/ACSAPM.1C00252/ASSET/IMAGES/LARGE/AP1C00252_0007.JPEG.
10. B. Guo and P. X. Ma, Conducting Polymers for Tissue Engineering, Biomacromolecules, 2018, 19(6), 1764,  DOI:10.1021/ACS.BIOMAC.8B00276.
11. H. Maddali, K. L. House, T. J. Emge and D. M. O’Carroll, Identification of the local electrical properties of crystalline and amorphous domains in electrochemically doped conjugated polymer thin films, RSC Adv., 2020, 10(36), 21454–21463,  10.1039/D0RA02796K.
12. S. Benaglia, S. Drakopoulou, F. Biscarini and R. Garcia, In operando nanomechanical mapping of PEDOT:PSS thin films in electrolyte solutions with bimodal AFM, Nanoscale, 2022, 14(38), 14146–14154,  10.1039/D2NR02177C.
13. K. Namsheer and C. S. Rout, Conducting polymers: a comprehensive review on recent advances in synthesis, properties and applications, RSC Adv., 2021, 11(10), 5659–5697,  10.1039/D0RA07800J.
14. F. Hu, Y. Xue, J. Xu and B. Lu, PEDOT-Based Conducting Polymer Actuators, Front. Robot. AI, 2019, 6, 486225,  DOI:10.3389/FROBT.2019.00114/BIBTEX.
15. M. S. Ting, J. Travas-Sejdic and J. Malmström, Modulation of hydrogel stiffness by external stimuli: soft materials for mechanotransduction studies, J. Mater. Chem. B, 2021, 9(37), 7578–7596,  10.1039/D1TB01415C.
16. M. S. Ting, et al., Conducting polymer hydrogels with electrically-tuneable mechanical properties as dynamic cell culture substrates, Biomater. Adv., 2022, 134, 112559,  DOI:10.1016/J.MSEC.2021.112559.
17. M. S. Ting, B. N. Narasimhan, J. Travas-Sejdic and J. Malmström, Soft conducting polymer polypyrrole actuation based on poly(N-isopropylacrylamide) hydrogels, Sens. Actuators, B, 2021, 343, 130167,  DOI:10.1016/J.SNB.2021.130167.
18. C. J. G. Abrego, et al., Multiscale Characterization of the Mechanical Properties of Fibrin and Polyethylene Glycol (PEG) Hydrogels for Tissue Engineering Applications, Macromol. Chem. Phys., 2022, 223(1), 2100366,  DOI:10.1002/MACP.202100366.
19. C. M. Tringides, M. Boulingre, A. Khalil, T. Lungjangwa, R. Jaenisch and D. J. Mooney, Tunable Conductive Hydrogel Scaffolds for Neural Cell Differentiation, Adv. Healthcare Mater., 2023, 12(7), 2202221,  DOI:10.1002/ADHM.202202221.
20. C. M. Tringides, et al., Viscoelastic surface electrode arrays to interface with viscoelastic tissues, Nat. Nanotechnol., 2021, 16(9), 1019–1029,  DOI:10.1038/s41565-021-00926-z.
21. R. Green, M. R. Abidian, R. Green and M. R. Abidian, Conducting Polymers for Neural Prosthetic and Neural Interface Applications, Adv. Mater., 2015, 27(46), 7620–7637,  DOI:10.1002/ADMA.201501810.
22. B. Lu, et al., Pure PEDOT:PSS hydrogels, Nat. Commun., 2019, 10(1), 1–10,  DOI:10.1038/s41467-019-09003-5.
23. B. O’Connor, et al., Correlations between mechanical and electrical properties of polythiophenes, ACS Nano, 2010, 4(12), 7538–7544,  DOI:10.1021/NN1018768/ASSET/IMAGES/LARGE/NN-2010-018768_0005.JPEG.
24. P. J. W. Sommerville, et al., Influence of Side Chain Interdigitation on Strain and Charge Mobility of Planar Indacenodithiophene Copolymers, ACS Polym. Au, 2022, 3(1), 59–69,  DOI:10.1021/ACSPOLYMERSAU.2C00034.
25. S. Zokaei, et al., Tuning of the elastic modulus of a soft polythiophene through molecular doping, Mater. Horiz., 2022, 9(1), 433–443,  10.1039/D1MH01079D.
26. S. Hultmark, et al., Impact of oxidation-induced ordering on the electrical and mechanical properties of a polythiophene co-processed with bistriflimidic acid, J. Mater. Chem. C, 2023, 11(24), 8091–8099,  10.1039/D2TC03927C.
27. C. M. Tringides, et al., Viscoelastic surface electrode arrays to interface with viscoelastic tissues, Nat. Nanotechnol., 2021, 16(9), 1019–1029,  DOI:10.1038/s41565-021-00926-z.
28. A. Savva, et al., Influence of Water on the Performance of Organic Electrochemical Transistors, Chem. Mater., 2019, 31(3), 927–937,  DOI:10.1021/acs.chemmater.8b04335.
29. C. Cendra, et al., Role of the Anion on the Transport and Structure of Organic Mixed Conductors, Adv. Funct. Mater., 2019, 29(5), 1807034,  DOI:10.1002/ADFM.201807034.
30. D. Melling, J. G. Martinez and E. W. H. Jager, Conjugated Polymer Actuators and Devices: Progress and Opportunities, Adv. Mater., 2019, 31(22), 1808210,  DOI:10.1002/ADMA.201808210.
31. Y. Wu, et al., Electrochemical actuation properties of a novel solution-processable polythiophene, Electrochim. Acta, 2007, 53(4), 1830–1836,  DOI:10.1016/J.ELECTACTA.2007.08.041.
32. P. R. Singh, S. Mahajan, S. Rajwade and A. Q. Contractor, EC-AFM investigation of reversible volume changes with electrode potential in polyaniline, J. Electroanal. Chem., 2009, 625(1), 16–26,  DOI:10.1016/J.JELECHEM.2008.10.005.
33. E. Smela, M. Kallenbach and J. Holdenried, Electrochemically driven polypyrrole bilayers for moving and positioning bulk micromachined silicon plates, J. Microelectromech. Syst., 1999, 8, 373–383 , Accessed: 23, 2023. [Online]. Available: https://orbit.dtu.dk/en/publications/electrochemically-driven-polypyrrole-bilayers-for-moving-and-posi.
34. E. Smela and N. Gadegaard, Surprising volume change in PPy(DBS): An atomic force microscopy study, Adv. Mater., 1999, 11(11), 953–957,  DOI:10.1002/(SICI)1521-4095(199908)11:11.
35. M. R. Gandhi, P. Murray, G. M. Spinks and G. G. Wallace, Mechanism of electromechanical actuation in polypyrrole, Synth. Met., 1995, 73(3), 247–256,  DOI:10.1016/0379-6779(95)80022-0.
36. M. Kaneko and K. Kaneto, Electrochemomechanical deformation of polyaniline films doped with self-existent and giant anions, React. Funct. Polym., 1998, 37(1–3), 155–161,  DOI:10.1016/S1381-5148(97)00175-2.
37. Q. Pei and O. Inganäs, Electroelastomers: Conjugated poly(3-octylthiophene) gels with controlled crosslinking, Synth. Met., 1993, 57(1), 3724–3729,  DOI:10.1016/0379-6779(93)90504-P.
38. E. Smela and N. Gadegaard, Volume change in polypyrrole studied by atomic force microscopy, J. Phys. Chem. B, 2001, 105(39), 9395–9405,  DOI:10.1021/JP004126U/ASSET/IMAGES/LARGE/JP004126UF00015.JPEG.
39. R. Giridharagopal, et al., Electrochemical strain microscopy probes morphology-induced variations in ion uptake and performance in organic electrochemical transistors, Nat. Mater., 2017, 16(7), 737–742,  DOI:10.1038/NMAT4918.
40. J. Gladisch, et al., Reversible Electronic Solid–Gel Switching of a Conjugated Polymer, Adv. Sci., 2020, 7(2), 1901144,  DOI:10.1002/ADVS.201901144.
41. M. Moser, et al., Controlling Electrochemically Induced Volume Changes in Conjugated Polymers by Chemical Design: from Theory to Devices, Adv. Funct. Mater., 2021, 31(26), 2100723,  DOI:10.1002/ADFM.202100723.
42. M. Moser, et al., Side Chain Redistribution as a Strategy to Boost Organic Electrochemical Transistor Performance and Stability, Adv. Mater., 2020, 32(37), 2002748,  DOI:10.1002/adma.202002748.
43. J. Gladisch, et al., An Electroactive Filter with Tunable Porosity Based on Glycolated Polythiophene, Small Sci., 2022, 2(4), 2100113,  DOI:10.1002/SMSC.202100113.
44. A. Savva, S. Wustoni and S. Inal, Ionic-to-electronic coupling efficiency in PEDOT:PSS films operated in aqueous electrolytes, J. Mater. Chem. C, 2018, 6(44), 12023–12030,  10.1039/C8TC02195C.
45. T. R. Cox and J. T. Erler, Remodeling and homeostasis of the extracellular matrix: implications for fibrotic diseases and cancer, Dis. Models Mech., 2011, 4(2), 165–178,  DOI:10.1242/DMM.004077.
46. Y. Marcus, Concentration dependence of ionic hydration numbers, J. Phys. Chem. B, 2014, 118(35), 10471–10476,  DOI:10.1021/JP5039255/ASSET/IMAGES/JP-2014-039255_M017.GIF.
47. R. Wu, B. D. Paulsen, Q. Ma and J. Rivnay, Mass and Charge Transport Kinetics in an Organic Mixed Ionic−Electronic Conductor, Chem. Mater., 2022, 34(21), 9699–9710,  DOI:10.1021/acs.chemmater.2c02476.
48. D. Moia, et al., Design and evaluation of conjugated polymers with polar side chains as electrode materials for electrochemical energy storage in aqueous electrolytes, Energy Environ. Sci., 2019, 12(4), 1349–1357,  10.1039/c8ee03518k.
49. A. Giovannitti, et al., Controlling the mode of operation of organic transistors through side-chain engineering, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(43), 12017–12022,  DOI:10.1073/PNAS.1608780113/SUPPL_FILE/PNAS.1608780113.SAPP.PDF.
50. A. D. Easley, T. Ma, C. I. Eneh, J. Yun, R. M. Thakur and J. L. Lutkenhaus, A practical guide to quartz crystal microbalance with dissipation monitoring of thin polymer films, J. Polym. Sci., 2022, 60(7), 1090–1107,  DOI:10.1002/POL.20210324.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mh01827j

‡ Equally contributing authors.

---