Molecularly induced order promotes charge separation through delocalized charge-transfer states at donor–acceptor heterojunctions

Abstract

The energetic landscape at the interface between electron donating and accepting molecular materials favors efficient conversion of intermolecular charge-transfer (CT) states into free charge carriers (FCC) in high-performance organic solar cells. Here, we elucidate how interfacial energetics, charge generation and radiative recombination are affected by molecular arrangement. We experimentally determine the CT dissociation properties of a series of model, small molecule donor–acceptor blends, where the used acceptors (B2PYMPM, B3PYMPM and B4PYMPM) differ only in the nitrogen position of their lateral pyridine rings. We find that the formation of an ordered, face-on molecular packing in B4PYMPM is beneficial to efficient, field-independent charge separation, leading to fill factors above 70% in photovoltaic devices. This is rationalized by a comprehensive computational protocol showing that, compared to the more amorphous and isotropically oriented B2PYMPM, the higher structural order of B4PYMPM molecules leads to more delocalized CT states. Furthermore, we find no correlation between the quantum efficiency of FCC radiative recombination and the bound or unbound nature of the CT states. This work highlights the importance of structural ordering at donor–acceptor interfaces for efficient FCC generation and shows that less bound CT states do not preclude efficient radiative recombination.

---

Koen Vandewal

Congratulations on 10 years of leadership in the field of materials science! Materials Horizons has consistently served as a primary resource for staying updated on the latest advancements in materials science. As a proud contributor since 2020, I eagerly anticipate the exciting future of the journal.

David Beljonne

As a member of the advisory board and as a contributing author, I have witnessed how Materials Horizons has contributed disseminating new ideas and concepts in materials science. Happy Anniversary!

Donato Spoltore

I always enjoy reading the papers published in Materials Horizons, a fundamental source to learn the newest developments in materials science. We are excited to contribute with this article, certain that it will inspire enlightening new studies. Congratulations on the first decade of successes and best wishes for the next decade at the forefront of materials science!

---

New concepts

Organic materials feature strong excitonic effects because of their low dielectric constants. Despite this, thermalized charge-transfer (CT) states efficiently separate into free charge carriers in organic solar cells. Several mechanisms have been proposed to rationalize this efficient charge generation, but a consensus is lacking. Here, we study vacuum deposited donor–acceptor blends consisting of several donors mixed with the acceptors B2PYMPM, B3PYMPM and B4PYMPM, which only differ in the nitrogen position of substituted pyridine rings. Remarkably, such a subtle change in the primary molecular structure drives strikingly large differences in the molecular packing. In particular, B4PYMPM adopts an ordered, face-on, molecular organization at surfaces and interfaces. Compared to the more amorphous and isotropically oriented B2PYMPM, the higher structural order in B4PYMPM leads to more delocalized interfacial CT states, which in turn foster efficient charge separation. Also, we find no correlation between the radiative recombination quantum efficiency and the bound or unbound character of the CT states. This is encouraging and helpful for guiding the design of new organic photovoltaic materials, as high radiative recombination efficiency and high CT state dissociation yield are required for highly efficient organic photovoltaics with low voltage losses.

1. Introduction

Blends of electron donating (D) and electron accepting (A) organic compounds find their applications in organic solar cells (OSCs) and organic light-emitting diodes (OLEDs). The power conversion efficiencies (PCEs) of OSCs exceed 18%,¹ thanks to the development of new strongly absorbing non-fullerene acceptors. Furthermore, D–A blends are regularly used as host materials for OLEDs with a low driving voltage and improved power efficiency.² Indeed, electroluminescence quantum efficiencies of 21.7% have been reported for D–A (or exciplex) OLEDs.^3,4 Recently, some of those visible light-emitting D–A blends have been discovered to also exhibit a high photovoltaic quantum efficiency.^5,6 These peculiar systems, as compared to the more commonly studied photovoltaic blends with optical gaps in the near-infrared, benefit from reduced non-radiative decay rates for their visible light-emitting charge-transfer (CT) states, but the origin of their efficient CT state dissociation has not been disclosed to date.

Because of low dielectric constants in organic materials, both the photo-induced local exciton (LE) and the CT state are expected to be strongly bound by Coulomb forces.⁷ This has raised a long-standing fundamental question: how can thermalized CT states overcome this binding energy and split into free charge carriers (FCC)? Over the years, several mechanisms have been proposed in the literature and, depending on the system under investigation, interface morphology,^8,9 energetic disorder,^10,11 electrostatic effects,¹² charge delocalization,^13–16 and entropic considerations^17,18 can be invoked to rationalize efficient charge generation in OSCs.

In this work, we study vacuum deposited small molecule D–A blends with relevance for organic photovoltaics and light emission, consisting of several donors mixed with the acceptors B2PYMPM, B3PYMPM and B4PYMPM, which only differ in the nitrogen position of substituted pyridine rings. These materials show a different preferential molecular orientation and structural order when forming a solid film,^19–21 and diodes based on these blends have strongly varying photovoltaic and electroluminescence characteristics.⁵ Here, through the analysis of the CT absorption and emission spectra and of the temperature dependence of the open-circuit voltage (V_OC), we determine whether the emissive CT states are in dynamic equilibrium with free charges, and therefore whether they are strongly bound or not.⁵ In B3PYMPM- and B2PYMPM-based blends with poor photovoltaic performance, we find that CT states are bound, and therefore the dissociation strongly depends on the electric field, while in B4PYMPM containing blends we find efficient, field-independent dissociation and fill factors (FFs) exceeding 70%. 2D grazing-incidence wide-angle X-ray scattering (GIWAXS) data reveal a relationship between face-on molecular stacking and efficient CT state dissociation. Multiscale computational modelling, combining molecular dynamics (MD), density functional theory (DFT) and microelectrostatic (ME) calculations as well as a tight-binding (TB) model to account for charge delocalization, suggests that horizontally aligned B4PYMPM molecules offer more delocalized states for charge separation and a shallower energetic landscape at the interface, allowing electrons to move along the direction perpendicular to the D:A heterojunction. Surprisingly, we find that the BF-DPB:B4PYMPM blend with unbound CT states and efficient charge carrier generation also exhibits the highest electroluminescence quantum efficiency. This indicates that emissive CT states are not necessarily strongly bound, which is encouraging for highly efficient organic photovoltaics with low non-radiative losses. In fact, non-radiative CT state decays are responsible for large V_OC losses and need to be suppressed to achieve higher PCEs in OSCs.²²

2. Results and discussion

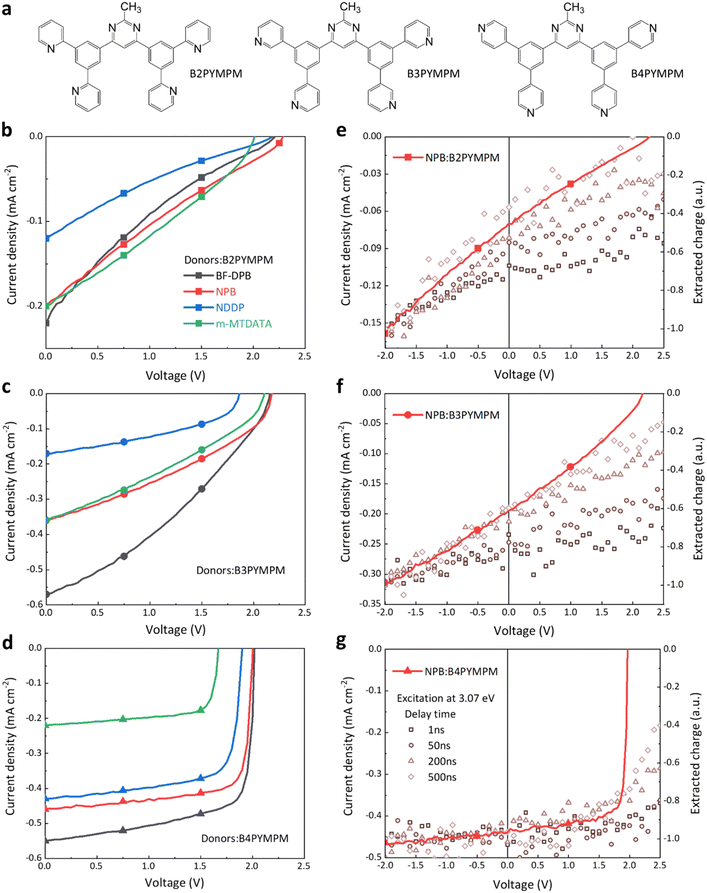
2.1 Chemical structures and photovoltaic performance

The electron acceptor molecules B2PYMPM, B3PYMPM, and B4PYMPM differ in the position of the nitrogen atom in the pyridine rings (see Fig. 1a). This small change in the chemical structure drives strikingly large differences in molecular packing and electron mobility.^20,23 Four different small-molecular donors, namely BF-DPB, NPB, NDDP, and m-MTDATA, were combined with the three acceptors. The chemical structure of the donors, energy levels, and device architecture are shown in Fig. S1 (ESI†). We characterized the photovoltaic and electroluminescence performance of these bulk-heterojunction (BHJ) D:A combinations, and their parameters are summarized in Table S1 (ESI†). Because of the large optical gap of the selected molecules, the main absorption peaks of photovoltaic external quantum efficiency curves (EQE_PV, Fig. S2, ESI†) are in the range of 300–400 nm, resulting in rather low photocurrents under AM 1.5G illumination. The V_OCs of B4PYMPM-containing devices are ∼0.2 V lower than those obtained with either B2PYMPM or B3PYMPM because of their decreased E_CT, resulting from the relatively lower LUMO energy of the former material (Fig. S1, ESI†).¹⁹ However, the most intriguing finding, as shown in Fig. 1b–d, is that regardless of the nature of the donor, B4PYMPM-based devices consistently produce very high fill factors (FFs > 70%); in contrast, FFs in B2PYMPM- or B3PYMPM-based devices are poor (∼20–40%). Low FFs can be a consequence of either poor charge transport or a poor and field-dependent dissociation of the CT states into FCC. The time-delayed collection field (TDCF) measurements (see Fig. 1e–g and discussion below) reveal that the latter process dominates in B2PYMPM and B3PYMPM devices, whereas efficient and nearly field-independent charge generation upon photoexcitation occurs in B4PYMPM systems.

Fig. 1 Chemical structures, photovoltaic performance, and time-delayed collection field (TDCF) measurements. (a) Chemical structures of three investigated acceptor molecules: B2PYMPM, B3PYMPM, and B4PYMPM. (b)–(d) Current–density voltage characteristics measured under simulated AM 1.5G solar illumination for devices based on three acceptors combined with four different donors. All these standard devices have a 30 nm thick active layer. Black, red, blue, and green colors are chosen for representing donor molecules BF-DPB, NPB, NDDP and m-MTADATA, respectively, while filled squares, circles, and triangles denoting B2PYMPM, B3PYMPM, and B4PYMPM acceptors, respectively. (e)–(g) Current density–voltage curves are represented as solid lines for NPB:B2PYMPM, NPB:B3PYMPM, and NPB:B4PYMPM. Devices for TDCF measurements have a 100 nm thick active layer. The relative number of generated charge carriers extracted in the TDCF measurement as a function of applied bias is shown on the right axis. A short laser pulse (∼4 ns) with a wavelength of 404 nm (3.07 eV) is used to excite samples, and the collection voltage (V_coll) is −3 V with a delay time in the range of 1–500 ns.

2.2 Time-delayed collection field (TDCF) measurements

Since high FFs were found for all B4PYMPM based systems, we focus on NPB-based devices, which can achieve a FF of 81% even with a 100 nm thick active layer (EQE_PV and J–V curves of the 100 nm device in Fig. S3, ESI†). This is convenient for TDCF measurements because active layers thicker than the usual 30 nm are required to minimize the capacitance and the corresponding RC rise time. Shown in Fig. 1e–g is the total charge extracted from the device for different delay times between the application of the laser pulse and of a strong reverse collection voltage (V_coll), as a function of applied bias. When V_coll is given 1 ns after pulsed illumination, the amount of free charges depends strongly on the applied voltage for the NPB:B2PYMPM and NPB:B3PYMPM combinations. This indicates a geminate recombination process occurring on a ns timescale.^24,25 Increasing the delay time up to 500 ns causes the field-dependence of the extracted charge to increase, which is the result of non-geminate recombination starting to take place at these timescales.^26–28 As a consequence of this strongly field-dependent charge generation and rapid non-geminate recombination, in B2PYMPM and B3PYMPM systems the FF is severely reduced. In contrast, a much weaker to no field-dependent generation is observed in B4PYMPM systems at timescales between 1–500 ns (Fig. 1g), suggesting much reduced geminate and non-geminate recombination. It was recently shown that both recombination processes are interlinked via the efficiency of CT dissociation,²⁹ as non-geminate recombination of FCC involves the reformation of the CT states. Efficient splitting of the CT states (as in devices with efficient FCC generation) will, therefore, slow down the effective rate of FCC recombination. As a result, the FF in B4PYMPM systems is significantly improved.

2.3 Charge-transfer state dissociation properties

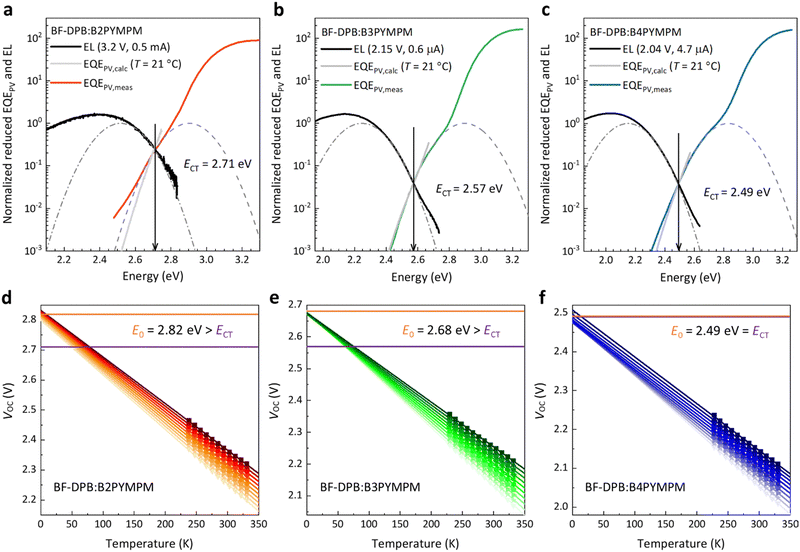
To further investigate the behaviour of the devices composed of the three different acceptors and support the hypothesis of efficient charge separation in B4PYMPM systems, we directly assessed the CT state dissociation properties through a combination of sensitive optical spectroscopy and temperature-dependent V_OC measurements. As shown in Fig. 2a–c, sensitive electroluminescence (EL) and EQE_PV measurements were performed to determine the energy of CT states (E_CT). For the BF-DPB:B2PYMPM combination, the E_CT value is 2.71 eV, which is larger than those of BF-DPB:B3PYMPM (E_CT = 2.57 eV) and BF-DPB:B4PYMPM (E_CT = 2.49 eV) combinations, following the same trend as the corresponding V_OC values (Table S2, ESI†). In order to determine whether the CT states are bound or unbound, the E_CT values of these blends are compared with E₀ (a detailed explanation can be found in the ESI,† paragraph 5, as well as in ref. 30). E₀ is determined as in Fig. 2d–f from the extrapolation of temperature-dependent suns-V_OC measurements to 0 K and it corresponds well with the activation energy of electroluminescence (Fig. S4, ESI†).⁵

Fig. 2 Sensitive EL and EQE_PV measurements and determination of E₀. (a)–(c) Normalized reduced electroluminescence (EL) and photovoltaic external quantum efficiency (EQE_PV) spectra as a function of the photon energy for three BF-DPB-based exemplary devices. The sensitive EL spectra are measured under low injection current conditions to make sure that injected charge carriers reach thermal equilibrium before recombination. Gray EQE_PV curves are calculated from EL spectra under the reciprocity assumption between absorption and emission and show an agreement with sensitively measured EQE_PV curves. The dashed curves are Gaussian fits of the EL and EQE_PV curves. The energy of charge-transfer states (E_CT) is obtained at the crossing point between appropriately scaled EL and EQE_PV curves, highlighted by vertical black arrows. (d)–(f) Temperature-dependent suns-V_OC measurements for corresponding exemplary devices, in which the temperature varies in the range of 223–333 K in steps of 10 K. For each intensity, the activation energy E₀ is obtained by extrapolating the temperature to 0 K. For the energy values with fitting errors smaller than 15 meV, the average value is taken and represented as E₀, shown in a horizontal orange line. The optically determined E_CT is plotted as a purple line.

When CT state dissociation into FCC is much faster than CT state decay, E₀ is expected to be equal to E_CT (detailed derivation in paragraph 5 of the ESI†). In this case, while it might still have a finite binding energy, the CT state behaves as it would be unbound since its binding energy can be quickly overcome within the lifetime of the CT state. This is the case for the BF-DPB:B4PYMPM system, where the experimentally determined E_CT is equal to E₀. Even upon reformation by encounter of positive and negative charges, there is a high probability for CT state dissociation, resulting in an equilibrium between FCC and CT states prior to decay. Consistently, for this material blend, efficient and field independent dissociation, FFs > 70% and photovoltaic internal quantum efficiency IQE_PV > 82% were measured.⁵ We want to stress once more that this result does not necessarily imply that the CT state has no binding energy. In fact, E_CT being equal to E₀ means that FCC are quickly formed before the CT state decays. In such a scenario, the value of E₀ − E_CT approaching zero (or even being slightly below zero) does not necessarily correspond to the CT state binding energy.³⁰ Contrarily, if CT state dissociation is slower or comparable to CT state decay, E₀ will be higher than E_CT, and will approximate the energy of an unbound electron–hole (e–h) pair E_FCC (detailed derivation in paragraph 5 of the ESI†). In this case, the CT state is bound (E₀ − E_CT > 0), as for B2PYMPM- and B3PYMPM-based blends, where the experimentally determined E₀ is significantly higher than E_CT. In these blends, e–h separation is slow so that the CT state decay becomes a competitive process, translating into a field-dependent FCC generation and a low FF.

This trend can be deduced and established not only for the BHJ systems employing BF-DPB as a donor material, but also for all other donors (Fig. S5–S7 and Table S3, ESI†). The same D:A combinations were also fabricated in a planar heterojunction (PHJ) structure and investigated as well. Their photovoltaic performance and parameters are shown in Fig. S8 and Table S4 (ESI†). In comparison to their BHJ counterparts, most of the PHJ devices exhibit higher FFs, which may be attributed to their lower non-geminate recombination rates associated to planar structures.³¹ However, we still measure considerable E₀ − E_CT energies for the B2PYMPM- and B3PYMPM-based systems (see Fig. S9, S10 and Table S5, ESI†). This is consistent with what we found in BHJ devices. All these results support the view that CT states in B4PYMPM-containing systems dissociate much faster than they decay, while for B2PYMPM- and B3PYMPM-based systems Coulombically bound e–h pairs cannot dissociate quickly.

Fig. 3a shows that the measured electroluminescence external quantum efficiencies (EQE_EL) of all investigated BHJ devices are not particularly dependent on E₀ − E_CT values. In fact, we find that B4PYMPM-based systems, where E₀ − E_CT is around 0, have a comparable or even higher EQE_EL as compared to the devices based on B2PYMPM and B3PYMPM. In particular, the EQE_EL of the BF-DPB:B4PYMPM blend reaches 1.5% (as compared to typical values for OSCs in the 0.0001–0.01% range),⁵ showing that fast dissociating CT states in equilibrium with FCC do not necessarily have lower emission efficiencies than strongly bound states. The relationship between FFs and the E₀ − E_CT values is illustrated in Fig. 3b. In B4PYMPM-containing systems, where the CT states are in equilibrium with FCC states, the FF values are high irrespective of the chosen donor molecule. In contrast, when CT states are bound such as in B2PYMPM- and B3PYMPM-based systems, the device FFs are lower due to an inefficient FCC generation.

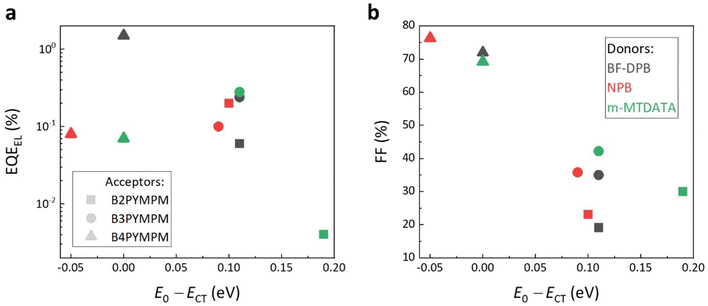Fig. 3 The relations between (a) EQE_EL, and (b) FF and E₀ − E_CT. The symbols in black, red, and green represent BF-DPB-, NPB-, and m-MTDATA-based BHJ devices, respectively. Filled squares, circles, and triangles denote acceptor molecules B2PYMPM, B3PYMPM, and B4PYMPM, respectively. The EQE_EL values are determined during the sensitive EL measurement; the injection conditions are shown together with sensitive EL curves. The FF values are obtained from JV curves and shown in Table S1 (ESI†).

2.4 Molecular orientation and packing

To elucidate whether the large differences in CT dissociation properties between the three acceptors could originate from morphological effects we surveyed the literature and carried out GIWAXS measurements. The molecular planes of B3PYMPM and B4PYMPM were reported to be oriented parallel to the substrate surface, unlike the ones of B2PYMPM. The difference in thin film morphology between the three acceptors was attributed to the formation of weak C–H⋯N hydrogen bonds (H-bonds) between molecules.^19–21 Moreover, the electron mobility of B4PYMPM was measured to be 10 times higher than that of B3PYMPM and 100 times higher than that of B2PYMPM.¹⁹ Using Bässler's disorder formalism,³² the energetic disorder was estimated to decrease from B2PYMPM to B4PYMPM. Similarly, the positional disorder was evaluated to be higher for B2PYMPM, compared to B3PYMPM and B4PYMPM, attributed to shorter intermolecular distance and well-ordered molecular orientations for the B4PYMPM film as well as dense-packing.¹⁹ Out-of-plane XRD patterns of the B3PYMPM and B4PYMPM film exhibited a broad halo peak, which shows a periodic structure with a short-range order formed in the direction normal to the substrate, while B2PYMPM showed none. The estimated molecular-stacking distance was ∼3.8 Å.²⁰

By conducting grazing-incidence wide-angle X-ray scattering (GIWAXS) measurements on both neat acceptor films and BF-DPB:acceptor blend films, we confirm the literature results discussed above. The 2D GIWAXS patterns of B2PYMPM, B3PYMPM and B4PYMPM pristine films on silicon substrates are presented in Fig. S11a–c (ESI†) and the corresponding population orientation analysis are shown in Fig. S11d–f (ESI†). In all three GIWAXS images a diffraction pattern at 1.7 Å⁻¹ on the Q_z axis is observed and attributed to the π–π stacking of molecules. From the population analysis we can deduce that B4PYMPM molecules are orientated 44.8% face-on with respect to the substrate, surpassing both B3PYMPM (30.8%) and B2PYMPM (12.2%). In fact, most of B2PYMPM molecules are isotropically oriented (62.6%), as shown in Fig. S11d and Table S6 (ESI†). The full width at half maximum of the ring in the Q_z direction 1.7 Å⁻¹ is 0.46 Å⁻¹ for B4PYMPM and 0.62 Å⁻¹ for B2PYMPM.

Compared to neat acceptor films, blends of the three acceptors with BF-DPB show a relatively higher isotropic percentage that, together with the significant increase in the peak width, suggests as expected a more amorphous molecular orientation in the blend (see Fig. S12 and Table S7, ESI†). However, B4PYMPM-based blend films still show the highest face-on ratio and the lowest isotropically oriented amount of material among blend films.

2.5 Modelling the interfacial charge-transfer exciton manifold

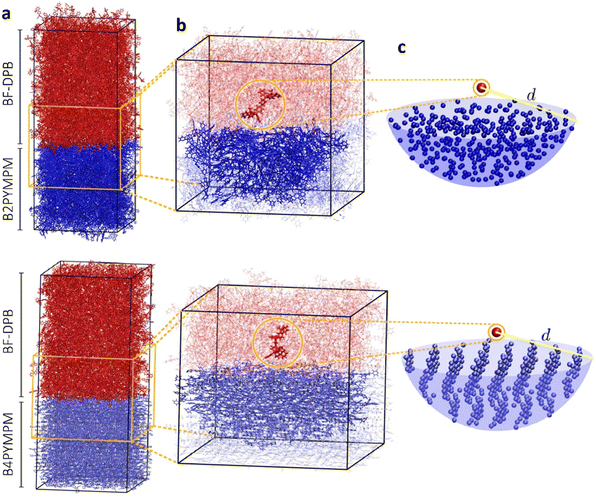
In an effort to understand the superior charge generation efficiency of B4PYMPM with respect to B3PYMPM and B2PYMPM, we set up and applied a multilevel computational approach that combines several techniques.^16,33 Charge delocalization effects on intermolecular e–h states were described with a tight-binding (TB) model. The model was parametrized starting from atomistic MD simulations for two D:A PHJ samples. MD simulations were not aimed at providing predictive morphologies, but rather realistic limiting-case heterointerfaces that were built following the experimental GIWAXS characterization and the literature data for bilayer systems: a BF-DPB:B2PYMPM junction between amorphous phases, and an interface between an amorphous BF-DPB phase and a crystalline B4PYMPM one (Fig. 4a). For each sample, a 2D-periodic 8 nm-thick slab centered at the heterointerface was extracted from the MD morphology (Fig. 4b) and employed in subsequent electronic structure calculations. DFT and microelectrostatic (ME) calculations were performed to assess the energy landscape of localized charge carriers for all the molecules at the interface, as well as the corresponding electron transfer integrals. This information was then utilized to construct a TB Hamiltonian for electron carriers in the acceptor phase that are Coulombically interacting with a fixed hole in the donor phase. More in detail, for each BF-DPB at the interface, the TB model includes all the acceptor molecules within a hemisphere of radius d (up to 6 nm) centered on the donor molecule being positively charged (Fig. 4b and c). Repeating this procedure for the different hole (donor) positions and diagonalizing the corresponding Hamiltonians allow spanning the manifold of delocalized e–h configurations, including interfacial CT excitons and (partially) space-separated e–h states. We remark in passing that we did not observe any net trend in the energy levels with distance arising from molecular multipole moments at the interface (Fig. S21, ESI†). Such band-bending effects, when present, can strongly impact the energetics of charge separation.^11,33 Similarly, we also excluded that entropy could assist charge separation in a significantly different way in the two systems (Fig. S24, ESI†), allowing us to focus on the potential energy profiles only.

Fig. 4 Illustration of the multiscale workflow for the modelling of electronic states at the BF-DPB:B2PYMPM (top) and BF-DPB:B4PYMPM (bottom) interfaces. (a) 2D periodic structure of planar heterojunctions obtained with molecular dynamics simulations. Transfer integrals and charge transport energy levels were computed for all the molecules within an (b) interfacial slab. A tight binding model describing electron states in the acceptor phase was then set up for every fixed position of the hole on a given donor molecule. The model includes all the acceptor molecules within a radius d from the hole. The donor molecule carrying the hole and the acceptor molecules included in a radial selection are highlighted with thicker lines in (b). (c) Point-like molecule representation of such a selection, showing the more ordered structure of the B4PYMPM phase, as compared to the amorphous B2PYMPM one.

The heat maps in Fig. 5a–d show the density of states (DOS) as a function of energy and e–h distance for localized (i.e. the diagonal elements of the TB Hamiltonian, panels Fig. 5a and c) and delocalized electrons (the energies of the eigenstates of the TB Hamiltonian, panels (Fig. 5b and d)), while panels Fig. 5e and f display the participation ratio (PR), quantifying the number of molecules over which a given CT state is delocalized.

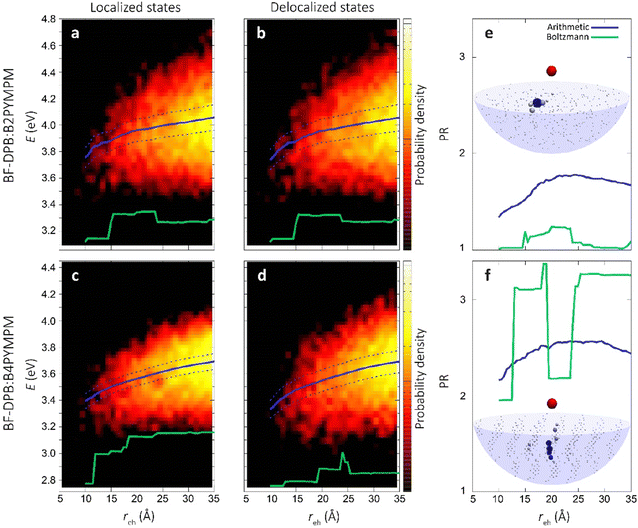Fig. 5 Role of charge delocalization. Evolution of the calculated CT DOS (a)–(d) and the PR (e) and (f) as a function of the electron–hole distance (r_eh) for BF-DPB:B2PYMPM (a) and (b), and BF-DPB:B4PYMPM (c) and (d) interfaces. The lines in each plot represent the arithmetic average with its standard deviation (solid and dashed blue lines, respectively) and the Boltzmann average at 300 K (in green). In panels (e) and (f) the inset shows a representative delocalized state for the BF-DPB:B2PYMPM (e) and the BF-DPB:B4PYMPM (f) samples. The color scale (from white to blue) and the volume of the spheres representing the acceptor molecules are proportional to the calculated site population (see the ESI†).

In Fig. 5a–d we also show the arithmetic (solid blue lines) and Boltzmann averages (green lines) over states at a given e–h distance, superimposed to the DOS map. While the arithmetic mean with its standard deviation (dashed blue lines) is a good estimator for the shape of the DOS, the Boltzmann average conveys information relevant to the thermalized charge carrier at 300 K (since the lowest energy states have higher statistical weight). From the arithmetic averages of the states near to the interface (Fig. 5b and d, solid blue lines) we estimate that E_CT amounts to ∼3.7 eV and ∼3.3 eV for BF-DPB:B2PYMPM and BF-DPB:B4PYMPM, respectively. This E_CT difference of ∼0.4 eV is in fair agreement with experimental measurements (Fig. 2a and c). In both systems, owing to the observed absence of net electrostatic forces at the D:A interface, the E_CT arithmetic averages follow roughly the same profile as a function of the distance, consistent with the Coulomb interaction between charged donors and acceptors. Regarding the separation of thermalized excitons, it is more appropriate to focus on Boltzmann-averaged profiles than on arithmetic averages, as the former reflects the properties of the states that are actually occupied at room temperature (the occupied DOS). We note that the Boltzmann average is somewhat more prone to sampling issues with respect to the arithmetic one. In fact, the spike in the DOS in the Boltzmann-averaged energy profile at around 20–25 Å in panel (d) and the corresponding drop in PR in panel (f) are ascribable to poor statistical sampling in that region. Nonetheless, we consider the Boltzmann average profile to be globally reliable and the differences in charge separation barrier between the two systems (Fig. 5a–d) to be genuine. For the B2PYMPM sample, the profile barely changes including or not charge delocalization effects (solid and green lines in Fig. 5a and b). This is due to the very small electron transfer integrals and the large energetic disorder in B2PYMPM (see Fig. S20–22 and Table S8, ESI†), which both concur in leading to almost fully localized states, i.e., with PRs close to unity (see Fig. 5e). Conversely, for the B4PYMPM sample, the low-energy states are delocalized over multiple acceptor units (PRs up to 3, see Fig. 5f), with a corresponding widening of the DOS (see Fig. 5d).

This different extent of charge delocalization has important consequences on the energetics of charge separation. We evaluated the energetic barrier (E_B, which is connected to E₀ − E_CT) for charge separation from the plots in Fig. 5b and d as the difference between the Boltzmann average energy (solid green lines) at the interface (∼10 Å) and its value at infinite distance (here assumed at ∼35 Å). In the B2PYMPM sample, interfacial CT excitons (r_eh < 10 Å) must overcome an E_B of ∼0.2 eV to move away from the hole (r_eh > 30 Å), irrespective of including or not delocalization effects. Conversely, a smaller barrier of ∼0.1 eV is found for charge carriers in BF-DPB:B4PYMPM, as a result of the more pronounced charge delocalization in this system.

Delocalization can also be quantified by the spatial spread of the states. Indeed, in B4PYMPM we found a larger spatial extension of the electronic wave function along the direction normal to the interface (see Table S9, ESI†), thereby speeding up the charge separation process. Thus, while charge delocalization is negligible in the B2PYMPM system, it plays a major role in BF-DPB:B4PYMPM, broadening the DOS and reducing the energy barrier that thermalized CT excitons must overcome to split into FCC. This difference in charge delocalization between the two systems, and its effect on the thermally-averaged charge separation profile, is in fair agreement with the experimental observations of a more strongly bound CT state for B2PYMPM-based systems.

The present theoretical analysis shows that the high charge generation efficiency of B4PYMPM-based blends can be explained by the higher structural order, which gives rise to larger transfer integrals and lower energetic disorder if compared to the B2PYMPM heterojunction, and by the face-on orientation that favors delocalization in the direction normal to the D : A interface. Both these factors concur to the formation of extended CT states with reduced e–h binding energy.²⁰

3. Conclusions

In conclusion, our work demonstrates how more delocalized states at the D:A interface enable an efficient dissociation of CT states, either formed upon exciton dissociation or by encounter of FCC. Joint computational and experimental results show that face-on oriented B4PYMPM molecules provide such delocalized CT states exhibiting field-independent charge generation, in contrast to less ordered, but chemically similar, B2PYMPM and B3PYMPM systems, which exhibit more localized and bound CT states. Moreover, even though CT states dissociate faster into FCC than they decay in the B4PYMPM system, its emission quantum efficiency is not lower than that of the more localized B2PYMPM- and B3PYMPM-based systems. This is encouraging, as a high radiative recombination efficiency, in combination with a high CT state dissociation yield, is required for achieving low voltage loss, highly efficient organic photovoltaics. This work shows that an interface with such favourable properties can be achieved by an ordered interfacial morphology enabling delocalized states in the direction perpendicular to the interface.

4. Experimental

4.1 Device preparation

The materials were purchased by Luminescence technology corp., Taiwan (NDDP, m-MTDATA, NPB, BPAPF, B2PYMPM, B3PYMPM, B4PYMPM); abcr GmbH, Germany (BPhen); Synthon, Germany (BF-DPB). The layers of the diodes were thermally evaporated at ultra-high vacuum (base pressure < 10⁻⁷ mbar) on a glass substrate with a pre-structured ITO contact (Thin Film Devices, USA). Glass substrates were cleaned in a multi-step wet process including rinsing with N-methyl-2-pyrrolidone, ethanol, and deionized water as well as treatment with ultraviolet ozone. Details on the device structure, donor molecules, and related energy levels are shown in Fig. S1, ESI.† All organic materials were purified 2–3 times by sublimation. The device area is defined by the geometrical overlap of the bottom and the top contact and equals 6.44 mm². To avoid exposure to ambient conditions, the organic part of the device was covered by a small glass substrate, glued on top.

4.2 Current–voltage characteristics

The J–V curves in the dark and under solar illumination were measured with a SMU (Keithley 2400, USA) at room temperature under ambient conditions. The cells were illuminated with a spectrally mismatch corrected intensity of 100 mW cm⁻² (AM1.5G) provided by a sun simulator (16 S–150 V.3 Solar Light Co., USA). Masks were used to minimize edge effects and to define an exact photoactive area (2.78 mm²). The intensity was monitored with a Hamamatsu S1337 silicon photodiode (calibrated by Fraunhofer ISE Freiburg, Germany). Light-intensity-dependent FF measurement of the CT-OLEDs were conducted by using three 385 nm APG2C1-385-r2 UV LEDs (Roithner, Austria) in series as the illumination source and a Keithley SMU 2635A to measure the current–voltage curve.

4.3 EQE_PV measurements

EQE_PV was measured using masks to minimize edge effects and to define an exact photoactive area (2.78 mm²). The EQE_PV was detected with a lock-in amplifier (Signal Recovery SR 7265) under monochromatic illumination (Oriel Xe Arc-Lamp Apex Illuminator combined with Cornerstone 260 1/4m monochromator, Newport, USA) using a calibrated mono-crystalline silicon reference diode (Hamamatsu S1337 calibrated by Fraunhofer ISE, Germany). For sensitively measured EQE_PV the light of a white high-power LED (LED Engin LZP-00CW00, USA), used for the high-E_CT devices, was chopped at 140 Hz and coupled into a monochromator (Newport Cornerstone 260 1/4m, USA). The resulting monochromatic light was focused onto the OSC, its current at short-circuit conditions was fed to a current pre-amplifier before it was analyzed with a lock-in amplifier (Signal Recovery 7280 DSP, USA). The time constant of the lock-in amplifier was chosen to be 1s and the amplification of the pre-amplifier was increased to resolve low photocurrents. The EQE_PV was determined by dividing the photocurrent of the OSC by the flux of incoming photons, which was measured using a calibrated Si and InGaAs photodiode (FDS100-CAL and FGA21-CAL, Thorlabs Inc., USA).

4.4 Electroluminescence measurements

The EL spectra were obtained with an Andor SR393i-B spectrometer equipped with a cooled Si and cooled InGaAs CCD detector array (DU420A-BR-DD and DU491A-1.7, UK). The spectral response of the setup was calibrated with a reference lamp (Oriel 63355). The emission spectrum of the OSCs was recorded at different injection currents with respect to voltages, which were lower than or at least similar to the V_OC of the device at 1 sun illumination. Additional certification of the EL measurements was determined by a flux calibrated Acton SpectraPro SP2560 monochromator coupled to a cooled Spec10LN Si CCD camera from Princeton Instruments.

4.5 EQE_EL measurements

The EQE_EL was measured by forward biasing the OSCs with either an Agilent 4155C parameter analyser or Keithley SMU and collecting the emitted radiation by an enhanced G10899-03K InGaAs photodetector from Hamamatsu. The absolute total photon flux determination was performed by placing the OSC at a distance of 18.3 mm from the photodetector. Knowledge about the spectral distribution of the cell emission, the spectral response of the InGaAs photodetector, and the assumption of a point source emitting uniformly into a half-sphere allowed for determination of the absolute EL photon flux from the OSC. Uncertainties in measured EQE_EL are expected to be governed by the small distance imprecision between the OSC and the photodetector (calibrated Si detector from Newport, 818-series with an active area of 1 cm²). To keep this uncertainty as little as possible, the measurement was conducted in different distances from the solar cell and always extrapolated to the full half sphere.

4.6 Temperature dependent suns-V_OC and EL measurements

For suns-V_OC measurements, a Keithley SMU2635A was controlling the LED (a white LED (APG2C3 NW, Roithner, Austria) for the OSCs and a 365 nm LED (APG2C1-365-r4, Roithner) for the CT OLEDs) to change the light intensity. A Keithley dual channel SMU2602A measures both the V_OC and the illumination intensity with a Newport 818-UV photodiode. To measure the EL, the dual channel SMU2602A applied a bias voltage to the sample and measures the photocurrent of a S2387-66R Si Photodiode (Hamamatsu, Japan), which was directly attached to the device, covering the whole active area. To change the cell temperature, the devices were placed in vacuum on a copper block, which was connected to a Peltier element from Peltron GmbH (Fürth, Germany), controlled by a BelektroniG HAT Control device (Freital, Germany).

4.7 TDCF measurements

The TDCF experiment was performed by using a laser pulse from a diode pumped, Q-switched Nd:YAG laser (NT242, EKSPLA) with a 6 ns pulse duration and a typical repetition rate of 500 Hz working at 404 nm to generate charges in the device. A pulse generator (Agilent 81150A) was used to apply the pre- and collection bias which are amplified by a home-built amplifier. The current through the device was measured via a grounded 10 Ω resistor in series with the sample and with a differential current probe recorded with an oscilloscope (DSO9104H). The pulse generator was triggered with a fast photodiode (EOT, ET-2030TTL). The fluence was determined with a CCD-camera in combination with a calibrated photodiode sensor (Ophir) and a laser-cut high-precision shadow mask to define the illuminated area.

4.8 GIWAXS measurements

The GIWAXS measurements were performed at BL11 (NCD-SWEET) at the ALBA synchrotron in Barcelona, Spain. For the measurements a Rayonix LX255-HS detector was used approximately 140 mm behind the sample. A beam energy of 12.4 keV, exposure time of 120 s and an incidence angle of 0.12° were used. The analysis of the scattering data was performed using WxDiff (© S.C.B.M.). The population analysis is performed by integrating the intensity along a Chi-Arc from 2° to 80° degrees in a specific Q range (ca. 1.4–1.9 Å⁻¹). The integrated intensity is corrected by cos(χ), due to a decrease in intensity at small χ angles close to the horizon, which results from the grazing-incidence geometry.^34,35

4.9 Computational methods

Bilayer samples were built by means of MD simulations and equilibrated at 298 K and 1 atm before being used for further calculations. Molecular geometries were then extracted from the last MD configuration and used to calculate the parameters for a model TB electronic Hamiltonian represented on a diabatic basis of localized molecular sites. Site energies were obtained with a combination of many-body evGW, DFT and ME calculations. Electron transfer integrals were computed at the DFT PBE0/def2-SVP level of theory. See the ESI† for a full description of the computational details and further results.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

X. J., L. S. and G. L. contributed equally to this work. X. J. is grateful for support from the China Scholarship Council (no. 201706140127) and the Graduate Academy of Technische Universität Dresden. The work in Bologna was performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Program; in particular, G. L. gratefully acknowledges the support of the Department of Industrial Chemistry, University of Bologna and the computer resources and technical support provided by CINECA. The work in Mons was supported by the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement no. 722651 (SEPOMO project). Computational resources were provided by the Consortium des Équipements de Calcul Intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under grant no. 2.5020.11, as well as the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles, infrastructure funded by the Walloon Region under grant agreement no. 1117545. L. S., G. L., L. M., G. D. and D. B. gratefully thank Xavier Blase for sharing the FIESTA code. D. B. is a FNRS Research Director. F. T. and S. C. B. M. would like to acknowledge support by the German Excellence Initiative via the Cluster of Excellence EXC 1056 “Center for Advancing Electronics Dresden (cfaed)” and support from the German Research Foundation (DFG, MA 3342/6 1). The GIWAXS experiments were performed at BL11 NCD-SWEET beamline at ALBA Synchrotron with the collaboration of ALBA staff. We would like to thank Eduardo Solano and Marc Malfois for their assistance during the beam time.

References

1. C. Li, J. Zhou, J. Song, J. Xu, H. Zhang, X. Zhang, J. Guo, L. Zhu, D. Wei, G. Han, J. Min, Y. Zhang, Z. Xie, Y. Yi, H. Yan, F. Gao, F. Liu and Y. Sun, Nat. Energy, 2021, 6, 605–613.
2. Q. Wang, Q.-S. Tian, Y.-L. Zhang, X. Tang and L.-S. Liao, J. Mater. Chem. C, 2019, 7, 11329–11360.
3. B. Liang, J. Wang, Z. Cheng, J. Wei and Y. Wang, J. Phys. Chem. Lett., 2019, 2811–2816.
4. M. Zhang, C.-J. Zheng, H. Lin and S.-L. Tao, Mater. Horizons, 2021, 8, 401–425.
5. S. Ullbrich, J. Benduhn, X. Jia, V. C. Nikolis, K. Tvingstedt, F. Piersimoni, S. Roland, Y. Liu, J. Wu, A. Fischer, D. Neher, S. Reineke, D. Spoltore and K. Vandewal, Nat. Mater., 2019, 18, 459–464.
6. X. Jia, E. C. Baird, J. Blochwitz-Nimoth, S. Reineke, K. Vandewal and D. Spoltore, Nano Energy, 2021, 89, 106404.
7. F. Gao and O. Inganäs, Phys. Chem. Chem. Phys., 2014, 16, 20291–20304.
8. V. Coropceanu, X.-K. Chen, T. Wang, Z. Zheng and J.-L. Brédas, Nat. Rev. Mater., 2019, 4, 689–707.
9. N. A. Ran, S. Roland, J. A. Love, V. Savikhin, C. J. Takacs, Y.-T. Fu, H. Li, V. Coropceanu, X. Liu, J.-L. Brédas, G. C. Bazan, M. F. Toney, D. Neher and T.-Q. Nguyen, Nat. Commun., 2017, 8, 79.
10. S. Athanasopoulos, H. Bässler and A. Köhler, J. Phys. Chem. Lett., 2019, 10, 7107–7112.
11. Y. Puttisong, Y. Xia, X. Chen, F. Gao, I. A. Buyanova, O. Inganäs and W. M. Chen, J. Phys. Chem. C, 2018, 122, 12640–12646.
12. G. D’Avino, S. Mothy, L. Muccioli, C. Zannoni, L. Wang, J. Cornil, D. Beljonne and F. Castet, J. Phys. Chem. C, 2013, 117, 12981–12990.
13. C. Deibel, T. Strobel and V. Dyakonov, Phys. Rev. Lett., 2009, 103, 036402.
14. N. Felekidis, A. Melianas and M. Kemerink, J. Phys. Chem. Lett., 2020, 11, 3563–3570.
15. A. A. Bakulin, A. Rao, V. G. Pavelyev, P. H. M. M. van Loosdrecht, M. S. Pshenichnikov, D. Niedzialek, J. Cornil, D. Beljonne and R. H. Friend, Science, 2012, 335, 1340–1344.
16. G. D’Avino, L. Muccioli, Y. Olivier and D. Beljonne, J. Phys. Chem. Lett., 2016, 7, 536–540.
17. B. A. Gregg, J. Phys. Chem. Lett., 2011, 2, 3013–3015.
18. S. N. Hood and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 4495–4500.
19. H. Sasabe, D. Tanaka, D. Yokoyama, T. Chiba, Y.-J. Pu, K. Nakayama, M. Yokoyama and J. Kido, Adv. Funct. Mater., 2011, 21, 336–342.
20. D. Yokoyama, H. Sasabe, Y. Furukawa, C. Adachi and J. Kido, Adv. Funct. Mater., 2011, 21, 1375–1382.
21. Y. Chen, X. Liu, S. Braun and M. Fahlman, ACS Appl. Mater. Interfaces, 2021, 13, 47218–47225.
22. P. Bi, S. Zhang, Z. Chen, Y. Xu, Y. Cui, T. Zhang, J. Ren, J. Qin, L. Hong, X. Hao and J. Hou, Joule, 2021, 5, 2408–2419.
23. A. De Nicola, A. Correa, A. Giunchi, L. Muccioli, G. D’Avino, J. Kido and G. Milano, Adv. Theory Simulations, 2021, 4, 2000302.
24. D. Veldman, Ö. İpek, S. C. J. Meskers, J. Sweelssen, M. M. Koetse, S. C. Veenstra, J. M. Kroon, S. S. van Bavel, J. Loos and R. A. J. Janssen, J. Am. Chem. Soc., 2008, 130, 7721–7735.
25. H. Cha, S. Wheeler, S. Holliday, S. D. Dimitrov, A. Wadsworth, H. H. Lee, D. Baran, I. McCulloch and J. R. Durrant, Adv. Funct. Mater., 2018, 28, 1704389.
26. D. Credgington, F. C. Jamieson, B. Walker, T.-Q. Nguyen and J. R. Durrant, Adv. Mater., 2012, 24, 2135–2141.
27. S. M. Hosseini, S. Roland, J. Kurpiers, Z. Chen, K. Zhang, F. Huang, A. Armin, D. Neher and S. Shoaee, J. Phys. Chem. C, 2019, 123, 6823–6830.
28. J. Kurpiers, T. Ferron, S. Roland, M. Jakoby, T. Thiede, F. Jaiser, S. Albrecht, S. Janietz, B. A. Collins, I. A. Howard and D. Neher, Nat. Commun., 2018, 9, 1–11.
29. S. Shoaee, A. Armin, M. Stolterfoht, S. M. Hosseini, J. Kurpiers and D. Neher, Sol. RRL, 2019, 3, 1900184.
30. K. Vandewal, Annu. Rev. Phys. Chem., 2016, 67, 113–133.
31. A. Foertig, A. Wagenpfahl, T. Gerbich, D. Cheyns, V. Dyakonov and C. Deibel, Adv. Energy Mater., 2012, 2, 1483–1489.
32. H. Bässler, Phys. Status Solidi, 1993, 175, 15–56.
33. G. Londi, S.-U.-Z. Khan, L. Muccioli, G. D’Avino, B. P. Rand and D. Beljonne, J. Phys. Chem. Lett., 2020, 11, 10219–10226.
34. J. Rivnay, S. C. B. B. Mannsfeld, C. E. Miller, A. Salleo and M. F. Toney, Chem. Rev., 2012, 112, 5488–5519.
35. D. E. Johnston, K. G. Yager, H. Hlaing, X. Lu, B. M. Ocko and C. T. Black, ACS Nano, 2014, 8, 243–249.

---

Footnotes

† Electronic supplementary information (ESI) available: Fig. S1–S24, Tables S1–S9, and six paragraphs. See DOI: https://doi.org/10.1039/d3mh00526g

‡ These three authors contributed equally.

§ Present address: Department of Chemical and Biomolecular Engineering, National University of Singapore, 4 Engineering Drive 4, Singapore 117585, Singapore.

---