Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrochemical lithiation-induced formation of disordered rocksalt†
Matthew J. A.
Leesmith
,
Nathan R.
Halcovitch
 and
Xiao
Hua
and
Xiao
Hua
 *
*
Department of Chemistry, Lancaster University, Lancaster LA1 4YB, UK. E-mail: x.hua1@lancaster.ac.uk
First published on 24th July 2023
Abstract
Cation disordered rocksalt (DRX) materials are promising electrode alternatives for next-generation battery technology due to their superior performances concerning capacity and rate capability. These materials are usually prepared via heat treatment or mechanochemical synthesis. Recently, several cation DRX oxides with desirable cycling behaviours have been prepared through electrochemical lithiation of a series of binary metal oxides that have a non-fcc oxygen sublattice. Capitalising on these findings, we strategically investigated two Mn oxides with unique oxygen structures. Through an analysis combining X-ray diffraction and pair distribution function techniques, an electrochemically active cation DRX phase was identified in both oxides upon electrochemical lithiation. Jointly with the earlier reports, our new findings constitute empirical evidence pointing to a general principle that underpins the electrochemical DRX transformation, opening up new opportunities for the development of higher energy density batteries.
1 Introduction
In response to an increasing global demand for cost-effective and high-performance rechargeable lithium-ion batteries (LIBs), the search for the next-generation electrode materials has transcended the realm of layered archetypes, which are typically represented by graphite for the anode and Li1+δNixMnyCozO2 for the cathode. Among the various newly explored electrode chemistries, cation disordered rocksalt (DRX) materials have attracted considerable interests. These materials are usually lithium transition metal oxides (Li1+xM1−xO2) or their fluorinated derivatives (Li1+xM1−xO2−yFy).1 They adopt a rocksalt (NaCl) structure where both cations and anions form an fcc packing. In particular, the cation sublattice can contain several metal species which are, in theory, randomly distributed. Recent reports show that not only do these materials exhibit desirable capacities (≈250 mA h g−1), larger than that from the current commercial materials benchmarked by the layered metal oxides (≈220 mA h g−1), but the Li migration in the DRX systems is also associated with a lower energy barrier leading to a faster ion mobility and hence a better rate performance.1 These merits render cation DRX materials one of the most promising electrode candidates1,2 for future LIB technologies. However, DRX structures are metastable and the conventional practice to access the cation disorder is via either thermal or mechanochemical synthesis. Whilst the disorder cannot be achieved thermally for all compositions, it can often be induced alternatively by extensive milling. Nevertheless, milling media such as container and beads inevitably introduce contaminants which can potentially cause unwanted metal doping.3 More importantly, as the relationship between the mechanical forces and entropy remains unclear, a better mechanistic understanding of the milling process is required for a systematic DRX material design.1Stepping outside the box, an emerging new method to access the non-equilibrium phases takes advantage of the electrochemical energy in a lithium-ion battery, i.e. via electrochemical lithiation. Whilst the first few “serendipitous” observations of lithiation-induced DRX formation was observed in α-V2O5 (ref. 4) and α-Fe2O3 (ref. 5) some decades ago, it is not until the recent renaissance of DRX chemistry that this irreversible metal oxide-to-DRX phase transition has been systematically studied and developed to innovate the DRX material synthesis.2,6,7 These efforts have in turn led to the discovery of two new systems, Nb2O5 (ref. 7) and TiO2,6,7 to join the ranks of the DRX-active metal oxides alongside V2O5 and Fe2O3. Interestingly, both Nb2O5 and TiO2 are well-known for their polymorphism, however, their phase transition to a DRX form has only been thus far observed in their amorphous counterparts; in contrast, α-V2O5 and α-Fe2O3 can both transform to a DRX phase in their bulk and/or nanostructured phases. Whilst it is obvious that all of these identified DRX-active metal oxides have a non-fcc oxygen sublattice which transforms into an fcc arrangement upon DRX conversion, questions come to mind if there is a general fundamental principle that underpins this phase transformation; more importantly, how this principle could direct us towards other metal oxides with a wider compositional and structural variation to enable the design of cation DRX materials with improved electrochemical properties.
With these questions in mind, we investigated the lithiation mechanisms of some Mn oxides which have non-fcc oxygen sublattices and large particle sizes (i.e. >100 nm). We chose Mn oxides as our model compounds largely due to their commercial relevance; their polymorphic nature also means that several commercially available systems, i.e. β-MnO2 and α-Mn2O3, have a non-fcc anion sublattice, rendering them ideal references for this study. It is also important to note that among those reported lithiation-induced DRX phases, LixNb2O5 and LixTiO2 are only suitable for anodes; whilst LixV2O5 and LixFe2O3 can principally function as cathodes, the former has been recently made known as an anode due to its unique multi-redox pathway allowing for additional Li storage at low voltages and the latter exhibits mediocre operating voltages somewhat compromising its energy density as a cathode. In comparison, the lithiation of MnO2 and its reversible process are supported by Mn4+/3+ redox, which should theoretically exhibit a desirable reaction voltage as a cathode.
Concerning that the structural complexity of the DRX transformation lies on an atomic level, X-ray scattering techniques via joint X-ray diffraction (XRD) and pair distribution function (PDF) analyses were employed to capture any potential formation of the DRX-related phases, as well as their reactivity during subsequent cycles. Excitingly, our analyses identified an electrochemically active DRX intermediate during the initial lithiation of both β-MnO2 and α-Mn2O3. We further extended our exploration to Cr2O3 and similar observation was made. These results collectively support an electrochemical DRX transformation from metal oxides with a non-fcc anion sublattice, providing empirical evidence to a general principle that may navigate us to a better design of the cation DRX electrodes for the development of high energy density batteries.
2 Results
2.1 Electrochemistry of MnO2
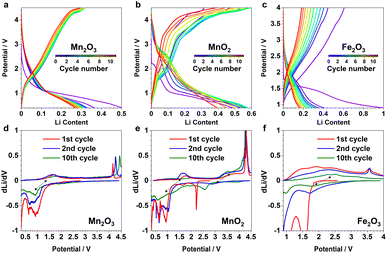
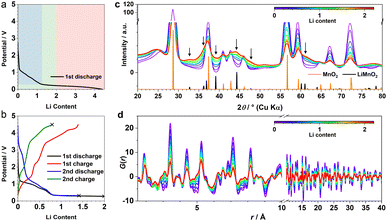
β-MnO2 adopts a rutile structure. Its initial discharge curve (Fig. 1a) shows a typical electrochemical profile of a multivalent metal oxide anode, which starts with a distinct voltage slope followed by a plateau. The slope has a capacity of about 1Li (per formula unit, highlighted in blue in Fig. 1a), which is conventionally defined as an “insertion” process forming a Li-inserted MnO2 intermediate (LixMnO2, 0 ≤ x ≤ 1).8 The voltage plateau, associated with a capacity of about 3Li, corresponds to a reaction commonly understood as “conversion”. This process undergoes Mn extrusion with concurrent Li2O formation. The 1st charge step and the following cycles follow a (relatively) reversible pathway between Mn (+Li2O) and zinc blende (zb-)MnO which differs significantly from the initial discharge and is discussed elsewhere.9 It is important to note that the particle size of the pristine metal oxides is known to have a large impact on the apparent voltage profile of the insertion process. The influence of a smaller particle usually manifests itself in the presence of a (pseudo)plateau in the slope region with a relatively large capacity.5 Because of the variation in material grain size among different reports, it is common to see distinct electrochemical profiles of the insertion cycle even for materials with the same crystal structure.5,102.2 XRD and PDF data of the 1st discharge
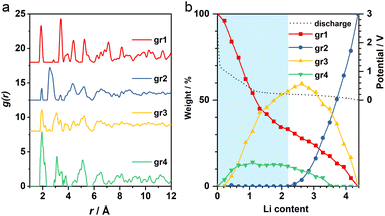
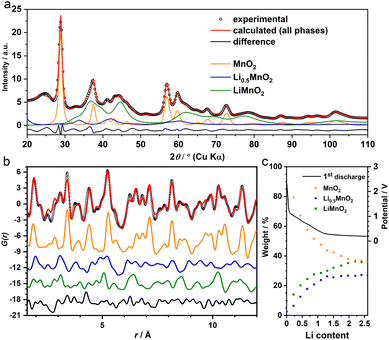
The operando X-ray total scattering data of MnO2 showed evident phase changes across the full discharge step (Fig. 1c and S1†). During the “insertion” step, the structure change is reflected by a significant reduction in both PDF and XRD peak intensities (Fig. 1c and d), with the latter accompanied by formation of new Bragg reflections (marked by black arrows in Fig. 1c). This suggests a drastic reduction in the structure coherence length, e.g. due to electrochemical pulverisation, with less notable changes in the (relative) atomic structures. During the “conversion” step, whilst the Bragg intensity continues to decrease, PDF peaks (≈2.5 Å) associated with new Mn local environments are observed (Fig. S1†), indicative of Mn nanoparticle formation.To analyse the PDF, a big data approach based on the Metropolis non-negative matrix factorisation (MMF) method11 (ESI†) was applied. We have previously established its protocol for the analysis of (both operando9,12 and ex situ13) PDF data to deconvolute any constituent phases involved in an electrode reaction,12 and demonstrated the advantage of this methodology in unravelling complex battery chemistry of conversion-type metal oxide9 and fluoride13 electrodes—systems that often involve unknown or nanostructured/amorphous intermediate phases during the cycling processes. Based on our MMF result, (at least) four components are required to describe the full lithiation process (Fig. 2a). Judging from the evolution of the derived phase ratios (Fig. 2b), gr1 and gr2 correspond to the starting (MnO2) and end (Mn + Li2O) phases, respectively, whereas gr3 and gr4 represent two potentially correlated intermediate phases.12 Surprisingly, whilst the onset of the voltage plateau—usually considered as the beginning of the “conversion” process where Mn is supposed to form—is seen when the nominal Li content (x) in LixMnO2 reaches ≈1, the actual extrusion of Mn (gr2) was not observed until x ≈ 2. This indicates that an additional process likely contributes to the capacity of the voltage plateau (1 ≤ x ≤ 2).
 | ||
| Fig. 2 (a) MMF-derived PDF components and (b) the corresponding weightings. The voltage curve is shown in black dotted line. Blue shade highlights the “insertion” regime. | ||
It is important to note that it is difficult to determine the actual Li content (x) in LixMnO2 precisely. This is largely due to the challenge in quantifying the capacity arising from electrolyte decomposition that is ubiquitous in all metal anode conversion anodes. For Mn oxides, within the voltage window of 1.0–0.3 V, whilst both MnO and Mn3O4 systems12 show a capacity of ≈1Li (per formula unit) entirely from non-Mn-associated redox, there is no comparable extra capacity in MnO2 anode based on the derived MMF phase evolutions (Fig. 2b). However, we did notice a slight reduction of the lithiation reaction rate at around x ≈ 1, which coincides with the onset of the voltage plateau and suggests that electrolyte side reaction may take place in parallel with the Mn redox. Taking this extra capacity into consideration, the Li content (x) contributing to the “insertion” process to form LixMnO2 is likely <2 (per formula unit).
2.3 Phase analysis
Given that we are only interested in the phase transition within the “insertion” cycle to form LixMnO2, our following study will focus on the first half of the lithiation (x ≤ 2). During this process, the absence of gr2, the much larger phase ratio of gr3, and earlier formation of gr4 collectively point to a two-step phase transitions from β-MnO2 to LixMnO2via sequential formation of gr4 and gr3 (Fig. 2b). To identify their structures and ensure their agreement with experiments in both long and short ranges, a series of joint refinement against both XRD and PDF data were performed. The initial structure models for gr4 and gr3 were obtained from literature.With respect to the gr3 phase, an earlier study of chemical lithiation of β-MnO2 reported a rutile to spinel-like (tetragonal Li1−δMnO2) phase transformation,8 pointing to a spinel-related structure (i.e. where the Mn ordering is equivalent to that in the spinel LiMn2O4) as the initial model. During this structure transition, the oxygen-sublattice undergoes a change from a tetragonal packed (tp) to an fcc arrangement. This is analogous to the transformation of the F−-sublattice we observed previously upon lithiation of FeF2, which forms an interfacial buffer phase with a nominal composition of Li2FeF4.13 This phase could be modelled using an orthorhombic structure (Cmmm, Fig. S2†) to accommodate the symmetry difference between the tetragonal parent (FeF2) and cubic end (LiF) phases during the tp-fcc transition.13 In light of the comparable change of the anion sublattice between β-MnO2 and FeF2, we therefore used the same interfacial structure (Li2MnO4) to model gr4. For charge balance, an assumption was made that half of the Li positions were occupied by Mn, leading to a composition of Li0.5MnO2.
The joint refinement was first attempted on the data collected at the state of Li 2.0—the end of “insertion” step. However, the agreement with the experiment is poor, particularly for the PDF data (Fig. S3†). In addition, whilst the main (111) reflection of the spinel-like phase was prominent in the chemically-lithiated system,8 this peak was not discernible in the operando XRD data (Fig. S4†). This suggests that even if the spinel motif forms, it only manifests itself in a short-range order and lacks a structure coherence along (at least) the [111] direction. To incorporate the disorder, we employed the cation DRX structure to model gr3. As the Jahn–Teller active Mn3+ is likely a dominant species in this LixMnO2 (0.5 ≤ x ≤ 1) phase (gr3), a symmetry lowered DRX-LiMnO2 structure (C2/m) was adopted. As expected, the refinement showed notable improvement in both long and short ranges (Fig. 3a and b). In particular, the Bragg peaks calculated from the refined DRX structure well align with the new reflections observed earlier in the experimental data (Fig. 1b) confirming that a symmetry lowered DRX phase provides a better description of the average structure of the gr3 intermediate. However, we also noticed the similarities in PDFs between the two intermediates (gr3 and gr4). To ensure they represent different phases (i.e. rather than two different Li concentrations from a solid-solution LixMnO2 series12), an additional refinement excluding the interfacial intermediate gr4 (i.e. with only MnO2 and the DRX phases considered) was performed. The refinement showed poor agreement with the experiment (Fig. S5†), demonstrating that the two intermediates are structurally different and are both required to model the XRD and PDF data. Following the structure assignments of the gr3 and gr4 phases, a series of refinements against the data across the whole insertion step were performed. The agreement between the refinement and the MMF results, particularly with respect to the phase ratio (Fig. 3c), is remarkable given that the MMF weightings are derived from a set of basis that are non-variable.
2.4 Reactivity of the DRX intermediate
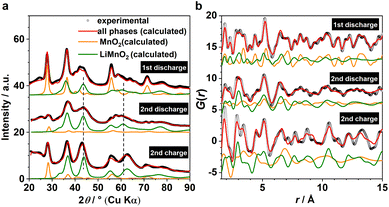
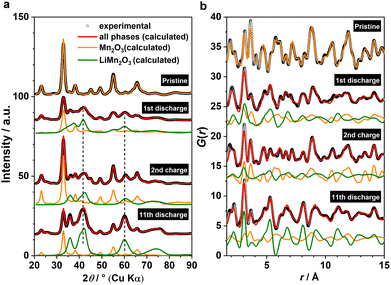
Based on the phase analysis, we now evaluate the reversibility of β-MnO2's tp-fcc phase transition, in particular with respect to the electrochemical reactivity of the DRX intermediate. Three ex situ samples within the insertion cycles were prepared for the laboratory X-ray total scattering measurements, including the end states of the 1st discharge, the 2nd discharge, and the 2nd charge (Fig. 1b). Both XRD and PDF data were extracted and analysed via refinement using the structure model identified from the analysis of the operando data (Fig. 4). Based on the results, all three phases, including β-MnO2 (gr2), interfacial-Li0.5MnO2 (gr4) and DRX-LixMnO2 (gr3), were required to model the three stages (Fig. 4). Judging by the relative Bragg peak intensities between these phases, it is evident that more MnO2 converted to DRX-LixMnO2 after the 2nd discharge. Upon the following charge, a noticeable shift of the DRX phase to higher 2θ angles can be seen. This shows a reduced lattice constant due to the extraction of Li, suggesting that this DRX phase is electrochemically reactive during the reversible insertion cycles. We note that this peak shift is also accompanied by an apparent increase of the MnO2 component. Whilst we do not exclude the probability of MnO2 reformation during the charging process, its apparent increase is likely due to the incoherence between different ex situ samples.In light of the observation of this DRX intermediate during the tp-fcc phase transition, a question comes to mind that if there are other non-fcc based metal oxides that may undergo a similar phase transformation to a cation DRX-related phase. We tested this hypothesis on α-Mn2O3 (bixbyite) as it has a non-fcc oxygen packing that resembles the fluoride sublattice in CaF2 with 25% anion vacancies (Fig. S6†). Several states of (dis)charge within the “insertion” cycle were measured ex situ via X-ray total scattering, including the end states of the 1st discharge, the 2nd charge and the 11th discharge (Fig. 5a). The 11th discharge (instead of in the early cycles) was chosen to improve the statistics concerning the incoherence among the ex situ measurements. The joint refinement against both XRD and PDF data confirmed the presence of a DRX intermediate (LixMn2O3) and that a third component wasn't required in the model (Fig. 5). Comparing between the end of 1st and 11th discharge, it is evident that more α-Mn2O3 has transformed to the DRX phase. Whilst an apparent increase of the parent α-Mn2O3 phase was observed based on the comparison between the end of 1st discharge and 2nd charge, this phase exhibits sharp Bragg peaks resembling those in the pristine, in turn suggesting its origin from unreacted α-Mn2O3 rather than a reconversion from the DRX—reconverted phase should show smaller particle sizes due to the inherent electrochemical pulverisation.12 In addition, a slight shift of the DRX peaks towards higher 2θ angles was also observed, indicating the redox activity of this DRX-LixMn2O3.
To further examine and verify this reactivity of the identified DRX species, multiple galvanostatic cycles of the “insertion” steps were performed for α-Mn2O3 and β-MnO2, and were compared to α-Fe2O3 (Fig. 6a–c); their corresponding redox processes are revealed in the dLi/dV plots (Fig. 6d–f). The initial discharge of these materials is largely underpinned by their irreversible phase transition to the DRX phases, hence the corresponding voltage curves all look distinct from the subsequent ones. But the following charge and discharge steps show comparable profile and redox features among different cycles, implying a reversible nature of the respective cycling process. As each state of (dis)charge contains multiple phases including unreacted pristine, DRX, and (possibly) surface/interfacial species, it is challenging to rationalise every redox feature without additional characterisations. However, based on the comparison among various cycles for the same material and across different systems, we can tentatively attribute the redox pairs located within 0.5–2 V (Fig. 6d and e), 2–4 V (Fig. 6e), 1.5–3 V (Fig. 6f) to Mn3+/2+, Mn4+/3+, and Fe3+/2+, respectively. The sharp peaks at high voltages (>3.5 V) are likely due to the additional capacity associated with oxygen and/or electrolyte reactions.14
3 Discussion
Our results suggest that both Mn oxides undergo an oxygen sublattice transformation from a non-fcc to an fcc arrangement. This transformation is accompanied by a concurrent reordering of the metal species to form a cation DRX phase. Therefore, up until now the confirmed DRX-active metal oxides (Fig. 7) include at least α-V2O5 (van de Waals/vdW oxide),2,4,15 MoxV2−xO5 (ReO3-related),16 α-Fe2O3 (corundum),5,12 TiO2 (amorphous),6,7 Nb2O5 (amorphous),6 β-MnO2 (rutile) and α-Mn2O3 (bixbyite). By comparison, Fe3O4 and Mn3O4, spinel-related phases with already an fcc oxygen sublattice, both form a cation ordered rocksalt upon lithiation despite a simultaneous migration of Fe/Mn from tetrahedral to octahedral sites.12 Whilst we cannot yet generalise these findings, they do constitute empirical evidence supporting a potential universal phenomenon, i.e. whether a metal oxide can be electrochemically converted to a cation DRX phase may have a dependence on the oxygen sublattice.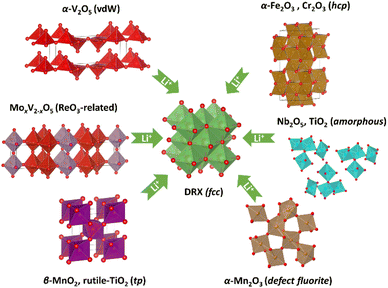 | ||
| Fig. 7 Identified phases and structure (or oxygen sublattice) types that can transform into a cation DRX phase via electrochemical lithiation. | ||
By way of an example, based on this empirical evidence and the hcp-fcc oxygen transition reported in α-Fe2O3, we envisage that some metal oxides with corundum structures may undergo comparable transformation. We tested this on Cr2O3 (Fig. S7a and b†), which is isostructural to hematite. Unsurprisingly, based on our simultaneous XRD and PDF refinement (Fig. S7c and d†), formation of a DRX-like phase—similar to that observed in α-Fe2O3—was identified. The derivative of the galvanostatic curves (Fig. S7b†) also shows a striking resemblance to that of α-Fe2O3 (Fig. 6f), implying that the formation and the subsequent reactions of Fe2O3 and Cr2O3's DRX phases could be fundamentally comparable.
In another example, according to the tp-fcc oxygen transition seen in β-MnO2 (rutile), it may be predicted that TiO2 (rutile) is also a DRX-active material. Whilst TiO2 has many polymorphic structures, the oxygen sublattice in both anatase and bronze phases are fcc-based; in contrast, rutile has a tp-oxygen, which is more closely related to the hcp-type in hematite.17 Upon a quick search in literature, a fast-charging DRX-LixTiO2 anode was indeed recently prepared using nanostructured TiO2 (rutile) via electrochemical lithiation.18 Remarkably, although rutile TiO2 has long been perceived as a mediocre anode due to is poor capacity as compared to the anatase and bronze polymorphs,19–21 this renewed understanding of nano rutile-TiO2 implies an important role of the crystallite size on metal oxides' electrochemical property, particularly with respect to its ability of DRX formation.
This particle size effect has previously been explored on α-Fe2O3 to maximise the DRX phase ratio upon the initial discharge, as well as the reversible capacity within the subsequent insertion cycles.5 The study revealed a capacity of nanoparticulate Fe2O3 (20 nm) almost twice as much as that of a submicron-sized (>100 nm) phase. It is known that nanomaterials possess a higher tolerance to lithiation-induced strain and atomic distortion.22 Thus, with respect to a significant structure change during the DRX formation, nanosized metal oxides can enable a facile Li insertion, generally leading to smaller polarisation, which in turn gives rise to a higher DRX conversion ratio within the desired voltage window. Because all of our pristine samples are commercial materials that have large crystallite sizes (of at least a few submicron), considerable starting phases remain unlithiated at the end of the initial discharge. This rationalises why only partial DRX conversion was observed in our work (Fig. 4 and 5).
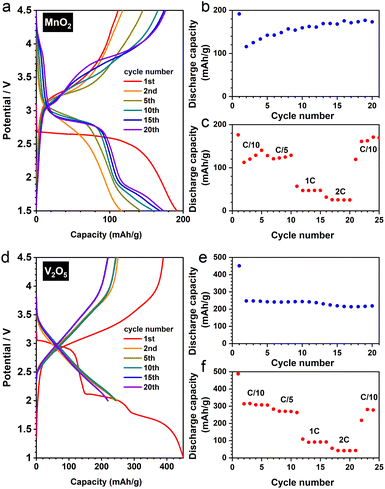
To verify this particle size effect, we synthesised nanostructured β-MnO2via a facile hydrothermal route.23 The as-prepared material adopts a nanorod morphology (Fig. S8a and b†), exhibiting significantly improved electrochemical performance (Fig. 8a–c) comparing to its bulk counterpart. The transformation of rutile to a DRX-like structure was confirmed by our joint XRD and PDF analysis (Fig. S8c and d†). Notably, the reversible cycling (i.e. after the first cycle) shows a gradually increased discharge capacity (Fig. 8b) with a slight change of voltage profile (Fig. 8a)—a redox pair becomes discernible around 4.0 V when the cycle number increases. These observations exhibit a resemblance to a DRX-LiMnO2 derived from mechanochemical synthesis,24 pointing to an analogous reaction mechanism between the two DRX materials prepared via distinct methods.
We further extended our investigation to the commercial α-V2O5, whose DRX derivative (Li3V2O5) shows a remarkable performance (Fig. 8d), reaching >200 mA h/g under a rate of C/5 after 20 cycles with a decent rate capability (Fig. 8e and f). Interestingly, the XRD and PDF analyses show that V2O5 does not require a nanostructured morphology (Fig. S9a†) to fully convert to the DRX phase (Fig. S9b and c†). Therefore, whilst downsizing the starting materials would in principle increase the yield of the DRX phase during the electrochemical synthesis, there is likely a structural dependence on the necessity of nanostructuring (or amorphisation) for DRX conversion, a cooperative effect—between structure types and particle sizes—that needs to be elucidated in future studies.
In addition to the crystal structure and particle size, we also anticipate that changing the chemical composition of the starting metal oxide by a strategic employment of dopants will modify the electronic structure of the corresponding DRX phase, in turn adjusting its operating voltage and specific capacity to enable the development of high energy density materials. This concept has been systematically tested in the MoxV2−xO5 system, in which the amount of V4+ increases with a higher concentration of Mo, leading to a reduced operating voltage of the cell.16
To avoid misleading readers, it is also important to point out that whilst we consider transition metal oxides (MaOb) precursors for the electrochemical synthesis of their DRX derivatives, the actual electrode materials contributing to the reversible redox reactions are the DRX phases, i.e. DRX-LixMaOb (x ≈ b − a)—but not the MaOb parent phases. Moreover, although we classify metal oxides based on their oxygen sublattice types, we do not mean that all non-fcc based metal oxides are definitely DRX-active; we also cannot exclude a potential metal dependence even if their oxide structures follow the crystallographic trend generalised in this work.
As a final point, it is worth noting that some compositions (in addition to DRX-LiMnO2), e.g. DRX-LiTiO2, have been prepared via both mechanochemical25 and electrochemical18 syntheses, but the electrochemically-achieved material was found to exhibit a higher capacity.18 Whilst the role of either synthetic protocol remains unestablished, their differences could potentially have a big impact on the derived DRX materials' physicochemical properties, including but not limited to phase purity, crystallite size (distribution), and cation short-range ordering, etc., which in turn could vary materials' electrochemical performances. As both of these synthetic approaches involve either mechanochemical or electrochemical grinding, the derived DRX materials usually have small particle sizes. These small particles, along with their structure disorder, render structure characterisation and phase analysis extremely challenging. Not only a plethora of techniques would be required to further our understanding of these DRX systems, a joint effort between experimentation and computation would also be crucial to unveil the phase transition mechanism between the distinct oxygen sublattices, to shed light into the underlying principle of the electrochemical synthesis for the preparation of high energy density DRX electrodes.
4 Conclusions
In summary, we studied the lithiation mechanism of β-MnO2 and α-Mn2O3 during their insertion cycles using operando and ex situ X-ray total scattering techniques. Based on a joint analysis combining XRD and PDF, an electrochemically active cation DRX phase was identified in both systems. Built upon the DRX-active metal oxides identified in earlier reports, our new result provides further empirical evidence hinting at a general phenomenon that a non-fcc oxygen sublattice may enable a transformation to a cation DRX phase upon electrochemical lithiation. In addition to the initial crystal structure of the metal oxides, we also discussed the impact of their crystallite size and chemical composition on the electrochemical properties of the derived cation DRX materials. Whilst additional experimental and computational supports are required to further our understanding of the DRX phase transition mechanisms and the underlying crystallographic principles, this study highlights an exciting new opportunity of using electrochemical synthesis to access high energy density DRX electrode materials.Author contributions
Matthew J. A. Leesmith: investigation, software. Nathan R. Halcovitch: investigation, methodology. Xiao Hua: conceptualization, supervision, investigation, formal analysis, software, methodology, plot, writing – original draft, writing – review & editing, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by a Research Grant via the Royal Society (GS\R2\222222) and a Research Enablement Grant via the Royal Society of Chemistry (E22-8441857550). The use of Diamond Light Source for access to beamline I15-1 (XPDF) is under Proposal CY22115-1. We also thank Dr Sara Baldock for the collection of the SEM data.Notes and references
- R. J. Clément, Z. Lun and G. Ceder, Energy Environ. Sci., 2020, 13, 345–373 RSC.
- H. Liu, Z. Zhu, Q. Yan, S. Yu, X. He, Y. Chen, R. Zhang, L. Ma, T. Liu, M. Li, R. Lin, Y. Chen, Y. Li, X. Xing, Y. Choi, L. Gao, H. S.-y. Cho, K. An, J. Feng, R. Kostecki, K. Amine, T. Wu, J. Lu, H. L. Xin, S. P. Ong and P. Liu, Nature, 2020, 585, 63–67 CrossRef CAS PubMed.
- T. Tsuzuki, Commun. Chem., 2021, 4, 143 CrossRef CAS PubMed.
- C. Delmas, H. Cognac-Auradou, J. M. Cocciantelli, M. Ménétrier and J. P. Doumerc, Solid State Ionics, 1994, 69, 257–264 CrossRef CAS.
- D. Larcher, C. Masquelier, D. Bonnin, Y. Chabre, V. Masson, J.-B. Leriche and J.-M. Tarascon, J. Electrochem. Soc., 2003, 150, A133–A139 CrossRef CAS.
- H. Xiong, H. Yildirim, E. V. Shevchenko, V. B. Prakapenka, B. Koo, M. D. Slater, M. Balasubramanian, S. K. R. S. Sankaranarayanan, J. P. Greeley, S. Tepavcevic, N. M. Dimitrijevic, P. Podsiadlo, C. S. Johnson and T. Rajh, J. Phys. Chem. C, 2012, 116, 3181–3187 CrossRef CAS.
- P. Barnes, Y. Zuo, K. Dixon, D. Hou, S. Lee, Z. Ma, J. G. Connell, H. Zhou, C. Deng, K. Smith, E. Gabriel, Y. Liu, O. O. Maryon, P. H. Davis, H. Zhu, Y. Du, J. Qi, Z. Zhu, C. Chen, Z. Zhu, Y. Zhou, P. J. Simmonds, A. E. Briggs, D. Schwartz, S. P. Ong and H. Xiong, Nat. Mater., 2022, 21, 795–803 CrossRef CAS PubMed.
- W. I. F. David, M. M. Thackeray, P. G. Bruce and J. B. Goodenough, Mater. Res. Bull., 1984, 19, 99–106 CrossRef CAS.
- X. Hua, P. K. Allan, C. Gong, P. A. Chater, E. M. Schmidt, H. S. Geddes, A. W. Robertson, P. G. Bruce and A. L. Goodwin, Nat. Commun., 2021, 12, 561 CrossRef CAS PubMed.
- H. Liu and C. P. Grey, J. Mater. Chem. A, 2016, 4, 6433–6446 RSC.
- H. S. Geddes, H. Blade, J. F. McCabe, L. P. Hughes and A. L. Goodwin, Chem. Commun., 2019, 55, 13346–13349 RSC.
- X. Hua, P. K. Allan, H. S. Geddes, E. Castillo-Martínez, P. A. Chater, T. S. Dean, A. Minelli, P. G. Bruce and A. L. Goodwin, Cell Rep. Phys. Sci., 2021, 2, 100543 CrossRef CAS.
- X. Hua, A. S. Eggeman, E. Castillo-Martínez, R. Robert, H. S. Geddes, Z. Lu, C. J. Pickard, W. Meng, K. M. Wiaderek, N. Pereira, G. G. Amatucci, P. A. Midgley, K. W. Chapman, U. Steiner, A. L. Goodwin and C. P. Grey, Nat. Mater., 2021, 20, 841–850 CrossRef CAS PubMed.
- Y. Y. Hwang, J. H. Han, S. H. Park, J. E. Jung, N. K. Lee and Y. J. Lee, Nanotechnology, 2022, 33, 182003 CrossRef PubMed.
- C. K. Christensen, D. R. Sørensen, J. Hvam and D. B. Ravnsbæk, Chem. Mater., 2019, 31, 512–520 CrossRef CAS.
- C. Delmas and H. Cognac-Auradou, J. Power Sources, 1995, 54, 406–410 CrossRef CAS.
- A. R. West and P. G. Bruce, Acta Crystallogr., Sect. B, 1982, 38, 1891–1896 CrossRef.
- P. Díaz-Carrasco, A. Duarte-Cárdenas, A. Kuhn and F. García-Alvarado, J. Power Sources, 2021, 515, 230632 CrossRef.
- X. Hua, Z. Liu, M. G. Fischer, O. Borkiewicz, P. J. Chupas, K. W. Chapman, U. Steiner, P. G. Bruce and C. P. Grey, J. Am. Chem. Soc., 2017, 139, 13330–13341 CrossRef CAS PubMed.
- Y. Ren, Z. Liu, F. Pourpoint, A. R. Armstrong, C. P. Grey and P. G. Bruce, Angew. Chem., Int. Ed., 2012, 51, 2164–2167 CrossRef CAS PubMed.
- M. Wagemaker, W. J. H. Borghols and F. M. Mulder, J. Am. Chem. Soc., 2007, 129, 4323–4327 CrossRef CAS.
- P. G. Bruce, B. Scrosati and J.-M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930–2946 CrossRef CAS PubMed.
- Y. Dong, K. Li, P. Jiang, G. Wang, H. Miao, J. Zhang and C. Zhang, RSC Adv., 2014, 4, 39167–39173 RSC.
- T. Sato, K. Sato, W. Zhao, Y. Kajiya and N. Yabuuchi, J. Mater. Chem. A, 2018, 6, 13943–13951 RSC.
- E. Baudrin, S. Cassaignon, M. Koelsch, J. P. Jolivet, L. Dupont and J. M. Tarascon, Electrochem. Commun., 2007, 9, 337–342 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta01740k |
| This journal is © The Royal Society of Chemistry 2023 |


![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , orange) and DRX-LiMn2O3 (
, orange) and DRX-LiMn2O3 (