Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Health risks due to intrusion into the drinking water distribution network: hydraulic modelling and quantitative microbial risk assessment†
Michael
Odhiambo
 a,
Victor
Viñas
a,
Victor
Viñas
 a,
Ekaterina
Sokolova
a,
Ekaterina
Sokolova
 *ab and
Thomas J. R.
Pettersson
*a
*ab and
Thomas J. R.
Pettersson
*a
aDepartment of Architecture and Civil Engineering, Chalmers University of Technology, Sweden. E-mail: Thomas.Pettersson@chalmers.se
bDepartment of Earth Sciences, Uppsala University, Sweden. E-mail: ekaterina.sokolova@geo.uu.se
First published on 21st April 2023
Abstract
Ageing water infrastructure is prone to increased physical deficiencies. These form pathways for pathogen intrusion into drinking water distribution networks (WDNs), hence posing major health risks to consumers. This study aimed at estimating the risk of infection from pipe breaks and intermittent water supply, which are some of the major causes of sustained low pressure within the WDN and hence the triggers for pathogen intrusion. Further, the effect of groundwater level on pathogen intrusion was investigated. Three risk scenarios were evaluated on the example of a real WDN in Sweden: (i) pipe break with no intrusion from leak holes, (ii) pipe break with intrusion due to leak holes, and (iii) insufficient water supply in the presence of leak holes. Pressure distribution from hydraulic modelling, estimated groundwater levels, and pathogen concentration in intruding water (from field study) were used to estimate the intrusion and the number of pathogens entering the WDN. Reference pathogens Campylobacter, Cryptosporidium, and norovirus were used in quantitative microbial risk assessment (QMRA) for assessing the health risks. Results indicated that the daily probability of infection exceeded an acceptable target value of 10−6 for most of the WDN and for all scenarios. The findings were consistent with the estimated annual burden of acute gastrointestinal illness in Sweden. The concentration of pathogens in intruding water and the duration of the low-pressure-causing event were observed to influence the probability of infection the most. The results from this study can be used to identify vulnerable sections in the WDN, which can be targeted for additional investment in monitoring and/or renewal.
Water impactWater suppliers are tasked with providing safe drinking water and need to assess health risks for consumers. We provide water suppliers with a sensible approach to carrying out quantitative microbial risk assessment (QMRA) with readily available data. This work is directly relevant to achieving sustainable development goals 3 good health and well-being and 6 clean water and sanitation. |
1 Introduction
Ageing water distribution networks (WDNs) are characterized by physical deficiencies such as pipe breaks, cracks, and leak holes. These deficiencies are the main causes of water loss through leakage, which greatly hinders the effective operational management of municipal WDNs. It represents reduced revenues and contributes to poor water quality.1 In the United States of America (USA), main pipe break is estimated to occur every 2 minutes leading to an estimated daily loss of 23 million cubic meters of clean drinking water.2 Worldwide, 126 billion cubic meters are estimated to be lost through leakages annually.3 In Sweden, 5000 repairs from pipe breaks and other leakages are estimated to occur annually, accounting for 10 to 15% of the total production losses.4 The deficiencies, pipe breaks, cracks, and leak holes can be pathways for pathogen intrusion in the WDN in case of inadequate pressure gradient (low pressure) in the WDNs and hence can cause risk to human health.5Pathogen intrusion in the WDNs can contaminate drinking water resulting in gastrointestinal illnesses (GII).6 Several studies have linked disease outbreaks to pathogen intrusion in the WDNs, for instance in Canada, surveillance reports between 1993 and 2008 estimated that broken pipes in WDNs contributed to 7% of waterborne disease outbreaks.7 In Sweden, from 1980 to 2007, 27 incidents accounting for 34% of total waterborne outbreaks were attributed to deficiencies in the WDNs.8 From 1971 to 1998, the USA reported 113 outbreaks associated with WDNs with over 21 thousand cases of illnesses, from which 498 people were hospitalized and 13 died.9 In May 2007, a documented low-pressure event in the WDN near a dairy cattle stable and a slaughterhouse was attributed to the campylobacteriosis outbreak in the Norwegian town of Røros. Investigations pointed out that consumption of drinking water from the tap as the cause of Campylobacter infection where 1500 people were affected.10 An estimated 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 infections occurred due to the outbreak of gastroenteritis in Montenegro, Podgorica town, in the period from August to September 2008. Norovirus was attributed to this infection, and it was suspected that the intrusion of pathogens in the WDN could have been caused by low-pressure events in the WDN due to a series of pump failures.11 Unhygienic meter replacement practices and repair of main pipe breaks in the WDN in Missouri, USA, were linked to the E. coli 0157:H7 outbreak between December 1989 to January 1990. The outbreak caused the death of 4 people, 32 hospitalizations and 243 incidences of diarrhoea.12,13 Overall, 37% of GII cases in Sweden may be attributed to pathogen intrusion in the WDN,14 while in the USA and Europe, 30% and 31% were observed, respectively.15 Previous studies16 have investigated the association of pathogen intrusion into distribution networks with the endemic level of GII. This includes studies in Canada, Australia, Sweden, the United Kingdom, Norway, and USA.
000 infections occurred due to the outbreak of gastroenteritis in Montenegro, Podgorica town, in the period from August to September 2008. Norovirus was attributed to this infection, and it was suspected that the intrusion of pathogens in the WDN could have been caused by low-pressure events in the WDN due to a series of pump failures.11 Unhygienic meter replacement practices and repair of main pipe breaks in the WDN in Missouri, USA, were linked to the E. coli 0157:H7 outbreak between December 1989 to January 1990. The outbreak caused the death of 4 people, 32 hospitalizations and 243 incidences of diarrhoea.12,13 Overall, 37% of GII cases in Sweden may be attributed to pathogen intrusion in the WDN,14 while in the USA and Europe, 30% and 31% were observed, respectively.15 Previous studies16 have investigated the association of pathogen intrusion into distribution networks with the endemic level of GII. This includes studies in Canada, Australia, Sweden, the United Kingdom, Norway, and USA.
Pipe breaks and intermittent (insufficient) supply are some of the major events that are responsible for sustained low pressure within the WDN and hence are the triggers for pathogen intrusion in the WDNs.5,17 When a break occurs on the main pipes in the WDN, high free flows are experienced which negatively impact the pressure within the WDN. With ageing of water distribution networks, and changing environmental conditions, pipe breaks, leaks and planned repairs are becoming more prevalent. WDNs with limited water supply are characterized by low pressure conditions, and due to changing hydrological regimes resulting from climate and land-use changes, insufficient water supply is expected to persist.5,18
To determine the public significance of these events, it is necessary to assess the associated risks to human health. This can help planners and managers prepare and respond to events when they occur. The key inputs for such estimations are duration and frequency of the events,5,19 concentration of pathogens in the soil water surrounding the pipes,5,6,15 the intrusion volumes of contaminated water, and the position of the pipes in relation to groundwater levels (GWLs).4 The position of the GWL is critical for intrusion to occur, if the pipe is located above the GWL, the risk of contaminated soil water intrusion will be lower.4 In Sweden, for example, about 20% of the pipes in WDNs are estimated to be located below the groundwater level, raising the risks of intrusion.4 While it may be possible to obtain some of these key input data through field measurements, others require hydraulic modelling, for instance, intrusion volumes due to low-pressure causing events in the WDN.3
Various approaches have been proposed to evaluate the risk of intrusion events occurring in WDNs and to assess potential mitigation measures.20,21 These include optimization studies to identify critical nodes for sensor placement;22–24 and geostatistical approaches for sensor placement and mitigation measures.25 Software tools are also available, such as IRA-WDS,26 and CANARY,27 which allow for predicting the occurrence of contamination events in the WDN. Many of the approaches developed focus on predicting the likelihood of contamination events occurring, and not necessarily the health consequences of these events. Studies that have tried to assess the impact of microbial contamination in the WDN have used the quantitative microbial risk assessment (QMRA) methodology to estimate infection risks.5,15,19,28–31 A conceptual model was developed by Besner et al.5 for assessing the risks of intrusion in the WDNs using hydraulic modelling and QMRA, and the conclusion was that the main uncertainties were associated with the magnitude and duration of low-pressure events and insufficient or lack of input data, for instance, data on failure frequencies and varying dose–response relationships. Using hydraulic modelling and QMRA, Blokker et al.6,15 determined human health risks after a main pipe repair event and observed that the risk was very dependent on the concentrations in the intruding water. Similar studies involving main pipe repair and intrusion from other low-pressure events indicate that the concentrations of pathogens in intruding water, duration and magnitude/intensity of the events have a great influence on the risk levels.4,19,31–36
While the previous studies focused on intrusion potential due to GWL as a constant estimated value over the entire WDN, this study explores further the effect of GWL variability on pathogen intrusion from pipe break events and insufficient water supply from the drinking water treatment plant. An area where most of the WDN pipes are perceived to be submerged below the groundwater level is investigated. Viñas et al.37 highlighted that QMRA has been applied to assess risks from regular operation, repairs, maintenance, and planned rehabilitation. For regular operations, though, not much has been done regarding the insufficient supply of water in the WDN, as most utilities across Europe have been able to meet their demands. This is quickly changing due to various reasons such as changing climatic conditions and land use,18 planned repairs from worn-out pipe sections, repairs due to extreme weather events, and pump shutdowns.5
This study aimed at estimating the risks of infection for drinking water consumers due to intrusion in a real WDN, using data readily available from the water supplier. The study expands on previous research by attempting to improve input parameters used for modelling, testing a variety of mitigation measures, and using epidemiological data to validate the results. The following research questions were adopted:
• What are the infection risks due to pathogen intrusion in the studied submerged WDN posed by the pipe break and intermittent/insufficient water supply events?
• What conditions within and around the WDN influence the infection risks to consumers' health?
• How can the calculated infection risks from intrusion be used for WDN renewal planning or strategic decision-making?
• Can the effects of intrusion on infection risk be adequately assessed with the proposed approach?
The following objectives were formulated in order to answer the research questions proposed:
• Define representative scenarios for intrusion events and calculate using the hydraulic model the pressure conditions in the pipes and potential volumes of intruded contaminated soil water.
• Assume representative concentration of pathogens in intruding contaminated soil water based on field study data from ongoing studies.
• Simulate the transport of pathogens in the WDN using a hydraulic model.
• Calculate the probability of infection using dose–response functions, in a QMRA model, and the simulated pathogen concentrations in the pipe network.
2 Methodology
The methodology included four major steps:1. Simulation of pressure levels in the WDN for scenarios of a pipe break and of an insufficient supply of water from the drinking water treatment plant.
2. Calculating the number of pathogens intruding into the WDN for different scenarios based on microbial concentrations in soil water from field studies.
3. Simulation of the spatial distribution of pathogens in the WDN after intrusion events.
4. Determining human health risk using spatial distribution of pathogens in the WDN as input data into a QMRA model.
2.1 Case study description
The study focused on a section of a water distribution network (WDN) in Skåne County, southern part of Sweden, with a total length of 13.5 km pipelines of varying diameters, ranging from 25 to 200 mm, including 457 nodes. The annual water supply in the study area is 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 m3 while total estimated water losses through leakage in the WDN are 0.054 l s−1 km−1, accounting for 27% of total water production. The WDN has a total of 280 metered service connections serving approximately 714 persons considering an estimated daily demand of 140 l p−1 d−1 in Sweden and excluding non-revenue water (water losses). The pipe network was laid between 1.5 m to 2 m below the ground surface within the same trench as stormwater and wastewater pipes. The staff at the site estimated that most sewer pipes are at the same elevation as drinking water pipes, with approximately 0.5 m distance in the horizontal direction between the pipes. It was further estimated that 100% of the pipes in the WDN were estimated to be below GWL, hence higher risks of intrusion were expected.
000 m3 while total estimated water losses through leakage in the WDN are 0.054 l s−1 km−1, accounting for 27% of total water production. The WDN has a total of 280 metered service connections serving approximately 714 persons considering an estimated daily demand of 140 l p−1 d−1 in Sweden and excluding non-revenue water (water losses). The pipe network was laid between 1.5 m to 2 m below the ground surface within the same trench as stormwater and wastewater pipes. The staff at the site estimated that most sewer pipes are at the same elevation as drinking water pipes, with approximately 0.5 m distance in the horizontal direction between the pipes. It was further estimated that 100% of the pipes in the WDN were estimated to be below GWL, hence higher risks of intrusion were expected.
2.2 Hydraulic modelling to determine pressure in the water distribution network
A pressure-driven analysis (PDA) model of EPANET version 2.2 was used for hydraulic modelling. This model uses the Wagner equation to determine nodal demands (qDi) based on available pressure (Pi), which is the difference between the hydraulic head (hi) and nodal elevation (Ei).38 Resultant pressure-dependent flows are determined using eqn (1).39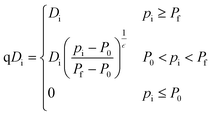 | (1) |
Head loss is the most critical setting in hydraulic modelling of WDNs with EPANET.40 Three models, i.e., Darcy–Weisbach (D–W), Hazen–Williams (H–W), and Chezy–Manning (C–M), can be used to determine head loss. Ignoring minor head losses, the three models of friction losses follow eqn (2).39
| hL = AqB | (2) |
The D–W model was adopted for this simulation, where the resistance coefficient, A, and flow exponent, B, are described by Rossman et al.39
The simulation period covered one week (168 hours), the hydraulic time step was set as 10 minutes, while the pattern and reporting time steps were set to one hour.
The following scenarios were investigated:
1. Pipe break – localized section, intrusion occurred only at the repair section, the WDN was assumed to have new pipes and hence no leakages are expected (PBNo leakage).
2. Pipe break – varying GWLs at different nodes and varying pipe pressure, the WDN was assumed to have leakage, and holes/cracks giving varying intrusion potential (PBLeakage).
3. Insufficient supply – insufficient water in the main pipes due to raw water shortage or process failures at the drinking water treatment plant.
| Hext = PL − (GWL + R) | (3) |
| ΔHint = Hext − Hp | (4) |
The GWLs in the study area were obtained from the observation boreholes near the project area provided by the Geological Survey of Sweden (SGU) (Fig. S3†). Boreholes were chosen with similar soil properties as in the project area. The relationship between the groundwater level in the borehole and the ground surface elevation of the boreholes was determined using regression analysis. Given the ground surface elevation of the nodes, the determined relationship was used to assume the groundwater level at every node. The GWLs, the pipe level (PL) and pipe radius (R) were used to determine the external piezometric head (Hext) acting on the pipe as shown in eqn (3).
Using the lowest nodal pressures (Hp) in the pipe and external piezometric head (Hext), the intrusion head potential (ΔHint) was determined, as shown in eqn (4), and used to calculate the nodal intrusion volume, further described in section 2.3.1.
2.3 Pathogen intrusions into the water distribution network
Pathogen intrusion into the WDN was determined based on the intrusion volume of soil water and assumptions on the pathogen concentrations in the intruded water based on field studies of E. coli concentration in the soil water and literature values on the pathogen concentrations in wastewater.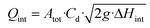 | (5) |
Using the drinking water leakage volume (Qout) during normal pressure (ΔHnormal), the size, total area (Atot), of the leakage holes on every pipe was determined by re-arranging the orifice equation as described by eqn (6).
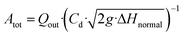 | (6) |
The intrusion volume into the WDN was calculated for every affected pipe section and node in all the scenarios. However, due to the vast number of nodes, sections of the WDN with similar characteristics (pressure, flow, elevation, and pipe size) were grouped, and the intrusion of each section was lumped into one node per section in the model. A total of 32 intrusion nodes were identified based on these criteria for all the scenarios except scenario 1 (Fig. S1†).
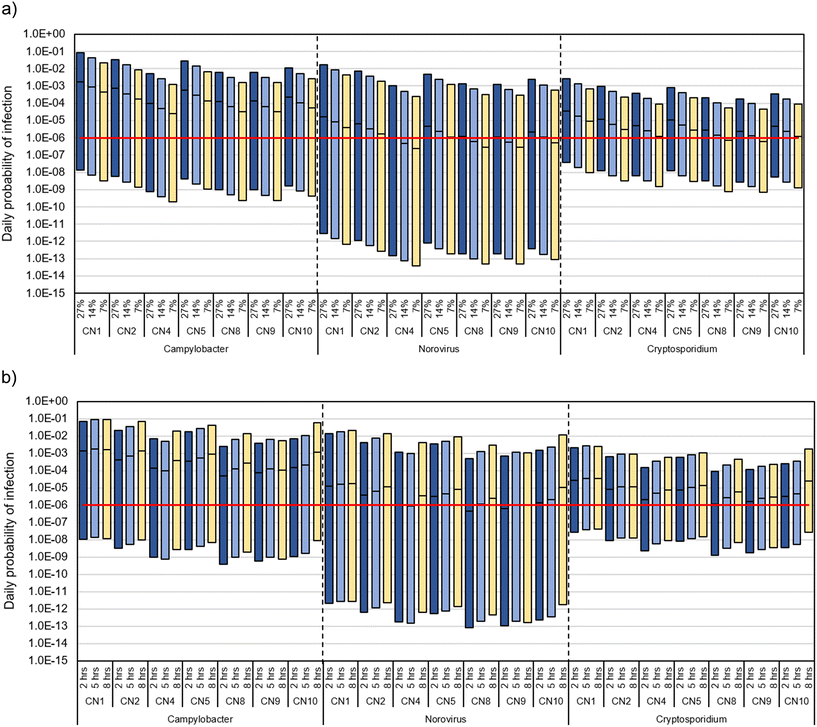
Additionally, for scenario 2 – pipe break with leakage and varying intrusion potential, to also test the effect of the leakage rate on the infection risk, the original leakage rate of 27% was reduced to a) 14% and to b) 7%, and thus the intrusion volumes were also reduced and hence the risks were recalculated for comparison.
The detection of E. coli in soil water was here assumed to indicate the presence of faecal pollution and potentially pathogens. In an unpublished study,42E. coli was detected in 22 out of 40 samples of soil water collected at the pipe level during pipe repairs. The detected E. coli concentrations varied between approx. 1 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units per 100 ml, indicating different levels of potential wastewater impact. As E. coli concentrations in untreated municipal wastewater are expected to vary between approx. 6 and 7
log10 units per 100 ml, indicating different levels of potential wastewater impact. As E. coli concentrations in untreated municipal wastewater are expected to vary between approx. 6 and 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units per 100 ml,43–46 the detected levels of E. coli in soil water indicate a dilution of at least 2
log10 units per 100 ml,43–46 the detected levels of E. coli in soil water indicate a dilution of at least 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units. Therefore, in this study, several dilution factors from 2 to 4
log10 units. Therefore, in this study, several dilution factors from 2 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units between the pathogen concentrations in wastewater and soil water were used, based on the unpublished study.
log10 units between the pathogen concentrations in wastewater and soil water were used, based on the unpublished study.
The average concentrations of the studied pathogens in untreated wastewater were reported to be: Campylobacter 1.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 per 100 ml,43 norovirus GI and GII 4.4
log10 per 100 ml,43 norovirus GI and GII 4.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 per 100 ml,47 and Cryptosporidium 0.3
log10 per 100 ml,47 and Cryptosporidium 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 per 100 ml.48 For norovirus, from literature, it was further assumed that 1 in 1000 detected gene copies were infectious.49
log10 per 100 ml.48 For norovirus, from literature, it was further assumed that 1 in 1000 detected gene copies were infectious.49
Based on the calculated flow rates of intruding soil water and the assumption of pathogen concentrations in wastewater and their reduction in soil water, the numbers of pathogens entering the system were calculated. The calculated numbers of pathogens entering the distribution network were further adjusted to reflect the reduced pathogen loads in the WDN due to leakages from the WDN.
For scenario 1, the total number of pathogens entering the WDN was inserted in the model in the affected node as initial water quality, representing cumulative intrusion over the entire 5 hour low-pressure period. This was inserted at the beginning of the water quality simulation at noon. A flow of 20 l s−1 was introduced at a node on the downstream end of the isolated section for 1 hour (12:00–13:00) to simulate flushing to remove intruded pathogens. The transport of the remaining pathogens was then simulated in the WDN. For scenarios 2 and 3, the numbers of pathogens entering the WDN were inserted in the model in the nodes as mass flow rates and were assumed to last the same time as the event period. The pathogen concentrations in critical nodes were obtained and used in the QMRA tool to calculate the risks to human health. The critical nodes were selected based on similar flow characteristics, the maximum hourly concentration, and the duration of concentration at the node.
2.4 Quantitative microbial risk assessment
Pathogen concentrations obtained from the hydraulic simulation for the selected downstream critical nodes were used as inputs to quantify the probability of infection for drinking water consumers. A triangular distribution was generated using each critical node's minimum, mode, and maximum pathogen concentrations. A Swedish consumption study recommended a gamma distribution of water consumption and an average daily consumption of 1 litre or 5 glasses of water per day.50 Hence, the consumption was assumed to be a gamma distribution with parameters α = 0.2 and β = 1 (Fig. S4†). The mean consumption volume used was 0.2 litres, which was considered a better representation of the volume of water consumed in one hour.The beta-Poisson dose–response relationship was used to calculate the probability of infection Pinf as shown in eqn (7).
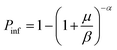 | (7) |
The dose–response parameters for the different reference pathogens were: Campylobacter (α = 0.024, β = 0.011),51 norovirus (α = 0.04, β = 0.055)52 and Cryptosporidium (α = 0.115, β = 0.176).53 For this study, it was assumed that everyone in the population was equally susceptible to the reference pathogen. The number of iterations in the Monte Carlo simulations to calculate Pinf was set to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
The probability of infection was calculated for selected critical nodes, i.e., nodes with the highest risk. The calculated Pinf was then converted to a daily risk by means of: daily risk = 1 − (1 − Pinf)n, where n is the duration of the intrusion event in hours. The acceptable risk target for daily probability of infection was set at 10−6, to account for short-term periods of heightened risk.54
3 Results
This section describes the results for pipe break scenario 1 – localized pipe break with no leakage in other sections of the WDN, pipe break scenario 2 – with leakage in other parts of the WDN, and scenario 3 – insufficient water supply. The results include output from the hydraulic simulations, i.e., calculated pathogen intrusions for all scenarios, the concentration of pathogens in the consumed water at critical times, and the resulting risk of infection for consumers.3.1 Pressure distribution
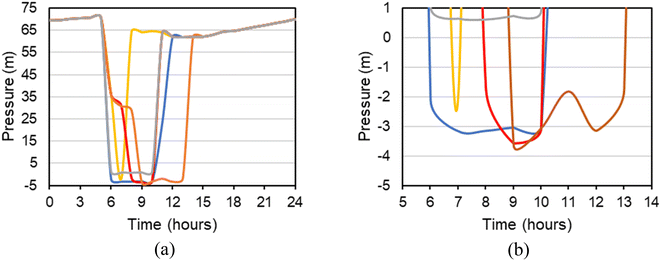
The graphs in Fig. 1 indicate the pressure distribution in the most affected intrusion node for each of the scenarios. The pressure drops were observed during the event periods, and the pressure resumed to normal after the end of the event as shown in Fig. 1(a). A similar trend was observed for the different nodes, however, the magnitude of the pressure at the nodes was different. The observed pressure during the events in the most affected nodes ranged from 0.7 m to −3.7 m (Fig. 1(b)). For scenario 2, different event periods (2, 5, and 8 hours) were tested and the lowest observed pressure ranged from −2 m to −3.7 m (Fig. 1(b)).3.2 Intrusion volumes/pathogens
The total number of pathogens entering the WDN varied depending on the unit intrusion volume of soil water, duration of the intrusion event, and pathogen concentration in the soil water (Table 1). Reduction factors between 2 and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units for the pathogen concentrations in wastewater and soil water were used for scenarios 1–3 lasting for 5 hours and with an estimated overall leakage rate of 27%. Higher intrusion volumes and hence higher pathogen intrusions into the WDN were observed in scenario 1 compared to scenarios 2 and 3 (Table 1). This was because in scenario 1, a relatively larger section of the WDN was assumed to have been replaced, and without leak holes, around the repair point (point intrusion), which contributed to higher intrusion volume while in other scenarios, most of the intrusions were assumed to originate from varied leak holes spread along the WDN (diffuse intrusion). Pathogens intruded into the WDN were assumed to be lost from the WDN through demands at the nodes, losses through leakages, and through cleaning the WDN's repaired or renewed pipe section using higher flow (commonly referred to as “flushing” by water producers). Flushing is commonly used when the intrusion is known as the case of scenario 1. Even though a higher concentration of pathogens intruded the WDN in scenario 1 compared to other scenarios, lower pathogen concentrations, consequently lower human health risks at the nodes, were observed in scenario 1 compared to scenario 2 (Fig. 3), and this can be attributed to flushing at the repair section in scenario 1. Generally higher concentrations in scenario 2 compared to scenario 3 (Fig. 3) can be attributed to lower internal pressure in the WDN during scenario 2. For scenario 2, the impacts of the leakage rate and event duration were further investigated. The initial leakage of 27% was reduced to 14% and then 7%, respectively, i.e., half and quarter of the original value. The total event period was changed from 5 to 2 and then 8 hours, and the resulting pathogen intrusions were noted, see Table 1. A pipe break event was divided into two parts as described in section 2.2.2 “detection time” which was the duration of free flow during a pipe break and “repair time” which represented the time the pipe was closed for actual repair. For total event periods of 2, 5 and 8 hours, the detection times were 1, 2 and 3 hours respectively, while the repair times were 1, 3, and 5 hours respectively. The pathogen intrusions were observed to be proportional to the detection time, while during the repair period, the pathogen intrusions were insignificant due to low or no flow downstream of the closed pipe, as the only supply source to this part of the WDN was cut off. This may however not be the case in WDNs with multiple reservoirs. In general, the intrusion volume and pathogen concentration in intruding soil water had a great influence on the number of pathogens intruding into the WDN.
log10 units for the pathogen concentrations in wastewater and soil water were used for scenarios 1–3 lasting for 5 hours and with an estimated overall leakage rate of 27%. Higher intrusion volumes and hence higher pathogen intrusions into the WDN were observed in scenario 1 compared to scenarios 2 and 3 (Table 1). This was because in scenario 1, a relatively larger section of the WDN was assumed to have been replaced, and without leak holes, around the repair point (point intrusion), which contributed to higher intrusion volume while in other scenarios, most of the intrusions were assumed to originate from varied leak holes spread along the WDN (diffuse intrusion). Pathogens intruded into the WDN were assumed to be lost from the WDN through demands at the nodes, losses through leakages, and through cleaning the WDN's repaired or renewed pipe section using higher flow (commonly referred to as “flushing” by water producers). Flushing is commonly used when the intrusion is known as the case of scenario 1. Even though a higher concentration of pathogens intruded the WDN in scenario 1 compared to other scenarios, lower pathogen concentrations, consequently lower human health risks at the nodes, were observed in scenario 1 compared to scenario 2 (Fig. 3), and this can be attributed to flushing at the repair section in scenario 1. Generally higher concentrations in scenario 2 compared to scenario 3 (Fig. 3) can be attributed to lower internal pressure in the WDN during scenario 2. For scenario 2, the impacts of the leakage rate and event duration were further investigated. The initial leakage of 27% was reduced to 14% and then 7%, respectively, i.e., half and quarter of the original value. The total event period was changed from 5 to 2 and then 8 hours, and the resulting pathogen intrusions were noted, see Table 1. A pipe break event was divided into two parts as described in section 2.2.2 “detection time” which was the duration of free flow during a pipe break and “repair time” which represented the time the pipe was closed for actual repair. For total event periods of 2, 5 and 8 hours, the detection times were 1, 2 and 3 hours respectively, while the repair times were 1, 3, and 5 hours respectively. The pathogen intrusions were observed to be proportional to the detection time, while during the repair period, the pathogen intrusions were insignificant due to low or no flow downstream of the closed pipe, as the only supply source to this part of the WDN was cut off. This may however not be the case in WDNs with multiple reservoirs. In general, the intrusion volume and pathogen concentration in intruding soil water had a great influence on the number of pathogens intruding into the WDN.
| Scenario | Pathogen reduction/leakage/repair time | Intrusion volume (l) | Campylobacter (No) | Cryptosporidium (No) | Norovirus (No) |
|---|---|---|---|---|---|
a For scenario 2, if nothing else is specified, the leakage rate is 27%, repair time is 5 hours, and pathogen reduction is 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units. log10 units.
|
|||||
| Scenario 1 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.9 × 103 | 7.5 × 103 | 7.5 × 102 | 9.5 × 103 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.9 × 103 | 5.7 × 102 | 5.7 × 101 | 7.2 × 102 | |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.9 × 103 | 5.7 × 101 | 5.7 × 100 | 7.2 × 101 | |
| Scenario 2a | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
1.2 × 103 | 3.2 × 103 | 3.2 × 102 | 4.0 × 103 |
| 14% leakage rate | 5.8 × 102 | 1.5 × 103 | 1.5 × 102 | 9.6 × 102 | |
| 7% leakage rate | 3.0 × 102 | 7.9 × 102 | 7.9 × 101 | 9.9 × 102 | |
| 2 hours repair time | 4.5 × 102 | 1.2 × 103 | 1.2 × 102 | 1.5 × 103 | |
| 8 hours repair time | 1.8 × 103 | 4.8 × 103 | 4.8 × 102 | 6.1 × 103 | |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
1.2 × 103 | 2.3 × 102 | 2.3 × 101 | 2.9 × 102 | |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
1.2 × 103 | 2.3 × 101 | 2.3 × 100 | 2.9 × 101 | |
| Scenario 3 | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.5 × 102 | 6.7 × 102 | 6.7 × 101 | 8.4 × 102 |
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.5 × 102 | 5.1 × 101 | 5.1 × 100 | 6.4 × 101 | |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction log10 unit reduction |
2.5 × 102 | 5.1 × 100 | 5.1 × 10−1 | 6.4 × 100 | |
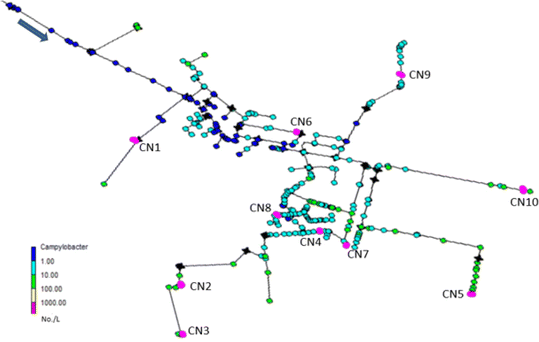
The location of the critical nodes, in which the highest concentrations and longest duration of pathogens were observed for all scenarios, are shown in Fig. 2.
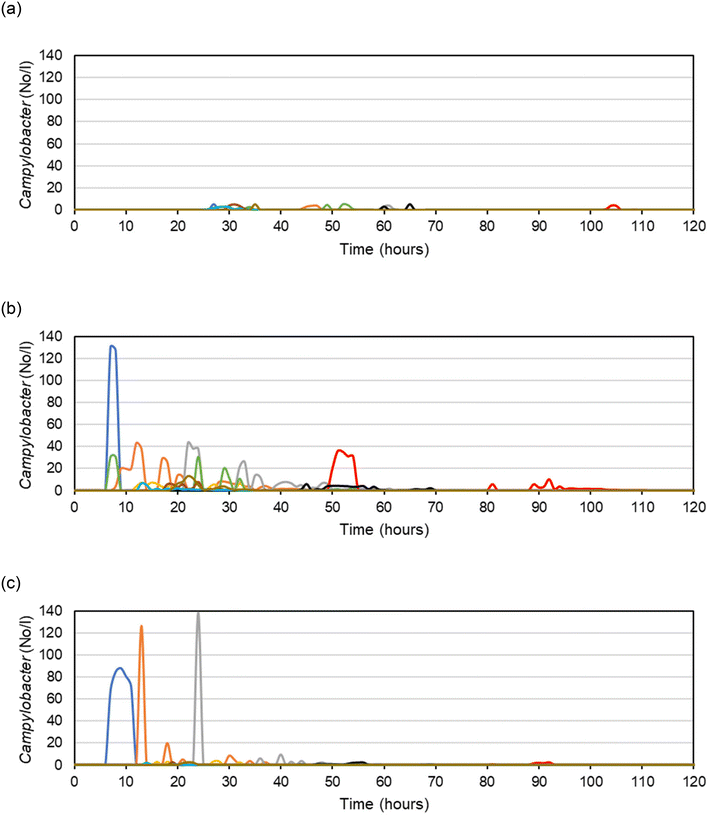
The time series plot for the selected critical nodes with maximum concentration and longest duration of Campylobacter for scenarios 1–3 (Fig. 3) shows that it takes up to approximately 100 hours for the concentration in the furthest nodes to return to 0 number per L, from the introduction of pathogens at hour 6 to around hour 110. Several nodes experienced peak concentrations at different times. For each scenario, the same trend was observed in the same nodes for the three different pathogens, because the same intrusion nodes were used. However, the pathogen concentrations at nodes were different due to varying numbers of pathogens intruding into the WDN.
From the time series of the pathogen concentrations at the critical nodes, triangular (T) distributions (minimum, mode, maximum) were used as input to the QMRA model for the health risks calculations for different scenarios.
3.3 Human health risks
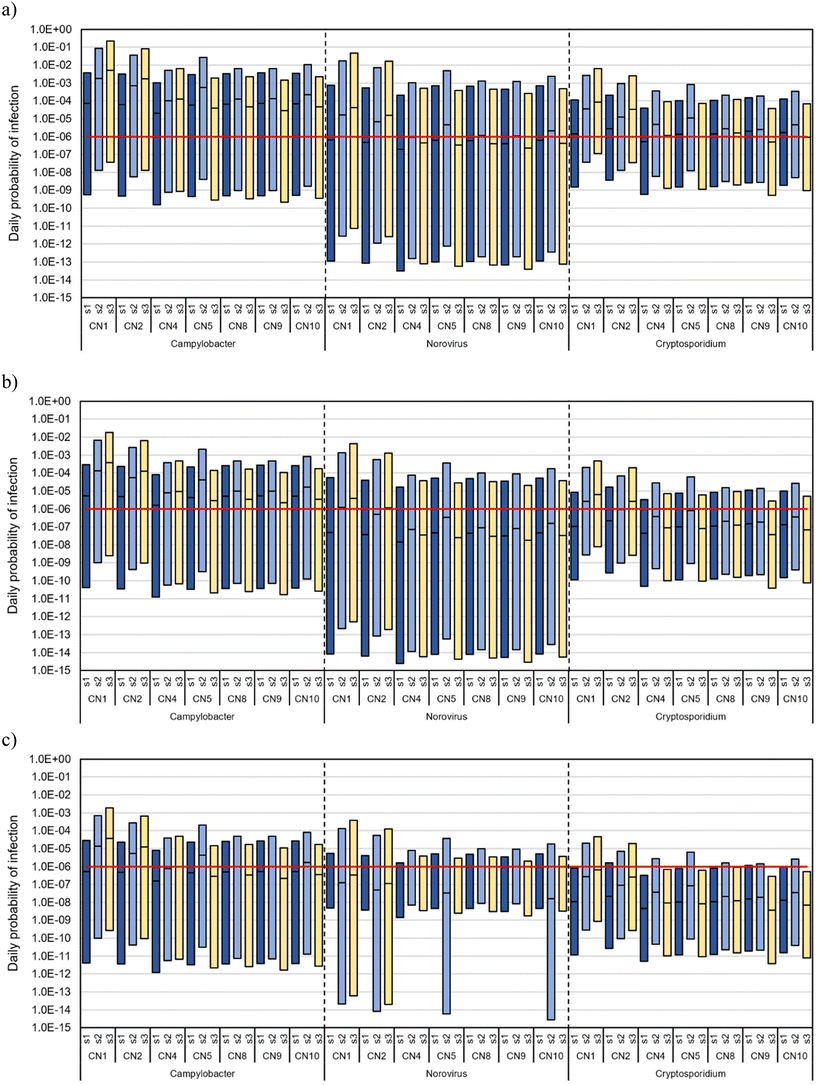
The estimated 75th percentile of the daily probability of infection (Fig. 4) was above the target value of 10−6 for all scenarios, all pathogens, and all tested log10 reductions between pathogen concentration in wastewater and soil water (with some few exceptions for Cryptosporidium for 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction). Although the risks for all pathogens were unacceptable, in general, the highest risks were observed for Campylobacter and the lowest risks were observed for norovirus.
log10 unit reduction). Although the risks for all pathogens were unacceptable, in general, the highest risks were observed for Campylobacter and the lowest risks were observed for norovirus.
The results shown in Fig. 5a indicated a reduced probability of infection with reduced leakage rate, which led to lower total area of leakage holes and hence reduced intrusion volume (eqn (5)). However, it can be noted that even low intrusion volumes in the WDN can still contribute to unacceptable risks during low-pressure events (Fig. 5a). The probability of infection exceeded the health target limit of 10−6 even when the leakage rate and hence the intrusion volume were reduced from the initial value (27%) to half (14%) and then to a quarter (7%).
Regarding the effect of the duration of the pipe break event, for this section of the WDN, it was observed that the intrusion was affected by the event detection period more than the time the pipe was closed for actual repair work. This was due to the low flow observed when the downstream WDN was isolated from the main water supply. From the observation of different durations of low-pressure events in scenario 2, it was found that the probability of infection was proportional to the low-pressure event duration (Fig. 5b).
4 Discussion
This research explored the practical approach of implementing hydraulic modelling and QMRA to support drinking water producers in Skåne, South of Sweden, in identifying risks to human health posed by the intrusion of pathogens in the WDN due to pipe break and intermittent/insufficient water supply, in areas prone to high groundwater levels. The study identified on a local scale, conditions that influence infection risk to human health and how the findings can be useful in renewal planning or decision-making of other mitigation measures. Resources should be channelled to where the need is greatest and where the most health gains can be realized. It is thus necessary that prioritization criteria are based on the best scientific information available.55 QMRA combined with hydraulic modelling is a structured way that utilizes a range of scientific information for decision support. With these tools, several conditions that influence the risk to human health in a WDN during intrusion were investigated. The key conditions identified include the concentration of pathogens in the soil water surrounding the pipes, the duration and magnitude of the low-pressure causing events, the intrusion volumes of contaminated water, and the position of the pipes in relation to groundwater levels.4.1 Impact of low-pressure events (duration and magnitude) and groundwater level on intrusion potential
The insufficient water supply into the WDN, and a pipe break, were the main investigated cause of low or negative pressure in the WDN. Pipe breaks could trigger sustained low-pressure conditions, due to increased free flow demand at the pipe break site, changed WDN hydraulics, such as flow reversals, because of the free flow and the closure of sections of the WDN, and higher demand during flushing.5 Field measurements in a WDN, with high-precision data loggers, indicated as low as −4 m of sustained negative pressures due to pipe breaks lasting more than 4 hours in 45% of the measurements.56,57 In other measurements involving transients of shorter durations, Gullick et al.58 detected negative pressure events which lasted less than 3 minutes but recorded as low as −10 m of pressure. This highlights the importance of the magnitude and duration of low-pressure events. With ageing pipes, and changes in climate and land use, pipe breaks and repairs are expected to occur more frequently in the future and increase incidences of sustained lower pressure conditions in WDNs.5,18The extent of the low pressure was influenced by the magnitude and duration of the event (Fig. 1). Scenario 2 with the highest free flow event (20 l s−1) recorded the lowest (negative) pressure compared to scenario 1 (with lower free flow) and scenario 3 (insufficient water supply). In scenario 3, the lowest pressure recorded was 0.65 m, which is a positive value but was still lower than the average GWL (0.8 m), hence triggering intrusion. The duration of the event was varied for the worst-case scenario 2, and lower pressures were observed with increased duration. The pathogen intrusions were observed to be proportional to the detection time (duration of free flow). Minor intrusions were observed during the repair period (time the pipe was closed for actual repair), this was attributed to low or no flow downstream of the closed pipe.
The WDN used had a single supply source, hence, isolating the breakpoint stopped the free flow, but also the water supply downstream, resulting in lower flows and flow reversals that continued for a short time before balancing out, and hence lower intrusions. This is different with a WDN with several sources, as flows would continue downstream of the isolated section due to attempted water supply from other sources hence continuously increasing the intrusion volume and hence pathogens. In scenario 1, although a high number of pathogens entered the WDN, the concentrations in critical nodes were much lower compared to other scenarios, because flushing was simulated. This highlights the ability to mitigate intrusion events when the source is known (scenario 1) or anticipated compared to an unknown source as is the case for leakages (scenarios 2 and 3).
For an intrusion to occur, there must be an intrusion potential due to the groundwater head, the pipes must be submerged in groundwater i.e., located below the GWL. In Sweden, approximately 20% of the pipes in WDNs are estimated to be below GWL.4 Negative or low-pressure in the WDN pipes and higher GWL in relation to pipe level resulted in higher intrusion potential, which in turn led to higher intrusion volumes and thus increased number of pathogens in the WDN. The intrusion estimates based on the dynamic groundwater level were compared to the estimates based on the constant groundwater level (Fig. S5†) The intrusion estimates based on dynamic groundwater level were deemed more realistic due to underestimation that was observed when constant groundwater levels were used (Fig. S5†). The pipes in the WDN were located between 1.5–2 m below ground, while the GWLs ranged from 0.5–3.5 m below ground level (Fig. S3†). This resulted in 0.58–0.67 m of pressure due to groundwater (Hext) and comparing various pressure events, the intrusion potential (Hint) varied from as low as 0.003 m in scenario 3 to 5.4 m in the worst-case scenario 2. Higher intrusion volume was recorded in scenario 2 as compared to scenario 3 due to lower/negative pressure and thus higher intrusion potential.
4.2 Risk to human health
The risk of infection is due to pathogens present in the soil water surrounding the WDN. In this study, the pathogens were assumed to come from the sewer pipes placed in the vicinity of the WDN. Malm et al.4 estimated that 80% of sewer pipes in Sweden are in the same trench as the pipes of the WDN. The total pathogens intruding into the network were influenced by the concentration in soil water and the intrusion volume. Intrusion volume was further influenced by the GWLs and the low-pressure event. Teunis et al.31 noted that the low-pressure event duration was the main factor influencing the viral intrusions in the WDN. Table 2 shows a summary of the change in daily probability of infection after applying different measures in the network. Increasing the wastewater dilution in the groundwater from 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log to 3
log to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log reduced the median (50th percentile) risk in scenario 2 by 92%, while further dilution to 4
log reduced the median (50th percentile) risk in scenario 2 by 92%, while further dilution to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log units reduced the risk by 99%. Reducing leakage by half (to 14%) and by three-fourths (to 7%) reduced the risk by 50%; and by 83% respectively compared to scenario 2. Reducing the repair time from 5 to 2 hours had mixed results: eight nodes showed a reduction in probability of infection while CN4 and CN6 showed an increase. Increasing the repair time from 5 to 8 hours mostly increased the probability of infection in the network, although a reduction was observed for some pathogens in CN1, CN2, and CN9 which can be attributed to changing hydraulic dynamics.
log units reduced the risk by 99%. Reducing leakage by half (to 14%) and by three-fourths (to 7%) reduced the risk by 50%; and by 83% respectively compared to scenario 2. Reducing the repair time from 5 to 2 hours had mixed results: eight nodes showed a reduction in probability of infection while CN4 and CN6 showed an increase. Increasing the repair time from 5 to 8 hours mostly increased the probability of infection in the network, although a reduction was observed for some pathogens in CN1, CN2, and CN9 which can be attributed to changing hydraulic dynamics.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 unit reduction, 27% leakage/intrusion rate, and 5 hours event period) for scenario 2 for varying log10 reduction, leakage, and repair time. For varying log10 reduction and leakage, an average of the variation for the three reference pathogens is shown due to the similarity of the values. Positive values indicate an increase in risk while negative values indicate a reduction in risk (“Campy” – Campylobacter, “Crypto” – Cryptosporidium)
log10 unit reduction, 27% leakage/intrusion rate, and 5 hours event period) for scenario 2 for varying log10 reduction, leakage, and repair time. For varying log10 reduction and leakage, an average of the variation for the three reference pathogens is shown due to the similarity of the values. Positive values indicate an increase in risk while negative values indicate a reduction in risk (“Campy” – Campylobacter, “Crypto” – Cryptosporidium)
| Critical node (CN) | Median Pinf for baseline scenario 2 | % variation of Pinf with measures (negative – reduction, positive – increase) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Campy | Norovirus | Crypto | 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 reduction log10 reduction |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 reduction log10 reduction |
Varying leakage/intrusion | 2 hour repair time | 8 hour repair time | ||||||
| 14% | 7% | Campy | Norovirus | Crypto | Campy | Norovirus | Crypto | ||||||
| 1 | 7.1 × 10−5 | 6.6 × 10−7 | 1.4 × 10−6 | −92.33 | −99.24 | −49.94 | −82.99 | −24.42 | −23.35 | −23.28 | −4.89 | 11.68 | −4.23 |
| 2 | 6.3 × 10−5 | 4.8 × 10−7 | 2.8 × 10−6 | −92.43 | −99.24 | −49.85 | −83.04 | −41.02 | −43.19 | −29.2 | 94.69 | 82.99 | −4.21 |
| 3 | 5.4 × 10−5 | 7.2 × 10−7 | 2.2 × 10−6 | −92.41 | −99.24 | −49.66 | −82.96 | −32.89 | −32.66 | −29.74 | 144.8 | 140.4 | 11.34 |
| 4 | 2.1 × 10−5 | 1.9 × 10−7 | 5.3 × 10−7 | −92.24 | −99.22 | −49.59 | −82.5 | 42.16 | 14.65 | −58.78 | 292.5 | 275.0 | 55.82 |
| 5 | 5.8 × 10−5 | 6.2 × 10−7 | 1.3 × 10−6 | −92.32 | −99.23 | −49.55 | −82.87 | −34.65 | −26.57 | −30.66 | 54.42 | 78.31 | 26.84 |
| 6 | 8.5 × 10−5 | 7.6 × 10−7 | 1.6 × 10−6 | −92.41 | −99.24 | −49.02 | −82.93 | 2020 | −17.83 | 2011 | 27.18 | 110.36 | 4.69 |
| 7 | 7.8 × 10−5 | 7.1 × 10−7 | 2.5 × 10−6 | −92.38 | −99.24 | −49.73 | −82.98 | −43.24 | −46.62 | −24.42 | 728.3 | 757.9 | 774.2 |
| 8 | 6.6 × 10−5 | 5.9 × 10−7 | 1.4 × 10−6 | −92.41 | −99.24 | −49.51 | −82.93 | −60.82 | −61.12 | −58.07 | 114.2 | 116.4 | 113.9 |
| 9 | 7.2 × 10−5 | 4.1 × 10−7 | 2.0 × 10−6 | −92.43 | −99.24 | −49.09 | −82.92 | −41.74 | −41.88 | −35.61 | −21.12 | −10.39 | 26.12 |
| 10 | 6.8 × 10−5 | 6.2 × 10−7 | 1.7 × 10−6 | −92.35 | −99.24 | −49.72 | −82.94 | −32.24 | −37.38 | −30.93 | 445.5 | 409.8 | 417.3 |
| Average | 6.3 × 10−5 | 5.8 × 10−7 | 1.7 × 10−6 | −92.37 | −99.24 | −49.57 | −82.91 | 175.1 | −31.60 | 169.0 | 187.6 | 197.2 | 142.2 |
To further assess the validity of the results, the infection risks for norovirus were compared to the estimated burden of acute gastrointestinal illness (AGI) in Sweden. The predicted incidence of AGI cases due to norovirus using the median daily infection risks for all scenarios was 0.07 cases/person-year (min, max: 0.02–4.4) [calculations not shown]. The incidence of AGI in Sweden has been estimated at 0.36 (ref. 59) and 0.43 (ref. 60) cases per person per year, with epidemiological studies in Scandinavia estimating the AGI proportion attributable to water distribution network incidents to be 37–38% (equivalent to 0.10–0.12 cases per person per year).14 Other studies have shown that excess cases due to tap water consumption may be in the range of 14–40%.61 Although available estimates of AGI incidence do not distinguish between the different pathogens, these estimates provide a theoretical upper limit to what risk estimates may reasonably be predicted.
4.3 Sources of uncertainties
In determining the infection risks due to various events in the WDN, the model and key inputs, for instance, the GWL, pressure distribution in the WDN during normal operation and during events, and pathogen concentrations in soil water, are critical. The model limitations and variability in these key inputs are a source of uncertainty, thus the assumptions made in this study may have impacted the estimated infection risks. In transport modelling of pathogens, turbulent flow conditions in the WDN were assumed and hence one-dimensional advection–reaction transport model was used in the hydraulic software. This implied that the constituents were travelling at the same velocity as the bulk fluid and hence deviations from the mean velocity, representing axial dispersion, were assumed to be relatively small and hence neglected.5,39,62 This assumption could have led to the overestimation of pathogen concentrations in pipes with laminar flow conditions, for instance, dead-end pipes, where dispersion may be significant.5 In estimating the GWLs, the assumption of uniformity in soil properties in the study area as the observed boreholes could have led to overestimations due to the heterogeneous nature of soils and the complex flow of water through soils. Similarly, groundwater variability with time could also have led to the overestimation of GWLs and hence the intrusion potential. However, it should be noted that the average GWLs were obtained from observation data over a long period between 1984 to 2022 to minimize the impact of this uncertainty (Fig. S3†).The lowest nodal pressure was used for determining the intrusion volume, and this may have been a source of overestimation as the pressure varied over the entire event period as seen in Fig. 1. Although the choice of PDA for calculating nodal pressures may have minimised the likelihood of overestimating intrusion volumes during a repair period, it may have had a lesser impact in overestimating the duration of negative pressures during free flow. A more sensitive transient analysis may be needed to properly assess the duration of negative pressures in the studied WDN, considering, e.g., surge protection devices present. The calculated probabilities of infection may effectively be the maximum risk that may occur in the network under an event resembling the scenarios tested in this study; hence, the conditions leading to unacceptable risks may not be realistic during the actual operation of the WDN. However, epidemiological studies carried out in Swedish WDNs have found an increased risk of GII connected to the WDN,14,63 suggesting that the modelled risk events occur in actual WDNs and contribute to the endemic level of disease.
The concentration of pathogens in intruding water was assumed to be the same at every node which may not be the case as the concentration may vary at different parts of the WDN. This is evidenced in a field study of pipeline repair sites in Gothenburg, in which only 22 out of 40 samples tested positive for E. coli. The concentrations also varied at different sites between 1 to 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10 units/100 ml.42 Other studies also indicate that not all sites sampled show the presence of pathogens.5,64,65
log10 units/100 ml.42 Other studies also indicate that not all sites sampled show the presence of pathogens.5,64,65
The risk of infection was estimated based on the volume of consumed water, however, given that the concentrations of pathogens in the WDN vary over time, the timing of exposure may also be critical to consider in QMRA.5,15,37,50 The timing of exposure was not included in this study due to the lack of suitable local patterns. Peak pathogen concentrations in the WDN may have coincided with other uses rather than drinking, such as taking a shower, flushing a toilet, and garden irrigation.37
4.4 Recommendations
Overall, the study identified nodes and sections of the WDN that may be prone to intrusion in case of low-pressure events and hence pose potential infection risks to water consumers. Similarly, critical nodes were identified where the risk was highest due to highest concentration or longest duration of pathogens. These sections can be targeted with monitoring measures or pipe replacements to improve operational efficiency. The concentration of pathogens and duration of low-pressure causing events were identified as the main factors influencing infection risk hence primary mitigation measures should aim at reducing the failure events as a priority or reducing the most influential factors such as the concentration of pathogens in soil water. Based on the assumptions used for the QMRA, reducing pathogen concentrations up to 10−5 No per l for all reference pathogens would result in the 75th percentile being within the acceptable risk target (calculations not shown). Pressure management in the WDN and leak detection and repair programs ought to be implemented. Installation of online monitoring devices such as pressure and water quality sensors as well as flow meters in the most vulnerable sections as identified in the study could reduce the probability of infection significantly. In the case of known repair points (scenario 1), flushing isolated sections can be very effective for reducing the pathogen loads in the network.6,15 Regular repair and maintenance of sewer pipes is important to reduce pathogen loads around the WDNs, and sampling of soil water along the pipes is recommended to determine the pathogen concentrations.5 Conclusions
• Hydraulic modelling in combination with QMRA indicates high risks of infection from pipe breaks and intermittent/insufficient water supply events, which are consistent with the estimated annual burden of acute gastrointestinal illness in Sweden. An intrusion occurring in the WDN would likely result in daily infection risks that exceed the acceptable risk of 10−6.• The concentration of pathogens in intruding soil water and the duration of the low-pressure causing event were observed to influence the risk of infection the most.
• Mitigation measures should aim at reducing the failure events as a priority or reducing the most influential factors, such as pathogen concentration in soil water around pipes and duration of low-pressure causing events, to minimize the impact when the events occur. The result from this study identifies vulnerable sections in the WDN indicating the potential targets for additional investment for monitoring and/or renewal.
• This study provides additional insights into estimating the infection risks from pipe breaks and other low-pressure-causing events in WDNs. It provides means to estimate the impact of groundwater on intrusion potential in WDNs.
Author contributions
Michael Odhiambo: methodology, formal analysis, visualization, investigation, writing – original draft, review & editing. Victor Viñas: formal analysis, investigation, visualization, writing – review & editing. Ekaterina Sokolova: conceptualization, methodology, supervision, writing – review & editing. Thomas Pettersson: conceptualization, methodology, supervision, funding acquisition, writing – review & editing.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The funding for this work was provided by Vinnova – Sweden's innovation agency – with the project Future City Water, project No. 2020-01842, and by the Gothenburg Region (GR). We would like to thank the staff at the anonymous municipality for providing information and data for the hydraulic modelling.References
- O. Giustolisi, D. Savic and Z. Kapelan, Pressure-Driven Demand and Leakage Simulation for Water Distribution Networks, J. Hydraul. Eng., 2008, 134, 626–635 CrossRef.
- ASCE, Water Infrastructure|American Society of Civil Engineers (ASCE)’s 2021 Infrastructure Report Card, https://infrastructurereportcard.org/cat-item/drinking-water/, (accessed 3 February 2022).
- T. AL-Washali, S. Sharma, R. Lupoja, F. AL-Nozaily, M. Haidera and M. Kennedy, Assessment of water losses in distribution networks: Methods, applications, uncertainties, and implications in intermittent supply, Resour., Conserv. Recycl., 2020, 152, 104515 CrossRef.
- A. Malm, O. Bergstedt, G. Axelsson, L. Barregård, B. Forsberg, J. Ljungqvist, T. Pettersson and Swedish Water, Assessment of health risks on the pipeline network in case of leakage (swedish), 2015.
- M. C. Besner, M. Prévost and S. Regli, Assessing the public health risk of microbial intrusion events in distribution systems: Conceptual model, available data, and challenges, Water Res., 2011, 45, 961–979 CrossRef CAS PubMed.
- M. Blokker, P. Smeets and G. Medema, QMRA in the drinking water distribution system, Procedia Eng., 2014, 89, 151–159 CrossRef.
- J. Wilson, J. Aramini, S. Clarke, M. Novotny, M. Quist and V. Keegan, Retrospective Surveillance for Drinking Water-Related Illnesses in Canada, 1993-2008: Final Report, NCCEH Rev.
- A. Malm, T. J. R. Pettersson and O. Bergstedt, Health effects of quality disturbances in Swedish water distribution networks (In Swedish), in Proceedings of the 7th Nordic Drinking Water Conference, DANVA, Copenhagen, 2010, pp. 97–101 Search PubMed.
- G. F. Craun and R. L. Calderon, Waterborne disease Outbreaks Caused by Distribution System Deficiencies, J. - Am. Water Works Assoc., 2001, 93, 64–75 CrossRef CAS.
- I. Jakopanec, K. Borgen, L. Vold, H. Lund, T. Forseth, R. Hannula and K. Nygård, A large waterborne outbreak of campylobacteriosis in Norway: The need to focus on distribution system safety, BMC Infect. Dis., 2008, 8, 1–11 CrossRef PubMed.
- D. Werber, D. Laušević, B. Mugoša, Z. Vratnica, L. Ivanović-Nikolić, L. Žižić, A. Alexandre-Bird, L. Fiore, F. M. Ruggeri, I. Di Bartolo, A. Battistone, B. Gassilloud, S. Perelle, D. Nitzan Kaluski, M. Kivi, R. Andraghetti and K. G. J. Pollock, Massive outbreak of viral gastroenteritis associated with consumption of municipal drinking water in a European capital city, Epidemiol. Infect., 2009, 137, 1713–1720 CrossRef CAS PubMed.
- E. E. Geldreich, K. R. Fox, J. A. Goodrich, E. W. Rice, R. M. Clark and D. L. Swerdlow, Searching for a water supply connection in the Cabool, Missouri disease outbreak of Escherichia coli 0157:H7, Water Res., 1992, 26, 1127–1137 CrossRef.
- D. L. Swerdlow, B. A. Woodruff, R. C. Brady, P. M. Griffin, S. Tippen, H. D. Donnell, E. Geldreich, B. J. Payne, A. Meyer, J. G. Wells, K. D. Greene, M. Bright, N. H. Bean and P. A. Blake, A waterborne outbreak in Missouri of Escherichia coli O157:H7 associated with bloody diarrhea and death, Ann. Intern. Med., 1992, 117, 812–819 CrossRef CAS PubMed.
- M. Säve-Söderbergh, J. Bylund, A. Malm, M. Simonsson and J. Toljander, Gastrointestinal illness linked to incidents in drinking water distribution networks in Sweden, Water Res., 2017, 122, 503–511 CrossRef PubMed.
- M. Blokker, P. Smeets and G. Medema, Quantitative microbial risk assessment of repairs of the drinking water distribution system, Microb. Risk Anal., 2018, 8, 22–31 CrossRef.
- V. Viñas, A. Malm and T. J. R. Pettersson, Overview of microbial risks in water distribution networks and their health consequences: Quantification, modelling, trends, and future implications, Can. J. Civ. Eng., 2018, 46, 149–159 CrossRef.
- J. J. Erickson, C. D. Smith, A. Goodridge and K. L. Nelson, Water quality effects of intermittent water supply in Arraiján, Panama, Water Res., 2017, 114, 338–350 CrossRef CAS PubMed.
- K. Simukonda, R. Farmani and D. Butler, Intermittent water supply systems: causal factors, problems and solution options, Urban Water J., 2018, 15, 488–500 CrossRef.
- J. Yang, M. W. LeChevallier, P. F. M. Teunis and M. Xu, Managing risks from virus intrusion into water distribution systems due to pressure transients, J. Water Health, 2011, 9, 291–305 CrossRef PubMed.
- N. Islam, A. Farahat, M. A. M. Al-Zahrani, M. J. Rodriguez and R. Sadiq, Contaminant intrusion in water distribution networks: Review and proposal of an integrated model for decision making, Environ. Rev., 2015, 23, 337–352 CrossRef.
- E. Z. Berglund, J. E. Pesantez, A. Rasekh, M. E. Shafiee, L. Sela and T. Haxton, Review of Modeling Methodologies for Managing Water Distribution Security, J. Water Resour. Plan. Manag., 2020, 146, 3120001 CrossRef PubMed.
- J. Berry, W. E. Hart, C. A. Phillips, J. G. Uber and J.-P. Watson, Sensor Placement in Municipal Water Networks with Temporal Integer Programming Models, J. Water Resour. Plan. Manag., 2006, 132, 218–224 CrossRef.
- A. Preis and A. Ostfeld, Contamination Source Identification in Water Systems: A Hybrid Model Trees–Linear Programming Scheme, J. Water Resour. Plan. Manag., 2006, 132, 263–273 CrossRef.
- S. Rathi, R. Gupta and L. Ormsbee, A review of sensor placement objective metrics for contamination detection in water distribution networks, Water Supply, 2015, 15, 898–917 CrossRef CAS.
- L. Perelman and A. Ostfeld, Topological clustering for water distribution systems analysis, Environ. Model. Softw., 2011, 26, 969–972 CrossRef.
- K. Vairavamoorthy, J. Yan, H. M. Galgale and S. D. Gorantiwar, IRA-WDS: A GIS-based risk analysis tool for water distribution systems, Environ. Model. Softw., 2007, 22, 951–965 CrossRef.
- U. S. EPA, Water Quality Event Detection Systems For Drinking Water Contamination Warning Systems: Development, Testing, and Application of CANARY, 2010 Search PubMed.
- R. G. Austin, C. Y. Choi, T. C. Balagopal and P. L. Gurian, in Water Distribution Systems Analysis 2010 - Proceedings of the 12th International Conference, WDSA 2010, 2012, pp. 459–470 Search PubMed.
- G. Ebacher, M.-C. Besner, J. Lavoie, B. S. Jung, B. W. Karney and M. Prévost, Transient Modeling of a Full-Scale Distribution System: Comparison with Field Data, J. Water Resour. Plan. Manag., 2011, 137, 173–182 CrossRef.
- R. Jamal, S. Mubarak, S. Q. Sahulka, J. A. Kori, A. Tajammul, J. Ahmed, R. B. Mahar, M. S. Olsen, R. Goel and J. Weidhaas, Informing water distribution line rehabilitation through quantitative microbial risk assessment, Sci. Total Environ., 2020, 739, 140021 CrossRef CAS PubMed.
- P. F. M. Teunis, M. Xu, K. K. Fleming, J. Yang, C. L. Moe and M. W. Lechevallier, Enteric virus infection risk from intrusion of sewage into a drinking water distribution network, Environ. Sci. Technol., 2010, 44, 8561–8566 CrossRef CAS PubMed.
- J. Yang, O. D. Schneider, P. K. Jjemba and M. W. Lechevallier, Microbial risk modeling for main breaks, J. - Am. Water Works Assoc., 2015, 107, E97–E108 CrossRef.
- M. V. Storey, N. J. Ashbolt and T. A. Stenström, Biofilms, thermophilic amoebae and Legionella pneumophila – a quantitative risk assessment for distributed water, Water Sci. Technol., 2004, 50, 77–82 CrossRef CAS PubMed.
- D. McInnis, A relative-risk framework for evaluating transient pathogen intrusion in distribution systems, Urban Water J., 2004, 1, 113–127 CrossRef.
- J. H. M. van Lieverloo, E. J. Mirjam Blokker and G. Medema, Quantitative microbial risk assessment of distributed drinking water using faecal indicator incidence and concentrations, J. Water Health, 2007, 5, 131–149 CrossRef PubMed.
- K. D. Mena, L. C. Mota, M. C. Meckes, C. F. Green, W. W. Hurd and S. G. Gibbs, Quantitative microbial risk assessment of a drinking water – wastewater cross-connection simulation, J. Environ. Eng. Sci., 2008, 7, 525–530 CrossRef CAS.
- V. Viñas, E. Sokolova, A. Malm, O. Bergstedt and T. J. R. Pettersson, Cross-connections in drinking water distribution networks: Quantitative microbial risk assessment in combination with fault tree analysis and hydraulic modelling, Sci. Total Environ., 2022, 831, 154874 CrossRef PubMed.
- S. Rathi and R. Gupta, Optimal sensor locations for contamination detection in pressure-deficient water distribution networks using genetic algorithm, Urban Water J., 2017, 14, 160–172 CrossRef.
- L. A. Rossman, H. Woo, M. Tryby, F. Shang, R. Janke and T. Haxton, Epanet 2.2 User's Manual, 2020.
- M. I. Sami, Effective placement of sensors for efficient early warning system in water distribution network, Master Thesis, Chalmers University of Technology, 2018 Search PubMed.
- J. Abrahamsson, J. Ansaker and G. Heinicke, in MRA - a model for Swedish water works (in Swedish), Swedish Water and Wastewater Association, Stockholm, 2009 Search PubMed.
- V. Viñas, M. Odhiambo, A. S. Mohammadi, O. Modin and T. J. R. Pettersson, Microbial Water Quality Sampling to Inform Health Risk Asssessments, 2023, Manuscript in preparation Search PubMed.
- J. A. Soller, M. E. Schoen, T. Bartrand, J. E. Ravenscroft and N. J. Ashbolt, Estimated human health risks from exposure to recreational waters impacted by human and non-human sources of faecal contamination, Water Res., 2010, 44, 4674–4691 CrossRef CAS PubMed.
- O. Dienus, E. Sokolova, F. Nyström, A. Matussek, S. Löfgren, L. Blom, T. J. R. Pettersson and P. E. Lindgren, Norovirus Dynamics in Wastewater Discharges and in the Recipient Drinking Water Source: Long-Term Monitoring and Hydrodynamic Modeling, Environ. Sci. Technol., 2016, 50, 10851–10858 CrossRef CAS PubMed.
- F. E. Eregno, I. Tryland, T. Tjomsland, M. Myrmel, L. Robertson and A. Heistad, Quantitative microbial risk assessment combined with hydrodynamic modelling to estimate the public health risk associated with bathing after rainfall events, Sci. Total Environ., 2016, 548-549, 270–279 CrossRef CAS PubMed.
- B. R. McMinn, N. J. Ashbolt and A. Korajkic, Bacteriophages as indicators of faecal pollution and enteric virus removal, Lett. Appl. Microbiol., 2017, 65, 11–26 CrossRef CAS PubMed.
- S. E. Eftim, T. Hong, J. Soller, A. Boehm, I. Warren, A. Ichida and S. P. Nappier, Occurrence of norovirus in raw sewage – A systematic literature review and meta-analysis, Water Res., 2017, 111, 366–374 CrossRef CAS PubMed.
- J. Ottoson, A. Hansen, T. Westrell, K. Johansen, H. Norder and T. A. Stenström, Removal of Noro- and Enteroviruses, Giardia Cysts, Cryptosporidium Oocysts, and Fecal Indicators at Four Secondary Wastewater Treatment Plants in Sweden, Water Environ. Res., 2006, 78, 828–834 CrossRef CAS PubMed.
- S. R. Seitz, J. S. Leon, K. J. Schwab, G. M. Lyon, M. Dowd, M. McDaniels, G. Abdulhafid, M. L. Fernandez, L. C. Lindesmith, R. S. Baric and C. L. Moe, Norovirus infectivity in humans and persistence in water, Appl. Environ. Microbiol., 2011, 77, 6884–6888 CrossRef CAS PubMed.
- M. Säve-Söderbergh, J. Toljander, I. Mattisson, A. Åkesson and M. Simonsson, Drinking water consumption patterns among adults - SMS as a novel tool for collection of repeated self-reported water consumption, J. Exposure Sci. Environ. Epidemiol., 2018, 28, 131–139 CrossRef PubMed.
- P. F. M. Teunis, W. van den Brandhof, M. Nauta, J. Wagenaar, H. van den Kerkhof and W. van Pelt, A reconsideration of the Campylobacter dose - Response relation, Epidemiol. Infect., 2005, 133, 583–592 CrossRef CAS PubMed.
- P. F. Teunis, C. L. Moe, P. Liu, S. E. Miller, L. Lindesmith, R. S. Baric, J. Le Pendu and R. L. Calderon, Norwalk virus: How infectious is it?, J. Med. Virol., 2008, 80, 1468–1476 CrossRef PubMed.
- P. F. M. Teunis, C. L. Chappell and P. C. Okhuysen, Cryptosporidium dose-response studies: Variation between hosts, Risk Anal., 2002, 22, 475–485 CrossRef PubMed.
- R. S. Signor and N. J. Ashbolt, Comparing probabilistic microbial risk assessments for drinking water against daily rather than annualised infection probability targets, J. Water Health, 2009, 7, 535–543 CrossRef CAS PubMed.
- S. Petterson, Z. Bradford-Hartke, S. Leask, L. Jarvis, K. Wall and P. Byleveld, Application of QMRA to prioritise water supplies for Cryptosporidium risk in New South Wales, Australia, Sci. Total Environ., 2021, 784, 147107 CrossRef CAS PubMed.
- M. C. Besner, G. Ebacher, J. Lavoie and M. Prévost, Low and Negative Pressures in Distribution Systems: Do They Actually Result in Intrusion?, Restoring Our Nat. Habitat - Proc. 2007 World Environ. Water Resour. Congr., 2007, pp. 1–10 Search PubMed.
- M. C. Besner, R. Broséus, J. Lavoie, G. Di Giovanni, P. Payment and M. Prévost, Pressure monitoring and characterization of external sources of contamination at the site of the payment drinking water epidemiological studies, Environ. Sci. Technol., 2010, 44, 269–277 CrossRef CAS PubMed.
- R. W. Gullick, M. W. Lechevallier, R. C. Svindland and M. J. Friedman, Occurrence of Transient Low and Negative Pressures in Distribution Systems, J. - Am. Water Works Assoc., 2004, 96, 52–66 CrossRef CAS.
- M. Edelstein, H. Merk, C. Deogan, A. Carnahan and A. Wallensten, Quantifying the incidence and cost of acute gastrointestinal illness in Sweden, 2013–2014, Epidemiol. Infect., 2016, 144, 2831–2839 CrossRef CAS PubMed.
- M. Säve-Söderbergh, J. Toljander, J. Bylund and M. Simonsson, Burden of gastrointestinal illness in Sweden-SMS as a tool for collecting self-reported gastrointestinal illness, Epidemiol. Infect., 2019, 147, e322 CrossRef PubMed.
- P. Payment, J. Siemiatycki, L. Richardson, G. Renaud, E. Franco and M. Prévost, A prospective epidemiological study of gastrointestinal health effects due to the consumption of drinking water, Int. J. Environ. Health Res., 1997, 7, 5–31 CrossRef.
- F. Hatam, M.-C. Besner, G. Ebacher and M. Prévost, Combining a Multispecies Water Quality and Pressure-Driven Hydraulic Analysis to Determine Areas at Risk During Sustained Pressure-Deficient Conditions in a Distribution System, J. Water Resour. Plan. Manag., 2018, 144, 04018057 CrossRef.
- K. Nygård, Y. Andersson, J. A. Røttingen, A. Svensson, J. Lindback, T. Kistemann and J. Giesecke, Association between environmental risk factors and campylobacter infections in Sweden, Epidemiol. Infect., 2004, 132, 317–325 CrossRef PubMed.
- M. R. Karim, M. Abbaszadegan and M. Lechevallier, Potential for pathogen intrusion during pressure transients, J. - Am. Water Works Assoc., 2003, 95, 134–146 CrossRef CAS.
- M. C. Besner, J. Lavoie, C. Morissette, P. Payment and M. Prévost, Effect of water main repairs on water quality, J. - Am. Water Works Assoc., 2008, 100, 95–109 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ew00720g |
| This journal is © The Royal Society of Chemistry 2023 |