 Open Access Article
Open Access ArticleCombined spectroscopic and computational study for optimising catalyst design in hydrocarbon transformations†
Matthew E.
Potter
 *a,
J. J. M.
Le Brocq
a,
A. E.
Oakley
*a,
J. J. M.
Le Brocq
a,
A. E.
Oakley
 a,
H.
Cavaye
a,
H.
Cavaye
 b,
Bart D.
Vandegehuchte
c and
Robert
Raja
b,
Bart D.
Vandegehuchte
c and
Robert
Raja
 *a
*a
aSchool of Chemistry, University of Southampton, Southampton, SO17 1BJ, UK. E-mail: M.E.Potter@soton.ac.uk; R.Raja@soton.ac.uk
bISIS Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Harwell Campus, Didcot, Oxon OX11 0QX, UK
cTotalEnergies OneTech Belgium, Zone Industrielle Feluy C, B-7181 Seneffe, Belgium
First published on 23rd August 2022
Abstract
Molecular interactions of hydrocarbons within the confined pores of heterogeneous catalysts can influence reaction pathways, which play a crucial role in determining the overall efficacy of catalytic transformations. We probe the interactions of n-butane with a solid-acid zeolite, mordenite, combining inelastic neutron scattering with DFT calculations. This reveals that the solid-acid sites within mordenite induce a conformer change, which could be key in designing optimised catalysts, for hydrocarbon transformations.
Hydrocarbon transformations are at the heart of industrial chemical processes, encompassing a wide range of reactions, such as cracking, alkylation and isomerisation.1 In particular, the acid-catalysed isomerisation of n-butane (herein referred to as ‘butane’) is vital for meeting the growing isobutane demand, as a precursor for branched alkylate fuels and as a calibrant.2 Zeolites, particularly mordenite (MOR)3,4 are among the broadly studied catalysts for this reaction and serve as model systems for understanding alkane–zeolite interactions. In the literature there are two widely accepted reaction mechanisms for butane isomerisation: the monomolecular and bimolecular pathways.2 Therefore, probing early reaction stages, including butane-Brønsted acid site interactions, would be of great interest in optimising alkane transformations within zeolites.
Inelastic neutron scattering (INS) is well suited to probing interactions between inorganic catalysts and hydrocarbon substrates,5,6 as the neutron scattering cross section of hydrogen is by far the largest of all elements. Thus, any hydrogen in a system will dominate the INS spectra, even when present in small quantities. As a result, INS has been widely used to investigate the orientation, or confinement of hydrocarbon substrates, or hydrogen itself, within porous framework catalysts.7,8 This has been used to gain a deeper understanding of adsorption and reaction pathways, particularly within solid acid catalysts, such as zeolites, where the proton acid site is often key to the transformation.9 Lennon et al. recently followed the INS spectra of propene in ZSM-5, monitoring the twisting motion of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond over 140 to 393 K,10 gaining valuable insights on the reaction pathway. In this work we present a combined INS (TOSCA)11 and Density Functional Theory (DFT) study (CRYSTAL17) aimed at observing the conformation of butane within the MOR pore, as a model system, at low temperatures. We will then extrapolate these findings, to high temperature processes, such as the butane isomerisation mechanism, to understand the role of confinement and the role of the acid site.
C bond over 140 to 393 K,10 gaining valuable insights on the reaction pathway. In this work we present a combined INS (TOSCA)11 and Density Functional Theory (DFT) study (CRYSTAL17) aimed at observing the conformation of butane within the MOR pore, as a model system, at low temperatures. We will then extrapolate these findings, to high temperature processes, such as the butane isomerisation mechanism, to understand the role of confinement and the role of the acid site.
The integrity of our mordenite sample was investigated using X-ray diffraction (Fig. S1, ESI†) and12,13 N2 physisorption (Fig. S2, ESI†),12,13 with ICP confirming the intended SiO2/Al2O3 molar ratio (experimental: 9.4, intended: 10). This confirms the expected MOR structure,14 with a unit cell containing 48 T-sites (Si) and 96 oxygen atoms, of which there are 10 crystallographically distinct O atoms and 4 distinct T sites (Fig. S3, ESI†). Scanning electron microscopy revealed the crystalline nature of the system (Fig. S4, ESI†), while 29Si solid state NMR (ssNMR) showed Si(OSi)4 being the main species, with some evidence of Si(OAl)1(OSi)3 (Fig. S5A, ESI†).1527Al ssNMR showed that Al(OSi)4 was the main feature with some extra-framework octahedral aluminium (AlO6) (Fig. S5B, ESI†).16 The main 1H ssNMR signal (Fig. S5C, ESI†) at 6.2 ppm represents Brønsted acid sites from aluminium substitution into the framework.17 Smaller signals due to the presence of silanol species were also seen (9.1 and 1.9 ppm).17 Catalysis data confirmed that the sample could isomerise butane, in addition to cracking, toward propane as a by-product. After 4 hours on stream, a conversion of 18 mol%, with a selectivity of 39 mol% to isobutane (Fig. S6, ESI†) was achieved.
The INS data focusses on the <2000 cm−1 range (Fig. S7, ESI†), for improved resolution on the butane signals, with emphasis on the <500 cm−1 region (Fig. S7B, ESI†). Bare MOR (MOR EXP, Fig. S7, ESI†) shares many features with previous work from Jobic et al. on hydrated mordenite.18 Notably these are hydroxonium vibrations (1371 cm−1), OH bridging groups (1090 cm−1), trisymmetric bending modes of hydroxonium species (902 cm−1) and hydroxonium rocking motions (435 cm−1).18
Our experimental ‘unconfined’ pure n-butane spectrum (Butane EXP) was also in excellent agreement with previous INS spectra.19 In particular, we highlight the two most intense signals at 237 and 266 cm−1, assigned to the in-phase and out-of-phase methyl torsion rotations respectively (Fig. S8, ESI†). Similarly, there are also prominent signals assigned as transverse –CH2– wags (167 cm−1), longitudinal in-plane acoustic C–C–C bending modes (427 cm−1), in-phase and out-of-phase –(CH2)n– rocking (732 cm−1) and mixed –(CH2)– rocking and twisting (804 and 837 cm−1) (Fig. S8, ESI†).7,10,19 Our DFT calculated INS spectrum of antiperiplanar ‘unconfined’ butane (Butane DFT) was in good agreement with the experimental ‘unconfined’ butane spectrum, confirming the expected conformation of n-butane (Fig. S8, ESI†). Comparing the calculated and experimental peaks showed a systematic deviation, as expected (Fig. S8C, ESI†),20,21 validating our approach.
Dosing MOR with gaseous butane modified the INS spectra (Butane + MOR EXP, Fig. 1 and Fig. S9, ESI†). In the 500–2000 cm−1 range (Fig. S9, ESI†) several of the butane signals have decreased in intensity or disappeared entirely. The signals most affected by this are the mixed –(CH2)– rocking and twisting (1007 and 1058 cm−1), –CH2– twisting and wagging (1292 cm−1) and CH3 scissoring and deformation (1538 cm−1).7,10,19 This is likely due to the confinement of butane within the mordenite system, prompting a change in symmetry of the butane species, or suppressing these motions. Focusing on the 0–500 cm−1 region (Fig. 1), we see a noticeable shift in the methyl torsion mode to significantly lower energy values of 217 and 258 cm−1, (from 237 and 266 cm−1 respectively). Further, incorporating butane into MOR shows a new peak at 368 cm−1. Peaks in this region could be a low energy acoustic C–C–C bend, or an overtone of lower-energy −CH2– wagging. Though as the spectra do not have any intense or defined signals in the −CH2– wagging range (150–175 cm−1), it is unlikely to be an overtone.7,10,19
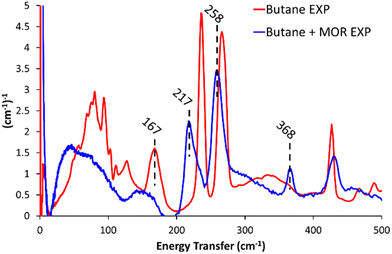 | ||
| Fig. 1 The difference in the experimental INS spectra on encapsulating butane into commercial mordenite (Butane + MOR EXP), compared to pure n-butane (Butane EXP), for <500 cm−1. | ||
DFT calculations were used to understand the experimental shift of the methyl torsions, and probe the shape of butane within the pore. This was done by comparing the calculated ‘unconfined’ butane spectrum (Butane DFT) with spectra calculated from optimised geometries of antiperiplanar butane in MOR.
Initially, purely siliceous MOR (Si-MOR) was used, to separate the influence of confinement and acidic interactions. The DFT model for Si-MOR (Si48O96) showed no irregularities and was fully optimised (Fig. S10A, ESI†), giving unit cell parameters of: a = 18.22 Å, b = 20.22 Å and c = 7.46 Å, with α = 90.00°, β = 90.03° and γ = 89.97°. The calculated INS spectra of this species showed very little intensity, as no hydrogen is present (Fig. S10B and C, ESI†).
A variety of initial geometries were considered and optimised with butane occupying the main pore, labelled as “Butane Si-MOR DFT X” (Fig. S11, ESI†). The DFT calculated geometries all gave binding energies in the region of −90 to −96 kJ mol−1 (Table S1, ESI†), due to the dispersion contributions. However, the calculated INS spectra of these geometries did not show the low energy shifts for the methyl torsions seen experimentally (Fig. 1, 2 and Fig. S11, ESI†). This suggests that confinement of antiperiplanar butane in Si-MOR is not the cause the experimental INS peak shift. To investigate the possibility of acid site interactions, an Al was placed in the T1 position of the MOR framework, with the associated proton positioned on O7, representing an associated acid site. The Al1Si47O96H1 system, with the acid site in the 12 membered-ring, was optimised before butane was introduced (Fig. S12A, ESI†). The unit cell parameters of this system showed little deviation from the ideal silicate system; a = 18.24 Å, b = 20.16 Å and c = 7.47 Å, with α = 90.03°, β = 90.21° and γ = 90.33°, as earlier, because the DFT calculated INS contributions in the 0–500 cm−1 region were miniscule (Fig. S12B and C, ESI†).
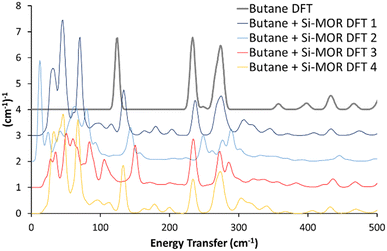 | ||
| Fig. 2 Comparing the calculated INS spectra of n-butane in siliceous mordenite for a range of geometries. In all cases, the experimental shifts of the butane torsional modes to lower energy values, on encapsulation in the mordenite pore (Fig. 1) were not replicated. See text for further details. Data is artificially incremented by 1 (cm−1)−1 for ease of reading. | ||
As with the purely siliceous framework, butane was introduced in a variety of different positions, relative to the framework, and to the acid site (Fig. S13, ESI†). These species were labelled as “Butane Al-MOR DFT X”. As with the siliceous MOR support, there was little change in the position of the methyl torsions, compared to the DFT calculated INS spectra of the ‘unconstrained’ butane (Fig. S13, ESI†). Interestingly the binding energy of butane for these systems ranged from −91 to −86 kJ mol−1 (Table S2, ESI†), slightly lower than the siliceous mordenite. This suggests that the presence of the acid site did not significantly strengthen the interactions between butane and the MOR framework, nor was it the cause of the shift of the methyl torsion.
Previous studies suggest that alkanes adopts distorted conformations within certain zeolite frameworks,22 transitioning from the typical antiperiplanar conformer (C–C–C–C dihedral angle of −180/180°) to a gauche-distorted conformer (Fig. S14, C–C–C–C dihedral angle of −60/60°, ESI†), herein referred to as “g-Butane”. The g-Butane DFT-calculated INS spectrum indeed replicates the experimentally observed shift of the in-phase methyl torsion to a lower energy value, compared to ‘unconfined n-butane’ (Fig. S15, ESI†). As this signal moves from 234 cm−1 (Butane DFT) to 219 cm−1 (g-Butane DFT), the out-of-phase methyl torsion shows no significant change. However, the g-Butane system presents a large signal centred at 333 cm−1, likely corresponding to the experimental MOR dosed butane (Butane + MOR EXP) signal at 368 cm−1. These findings suggest that butane may adopt a gauche-distorted conformation within a MOR pore. To investigate this further, INS spectra were calculated using DFT for g-butane confined in siliceous and acidic MOR systems.
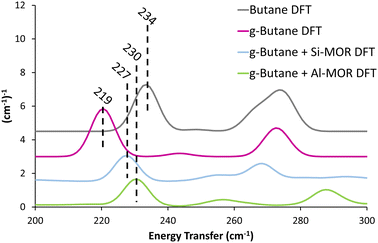 | ||
| Fig. 3 Calculated INS spectra of unconfined antiperiplanar n-butane (Butane DFT) and gauche distorted butane unconfined (g-Butane DFT), within siliceous (Si-MOR) and acidic (Al-MOR) mordenite pores shows the deviation in the methyl torsion peak position between the conformers, akin to the experimental findings (Fig. 1). Spectra are artificially shifted by 1.5 (cm−1)−1 for ease of reading. | ||
The DFT calculated INS spectra of g-butane in Si-MOR and Al-MOR are shown in Fig. 4 and Fig. S15 (ESI†), where they are compared with the DFT calculated spectra of ‘unconfined’ Butane. In both Si-MOR and Al-MOR the g-butane shows a shift of the in-phase methyl torsion to a lower energy value (Fig. 3), relative to the ‘unconfined system’, along with a significant signal at 336 cm−1 emerging (Fig. S15, ESI†), replicating the experimental INS findings. This strongly supports the idea that butane has indeed adopted a gauche-distorted conformer inside the mordenite species. To investigate the role of the acid site and confinement further, the energy profiles on rotating the dihedral C–C–C–C bond were calculated with DFT, which contrasted ‘unconfined’ butane, with butane in purely siliceous MOR (Si-MOR) and butane in acidic mordenite (Al-MOR).
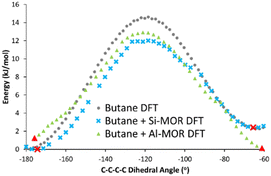 | ||
| Fig. 4 DFT calculated energy of rotation about the C–C–C–C dihedral angle in n-butane, transitioning from the antiperiplanar (−180°) to the gauche conformer (−60°) for butane when unconfined (Butane DFT), in siliceous mordenite (Butane + Si-MOR DFT) and acidic Al-substituted mordenite (Butane + Al-MOR DFT). Red symbols represent minima, as confirmed by frequency calculations, as shown in Fig. 3 and Fig. S15 (ESI†). Final Gauche conformers (Fig. S16, ESI†) were determined based on the progression of C–C–C–C dihedral angle in the optimisation sequence. | ||
The binding energies of butane within mordenite were compared between the B3LYP and PBE functionals, which showed excellent agreement. However, we note that the choice of dispersion correction plays a vital role in the final energy (see Table S3, ESI†). The difference in energy between gauche and antiperiplanar ‘unconfined’ n-butane, was compared for n-butane lying along the B axis (Tables S1 and S2, ESI†), as this was the lowest energy configuration for the Al-MOR system (Table S2, ESI†), and thus best represents our ‘real’ acidic mordenite used experimentally. Here the rotation barrier is in good agreement with previous literature (Fig. 4 and Table 1).23 Confining butane in siliceous MOR (Butane + Si-MOR DFT) does not seem to significantly influence the relative energy values of the antiperiplanar and gauche-distorted butanes (Table 1 and Fig. 4), compared to the ‘unconfined’ system. The gauche-distorted conformer of ‘unconfined’ butane is 2.3 kJ mol−1 higher in energy than the antiperiplanar conformation, while a difference of 2.4 kJ mol−1 is seen in Si-MOR. However, confinement does lower the energy barrier for rotation, amounting to 12.0 kJ mol−1 in Si-MOR, while ‘unconfined’ butane has a rotation barrier of 14.6 kJ mol−1, suggesting butane can rotate more easily inside the pore. In contrast, the acidic MOR system (Al-MOR) stabilises the gauche configuration, which becomes more stable than the antiperiplanar conformation, by 1.2 kJ mol−1. Therefore, the DFT calculations show that proximity to the acid site, and not necessarily confinement, is the key factor in the gauche conformer being adopted (Fig. S16, ESI†).
| Energy (kJ mol−1) | ||||
|---|---|---|---|---|
| System | Antiperiplanar bindinga | Gauche bindingb | Transition statec | Relative gauche energyd |
| a Energy of local minima in the 175–185° region, relative to ‘unconfined’ butane and empty framework. b Energy of local minima in the 55–65° region, relative to ‘unconfined’ butane and empty framework. c Energy of local maxima in the 60–180° along the dihedral angle energy profile. d Gauche energy – antiperiplanar energy. | ||||
| Butane DFT | N/A | N/A | +14.6 | +2.3 |
| Butane + Si-MOR DFT | −90.9 | −88.5 | +12.0 | +2.4 |
| Butane + Al-MOR DFT | −91.4 | −94.2 | +12.9 | −1.2 |
From the energy differences between the two conformers the relative populations of gauche and antiperiplanar butane at isomerisation temperatures can be calculated using a Boltzmann distribution (Fig. S17, ESI†). This method doesn’t consider entropy differences between the two states. However, the main entropic contributions will arise from the molecule becoming confined within a pore, regardless of the conformation. As such, we do not anticipate that there will be a significant change in entropy between the two conformations.24
At temperatures <100 K almost all butane in acidic mordenite will be in the gauche conformer (Butane Al-MOR DFT). This is in excellent agreement with our INS findings, at 20 K. When combined with our DFT study, this shows that in acidic mordenite butane mostly favoured the gauche conformer. We see the reverse when butane is both ‘unconfined’ (Butane DFT) or in siliceous mordenite (Butane Si-MOR DFT), where butane is exclusively antiperiplanar at low temperatures (<20 K, Fig. S17, ESI†). This also reproduces the experimental INS results for the ‘unconfined’ butane system. Extrapolating to the butane isomerisation temperature range (550–800 K), shows large amounts of both conformers exist in all systems, due to the small energy difference (<2.5 kJ mol−1 in all cases). Despite this, the existence of alternative conformers has not (to the best of our knowledge) been considered previously in mechanistic or computational studies, on butane isomerisation.3,25,26 It is possible that the existence of multiple conformers could play an important role in many reaction mechanisms and processes, both from an experimental and theoretical viewpoint. Suggesting, butane's preference for the gauche conformer, within acidic mordenite could be linked to the superior activity of mordenite for butane isomerisation, which has not yet been considered in the catalyst design. However this requires further investigation.
We have explored the interactions of butane within mordenite, a solid-acid catalyst widely used for the industrially significant butane isomerisation reaction. We demonstrate, through a combined experimental and computational study that confining butane near an acid site, within the main mordenite pore, affects the favoured conformation of the butane molecule. While unconfined butane, and butane dosed siliceous mordenite favours the expected antiperiplanar butane conformer, the acidic mordenite stabilises the gauche-distorted conformer. The influence of alternative conformers has not yet been explored for butane isomerisation. This could prove to be a key factor in catalyst design and directing reaction pathways, not just in butane isomerisation, but for many processes. As such this is a factor that must be considered and investigated in a wider range of system and catalytic reactions.
Conflicts of interest
Authors declare they have no conflicts of Interest.Notes and references
- J. T. F. Degnan, Top. Catal., 2000, 13, 349 CrossRef.
- M. E. Potter, J. J. M. Le Brocq, A. E. Oakley, E. B. McShane, B. D. Vandegehuchte and R. Raja, Catalysts, 2020, 10, 1099 CrossRef CAS.
- M. J. Wulfers and F. C. Jentoft, J. Catal., 2015, 330, 507 CrossRef CAS.
- T. Kurniawan, O. Muraza, A. S. Hakeem, I. A. Bakare, T. Nishitoba, T. Yokoi, Z. H. Yamani and A. M. Al Amer, Energy Fuels, 2017, 31, 12691 CrossRef CAS.
- L. Lin, Q. Mei, X. Han, S. F. Parker and S. Yang, Top. Catal., 2020, 64, 593 CrossRef.
- A. J. O'Malley, S. F. Parker and C. R. A. Catlow, Chem. Commun., 2017, 53, 12164 RSC.
- A. P. Hawkins, A. J. O’Malley, A. Zachariou, P. Collier, R. A. Ewings, I. P. Silverwood, R. F. Howe, S. F. Parker and D. Lennon, J. Phys. Chem. C, 2018, 123, 417 CrossRef.
- L. Lin, A. M. Sheveleva, I. da Silva, C. M. A. Parlett, Z. Tang, Y. Liu, M. Fan, X. Han, J. H. Carter, F. Tuna, E. J. L. McInnes, Y. Cheng, L. L. Daemen, S. Rudic, A. J. Ramirez-Cuesta, C. C. Tang and S. Yang, Nat. Mater., 2020, 19, 86 CrossRef CAS PubMed.
- M. Jiménez-Ruiz, D. S. Gahle, T. Lemishko, S. Valencia, G. Sastre and F. Rey, J. Phys. Chem. C, 2020, 124, 5436 CrossRef.
- A. P. Hawkins, A. Zachariou, S. F. Parker, P. Collier, I. P. Silverwood, R. F. Howe and D. Lennon, ACS Omega, 2020, 5, 7762 CrossRef CAS PubMed.
- https://doi.org/10.5286/ISIS.E.RB1920057 .
- J.-S. Lin, J.-J. Wang, J. Wang, I. Wang, R. J. Balasamy, A. Aitani, S. Al-Khattaf and T.-C. Tsai, J. Catal., 2013, 300, 81 CrossRef CAS.
- J. Groen, T. Sano, J. Moulijn and J. Pérez-Ramírez, J. Catal., 2007, 251, 21 CrossRef CAS.
- W. M. Meier, Z. Kristallogr., 1961, 115, 439 CrossRef CAS.
- K. Gong, Z. Liu, L. Liang, Z. Zhao, M. Guo, X. Liu, X. Han, X. Bao and G. Hou, J. Phys. Chem. Lett., 2021, 12, 2413 CrossRef CAS PubMed.
- M. Ravi, V. L. Sushkevich and J. A. van Bokhoven, J. Phys. Chem. C, 2019, 123, 15139 CrossRef CAS.
- G. Paul, C. Bisio, I. Braschi, M. Cossi, G. Gatti, E. Gianotti and L. Marchese, Chem. Soc. Rev., 2018, 47, 5684 RSC.
- H. Jobic, M. Czjzek and R. A. Van Santen, J. Phys. Chem., 2002, 96, 1540 CrossRef.
- W. B. Nelligan, D. J. LePoire, T. O. Brun and R. Kleb, J. Chem. Phys., 1987, 87, 2447 CrossRef CAS.
- Y. Li, W. Guo, W. Fan, S. Yuan, J. Li, J. Wang, H. Jiao and T. Tatsumi, J. Mol. Catal. A: Chem., 2011, 338, 24 CrossRef CAS.
- A. Pulido, M. R. Delgado, O. Bludský, M. Rubeš, P. Nachtigall and C. O. Areán, Energy Environ. Sci., 2009, 2, 1187 RSC.
- P. K. Ghorai, J. Phys. Chem. B, 2010, 114, 6492 CrossRef CAS PubMed.
- Y. Mo, J. Org. Chem., 2010, 75, 2733 CrossRef CAS PubMed.
- R. Y. Brogaard, C.-M. Wang and F. Studt, ACS Catal., 2014, 4, 4504 CrossRef CAS.
- Z. Hong, K. B. Fogash, R. M. Watwe, B. Kim, B. I. Masqueda-Jiménez, M. A. Natal-Santiago, J. M. Hill and J. A. Dumesic, J. Catal., 1998, 178, 489 CrossRef CAS.
- E. García, M. A. Volpe, M. L. Ferreira and E. Rueda, J. Mol. Catal. A: Chem., 2003, 201, 263 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Including full experimental details, experimental INS spectra, calculated DFT geometries and DFT calculated INS spectra. See DOI: https://doi.org/10.1039/d2cc02003c |
| This journal is © The Royal Society of Chemistry 2022 |
