Slow magnetic relaxation in a {Co^IICo^III₂} complex containing a high magnetic anisotropy trigonal bipyramidal Co^II centre

Abstract

We report a trinuclear mixed-valence {Co^IICo^III₂} complex, where the Co^II centre adopts a trigonal bipyramidal geometry, leading to a large, easy-plane magnetic anisotropy and field-induced slow magnetic relaxation with a Raman-like relaxation process.

---

Single-Molecule Magnets (SMMs) show promise in a number of technological applications such as molecular spintronics,¹ high-density information storage,² and qubits for quantum computation.³ When the magnetic properties arise from a single paramagnetic ion in an appropriate ligand field, then these molecules are often referred to as Single-Ion Magnets (SIMs). The origin of SMM and SIM behaviour is the presence of an energy barrier (ΔE/k_B) that prevents the reorientation of magnetisation between the M_S = ±S components of the ground state S. Magnetic anisotropy, which depends on the spin–orbit contribution,⁴ is difficult to control in polymetallic systems, and hence recent research has been focused on monometallic systems. Monometallic Co^II complexes have been found to exhibit both large negative (easy-axis) and large positive (easy-plane) magnetic anisotropy when found in tetracoordinate, pentacoordinate and hexacoordinate geometries.⁵ More specifically, Co^II ions with an ideal trigonal bipyramidal geometry are expected to exhibit a high easy-plane anisotropy.⁶

We are working towards the synthesis of coordination complexes containing at least one high magnetic anisotropy centre, such as trigonal bipyramidal (TBP) Co^II, in order to boost the barrier ΔE/k_B. Herein, we report the complex [Co^IICo^III₂(μ₃-OH)(μ-pz)₄(DBM)₃]·2MeCN (1·2MeCN) (Fig. 1), which is a new solvate of a previously reported {Co₃} complex, obtained by a different synthetic procedure.⁷

Fig. 1 The molecular structure of 1. Colour code: Co^II: dark pink (the dark pink polyhedron represents the TBP geometry), Co^III: light pink (the light pink polyhedra represent the octahedral geometry), O: red, N: blue, C: grey. Hydrogen atoms are omitted for clarity.

Complex 1 is a mixed-valence isosceles triangle of Co^II/Co^III ions synthesised from the reaction of CoCl₂·6H₂O with Hpz (pyrazole) and HDBM (dibenzoylmethane) in MeOH/MeCN in the presence of NEt₃ (see the ESI†). The crystallographic data can be found in Table S1 (see the ESI†). The Co^II centre (Co1) is five-coordinate adopting a slightly distorted TBP geometry, while the two diamagnetic Co^III ions (Co2 and Co3) adopt an octahedral geometry. The oxidation states of Co^II and Co^III were confirmed using Bond Valence Sum (BVS) analysis.⁸ Continuous shape measures (CShMs),⁹ which provide an estimate of the distortion from the ideal TBP geometry for Co1, give a value of 0.33 (where 0 corresponds to the ideal polyhedron), confirming a small distortion (Table S2 and Fig. S3 ESI†). The crystal packing is shown in Fig. S4.† Intermolecular interactions are present through hydrogen–π and π–π interactions between the phenyl and pyrazolate rings of neighbouring molecules, while the shortest intermolecular Co1⋯Co1′ distance is ∼9.3 Å.

Direct current (dc) magnetic susceptibility measurements were performed on a polycrystalline sample of 1 restrained in eicosane in the 290–2 K temperature range in an applied magnetic field of 1000 Oe (Fig. 2). The χ_MT value at room temperature (2.45 cm³ mol⁻¹ K) corresponds to a high-spin Co^II ion and indicates a spin–orbit coupling contribution (the Co^III ions are diamagnetic so for g = 2, S = 3/2, χ_MT = 1.88 cm³ mol⁻¹ K). Upon cooling, χ_MT decreases slowly until ∼50 K to reach 2.16 cm³ mol⁻¹ K and then decreases rapidly below ∼50 K to reach 1.40 cm³ mol⁻¹ K at 2 K, indicating zero-field splitting of the ground state. Additionally, magnetisation versus field plots at 2, 4 and 6 K did not saturate at the highest available field of 5 T, a further indication of the presence of magnetic anisotropy (Fig. 2 inset).

Fig. 2 Variable temperature dc susceptibility data for 1 in a field of 1000 Oe from 290–2 K. Inset: Magnetisation versus field plots at temperatures 2, 4, and 6 K for 1. The red solid lines represent the fit (see the text for details).

Microanalysis and powder X-ray diffraction carried out on ground and non-ground samples (Fig. S1 and S2†) show that the lattice solvent is easily lost. Such desolvation could cause changes in the crystal packing, resulting in small changes of the local cobalt environment and hence small changes to the Co^IIg values and zero-field splitting (ZFS) parameters. High frequency EPR studies on 1 (Fig. S5†) are in agreement and suggest the presence of two discrete species within the microcrystalline powder sample in an ∼50 : 50 ratio, having distinct ZFS parameters. Analysis of the EPR data gives the parameters for the two species as: g_x = g_y = 2.18, g_z = 2.07 with an E/D ratio ∼0.13 and g_x = g_y = 2.23, g_z = 2.08 with an E/D ratio ∼0.17 (see the ESI†). Using the average of these two sets, g_x = g_y = 2.205, g_z = 2.075, the dc magnetic susceptibility data and the magnetisation curves of 1 were fitted simultaneously using the program PHI¹⁰ (Fig. 2), as described by the following effective Hamiltonian equation (1):

The first and second terms represent the axial and rhombic ZFS terms, parameterised by D and E, respectively, Ŝ is the spin operator with components Ŝ_i (i = x, y, z), and the final term denotes the Zeeman interaction with the local magnetic field, , parameterised through the Landé 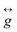tensor. Fixing the values of g_x = g_y = 2.205 and g_z = 2.075, and χ_TIP = 0.0009 cm³ mol⁻¹, where χ_TIP stands for the contribution of temperature-independent paramagnetism arising from two Co^III and one TBP Co^II,¹¹ we were able to extract the ZFS parameters D = +23.85 (±0.17) cm⁻¹ and E = +4.04 (±0.09) cm⁻¹. The E/D ratio extracted from the fitting of the magnetic data is ∼0.17, consistent with the EPR studies. The magnitude of D is also consistent with previously reported Co^II centres in TBP geometry with easy-plane anisotropy.^12,13

The relatively high value of the transverse anisotropy indicates significant mixing of the M_S = ±3/2 and ±1/2 levels, and can be attributed to the small deviation from the ideal TBP geometry and/or the different nature of the ligands in the equatorial positions.¹³ Only a few examples of Co^II in TBP geometry with easy-plane anisotropy have been found to show slow relaxation of the magnetisation.¹³ Therefore, we performed alternating current (ac) magnetic susceptibility measurements. In zero applied dc field, 1 does not display any out-of-phase ac signals, due to efficient zero-field quantum tunnelling. However, by using an applied dc field to suppress tunnelling, compound 1 does display slow magnetic relaxation at low temperature. Variable dc fields (500–5000 Oe) were applied to 1 at 2 K in order to obtain the optimum dc field at which the characteristic relaxation time of the magnetisation (τ) possesses the largest value (Fig. S7, ESI†). The characteristic relaxation times for each field were calculated using CC-FIT,¹⁴ and the τ_max value was obtained at 1000 Oe. The frequency dependence of the in-phase and out-of-phase magnetic susceptibility was measured under the optimum dc field for the range of temperatures 1.8–8 K (Fig. 3).

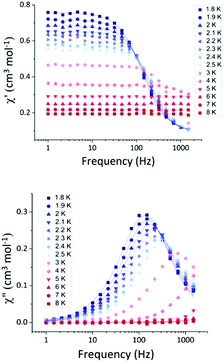Fig. 3 Frequency dependent in-phase (top) and out-of-phase (bottom) susceptibility signals for complex 1 in a 1000 Oe dc applied magnetic field, in the temperature range 1.8–8 K. The solid lines correspond to the fit (CC-FIT).¹⁴

The fitting of the Cole–Cole plot (out-of-phase versus in-phase signals) for 1 was performed using CC-FIT¹⁴ (Fig. 4), resulting in small values of the Cole–Cole parameter α (0.08–0.02) indicative of a relatively narrow distribution of relaxation times. The τ values were used to construct an Arrhenius plot for the temperatures 1.8–5 K, from which the relaxation parameters of ΔE/k_B (energy barrier) and τ₀ (pre-exponential factor) at higher temperatures were extracted for 1 (Fig. S8, ESI†). Fitting within the linear region (Orbach relaxation mechanism), the values ΔE/k_B = 23.18 (±2.2) K and τ₀ = 1.14 × 10⁻⁷ s were extracted. However, the value of ΔE/k_B is smaller than the calculated energy difference between the ground and first excited state of ∼50 cm⁻¹, a clear indication that other relaxation processes need to be considered. Using eqn (2), we attempted to fit the τ⁻¹versus T data but we were not able to extract reasonable values. The terms are the direct, tunnelling, Raman and Orbach contributions, in that order.¹⁵

τ⁻¹ = B + CTⁿ (3)

Fig. 4 The Cole–Cole plot of the ac magnetic susceptibility of 1 at 1000 Oe (top). The solid lines correspond to the fit (CC-FIT). The plot of τ⁻¹versus T for 1 in the temperature range 1.8–5 K (bottom). The red solid line corresponds to the fit using eqn (3) (see the text for details).

In order to avoid over-parameterisation we attempted to fit the τ versus field (H) plot using only the terms for direct and tunnelling processes (which are dependent on the field) to extract the parameters A, B₁, and B₂. However, all efforts were unsuccessful, an indication that there is a more complicated dependence of τ with the field. Therefore, using only the tunnelling (expressed as the parameter B) and Raman contributions (see eqn (3)) we were able to fit the τ⁻¹versus T plot (Fig. 4) affording the values B = 926 s⁻¹, C = 2.3 K⁻ⁿ s⁻¹ and n = 6.6. The exponent factor n in the Raman process should be equal to 9 for Kramers' ions, or 5 in the presence of low-lying states. However, lower values for n have been reported in cases where acoustic and optical phonons are involved.^15,16

In conclusion, [Co^IICo^III₂(μ₃-OH)(μ-pz)₄(DBM)₃] is the only reported example of a mixed-valence Co^II/Co^III polynuclear complex containing a single trigonal bipyramidal Co^II centre that gives rise to slow magnetic relaxation.¹⁷ In the case of 1, this arises from a large, easy-plane magnetic anisotropy. To obtain the zero-field splitting parameters, we used high frequency EPR measurements to extract the g factors. These were then fixed in the simultaneous fitting of the dc magnetic susceptibility and magnetisation data to give the parameters D = +23.85 (±0.17) cm⁻¹ and E = +4.04 (±0.09) cm⁻¹. Furthermore, it has been demonstrated recently how the magnetic anisotropy of octahedral Co^II is transferred to the overall magnetic anisotropy of a polymetallic {Cr₇Co} system. This is of interest for quantum information processing, especially in relation to molecules with a large spin ground state that is characterised by a large, easy-plane anisotropy.¹⁸ Hence, the next step is to develop a route to incorporate high magnetic anisotropy trigonal bipyramidal Co^II centres into exchange-coupled polymetallic systems that contain multiple paramagnetic centres.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

MM acknowledges the support from The UK Engineering and Physical Sciences Research Council (EP/J018147/1). A portion of this work was performed at the NHMFL, which is supported by the NSF (DMR-1157490 and DMR-1644779) and the State of Florida. SH also acknowledges the support from the NSF (DMR-1610226). The data that underpin this work are available at http://dx.doi.org/10.5525/gla.researchdata.618.

Notes and references

1. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179.
2. J. Bartolome, F. Luis and J. F. Fernández, in Molecular Magnets: Physics and Applications, Springer, Verlag, Berlin Heidelberg, 2014.
3. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357.
4. B. N. Figgis, Introduction to ligand fields, Wiley-VCH, New York, 1966; B. N. Figgis, M. Gerloch, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1968, 2086; R. B. Bentley, M. Gerloch, J. Lewis and P. N. Quested, J. Chem. Soc. A, 1971, 3751; A. K. Gregson, R. L. Martin and S. Mitra, J. Chem. Soc., Dalton Trans., 1976, 1458.
5. Y. Rechkemmer, F. D. Breitgoff, M. van der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. van Slageren, Nat. Commun., 2016, 7, 10467; V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792; C. Rajnák, J. Titiš, J. Moncol′, F. Renz and R. Boča, Eur. J. Inorg. Chem., 2017, 11, 1520; C. Rajnák, J. Titiš, O. Fuhr, M. Ruben and R. Boča, Inorg. Chem., 2014, 53, 8200; F. Shao, B. Cahier, E. Rivière, R. Guillot, N. Guihéry, V. E. Campbell and T. Mallah, Inorg. Chem., 2017, 56, 1104; F. Shao, B. Cahier, N. Guihéry, E. Rivière, R. Guillot, A. Barra, Y. Lan, W. Wernsdorfer, V. E. Campbell and T. Mallah, Chem. Commun., 2015, 51, 16475; D. Sertphon, K. S. Murray, W. Phonsri, J. Jover, E. Ruiz, S. G. Telfer, A. Alkaş, P. Harding and D. J. Harding, Dalton Trans., 2018, 47, 859.
6. S. Gomez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010.
7. M. Łukasiewicz, Z. Ciunik, J. Mazurek, J. Sobczak, A. Staroń, S. Wołowiec and J. J. Ziółkowski, Eur. J. Inorg. Chem., 2001, 1575.
8. N. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 192.
9. M. Pinsky and D. Avnir, Inorg. Chem., 1998, 37, 5575; S. Alvarez and M. Llunell, J. Chem. Soc., Dalton Trans., 2000, 3288.
10. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164.
11. R. Herchel and R. Boča, Dalton Trans., 2005, 1352; J. S. Wood, J. Chem. Soc. A, 1969, 1582.
12. R. Boča, L. Dlháň, W. Linert, H. Ehrenberg, H. Fuess and W. Haase, Chem. Phys. Lett., 1999, 307, 359; R. Herchel and R. Boča, Dalton Trans., 2005, 1352; C. Rajnák, J. Titiš, I. Šalitroš, R. Boča, O. Fuhr and M. Ruben, Polyhedron, 2013, 65, 122; B. Cahier, M. Perfetti, G. Zakhia, D. Naoufal, F. ElKhatib, R. Guillot, E. Rivière, R. Sessoli, A.-L. Barra, N. Guihéry and T. Mallah, Chem. – Eur. J., 2017, 23, 3648; D. Schweinfurth, J. Krzystek, M. Atanasov, J. Klein, S. Hohloch, J. Telser, S. Demeshko, F. Meyer, F. Neese and B. Sarkar, Inorg. Chem., 2017, 56, 5253.
13. T. J. Woods, M. F. Ballesteros-Rivas, S. Gómez-Coca, E. Ruiz and K. R. Dunbar, J. Am. Chem. Soc., 2016, 138, 16407; N. Nedelko, A. Kornowicz, I. Justyniak, P. Aleshkevych, D. Prochowicz, P. Krupiński, O. Dorosh, A. Ślawska-Waniewska and J. Lewiński, Inorg. Chem., 2014, 53, 12870; A. K. Mondal, T. Goswami, A. Misra and S. Konar, Inorg. Chem., 2017, 56, 6870; C. Rajnák, J. Titiš, I. Šalitroš, R. Boča, O. Fuhr and M. Ruben, Polyhedron, 2013, 65, 122.
14. CC-FIT Copyright © 2014 Nicholas F. Chilton; Y.-N. Guo, G.-F. Xu, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 9953.
15. Y. Zhang, S. Gomez-Coca, A. J. Brown, M. R. Saber, X. Zhanga and K. R. Dunbar, Chem. Sci., 2016, 7, 6519.
16. D. Shao, L. Zhang, L. Shi, Y. Zhang and X. Wang, Inorg. Chem., 2016, 55, 10859; L. Chen, S. Chen, Y. Sun, Y. Guo, L. Yu, X. Chen, Z. Wang, Z. W. Ouyang, Y. Songa and Z. Xued, Dalton Trans., 2015, 44, 11482; E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130.
17. Y. Zhu, C. Cui, Y. Zhang, J. Jia, X. Guo, C. Gao, K. Qian, S. Jiang, B. Wang, Z. Wang and S. Gao, Chem. Sci., 2013, 4, 1802; V. Chandrasekhar, A. Dey, A. J. Mota and E. Colacio, Inorg. Chem., 2013, 52, 4554; D. Wu, X. Zhang, P. Huang, W. Huang, M. Ruan and Z. W. Ouyang, Inorg. Chem., 2013, 52, 10976; E. A. Buvaylo, V. N. Kokozay, O. Y. Vassilyeva, B. W. Skelton, A. Ozarowski, J. Titiš, B. Vranovičová and R. Boča, Inorg. Chem., 2017, 56, 6999; S. Manna, A. Bhunia, S. Mistri, J. Vallejo, E. Zangrando, H. Puschmann, J. Cano and S. C. Manna, Eur. J. Inorg. Chem., 2017, 19, 2585; S. Mandal, S. Mondal, C. Rajnák, J. Titiš, R. Boča and S. Mohanta, Dalton Trans., 2017, 46, 13135.
18. E. Garlatti, T. Guidi, A. Chiesa, S. Ansbro, M. L. Baker, J. Ollivier, H. Mutka, G. A. Timco, I. Vitorica-Yrezabal, E. Pavarini, P. Santini, G. Amoretti, R. E. P. Winpenny and S. Carretta, Chem. Sci., 2018, 9, 3555.

---

Footnotes

† Electronic supplementary information (ESI) available: Further experimental details. CCDC 1838443. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt01997e

‡ Current address: Institute for Integrated Cell-Material Sciences (WPI-iCeMS), Kyoto University, Yoshida, Sakyo-ku, Kyoto 606-8501, Japan.

§ Current address: School of Chemistry, The University of Manchester, Manchester M13 9PL, U.K.

---