Taking the green fluorescence out of the protein: dynamics of the isolated GFP chromophore anion

Abstract

The green fluorescent protein (GFP) is employed extensively as a marker in biology and the life sciences as a result of its spectacular fluorescence properties. Here, we employ femtosecond time-resolved photoelectron spectroscopy to investigate the ultrafast excited state dynamics of the isolated GFP chromophore anion. Excited state population is found to decay bi-exponentially, with characteristic lifetimes of 330 fs and 1.4 ps. Distinct photoelectron spectra can be assigned to each of these timescales and point to the presence of a transient intermediate along the decay coordinate. Guided by ab initio calculations, we assign these observations to twisting about the C–C–C bridge followed by internal conversion to the anion ground state. The dynamics in vacuo are very similar to those observed in solution, despite the difference in absorption spectra between the two media. This is consistent with the protein environment restricting rotation about the C–C–C bond in order to prevent ultrafast internal conversion and preserve the fluorescence.

---

1 Introduction

Fluorescent proteins have revolutionised molecular biology. They can be fused to other proteins without interfering with their function, allowing them to serve as efficient fluorescent probes. The green fluorescent protein (GFP) was the first such protein to be discovered^1,2 and, together with its family of variants, is the most widely used fluorescent protein for in vivo monitoring of biological processes. Despite the fact that there have been numerous experimental and theoretical investigations of the fundamental photophysics and photochemistry that underpin the photobiology of GFP,^3–6 the role of the protein environment around the central chromophore is still not completely understood. It has been suggested that the environment of the chromophore inside the protein is similar to that in vacuo,^7–9 however the isolated chromophore was found to be non-fluorescent,⁷ and the dominant pathway for excited state relaxation in the gas-phase still remains an open question.

A widely used model chromophore for wild-type GFP is p-hydroxybenzylidene-2,3-dimethylimidazolinone (HBDI, the relevant anionic deprotonated form is shown in Fig. 1). The chromophore is buried within an eleven-stranded β-barrel that forms the protein and has two characteristic absorption bands centred around 395 nm and 480 nm, which are attributed to the neutral and anionic forms of the chromophore, respectively.^3,10 Excitation of either form of the chromophore results in a strong fluorescence (Φ = 0.79) from the anionic chromophore (the neutral form undergoes excited state proton transfer, forming the fluorescent anionic form).¹¹ The fluorescence is lost when the protein is denatured but returns upon renaturation or cooling below the glass transition.¹² In solution, the chromophore was found to be virtually non-fluorescent,¹³ which has been attributed to a fast non-radiative decay channel becoming accessible. Interestingly, the absorption maximum of the chromophore in solution varies with the choice of solvent, but the excited state lifetimes show relatively little dependence on the solvent, except for extremely viscous solvents, such as glycol, in which the excited state lifetime becomes significantly longer.^14–16 Consistent with experiment, theoretical investigations indicate that the ultrafast non-radiative decay observed in solution involves motion on the excited state surface, initially involving a geometry change from the Franck–Condon region (FC) to the fluorescent state (FS) on a timescale of tens of femtoseconds, then away from the FS via rotation about the C4–C7 bond (torsional angle ϕ, Fig. 1), followed by internal conversion to the ground state.^15,17 This rotation appears to be inhibited in the protein environment, making fluorescence from the excited state the primary decay channel. High viscosity solvents or freezing below the glass transition temperature similarly prevent free rotation around ϕ, leading to the observed slowing down of the non-radiative decay.^16,18

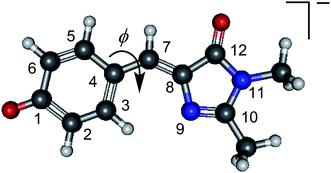Fig. 1 The structure of deprotonated p-hydroxybenzylidene-2,3-dimethylimidazolinone anion, a model for the GFP chromophore, with the atomic numbering and torsional angle, ϕ, referred to in the manuscript.

The electronic absorption spectrum of the isolated HBDI⁻ chromophore is similar to that of the native protein in its anionic form.⁹ This suggests that the protein environment does not induce significant differences in electronic character or excitation energy between the ground and first excited singlet ππ* state around the Franck–Condon region in the chromophore. While the similarities in absorption spectra of the isolated chromophore and the chromophore within the protein environment are striking, their decay pathways are clearly different because in the gas-phase the chromophore is non-fluorescent. This leads to the question of how, and on what timescale, the isolated chromophore decays, which is the focus of this contribution.

We probe directly the electronic relaxation pathway of an isolated model GFP chromophore anion (HBDI⁻, Fig. 1) following excitation to the first electronically excited ππ* state, S₁. Using anion time-resolved photoelectron spectroscopy,^19,20 we track the evolution of excited state population and interpret our results with the help of ab initio calculations. The results reveal that sub-picosecond dynamics are occurring on the S₁ excited state followed by internal conversion. Our results are remarkably similar to the dynamics observed in solution.^15,21,22 Comparison of the results with our calculations suggests that the excited state undergoes rapid (sub-picosecond) motion from the FC region towards a twisted intermediate (TI), which subsequently undergoes internal conversion to the anion ground state, as has previously been suggested to explain the dynamics in solution.^15,17 The decay mechanisms in vacuo and in solution appear identical, despite theoretical studies that suggest otherwise.¹⁸

2 Methods

2.1 Experimental

Isolated HBDI⁻ molecules are excited with 500 nm (2.48 eV) femtosecond laser pulses, just below the maximum of the S₁ ← S₀ transition (Fig. 2).^7–9 This excitation energy is resonant with the S₁ excited state but below the maximum in the direct photodetachment spectrum around 2.7–2.9 eV,^23–25 thus minimising direct and indirect electron loss channels in the anion. Excited state population is subsequently projected into the photodetachment continuum after a delay t, using an 800 nm (1.55 eV) probe pulse (this is sufficient to detach electrons from the excited state but not the ground state, so the experiment is sensitive to excited state dynamics only). Photoelectron images are recorded for a series of pump–probe delays.

Fig. 2 Energy level diagram of HBDI⁻ and excitation scheme employed in the current investigation. Population is transferred into the S₁ excited state with a 500 nm (2.48 eV) photon, and the S₁ population probed at 800 nm (1.55 eV). Shown on the right are two representative photoelectron spectra, recorded when the probe arrives before the pump (t < 0, green) and with both pulses overlapped temporally (t = 0, red). Both spectra show a large, non-dynamic feature at low electron kinetic energy (eKE) due to indirect electron detachment from the anion (see text for details). The pump–probe signature of the excited state is observed as a broad feature peaking at eKE = 1.1 eV.

Full details of the experimental apparatus have been reported previously and only details pertinent to the current experiment are given here.^26,27 The GFP chromophore was synthesised using the method reported by Voliani et al.²⁸ Anions were transferred into the gas-phase by electrospraying a 1 mM solution of HBDI in 90 : 10 methanol–water, with NaOH added dropwise until a colour change from pale-yellow to dark-yellow was observed. Anions were subsequently trapped in a ring electrode trap, and injected co-linearly into a Wiley–McLaren time-of-flight mass spectrometer at 500 Hz repetition rate. Isolated HBDI⁻ were observed as a single peak at 219 Da and the laser-ion delay adjusted such that only HBDI⁻ were intersected by femtosecond pump and probe laser pulses in the centre of a velocity-map imaging (VMI) setup.^27,29 Photoelectrons were collected in the direction mutually perpendicular to the ion and laser beams. Photoelectron images were acquired for approximately 2 × 10⁵ laser shots per delay and the resulting images were deconvoluted using the polar onion-peeling routine;³⁰ yielding photoelectron spectra and angular distributions. The VMI spectrometer was calibrated using photodetachment from I⁻ and has a typical electron kinetic energy (eKE) resolution ΔeKE/eKE of 5%.

The excitation (pump) and detachment (probe) laser pulses were derived from a commercial Ti:Sapphire oscillator and amplifier system (Spectra Physics Tsunami and Spitfire XP Pro). Pump pulses at 500 nm were obtained by sum-frequency generation of the output from an optical parametric amplifier with the fundamental 800 nm. Typical pump–probe intensities in the interaction region were on the order of 2 × 10¹⁰ W cm⁻². Pump and probe pulses were delayed relative to each other using an optical delay line and a cross-correlation with full-width at half-maximum (FWHM) of 130 fs was measured in a thin β-barium borate crystal.

2.2 Computational

The molecular geometries along the excited state reaction coordinate of a simplified model GFP chromophore anion with a hydrogen terminated imidazole group (p-hydroxybenzylidene-imidazolinone, HBI⁻) were determined by a potential energy surface (PES) scan calculation. The simplified model chromophore was chosen to reduce computational expense as removal of the methyl groups is unlikely to have a significant effect on the energetics of the chromophore.³¹

We employed the complete active space self-consistent field (CASSCF) level of theory with a 6-31G* basis set¹⁷ using MOLPRO 2010.1.³² Ideally, the complete active space should include all p-orbitals antisymmetric to the molecular plane, which would require CASSCF(16/14), a calculation with 16 electrons in 14 orbitals. To reduce the computational cost, we employed an incomplete active space of 12 electrons in 11 orbitals.¹⁷ The 3 orbitals and 4 electrons that were excluded were considered to have least influence on the conjugation and were the lowest and highest sets of benzene valence p-orbitals on the phenol moiety (i.e. the lowest HOMO and the highest LUMO) and the lone pair on the N11 atom. A two-root (S₀, S₁) state-average procedure was used to avoid CASSCF convergence problems in all calculations. The CASSCF PES scan calculation was performed on the GFP chromophore anion for the torsional angle ϕ. Once we obtained the anion geometries, we reduced the number of electrons by one to be able to calculate single-state CASSCF energies for the radical of the same geometry in its ground D₀ state.

To improve the energy profile of the CASSCF calculations, single-state, single-point, multiconfigurational second-order perturbation theory (CASPT2) calculations were performed with the ANO-pVDZ basis set for both the anion and radical at key geometries using MOLCAS7.6.^32–35

3 Results

Fig. 2 shows two representative photoelectron spectra, with the probe pulse arriving before the pump (t < 0, green line), and when pump and probe are overlapped temporally (t = 0, red line). The former is identical to a pump-only photoelectron spectrum, indicating that the probe alone is not resonant with any transition within the chromophore. This spectrum shows a large feature at eKE < 0.2 eV, arising primarily from indirect electron loss following excitation of the S₁ state at 2.48 eV.^8,23–25 A second feature, centred at eKE = 1.96 eV, requires at least two photons and is consistent with resonant two-photon detachment via the S₁ excited state, as seen previously in single-photon photoelectron spectra of HBDI⁻.²³ When pump and probe are temporally overlapped, an additional photoelectron feature can be discerned at eKE = 1.1 eV. Given the probe energy of 1.55 eV, this feature is consistent with excitation of the S₁ state by the pump pulse, followed by detachment with a probe photon. Hence, this feature is a direct measure of the population in the S₁ state.

Time-resolved photoelectron spectra are shown in Fig. 3(a), with pump-only and probe-only signals subtracted from pump–probe spectra, leaving only the time-resolved S₁ excited state photoelectron signal as a function of time. For clarity and later comparison, Fig. 3(b) is a contour map of the same data. A rapid rise in photoelectron signal is observed at t = 0, with maximum intensity at eKE = 1.1 eV. The photoelectron spectrum at t = 0 is asymmetric with a decaying tail towards low eKE. With increasing pump–probe delay the high eKE side of this feature decays on a sub-picosecond timescale, leaving a broad feature centred around eKE = 0.6 eV, which subsequently decays on a picosecond timescale.

Fig. 3 Time-resolved photoelectron spectroscopy results for HBDI⁻ following excitation of the S₁ excited state at 500 nm (2.48 eV) and probing with 800 nm (1.55 eV). (a) Experimental photoelectron spectra as a function of pump–probe delay; (b) contour plot of the data shown in (a); (c) simulated time-resolved photoelectron data, modelled using the timescales and coefficients extracted from the fitting procedure described in the text.

The observed dynamics were fitted to a sum of exponentially decaying spectral profiles convoluted with a Gaussian cross-correlation function, g(t),

where the coefficients c_i(eKE) represent the intensity of the i^th decay at a given eKE, and τ_i is its corresponding lifetime. Two contributions were sufficient to fit the time-resolved dataset and the resultant lifetimes are τ₁ = 330 fs and τ₂ = 1.4 ps. The resultant S(eKE,t) is plotted in Fig. 3(c), and reproduces the experimental data (Fig. 3(b)) remarkably well, with an adjusted R² = 0.98 (see ESI†). The spectra of the individual fit coefficients, c₁(eKE) and c₂(eKE), are shown in Fig. 4(a), where positive values indicate exponential decay and negative values indicate exponential growth at the respective timescales.

Fig. 4 (a) Spectral components of the fast (c₁(eKE), 330 fs, green trace) and slow (c₂(eKE), 1.4 ps, blue trace) decay coefficients extracted from the data using equation (1). The sum of the two components (red trace) represents the photoelectron spectrum of the initially excited state, that decays on a 330 fs timescale. (b) Integrated photoelectron spectra of the initially excited state that decays on a 330 fs timescale (red), the longer lived state whose population rises with a 330 fs timescale and decays on a 1.4 ps timescale (blue) and the total integrated photoelectron spectrum (black) together with experimental data (black circles).

The spectrum obtained for c₁(eKE), corresponding to a timescale of 330 fs, shows a decay of intensity in the spectral region eKE > 0.6 eV, while concomitantly a rise is observed for eKE < 0.6 eV. This suggests an evolution along the excited state potential energy surface with a characteristic lifetime of 330 fs, from a point along S₁ producing photoelectrons with high eKE to a point leading to photoelectrons with lower eKE. The remaining population, described by the coefficient c₂(eKE), has a broad eKE distribution peaking around 0.6 eV (Fig. 4(a)) and a lifetime of 1.4 ps. The spectral shape of this feature shows no further changes as indicated by the fact that only a single timescale is required to reproduce the spectrum at long delays. The photoelectron spectrum associated with the 330 fs timescale can be reconstructed by summing the coefficients of the fit, as explained in the ESI,† and this is shown in Fig. 4(a) as a solid red line.

The decay times and their relative weights obtained from the global fit have also been used to reproduce the total integrated photoelectron signal as shown in Fig. 4(b). The fast and slow decaying components clearly show the origin of the bi-exponential decay that has also been observed in solution and the overall fit is in excellent agreement with the experimentally measured photoelectron signal. At long times, however, the total integrated photoelectron signal does not decay to zero. Instead, about 2% of the photoelectron signal at t = 0 remains and decays on a timescale exceeding the current experiment (10 ps). This residual signal indicates that a very small fraction of the population remains in the excited state.

4 Discussion

To interpret the photoelectron spectra, we have performed ab initio calculations of a model GFP chromophore anion, HBI⁻. Specifically, we have calculated the energy of the anion S₀ and S₁ states and the neutral D₀ state at a number of key geometries along the potential energy surface of the S₁ excited state. A summary of the results from our calculations is provided in Fig. 5. In agreement with previous studies,^15,17 we identify three key geometries along the minimum energy path of the S₁ excited state: the Franck–Condon (FC) geometry corresponds to the geometry initially excited from S₀; the fluorescent state (FS) is a shallow minimum on S₁; and a twisted intermediate (TI) in which rotation about the central C4–C7 bond (ϕ, Fig. 1) by 90° has occurred. Note that an additional TI geometry can be accessed by rotation about the C7–C8 bond. This process was found to possess a small potential barrier in the gas-phase, making ϕ torsion the more likely deactivation pathway, although not necessarily exclusive.¹⁷

Fig. 5 Schematic potential energy curves of S₁ and D₀ along the reaction coordinate (minimum energy path, MEP) from FC → FS → TI, together with the CASPT2 calculated energies and the state-averaged CASSCF S₁ orbitals for the FC and TI geometries. After TI, decay back to the S₀ anion ground state is likely to occur by internal conversion.

The FC and FS geometries are connected primarily by a stretching of the allyl C–C bond occurring on a timescale of tens of femtoseconds.¹⁷ Calculated S₁ potential energy surfaces indicate that the surface connecting the FC and FS is rather flat along the minimum energy path.¹⁷ Our calculations show that the geometry change from FC to FS induces only a small change in the D₀ energy, suggesting that the photoelectron spectra of the FC and FS geometries are similar. Moreover, based on the timescale associated with motion from FC to FS, both geometries will be populated during the laser excitation. Hence we conclude that the photoelectron spectrum corresponding to the fast lifetime (τ₁ = 330 fs) corresponds to a combination of the photoelectron spectra of FC and FS (Fig. 4(a), red trace).

After the formation of the FS geometry, theory predicts the presence of a negligible (0.02 eV) barrier between the FS and TI. This motion involves a significant change in reaction coordinate on the S₁ state, as initial stretching of the C–C–C bridge is replaced by a rotation about weakened bonds. From our calculations, this motion leading from FC → FS → TI is associated with a significant stabilisation of S₁ by 0.49 eV, which is in qualitative agreement with Olivucci et al.¹⁷ and quantitative agreement with more recent calculations.³¹ Concomitantly, the energy of D₀ increases by 0.54 eV along this mode with respect to the energy of the FC geometry, as indicated in Fig. 5. This picture is in good agreement with the observations in Fig. 3(a and b) and Fig. 4(a): after the decay of the initial geometries on the S₁ state, a new feature emerges at a lower eKE, redshifted by 0.5 eV, and broadened substantially. The spectral shift and increased spectral width can be attributed to the divergence of the D₀ and S₁ potential energy surfaces. The TI will be formed vibrationally hot as the internal energy must be conserved in the gas-phase. We have not performed a Franck–Condon analysis as the effective temperature is non-Boltzmann and the mode distribution unknown.

The conceptual picture of the dynamics of the isolated GFP chromophore anion is as follows. Initial excitation leads to the formation of the FC (see Fig. 5), which evolves to the FS geometry within the time resolution of our experiment (sub-100 fs). From the FS, the system undergoes a rotation about the C–C–C bridge on a 330 fs timescale, consistent with timescales observed for similar motions in biological chromophores such as rhodopsin.³⁶ The TI subsequently decays on a 1.4 ps timescale, most likely by internal conversion to the S₀ ground state in a single exponential fashion. Unlike the initial motion from the FC/FS to TI geometries, the decay of the TI in the S₁ state does not involve spectral changes.

The decay lifetimes found by global fitting are in remarkable quantitative agreement with the excited state dynamics of HBDI⁻ in solution, as measured by fluorescence up-conversion, where a bi-exponential decay with characteristic lifetimes of 340 fs and 1.1 ps was observed in methanol.^15,21,22 The timescales were found to be almost insensitive to polarity¹⁵ or viscosity,²¹ with the exception of very large viscosities which lead to a substantially longer lifetime of the excited state.¹⁶ The dynamics were interpreted as a fast initial motion along a vibrational coordinate on the S₁ state, followed by intramolecular vibrational redistribution and decay from the formed intermediate. Our mechanistic model is consistent with these experiments and comparison with our quantum chemistry calculations leads us to interpret the second step as a rotation about one of the C–C bonds in the bridge. The similarity between the gas-phase and solution also hints at the minor role that autodetachment from S₁ plays in the decay dynamics, a pathway that is energetically inaccessible in solution. This is in agreement with recent photoelectron spectroscopic results on HBDI⁻.^23–25 Furthermore, our spectra do not show any evidence for such dynamics (at eKE < 0.1 eV), although the resultant signals would be expected to be small and on a large background. Nonetheless, even if competitive autodetachment was taking place, one might expect that only the timescales would be affected and the spectral features arising from S₁ photodetachment would remain mostly unchanged.

Previous theoretical studies have suggested a difference in the decay pathways accessible to the chromophore in solution and in the gas-phase. Specifically, in solution, both rotation about the C7–C8 or C4–C7 bonds are barrierless. In the gas-phase, a barrier to rotation about C7–C8 leads to a preferential deactivation pathway involving C4–C7 rotation.¹⁷ However, the most striking difference is the energy gap between the S₀ and S₁ states following rotation about either bonds. In solution, the TI associated with rotation around the C4–C7 bond has a much larger S₀–S₁ gap than in the gas-phase and also significantly larger than the TI formed following rotation of the C7–C8 bond.¹⁷ Hence, it was concluded that rotation about the C7–C8 bond will lead to more rapid decay in solution. Rotation about the C4–C7 bond would lead to a bottleneck in the dynamics and some population could remain trapped on the excited state. From our experimental data, the remarkable qualitative and quantitative agreement between the measured excited state decay in solution and in vacuo would suggest that similar relaxation pathways are accessed in both environments, although we cannot definitively assign the rotation to a specific bond.

The striking insensitivity of the relaxation dynamics to the environment is surprising for two reasons. Firstly, the maximum of the gas-phase absorption spectrum of the anion GFP chromophore is very similar to that of GFP within the protein.^9,37 In contrast, the absorption spectrum in solution is blue shifted by ∼0.3 eV in water¹³ and suggests that either the FC structures may be different or that electronic states are destabilised or stabilised to differing extents in solution. One might expect that this would have some bearing on the excited state dynamics, although it should be pointed out that the coincidence of the gas-phase and protein absorption spectra may be accidental and result from a cancellation between blue-shifting and red-shifting interactions in the protein. Secondly, it is well-known that when the environment is the GFP β-barrel protein, the dynamics are on a nanosecond timescale³ and have slowed down by 3 orders of magnitude with respect to the isolated chromophore dynamics determined here. This is at odds with the observed insensitivity of the environment on the excited state dynamics. In the protein, the weakly fluorescent TI is almost never reached and the chromophore is trapped in the FS geometry. In both the gas-phase and solution, the chromophore leaves the FS geometry on a 330 fs timescale to form the TI intermediate via a negligible barrier.^15,17 The observed discrepancy points to a large influence of the protein environment on the S₁ excited state potential energy surface. The TI is accessed via a rotation about the bridging C–C bonds, which appears to be dramatically restricted if the chromophore is embedded in the protein barrel. On the imidazole side, the chromophore is covalently bound to the protein, while the hydroxy-anion is restricted by hydrogen bonds.^2,38,39 From the comparison of the dynamics of the GFP chromophore in the gas-phase and in water, it is clear that the solvation of the phenoxy anion and H-bonding alone are insufficient to cause significant changes in excited state dynamics. In terms of covalent bonding, the addition of bulky groups on the GFP chromophore does influence the dynamics, but by less than one order of magnitude.⁴⁰ Hence, it must be the concerted action of the protein on both sides of the chromophore that restricts the motion, leading to a large barrier on the S₁ state that prevents the TI from being formed and thus establishes fluorescence as the primary decay channel.

5 Conclusions

We have measured the ultrafast relaxation dynamics of an isolated model GFP chromophore using time-resolved photoelectron spectroscopy. The resulting deactivation pathway was found to proceed via two distinct coordinates. Initially, the excited state evolves from the FC region to the FS geometry, on timescales faster than the time resolution of the current experiment. From the FS a rotation about the bridging C–C bond leads to the formation of a twisted intermediate geometry on a timescale of 330 fs. This subsequently undergoes internal conversion to the anionic ground state in 1.4 ps. These results are in quantitative agreement with measurements of the same chromophore in solution and suggest that a similar relaxation pathway is operative.

A key feature of the current experiment is that we have essentially measured the photoelectron spectra of the transient intermediates in the GFP chromophore. The FC/FS and the TI geometries are represented by the photoelectron spectra shown in Fig. 4(a). These photoelectron spectra will serve as important benchmarks for quantum dynamics calculations of the involved intermediates. Moreover, the S₁ potential energy surface can be refined in conjunction with excited state dynamics calculations, providing an important step towards a complete understanding of the photophysics of the GFP chromophore. This goal lies at the heart of understanding the photophysics and photochemistry that underpin the fluorescence properties of GFP and current experiments in our groups are aimed at introducing the protein scaffold incrementally in an attempt to identify the key and minimal structural requirements that lead to fluorescence. Moreover, it is only through the deep insight provided in the current experiment that one may hope to develop the predictive capabilities of new biological probes with finely tuned properties.

Acknowledgements

CRSM and HHF are grateful to M.A. Robb for useful discussions and his guidance with the quantum chemistry calculations, the EPSRC UK National Service for Computational Chemistry Software (NSCCS), H. Tsui for advice in its use and R.J. Fitzmaurice for synthesising the HBDI chromophore. JRRV is grateful to the EPSRC (EP/D073472) for funding. ASC is funded by the Leverhulme Trust.

References

1. O. Shimomura, F. H. Johnson and Y. Saiga, J. Cell. Comp. Physiol., 1962, 59, 223–239.
2. R. Y. Tsien, Annu. Rev. Biochem., 1998, 67, 509–544.
3. M. Chattoraj, B. A. King, G. U. Bublitz and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 8362–8367.
4. M. Zimmer, Chem. Rev., 2002, 102, 759–782.
5. S. Bonsma, R. Purchase, S. Jezowski, J. Gallus, F. Könz and S. Völker, ChemPhysChem, 2005, 6, 838–849.
6. S. R. Meech, Chem. Soc. Rev., 2009, 38, 2922–2934.
7. M. W. Forbes and R. A. Jockusch, J. Am. Chem. Soc., 2009, 131, 17038–17039.
8. M. W. Forbes, A. M. Nagy and R. A. Jockusch, Int. J. Mass Spectrom., 2011, 308, 155–166.
9. S. B. Nielsen, A. Lapierre, J. U. Andersen, U. V. Pedersen, S. Tomita and L. H. Andersen, Phys. Rev. Lett., 2001, 87, 228102.
10. R. Heim, D. C. Prasher and R. Y. Tsien, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12501–12504.
11. G. H. Patterson, S. M. Knobel, W. D. Sharif, S. R. Kain and D. W. Piston, Biophys. J., 1997, 73, 2782–2790.
12. N. M. Webber, K. L. Litvinenko and S. R. Meech, J. Phys. Chem. B, 2001, 105, 8036–8039.
13. H. Niwa, S. Inouye, T. Hirano, T. Matsuno, S. Kojima, M. Kubota, M. Ohashi and F. Tsuji, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13617–13622.
14. A. D. Kummer, C. Kompa, H. Niwa, T. Hirano, S. Kojima and M. E. Michel-Beyerle, J. Phys. Chem. B, 2002, 106, 7554–7559.
15. D. Mandal, T. Tahara and S. R. Meech, J. Phys. Chem. B, 2004, 108, 1102–1108.
16. R. Gepshtein, D. Huppert and N. Agmon, J. Phys. Chem. B, 2006, 110, 4434–4442.
17. M. E. Martin, F. Negri and M. Olivucci, J. Am. Chem. Soc., 2004, 126, 5452–5464.
18. P. Altoe, F. Bernardi, M. Garavelli, G. Orlandi and F. Negri, J. Am. Chem. Soc., 2005, 127, 3952–3963.
19. A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758.
20. J. R. R. Verlet, Chem. Soc. Rev., 2008, 37, 505–517.
21. D. Mandal, T. Tahara, N. M. Webber and S. R. Meech, Chem. Phys. Lett., 2002, 358, 495–501.
22. K. L. Litvinenko, N. M. Webber and S. R. Meech, J. Phys. Chem. A, 2003, 107, 2616–2623.
23. D. A. Horke and J. R. R. Verlet, Phys. Chem. Chem. Phys., 2012, 14, 8511–8515.
24. C. R. S. Mooney, M. E. Sanz, A. R. McKay, R. J. Fitzmaurice, A. E. Aliev, S. Caddick and H. H. Fielding, J. Phys. Chem. A, 2012, 116, 7943–7949.
25. Y. Toker, D. B. Rahbek, B. Klaerke, A. V. Bochenkova and L. Andersen, Phys. Rev. Lett., 2012, 109, 128101.
26. J. Lecointre, G. M. Roberts, D. A. Horke and J. R. R. Verlet, J. Phys. Chem. A, 2010, 114, 11216–11224.
27. D. A. Horke, G. M. Roberts, J. Lecointre and J. R. R. Verlet, Rev. Sci. Instrum., 2012, 83, 063101.
28. V. Voliani, R. Bizzarri, R. Nifosi, S. Abbruzzetti, E. Grandi, C. Viappiani and F. Beltram, J. Phys. Chem. B, 2008, 112, 10714–10722.
29. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477–3484.
30. G. M. Roberts, J. L. Nixon, J. Lecointre, E. Wrede and J. R. R. Verlet, Rev. Sci. Instrum., 2009, 80, 053104.
31. C. Filippi, M. Zaccheddu and F. Buda, J. Chem. Theory Comput., 2009, 5, 2074–2087.
32. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson, M. Wang and A. Wolf, MOLPRO, version 2010.1, a package of ab initio programs, 2010.
33. G. Karlström, R. Lindh, P.-A. Malmqvist, B. O. Roos, U. Ryde, V. Veryazov, P.-O. Widmark, M. Cossi, B. Schimmelpfennig, P. Neogrady and L. Seijo, Comput. Mater. Sci., 2003, 28, 222–239.
34. V. Veryazov, P.-O. Widmark, L. Serrano-Andrs, R. Lindh and B. O. Roos, Int. J. Quantum Chem., 2004, 100, 626–635.
35. F. Aquilante, L. De Vico, N. Ferr, G. Ghigo, P.-Å. Malmqvist, P. Neogrdy, T. B. Pedersen, M. Pitok, M. Reiher, B. O. Roos, L. Serrano-Andrs, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247.
36. P. Kukura, D. W. McCamant, S. Yoon, D. B. Wandschneider and R. A. Mathies, Science, 2005, 310, 1006–1009.
37. L. H. Andersen, A. Lapierre, S. B. Nielsen, I. B. Nielsen, S. U. Pedersen, U. V. Pedersen and S. Tomita, Eur. Phys. J. D, 2002, 20, 597–600.
38. M. Orm, A. B. Cubitt, K. Kallio, L. A. Gross, R. Y. Tsien and S. J. Remington, Science, 1996, 273, 1392–1395.
39. F. Yang, L. G. Moss and G. N. Phillips, Nat. Biotechnol., 1996, 14, 1246–1251.
40. J. Conyard, M. Kondo, I. A. Heisler, G. Jones, A. Baldridge, L. M. Tolbert, K. M. Solntsev and S. R. Meech, J. Phys. Chem. B, 2011, 115, 1571–1577.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c2sc21737f

‡ These authors contributed equally to this work.

---