Open Access Article
Open Access ArticleQuantum vibrational spectroscopy with classical trajectories
Riccardo Conte
 *a,
Chiara Aieta
*a,
Chiara Aieta
 *ab and
Michele Ceotto
*ab and
Michele Ceotto
 *a
*a
aDipartimento di Chimica, Università degli Studi di Milano, via Golgi 19, 20133 Milano, Italy. E-mail: riccardo.conte1@unimi.it; chiara.aieta@unimi.it; michele.ceotto@unimi.it
bDepartment of Chemistry, Princeton University, Princeton, NJ 08544, USA
First published on 28th January 2026
Abstract
Vibrational spectroscopy is a technique of wide use in fields like analytical chemistry, biomedical applications, and pharmacology. The technique is cost-effective and very popular. However, a reliable assignment of vibrational spectra may be hard to achieve for large molecular systems or when nuclear quantum effects (NQEs) are sizeable. These aspects hamper the effectiveness of vibrational spectroscopy as an analytical and characterization tool. Computational approaches may help overcome the shortcomings of a purely experimental investigation. For instance, classical molecular dynamics is computationally cheap and easy to perform by a non-expert user as well, but it cannot account for NQEs. The latter can be included in an affordable way if approximate quantum mechanical methods based on classical trajectories are employed. Herein, we review the main theoretical approaches based on classical trajectories and able to deal with NQEs in vibrational spectroscopy. We start by reporting on the possibility to employ methods derived from the path integral representation of quantum mechanics, i.e. semiclassical (SC) dynamics, centroid molecular dynamics (CMD), ring polymer molecular dynamics (RPMD), and their variants. Then, other techniques like the quantum thermal bath (QTB) and the quasi-classical trajectory (QCT) method are highlighted. All but SC methods are based on a fully classical real-time propagation. This review aims at increasing the awareness of useful and ready-to-use classical-trajectory-based computational techniques among the broader community of experimental researchers, developers, and applied scientists, who employ vibrational spectroscopy in their everyday activity.
1 Introduction
Vibrational spectroscopy as an investigation and analysis tool is adopted in many research fields. Even if there is no need to stress this aspect, we find it useful to remind the reader about the range of uses of IR and Raman spectroscopies, which are the main techniques adopted in vibrational spectroscopy.For instance, vibrational spectroscopy is employed to better understand biological functions;1 it is adopted for medical diagnostics and identification of biomarkers of degenerative disease,2 and it is being developed for use in virology.3
A modern and innovative branch of clinical medicine is based on IR and, mainly, Raman spectroscopy of plasma or saliva samples.4–7 This approach has the advantage of being non-invasive and cost-effective, so that its adoption for early clinical diagnosis, disease research, and also drug discovery is currently considered at the frontier of clinical medicine.
In the field of virology, viruses are generally characterized by means of electron microscopy and mass spectroscopy, which allow one to determine the virus morphology and chemical composition.8,9 The first Raman investigation of a virus involved the turnip yellow mosaic virus, and it was focused on the secondary structure of its coat protein and RNA.10 From there, vibrational spectroscopy has gained in importance, and it has been employed both to study virus–cell interactions and as a tool for monitoring viral infections. For instance, Fourier transform infrared (FTIR) spectroscopy has permitted researchers to study the kinetics of the development of the herpes simplex virus,11 or to profile mouse kidney cells infected with the murine sarcoma virus.12 Other uses of vibrational spectroscopy in virology include serum analysis to assist the reverse transcription polymerase chain reaction technique in virus identification.13–15 Viruses are made of proteins, lipids, and nucleic acids, so they are expected to be characterized by very signal-rich spectra, which need some kind of theoretical or computational processing before a reliable assignment of spectroscopic features can be achieved.
Materials science is another field in which vibrational spectroscopy is widely employed. For instance, surface-enhanced Raman scattering (SERS) is an advanced Raman technique used to study surface phenomena like catalysis or polymer formation, biosensing, and single-molecule sensing.16 The first use of SERS dates back to 1974 when Raman spectra of pyridine on roughened silver were collected.17 Nowadays, SERS is employed for detection of biological samples and diseases like cancer, Alzheimer's, and Parkinson's.18–20 It is also used in conjunction with electrochemistry to unravel the behavior of molecules in different oxidation states21 and to detect chemicals in very low concentrations.22 Materials science takes advantage of the general features of vibrational spectroscopy like the rapidity of the analysis, the property of being cost effective, and its non-destructive handling of materials, which can be analyzed without damage.
Other reasons to employ vibrational spectroscopy are in common with molecular science. Specifically, IR and Raman techniques allow one to gain information on electronic properties like polarizabilities and dipole moments,23 in addition to detailed knowledge about geometry and symmetry useful to characterize chemical species. In particular, we point out the possibility to study intermolecular forces, i.e. interactions between adsorbed molecules and the materials surface or hydrogen bonds and other types of interactions in solvated systems.24,25
This short overview clearly does not cover all fields of application of vibrational spectroscopy techniques. In all cases, the gain one would get by combining experimental IR or Raman studies with high-level application of theoretical and computational tools is evident. Nowadays, machine learning approaches are more and more used, and they can be useful in assigning vibrational spectroscopic features.2,26–31 However, they are not able to provide direct physical insights. For a comprehensive understanding and application of vibrational spectroscopy, one should look for theoretical approaches able to clarify the assignment of very complex spectra and detect quantum spectroscopic effects. Experiments are described by quantum mechanics, but popular computational tools often neglect it.
Herein, we present a review of the main theoretical and computational approaches to vibrational spectroscopy to describe quantum effects in a computationally cost-effective way, i.e. based on the evolution of classical trajectories. We remark on the strengths and shortcomings of the illustrated methods, with the aim of familiarizing the non-expert reader with some methods to assist and improve experimental research. Before drawing our conclusions, we point the reader eager to practice the reviewed methods to some available free software. This review is about linear spectroscopy, but many of the techniques described here can be adapted and employed for studies involving non-linear spectroscopies.
2 A rigorous starting point: Feynman's path integral representation of quantum mechanics and correlation functions
The starting point to come up with an approximation of quantum mechanics by means of classical trajectories is represented by Feynman's path integral formulation of quantum mechanics.32 Within this formalism, the probability amplitude to go from one point in space x to another one x′ in a time t is obtained as a weighted sum over all possible paths x(t) linking the two points. The weight depends on the classical action S[x(t)]
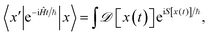 | (1) |
A different treatment of Feynman's path integrals is the one based on Wick's rotation36
| t → iτ, | (2) |
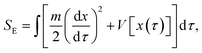 | (3) |
Path integral molecular dynamics (PIMD) is based on imaginary-time path integrals, and it is used to compute thermal expectation values of functions of position operators.37–39 If one looks for a quantum dynamical description, i.e. a real-time representation which is necessary for spectroscopy calculations, one way is to work in imaginary time and then, by means of a reverse Wick's rotation, go back to the real-time domain. An alternative, less rigorous, but more practical approach is used by methods derived from PIMD, like centroid molecular dynamics40 and ring polymer molecular dynamics,41 which heuristically move from the PIMD calculation to a real-time simulation to evaluate a Kubo transform.42
From the previous paragraphs, it is clear that SC methods include a set of approaches directly related to quantum dynamics, while path integral methods are expected to treat quantum dynamics in a more approximate way. However, both kinds of approaches work in a time-dependent fashion and can be employed for vibrational spectroscopy calculations starting from a suitable correlation function. The choice of a time-dependent approach to the calculation of time-independent quantities may appear cumbersome, but it is justified from the point of view of reduced computational cost when trajectories evolved classically. The unavoidable but limited loss in accuracy is compensated by the possibility to push calculations to deal with larger systems, including solvated or condensed phase ones.
The basic spectroscopic calculation to perform with SC dynamics is the so-called vibrational power spectrum, which provides the vibrational density of states obtained by Fourier transforming the survival amplitude of an arbitrary quantum wavepacket. The peaks appearing in the power spectrum are located at eigenenergies of the vibrational Hamiltonian, and transition frequencies can be obtained as differences between eigenenergies. The density of states I(E) is obtained from
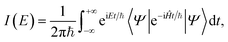 | (4) |
Another correlation function employed in SC spectroscopy is the Boltzmann-averaged dipole (µ) autocorrelation function, i.e. the autocorrelation function that, in the framework of linear response theory, upon being Fourier transformed returns the absorption lineshape σ(ω). The latter is directly related to the IR spectrum through a frequency-dependent refractive index n′(ω)43,44
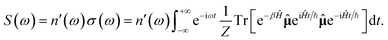 | (5) |
A different correlation function, the Kubo time correlation function,42 is employed by CMD, RPMD and other approaches derived from them. The IR spectrum based on Kubo's formula is calculated as
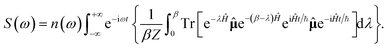 | (6) |
To conclude the description of the correlation functions more commonly adopted in spectroscopic calculations, we notice that classical molecular dynamics (MD) employs yet another type of correlation function. In the calculation of classical power spectra, it is the velocity autocorrelation function which is Fourier transformed
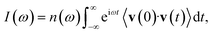 | (7) |
The classical calculation can be performed in an NVE ensemble, in which case, if the initial energy of the system is chosen following a harmonic quantization of vibrational energy levels, the approach is termed the quasi-classical trajectory48 (QCT) or quasi-classical molecular dynamics method.49 The classical calculation can also be performed at a chosen temperature by coupling a thermostat to the system and waiting for equilibration before starting the run from which the frequencies are to be extracted. Different from SC power spectra (and SC frequencies), the classical power spectra (and classical frequencies) are dependent on the temperature or trajectory energy.48 Simply, by substituting v with µ in eqn (7), one can calculate the classical absorption lineshape (related to the classical IR spectrum through a frequency-dependent refractive index), in which case, the average 〈·〉 of eqn (7) is performed over the three Cartesian components of the molecular dipole. In general, eqn (5)–(7) can also be adopted for the calculation of Raman spectra, provided the polarizability tensor α is employed in the correlation functions.
3 Vibrational spectroscopy with semiclassical methods
In our review of SC approaches, we deal with SC power spectra. Introduction of a stationary phase approximation into eqn (1), followed by adoption of Miller's initial value representation,50 derivation of the Heller–Herman–Kluk–Kay (HHKK) SC propagator (often indicated simply as the Herman–Kluk (HK) propagator),35 and finally application of Kaledin and Miller's time averaging technique51,52 led to a practical formula for calculating SC power spectra of a molecular system made of Nvib vibrational degrees of freedom
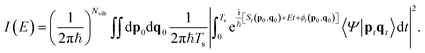 | (8) |
Eqn (8) is known as the time averaged semiclassical initial value representation (TA SCIVR). Evaluation of eqn (8) is done through Monte Carlo (MC) integration and based on running classical trajectories from initial conditions (p0, q0). The chosen simulation time Ts should be both long enough to cover several vibrational periods and short enough not to deteriorate the SC propagator. A common choice for molecular systems is Ts ≈ 600 fs, since the fundamental frequencies of interest generally have vibrational periods between 10 and a couple hundreds of fs. All quantities appearing in the time integrand of eqn (8) depend on the classical trajectories. Specifically, ϕt(p0, q0) is the phase of the Herman–Kluk prefactor and 〈Ψ|ptqt〉 is the quantum overlap of the chosen arbitrary state |Ψ〉 with the coherent state |ptqt〉.
Shalashilin and Child exploited the properties of coherent states to develop their coupled coherent states (CCS) theory,53–55 showing it was able to reproduce both the linearized coherent state matrix element of the HK propagator and the coherent state overlap of Heller's thawed Gaussian propagator56 (another type of semiclassical propagator based on a single trajectory that we document later).
We point out that eqn (8) provides a way to describe nuclear quantum effects on the basis of an extremely short dynamics. From this point of view, the method is very attractive. However, there are some drawbacks that prevent the application of eqn (8) “as is” to large systems. First of all, a large number of trajectories must be evolved to reach convergence in MC integration. This number increases fast with the dimensionality of the system. Furthermore, the time evolution of ϕt(p0, q0) requires calculation of Hessian matrices, which is computationally expensive. Much work has been done in reducing the number of Hessian calculations required, including adoption of machine learning methods or limitation of Hessian calculations to a subsystem.57–62 Last, the Fourier transform signal is concealed by noise when the 〈Ψ|ptqt〉 overlap is too high-dimensional.63 Therefore, a method based on just a few trajectories and able to work in reduced dimensionality without relevant loss of accuracy was the goal of further theoretical advance.
3.1 Reproducing quantum tunneling splittings
A first advance, introduced by Ceotto, and known as multiple coherent states semiclassical initial value representation (MC SCIVR), is based on a tailored choice of reference states and trajectories to minimize the computational overhead of the calculation.64 MC SCIVR has been used in numerous investigations,65–67 but here we focus on a study about the vibrational spectrum of non-rotating ammonia.68 This spectrum is characterized by tunneling splitting due to the umbrella or pyramidal inversion of NH3. Fig. 1 shows the MC-SCIVR results for NH3 and ND3, based on the evolution of just 8 tailored trajectories for each study. The splitting of fundamental mode 2 is evident in the NH3 case (the two signals originated from the splitting are labeled as 2+1 and 2−1), while it is missing (because it is too small for the resolution of the calculation) in the deuterated case. This demonstrates not only the quantum nature of the reported effect but also that calculations of spectra involving tunneling are very challenging for SCIVR methods. Only shallow tunneling is described, and tiny splittings (up to a few cm−1) are hard to be detected. However, this is a first example of the ability of SC methods to describe NQEs in molecular systems.3.2 Reproducing quantum interference effects
Another way in which NQEs appear in a vibrational spectrum is in the form of a frequency shift of the spectroscopic signal associated with a fundamental transition, if compared to the corresponding classical estimate. Classical simulations are certainly able to account for the anharmonicity of the potential. In this way, they provide frequency and intensity estimates of fundamentals which differ from the harmonic ones. However, by definition, they are not able to detect the additional features associated with phenomena like quantum real-time coherence and quantum interference (not to say tunneling).In SC calculations, the type of NQEs mentioned above are naturally included because of the real-time path-integral origin of the method. An example of this is found in the vibrational spectrum of protonated glycine tagged with 3 hydrogen molecules.69 To deal with this system, the divide-and-conquer semiclassical initial value representation (DC SCIVR) technique,63,70 combined with MC SCIVR, has been introduced and adopted by our group. The advance introduced by DC SCIVR concerns the possibility to work in reduced dimensionality within subsets obtained by means of a sensible partition of vibrational modes according to their mutual coupling. This means that the semiclassical calculations are performed in reduced dimensional subspaces made of modes strongly coupled to each other. In DC SCIVR, trajectories are still full dimensional though, so coupling and interference with all other modes are still accounted for. Several methods to determine the best subspace partition have been worked out, including a genetic algorithm and approaches based on the investigation of the off-diagonal elements of the Hessian matrix.71,72 DC SCIVR allows one to overcome the issues related to the typical low signal-to-noise ratio of systems exceeding 20–30 vibrational degrees of freedom.
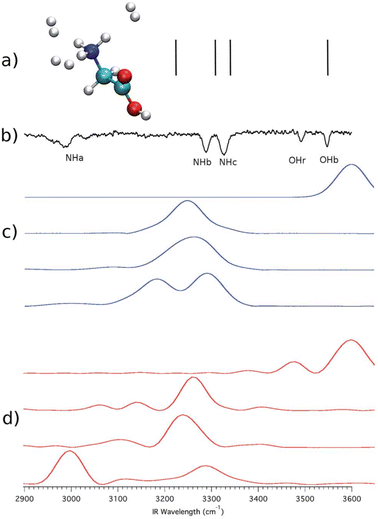
With reference to the protonated glycine tagged with 3 hydrogen molecules mentioned above, Fig. 2 reports the scaled harmonic estimates (i.e. frequencies obtained by scaling the harmonic estimates by a factor) of the high-frequency fundamentals – vertical lines in panel (a): quantum effects are missing since the scaled harmonic estimate for the fundamental frequency of the mode named NHa is totally off the mark if compared to the experiment in panel (b). A more accurate description of anharmonicity is given by the QCT simulation of panel (c). QCT methods return anharmonic classical estimates of fundamental frequencies.49 However, the presence of the NH3+ rotor and the interaction with the three hydrogen molecules lead to quantum interference effects between the quantum states just below and above the rotational barrier. This effect cannot be accounted for by the QCT calculation. The NQE is evident from the experiment, and it appears under the form of an additional shift in the signal of the NHa stretch compared to the QCT estimate. Only the DC-SCIVR calculation (see panel d) is able to reproduce this NQE, which is distinctive of one of the fundamental frequencies of vibration. Remarkably, QCT calculations of panel (c) and DC-SCIVR calculations of panel (d) were performed using exactly the same classical trajectories.
3.3 Reproducing anharmonic overtones and combination bands
Quantum features in vibrational spectra are certainly not limited to fundamental transitions. They also involve combination bands and overtones, whose calculation requires a proper quantum treatment. Single-trajectory classical estimates of the vibrational frequency of such spectral features return the sum of fundamental transition frequencies they are made of in a harmonic-like fashion, with small deviations in multi-trajectory calculations.73 In other words, classical methods are able to account for the anharmonicity of the 3Nat − 6-dimensional PES (Nat being the number of atoms in the system), and they account for some anharmonicity of the Nvib = 3Nat − 6 fundamental vibrations. However, classical methods can only algebraically combine these 3Nat − 6 fundamental frequencies to approximate combination bands and overtones; so, due to the lack of real-time coherences and quantum interferences, they do not account for the entire anharmonic shifts typical of a quantum treatment of combination bands and overtones.The importance of this topic is evident in studies where the role of combination bands and their correct quantum description is crucial. A remarkable example is the bending–libration combination band in water clusters and liquid water. Imagine to build larger and larger water clusters until the central H2O monomer shows spectroscopic features in agreement with those of liquid water. What one finds out is that if the requirement is just that the fundamental bands be in agreement with those of liquid water, then this is accomplished even by small water clusters. When the requirement additionally includes the bending–libration combination band, DC SCIVR points out that it is the water cluster made of 21 monomers which is the first one to match liquid water in all aspects.74 Fig. 3 shows that the 19-mer is characterized by OH stretches that go outside the Raman signal produced by monomers which are tetrahedrally coordinated in liquid water, i.e. those representative of bulk liquid water.75 The 21-mer has all features in common with liquid water, and these features, in the larger 23-mer, resemble liquid water even more.
 | ||
| Fig. 3 Power spectra of the central monomer. The peaks corresponding to bending (darker color nuances), stretching (lighter color nuances), and most coupled bending–libration modes (blue) of (H2O)19 (top), (H2O)21 (middle), and (H2O)23 (bottom) are reported. The liquid water IR spectrum is shown as shaded gray areas, and the MCR-Raman band (from ref. 75) for the stretching of tetrahedrally coordinated monomers in liquid water (light blue) is also presented. Reproduced from A. Rognoni, R. Conte and M. Ceotto, Chem. Sci., 2021, 12, 2060–2064. | ||
3.4 Dealing with large dimensional systems
As anticipated, the DC-SCIVR technique was developed to deal with large dimensional systems. DC-SCIVR simulations are still based on full dimensional classical dynamics, but eqn (8) is projected onto and evaluated in subspaces. Calculations in the chosen subspaces are made possible by introduction of an approximate projected potential.71A remarkable example of the ability of DC SCIVR to reproduce power spectra of large dimensional systems is the study of C4![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C5
O and C5![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C6 stretching vibrations of thymidine solvated by water. The two vibrations are well separated in frequency (about 50 cm−1) in gas-phase thymidine, while their signals coalesce when thymidine is solvated by water.76,77 The solvent was described explicitly by means of more than 300 water molecules organized in a droplet model with a repulsive wall on the edge of the solvation sphere. DC SCIVR was used in conjunction with a QM/MM scheme with polarizable embedding to describe the two vibrations and was successful in reproducing the degeneracy of the two vibrations for solvated thymidine. It was found to be essential to use a polarizable force field for the MM region, while the QM part was treated at the DFT-B3LYP/6-31G* level of theory.78
C6 stretching vibrations of thymidine solvated by water. The two vibrations are well separated in frequency (about 50 cm−1) in gas-phase thymidine, while their signals coalesce when thymidine is solvated by water.76,77 The solvent was described explicitly by means of more than 300 water molecules organized in a droplet model with a repulsive wall on the edge of the solvation sphere. DC SCIVR was used in conjunction with a QM/MM scheme with polarizable embedding to describe the two vibrations and was successful in reproducing the degeneracy of the two vibrations for solvated thymidine. It was found to be essential to use a polarizable force field for the MM region, while the QM part was treated at the DFT-B3LYP/6-31G* level of theory.78
Another field of application of DC SCIVR to large dimensional systems is materials science. Several applications have been devoted to the spectroscopic study of the molecular adsorption on anatase TiO2 surfaces in which the full-dimensional dynamics of the adsorbate, the solid surface and the solid bulk were taken into account to come up with a quantum anharmonic estimate of the adsorbate energy levels.79 Investigations of adsorption on anatase of molecules like water,79 NOx species,80 and formic acid dimer81 have been presented. The latter study was particularly interesting because it served as a prototype for adsorption of gas-phase Brønsted acid on oxides. Calculations were performed with density functional theory employing plane waves for the solid. The results were compared to low temperature experiments, which clarified that the acid proton forms a very strong hydrogen bond with surface oxygen. This explains a substantial amount of redshift compared to free OH bonds, which makes the OH stretching involved in the adsorption elusive and puzzling to be assigned in the experimental spectrum.
We notice that the family of SCIVR methods has been built in a hierarchical way moving from TA SCIVR to MC SCIVR and to DC SCIVR. All these methods can be used with any kind of description of the potential energy surface (PES) of the system under investigation. This includes common force fields, fitted ab initio PES, “on-the-fly” evaluation of the potential energy, and QM/MM schemes.82–87
3.5 Calculation of IR spectra and absorption intensities
Semiclassical IR spectroscopy is based on eqn (5), which states that the IR spectrum (S(ω)) is strictly related to the absorption lineshape. Even if the inverse temperature β plays an important role in shaping the absorption lineshape, for molecules with well separated quantum vibrational levels, or when one is interested in vibrations at frequencies higher than the THz region, the β → +∞ limit, i.e. the zero-temperature limit, is representative of the room temperature spectrum as well. In the zero-temperature limit, it is possible to rearrange eqn (5) in a suitable way for using semiclassical propagators and the time average approach. In our group, we have worked out a semiclassical infrared method (SC IR), which is able to reproduce very accurate IR spectra compared to quantum mechanical exact calculations or experimental spectra.88 However, the method is numerically applicable only to small systems, so we worked out an extended version of it, named extended semiclassical infrared (e-SC IR), starting from the analytical dynamics of a harmonic oscillator and inserting in the new theory the features of MC SCIVR.89 It turns out that e-SC IR can be directly employed to study molecular systems of any size without the need to adopt the DC-SCIVR technique. Not surprisingly, the method is not as accurate as the parent SC IR, but it has allowed us to get IR spectra for glycine and ethanol (see Fig. 4 for the IR spectrum of the latter), and applications to larger and larger systems are underway. | ||
| Fig. 4 e-SC-IR spectrum of non-rotating gas-phase ethanol. Reproduced from C. Lanzi, C. Aieta, M. Ceotto and R. Conte, J. Chem. Phys., 2025, 163, 024122 with the permission of AIP Publishing. | ||
SC IR and e-SC IR are not the first attempts to develop SC methods able to calculate IR spectra. To this end, two semiclassical approaches were already presented by our group. One method starts from SC power spectra calculations and, from there, SC vibrational wavefunctions are obtained as linear combinations of a harmonic basis set. Eventually, the IR spectrum is calculated by means of a state-to-state approach.90 One advantage of this method is that the obtained wavefunctions can be used for different purposes, for instance, visualization of nuclear vibrational densities.91,92 The main drawback is that as the vibrational states get more energetic a huge number of harmonic basis set elements contribute to the SC wavefunction, making the IR spectrum calculation cumbersome. The other anticipated method takes advantage of the power spectrum lineshape, and from there it reconstructs the IR spectrum.93 The advantage of this method is that bigger systems can be treated. However, both approaches are not amenable to be applied in conjunction with DC SCIVR, because they rely on full-dimensional calculations of power spectra, while DC SCIVR performs calculations in several reduced dimensional subsets, so their range of applicability is in principle narrower than that of e-SC IR.
SC calculations able to provide absorption intensities also include vibronic, photoabsorption, and photoemission spectra.94 In this field, the work of the Vaníček group is a landmark. Different from the SC methods described above, they adopted a thawed Gaussian approximation (TGA).56 The main feature of TGA methods is that they are based on a single classically evolved trajectory, and they require the width of the Gaussian (as well as its phase) to be evolved in time according to the associated time-dependent Schrödinger equation. Therefore, TGA approaches are more robust than other single-trajectory-based SC methods even if they are generally less accurate. The latter aspect is not a severe drawback in applications for vibronic spectroscopy in which the energies at play are large compared to vibrational spectroscopy ones. For instance, the calculation of the photoemission spectrum of oligothiophenes, in which vibronic transitions are present, was a successful application of TGA (see Fig. 5).95
Further advances in the field have been undertaken both theoretically and regarding the range of applications. For instance, the photoabsorption spectrum of benzene was calculated by means of TGA.96 Furthermore, the possibility of calculations of finite-temperature vibronic spectra was introduced with the theory of thermofield dynamics at basically no additional, or very reduced, computational cost.97–99 Thawed Gaussian Ehrenfest dynamics was shown to be a viable route to investigate the physics of processes at conical intersections,100 and applications to two-dimensional electronic spectra were undertaken.101
The huge flexibility of SCIVR methods is also demonstrated by possible applications to the non-adiabatic dynamics field.102–106 More specialized work was performed by the Ananth group, where path-integral based approaches to non-adiabatic processes both in the SC and ring-polymer frameworks were developed.107–110 The Vaníček group introduced an SC method for computing time-resolved non-adiabatic electronic spectra111 and later proposed accurate integrators for non-adiabatic dynamics.112 Quite recently, our group employed the time average approach to compute non-adiabatic vibronic spectra.113 A comparison between different approaches to non-adiabatic dynamics was performed by the Shalashilin group by means of their ab initio multiple cloning method based on trajectory and Gaussian wavepacket evolution.114,115
Herman–Kluk and thawed Gaussian SC propagators have been demonstrated to be strictly intertwined. The thawed Gaussian propagator can be obtained as an approximation to the HK one, and by means of a refined cellularization approach one can move from Heller's thawed Gaussian propagator to the HK one.116 The two propagators can also be combined to describe different portions of a larger system. For instance, the more accurate Herman–Kluk propagator can be adopted for the target molecule and the thawed Gaussian one for the environment. The Grossmann group has developed this mixed (or hybrid) SC theory, including application to IR spectroscopy in the limit of high temperatures and upon partial linearization of the propagator.117–120 SC approaches can tackle spectroscopy studies by describing the environment in a linearized framework, the so-called linearized semiclassical initial value representation (LSC-IVR),121–126 or in a full-dimensional fashion.78,127 If possible, the full-dimensional approach, in the sense that the full, non-linearized propagator is employed, is to be preferred because if the semiclassical propagator is linearized, then quantum coherences are lost.128
3.6 Possible ways to improve the accuracy of semiclassical vibrational spectroscopy
The results obtained with SC methods have been often and successfully compared to the outcomes of fully quantum approaches. We recall two investigations in which comparisons to MCTDH results were performed. One study by the Pollak and Burghardt groups concerned the vibronic absorption spectrum of formaldehyde,129 and another one was a study of the vibrational spectrum of the Zundel cation by our group.130 In an investigation of the smallest amino acid, i.e. glycine, SC results have been compared to second-order vibrational perturbation theory (VPT2) ones.131Notwithstanding, attempts to improve the accuracy of the SC propagator have been undertaken. To this purpose, an approach developed in our group is the adiabatically switched semiclassical initial value representation (AS SCIVR).132 This method can be used in conjunction with any of the other SCIVR methods mentioned above, and some applications have been performed.133,134 Based on the adiabatic theorem, AS SCIVR prepares the initial conditions of trajectories used for the SC calculations. The approach improves the stability of the classical trajectories and generally allows one to get more accurate and precise SC frequency estimates at the cost of a preliminary short classical dynamics. For instance, AS SCIVR has been adopted in two studies involving the ethanol and ethylene glycol molecules for which experimental data and vibrational configuration interaction (VCI) calculations were available. In both investigations, AS SCIVR demonstrated very good accuracy. In the case of ethanol,135 AS SCIVR was able to get for the trans-ethanol isomer the Fermi resonance involving the CH2 symmetric stretch and the overtone of a CH2 motion at a lower frequency. The AS-SCIVR description of this Fermi resonance was in better agreement with the experiment than VCI results. Furthermore, AS SCIVR was able to estimate the zero-point energy of trans- and gauche-ethanol in very good agreement with benchmark diffusion MC calculations.136 In the case of ethylene glycol,84 AS-SCIVR results were close to benchmark VCI ones and more accurate than thermostatted ring polymer molecular dynamics (TRPMD) calculations. It is worth noticing that while MC SCIVR introduces an approximation to the SC propagator by slashing the number of needed trajectories, AS SCIVR improves on the initial conditions of the trajectories to reach faster convergence in the semiclassical calculations. In principle, one can use AS SCIVR followed by MC SCIVR133,134 to improve the stability of the MC-SCIVR trajectories.
Two other very rigorous approaches able to enhance the accuracy of semiclassical calculations were introduced. They are the ℏ series approach worked out by Kay137 and the correction operator method introduced by Pollak.138,139 Even if both methods provide a rigorous way to improve calculations, they work directly on the propagator rather than on its time averaged version. Furthermore, they can become impractical when dealing with high-dimensional systems, and their application so far has been limited to low-dimensional or model systems.140
An alternative SCIVR approach, which has been recently developed in Xin-Zheng Li's group, makes use of the filter diagonalization technique.141,142 The advantage of this method is that a much shorter time evolution is required, which helps keeping trajectories stable. Furthermore, the divide-and-conquer technique can be adopted, allowing one to tackle large dimensional systems. The approach was also shown to improve in some instances the accuracy of results compared to those obtained with the time average technique.
Another very recent advance has been obtained by adopting MCTDH to calculate the coherent state overlap within the SC framework. The method has been applied to on-the-fly dynamics with promising results.143
4 Vibrational spectroscopy with centroid and ring polymer molecular dynamics
We next move on to discuss the arguably most popular class of classical-trajectory-based approaches. CMD and RPMD have been constantly developing in the last 20 years, and improvements over the initial formulations have been introduced. These approaches are strictly related to path integral molecular dynamics starting from the mapping of each quantum particle onto a ring polymer of quasi-particles known as beads. For this reason, they are sometimes collectively named PIMD methods.When looking at static or thermodynamical properties of a quantum system, the quantum Boltzmann-averaged expectation value of an observable A, which is a function of the position operator, given by
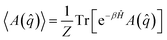 | (9) |
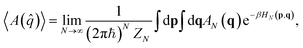 | (10) |
4.1 Exact treatment of the Kubo time correlation function and Matsubara dynamics
As anticipated, spectroscopic signals can be obtained from the Fourier transform of the Kubo time correlation function, as reported in eqn (6). Shi and Geva149 demonstrated that the Kubo time correlation function for two generic operators Â(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ) and
) and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) (
(![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) ) of a quantum particle subject to the Hamiltonian Ĥ (in the case of IR spectroscopy, Â and
) of a quantum particle subject to the Hamiltonian Ĥ (in the case of IR spectroscopy, Â and ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) are the dipole momentum operator µ) can be recast as the quantum dynamical propagation of an ensemble of imaginary-time Feynman paths involving two functions AN(q) and BN(z), i.e.
are the dipole momentum operator µ) can be recast as the quantum dynamical propagation of an ensemble of imaginary-time Feynman paths involving two functions AN(q) and BN(z), i.e.
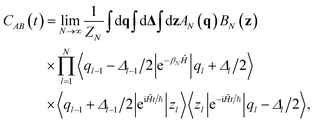 | (11) |
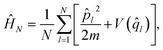 | (12) |
Matsubara dynamics exploits the property of ĤN being invariant for a cyclic permutation of replicas to introduce a set of Fourier variables or modes (Qi, i = 1, …, N), which can be defined starting from the ring polymer coordinates q. The centroid is characterized by zero Fourier frequency, while the non-zero frequency modes are the fluctuation modes describing thermal fluctuations around the centroid. Matsubara dynamics is based on retaining for the dynamics-only M low-frequency modes (the Matsubara dynamical modes) of the original N (N → ∞) modes, while all N modes are still retained for the quantum statistics. So, in Matsubara dynamics, the potential VN(q) is replaced by a potential of mean force150
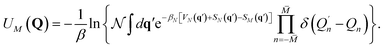 | (13) |
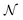 is an appropriate normalization factor, Q is the collection of Matsubara dynamical modes, Qn and
is an appropriate normalization factor, Q is the collection of Matsubara dynamical modes, Qn and 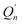 are two generic Matsubara dynamical modes, q′ runs over the set of all N beads,
are two generic Matsubara dynamical modes, q′ runs over the set of all N beads, ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) is equal to (M − 1)/2 and
is equal to (M − 1)/2 and
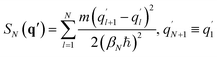 | (14) |
The Matsubara dynamics (M modes) evolved under the classical Hamiltonian HM(P, Q) = P2/2m + UM(Q), where P is the vector of momenta conjugate to Q, and the quantum Kubo correlation function is approximated as
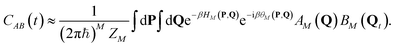 | (15) |
4.2 Centroid molecular dynamics and ring polymer molecular dynamics
Matsubara dynamics is impractical, but by appropriate approximation it is possible to derive two much more practical and popular methods: CMD and RPMD. Historically, CMD and RPMD have not been introduced as approximations to Matsubara dynamics but as heuristic interpretation of the PIMD real-time dynamics. In CMD and RPMD, the real-time dynamics of the PIMD ring polymer is not just a way to get an efficient quantum Boltzmann sampling, but it is exploited to calculate approximate real-time correlation functions derived from the Kubo one.
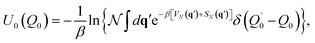 | (16) |
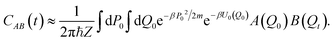 | (17) |
The potential of mean force in eqn (16) is computationally expensive to evaluate at each step of the dynamics. Its common evaluation is based on the introduction of fictitious masses for the fluctuation modes much lighter than the mass of the centroid. This procedure is often called the adiabatic approximation.153–155 Furthermore, thermostats are usually coupled to the fluctuation modes to ensure the correct canonical sampling, while the centroid is left unthermostated not to spoil the evaluation of the correlation function.156 Numerous applications of CMD to vibrational spectroscopy can be found in the literature, which include, for instance and far from being exhaustive, studies of the vibrational motion of liquid water,157,158 high pressure ices,159 and protonated methane (CH5+).160
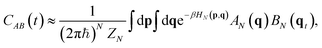 | (18) |
If one applies basic RPMD to perform vibrational spectroscopy calculations, though, some issues arise. First of all, it is not possible to rely on the bead dynamics for the calculation of the correlation function because the harmonic springs would spoil the true frequencies of vibration of the system. Therefore, RPMD must also rely on the dynamics of the centroid for spectroscopy calculations. However, the presence of spurious peaks in the spectra is unavoidable due to the coupling of the centroid motion with that of the beads. Thermostatted ring polymer molecular dynamics has been introduced to alleviate this problem.161,162 In TRPMD, a set of thermostats is coupled to the fluctuation modes to damp their vibrational motions at the cost of widening the spectral lineshapes.45 Several applications of (T)RPMD to IR spectroscopy have been reported in the literature, including analysis of ethylene glycol,163 non-linear spectroscopy,164 analysis of Lennard-Jones liquids,165 and a study of hydrazine in an ab initio fashion,166 to give some representative examples.
Fig. 6 shows a comparison of the accuracy of different imaginary-time path integral methods for the two-dimensional Champagne bottle model, as reported by Trenins and Althorpe.150 Two absorption bands are visible: the low frequency one is a rotational band, while the high frequency one is due to the stretching mode which mimics the OH stretching in water. Results at four different temperatures are presented. A striking difference between the two bands is that while the absorption maximum of the rotational band shifts with temperature, the maximum of the stretch band is basically independent of it. This is because the involved rotational energy levels are close together, while the spacing between vibrational energy levels is larger. The investigated temperature range extends enough to change the populations of rotational levels in a way that the peak of absorption is temperature-dependent, while the change of population in vibrational levels is negligible. Matsubara dynamics with M ranging from 1 (at T = 800 K) to 5 (at T = 200 K) is the most accurate simulation. The slight blue shift compared to the exact quantum mechanical results and other small discrepancies is due to the neglect of real-time coherence effects. The TRPMD simulation also suffers from some blue shifts and, as anticipated, widens the band. The CMD calculation is characterized by a sizeable red shift of the stretch band at 200 K.167 This issue of CMD is known as the curvature problem, and it is related to the Cartesian description of the centroid motion. Some methods, which we label as post-CMD, have been recently developed to overcome this issue and improve CMD accuracy.
 | ||
| Fig. 6 IR spectra for a two-dimensional Champagne bottle model (see ref. 150 for details). The vertical dashed line indicates the center of the quantum mechanical stretch peak. The low-frequency band is due to rotational motion. Reproduced from G. Trenins and S. C. Althorpe, J. Chem. Phys., 2018, 149, 014102 with the permission of AIP publishing. | ||
The quasi-centroid molecular dynamics method (QCMD) is based on the definition of an appropriate set of curvilinear coordinates, so that the coupling of the centroid with the N − 1 fluctuation modes is minimized. The propagation is still performed in Cartesian coordinates, but a curvilinear potential of mean force is defined and employed. QCMD is able to correct the red shift of CMD in evaluating the fundamental OH stretching frequency.168 The different dynamics of the quasi-centroid compared to the centroid one may also affect the static properties, so to confirm the reliability of QCMD calculations, it is essential to compare static averages obtained from QCMD with those of a standard PIMD simulation. The main issues arising when practically applying QCMD lie in the necessity to define for each system a set of appropriate curvilinear coordinates, which is not always straightforward, and in the determination of a computationally effective way to estimate the curvilinear potential of mean force. The second problem has been levied by introducing the fast quasi-centroid molecular dynamics method (f-QCMD),170–172 which provides an efficient way to calculate the difference between the quasi-centroid potential of mean force and the classical potential, i.e. the so-called quantum correction potential. f-QCMD achieves the goal by means of a series of pairwise terms extracted from short-time PIMD simulations.173 The approach is up to 100 times faster than the parent QCMD.
The temperature-elevated path integral coarse-graining simulations (Te PIGS) method employs a different approach to estimate the quantum correction potential.174 The method gets its foundation from the observation that the quantum correction potential usually changes very slowly with temperature. If this holds true for the system under investigation, then one can get a reliable estimate of the quantum correction potential as the high temperature difference between the potential of mean force used in CMD and the classical potential. The advantage of working with the CMD potential of mean force, which is accurate at high temperatures, is that the search for a set of appropriate curvilinear coordinates is no longer needed, thus also overcoming the first of the two problems mentioned above. This property makes Te PIGS ideally the most suitable post-CMD approach for calculations involving large-dimensional systems.146,175,176 Fig. 7 shows results from ref. 171 in adopting the post-CMD methods to calculate the IR spectrum of liquid water at 300 K based on the analytical qTIP4P/F PES and associated dipole surface.
Fig. 7 demonstrates that QCMD, f-QCMD, and Te PIGS are in very good agreement between each other and are able to describe accurately the three bands of fundamentals characterizing liquid water. These are the libration band below 1000 cm−1, the bending band centered just above 1600 cm−1, and the stretching band with the absorption maximum just below 3500 cm−1. We notice that the classical simulation is characterized by a blue shift. This is an anticipated result, since at 300 K a classical simulation is missing most of the anharmonicity of the potential, and the signal is found closer to the harmonic estimate. As expected, the post-CMD methods allow for a correct quantum thermal sampling, and classical anharmonicities of the potential are correctly described. On the other hand, they are still based on just the centroid dynamics and are missing the real-time coherence effects. This leads to (small) discrepancies in the evaluation of fundamental bands and to the inability to describe the bending–libration combination band between 2000 and 2500 cm−1. The issue about this combination band is not only limited to the calculated absorption intensity, for which a correction term from Matsubara dynamics has been worked out,177 but also concerns the frequency of the band which, being the simulation based on a classical real-time propagator, is found at the sum of fundamental frequencies, missing the anharmonicity related to nuclear quantum effects.
Post-CMD methods are continuously being developed. As an example, the hybrid-CMD method has recently appeared in an effort to solve the curvature problem in a computationally efficient way relying on a hybrid of QCMD and CMD.178
5 Vibrational spectroscopy with other classical-trajectory based approaches
Methods derived from imaginary-time path integration have the property to correctly sample the quantum Boltzmann statistics, while, as already discussed, the real time dynamics was only heuristically introduced. Methods that build on a specular scheme also exist and have been employed in vibrational spectroscopy. In these approaches, the focus is on the real time dynamics performed by means of classical molecular dynamics, while the energy of the trajectories is set by enforcing the quantum statistics into molecular dynamics. In the following, we will review two approaches that fall into this category, namely the quantum thermal bath (QTB) and the QCT methods.5.1 The quantum thermal bath method
The QTB method was introduced by Dammak et al. about 15 years ago based on the idea to exploit the link between energy quantization and its spectral density at thermal equilibrium.179 Specifically, the fluctuation–dissipation theorem180 states that when dissipation converts the energy of a dynamical system into heat, then there is a response related to thermal fluctuations to preserve detailed balance. One can practically exploit the theorem by adding both a frictional term and a Gaussian random force term (related to the thermal fluctuations) to the molecular dynamics of the system under investigation. In this way, by appropriately modifying the equations of motion, one can enforce the desired quantum thermal statistics into molecular dynamics. The modified equations of motion are known as the Langevin equations of motion, i.e.
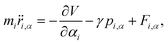 | (19) |
The spectrum of the random force Fi,α provides the link with the quantum thermal statistics to be enforced into the dynamics. The stochastic force spectrum (I) is defined by the fluctuation–dissipation theorem as
| IFi,αFj,β(ω) = 2miγδijδαβΘ(ω, T). | (20) |
The Kronecker deltas mean the random forces acting on different atoms (δij) or with different components (δαβ) are uncorrelated. Θ(ω, T) is the quantum average energy for a harmonic oscillator of frequency ω at temperature T given by
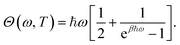 | (21) |
The spectrum I in eqn (20) can also be calculated by means of a Fourier transform of the random force autocorrelation function. Therefore, once I is determined through eqn (20) for the temperature T of interest, by means of the inverse Fourier transform one gets the autocorrelation, and from there it is possible to numerically generate the Gaussian random force necessary to include the quantum thermal statistics into the dynamics.181,182 We notice that through eqn (19)–(21) each vibrational mode is thermalized at an effective temperature to include the zero-point motion.
The first applications of QTB were devoted to reproducing statistical quantum effects in a variety of chemical and condensed-matter problems, including the heat capacity of an MgO crystal and the radial distribution function of nonsuperfluid 4He.179 Later, some models for proton-transfer IR spectroscopy were investigated,183 and power spectra of neon and argon clusters as well as IR spectra of water clusters were reported.184 However, the method suffers from zero-point energy leakage.185 The adaptive quantum thermal bath technique (adQTB) was introduced to mitigate this drawback.186
The adQTB approach employs two frequency-dependent friction coefficients (one for the Langevin equation of motion and one for the fluctuation–dissipation theorem) and deviations from the quantum fluctuation–dissipation theorem are minimized along the QTB trajectory. There is a numerical overhead in using adQTB compared to QTB because the two frictional parameters must be adapted, but this overhead is often affordable even when dealing with large dimensional molecular or condensed phase systems. One shortcoming of QTB simulations, being based on a classical propagation of the dynamics, is the lack of real time coherence and the inability to describe quantum interference. Therefore, in vibrational spectroscopy, QTB methods are expected to miss anharmonicity, especially in approximating quantum combination bands and overtones.
A recent application of adQTB involved the IR (vibro-rotational) spectrum of liquid water.187 In a second study,128 focused on the intensity of bands located at the sum of bending and stretching frequencies and at twice the stretching frequencies of gas-phase water, the advantage of adQTB over previous PIMD results was remarked (even though Benson and Althorpe – basically at the same time – pointed out that through a Matsubara-derived post-multiplication factor QCMD intensities can also be improved177). These studies demonstrated that sampling can play a surprising role in determining the IR intensities in a trajectory-based method. Discrepancies from exact results related to the use of a classical propagator are not always due to the missed real time coherences, since a more accurate description of quantum correlation descending from a better sampling can account for some of the deviations in intensities. However, it still holds that adoption of a classical propagator prevents from a full description of the frequency anharmonicity typical of quantum and experimental combination bands and overtones.
5.2 Quasi-classical trajectory molecular dynamics
A simple way to include a quantum amount of energy into classical molecular dynamics is to start the simulation with initial conditions based on a harmonic quantization of the vibrational energy. This approach, named quasi-classical trajectory or sometimes quasi-classical trajectory molecular dynamics, has largely been adopted for classical scattering studies where the main interest is to predict the product outcome and branching ratios depending on the initial vibrational state excitation.188,189The same setup can be adopted in vibrational studies to calculate the Fourier transform of classical autocorrelation functions. Specifically, the velocity or momentum autocorrelation function is employed to calculate power spectra and get a classical estimate of the density of states. The dipole autocorrelation function is used to calculate IR spectra. For instance, in the case of a power spectrum I(ω)
 | (22) |
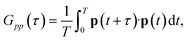 | (23) |
QCT can be employed as a term of comparison by other methods to determine their ability to describe NQEs. A relevant example of this is presented in Fig. 2. Several spectroscopic systems have been investigated by means of QCT, ranging, for instance, from small molecules48 to protonated and neutral water clusters49,194,195 and biomolecules.87,196
A way to increase the accuracy of QCT calculations is by improving the initial conditions by means of the adiabatic switching technique.197–200 The approach is quite similar to the one used in the AS-SCIVR method. The difference between the two approaches lies in the propagation performed after the preliminary adiabatic switching run: in the case of AS SCIVR, the final trajectory propagation is semiclassical and able to describe NQEs including real-time coherences and quantum interferences, while in the case of QCT it is fully classical.
6 Free software available
Table 1 reports on free software associated with the spectroscopic methods reviewed previously.7 Conclusions
We go back to one of the main goals anticipated in the Introduction, which is to provide researchers interested in vibrational spectroscopy with an overview of different computational approaches. We notice that there are several classical trajectory-based methods available for spectroscopy investigations ranging from isolated gas-phase molecules to condensed matter. All of them go beyond classical molecular dynamics and include NQEs even if to different extents.Semiclassical methods, being derived from real-time path integration, naturally describe all kinds of NQEs including those related to real-time quantum propagation, which are neglected by PIMD methods, QTB, and QCT. The computational cost of SC approaches is generally higher, but still affordable (in the few-trajectory versions) for spectroscopy investigations of solvated and condensed phase systems or materials. SC approaches have been developed for both power spectra and IR calculations. PIMD methods and (ad)QTB provide more approximate results, especially when dealing with purely quantum features like combination bands and overtones. However, the quantum thermal statistics is correctly taken into account, zero-point energy leakage avoided, and anharmonicity related to zero-point energy accounted for. QCT is perhaps the most straightforward way to include zero-point energy anharmonicity in molecular dynamics simulations, and it may serve as a preliminary investigation of the main vibrational features of complex systems.
The classical-trajectory-based approaches presented here have the advantage of not requiring any particular treatment or representation of the PES. The PES can be employed as is, in full dimensionality, and, when necessary, also in an “on-the-fly” fashion. This feature makes the reviewed approaches more direct and easy-to-use than other quantum time-independent or time-dependent techniques. All methods calculate the spectra by means of an appropriate Fourier transform. So, even if we have focused on power and IR spectra, generalization to Raman spectroscopy is doable.
The illustrated methods can be sorted hierarchically according to the amount and accuracy of NQEs they are able to describe. All of them are steadily advanced, but some of them have enjoyed more development efforts than others. Classical molecular dynamics by definition misses all NQEs. QCT introduces in an approximate and sensible way anharmonicity effects related to the zero-point energy. PIMD and QTB methods provide an exact or very accurate description of the quantum statistics, but they miss real-time coherences and quantum interferences. Therefore, they are better suited to investigate systems characterized by a mild quantum character. Conversely, the semiclassical methods presented here are able to describe all NQEs, but they are limited to estimate tunneling in the shallow regime. Very recently, two of us presented an evaluation of the quantumness of SC and PIMD methods, demonstrating the predominant quantum character of the former.73 Semiclassical methods are accurate in describing NQEs, well developed, and able to reproduce the spectroscopy of a large range of systems including predominantly quantum ones.
Finally, we briefly mention a different family of promising methods based on the nuclear electronic orbital (NEO) approach.206–208 The NEO approach is a multicomponent quantum chemistry method in which selected nuclei are treated on the same footing as electrons, while the remaining nuclei are treated as classical point charges, as in conventional electronic-structure calculations. Exploiting the same implementation as conventional electronic-structure codes, the NEO approach provides vibronic energy levels for the quantum subsystem composed of protons and electrons, including non-Born–Oppenheimer effects.209–214 NEO methods are very attractive for quantum vibrational spectroscopy as most of the sizeable NQEs are usually related to protons (for instance, tunneling and real-time coherence effects). However, the NEO vibronic energy levels computed with multicomponent quantum chemistry calculations are not directly comparable to vibrational spectroscopy experiments because they are determined for fixed heavy nuclei.215,216 The NEO approach invokes the Born–Oppenheimer separation between the quantum protons and the classical nuclei, and the NEO potential energy surface depends on only the coordinates of the classical nuclei. Consequently, vibrational spectroscopy methods based on the NEO approaches need to account for the feedback between the classical nuclei and the electron-proton quantum subsystem. As far as trajectory methods are concerned, combining the real-time NEO time-dependent density functional theory (RT-NEO) method217 with Ehrenfest dynamics218,219 was shown to be suitable for spectroscopic goals.218,220–222 The RT-NEO method propagates the electronic and protonic densities numerically according to the time-dependent Schrödinger equation. At the same time, the classical nuclei evolve on a mean field potential generated by the proto-electronic wave-function according to classical equations of motion. This is an active field of research, and the new NEO-QCT technique is being developed at the time of writing. A related technique, named constrained NEO (CNEO), has recently been introduced.223,224 The CNEO approach constructs an extended energy surface that depends on the coordinates of the classical nuclei and the position expectation values of the quantum nuclei. The CNEO potential energy surface is obtained by constraining the position expectation value of the quantum nuclear position operator. Since the CNEO potential energy surface has a dimensionality corresponding to that of a conventional electronic surface, a classical MD trajectory can be propagated to calculate the correlation functions required to simulate vibrational spectra.225 In this way, adiabatic dynamics can be adopted with the CNEO approach.In the hierarchical sorting of approaches presented above, the NEO approaches could in principle provide the best NQE description of all reviewed methods. The price for that is the additional computational overhead of the proto-electronic calculations.
We have presented a review of theoretical methods adopted in vibrational spectroscopy and based on the evolution of classical trajectories at best of our knowledge. We apologize for any methodology we may have missed.
Author contributions
Riccardo Conte: conceptualization, writing – original draft and review; Chiara Aieta: conceptualization, writing – original draft and review; Michele Ceotto: conceptualization, writing – original draft and review.Conflicts of interest
The authors declare no conflicts of interest.Abbreviations
| NQEs | Nuclear quantum effects |
| SC | Semiclassical |
| SCIVR | Semiclassical initial value representation |
| MC SCIVR | Multiple coherent semiclassical initial value representation |
| DC SCIVR | Divide-and-conquer semiclassical initial value representation |
| AS SCIVR | Adiabatically switched semiclassical initial value representation |
| SC-IR | Semiclassical infrared |
| eSC-IR | Extended semiclassical infrared |
| PIMD | Path integral molecular dynamics |
| CMD | Centroid molecular dynamics |
| (T)RPMD | (Thermostatted) ring polymer molecular dynamics |
| QCMD | Quasi-centroid molecular dynamics |
| Te PIGS | Temperature-elevated path integral coarse-graining simulations |
| (ad)QTB | (Adaptive) quantum thermal bath |
| QCT | Quasi-classical trajectory |
| NEO | Nuclear-electronic orbital |
| cNEO | Constrained nuclear-electronic orbital |
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Acknowledgements
The authors warmly thank Dr Jia-Xi Zeng for carefully reading the manuscript. C. A. thanks the European Commission for support through a Marie Curie “Global” Fellowship for the project “NEOSC” (G.A. No. 101106284—NEOSC—HORIZON-MSCA-2022-PF-01). M. C. acknowledges financial support from the European Research Council (Grant Agreement No. (647107)—SEMICOMPLEX—ERC-2014-CoG under the European Union's Horizon 2020 and No. 101081361—SEMISOFT—ERC-2022-POC2 under Horizon Europe research and innovation programme).Notes and references
- H. J. Byrne, F. Bonnier, A. Casey, M. Maher, J. McIntyre, E. Efeoglu and Z. Farhane, Appl. Opt., 2018, 57, E11–E19 CrossRef CAS PubMed.
- N. M. Ralbovsky and I. K. Lednev, Chem. Soc. Rev., 2020, 49, 7428–7453 Search PubMed.
- Z. Farhane, F. Bonnier, A. Casey and H. J. Byrne, Analyst, 2015, 140, 4212–4223 RSC.
- M. Casella, A. Lucotti, M. Tommasini, M. Bedoni, E. Forvi, F. Gramatica and G. Zerbi, Spectrochim. Acta, Part A Mol. Biomol. Spectrosc., 2011, 79, 915–919 CrossRef CAS PubMed.
- A. Gualerzi, S. Niada, C. Giannasi, S. Picciolini, C. Morasso, R. Vanna, V. Rossella, M. Masserini, M. Bedoni and F. Ciceri, et al., Sci. Rep., 2017, 7, 9820 Search PubMed.
- M. J. Baker, H. J. Byrne, J. Chalmers, P. Gardner, R. Goodacre, A. Henderson, S. G. Kazarian, F. L. Martin, J. Moger and N. Stone, et al., Analyst, 2018, 143, 1735–1757 Search PubMed.
- A. Gualerzi, S. A. A. Kooijmans, S. Niada, S. Picciolini, A. T. Brini, G. Camussi and M. Bedoni, J. Extracell. Vesicles, 2019, 8, 1568780 Search PubMed.
- K. R. Richert-Pöggeler, K. Franzke, K. Hipp and R. G. Kleespies, Front. Microbiol., 2019, 9, 3255 Search PubMed.
- A. Milewska, J. Ner-Kluza, A. Dabrowska, A. Bodzon-Kulakowska, K. Pyrc and P. Suder, Mass Spectrom. Rev., 2020, 39, 499–522 Search PubMed.
- K. Hartman, P. McDonald-Ordzie, J. Kaper, B. Prescott and G. Thomas Jr, Biochemistry, 1978, 17, 2118–2123 Search PubMed.
- V. Erukhimovitch, I. Mukmanov, M. Talyshinsky, Y. Souprun and M. Huleihel, Spectrochim. Acta, Part A Mol. Biomol. Spectrosc., 2004, 60, 2355–2361 Search PubMed.
- M. Huleihel, V. Erukhimovitch, M. Talyshinsky and M. Karpasas, Appl. Spectrosc., 2002, 56, 640–645 Search PubMed.
- J. Saade, M. T. T. Pacheco, M. R. Rodrigues and L. Silveira Jr, J. Spectrosc., 2008, 22, 387–395 Search PubMed.
- S. Khan, R. Ullah, A. Khan, N. Wahab, M. Bilal and M. Ahmed, Biomed. Opt. Express, 2016, 7, 2249–2256 Search PubMed.
- S. Roy, D. Perez-Guaita, S. Bowden, P. Heraud and B. R. Wood, Clinical Spectroscopy, 2019, 1, 100001 CrossRef.
- B. Sharma, R. R. Frontiera, A.-I. Henry, E. Ringe and R. P. Van Duyne, Mater. Today, 2012, 15, 16–25 Search PubMed.
- M. Fleischmann, P. J. Hendra and A. J. McQuillan, Chem. Phys. Lett., 1974, 26, 163–166 Search PubMed.
- M. Y. Sha, H. Xu, M. J. Natan and R. Cromer, J. Am. Chem. Soc., 2008, 130, 17214–17215 Search PubMed.
- J.-H. An, W. A. El-Said, C.-H. Yea, T.-H. Kim and J.-W. Choi, J. Nanosci. Nanotechnol., 2011, 11, 4424–4429 CrossRef CAS PubMed.
- H. T. Beier, C. B. Cowan, I.-H. Chou, J. Pallikal, J. E. Henry, M. E. Benford, J. B. Jackson, T. A. Good and G. L. Coté, Plasmonics, 2007, 2, 55–64 CrossRef CAS.
- A. H. Flood, J. F. Stoddart, D. W. Steuerman and J. R. Heath, Science, 2004, 306, 2055–2056 Search PubMed.
- C. L. Brosseau, F. Casadio and R. P. Van Duyne, J. Raman Spectrosc., 2011, 42, 1305–1310 Search PubMed.
- A. N. Egorochkin, O. V. Kuznetsova, N. M. Khamaletdinova and L. G. Domratcheva-Lvova, J. Organomet. Chem., 2011, 696, 2199–2205 Search PubMed.
- C. Fecko, J. Eaves, J. Loparo, A. Tokmakoff and P. Geissler, Science, 2003, 301, 1698–1702 Search PubMed.
- B. Auer, R. Kumar, J. Schmidt and J. Skinner, Proc. Natl. Acad. Sci., 2007, 104, 14215–14220 CrossRef CAS PubMed.
- P. O. Dral, A. Owens, S. N. Yurchenko and W. Thiel, J. Chem. Phys., 2017, 146, 244108 Search PubMed.
- A. P. Bartok, S. De, C. Poelking, N. Bernstein, J. R. Kermode, G. Csanyi and M. Ceriotti, Sci. Adv., 2017, 3, e1701816 Search PubMed.
- W. Fu and W. S. Hopkins, J. Phys. Chem. A, 2018, 122, 167–171 Search PubMed.
- K. T. Schütt, H. E. Sauceda, P.-J. Kindermans, A. Tkatchenko and K.-R. Müller, J. Chem. Phys., 2018, 148, 241722 Search PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 Search PubMed.
- P. Schienbein, J. Chem. Theory Comput., 2023, 19, 705–712 Search PubMed.
- R. P. Feynman, Rev. Mod. Phys., 1948, 20, 367 CrossRef.
- F. Grossmann and A. L. Xavier, Phys. Lett. A, 1998, 243, 243–248 CrossRef CAS.
- W. H. Miller, Mol. Phys., 2002, 100, 397–400 CrossRef CAS.
- M. F. Herman and E. Kluk, Chem. Phys., 1984, 91, 27–34 CrossRef CAS.
- R. P. Feynman and A. R. Hibbs, Quantum mechanics and path integrals, McGraw-Hill, 1965 Search PubMed.
- D. Marx and M. Parrinello, Z. Phys. B, 1994, 95, 143–144 CrossRef CAS.
- D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077–4082 CrossRef CAS.
- M. E. Tuckerman, D. Marx, M. L. Klein and M. Parrinello, J. Chem. Phys., 1996, 104, 5579–5588 Search PubMed.
- J. Cao and G. A. Voth, J. Chem. Phys., 1994, 100, 5106–5117 Search PubMed.
- I. R. Craig and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, 3368–3373 CrossRef CAS PubMed.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586 CrossRef.
- D. A. McQuarrie, Statistical Mechanics, Harper-Collins, 1976 Search PubMed.
- X. Sun, H. Wang and W. H. Miller, J. Chem. Phys., 1998, 109, 4190–4200 CrossRef CAS.
- S. C. Althorpe, Annu. Rev. Phys. Chem., 2024, 75, 397–420 CrossRef CAS PubMed.
- T. Matsubara, Progr. Theor. Phys., 1955, 14, 351–378 CrossRef.
- T. J. Hele, M. J. Willatt, A. Muolo and S. C. Althorpe, J. Chem. Phys., 2015, 142, 191101 CrossRef PubMed.
- R. Conte, C. Aieta, G. Botti, M. Cazzaniga, M. Gandolfi, C. Lanzi, G. Mandelli, D. Moscato and M. Ceotto, Theor. Chem. Acc., 2023, 142, 53 Search PubMed.
- C. Qu and J. M. Bowman, J. Phys. Chem. Lett., 2018, 9, 2604–2610 Search PubMed.
- W. H. Miller, J. Chem. Phys., 1970, 53, 3578–3587 Search PubMed.
- A. L. Kaledin and W. H. Miller, J. Chem. Phys., 2003, 118, 7174–7182 CrossRef CAS.
- A. L. Kaledin and W. H. Miller, J. Chem. Phys., 2003, 119, 3078–3084 Search PubMed.
- D. V. Shalashilin and M. S. Child, J. Chem. Phys., 2001, 115, 5367–5375 Search PubMed.
- M. Child and D. Shalashilin, J. Chem. Phys., 2003, 118, 2061–2071 CrossRef CAS.
- D. V. Shalashilin and M. S. Child, Chem. Phys., 2004, 304, 103–120 CrossRef CAS.
- E. J. Heller, J. Chem. Phys., 1975, 62, 1544–1555 CrossRef CAS.
- H. Wu, M. Rahman, J. Wang, U. Louderaj, W. Hase and Y. Zhuang, J. Chem. Phys., 2010, 133, 074101 CrossRef CAS PubMed.
- M. Ceotto, Y. Zhuang and W. L. Hase, J. Chem. Phys., 2013, 138, 054116 CrossRef PubMed.
- R. Conte, F. Gabas, G. Botti, Y. Zhuang and M. Ceotto, J. Chem. Phys., 2019, 150, 244118 CrossRef PubMed.
- T. Begusic, M. Cordova and J. Vanicek, J. Chem. Phys., 2019, 150, 154117 CrossRef PubMed.
- M. Cazzaniga, M. Micciarelli, F. Moriggi, A. Mahmoud, F. Gabas and M. Ceotto, J. Chem. Phys., 2020, 152, 104104 CrossRef CAS PubMed.
- M. Gandolfi and M. Ceotto, J. Chem. Theory Comput., 2021, 17, 6733–6746 CrossRef CAS PubMed.
- M. Ceotto, G. Di Liberto and R. Conte, Phys. Rev. Lett., 2017, 119, 010401 CrossRef PubMed.
- M. Ceotto, S. Atahan, G. F. Tantardini and A. Aspuru-Guzik, J. Chem. Phys., 2009, 130, 234113 CrossRef PubMed.
- M. Ceotto, S. Atahan, S. Shim, G. F. Tantardini and A. Aspuru-Guzik, Phys. Chem. Chem. Phys., 2009, 11, 3861–3867 RSC.
- M. Ceotto, D. Dell'Angelo and G. F. Tantardini, J. Chem. Phys., 2010, 133, 054701 Search PubMed.
- M. Ceotto, S. Valleau, G. F. Tantardini and A. Aspuru-Guzik, J. Chem. Phys., 2011, 134, 234103 Search PubMed.
- R. Conte, A. Aspuru-Guzik and M. Ceotto, J. Phys. Chem. Lett., 2013, 4, 3407–3412 Search PubMed.
- A. Masson, E. R. Williams and T. R. Rizzo, J. Chem. Phys., 2015, 143, 104313 Search PubMed.
- F. Gabas, G. Di Liberto, R. Conte and M. Ceotto, Chem. Sci., 2018, 9, 7894–7901 RSC.
- G. Di Liberto, R. Conte and M. Ceotto, J. Chem. Phys., 2018, 148, 014307 Search PubMed.
- M. Gandolfi, A. Rognoni, C. Aieta, R. Conte and M. Ceotto, J. Chem. Phys., 2020, 153, 204104 Search PubMed.
- J.-X. Zeng, R. Conte and M. Ceotto, J. Chem. Phys., 2025, 163, 194114 Search PubMed.
- A. Rognoni, R. Conte and M. Ceotto, Chem. Sci., 2021, 12, 2060–2064 Search PubMed.
- D. Ben-Amotz, J. Am. Chem. Soc., 2019, 141, 10569–10580 Search PubMed.
- L. Beyere, P. Arboleda, V. Monga and G. Loppnow, Can. J. Chem., 2004, 82, 1092–1101 Search PubMed.
- F. Gabas, R. Conte and M. Ceotto, J. Phys. Chem. Lett., 2022, 13, 1350–1355 Search PubMed.
- D. Moscato, G. Mandelli, M. Bondanza, F. Lipparini, R. Conte, B. Mennucci and M. Ceotto, J. Am. Chem. Soc., 2024, 146, 8179–8188 CrossRef CAS PubMed.
- M. Cazzaniga, M. Micciarelli, F. Gabas, F. Finocchi and M. Ceotto, J. Phys. Chem. C, 2022, 126, 12060–12073 Search PubMed.
- L. Mino, M. Cazzaniga, F. Moriggi and M. Ceotto, J. Phys. Chem. C, 2023, 127, 437–499 CrossRef CAS PubMed.
- E. Fallacara, F. Finocchi, M. Cazzaniga, S. Chenot, S. Stankic and M. Ceotto, Angew. Chem., Int. Ed., 2024, 63, e202409523 CrossRef CAS PubMed.
- R. Conte, C. Aieta, M. Cazzaniga and M. Ceotto, J. Phys. Chem. Lett., 2024, 15, 7566–7576 Search PubMed.
- R. Conte, G. Mandelli, G. Botti, D. Moscato, C. Lanzi, M. Cazzaniga, C. Aieta and M. Ceotto, Chem. Sci., 2025, 16, 20–28 Search PubMed.
- A. Nandi, R. Conte, P. Pandey, P. L. Houston, C. Qu, Q. Yu and J. M. Bowman, J. Chem. Theory Comput., 2025, 21, 5208–5220 CrossRef CAS PubMed.
- R. Conte and M. Ceotto, in Quantum Chemistry and Dynamics of Excited States: Methods and Applications, John Wiley & Sons, 2021 Search PubMed.
- R. Conte, M. Ceotto, et al., in Vibrational Dynamics of Molecules, Wiley, 2022, pp. 378–415 Search PubMed.
- D. Moscato, F. Gabas, R. Conte and M. Ceotto, J. Biomol. Struct. Dyn., 2023, 41, 14248–14258 CrossRef CAS PubMed.
- C. Lanzi, C. Aieta, M. Ceotto and R. Conte, J. Chem. Phys., 2024, 160, 214107 Search PubMed.
- C. Lanzi, C. Aieta, M. Ceotto and R. Conte, J. Chem. Phys., 2025, 163, 024122 CrossRef CAS PubMed.
- M. Micciarelli, R. Conte, J. Suarez and M. Ceotto, J. Chem. Phys., 2018, 149, 064115 CrossRef PubMed.
- C. Aieta, M. Micciarelli, G. Bertaina and M. Ceotto, Nat. Commun., 2020, 11, 4384 CrossRef PubMed.
- C. Aieta, G. Bertaina, M. Micciarelli and M. Ceotto, J. Chem. Phys., 2020, 153, 214117 Search PubMed.
- M. Micciarelli, F. Gabas, R. Conte and M. Ceotto, J. Chem. Phys., 2019, 150, 184113 Search PubMed.
- E. J. Heller, Acc. Chem. Res., 1981, 14, 368–375 CrossRef CAS.
- M. Wehrle, M. Sulc and J. Vanicek, J. Chem. Phys., 2014, 140, 244114 CrossRef PubMed.
- A. Patoz, T. Begusic and J. Vanicek, J. Phys. Chem. Lett., 2018, 9, 2367–2372 CrossRef CAS PubMed.
- C. S. Reddy and M. D. Prasad, J. Phys. Chem. A, 2016, 120, 2583–2590 CrossRef CAS PubMed.
- T. Begušić and J. Vaníček, J. Chem. Phys., 2020, 153, 024105 CrossRef PubMed.
- K. Polley and R. F. Loring, J. Chem. Phys., 2022, 156, 124108 Search PubMed.
- A. Scheidegger and J. J. Vaníček, arXiv, 2025, preprint, arXiv:2504.05922, DOI:10.48550/arXiv.2504.05922.
- T. Begušić and J. Vaníček, J. Phys. Chem. Lett., 2021, 12, 2997–3005 CrossRef PubMed.
- H.-D. Meyer and W. H. Miller, J. Chem. Phys., 1979, 70, 3214–3223 Search PubMed.
- M. F. Herman, J. Chem. Phys., 1995, 103, 8081–8097 CrossRef CAS.
- G. Stock and M. Thoss, Phys. Rev. Lett., 1997, 78, 578 CrossRef CAS.
- M. Thoss and G. Stock, Phys. Rev. A, 1999, 59, 64 CrossRef CAS.
- N. Ananth, C. Venkataraman and W. H. Miller, J. Chem. Phys., 2007, 127, 084114 CrossRef PubMed.
- N. Ananth, J. Chem. Phys., 2013, 139, 124102 Search PubMed.
- M. S. Church, T. J. H. Hele, G. S. Ezra and N. Ananth, J. Chem. Phys., 2018, 148, 102326 CrossRef PubMed.
- M. S. Church and N. Ananth, J. Chem. Phys., 2019, 151, 134109 CrossRef PubMed.
- S. Malpathak, M. S. Church and N. Ananth, J. Phys. Chem. A, 2022, 126, 6359–6375 CrossRef CAS PubMed.
- T. Zimmermann and J. Vaníček, J. Chem. Phys., 2014, 141, 134102 CrossRef PubMed.
- S. Choi and J. Vaníček, J. Chem. Phys., 2021, 155, 124104 CrossRef CAS PubMed.
- D. Moscato, M. Gandolfi and M. Ceotto, J. Chem. Phys., 2025, 162, 234108 CrossRef CAS PubMed.
- V. M. Freixas, A. J. White, T. Nelson, H. Song, D. V. Makhov, D. Shalashilin, S. Fernandez-Alberti and S. Tretiak, J. Phys. Chem. Lett., 2021, 12, 2970–2982 CrossRef CAS PubMed.
- V. M. Freixas, W. Malone, X. Li, H. Song, H. Negrin-Yuvero, R. Pérez-Castillo, A. White, T. R. Gibson, D. V. Makhov and D. V. Shalashilin, et al., J. Chem. Theory Comput., 2023, 19, 5356–5368 CrossRef CAS PubMed.
- S. V. Antipov, F. Kröninger and J. J. Vaníček, J. Chem. Phys., 2025, 163, 154107 CrossRef CAS PubMed.
- F. Grossmann, J. Chem. Phys., 2006, 125, 014111 CrossRef PubMed.
- M. Buchholz, F. Grossmann and M. Ceotto, J. Chem. Phys., 2016, 144, 094102 CrossRef PubMed.
- M. Buchholz, F. Grossmann and M. Ceotto, J. Chem. Phys., 2017, 147, 164110 CrossRef PubMed.
- M. Buchholz, F. Grossmann and M. Ceotto, J. Chem. Phys., 2018, 148, 114107 CrossRef PubMed.
- X. Sun, H. Wang and W. H. Miller, J. Chem. Phys., 1998, 109, 7064–7074 CrossRef CAS.
- J. A. Poulsen, G. Nyman and P. J. Rossky, J. Chem. Phys., 2003, 119, 12179–12193 CrossRef CAS.
- J. Liu and W. H. Miller, J. Chem. Phys., 2007, 127, 114506 CrossRef PubMed.
- J. Liu and W. H. Miller, J. Chem. Phys., 2008, 128, 144511 CrossRef PubMed.
- J. Liu, Int. J. Quantum Chem., 2015, 115, 657–670 CrossRef CAS.
- J. A. Poulsen and G. Nyman, Entropy, 2025, 27, 702 CrossRef CAS PubMed.
- F. Grossmann, Phys. Scr., 2016, 91, 044004 CrossRef.
- T. Plé, S. Huppert, F. Finocchi, P. Depondt and S. Bonella, J. Chem. Phys., 2021, 155, 104108 Search PubMed.
- M. Bonfanti, J. Petersen, P. Eisenbrandt, I. Burghardt and E. Pollak, J. Chem. Theory Comput., 2018, 14, 5310–5323 CrossRef CAS PubMed.
- G. Bertaina, G. Di Liberto and M. Ceotto, J. Chem. Phys., 2019, 151, 114307 CrossRef CAS PubMed.
- F. Gabas, R. Conte and M. Ceotto, J. Chem. Theory Comput., 2017, 13, 2378 CrossRef CAS PubMed.
- R. Conte, L. Parma, C. Aieta, A. Rognoni and M. Ceotto, J. Chem. Phys., 2019, 151, 214107 CrossRef PubMed.
- G. Botti, M. Ceotto and R. Conte, J. Chem. Phys., 2021, 155, 234102 CrossRef CAS PubMed.
- G. Botti, C. Aieta and R. Conte, J. Chem. Phys., 2022, 156, 164303 CrossRef CAS PubMed.
- R. Conte, A. Nandi, C. Qu, Q. Yu, P. L. Houston and J. M. Bowman, J. Phys. Chem. A, 2022, 126, 7709–7718 CrossRef CAS PubMed.
- A. Nandi, R. Conte, C. Qu, P. L. Houston, Q. Yu and J. M. Bowman, J. Chem. Theory Comput., 2022, 18, 5527–5538 CrossRef CAS PubMed.
- K. G. Kay, Chem. Phys., 2006, 322, 3–12 CrossRef CAS.
- S. Zhang and E. Pollak, J. Chem. Phys., 2003, 119, 11058–11063 CrossRef CAS.
- E. Pollak, in The Semiclassical Initial Value Series Representation of the Quantum Propagator, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp. 259–271 Search PubMed.
- R. Conte and E. Pollak, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 036704 CrossRef PubMed.
- J.-X. Zeng, S. Yang, Y.-C. Zhu, W. Fang, L. Jiang, E.-G. Wang, D. H. Zhang and X.-Z. Li, J. Phys. Chem. A, 2023, 127, 2902–2911 CrossRef CAS PubMed.
- J.-X. Zeng and X.-Z. Li, Computational Materials Today, 2025, 6, 100032 CrossRef.
- M. Tsumura and Y. Kurashige, J. Chem. Theory Comput., 2025, 21, 11401–11414 Search PubMed.
- O. Marsalek and T. E. Markland, J. Phys. Chem. Lett., 2017, 8, 1545–1551 CrossRef CAS PubMed.
- C. John, T. Spura, S. Habershon and T. D. Kühne, Phys. Rev. E, 2016, 93, 043305 CrossRef PubMed.
- V. Kapil, D. P. Kovács, G. Csányi and A. Michaelides, Faraday Discuss., 2024, 249, 50–68 RSC.
- M. Ceriotti, M. Parrinello, T. E. Markland and D. E. Manolopoulos, J. Chem. Phys., 2010, 133, 124104 Search PubMed.
- M. Ceriotti and D. E. Manolopoulos, Phys. Rev. Lett., 2012, 109, 100604 CrossRef PubMed.
- Q. Shi and E. Geva, J. Chem. Phys., 2003, 118, 8173–8184 CrossRef CAS.
- G. Trenins and S. C. Althorpe, J. Chem. Phys., 2018, 149, 014102 CrossRef PubMed.
- A. Prada, E. S. Pós and S. C. Althorpe, J. Chem. Phys., 2023, 158, 114106 CrossRef CAS PubMed.
- J. Cao and G. A. Voth, J. Chem. Phys., 1996, 104, 273–285 CrossRef CAS.
- J. Cao and G. J. Martyna, J. Chem. Phys., 1996, 104, 2028–2035 Search PubMed.
- D. Marx, M. E. Tuckerman and G. J. Martyna, Comput. Phys. Commun., 1999, 118, 166–184 Search PubMed.
- T. D. Hone, P. J. Rossky and G. A. Voth, J. Chem. Phys., 2006, 124, 154103 Search PubMed.
- A. Pérez, M. E. Tuckerman and M. H. Müser, J. Chem. Phys., 2009, 130, 184105 Search PubMed.
- F. Paesani, S. S. Xantheas and G. A. Voth, J. Phys. Chem. B, 2009, 113, 13118–13130 CrossRef CAS PubMed.
- G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2015, 11, 1145–1154 CrossRef CAS PubMed.
- T. Ikeda, J. Chem. Phys., 2018, 148, 102332 CrossRef PubMed.
- S. D. Ivanov, A. Witt and D. Marx, Phys. Chem. Chem. Phys., 2013, 15, 10270–10299 RSC.
- M. Rossi, M. Ceriotti and D. E. Manolopoulos, J. Chem. Phys., 2014, 140, 234116 CrossRef PubMed.
- M. Rossi, V. Kapil and M. Ceriotti, J. Chem. Phys., 2018, 148, 102301 CrossRef PubMed.
- M. Arandhara and S. G. Ramesh, Phys. Chem. Chem. Phys., 2024, 26, 19529–19542 RSC.
- T. Begušić, X. Tao, G. A. Blake and T. F. Miller, J. Chem. Phys., 2022, 156, 131102 CrossRef PubMed.
- Z. Tong, P. E. Videla, K. A. Jung, V. S. Batista and X. Sun, J. Chem. Phys., 2020, 153, 034117 CrossRef CAS PubMed.
- A. Kaczmarek, M. Shiga and D. Marx, J. Phys. Chem. A, 2009, 113, 1985–1994 CrossRef CAS PubMed.
- A. Witt, S. D. Ivanov, M. Shiga, H. Forbert and D. Marx, J. Chem. Phys., 2009, 130, 194510 CrossRef PubMed.
- G. Trenins, M. J. Willatt and S. C. Althorpe, J. Chem. Phys., 2019, 151, 054109 CrossRef.
- S. D. Ivanov, A. Witt, M. Shiga and D. Marx, J. Chem. Phys., 2010, 132, 031101 CrossRef PubMed.
- T. Fletcher, A. Zhu, J. E. Lawrence and D. E. Manolopoulos, J. Chem. Phys., 2021, 155, 231101 CrossRef CAS PubMed.
- J. E. Lawrence, A. Z. Lieberherr, T. Fletcher and D. E. Manolopoulos, J. Phys. Chem. B, 2023, 127, 9172–9180 CrossRef CAS PubMed.
- A. Z. Lieberherr, S. T. Furniss, J. E. Lawrence and D. E. Manolopoulos, J. Chem. Phys., 2023, 158, 234106 CrossRef CAS PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS PubMed.
- F. Musil, I. Zaporozhets, F. Noé, C. Clementi and V. Kapil, J. Chem. Phys., 2022, 157, 181102 CrossRef CAS PubMed.
- J. Wang, S. Olsson, C. Wehmeyer, A. Pérez, N. E. Charron, G. De Fabritiis, F. Noé and C. Clementi, ACS Cent. Sci., 2019, 5, 755–767 CrossRef CAS PubMed.
- J. Castro, G. Trenins, V. Kapil and M. Rossi, J. Chem. Phys., 2025, 163, 204102 CrossRef CAS PubMed.
- R. L. Benson and S. C. Althorpe, J. Chem. Phys., 2021, 155, 104107 CrossRef CAS PubMed.
- D. K. Limbu, N. London, M. O. Faruque and M. R. Momeni, J. Chem. Phys., 2025, 162, 014111 CrossRef CAS PubMed.
- H. Dammak, Y. Chalopin, M. Laroche, M. Hayoun and J.-J. Greffet, Phys. Rev. Lett., 2009, 103, 190601 CrossRef PubMed.
- H. B. Callen and T. A. Welton, Phys. Rev., 1951, 83, 34 CrossRef.
- A. Maradudin, T. Michel, A. McGurn and E. Méndez, Ann. Phys., 1990, 203, 255–307 CAS.
- B. Leimkuhler and C. Matthews, Appl. Math. Res. eXpress, 2013, 2013, 34–56 Search PubMed.
- M. Basire, D. Borgis and R. Vuilleumier, Phys. Chem. Chem. Phys., 2013, 15, 12591–12601 RSC.
- J. Hernández-Rojas, F. Calvo and E. G. Noya, J. Chem. Theory Comput., 2015, 11, 861–870 CrossRef PubMed.
- F. Brieuc, Y. Bronstein, H. Dammak, P. Depondt, F. Finocchi and M. Hayoun, J. Chem. Theory Comput., 2016, 12, 5688–5697 CrossRef CAS PubMed.
- E. Mangaud, S. Huppert, T. Plé, P. Depondt, S. Bonella and F. Finocchi, J. Chem. Theory Comput., 2019, 15, 2863–2880 CrossRef CAS PubMed.
- N. Mauger, T. Plé, L. Lagardère, S. Bonella, E. Mangaud, J.-P. Piquemal and S. Huppert, J. Phys. Chem. Lett., 2021, 12, 8285–8291 CrossRef CAS PubMed.
- C. Chen, B. Braams, D. Y. Lee, J. M. Bowman, P. L. Houston and D. Stranges, J. Phys. Chem. A, 2011, 115, 6797–6804 CrossRef CAS PubMed.
- A. W. Jasper, J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2013, 117, 12243–12255 CrossRef CAS PubMed.
- L. Da-hong and W. L. Hase, J. Chem. Phys., 1988, 89, 6723–6735 CrossRef.
- W. H. Miller, W. L. Hase and C. L. Darling, J. Chem. Phys., 1989, 91, 2863–2868 CrossRef CAS.
- G. Czakó, A. L. Kaledin and J. M. Bowman, J. Chem. Phys., 2010, 132, 164103 CrossRef PubMed.
- Z. Jiang, L. Zhang, L. Bonnet, D. Yang and B. Jiang, J. Chem. Phys., 2025, 163, 014706 CrossRef CAS PubMed.
- N.-T. Van-Oanh, C. Falvo, F. Calvo, D. Lauvergnat, M. Basire, M.-P. Gaigeot and P. Parneix, Phys. Chem. Chem. Phys., 2012, 14, 2381–2390 RSC.
- D. Barbiero, G. Bertaina, M. Ceotto and R. Conte, J. Phys. Chem. A, 2023, 127, 6213–6221 CrossRef CAS PubMed.
- G. Botti, M. Ceotto and R. Conte, J. Phys. Chem. Lett., 2023, 14, 8940–8947 CrossRef CAS PubMed.
- E. A. Solovev, Zh. Eksp. Teor. Fiz., 1978, 75, 1261–1268 Search PubMed.
- R. T. Skodje, F. Borondo and W. P. Reinhardt, J. Chem. Phys., 1985, 82, 4611–4632 CrossRef CAS.
- B. R. Johnson, J. Chem. Phys., 1985, 83, 1204–1217 CrossRef CAS.
- C. Qu and J. M. Bowman, J. Phys. Chem. A, 2016, 120, 4988–4993 CrossRef CAS PubMed.
- M. Ceriotti, J. More and D. E. Manolopoulos, Comput. Phys. Commun., 2014, 185, 1019–1026 CrossRef CAS.
- Y. Litman, V. Kapil, Y. M. Y. Feldman, D. Tisi, T. Begušić, K. Fidanyan, G. Fraux, J. Higer, M. Kellner, T. E. Li, E. S. Pós, E. Stocco, G. Trenins, B. Hirshberg, M. Rossi and M. Ceriotti, J. Chem. Phys., 2024, 161, 062504 CrossRef CAS PubMed.
- M. Ceriotti, M. Rossi, V. Kapil, Y. Litman, et al., i-Pi code, 2024, https://ipi-code.org/, accessed on September 27, 2025 Search PubMed.
- R. Conte, M. Gandolfi, D. Moscato, C. Aieta, S. Valtolina and M. Ceotto, J. Comput. Chem., 2025, 46, e70118 CrossRef CAS PubMed.
- M. Gandolfi, D. Moscato, C. Aieta, M. Pindaro, E. Campana, S. Valtolina and M. Ceotto, A web platform for time averaged Fourier transform of autocorrelated data, 2024, http://semisoft.unimi.it/, accessed on September 25, 2025 Search PubMed.
- S. P. Webb, T. Iordanov and S. Hammes-Schiffer, J. Chem. Phys., 2002, 117, 4106–4118 CrossRef CAS.
- F. Pavošević, T. Culpitt and S. Hammes-Schiffer, Chem. Rev., 2020, 120, 4222–4253 CrossRef PubMed.
- S. Hammes-Schiffer, J. Chem. Phys., 2021, 155, 030901 CrossRef CAS PubMed.
- M. V. Pak, A. Chakraborty and S. Hammes-Schiffer, J. Phys. Chem. A, 2007, 111, 4522–4526 CrossRef CAS PubMed.
- K. R. Brorsen, Y. Yang and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2017, 8, 3488–3493 CrossRef CAS PubMed.
- F. Pavošević, T. Culpitt and S. Hammes-Schiffer, J. Chem. Theory Comput., 2018, 15, 338–347 CrossRef PubMed.
- T. Culpitt, Y. Yang, F. Pavošević, Z. Tao and S. Hammes-Schiffer, J. Chem. Phys., 2019, 150, 201101 CrossRef PubMed.
- C. L. Malbon and S. Hammes-Schiffer, J. Chem. Theory Comput., 2025, 21, 3968–3980 CrossRef CAS PubMed.
- R. J. Stein, C. L. Malbon and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2025, 16, 7718–7724 Search PubMed.
- Y. Yang, T. Culpitt and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2018, 9, 1765–1770 CrossRef CAS PubMed.
- S. M. Garner, S. Upadhyay, X. Li and S. Hammes-Schiffer, J. Phys. Chem. Lett., 2024, 15, 6017–6023 CrossRef CAS PubMed.
- L. Zhao, Z. Tao, F. Pavošević, A. Wildman, S. Hammes-Schiffer and X. Li, J. Phys. Chem. Lett., 2020, 11, 4052–4058 CrossRef CAS PubMed.
- L. Zhao, A. Wildman, Z. Tao, P. Schneider, S. Hammes-Schiffer and X. Li, J. Chem. Phys., 2020, 153, 224111 CrossRef CAS PubMed.
- L. Zhao, A. Wildman, F. Pavošević, J. C. Tully, S. Hammes-Schiffer and X. Li, J. Phys. Chem. Lett., 2021, 12, 3497–3502 CrossRef CAS PubMed.
- D. B. Williams-Young, A. Petrone, S. Sun, T. F. Stetina, P. Lestrange, C. E. Hoyer, D. R. Nascimento, L. Koulias, A. Wildman and J. Kasper, et al., Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1436 CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. Lee Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- J. C. Tully, Chem. Phys. Lett., 2023, 816, 140396 CrossRef CAS.
- X. Xu and Y. Yang, J. Chem. Phys., 2020, 152, 084107 CrossRef CAS PubMed.
- X. Xu and Y. Yang, J. Chem. Phys., 2020, 153, 074106 CrossRef CAS PubMed.
- Z. Chen and Y. Yang, J. Phys. Chem. Lett., 2023, 14, 279–286 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2026 |