Accessing metal-specific orbital interactions in C–H activation with resonant inelastic X-ray scattering

Abstract

Photochemically prepared transition-metal complexes are known to be effective at cleaving the strong C–H bonds of organic molecules in room temperature solutions. There is also ample theoretical evidence that the two-way, metal to ligand (MLCT) and ligand to metal (LMCT), charge-transfer between an incoming alkane C–H group and the transition metal is the decisive interaction in the C–H activation reaction. What is missing, however, are experimental methods to directly probe these interactions in order to reveal what determines reactivity of intermediates and the rate of the reaction. Here, using quantum chemical simulations we predict and propose future time-resolved valence-to-core resonant inelastic X-ray scattering (VtC-RIXS) experiments at the transition metal L-edge as a method to provide a full account of the evolution of metal–alkane interactions during transition-metal mediated C–H activation reactions. For the model system cyclopentadienyl rhodium dicarbonyl (CpRh(CO)₂), we demonstrate, by simulating the VtC-RIXS signatures of key intermediates in the C–H activation pathway, how the Rh-centered valence-excited states accessible through VtC-RIXS directly reflect changes in donation and back-donation between the alkane C–H group and the transition metal as the reaction proceeds via those intermediates. We benchmark and validate our quantum chemical simulations against experimental steady-state measurements of CpRh(CO)₂ and Rh(acac)(CO)₂ (where acac is acetylacetonate). Our study constitutes the first step towards establishing VtC-RIXS as a new experimental observable for probing reactivity of C–H activation reactions. More generally, the study further motivates the use of time-resolved VtC-RIXS to follow the valence electronic structure evolution along photochemical, photoinitiated and photocatalytic reactions with transition metal complexes.

---

Introduction

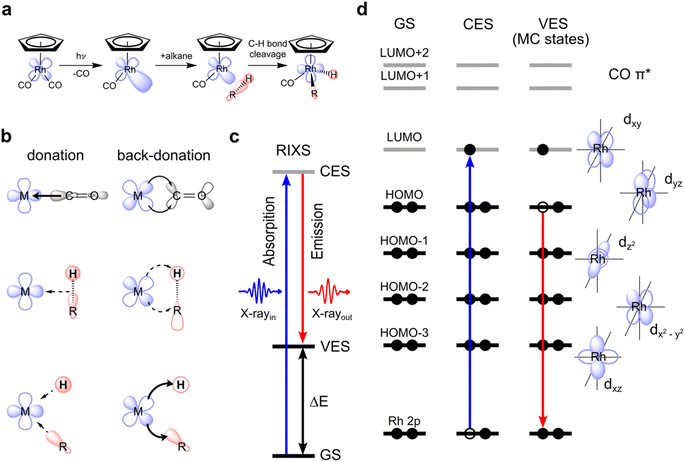
Carbon–hydrogen (C–H) bonds are among the strongest chemical linkages in nature and thus inherently unreactive. Still, manipulating carbon–hydrogen bonds holds the key to numerous molecular transformations that are essential in organic and metal–organic synthesis within the context of “green chemistry”, the design of new pharmaceuticals or the transformation of low molecular weight hydrocarbons to high energy density liquid fuels.¹ However, since C–H bonds lack considerable polarity, their manipulation via activation and functionalization is challenging due to significant energy barriers needed to be overcome under ambient conditions. One way of activating C–H bonds is using photo-triggered transition metal complexes.^2,3 Photochemical C–H activation with transition metal complexes involves the dissociation of one or several ligands from the photo-excited transition metal complex in a room-temperature solution to generate a low-valent reactive metal center that then facilitates C–H bond cleavage in alkanes from solution. The most common metal complexes effectuating photoinitiated C–H activation are second or third row transition metal carbonyls and dihydrides, where the loss of a carbonyl or dihydride ligand creates a reactive metal center. The open coordination site at the metal then enables the binding of an alkane to form a so-called σ-alkane complex followed by subsequent C–H bond cleavage in an oxidative addition step by insertion of the metal into the C–H bond. Apart from this photoinduced C–H activation, there are numerous examples of C–H activation by transition-metal complexes which are not photoinitiated.^4–6 Often, they involve so-called “agostic interactions”,⁷ a considerably different way of facilitating the breaking of the C–H bond compared to the metal–alkane interactions in a σ-complex.⁸

Still, the various mechanisms of C–H activation by transition-metal complexes, be they photoinduced or not, can in fact be generally related to specific charge-transfer interactions between the metal d and C–H orbitals. The orbital symmetry (σ or π) and the direction of these interactions (metal to C–H donation or back-donation) can vary in incremental steps from case to case, thus forming a continuous range of charge-transfer mechanisms. Depending on the detailed nature of the orbital interactions and the overall charge transfer, a given complex can be placed in this continuum.⁹ Photoinitiated C–H activation via oxidative addition of an alkane to a transition metal constitutes a prominent mechanism within this spectrum.

The relevant charge-transfer interactions in C–H activation by transition metals were initially conceptualized on an orbital level by Sailard and Hoffmann.¹⁰ It was proposed that C–H σ to metal-d (LMCT) charge donation and metal d to C–H σ* (MLCT) charge back-donation act as the basic metal–alkane bonding and C–H bond cleavage interactions. C–H to metal donation was proposed to be essential in binding of the C–H bond to the metal center. Both C–H to metal charge donation and metal to C–H charge back-donation would then act in opposite directions but work in tandem to weaken the C–H bond and ultimately cleave it. The “two-way” charge transfer interactions between C–H and the metal^10,11 act differently when binding the C–H group in a σ-complex compared to when cleaving the C–H bond and forming the final metal–carbon and metal–hydride bonds. It is therefore important to quantify the relative strength of these opposing modes of charge-transfer interactions for the different intermediates at the different stages of the reaction. Based on the above considerations, a generalized correlation diagram for how orbitals interact in the relevant intermediates in C–H activation by transition-metal complexes has been developed.^10,12 Computational approaches with energy decomposition schemes have attempted to estimate the relative strength of charge donation and back-donation. A general consensus, however, is lacking, because it is debated whether an unambiguous descriptor of the underlying orbital interactions actually exists. In addition, the means to experimentally access the hypothesized orbital interactions directly are missing to date. In terms of new experimental insight, it is access to the electronic structure of the σ-complex, the crucial intermediate in the activation process, that is of prime importance, since the transition-state, which is the point of focus of most computational studies, cannot be accessed experimentally. Time-resolved infrared spectroscopy has been used to identify reaction intermediates, including σ-complexes, by following IR marker modes (like the CO stretching frequency).^13–17 Relating the details of orbital-specific metal–alkane interactions in σ-complexes to the IR marker modes, however, is comparably indirect. Experimentally determining the electronic structure properties, which drive C–H bond cleavage with transition metal complexes, by accessing the two-way charge-transfer interactions in an orbital-specific way and determining the relative strengths of the opposite components, thus remain challenging to date.

Using time-resolved X-ray absorption spectroscopy at the transition metal L-edge, we were recently able to observe the metal–alkane orbital interactions, which are operative in photoinduced C–H activation.¹⁸ We demonstrated, how with this atom-specific probe we could follow the evolution of orbital interactions and orbital populations as a function of time.^19,20 This enabled us to dissect the C–H σ to metal d charge donation and metal d to C–H σ* (MLCT) charge back-donation in C–H activation.¹⁸ For photoinitiated C–H activation with CpRh(CO)₂ (where Cp is cyclopentadienyl) in octane solution, time-resolved X-ray absorption spectroscopy at the Rh L-edge gave access to the two-way charge-transfer interactions between Rh and the C–H group in the essential CpRh(CO)–octane σ-complex reaction intermediate. Metal L-edge X-ray absorption spectroscopy, however, is based on transitions of metal 2p core electrons to unoccupied molecular orbitals. The method is hence primarily sensitive to the unoccupied anti-bonding counterparts of the occupied bonding orbitals.²¹ For a full account of the two-way charge-transfer interactions and thus experimental access to the full correlation diagram for C–H activation by transition-metal complexes, it is therefore necessary to also probe the occupied orbitals.^22,23 Here, using quantum chemical simulations, we predict how valence-to-core resonant inelastic X-ray scattering (VtC-RIXS) at transition metal L-edges^20,24–28 can be used to probe changes of orbital interactions in both, occupied and unoccupied orbitals. We show this by focusing on the decisive intermediates along the photoinitiated C–H activation pathway and we use CpRh(CO)₂ to demonstrate our approach. By dissecting donation and back-donation interactions between Rh and an incoming C–H group on an orbital level we can now relate computationally established mechanisms and notions for reactivity in C–H activation by transition-metal complexes to the newly proposed experimental observables.

Results and discussion

Accessing C–H activation by CpRh(CO)₂ with time-resolved VtC-RIXS at the Rh L-edge

C–H activation by CpRh(CO)₂ is initiated by the photo-dissociation of a single CO moiety within 370 fs leading to the formation of a highly reactive undercoordinated singlet CpRhCO complex¹⁸ (see schematic depiction of the overall process in Fig. 1(a)). It has been conclusively established that CpRhCO binds with an alkane, both when performed in an argon matrix with methane or in an alkane solution.^{16,18,29–34} In octane solution, a σ-complex forms within 2 ps by the association of a C–H group to CpRhCO.¹⁸ σ-complex formation is followed by C–H activation via oxidative addition to the Rh center on nanosecond timescales, forming two new Rh–C and Rh–H bonds. We do not focus here on the photo-dissociation of CO from CpRh(CO)₂ which involves excited states and complex photochemical dynamics. Instead, we address how metal–ligand bonding drives the formation of the σ-complex and the subsequent C–H bond activation, which exclusively involve singlet ground states. CpRh(CO)₂ serves as an ideal model system for this, where electronic interactions are the predominant drivers, in contrast to other cases, where steric and cooperative effects dominate C–H bond activation.^31,35 CpRh(CO)₂ is therefore well suited as a demonstrative case to show how the orbital correlation diagram for C–H activation by transition-metal complexes can be made accessible with VtC-RIXS in future experiments. This proposed spectroscopic approach can then be extended to transition-metal systems also having varied degrees of reactivity as will be discussed at the end of this study.

Fig. 1 Metal–ligand orbital interactions in photoinitiated C–H bond activation by CpRh(CO)₂ probed using VtC-RIXS. (a) Schematic depiction of the key intermediates and reaction steps in photo-initiated C–H activation by CpRh(CO)₂. (b) Conceptual depiction of charge donation and back-donation interactions between the metal (M) and one ligand in the original M–CO configuration, in the M–alkane σ-complex configuration and in the final M–C–H metal hydride product (arrows denote the direction of charge transfer interaction, their thicknesses indicate the proposed relative strengths of the charge transfer). (c) State picture of the RIXS process (total energy many-electron picture), with excitation from the initial ground state (GS) to the intermediate core-excited state (CES) with incident photon energy X-ray_in and inelastic scattering to the final valence-excited state (VES) with the measured scattered photon energy X-ray_out and the resulting energy transfer ΔE. (d) Corresponding orbital picture (orbital energy one-electron picture) where a Rh 2p electron is promoted to a vacant molecular orbital (here of Rh 4d character) via a 2p → 4d transitions, followed by transition of an electron from an occupied 4d orbital to fill the hole on the 2p orbital (via 4d → 2p transitions), creating the metal-centered (MC) d–d valence-excited final states.

The main orbital interactions here are the C–H σ to Rh 4d (LMCT) charge donation and the Rh 4d to C–H σ* (MLCT) charge back-donation. C–H to Rh charge donation is responsible for σ-complex formation. Rh to C–H back-donation in contrast drives the oxidative addition step^10,18 with a resulting transfer of charge density from Rh to the C–H moiety and, eventually, oxidation of the Rh center (see Fig. 1(b)). Inspecting the valence molecular orbitals of CpRh(CO)₂ reveals that the lowest unoccupied molecular orbital (LUMO) is predominantly a d_xy orbital, with the highest occupied molecular orbital (HOMO), HOMO−1, HOMO−2 and HOMO−3 being the d_yz, d_z², d_xz and d_x²–y² orbitals, respectively (see Fig. S1†). These Rh 4d orbitals change and rehybridize across the reaction coordinate and, as we will show, the varying interactions of occupied MOs (specifically HOMO to HOMO−3) can be made accessible with Rh L-edge VtC-RIXS.

The VtC-RIXS process (denoted as RIXS hereafter) can be rationalized by the excitation of the system from the initial ground state (GS in Fig. 1(c)) to an intermediate core-excited state (CES in Fig. 1(c)) through the absorption of an incident X-ray photon, followed by inelastic scattering to a final valence-excited state (VES in Fig. 1(c)). The RIXS process can therefore often be approximated by an initial X-ray absorption step (as in X-ray absorption, spectroscopy, XAS) followed by an X-ray emission step (as in X-ray Emission Spectroscopy, XES). By knowing the energy of the incident photon and measuring the energy of the scattered photon, their difference, and thus the energy being transferred to the system, can be determined (ΔE in Fig. 1(c)). This energy transfer thus is a direct measure of the transition energies from the ground to valence-excited states. Resonant enhancement at the Rh L absorption edge makes the method specific to the Rh center. We further use the one-electron picture interpretation of the RIXS process to demonstrate sensitivity to specific molecular orbitals. The one-electron picture interpretation is well justified here because each transition between ground, core-excited and valence-excited states can be unambiguously assigned to transitions between Rh 2p, unoccupied and occupied molecular orbitals. This is illustrated for transitions between Rh 2p, HOMO and LUMO orbitals in Fig. 1(d): The incident X-ray photon promotes an electron from the Rh 2p core orbitals to the unoccupied d_xy-LUMO. Subsequently, an electron from the HOMO can be thought to fill the Rh 2p core hole (the HOMO will have to have at least some Rh 4d character to have substantial intensity in the related dipole transition), leaving the system in a valence-excited final state of metal-centered (MC) character. The measured energy transfer (ΔE in Fig. 1(c)) reflects the energy of the respective MC state and, within the one-electron picture interpretation, this energy transfer can also be approximately assigned to the energy of the HOMO–LUMO transition. Considering that other electrons from other occupied molecular orbitals with Rh 4d character (HOMO−1, HOMO−2, …) can also fill the Rh 2p core hole, it is evident that this gives access to the HOMO−1, HOMO−2, to LUMO transition energies and thereby to the orbital-interaction energies involving all occupied orbitals accessible by p–d dipole transitions. Additionally, and again within the one-electron picture interpretation, the RIXS intensities of the HOMO, HOMO−1, HOMO−2, to LUMO transitions scale with the amount of Rh 4d character in the occupied molecular orbitals (mainly by orbital overlap). RIXS intensities therefore provide information on hybridization of the Rh 4d orbitals with surrounding ligand orbitals.

Here, we show with simulated VtC-RIXS signatures of the CpRhCO–octane σ-complex and the final activated product complex CpRhCO–R–H in their S₀ ground states (see Fig. 1(a)) how the electronic structure changes along σ-complex formation and C–H activation can be accessed and verified by future experiments. We benchmark the theoretical methods used in our predictive study here against measured steady-state VtC-RIXS spectra of CpRh(CO)₂ and a structurally related compound. Finally, the accuracy in theoretically reproducing the measured Rh L-edge X-ray absorption spectra in our earlier study¹⁸ for these same intermediates at a similar level of theory provides additional confidence in the simulation method used here.

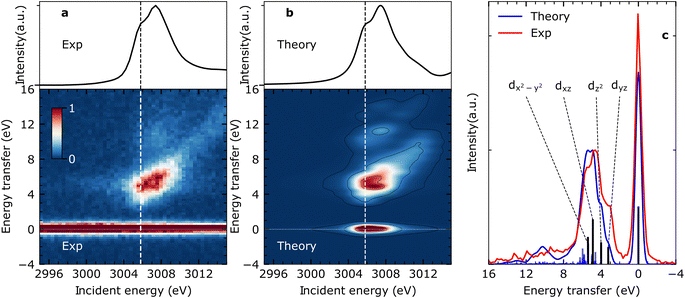
Steady-state VtC-RIXS spectra of CpRh(CO)₂ – comparison between experiment and theory

Fig. 2(a) shows the measured steady-state X-ray absorption spectra and RIXS intensities of CpRh(CO)₂ (for experimental details see Methods section). The experimental data are compared to the calculated X-ray absorption spectra and RIXS maps (Fig. 2(b)). Calculations were done using the restricted orbital subspace time dependent density functional theory (TD-DFT) method^26,27,36 (see computational details in Methods Section). The simulated X-ray absorption and RIXS spectra reproduce all features of the experimental spectra. This is evidenced in a more quantitative evaluation in Fig. 2(c), where cuts through the experimental and theoretical RIXS maps at the pre-edge peak in the Rh L-edge X-ray absorption spectrum at ∼3005.8 eV are displayed. This pre-edge excitation corresponds to the transitions of Rh 2p electrons to the LUMO having prominent Rh 4d_xy character¹⁸ (see Fig. 1(d)). The RIXS spectrum taken at the X-ray absorption pre-edge at 3005.8 eV (see Fig. 2(c)) therefore reflects the HOMO, HOMO−1 → 4d_xy (LUMO) transitions or, correspondingly, the energies of respective d–d (MC) valence-excited states. The simulated RIXS spectrum reproduces all relevant peaks in terms of both, energies and intensities. The calculated energy transfers are slightly overestimated, but their relative splittings are reproduced. The four transitions with highest intensities can be assigned to the four strong 4d_yz, 4d_z², 4d_xz, and 4d_x²–y² → 4d_xy orbital transitions (dark blue sticks in Fig. 2(c), labeled as d_yz, d_z², d_xz and d_x²–y²). This assignment is additionally verified using ab initio methods (see Fig. S1 in ESI† for MOs). Based on the good agreement between calculated and measured RIXS maps of CpRh(CO)₂, we proceed to tracking changes in Rh specific orbital interactions across the C–H activation reaction coordinate with Rh L-edge VtC-RIXS by predicting the X-ray absorption spectra and RIXS maps for the various reaction intermediates of CpRh(CO)₂ upon C–H activation.

Fig. 2 VtC-RIXS of CpRh(CO)₂ as a probe of MC d–d final states. (a) Experimental Rh L-edge X-ray absorption spectrum (top) and Rh L-edge RIXS map (bottom) for CpRh(CO)₂. (b) Simulated Rh L-edge X-ray absorption spectra and RIXS map at the TD-DFT level of theory. X-ray absorption spectra result from integration of RIXS intensities in a given incident-energy range along the energy-transfer axis. Vertical dashed lines in (a) and (b) indicate the energy of 3005.8 eV at which cuts were obtained to target the valence-excited MC states or, alternatively, HOMO, HOMO−1, to LUMO transitions. (c) Cuts from the experimental and simulated RIXS maps at 3005.8 eV. The dominant peaks correspond to transitions from the ground to MC states or, alternatively, to the HOMO, HOMO−1, HOMO−2, HOMO−3 (4d_yz, 4d_z², 4d_xz, and 4d_x²–y², respectively) to 4d_xy LUMO orbital transitions.

Predicting Rh L-edge RIXS signatures across the C–H activation pathway

The calculated Rh L-edge X-ray absorption spectra and RIXS maps of the essential intermediates along the C–H activation pathway of CpRh(CO)₂ are displayed in Fig. 3(a)–(d). We focus here on an analysis of the RIXS spectra taken at the X-ray absorption pre-edge peaks corresponding to Rh 2p → LUMO transitions (dashed lines in Fig. 3(a)–(d), because the corresponding HOMO, HOMO−1, to LUMO transitions are most informative on the Rh-ligand frontier-orbital interactions).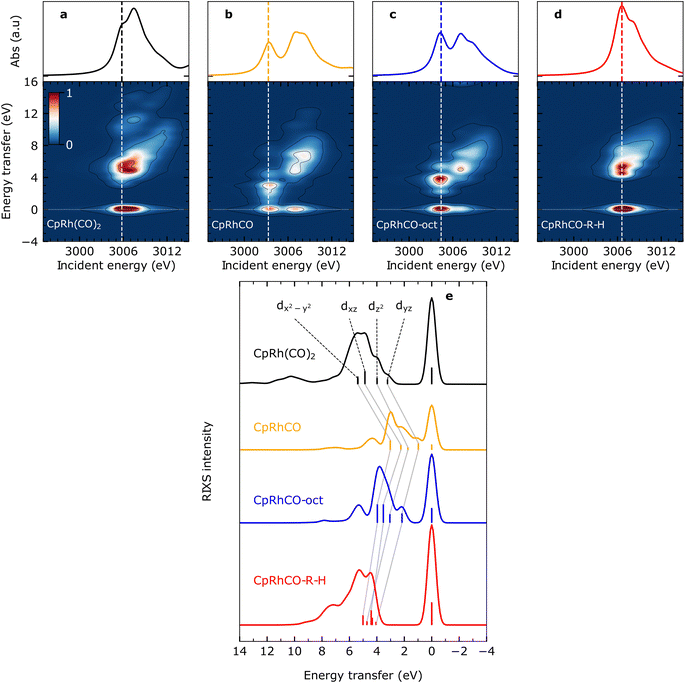

Fig. 3 Simulated VtC-RIXS for key intermediates upon C–H activation in octane by CpRh(CO)₂. Simulated Rh L₃-edge RIXS maps for (a) CpRh(CO)₂, (b) free fragment CpRhCO, (c) sigma-complex CpRhCO–octane (abbreviated as CpRhCO-oct) and (d) final activated product complex CpRhCO–R–H (along with the Rh L₃-edge X-ray absorption spectra on top of the panels). (e) Cuts through the RIXS maps for the four intermediates in (a–d) at incidence energies of pre-edge excitation (indicated by the vertical lines in panels (a–d)). As in Fig. 2(c), the RIXS transitions are labeled according to the involvement of the four occupied Rh 4d orbitals (gray lines connect the corresponding transitions and the evolution of their energies and intensities along the reaction pathway).

We start by simulating the VtC-RIXS signature for the free CpRhCO fragment in a singlet ground state and follow with the RIXS maps in Fig. 3 what effects CO removal has on the frontier orbitals. Upon CO removal, the energy transfers of all RIXS features at the X-ray absorption pre-edge have considerably decreased by several eV along the energy-transfer axis compared to CpRh(CO)₂ (compare Fig. 3(b) and (a)). These red-shifts reflect the overall reduction of covalent interactions of the frontier orbitals when a strongly bound ligand is removed. This is quantified by the cut through the RIXS map of CpRhCO at the X-ray absorption pre-edge (see Fig. 3(e)). Compared to the corresponding cut for CpRh(CO)₂, CO removal decreases the energy transfers of the d_yz, d_z², d_xz and d_x²–y² RIXS peaks. These shifts correspond to how the 4d_yz, 4d_z², 4d_xz, and 4d_x²–y² → 4d_xy orbital transition energies from occupied orbitals to the LUMO decrease (correspondingly, these shifts reflect how energies of d–d (MC) states decrease when removing the CO from CpRh(CO)₂). The red-shift of the lowest-energy d_yz RIXS peak from 3 eV in CpRh(CO)₂ to 1 eV in CpRhCO (see Fig. 3(e)) is particularly informative: It corresponds directly to the decrease of the HOMO–LUMO 4d_yz → 4d_xy transition and hence reflects the destabilization of the HOMO (d_yz), or, more precisely, the reduction of the HOMO–LUMO energy separation. The HOMO (d_yz) orbitals in both CpRh(CO)₂ and CpRhCO are associated with Rh 4d to CO (π*) back-donation. Removal of CO from CpRh(CO)₂ frustrates this interaction, thereby destabilizing the HOMO (d_yz) and stabilizing the LUMO (d_xy). The red shift of the d_yz RIXS peak (4d_yz → 4d_xy transition) quantifies this stabilization/destabilization. This is accompanied by an increase in intensity of that peak due to the increase of Rh d_yz character in the HOMO, when back-donation is frustrated upon CO removal (due to the dipole-allowed nature of the 4d_yz → 2p transitions in the RIXS process). Note that, additionally, the pre-edge peak in the Rh L-edge X-ray absorption spectrum red-shifts from 3005.8 eV in CpRh(CO)₂ to 3003.3 eV in CpRhCO (compare top panels in Fig. 3(a) and (b)). This corresponds to a decrease of the 2p → LUMO (4d_xy) transition energy and reflects the stabilization of the LUMO orbital as CO is removed and a vacant coordination site is created at the Rh center in the free CpRhCO fragment.¹⁸ This is a manifestation of the creation of what has been termed “hole on the metal” by Hoffman et al.³⁷

Upon octane C–H coordination to the vacant site in the free fragment and thus formation of the CpRhCO–octane σ-complex, all d_yz, d_z², d_xz and d_x²–y² RIXS peaks at the X-ray absorption pre-edge shift back to higher energies (Fig. 3(e)), indicating the recovery of covalent interactions at the Rh center to a certain degree. Specifically, C–H to Rh coordination shifts the HOMO–LUMO 4d_yz → 4d_xy transition (d_yz RIXS peak) back from 1 eV in the free CpRhCO fragment to slightly more than 2 eV in the σ-complex (Fig. 3(e)). The related recovery of the HOMO–LUMO energy separation directly reflects the increase of underlying charge donation and back-donation interactions. The emerging Rh 4d to C–H σ* (MLCT) charge back-donation stabilizes the HOMO (accompanied with some increase in C–H σ* character in the HOMO and a corresponding slight decrease of the intensity of the d_yz RIXS peak). The new or increased C–H σ to Rh 4d (LMCT) charge donation destabilizes the “hole on the metal” LUMO orbital in the CpRhCO–octane σ-complex compared to the free CpRhCO fragment. Correspondingly, the X-ray absorption pre-edge shifts back as well from 3003.3 eV in CpRhCO to 3004.4 eV in CpRhCO–octane (see Fig. 3(b) and (c) top).

Importantly, we note that the energies of the d_yz RIXS peaks (HOMO–LUMO 4d_yz → 4d_xy transition energies) amount to only slightly more than 2 eV in the σ-complex compared to 3 eV in CpRh(CO)₂ (Fig. 3(e)). This difference suggests a smaller HOMO–LUMO energy separation in CpRh–CO–octane compared to CpRh(CO)₂. This is a direct manifestation of the weaker Rh 4d to C–H σ* back-donation in CpRhCO–octane compared to the Rh 4d to CO π* back-donation in CpRh(CO)₂ (a corresponding effect on the LUMO orbitals of the two structures can be seen in the difference in Rh L-edge X-ray absorption pre-edge energies). Our Mullikan population analysis of orbitals shows that the Rh 4d character of the HOMOs for CpRhCO–octane and CpRh(CO)₂ amount to 38.1% and 22.5%, respectively. This difference can be related to the smaller overlap of Rh 4d and C–H σ* orbitals in CpRhCO–octane compared to the overlap of Rh 4d and CO π* orbitals in CpRh(CO)₂ and a correspondingly smaller degree of hybridization. In RIXS, the difference in 4d character can be directly observed from the higher intensity of the d_yz peak in CpRhCO–octane compared to CpRh(CO)₂ (see Fig. 3(e)).

Oxidative addition of the C–H bond to the Rh center in the final step of the reaction pushes the C–H group closer to the Rh center, thereby increasing both C–H σ to Rh 4d_xy donation and Rh 4d_yz to C and H σ* charge back-donation. As Fig. 3(e) clearly shows, oxidative addition shifts all d_yz, d_z², d_xz and d_x²–y² RIXS peaks at the X-ray absorption pre-edge to higher energies compared to the CpRhCO–octane σ-complex (correlating with the increase of covalent interaction in the final hydride product CpRhCO–R–H). The d_yz RIXS peak, in particular, red shifts from slightly more than 2 eV in CpRhCO–octane to above 4 eV in CpRhCO–R–H (Fig. 3(e)). This notable shift of the HOMO–LUMO 4d_yz → 4d_xy transition to an energy even higher than in CpRh(CO)₂ (3 eV) is reflective of a substantial increase of Rh 4d_yz to C and H σ* back-donation and a related stabilization of the HOMO (d_yz) when the metal hydride with covalent Rh–C and Rh–H bonds is formed. The d_yz RIXS peak also significantly decreases in intensity, resulting in it no longer being identifiable as a separate peak as in CpRh(CO)₂, CpRhCO, and CpRhCO–octane (see Fig. 3(e)). This directly points to the significant loss of 4d_yz character in the HOMO as Rh 4d_yz to C and H σ* charge back-donation increase. Our Mullikan population analysis reveals that the 4d character of the HOMO drops from 38.1% in CpRhCO–octane to 15.5% in CpRhCO–R–H and much lower than the 22.5% in CpRh(CO)₂. We also note that the overall energy spread, over which the d_yz, d_z², d_xz and d_x²–y² RIXS peaks are distributed, decreases from around than 2 eV in CpRh(CO)₂, CpRhCO and CpRhCO–octane to around 1 eV in the final metal hydride CpRhCO–R–H (Fig. 3(e)). An explanation of this is given below.

As a final note, the strong C and H σ to Rh 4d_xy donation in the final metal hydride destabilizes the LUMO (while the Rh 4d_yz to C and H σ* charge back-donation stabilizes the LUMO+1). Consistently, the X-ray absorption pre-edge peak shifts from 3004.4 eV in the CpRhCO–octane σ-complex to 3006.6 eV in CpRhCO–R–H (Fig. 3(c) and (d), top) (notably to a higher incident energy as in CpRh(CO)₂ where it is at 3005.8 eV due to the stronger R and H versus CO ligand to Rh charge donation).

Motivated by the stringent consistency between changes in orbital interactions and changes in the simulated RIXS spectra at the X-ray absorption pre-edge across the reaction coordinate, we now turn to a more explicit prediction of experimental observables and, alongside, a more detailed analysis of the final oxidative addition step of the reaction. In future pump-probe experiments, the ground-state CpRh(CO)₂ species will be photoexcited and the emerging reaction intermediates will be measured against a background of un-excited CpRh(CO)₂. For measurements of the CpRhCO free fragment and of the CpRhCO–octane σ-complex, the calculated RIXS maps and spectra in Fig. 3 serve as good predictions, because their X-ray absorption pre-edges are well separated from the absorption edges of CpRh(CO)₂. By tuning the incident energies to the easily identifiable respective pre-edge resonances, the RIXS spectra of CpRhCO and CpRhCO–octane can be straightforwardly measured. For the final CpRhCO–R–H metal hydride product, though, the situation is more complicated because its Rh L-edge X-ray absorption spectrum as well as RIXS map strongly overlap with the corresponding spectral features of ground-state CpRh(CO)₂ (Fig. 3(a), (d) and (e)). To isolate detailed changes in electronic structure upon metal hydride formation compared to un-excited CpRh(CO)₂, we therefore predict and analyze RIXS difference maps, where the simulated RIXS intensities of the ground-state CpRh(CO)₂ species (as a reference) are subtracted from the simulated RIXS intensities of the final metal hydride product. This approach is commonly applied in pump-probe experiments and was shown before to render adequate RIXS intensities of reaction intermediates.²⁰ The more subtle changes in RIXS intensities are emphasized and the information needed to relate changes in RIXS intensities to an overall orbital correlation diagram for the oxidative addition step is revealed.

The calculated RIXS difference maps for the CpRhCO–octane σ-complex and the metal hydride product CpRhCO–R–H are shown in Fig. 4(a) and (b) (for completeness, equivalent data of CpRhCO are shown in Fig. S2†). Cuts through these simulated difference maps (rendering RIXS difference spectra) are compared in Fig. 4(c) for the two species and reveal the valence electronic-structure changes along the reaction coordinate of oxidate addition in C–H activation. These differences reflect the peak shifts discussed above and, in addition, make visible the more subtle changes in peak intensities (changes in Rh 4d character in the occupied 4d_yz, 4d_z², 4d_xz and 4d_x²–y² orbitals). The RIXS difference map of CpRhCO–octane can be almost exclusively described by the depletion of ground-state CpRh(CO)₂ intensities (compare negative, blue-marked, intensities in Fig. 4(a) with the RIXS map of CpRh(CO)₂ in Fig. 3(a)) and the shifted RIXS intensities of CpRhCO–octane (compare positive, red-marked, intensities in Fig. 4(a) with the RIXS map of CpRhCO–octane in Fig. 3(b)). The corresponding RIXS difference spectrum of CpRhCO–octane at the X-ray absorption pre-edge shown in Fig. 4(c) thus almost exclusively exhibits positive intensities only (with some negative intensities due to spectral overlap of RIXS intensities in the RIXS maps of CpRhCO–octane and depleting CpRh(CO)₂ at energy transfers above 5–6 eV).

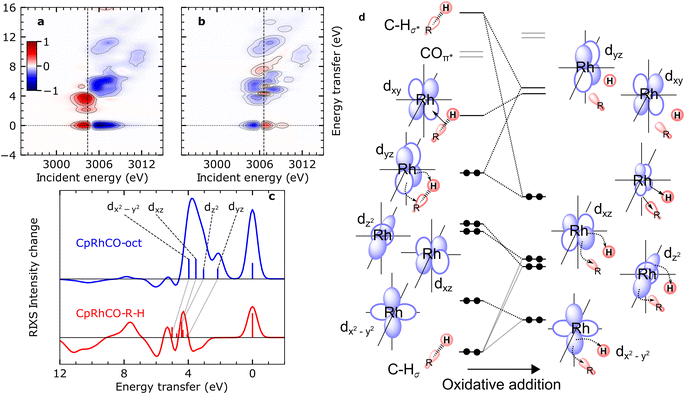Fig. 4 Simulated VtC-RIXS difference signatures for the oxidation addition step vs. the orbital correlation diagram. (a) and (b) RIXS difference maps of CpRhCO–octane and CpRhCO–R–H, respectively, obtained by subtracting the RIXS map of CpRh(CO)₂ shown in Fig. 3(a) from the RIXS maps shown in Fig. 3(c) and (d). Red regions denote positive intensity, blue regions denote depletion. Vertical lines indicate incidence energies where RIXS cuts were obtained. (c) Cuts in the difference RIXS maps for CpRhCO–octane (red) and CpRhCO–R–H (blue). Individual peaks are labeled by the occupied 4d orbitals as in Fig. 2 and 3. Gray lines illustrate the evolution of RIXS peaks upon oxidative addition. (d) Correlation diagram as motivated and derived from interpreting the RIXS spectra for CpRhCO–octane and CpRhCO–R–H from panel (c).

The simulated RIXS difference map of the final CpRhCO–R–H in Fig. 4(b) is more complex as expected. Intensities at zero energy transfer reflect the blue shift of the X-ray absorption pre-edge in CpRhCO–R–H compared to CpRh(CO)₂ (see the opposite pattern in Fig. 4(a) at zero energy transfers due to the opposite red shift of the X-ray absorption pre-edge in CpRhCO–octane compared to CpRh(CO)₂). A cut at the X-ray absorption pre-edge (at 3006.6 eV, Fig. 4(c)) clearly shows strong intensity modulations in both, positive and negative directions (in contrast to the CpRhCO–octane RIXS difference spectrum). The negative-intensity feature at 3–4 eV for CpRhCO–R–H reflects the aforementioned reduced intensity of the d_yz RIXS peak in CpRhCO–R–H with respect to CpRh(CO)₂ and the correspondingly lower Rh 4d character in the 4d_yz HOMO in CpRhCO–R–H compared to CpRh(CO)₂. This depletion of Rh 4d character is a clear indication of oxidation as it can be interpreted as an increase in Rh 4d to C–H σ* charge back-donation to the point of the metal getting oxidized from Rh(I) to Rh(III).

Our predictions and analysis offer a unique way to motivate, verify and extend the orbital correlation diagrams for C–H activation by transition-metal complexes proposed by Ess and coworkers.¹²Fig. 4(d) shows the correlation diagram for the oxidative addition step, which we extract from our calculations and directly correlate with the calculated RIXS intensities and energies. The changes in energies and hybridization of the most relevant unoccupied molecular orbitals, i.e., of LUMO, LUMO+1, LUMO+2, LUMO+3, were reported earlier based on our combination of calculations and measured X-ray absorption spectra (as indicated in Fig. 4(d), they are fully consistent with the changes reported here for the occupied orbitals).¹⁸ With RIXS, we show how one can additionally track the changes in energies and hybridization of the occupied orbitals. The changes in the Rh 4d_yz HOMO discussed so far, are depicted in our extended correlation diagram in Fig. 4(d). With future time-resolved Rh L-edge RIXS experiments, these changes and the related correlation diagram will become accessible experimentally. Specific intensity variations of the other RIXS peaks relating to HOMO−1 to HOMO−3 are less clear because shifts in the peaks strongly interplay with variations in peak intensities. Still, when comparing the RIXS difference cuts at the X-ray absorption pre-edges of the CpRhCO–octane σ-complex and of the final CpRhCO–R–H product in Fig. 4(c), we can state that CpRhCO–R–H exhibits stronger negative intensities. This reduced RIXS intensity reflects an overall decrease of Rh 4d character in the Rh-centered occupied orbitals, which are involved in formation of the new covalent Rh–C and Rh–H bonds.

Inspection of the molecular orbitals of CpRhCO–R–H (see Fig. S3†) indeed shows that the 4d_x²–y² (HOMO−3 in CpRhCO–octane and CpRhCO–R–H) and 4d_z² (HOMO−1 in CpRhCO–octane and HOMO−2 in CpRhCO–R–H, see Fig. 4(d)) hybridize with the C sp³ and H s orbitals as they are favorably oriented in space to form the corresponding bonding overlaps for the new Rh–C and Rh–H bonds (Fig. 4(d)). We also find that in CpRhCO–R–H, the HOMO−1 and HOMO−2 stabilize more than HOMO−2 and HOMO−4, resulting in an energetic cross-over between the HOMO−2 and HOMO−3. This behavior also explains the decrease in the earlier-mentioned energy spread of d_yz, d_z², d_xz and d_x²–y² RIXS peaks. At the same time, the Rh character in these orbitals significantly decreases. Our Mulliken population analysis yields a decrease from 72.9% to 60.9% for 4d_x²–y² HOMO−3 and from 77% to 34% for 4d_z² HOMO−1/HOMO−2 when going from CpRhCO–octane to CpRhCO–R–H. The 4d_xz (HOMO−2 in CpRhCO–octane and HOMO−1 in CpRhCO–R–H, see Fig. 4(d)), finally, is also stabilized upon oxidative addition and, accordingly, significantly loses Rh 4d character as the covalent bonds are formed. According to the Mulliken population analysis, the Rh 4d character in the 4d_xz orbital decreases from 80.8% to 59%.

These quantum-chemical predictions directly relate to experimental RIXS observables, as we show, and can be used to construct and conceptualize the entire correlation diagram in Fig. 4(d). By explicitly considering covalent interactions involving all occupied 4d orbitals, we extend upon previous theoretical concepts, which were purely based on charge donation and back-donation interactions. RIXS, we predict, will also enable revealing how varying degrees of C–H σ* to metal-d (LMCT) charge donation and metal-d to C–H σ* (MLCT) charge back-donation, as induced by different spectator ligands for instance, influence the overall reactivity towards C–H activation. We demonstrate this in the last section of our study.

Predicting RIXS fingerprints of spectator ligand effects in C–H activation

It has previously been demonstrated using NMR spectroscopy and time-resolved IR spectroscopy how differences in the spectator ligands of transition-metal complexes effectuate the propensity of different σ-complexes towards C–H activation.¹³ Following this approach, we recently reported trends in orbital energies and hybridization of unoccupied orbitals, which determine the varying reactivity towards C–H activation for two different σ-complexes, CpRhCO–octane and Rh(acac)(CO)–octane¹⁸ (where acac = acetylacetonate). Similar to CpRh(CO)₂, the formation of the Rh(acac)(CO)–octane σ-complex follows CO dissociation from Rh(acac)(CO)₂ in octane solution. The RIXS spectrum of Rh(acac)(CO)₂ was also measured and simulated using the above-mentioned protocol and we show the agreement of simulated and measured RIXS maps in Fig. S4.†

In contrast to the CpRhCO–octane σ-complex, Rh(acac)(CO)–octane constitutes a particularly stable σ-complex that does not facilitate C–H activation.³⁸ Here, we trace these observations back to changes in the occupied orbitals. In Fig. 5(a) and (b), the simulated RIXS difference maps for the two σ-complexes Rh(acac)(CO)–octane and CpRhCO–octane are shown. As can be seen, the d_yz RIXS peak (HOMO–LUMO 4d_yz → 4d_xy transition) in Rh(acac)(CO)–octane is merged at high energies with the other (d_z², d_xz and d_x²–y²) RIXS peaks. For CpRhCO–octane, it is instead clearly separated at an energy of slightly more than 2 eV. This observation is even more apparent in the cuts through the RIXS difference maps at the respective X-ray absorption pre-edges in Fig. 5(c). The higher HOMO–LUMO 4d_yz → 4d_xy transition energy in Rh(acac)(CO)–octane compared to CpRhCO–octane is due to stronger C–H σ to Rh 4d_xy charge donation, leading to greater destabilization of the LUMO in Rh(acac)(CO)–octane compared to CpRhCO–octane and a greater stabilization of HOMO in Rh(acac)(CO)–octane than in CpRhCO–octane. This stabilization of the HOMO correlates with decreased hybridization of Rh 4d_yz with the σ* orbital of the C–H group in Rh(acac)(CO)–octane and hence a frustrated Rh 4d_yz to C–H σ* charge back-donation. We also note that the integrated intensity of all d_yz, d_z², d_xz, and d_x²–y² RIXS peaks is higher in Rh(acac)(CO)–octane compared to CpRhCO–octane, indicating increased Rh 4d character of HOMO−1, HOMO−2 and HOMO−3. This reflects the more ionic complex Rh(acac)(CO)–octane¹⁸ with a higher effective oxidation of the Rh(I) center compared to CpRh(CO)–octane. In our previous study based on X-ray absorption spectroscopy,¹⁸ we established that C–H σ to Rh 4d_xy donation is stronger in Rh(acac)(CO)–octane compared to CpRhCO–oct, thereby contributing to a more stable σ-complex. Based on the simulated RIXS signatures shown here, we demonstrate that this notion can be extended by establishing in future RIXS experiments that the Rh 4d_yz to C–H σ* charge back-donation is also frustrated in Rh(acac)(CO)–octane and that the reduced hybridization with the C–H σ* orbital contributes to preventing C–H activation in the Rh(acac)(CO)–octane σ-complex.

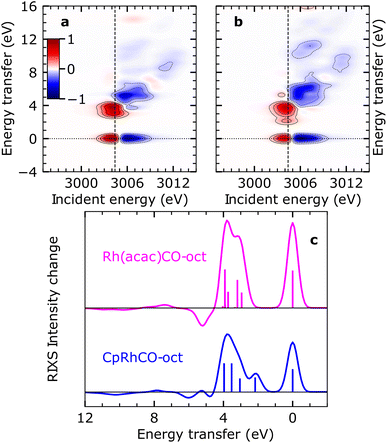Fig. 5 Simulated VtC-RIXS difference signatures as fingerprints of σ-complex reactivity. (a) Difference RIXS map of Rh(acac)(CO)–octane obtained by subtracting the calculated RIXS map of Rh(acac)(CO)₂, as shown in Fig. S4 in the ESI,† from the calculated RIXS map of Rh(acac)(CO)–octane. (b) Difference RIXS map of CpRhCO–octane (same as in Fig. 4(a)). (c) Cuts through the difference RIXS maps in (a) and (b) at the X-ray absorption pre-edge at 3004.4 eV (dashed lines in (a) and (b)) for Rh(acac)(CO)–octane (top) and CpRhCO–octane (bottom).

Conclusion

By simulating the valence-to core resonant inelastic X-ray scattering (VtC-RIXS) signatures at the transition metal L-edge for various key intermediates in a photochemical C–H activation reaction with a transition metal complex, we have predicted how VtC-RIXS can be used to dissect and understand the decisive orbital interactions which drive the reaction. By comparison to experimental VtC-RIXS data of CpRh(CO)₂, a well-studied model system, we were able to benchmark and validate the accuracy of our computational predictions with TD-DFT. Since C–H activation by CpRh(CO)₂ is mainly governed by electronic effects, spectroscopic signatures could be assigned to the changes in covalent interactions such as charge donation and back-donation across the reaction pathway without interference of other (e.g. steric) effects. This allows to extend the established correlation diagram for the oxidative addition step in the C–H activation process by including changes in covalency over the full 4d manifold. We predict that these changes can be directly extracted from the changes in energies and intensities of VtC-RIXS peaks, which reflect the evolving character of the relevant occupied and unoccupied Rh 4d orbitals.

A robust theoretical description of how VtC-RIXS probes the evolution of valence orbitals and as such, molecular bonds, during chemical reactions constitutes a critical step towards the experimental realization of such investigations. With RIXS being an extremely photon-hungry technique, particularly in the VtC regime, time-resolved experiments have thus far been challenging or outright unfeasible even at intense X-ray free-electron laser sources. However, with already or soon-to-be operating X-ray free-electron lasers like the European XFEL (Hamburg, Germany) and the LCLS-II (Stanford, USA), which provide kHz to MHz repetition rates and thus orders of magnitude increases in average X-ray flux compared to other X-ray free-electron laser sources,³⁹ VtC-RIXS experiments as proposed here will become routinely feasible. We anticipate future experimental studies with time-resolved VtC-RIXS at transition metal L-edges to yield unique information on the evolution of frontier-orbital interactions in a range of photochemical and photocatalytic reactions in solution. The resulting experimental extraction and verification of orbital correlation diagrams will reveal how covalent metal–ligand interactions drive catalytic function.

Materials and methods

Computational details

The quantum chemical computations were performed using the ORCA program package⁴⁰ and Open-MOLCAS.⁴¹ All the geometries were optimized at the TPSSh/def2-TZVP level of theory^42,43 followed by frequency computations. No imaginary normal modes were found confirming that the optimized structures are intermediates in the reaction pathway. Solvent effects were taken into account by incorporating the CPCM polar continuum model with hexane as the solvent⁴⁴ for all computations done in ORCA. X-ray absorption and VtC RIXS spectra were computed in ORCA using the restricted orbital subspace TD-DFT method³⁶ within the Tamm-Damcoff approximation.⁴⁵ Second order relativistic effects were taken into account using the ZORA method.⁴⁶ The SARC-ZORA-TZVPP basis set was used for the Rh atom and ZORA-def2-TZVPP for the rest of the atoms.⁴⁷ The three Rh 2p orbitals were rotated into the restricted orbital subspace, which also consisted of 20 occupied orbitals and 20 unoccupied orbitals. The core-excited states (intermediate states) and valence-excited states (final states) were computed by considering excitations from the occupied orbital subspace (20 + 3 orbitals) into the 20 selected unoccupied orbitals. The 0–16 eV energy range on the energy loss axis was accounted for and covered by solving for 420 valence-excited states for CpRh(CO)₂ and CpRhCO and 400 valence-excited states for CpRhCO–oct and CpRhCO–C–H. For all species, 60 core-excited states were calculated. All the transition dipole moments for excitations from the ground state to core-excited states and the decay from core-excited states to valence-excited states were computed using the Multi-Wfn program package.⁴⁸

The RIXS intensities were computed using the Kramers–Heisenberg formula. The discrete intensities were convoluted along the incident energy axis with a Voigt profile consisting of a 1.9 eV FWHM Lorentzian function to account for the core–hole lifetime⁴⁹ and a Gaussian function of 0.6 eV FWHM. On the energy transfer axis, the intensities were broadened with Gaussian of 0.7 eV FWHM. A shift of −22.2 eV in the incident energy axis was applied to the calculated spectrum of CpRh(CO)₂ to align it with experimental spectrum. The same shift was applied to all other calculated species reproducing relative shifts determined experimentally.¹⁸

RIXS calculations for the different species were also carried out at the Restricted Active Space Perturbation Theory (RASPT2) level of theory^50,51 in Open-MOLCAS. For the RASPT2 computations, the Douglas–Kroll–Hess–Hamiltonian⁵² was used to account for the zeroth order relativistic effect along with Sapporo-DKH3-DZP-2012 ⁵³ basis set for Rh and the cc-pVDZ-DK basis set⁵⁴ for all other atoms. We used three 2p orbitals with six electrons in the RAS1 space for all the species. The RAS2 space was varied accordingly for different species. We used 10 electrons in 10 orbitals in the RAS2 space for computing the RIXS maps for CpRh(CO)₂ and 10 electrons in 8 orbitals for CpRhCO. For CpRhCO–octane and CpRhCO–R–H, the RAS2 orbitals consisted of 10 electrons in 9 orbitals. A total of 50 singlet ground and valence-excited states were solved using state-averaging. A total of 40 core-excited states were solved using the HEXS keyword in RASSCF.⁵⁵ Subsequently, RASPT2 computations were performed to account for dynamical correlation. The discrete transitions were convoluted in the same way as described earlier for TD-DFT. The spectra are again shifted by −67.1 eV in the incident energy axis. Unlike in TD-DFT, this constant shift does not consistently reproduce the relative shifts determined from experiment¹⁸ for RASPT2. The RASPT2 spectra are shown in Fig. S5–S8 in the ESI.† A discussion on the comparison between the RIXS spectra simulated at the TDDFT and RASPT2 level of theory is provided in the ESI after Fig. S8.†

Experimental details

The VtC-RIXS experiments were performed using the Alvra instrument of the Swiss Free Electron Laser (SwissFEL). CpRh(CO)₂ was purchased from HetCat, Rh(acac)(CO)₂ from Sigma-Aldrich. The samples were dissolved at 20 mM concentration in decane and octane, respectively (purchased from Sigma-Aldrich). The sample was delivered into the experimental chamber via a cylindrical liquid jet with a diameter of 75 μm. The sample was collected by a catcher system below the interaction zone and recirculated into the sample reservoir. The experimental chamber was kept under 500 mbar He atmosphere to minimize X-ray scattering noise and increase the X-ray transmission. The incidence energy of the X-rays was tuned across the Rh L₃-edge between 2995 eV and 3015 eV using a Si(111) monochromator with a bandwidth of ∼0.4 eV. The X-ray focus spot size was ∼20 × 20 μm² on the sample.

The VtC-RIXS data was collected in parallel to time-resolved X-ray absorption measurements at a repetition rate of 100 Hz. To only include steady-state data, every second XFEL shot impinging on the sample was selected for the current analysis, thus reducing the effective repetition rate to 50 Hz. While time-resolved VtC-RIXS data were recorded, the S/N level did not allow for the extraction of spectroscopic information, and hence only experimental steady state spectra are presented in this paper. The data was recorded using a von-Hamos type X-ray emission spectrometer equipped with a 250 mm cylindrically bent Si(111) segmented crystal and a Jungfrau 4.5 M detector. The energy axis of the spectrometer was calibrated with respect to the elastic scattering. The energy resolution of the spectrometer was ∼0.8 eV as determined by fitting the elastic scattering below the absorption onset at 2995 eV. Each pixel of the raw single-shot Jungfrau images was corrected for pedestal levels and gains before retrieving the deposited energy in keV.^56,57 Low and high energy thresholds of 2.0 and 10.0 keV, respectively, were applied for each pixel to minimize noise and eliminate unphysical counts. In order to enhance further the signal-to-noise of the VtC-X-ray emission line, two regions of interest (ROIs) were selected on the 2D detector and subtracted from each other. The first (signal) was placed around the VtC line, whereas the second one (background) was located at the same position along the dispersive axis but offset along the non-dispersive axis.

Data availability

All data supporting the findings of this study are available from the corresponding authors upon reasonable request.

Author contributions

A. B., R. M. J. and P. W. originated the project concept. A. B., M. C. and M. O. performed the theoretical calculations. A. B., R. M. J, M. O. and P. W. analyzed the computational results. R. M. J., T. L., R.-P. W., J. H., R. S., E. B., V. K., A. K., A. W., D. O., C. A., C. M., P. J. M. J., C. C., C. B., N. H. and P. W. planned and executed the experiments. R. M. J., T. L., and C. C. analyzed the experimental data. A. B. R. M. J. and P. W. wrote the paper with input from all the authors.

Conflicts of interest

The authors declare no conflicts interest.

Acknowledgements

We acknowledge the Paul Scherrer Institut, Villigen, Switzerland for provision of beamtime at the Alvra beamline of SwissFEL. The computations were partly enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX partially funded by the Swedish Research Council through grant agreement no. 2021-22968 and 2022-22975. The computations were also partly enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) and the Swedish National Infrastructure for Computing (SNIC) at NSC and PDC partially funded by the Swedish Research Council through grant agreement no. 2022/1-14, 2023/1-8, 2022-06725 and no. 2018-05973. M. O. acknowledges funding from the Swedish Research Council (grant agreement no. 2021-04521). A. B. and P. W. acknowledge funding from the Carl Tryggers Foundation (contract CTS 19:399). P. W. acknowledges funding from the Swedish Research Council (grant agreement no. 2019-04796). J. H. and N. H. acknowledge funding from the Cluster of Excellence “CUI: Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG), EXC 2056, project ID 390715994. R.-P. W. acknowledges funding from the German Ministry of Education and Research (BMBF), project ID 05K19GU2. V. K., A. K., and C. B. acknowledge support from the Swiss National Science Foundation (SNSF) through the NCCR:MUST. A. W. acknowledges the National Science Centre, Poland (NCN), for partial support through grant no. 2019/03/X/ST3/00035.

References

1. K. I. Goldberg and A. S. Goldman, Acc. Chem. Res., 2017, 50, 620–626.
2. B. A. Arndtsen, R. G. Bergman, T. A. Mobley and T. H. Peterson, Acc. Chem. Res., 1995, 28, 154–162.
3. A. J. Lees and A. A. Purwoko, Coord. Chem. Rev., 1994, 132, 155–160.
4. C. Jia, T. Kitamura and Y. Fujiwara, Acc. Chem. Res., 2001, 34, 633–639.
5. C. P. Lenges and M. Brookhart, J. Am. Chem. Soc., 1999, 121, 6616–6623.
6. S. Murai, F. Kakiuchi, S. Sekine, Y. Tanaka, A. Kamatani, M. Sonoda and N. Chatani, Nature, 1993, 366, 529–531.
7. T. Matsubara, N. Koga, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 1998, 120, 12692–12693.
8. M. Brookhart, M. L. H. Green and G. Parkin, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914.
9. K. M. Altus and J. A. Love, Commun. Chem., 2021, 4, 173.
10. J. Y. Saillard and R. Hoffmann, J. Am. Chem. Soc., 1984, 106, 2006–2026.
11. E. A. Cobar, R. Z. Khaliullin, R. G. Bergman and M. Head-Gordon, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6963–6968.
12. D. H. Ess, W. A. Goddard and R. A. Periana, Organometallics, 2010, 29, 6459–6472.
13. G. E. Ball, C. M. Brookes, A. J. Cowan, T. A. Darwish, M. W. George, H. K. Kawanami, P. Portius and J. P. Rourke, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6927–6932.
14. S. E. Bromberg, H. Yang, M. C. Asplund, T. Lian, B. K. McNamara, K. T. Kotz, J. S. Yeston, M. Wilkens, H. Frei, R. G. Bergman and C. B. Harris, Science, 1997, 278, 260–263.
15. E. P. Wasserman, C. B. Moore and R. G. Bergman, Science, 1992, 255, 315–318.
16. M. W. George, M. B. Hall, O. S. Jina, P. Portius, X.-Z. Sun, M. Towrie, H. Wu, X. Yang and S. D. Zaric, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20178–20183.
17. A. J. Cowan, P. Portius, H. K. Kawanami, O. S. Jina, D. C. Grills, X.-Z. Sun, J. McMaster and M. W. George, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6933–6938.
18. R. M. Jay, A. Banerjee, T. Leitner, R.-P. Wang, J. Harich, R. Stefanuik, H. Wikmark, M. R. Coates, E. V. Beale, V. Kabanova, A. Kahraman, A. Wach, D. Ozerov, C. Arrell, P. J. M. Johnson, C. N. Borca, C. Cirelli, C. Bacellar, C. Milne, N. Huse, G. Smolentsev, T. Huthwelker, M. Odelius and P. Wernet, Science, 2023, 380, 955–960.
19. R. M. Jay, K. Kunnus, P. Wernet and K. J. Gaffney, Annu. Rev. Phys. Chem., 2022, 73, 187–208.
20. P. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. De Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81.
21. R. K. Hocking, E. C. Wasinger, Y. L. Yan, F. M. F. Degroot, F. A. Walker, K. O. Hodgson, B. Hedman and E. I. Solomon, J. Am. Chem. Soc., 2007, 129, 113–125.
22. H. Lim, M. T. Brueggemeyer, W. J. Transue, K. K. Meier, S. M. Jones, T. Kroll, D. Sokaras, B. Kelemen, B. Hedman, K. O. Hodgson and E. I. Solomon, J. Am. Chem. Soc., nd., 145, 16015–16025.
23. N. Lee, T. Petrenko, U. Bergmann, F. Neese and S. DeBeer, J. Am. Chem. Soc., 2010, 132, 9715–9727.
24. R. M. Jay, S. Eckert, M. Fondell, P. S. Miedema, J. Norell, A. Pietzsch, W. Quevedo, J. Niskanen, K. Kunnus and A. Föhlisch, Phys. Chem. Chem. Phys., 2018, 20, 27745–27751.
25. R. M. Jay, J. Norell, S. Eckert, M. Hantschmann, M. Beye, B. Kennedy, W. Quevedo, W. F. Schlotter, G. L. Dakovski, M. P. Minitti, M. C. Hoffmann, A. Mitra, S. P. Moeller, D. Nordlund, W. Zhang, H. W. Liang, K. Kunnus, K. Kubiček, S. A. Techert, M. Lundberg, P. Wernet, K. Gaffney, M. Odelius and A. Föhlisch, J. Phys. Chem. Lett., 2018, 9, 3538–3543.
26. E. Biasin, D. R. Nascimento, B. I. Poulter, B. Abraham, K. Kunnus, A. T. Garcia-Esparza, S. H. Nowak, T. Kroll, R. W. Schoenlein, R. Alonso-Mori, M. Khalil, N. Govind and D. Sokaras, Chem. Sci., 2021, 12, 3713–3725.
27. D. R. Nascimento, E. Biasin, B. I. Poulter, M. Khalil, D. Sokaras and N. Govind, J. Chem. Theory Comput., 2021, 17, 3031–3038.
28. K. Kunnus, W. Zhang, M. G. Delcey, R. V. Pinjari, P. S. Miedema, S. Schreck, W. Quevedo, H. Schröder, A. Föhlisch, K. J. Gaffney, M. Lundberg, M. Odelius and P. Wernet, J. Phys. Chem. B, 2016, 120, 7182–7194.
29. J. B. Asbury, H. N. Ghosh, J. S. Yeston, R. G. Bergman and T. Lian, Organometallics, 1998, 17, 3417–3419.
30. M. C. Asplund, P. T. Snee, J. S. Yeston, M. J. Wilkens, C. K. Payne, H. Yang, K. T. Kotz, H. Frei, R. G. Bergman and C. B. Harris, J. Am. Chem. Soc., 2002, 124, 10605–10612.
31. A. L. Pitts, A. Wriglesworth, X. Z. Sun, J. A. Calladine, S. D. Zarić, M. W. George and M. B. Hall, J. Am. Chem. Soc., 2014, 136, 8614–8625.
32. A. J. Rest, I. Whitwell, W. A. G. Graham, J. K. Hoyano and A. D. McMaster, J. Chem. Soc., Dalton Trans., 1987, 1181–1190.
33. A. A. Bengali, B. A. Arndtsen, P. M. Burger, R. H. Schultz, B. H. Weiller, K. R. Kyle, C. B. Moore and R. G. Bergman, Pure Appl. Chem., 1995, 67, 281–288.
34. S. T. Belt, F. W. Grevels, W. E. Klotzbuecher, A. McCamley and R. N. Perutz, J. Am. Chem. Soc., 1989, 111, 8373–8382.
35. N. Gorgas, A. J. P. White and M. R. Crimmin, J. Am. Chem. Soc., 2022, 144, 8770–8777.
36. V. Vaz da Cruz, S. Eckert and A. Föhlisch, Phys. Chem. Chem. Phys., 2021, 23, 1835–1848.
37. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1982, 21, 711–724.
38. T. P. Dougherty, W. T. Grubbs and E. J. Heilweil, J. Phys. Chem., 1994, 98, 9396–9399.
39. R. Schoenlein, T. Elsaesser, K. Holldack, Z. Huang, H. Kapteyn, M. Murnane and M. Woerner, Philos. Trans. R. Soc., A, 2019, 377, 20180384.
40. F. Neese, WIREs Comput. Mol. Sci., 2022, 12, 1–15.
41. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D.-C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117.
42. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
43. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
44. M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Chem. Phys., 2001, 114, 5691–5701.
45. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299.
46. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
47. J. D. Rolfes, F. Neese and D. A. Pantazis, J. Comput. Chem., 2020, 41, 1842–1849.
48. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
49. J. L. Campbell and T. Papp, At. Data Nucl. Data Tables, 2001, 77, 1–56.
50. P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194.
51. P. Å. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109.
52. M. Reiher, O. Salomon and B. Artur Hess, Theor. Chem. Accounts Theory, Comput. Model. (Theoretica Chim. Acta), 2001, 107, 48–55.
53. T. Noro, M. Sekiya and T. Koga, Theor. Chem. Acc., 2012, 131, 1124.
54. W. A. de Jong, R. J. Harrison and D. A. Dixon, J. Chem. Phys., 2001, 114, 48.
55. M. G. Delcey, L. K. Sørensen, M. Vacher, R. C. Couto and M. Lundberg, J. Comput. Chem., 2019, 40, 1789–1799.
56. S. Redford, M. Andrä, R. Barten, A. Bergamaschi, M. Brückner, S. Chiriotti, R. Dinapoli, E. Fröjdh, D. Greiffenberg, K. S. Kim, J. H. Lee, C. Lopez-Cuenca, M. Meyer, D. Mezza, A. Mozzanica, S.-Y. Park, C. Ruder, B. Schmitt, X. Shi, D. Thattil, G. Tinti, S. Vetter and J. Zhang, J. Instrum., 2020, 15, C02025.
57. A. Mozzanica, M. Andrä, R. Barten, A. Bergamaschi, S. Chiriotti, M. Brückner, R. Dinapoli, E. Fröjdh, D. Greiffenberg, F. Leonarski, C. Lopez-Cuenca, D. Mezza, S. Redford, C. Ruder, B. Schmitt, X. Shi, D. Thattil, G. Tinti, S. Vetter and J. Zhang, Synchrotron Radiat. News, 2018, 31, 16–20.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3sc04388f

‡ These authors contributed equally to this work.

§ Present address: Department of Physics and Astronomy, Uppsala University, 751 20 Uppsala, Sweden.

¶ Present address: Stanford PULSE Institute, SLAC National Accelerator Laboratory, Stanford University, Menlo Park, CA 94025, USA.

|| Present address: Physical Sciences Division, Pacific Northwest National Laboratory, Richland, WA 99352, USA.

---