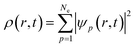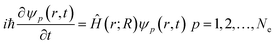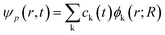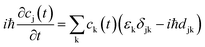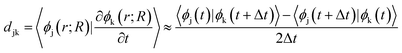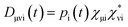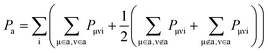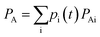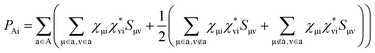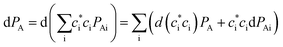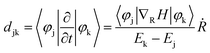Insights into photoinduced carrier dynamics and hydrogen evolution reaction of organic PM6/PCBM heterojunctions†
Xiao-Ying
Xie
*a,
Xiang-Yang
Liu
 b,
Wei-Hai
Fang
b,
Wei-Hai
Fang
 c and
Ganglong
Cui
c and
Ganglong
Cui
 *c
*c
aThe Laboratory of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Yantai University, Yantai, 264005, China. E-mail: xiaoying.xie@mail.bnu.edu.cn
bCollege of Chemistry and Material Science, Sichuan Normal University, Chengdu 610068, China
cKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, China. E-mail: ganglong.cui@bnu.edu.cn
First published on 9th November 2022
Abstract
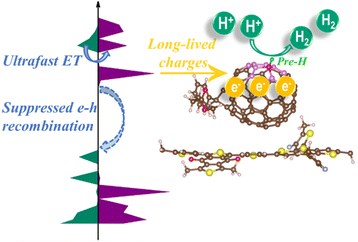
Efficient spatial separation of photogenerated charge carriers across donor/acceptor interfaces has stimulated intense research efforts in photocatalysis fields ascribed to distinctive electronic structure properties of related constituents. Leveraging electronic structure calculations in combination with ab initio-based non-adiabatic carrier dynamics simulations, this study reports ultrafast electron transfer and suppressed nonradiative electron–hole recombination at the interface of PM6/PCBM organic semiconductor heterojunctions, which leads to long-lived charges taking part in hydrogen evolution. The photoinduced dynamical processes are dominantly influenced by energy gaps and non-adiabatic couplings between frontier donor and acceptor states. In addition, hydrogen evolution sites at PM6/PCBM heterojunctions are unveiled by means of first-principles calculations, which suggest that the reaction activity heavily depends on H-adsorbed sites. The activity on the C atoms at the junction of three benzene rings (C666) is much lower than that on the C atoms connected with one pentagon ring and two benzene rings (C665). Nevertheless, the former can be significantly improved via pre-hydrogenating the adjacent C665 atom. This work reveals new photophysical and photochemical properties of PM6/PCBM heterojunctions in detail and provides useful perspectives for performance improvements of photocatalytic materials based on organic donor–acceptor heterojunctions.
Introduction
Due to the grand challenge of climate change and depletion of fossil resources, researchers are paying gradually increasing attention to alternative renewable energy.1 Among them, solar energy is one of main research subjects owing to its abundance in nature.2 However, its wide application is greatly hindered by low energy density, diffusion, and intermittency of radiant sunlight. Alternatively, the storage of solar energy in chemical bonds via efficient photocatalytic techniques is much more practical and has sparked intense interest in various fields of solar energy utilization.3 A typical example is solar-driven H2 generation,4–6 in which produced hydrogen fuel has been regarded as one of the most appealing green energy carriers due to its high energy capacity and combustion without bringing extra environmental pollution.6–12 It should be noted that efficient photocatalysts are of great significance in converting solar to chemical energy.13–15Conventional inorganic semiconductors, especially metal oxides, have been employed in photocatalytic systems for decades.13,16–21 Nevertheless, absorption of inorganic photocatalysts usually falls into UV regime ascribed to large intrinsic band gaps, which significantly reduces sunlight harvesting capacity.16,22 Recently, organic semiconductor photocatalysts have gained notable attention because their light absorption and energy levels can be precisely modulated in synthetic processes, thereby enabling excellent photo-response in solar spectrum and high solar-to-hydrogen conversion efficiency.23 In 2009, Wang et al. reported that carbon nitride can be used for hydrogen production by solar-driven water splitting.24 Subsequently, a variety of organic materials involving conjugated microporous polymers (CMPs), covalent organic frameworks (COFs), covalent triazine-based frameworks (CTFs), etc. are explored as photocatalysts for hydrogen evolution.23,25–31 Considering a spectrum of organic building blocks and a variety of synthetic techniques, there should be a wide range of potential organic polymer photocatalysts with outstanding photocatalytic hydrogen evolution performance. Bai and co-workers have screened a large group of linear polymers by means of high-throughput approaches to explore the correlation between polymer structures and their photocatalytic hydrogen evolution activities, which provides valuable insights for future design and synthesis of photocatalysts with optimized performances.25 Unfortunately, organic materials have generally suffered from insufficient interfacial charge separation, impeding the improvement of their photocatalytic activities.
The construction of donor/acceptor heterojunctions has recently emerged as an ideal solution for enhancing charge spatial separation at the interface and harvesting long-lived charge carriers.32–37 Donor/acceptor heterojunctions with type II energy level offset benefit electron–hole pair dissociation into free charge carriers, as shown in Fig. S1,† leading to good charge separation. For example, upon excitation of the α moiety, the hole within the α moiety can flow into the β one whereas the photogenerated electron remains within the α domain. In addition, the electron and hole are separately confined within the two different components, thus the electron–hole recombination is suppressed. For instance, a robust panchromatic ternary polymer dots capable of producing hydrogen with excellent and stable performances have been fabricated.38 High external quantum efficiency for hydrogen evolution reduction (HER) is inherently beneficial from energy and charge transfer from conjugated polymers (PFBT and PFODTBT) to ITIC molecules on the time scale of sub-picosecond.38 Liu et al. have designed two novel donor/acceptor conjugated polymers based on dibenzothiophene-S,S-dioxide and thiophene derivatives. The suitable band gaps and promoted charge separation efficiencies result in an outstanding hydrogen generation rate.39 Kosco and co-workers have exploited organic heterojunctions composed of polymer PTB7-Th and non-fullerene EH-IDTBR as hydrogen generation photocatalysts, which exhibit greatly increased photocatalytic activities when varying nanomorphology from a core–shell structure to an inter-mixed donor/acceptor blend.32 Just recently, they have further assembled conjugated polymer PBDB-T-2F (PM6) and electron acceptor fullerene [6,6]-phenyl C71 butyric acid methyl ester (PCBM) to form an organic semiconductor heterojunction, which can effectively drive photocatalytic hydrogen evolution.40 The excellent photocatalytic performance is dominantly beneficial from intrinsically long-lived charges. Generally, photocatalytic materials used in experiments are rather complicated and it is thus difficult to explore their structure–activity relationships in detail.
The underlying photo-physical and -chemical properties in organic donor/acceptor semiconductor heterojunctions are desirable to be thoroughly understood for further improving photocatalytic hydrogen evolution activities. To address these issues in organic PM6/PCBM heterojunctions, we firstly explore photoinduced charge carrier dynamics with the aid of static electronic structure calculations and our recently developed non-adiabatic molecular dynamics simulations. The results confirm an ultrafast electron transfer from the light harvester PM6 to the electron acceptor PCBM leading to long-lived charge separated states in PM6/PCBM. In addition, atomic-level insights into the photoinduced charge relaxation dynamics at the donor/acceptor interface are complemented. The PM6/PCBM heterojunctions are found can be used for photocatalytic hydrogen production, yet the hydrogen generation mechanism is still missing. Hence, we also study the hydrogen evolution mechanism in PM6/PCBM heterojunction and reveal the preferable reaction sites. Our present work provides a comprehensive understanding on the excellent photocatalytic hydrogen evolution activity of PM6/PCBM, which may aid the rational design of organic photocatalysts for hydrogen production.
Simulation methods
Nonadiabatic dynamics methods
Nonadiabatic carrier transfer dynamics simulations are performed employing Tully's fewest-switches surface-hopping (FSSH) methods on the basis of density functional theory.41–44 An interacting many-body system can be mapped to a system of noninteracting particles with equal electron density based on time-dependent density functional theory in Kohn–Sham framework. In result, time-dependent charge density ρ(r, t) of an interacting system is acquired from a set of time-dependent Kohn–Sham orbitals ψp(r, t)45–49Electron density evolution eventually results in a set of single-electron equations for evolution of Kohn–Sham orbitals ψp(r, t)50–54
If expanding time-dependent electron or hole wavefunction ψp(r, t) in terms of interested unoccupied or occupied adiabatic Kohn–Sham orbitals ϕk(r, t) calculated from density functional theory calculations along adiabatic molecular dynamics trajectories
the energy of the kth adiabatic state (εk) can be directly obtained from density functional theory calculations and the nonadiabatic coupling between adiabatic states j and k (djk) can be calculated numerically through finite difference methods as overlaps of adiabatic states at times t and t + Δt:
In which ϕj(t) and ϕk(t + Δt) are wave functions of adiabatic states j and k at times t and t + Δt, respectively. Previous algorithms are primarily implemented with plane wave basis sets.55,56 Recently, we have implemented this nonadiabatic carrier dynamics method with Gaussian basis sets with CP2K57 and have widely applied to study the photoinduced carrier dynamics of a series of periodic systems.57–65
Carrier transfer analysis
In order to estimate electron or hole transfer from one to another fragment in nonadiabatic dynamics simulations, we have developed an efficient density-matrix based method. First, we can define a density matrix D in terms of atomic orbitals χμwhere pi(t) is time-dependent occupation number of the ith adiabatic state calculated on the basis of above expanding coefficients ci(t); χμi is the μth atomic orbital coefficient of the ith adiabatic state.
Similar to Mulliken charge analysis,66 we have then defined a population matrix P using density matrix D and atomic overlap matrix S
| Pμνi = DμνiSμν |
Finally, we can obtain the ath atomic charge through summing all basis functions μ belonging to that atom and all involved adiabatic states i
It's noteworthy that if only an atomic orbital belongs to the ath atom, just half of Pμνi is used, as done by Mulliken charge analysis method. Accordingly, the total number of electrons on a fragment A is the sum of all atomic charges belonging to that fragment
In such a case, the differentiation of PA is then derived as
in which the first term has variational occupations for adiabatic states i and the second term has constant adiabatic state occupations but changeable electron population. These two terms correspond to nonadiabatic and adiabatic electron transfer contributions. The former is primarily caused by state hopping between different adiabatic states and the latter is mainly originated from changes of adiabatic states induced by atomic motions. It's noteworthy that we use Gaussian basis sets in our simulations. As a result, molecular coefficients χμi are real numbers. Although adiabatic states' expanding coefficients ci(t) are complex numbers, they are not directly used; instead, their 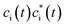 products, which are real numbers, are used for calculating time-dependent occupation number pi(t) of the ith adiabatic state.
products, which are real numbers, are used for calculating time-dependent occupation number pi(t) of the ith adiabatic state.
Computational details
The geometry optimization and the adiabatic ab initio molecular dynamics (AIMD) simulations are carried out employing the density functional theory (DFT) method implemented in the Quickstep/CP2K software package.57 Exchange-correlation interaction is described by Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).67 Meanwhile, the DZVP-MOLOPT-SR-GTH basis sets and Goedecker–Teter–Hutter pseudopotentials are adopted.68–72 The empirical dispersion correction method is evoked in our simulations to consider the van der Waals (vdW) interactions.73 To obtain more accurate density of states (DOS), Heyd–Scuseria–Ernzerhof (HSE06) functional with the auxiliary density matrix method (ADMM) is applied.74–76 In our calculations, only the gamma point is considered.For the non-adiabatic molecular dynamics simulations, the geometry is firstly heated to 300 K using the Nosé–Hoover chain thermostat and equilibrated for about 1 ps in the canonical ensemble.77,78 Subsequently, a 1 ps microcanonical trajectory with the nuclear time step of 1 fs is propagated, from which 100 initial conditions are randomly selected.79–81 1000 surface-hopping trajectories are propagated for 500 fs with a time step of 1 fs for every initial condition to simulate the photogenerated electron dynamics, resulting in total of 100 × 1000 trajectories for subsequent nonadiabatic dynamics simulations. The empirical quantum decoherence correction with the value of 0.1 a.u. is considered in our surface-hopping dynamics simulations as Granucci et al. proposed.82 The dynamical results listed in the present work are averaged over all the prepared trajectories. Discussion about excitonic effects is given in the ESI (Fig. S2 and Table S1†). More details on the dynamical simulations can be found in our reported studies.
Vienna ab initio simulation package (VASP) within the framework of DFT is employed to obtain the reasonable reaction intermediates along the H2 generation process.83,84 Similar to the above, PBE functional involved with long-range dispersion correction (PBE + D3) is firstly applied to optimize the geometry, and then the energy is recalculated using more accurate HSE06 + D3.67,73,85,86 The core-valence electron interaction is treated using the projector augmented-wave (PAW) method.87 The Gibbs free energy (ΔG) is calculated according to the following definition:
| ΔG = ΔE + ΔEZPE − TΔS |
Results and discussion
Geometry and electronic structures of the PM6/PCBM heterojunction
Polymer PM6 always serves as an electron donor in photovoltaic or photocatalytic devices owing to its strong visible light absorption. By contrast, fullerenes and their analogues are well-known photo-excited electron acceptors due to their superior electron affinity and carrier mobility.89 The organic donor/acceptor semiconductor heterojunctions studied in the present work are constructed via stacking a PCBM on the polymer PM6 surface with different orientations (Fig. S3†). As listed in Table S2,† the adsorption energies are larger for composites with a “lying” PCBM (0.49 ∼ 0.61 eV) than those with a “standing” PCBM (0.38 ∼ 0.42 eV). So, a relatively stable structure with a “lying” PCBM on the PM6 surface is selected for the further discussion (denoted as PM6/PCBM hereafter, Fig. S3a†). As shown in Fig. 1a, the distance between PCBM and PM6 is 3.20 Å in the PBE + D3 optimized PM6/PCBM structure. The calculated adsorption energies of PCBM on the PM6 surface are 0.55 and 0.54 eV at the PBE + D3 and HSE06 + D3 levels, respectively, suggesting modest physical adsorption between the two components.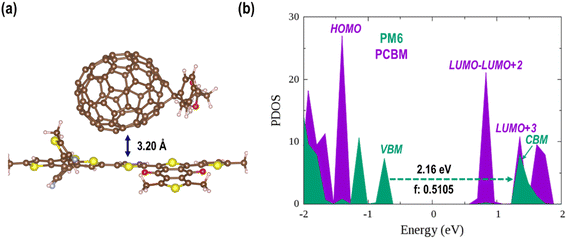 | ||
| Fig. 1 (a) The PBE + D3 optimized PM6/PCBM structure and (b) its PDOS calculated by HSE06 functional with the vdW correction. The relevant result calculated at the PBE + D3 level is shown in Fig. S4.† | ||
Projected density of states (PDOS) can give us important information on the charge transfer and relaxation within the donor/acceptor heterojunctions. Fig. S4 in the ESI† and Fig. 1b show the PDOS of optimized PM6/PCBM at the PBE + D3 and HSE06 + D3 levels, respectively. Obviously, both computational methods show that four PCBM states, including the lowest unoccupied molecular orbital (LUMO), lie in between the valence band maximum (VBM) and conduction band minimum (CBM) of polymer PM6, while the highest occupied molecular orbital (HOMO) of PCBM is below the VBM of PM6, indicating that the organic PM6/PCBM nanohybrids belong to type-II heterojunctions, in agreement with the experimental observations.40 In particular, the LUMO+3 state of PCBM is rather close to the CBM of PM6 with a small energy gap of only 0.04 [0.06] eV at the HSE06 + D3 [PBE + D3] level, implying an ultrafast interfacial electron transfer process from PM6 to PCBM would occur. By contrast, sequential electron migration from LUMO+3 to the three nearly degenerate energy levels, i.e., LUMO+2, LUMO+1, and LUMO, is suppressed owing to a relatively large energy gap between the LUMO+3 and LUMO+2 states of PCBM, which is calculated to be 0.47 [0.38] eV at the HSE06 + D3 [PBE + D3] level. Taken together, the polymer PM6 can quickly donate photogenerated electron after the band gap excitation, while the transferred electron would be trapped in the PCBM acceptor considering the large energy span between the LUMO+3 and LUMO+2 states. The overall band gap of the organic PM6/PCBM heterojunction is estimated to be 1.56 eV at the HSE06 + D3 level and it's decreased to 0.98 eV when PBE functional is employed due to the underestimation of GGA functional. It's evident that the considerable band gap is beneficial for impeding electron–hole recombination and achieving long-lived charge-separated states, thus improving the photocatalytic performance.90–92
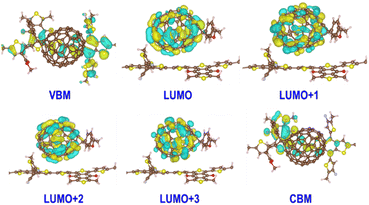
Based on the transition dipole moments calculations, the electron transition from VBM to CBM of PM6 is allowed with a large oscillator strength of 0.5105 (Table S3†). The computed electron excitation energy is 2.16 eV at the HSE06 + D3 level, in line with the experimentally utilized excitation energy of 2.25 eV.40 The corresponding oscillator strength, 0.4296, is also large calculated at the PBE + D3 level, but the excitation energy is reduced to 1.53 eV owing to the underestimation of PBE functional as mentioned above. Fig. 2 presents the spatial distributions of the relevant states. Obviously, both VBM and CBM localize at PM6 moiety and feature π character, demonstrating that the π → π* transition in PM6 will take place upon excitation. While the four states lying below the CBM (LUMO, LUMO+1, LUMO+2, and LUMO+3) primarily reside at the PCBM moiety, indicating the electron transfer from PM6 to PCBM is favorable in the organic donor/acceptor heterojunctions.
The charge separation dynamics at the PM6/PCBM interface
Long-lived charge carriers are desirable for photocatalytic reactions, such as H2 evolution reaction (HER), CO2 reduction reaction (CO2RR), and N2 reduction reaction (NRR), which can be achieved in donor/acceptor heterojunctions via effective charge spatial separation. Next, we will apply our recently developed NAMD to complete the description of the charge transfer, relaxation, and recombination in PM6/PCBM heterojunctions, thus shedding light on the generation of long-lived charge-separated states. As discussed above, the excited electron would initially occupy the CBM of PM6 upon absorption of a photon with 2.16 eV energy. In order to study the photoinduced electron transfer process between the PM6 and PCBM components, five states (CBM of PM6, LUMO+3, LUMO+2, LUMO+1, and LUMO of PCBM) are involved in the non-adiabatic dynamics simulations.Fig. 3a shows the time-dependent populations of involved states within 500 fs simulation time. It's clear that the population of CBM, the initially electron populated state, is reduced to ca. zero in the first 400 fs. Correspondingly, the amount of electron populated at the LUMO+3 state increases rapidly to its maximum within 400 fs, and then begins to decrease at a relatively slow rate. By contrast, the amount of electron populated at the LUMO+2 or LUMO+1 state is slightly increased within the 500 fs simulations. The population of the LUMO state monotonously grows up and reaches ca. 0.1 in the end. Fig. 4 displays the time-dependent energies of relative states in the non-adiabatic dynamics simulations. Obviously, the energy gap between CBM and LUMO+3 states is small with an average value of 0.11 eV during the non-adiabatic dynamics, consistent with the sharp electron amount decrease in CBM as presented in Fig. 3a, indicating that a fast electron transfer from PM6 to PCBM is favourable. In addition, the spatial distribution of LUMO+3 and CBM gets delocalized in the molecular dynamics as shown in Fig. S5,† contributing to the ultrafast electron transfer from PM6 to PCBM. The time constant for electron transfer is estimated to be 250 fs using a mono-exponential decay function to fit the time-dependent electron amount localized on the PM6 fragment (see Fig. 3b), which is in good agreement with the within 1 ps timescale for electron transfer observed by the experiment.40
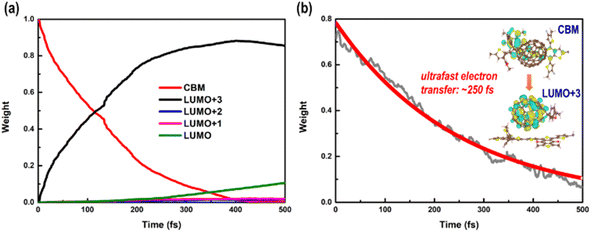 | ||
| Fig. 3 (a) Time-dependent state populations of CBM in PM6 and LUMO+x (x = 0–3) in PCBM and (b) time-dependent electron amount localized on the PM6 fragment in the nonadiabatic dynamics simulations. | ||
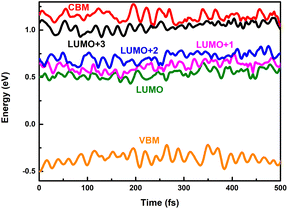 | ||
| Fig. 4 Time-dependent energies of VBM and CBM of PM6 and LUMO+x (x = 0–3) of PCBM in the nonadiabatic dynamics simulations. | ||
As shown in Fig. 3a, the electron can be rapidly populated at the LUMO+3 state of PCBM, whereas the successive migration to lower band containing the LUMO+2, LUMO+1, and LUMO states is heavily stuck. Nonadiabatic coupling djk, which can be expressed as:
| ΔE/eV | |NAC|/ps−1 | |
|---|---|---|
| CBM → LUMO+3 | 0.11 | 69.53 |
| LUMO+3 → LUMO+2 | 0.34 | 12.74 |
| LUMO → VBM | 0.89 | 0.56 |
An ideal photocatalyst is not only required to separate the charge carriers rapidly, but also desired to maintain the charge separated for a long time. Subsequently, we will take the electron–hole recombination process into consideration. It's widely accepted that energy gap and nonadiabatic coupling are the two crucial factors determining the efficiency of nonadiabatic transition. The band gap between the LUMO state of PCBM and the VBM of PM6 is rather large (see Fig. 4). The average value is estimated to be 0.89 eV, which is more than eight times of that of the energy gap between CBM and the LUMO+3 state (see Table 1). Thus, the considerable energy differences are responsible for the slow electron–hole recombination. According to the expression of nonadiabatic coupling, djk is inversely proportional to the energy difference while proportional to the interstate coupling. Whether interstate coupling or energy difference governs the nonadiabatic couplings is specifically dependent on the studied systems. In most cases of dynamics simulations of materials, the wave function properties maintain essentially constant while the energy differences play an important role. However, the interstate coupling based on the wave function properties makes significant contributions in the present studied PM6/PCBM system. The calculated nonadiabatic coupling of electron–hole recombination is just 0.56 ps−1, two orders of magnitude smaller than that of above-stated electron transfer (Table 1). Therefore, both the large energy gaps and remarkably small nonadiabatic couplings reduce the electron–hole recombination significantly.
In brief, a dramatically long-lived charge-separated state can be achieved in the organic PM6/PCBM heterojunctions through efficient spatial separation of the photogenerated charge carriers across the donor/acceptor interface and the suppressed electron–hole recombination, consequently providing potential applications to trigger photoredox reactions in photocatalysis.
Hydrogen evolution reaction mechanisms in the PM6/PCBM heterojunction
In terms of the photogenerated charges in PM6/PCBM with an ultralong lifetime, their applications in photocatalysis are extremely promising. Kosco et al. have found that such organic donor/acceptor heterojunction exhibits outstanding performance for photocatalytic H2 evolution.40 However, the detailed mechanisms of the H2 generation are yet to be clarified, which impedes further advances. With the assistance of the first-principles calculations, an in-depth understanding of the photocatalytic hydrogen evolution process in the PM6/PCBM heterojunctions can be revealed.The widely accepted H2 generation process is: 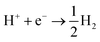 , in which one proton acquires an electron to generate hydrogen. As discussed above, the photogenerated electron would be transferred to the PCBM fragment on the femtosecond timescale, so the reduction reaction prefers to occur at PCBM, which is also in agreement with the experiment.40 There are two distinct types of C atoms acting as potential active sites at PCBM, i.e., C665 or C666, which is representative of the C atom at the junction of one pentagon ring with two benzene rings or at the junction of three benzene rings (see Fig. 5b and c). To investigate the photocatalytic hydrogen evolution activity at these two kinds of sites, we calculate the binding Gibbs free energy of H*, which has been well-accepted as the crucial indicator to evaluate the catalyst performance for H2 generation. Based on the Gibbs free energy profiles as depicted in Fig. 5a, the H adsorption energies at C665 and C666 sites are 0.54 eV and 1.11 eV, respectively. The energy required for hydrogen adsorption is reduced by half via altering the binding sites from C666 to C665, indicating the H2 production is more efficient at the C665 sites than at the C666 sites.
, in which one proton acquires an electron to generate hydrogen. As discussed above, the photogenerated electron would be transferred to the PCBM fragment on the femtosecond timescale, so the reduction reaction prefers to occur at PCBM, which is also in agreement with the experiment.40 There are two distinct types of C atoms acting as potential active sites at PCBM, i.e., C665 or C666, which is representative of the C atom at the junction of one pentagon ring with two benzene rings or at the junction of three benzene rings (see Fig. 5b and c). To investigate the photocatalytic hydrogen evolution activity at these two kinds of sites, we calculate the binding Gibbs free energy of H*, which has been well-accepted as the crucial indicator to evaluate the catalyst performance for H2 generation. Based on the Gibbs free energy profiles as depicted in Fig. 5a, the H adsorption energies at C665 and C666 sites are 0.54 eV and 1.11 eV, respectively. The energy required for hydrogen adsorption is reduced by half via altering the binding sites from C666 to C665, indicating the H2 production is more efficient at the C665 sites than at the C666 sites.
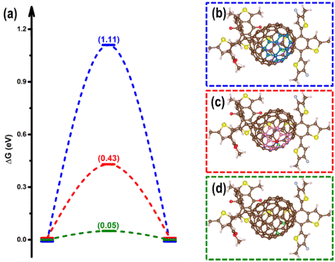 | ||
| Fig. 5 (a) The HSE06 + D3 calculated free energy profiles for hydrogen evolution at the C666 site (blue), C665 site (red), and C666 site with adjacent C665 site pre-hydrogenated (green). The free energy diagrams obtained at the PBE + D3 level are listed in Fig. S6.† Corresponding optimized structures of hydrogen adsorbed at the C666 site (b), C665 site (c), as well both C666 and C665 sites (d) of the PM6/PCBM heterojunctions. The pentagon and benzene rings surrounding the C665 and C666 sites are highlighted in (b) and (c). | ||
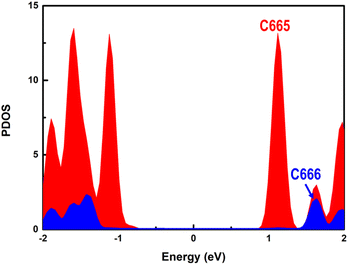
The higher photocatalytic hydrogen evolution activity of the C665 sites in comparison with the C666 sites can be understood in two aspects. The PDOS of C665 and C666 are separately presented in Fig. 6. It's clear that the CBM of C665 locates much lower than the CBM mainly derived from the C666 atoms, indicating the fate of the electrons generated upon photoexcitation is to concentrate at the C665 sites, where H+ species can be effectively reduced to H2. On the other hand, parallel to the well-known d-band center theory,93–97 it can be deduced that the binding strength of H adsorbates is much stronger with the C665 versus C666 sites since the energy of the C665 valence band is higher than that of the C666 valence band (see Fig. 6).98,99 Moreover, more than three-quarters of the C atoms in PCBM are assigned to the C665 sites. Plenty of C665 sites with high activity further improves the photocatalytic performance of the organic PM6/PCBM heterojunctions.
Based on the above results, the C666 sites in PCBM are insufficiently active for H2 production due to the large energy consumed for H binding. Is there a facile solution to advance the photocatalytic activity of the C666 sites? Astonishingly, we find that the binding of H at the C666 sites can be significantly enhanced through pre-adsorption of a hydrogen at the adjacent C665 atom. As stated above, the adsorption of H at the C665 is favorable. As the green line in Fig. 5a depicts, the Gibbs free energy change for H adsorption at the C666 site is remarkably reduced to 0.05 eV from 1.11 eV when a neighbor C665 site has been attached by a hydrogen (see Fig. 5d), which is comparable to that of excellent Pt catalyst (−0.09 eV).100 Bader charge analysis shows a higher accumulation of electrons at C666 sites (increased by 0.13 |e|) via hydrogenation of an adjacent C665 atom. The results are consistent with previous works, which indicate that hydrogenation can be a practical strategy to enhance the performance of HER, CO2RR, and NRR via refining the electronic density of the active sites.101–105 The results imply that the C666 sites can serve as superior hydrogen evolution sites given one surrounding C665 site has been hydrogenated.
Conclusions
PM6/PCBM shows remarkable promise in photocatalytic H2 evolution. Detailed mechanisms of the H2 generation are desired to further optimize the photocatalytic performance of such organic semiconductor heterojunctions. Long-lived charges and suitable reaction sites play essential roles in boosting activity of photocatalysts. In this article, we comprehensively explore the photoinduced carrier dynamics and hydrogen evolution reaction sites of organic PM6/PCBM heterojunctions, which are summarized in Fig. 7. Photogenerated electrons are rapidly extracted from the donor polymer PM6 into acceptor PCBM occurring within 1 ps after photoexcitation of the nanocomposite. The large energy gap and small nonadiabatic coupling between the VBM of PM6 and LUMO of PCBM heavily suppress the recombination of electron–hole pairs. As a result, long-lived electrons can be effectively achieved on the PCBM fragment, which will readily reduce proton to hydrogen at suitable sites. According to the calculated binding Gibbs free energy of H*, it's evident that the C665 sites exhibit higher photocatalytic H2 evolution activity in comparison with the C666 sites. However, the photocatalytic activity of C666 can be significantly enhanced through pre-hydrogenation of the adjacent C665 atom. The explicit structure–activity relationship in PM6/PCBM is revealed by the combination of static electronic structure calculations and nonadiabatic ab initio molecular dynamics simulations, thus providing insights into rational design and synthesis photocatalysts with high H2 evolution activity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by National Key Research and Development Program of China (No. 2021YFA1500703; G. C.); National Natural Science Foundation of China (No. 22103067; X. X.) and Natural Science Foundation of Shandong Province (No. ZR2021QB105; X. X.), and the Fundamental Research Funds for the Central Universities (G. C.).Notes and references
- M. I. Hoffert, K. Caldeira, G. Benford, D. R. Criswell, C. Green, H. Herzog, A. K. Jain, H. S. Kheshgi, K. S. Lackner and J. S. Lewis, et al. , Science, 2002, 298, 981–987 CrossRef CAS PubMed.
- N. S. Lewis, Science, 2007, 315, 798–801 CrossRef CAS PubMed.
- F. Creutzig, P. Agoston, J. C. Goldschmidt, G. Luderer, G. Nemet and R. C. Pietzcker, Nat. Energy, 2017, 2, 17140 CrossRef.
- G. Zhang, Z. A. Lan and X. Wang, Chem. Sci., 2017, 8, 5261–5274 RSC.
- Q. Xiang, J. Yu and M. Jaroniec, Chem. Soc. Rev., 2012, 41, 782–796 RSC.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- M. Kitano and M. Hara, J. Mater. Chem., 2010, 20, 627–641 RSC.
- D. J. Durbin and C. Malardier-Jugroot, Int. J. Hydrogen Energy, 2013, 38, 14595–14617 CrossRef CAS.
- R. Asahi, T. Morikawa, H. Irie and T. Ohwaki, Chem. Rev., 2014, 114, 9824–9852 CrossRef CAS PubMed.
- M. Ball and M. Weeda, Int. J. Hydrogen Energy, 2015, 40, 7903–7919 CrossRef CAS.
- J. Zhang, Y. Chen and X. Wang, Energy Environ. Sci., 2015, 8, 3092–3108 RSC.
- M. Karayilan, W. P. Brezinski, K. E. Clary, D. L. Lichtenberger, R. S. Glass and J. Pyun, Angew. Chem., Int. Ed., 2019, 58, 7537–7550 CrossRef CAS PubMed.
- F. E. Osterloh, Chem. Soc. Rev., 2013, 42, 2294–2320 RSC.
- Y. Zheng, L. Lin, B. Wang and X. Wang, Angew. Chem., Int. Ed., 2015, 54, 12868–12884 CrossRef CAS PubMed.
- Q. Wang and K. Domen, Chem. Rev., 2020, 120, 919–985 CrossRef CAS PubMed.
- A. Fujishima and K. Honda, Nature, 1972, 238, 37–38 CrossRef CAS PubMed.
- X. Chen, S. Shen, L. Guo and S. S. Mao, Chem. Rev., 2010, 110, 6503–6570 CrossRef CAS PubMed.
- L. Liu, X. Gu, Z. Ji, W. Zou, C. Tang, F. Gao and L. Dong, J. Phys. Chem. C, 2013, 117, 18578–18587 CrossRef CAS.
- L. Liu, Z. Ji, W. Zou, X. Gu, Y. Deng, F. Gao, C. Tang and L. Dong, ACS Catal., 2013, 3, 2052–2061 CrossRef CAS.
- Y. Ma, X. Wang, Y. Jia, X. Chen, H. Han and C. Li, Chem. Rev., 2014, 114, 9987–10043 CrossRef CAS PubMed.
- W. Zou, L. Zhang, L. Liu, X. Wang, J. Sun, S. Wu, Y. Deng, C. Tang, F. Gao and L. Dong, Appl. Catal., B, 2016, 181, 495–503 CrossRef CAS.
- Y. Goto, T. Hisatomi, Q. Wang, T. Higashi, K. Ishikiriyama, T. Maeda, Y. Sakata, S. Okunaka, H. Tokudome and M. Katayama, et al. , Joule, 2018, 2, 509–520 CrossRef CAS.
- Y. Wang, A. Vogel, M. Sachs, R. S. Sprick, L. Wilbraham, S. J. A. Moniz, R. Godin, M. A. Zwijnenburg, J. R. Durrant and A. I. Cooper, et al. , Nat. Energy, 2019, 4, 746–760 CrossRef CAS.
- X. Wang, K. Maeda, A. Thomas, K. Takanabe, G. Xin, J. M. Carlsson, K. Domen and M. Antonietti, Nat. Mater., 2009, 8, 76–80 CrossRef CAS PubMed.
- Y. Bai, L. Wilbraham, B. J. Slater, M. A. Zwijnenburg, R. S. Sprick and A. I. Cooper, J. Am. Chem. Soc., 2019, 141, 9063–9071 CrossRef CAS PubMed.
- C. Dai and B. Liu, Energy Environ. Sci., 2020, 13, 24–52 RSC.
- K. Sakaushi and M. Antonietti, Acc. Chem. Res., 2015, 48, 1591–1600 CrossRef CAS PubMed.
- G. Zhang, Z.-A. Lan and X. Wang, Angew. Chem., Int. Ed., 2016, 55, 15712–15727 CrossRef PubMed.
- V. S. Vyas, V. W.-h. Lau and B. V. Lotsch, Chem. Mater., 2016, 28, 5191–5204 CrossRef CAS.
- Y.-L. Wong, J. M. Tobin, Z. Xu and F. Vilela, J. Mater. Chem. A, 2016, 4, 18677–18686 RSC.
- E. Lanzarini, M. R. Antognazza, M. Biso, A. Ansaldo, L. Laudato, P. Bruno, P. Metrangolo, G. Resnati, D. Ricci and G. Lanzani, J. Phys. Chem. C, 2012, 116, 10944–10949 CrossRef CAS.
- J. Kosco, M. Bidwell, H. Cha, T. Martin, C. T. Howells, M. Sachs, D. H. Anjum, S. Gonzalez Lopez, L. Zou and A. Wadsworth, et al. , Nat. Mater., 2020, 19, 559–565 CrossRef CAS PubMed.
- H. Yang, X. Li, R. S. Sprick and A. I. Cooper, Chem. Commun., 2020, 56, 6790–6793 RSC.
- P. Fortin, S. Rajasekar, P. Chowdhury and S. Holdcroft, Can. J. Chem., 2018, 96, 148–157 CrossRef CAS.
- L. Lu, T. Zheng, Q. Wu, A. M. Schneider, D. Zhao and L. Yu, Chem. Rev., 2015, 115, 12666–12731 CrossRef CAS PubMed.
- Y.-X. Liu, M. A. Summers, S. R. Scully and M. D. McGehee, J. Appl. Phys., 2006, 99, 093521 CrossRef.
- G. Yu, J. Gao, J. C. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789–1791 CrossRef CAS.
- A. Liu, L. Gedda, M. Axelsson, M. Pavliuk, K. Edwards, L. Hammarström and H. Tian, J. Am. Chem. Soc., 2021, 143, 2875–2885 CrossRef CAS PubMed.
- Y. Liu, J. Wu and F. Wang, Appl. Catal., B, 2022, 307, 121144 CrossRef CAS.
- J. Kosco, S. Gonzalez-Carrero, C. T. Howells, T. Fei, Y. Dong, R. Sougrat, G. T. Harrison, Y. Firdaus, R. Sheelamanthula and B. Purushothaman, et al. , Nat. Energy, 2022, 7, 340–351 CrossRef CAS.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- J. C. Tully and R. K. Preston, J. Chem. Phys., 1971, 55, 562–572 CrossRef CAS.
- S. Hammes-Schiffer and J. C. Tully, J. Chem. Phys., 1994, 101, 4657–4667 CrossRef CAS.
- A. V. Akimov, A. J. Neukirch and O. V. Prezhdo, Chem. Rev., 2013, 113, 4496–4565 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- R. G. Parr and W. T. Yang, Density-Functional Theory of Atoms and Molecules, Oxford University Press, Dordrecht, 1994 Search PubMed.
- K. Fiolhais, F. Nogueira and M. Marques, A Primer in Density Functional Theory, Springer: Berlin, Dordrecht, 2003 Search PubMed.
- M. A. L. Marques, C. A. Ullrich, F. Nogueira, A. Rubio, K. Burke and E. K. U. Gross, Time-Dependent Density Functional Theory, Springer, Berlin, Dordrecht, 2006 Search PubMed.
- I. Franco and S. Tretiak, J. Am. Chem. Soc., 2004, 126, 12130–12140 CrossRef CAS PubMed.
- M. A. L. Marques and E. K. U. Gross, Annu. Rev. Phys. Chem., 2004, 55, 427–455 CrossRef CAS PubMed.
- M. A. Marques, X. López, D. Varsano, A. Castro and A. Rubio, Phys. Rev. Lett., 2003, 90, 258101 CrossRef PubMed.
- S. Tretiak, K. Igumenshchev and V. Chernyak, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 033201 CrossRef.
- R. Baer, T. Seideman, S. Ilani and D. Neuhauser, J. Chem. Phys., 2004, 120, 3387–3396 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Am. Chem. Soc., 2014, 136, 1599–1608 CrossRef CAS PubMed.
- A. V. Akimov and O. V. Prezhdo, J. Chem. Theory Comput., 2013, 9, 4959–4972 CrossRef CAS PubMed.
- T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- X.-Y. Liu, X.-Y. Xie, W.-H. Fang and G. L. Cui, J. Phys. Chem. A, 2018, 122, 9587–9596 CrossRef CAS PubMed.
- X.-Y. Liu, W.-K. Chen, W.-H. Fang and G. L. Cui, J. Phys. Chem. Lett., 2019, 10, 2949–2956 CrossRef CAS PubMed.
- X.-Y. Xie, X.-Y. Liu, Q. Fang, W.-H. Fang and G. L. Cui, J. Phys. Chem. A, 2019, 123, 7693–7703 CrossRef CAS PubMed.
- X.-Y. Xie, J.-J. Yang, X.-Y. Liu, Q. Fang, W.-H. Fang and G. L. Cui, Phys. Chem. Chem. Phys., 2021, 23, 13503–13511 RSC.
- X.-Y. Liu, J.-J. Yang, W.-K. Chen, A. V. Akimov, W.-H. Fang and G. L. Cui, J. Phys. Chem. Lett., 2021, 12, 1131–1137 CrossRef CAS PubMed.
- X.-Y. Liu, Z.-W. Li, W.-H. Fang and G. L. Cui, J. Phys. Chem. A, 2020, 124, 7388–7398 CrossRef CAS PubMed.
- J.-J. Yang, Z.-W. Li, X.-Y. Liu, W.-H. Fang and G. L. Cui, Phys. Chem. Chem. Phys., 2020, 22, 19542–19548 RSC.
- J.-J. Yang, X.-Y. Liu, Z.-W. Li, T. Frauenheim, C. Yam, W.-H. Fang and G. L. Cui, Phys. Chem. Chem. Phys., 2021, 23, 6536–6543 RSC.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- W. Chu, W. A. Saidi, Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, J. Am. Chem. Soc., 2016, 138, 13740–13749 CrossRef CAS PubMed.
- Q. Zheng, W. A. Saidi, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, Nano Lett., 2017, 17, 6435–6442 CrossRef CAS PubMed.
- Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, W. A. Saidi and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 205417 CrossRef CAS.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- A. Melianas, F. Etzold, T. J. Savenije, F. Laquai, O. Inganäs and M. Kemerink, Nat. Commun., 2015, 6, 8778 CrossRef CAS PubMed.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- Y. Wei, W.-H. Fang, Q. Fang and R. Long, J. Phys. Chem. C, 2018, 122, 7041–7050 CrossRef CAS.
- X. Zhao, H. Lu, W.-H. Fang and R. Long, Nanoscale, 2022, 14, 4644–4653 RSC.
- V. Stamenkovic, B. S. Mun, K. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Phys. Rev. Lett., 2004, 93, 156801 CrossRef CAS PubMed.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129 CAS.
- B. Hammer and J. K. Nørskov, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- J. Tian, Z. Zhou, S. Zhang, Z. Li, L. Shi, Q. Li and J. Wang, J. Mater. Chem. A, 2021, 9, 11753–11761 RSC.
- X. Bai, C. Ling, L. Shi, Y. Ouyang, Q. Li and J. Wang, Sci. Bull., 2018, 63, 1397–1403 CrossRef CAS.
- J. K. Nørskov, T. Bligaard, A. Logadottir, J. R. Kitchin, J. G. Chen, S. Pandelov and U. Stimming, J. Electrochem. Soc., 2005, 152, J23 CrossRef.
- M. Ziemba, M. Radtke, L. Schumacher and C. Hess, Angew. Chem., Int. Ed., 2022, 61, e202209388 CrossRef CAS PubMed.
- D. Wang, X. Jiang, Z. Lin, X. Zeng, Y. Zhu, Y. Wang, M. Gong, Y. Tang and G. Fu, Small, 2022, 18, 2204063 CrossRef CAS PubMed.
- G. Jia, Y. Wang, X. Cui, H. Zhang, J. Zhao, L. H. Li, L. Gu, Q. Zhang, L. Zheng and J. Wu, et al. , Matter, 2022, 5, 206–218 CrossRef CAS.
- X.-Y. Xie, P. Xiao, W.-H. Fang, G. L. Cui and W. Thiel, ACS Catal., 2019, 9, 9178–9187 CrossRef CAS.
- C. Ling, Y. Zhang, Q. Li, X. Bai, L. Shi and J. Wang, J. Am. Chem. Soc., 2019, 141, 18264–18270 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta07170c |
| This journal is © The Royal Society of Chemistry 2022 |