Electron diffraction of 1,4-dichlorobenzene embedded in superfluid helium droplets†
Stephen D.
Bradford
a,
Yingbin
Ge
 b,
Jie
Zhang
b,
Jie
Zhang
 a,
Marisol
Trejo
a,
Dale
Tronrud
a and
Wei
Kong
a,
Marisol
Trejo
a,
Dale
Tronrud
a and
Wei
Kong
 *a
*a
aDepartment of Chemistry, Oregon State University, Corvallis, OR 97331, USA. E-mail: wei.kong@oregonstate.edu; Tel: +1 541-737-6714
bDepartment of Chemistry, Central Washington University, Ellensburg, WA 98926, USA
First published on 7th November 2022
Abstract
We perform electron diffraction of 1,4-dichlorobenzene (C6H4Cl2, referred to as 2ClB) embedded in superfluid helium droplets to investigate the structure evolution of cluster growth. Multivariable linear regression fittings are used to determine the concentration and the best model structures of the clusters. At a droplet source temperature of 22 K with droplets containing on average 5000 He atoms, the fitting results agree with the doping statistics modeled using the Poisson distribution: the largest molecular clusters are tetramers, while the abundances of monomers and dimers are the highest and are similar. Molecular dimers of 2ClB are determined to have a parallel structure with a 60° rotation for the Cl–Cl molecular axes. However, a better agreement between experiment and fitting is obtained by reducing the interlayer distance that had been calculated using the density functional theory for dimers. Further calculations using the highest level quantum mechanical calculations prove that the reduction in interlayer distance does not significantly increase the energy of the dimer. Cluster trimers adopt a dimer structure with the additional monomer slanted against the dimer, and tetramers take on a stacked structure. The structure evolution with cluster size is extraordinary, because from trimer to tetramer, one monomer needs to be rearranged, and neither the trimer nor the tetramer adopts the corresponding global minimum structure obtained using high level coupled-cluster theory calculations. This phenomenon may be related to the fast cooling process in superfluid helium droplets during cluster formation.
1. Introduction
Solving atomic structures, particularly structures of biological macromolecules, is of paramount importance in modern science. To overcome the recalcitrant problem of crystallization in single crystal X-ray diffraction, several new methods have been invented such as diffraction-before-destruction1–3 and cryo-electron microscopy.4–6 Our group is currently working on a new technique called serial single molecule electron diffraction imaging (SS-EDI).7 This method involves aligning molecules in superfluid helium droplets using an elliptically polarized laser8,9 and performing electron diffraction. By aligning the molecules of interest in a specific orientation, the signal-to-noise ratio of the diffraction image can be improved with each successive diffraction event. Subsequent change in sample orientation ensures complete sampling of projections for three dimensional information.As we attempt to develop the first prototype of this idea, we have taken advantage of the cluster forming tendency of superfluid helium droplets and performed electron diffraction of neutral and cationic molecular clusters embedded in superfluid helium droplets.10,11 Our work on I2 has revealed the presence of halogen bond from iodine clusters in droplets,12 and our work on CS2 has confirmed the gas phase structure of dimers but solid-like structure for trimers.13 The structure evolution of clusters with increasing units of monomers has painted a varied path for different species, trapping some in metastable states, while allowing others to find the global minimum.14–16
In this work, we report the structure of 1,4-dichlorobenzene (C6H4Cl2, 2ClB) clusters embedded in superfluid helium droplets. This work is partially motivated by the two competing structures of benzene dimers, either parallel or T-shape, depending on the charge of the dimer.17,18 Although with the substitution of the two heavy atoms, 2ClB may not be representative of benzene, it is an easy starting point of investigation and the heavy atoms are advantageous for diffraction. There is currently no information on the structures of 2ClB clusters in the gas phase. Crystalline 2ClB has 3 reported structures determined using X-ray diffraction,19 including the α structure at room temperature, the highly symmetric β structure more common at higher temperatures (>325 K), and the γ structure at lower temperatures (100 K). These structures can also interchange given appropriate conditions and sufficient time. We discover that under our current experimental conditions, only gas phase clusters can form within superfluid helium droplets, and that the growth pattern of these clusters does not converge to any of the crystal structures. The fast cooling rate of superfluid helium might trap the clusters in metastable geometries,20,21 away from the global minimum or any intermediate state of crystal forms. We also notice a discrepancy between experiment and calculation on the interlayer distance of a dimer, and the reduced distance from experiment is validated from a high level calculation using the most extensive available basis set. Further experiments involving larger helium droplets will need to be conducted to observe bulk crystal formation or confirm the amorphous state of 2ClB formed in superfluid helium droplets.
2. Experimental setup
The experimental setup has been explained in previous publications.10,22,23 A cryostat (Sumitomo, SRDK-408SW) pre-cools the helium gas to 22 K held at 70 atm in a pulse valve (termed DPV in the following, E-L-5-8-C-Unmounted Cryogenic Copper Even-Lavie valve) of 50 μm in nozzle diameter. The release of helium into the source chamber at 5 Hz causes the pressure in the chamber to rise from 3 × 10−7 torr to 3 × 10−6 torr. Superfluid helium droplets formed through isentropic expansion travel approximately 20 cm to pass through a 2 mm skimmer cone to enter the doping chamber. The sample, 1,4-dichlorobenzene (Sigma Aldrich, 99.99% purity) is introduced into the doping chamber via a heated sample pulse valve (SPV, Parker series 9, with a 500 μm nozzle diameter). The vacuum of the doping chamber is raised from 3 × 10−8 torr to 5 × 10−5 torr when the SPV is in operation at 10 Hz. At 70 °C, the vapor pressure of the sample is 60 torr (7.9 × 103 Pa).24 The doping chamber is separated from the diffraction chamber via another cone (5 mm in diameter). The vacuum level of the diffraction chamber rises from 1 × 10−8 torr to 5 × 10−8 torr when the SPV is on, but it does not change with the operation of the DPV.During diffraction, a pulsed electron beam (Kimball physics, EFPS-6210B) with a duration of 30 μs, an energy of 40 keV, a current of roughly 1 mA, and a beam diameter of 3 mm, intersects with the doped helium droplets. A phosphor screen (Beam Imaging Solutions, P43) of 40 mm in diameter located directly below the electron beam receives the diffracted electrons and produces fluorescence, which is recorded by an Electron Multiplying Charge Coupled Device camera (iXon Ultra, Andor Technology). The flux of the electron beam is measured via a Faraday cup located at the center of the phosphor screen.
2.1 Characterization of doping conditions
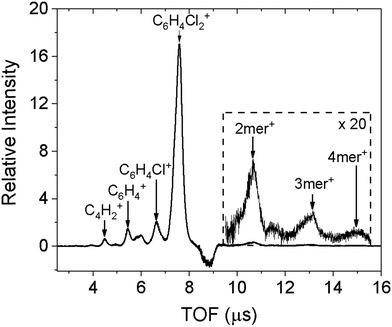
The doped droplets can be characterized using a time-of-flight (TOF) mass spectrometer arranged coaxial with the droplet beam. The fourth harmonic of a pulsed Nd:YAG (Quantel, Brilliant) laser at 266 nm ionizes the dopant molecules via two-photon ionization (ionization energy of 2ClB: 8.92 eV),24 and ionization further results in ejection of the doped ions.25 The bare ions are accelerated and detected by a set of microchannel plates in the TOF spectrometer. The resulting spectrum is shown in Fig. 1. In addition to the predominant parent peak, three fragments with decreasing intensities are also observable, corresponding to sequential loss of chlorine atoms and a few additional carbon and hydrogen atoms. Molecular clusters are also present, ranging from dimer to tetramer, as shown in the inset. We believe that fragmentation is caused by the ionization laser, hence the diffraction profile should contain contributions from gas phase monomers to tetramers. This point will be confirmed when fitting the diffraction profiles.The negative peak at 8.8 μs corresponds to a contaminant present in the diffraction chamber. The experiment is conducted with active background subtraction: the SPV and the laser (or the pulsed electron gun in the diffraction experiment) operate at 10 Hz, while the DPV operates at 5 Hz. Only the difference spectrum obtained when the DPV is on and off is attributed to the doped sample. The contaminant is present in both mass spectra, however, when the DPV is on, the leading portion of the droplet beam removes the ambient contaminant from the ionization region, resulting in a smaller signal of the contaminant and therefore a negative contribution in the difference spectrum.
To ensure that helium does not overwhelm the detector,10 we need to minimize its contribution by reducing the amount of undoped helium droplets. To achieve this, we can monitor the intensity of the parent peak while increasing the doping pressure of the sample: the signal will increase until a turning point when the signal will begin to decrease. This is because sufficient collisions of the sample with the droplets have started to destroy some of the smaller droplets, preventing them from reaching the diffraction region. Further increase in doping pressure shifts the Poisson distribution to increasingly large molecular clusters inside the droplets, and significantly reduces the number of undoped droplets. Consequently, the actual diffraction intensity, monitored at the half radius of the diffraction screen, is reduced by 90% compared with that of neat droplets, due to the destruction of small droplets.
2.2 Modeling doping conditions using Poisson distribution
We measured the size of the helium droplets using benzene as a dopant in a previous experiment.13 The ionization threshold of benzene is 9.24 eV,26 resulting in minimal excess energy when ionized via two photons at 266 nm (9.35 eV in total). The photostability of benzene is also advantageous for maintaining the integrity of the droplet, compared with its chloro-substituted species. The mass spectrum of benzene doped helium droplets contains only parent ions and clusters ions, showing no sign of fragmentation. Under the current droplet source conditions, three different size groups containing 150, 800 and 5000 helium atoms have been determined.13 From the heat capacity of 2ClB,27 pickup of one monomer will result in evaporation of 500 He atoms,28 about 10% of the total size of the largest cluster. To model using Poisson statistics,29 the cross section of a helium droplet should be relatively constant during successive doping, which is adequate for the group with the largest size, while the first two groups with smaller sizes are destroyed in the doping region. We have also compared the results obtained using the Markovian arrival process,13 taking into consideration the reduction in droplet size during successive doping events, but the results are almost identical to those of the simple Poisson distribution.2.3 Calculation methods
All calculations including density functional theory (DFT) and coupled-cluster single, double, and perturbative triple excitations (CCSD(T)) were carried out using the Gaussian 16 program.30 The structures of 2ClB and 2ClB clusters were optimized using the B3LYP functional31–33 coupled with Grimme's D3BJ empirical dispersion corrections,34 hereafter referred to as the B3LYP-D3BJ method. The valence double-ζ 6-31G(d) basis sets were employed for the C, H, and Cl atoms during geometry optimization. Vibrational frequency calculations were carried out at the same B3LYP-D3BJ/6-31G(d) level of theory to ensure that the optimized structures are all local minima without any imaginary frequencies. To determine the relative energies of the local minima accurately, CCSD(T)35 single-point energy calculations were carried out on the optimized structures from B3LYP-D3BJ using the same 6-31G(d) basis sets, hereafter referred to as the CCSD(T)//B3LYP-D3BJ/6-31G(d) calculations. The “//” sign is used to separate the higher-level method for the single-point energy calculation and the lower-level method for the geometry optimization calculation. The CCSD(T) method, known as the “gold standard” in quantum chemistry, was chosen to compute the single-point energies because its high level of accuracy is needed to determine the reliable energy rankings for the 2ClB cluster structures with small energy spacings. The downside of using the CCSD(T) method is that the computing time of a CCSD(T) energy calculation scales as O(N7), where N is the size of the system. When the size of the system doubles, the computing time increases by 27 = 128 fold in theory. The actual computing time scale is even worse than O(N7) due to the limitation of the available memory and the less-than-ideal parallelization across multiple CPUs. For example, the CCSD(T)/6-31G(d) single-point energy calculation of the dimer took ∼3 CPU days on a Linux cluster that consists of thirty two 2.9 GHz Xeon E5-2690 processors, while the CCSD(T) calculations of the tetramer took between 500 and 800 CPU days on the same Linux cluster. Because of their prohibitive computing cost, the CCSD(T)/6-31G(d) single-point calculations were performed for the monomer, dimers, trimers, and tetramers of 2ClB.Several comparative calculations have been performed to validate the optimization method. To ensure that the valence double-ζ 6-31G(d) basis sets are suitable for geometry optimization of 2ClB clusters at the B3LYP level, B3LYP/6-311G(d,p) and B3LYP/6-311++G(d,p) single-point calculations were carried out on the optimized structures from the B3LYP-D3BJ/6-31G(d) calculations. The employment of the larger valence triple-ζ 6-311G(d,p) and 6-311++G(d,p) basis sets in the B3LYP calculation generated similar binding energies as those obtained using the 6-31G(d) basis sets. To ensure that the B3LYP-D3BJ method is suitable for geometry optimization of 2ClB clusters, another widely used density functional theory method, ωB97X-D,36 was also used to carry out the optimization calculation followed by the CCSD(T) single-point calculation. The CCSD(T)//ωB97X-D/6-31G(d) binding energies agree with those from CCSD(T)//B3LYP-D3BJ/6-31G(d) calculations. These comparative studies of using different combinations of DFT methods and basis sets suggest that the B3LYP-D3BJ/6-31G(d) calculations provide reasonably accurate structures of 2ClB and 2ClB clusters. The results of these comparative studies are graphed in Fig. S1 in the ESI.†
3. Results
3.1 Calculation results
Our B3LYP-D3BJ/6-31G(d) calculations of gas phase clusters result in local minimum structures of one dimer, five trimers, ten tetramers, seven pentamers, and seven hexamers. Only a few of the most stable structures are listed in Fig. 2, while a complete list of all trimer and tetramer structures with the CCSD(T)//B3LYP-D3BJ/6-31G(d) relative energies, along with the optimized pentamer and hexamer structures at the B3LYP-D3BJ/6-31G(d) level, are provided in the ESI.† The gas phase dimer structure has a binding energy of 17.2 kJ mol−1, and it consists of two quasi parallel monomers separated by 3.3 Å with a 60° rotation between the Cl–Cl molecular axes. In comparison, the most compact crystal cuts from the α, β, and γ structures have intermolecular spacings of 3.46 Å, 3.43 Å, 2.21 Å, but with in-plane shifts of 1.7 Å along the c axis for the α and β structures, and of 5.5 Å along the b axis for the γ structure. There are no rotations between the molecular axes for all crystal structures.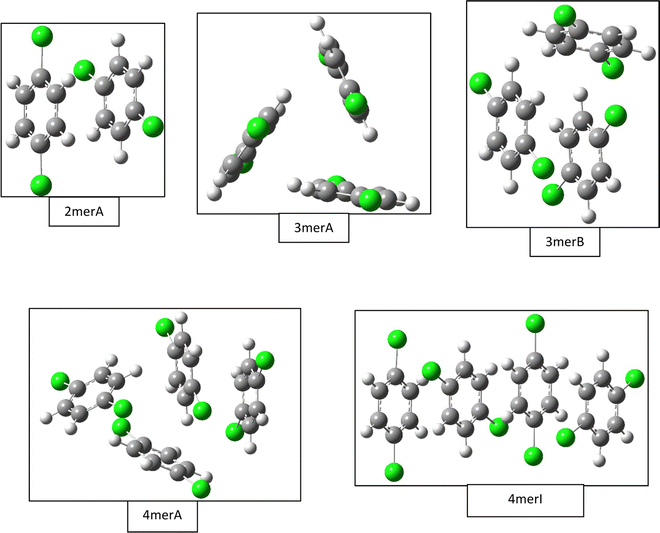 | ||
| Fig. 2 Selected gas phase structures from density functional theory calculations. Structures for the dimer (2merA), trimer (3merA), and tetramer (4merA) are the global minima, while other structures including trimer (3merB) and tetramer (4merI) are results from fittings of the experimental data (see Fig. 4). | ||
The most stable trimer (3merA) is triangular in shape and has the highest symmetry among all converged structures. The ultrastability of this global minimum structure can be understood by visualizing its sixth highest-occupied molecular orbital (denoted by HOMO−5) in Fig. 3. While the top six HOMOs are all linear combinations of the six nearly degenerate π orbitals (two from each benzene ring), only HOMO−5 involves significant electron delocalization over all three benzene rings, similar to the intermolecular electron delocalization identified previously in benzene trimers.37
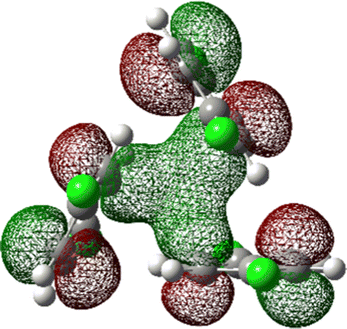 | ||
| Fig. 3 HOMO−5 of the global minimum structure of the 2ClB trimer (3merA) at the CCSD(T)//B3LYP-D3BJ/6-31G(d) level of theory. | ||
Several higher energy trimer structures have a 2+1 motif, consisting of a parallel dimer of different displacements and relative rotations, with a third monomer slanted against the dimer, as represented by 3merB in Fig. 2. Other structures have non-parallel and irregularly stacked molecular planes, and are generally termed “clam” shape. The most stable structure with the 2+1 motif is very similar in energy to that of the lowest energy structure (3merA), differing by only 2.6 kJ mol−1 at the CCSD(T)//B3LYP-D3BJ/6-31G(d) level.
Fig. 2 shows only two tetramer structures, including the most stable tetramer (4merA) and the tetramer that fits the best in the statistical model (4merI). The most stable tetramer 4merA has a 3+1 motif, containing the most stable trimer structure (3merA) of a triangular shape and a fourth monomer aligned in parallel with one of the three sides of the triangle. The structure of 4merI contains two parallel stacked dimers with a molecular axis rotation of 60°. These two tetramer structures, 4merA and 4merI, differ in energy by 11.7 kJ mol−1. The other eight tetramer structures with relative energies can be found in the ESI.†
3.2 Experimental results
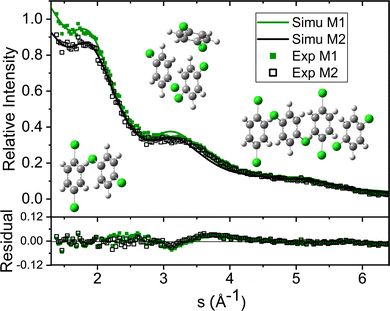
The experimental diffraction profiles from doped droplets and neat droplets are shown in Fig. 4, together with the final fitting result, contributions from the helium background, and contributions from clusters of 2ClB. The vertical axis corresponds to the radial profile of the circularly symmetric diffraction pattern I(s), while the horizontal axis corresponds to the momentum transfer s in units of Å−1:38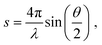 | (1) |
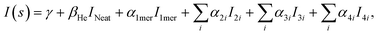 | (2) |
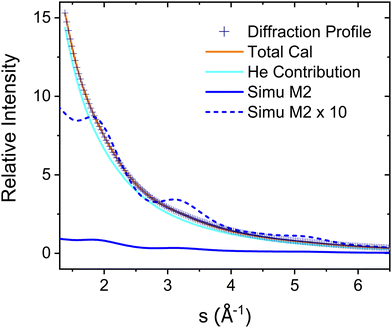 | ||
| Fig. 4 Experimental diffraction profile, fitting (Total Cal), helium contribution, and simulated dopant contributions of 2ClB (Simu M2) embedded in superfluid helium droplets. The difference between the experimental and simulated profiles is shown in Fig. 5. | ||
The model structures in the fitting include those from computation and from cuts of the crystal structures as shown in the ESI.† Altogether we investigated 32 structures of clusters, including one monomer, 5 dimers, 10 trimers and 16 tetramers. No larger clusters than tetramers are considered because droplets containing larger molecular clusters should have a limited transmission efficiency into the diffraction region.40 Assuming that 500 He atoms are removed upon pickup of one 2ClB molecule, and even without consideration of the binding energies of the molecular cluster, a droplet containing 5000 atoms will be reduced to 3000 atoms after picking up 4 monomers. At this size and after bombarding with 4 molecules, transmission of the droplet into the diffraction region is significantly reduced.
The large number of fitting parameters in eqn (2) poses a statistical problem, hence we separated the structures of 5 dimers into 2 groups (the second group contains 1 repeated structure from the first group), the 10 trimer structures into 4 groups (with 2 structures repeated in the last group), and the 16 tetramers into 6 groups (with 2 structures repeated in the last group), so that each group contains 3 structures, i.e. 3 independent fitting parameters. We then fitted all possible combinations of these groups of dimers, trimers, and tetramers, with each fitting containing 12 independent parameters for the multilinear regression, including the baseline γ, the droplet fraction β, the monomer coefficient α1mer, and 9 fitting parameters from the cluster groups. The fitting results are then ranked according to the Akaike information criterion (AIC):41
| AIC = m·ln(σ2) + 2k, | (3) |
We also rely on the doping statistics to eliminate fitting results that have low AIC values but contain unrealistic contributions from different sized clusters. For example, at a doping pressure of 2 × 10−5 Pa for helium droplets containing 5000 helium atoms, the Poisson distribution predicts that dopant cluster sizes ranging from 1 to 4 should have abundances of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.98
0.98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.65
0.65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.32, hence fittings containing negligible contributions of monomers are eliminated. Similarly, fittings containing no contribution of dimers but statistically significant contributions of trimers, or no contributions of trimers but statistically significant contributions of tetramers, are also eliminated.
0.32, hence fittings containing negligible contributions of monomers are eliminated. Similarly, fittings containing no contribution of dimers but statistically significant contributions of trimers, or no contributions of trimers but statistically significant contributions of tetramers, are also eliminated.
Unfortunately, the results from all 48 fittings, even with the above considerations, showed no clear preference for one or a few models over the rest. However, a consistent conclusion from all the fittings was that only the gas phase dimer was statistically significant, while all cuts of dimers from the three crystal structures were insignificant. We therefore concluded that dimers in droplets are of the gas phase structure. We then used the gas phase dimer structure and performed 24 more fittings with the trimer and tetramer groups. With the reduced number of fitting parameters (10 instead of 12, due to removal of two parameters associated with crystalline dimers), only one model was favored statistically within the constraint of Poisson distribution.
The green symbols and solid lines labeled M1 in Fig. 5 represent the net contribution of 2ClB clusters from experiment and from fitting, after removing the contribution of helium. The residue in the bottom panel is generally satisfactory, except for the region from s = 2 to 4. We first suspected that chlorine atoms could be lost due to heating in the sample pulse valve, so we tried to remove one or both chlorine from 2ClB from the test structures, and in both cases, the fitting quality deteriorated dramatically. To test whether the structures of clusters contain systematic problems, we reduced the interlayer distance of the dimers by 4%, while maintaining the tilt angle between the two molecular planes. The result improved statistically, with the AIC value lowered by 45. We then performed a single point calculation using CCSD(T)/6-311++G(d,p)//B3LYP/6-31G(d) for dimer structures with reduced interlayer distances by 2% and 4%, and the resulting energies are 0.0 and 0.8 kJ mol−1 above that of the original structure. This result suggests that the B3LYP method does slightly overestimate the interlayer distance. We also adjusted the relative orientation of the two molecules in the dimer, but the fitting quality was statistically the same within 5° of rotation, beyond which the fit became progressively worse. We also adjusted the spacing of the optimal trimer structure 3merB, which also resulted in a worse fitting result. At this stage, we do not have further ideas on improving the fitting quality in the region between s = 3.2 and 4. The black symbols and solid line labeled M2 in Fig. 5 represent the fitting result: improvements in the region below s = 3.2 can be observed.
Table 1 lists the coefficients of the fitting result using the reduced dimer distance, and Poisson statistics. In this result, the trimer is of the 2+1 (3merB) motif, 2.6 kJ mol−1 above the global minimum (3merA), and the tetramer is stacked (4merI), 11.7 kJ mol−1 above the global minimum (4merA). The ratio of contributions from monomer through tetramer is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.24
1.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.33
0.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.19. The value of β is 0.119, hence after the sample is doped into the helium droplets, only 11.9% of the helium remains to carry the sample downstream. This value is consistent with the loss in diffraction intensity due to sample doping as explained in Section 2.1.
0.19. The value of β is 0.119, hence after the sample is doped into the helium droplets, only 11.9% of the helium remains to carry the sample downstream. This value is consistent with the loss in diffraction intensity due to sample doping as explained in Section 2.1.
| Fitting parameter | Ratio to monomer | Poisson ratio to monomer | |
|---|---|---|---|
| Monomer | 2.70 × 10−3 ± 2.8 × 10−4 | 1 | 1 |
| 2merA | 3.34 × 10−3 ± 4.1 × 10−4 | 1.24 | 0.98 |
| 3merB | 8.96 × 10−4 ± 2.3 × 10−4 | 0.33 | 0.65 |
| 4merE | 5.13× 10−4 ± 4.8 × 10−5 | 0.19 | 0.32 |
| Helium | 1.19 × 10−1 ± 2.8 × 10−4 |
We note here that the above exercise is suggestive of the resolving power of our diffraction experiment, although some caution is warranted. The initial discrepancy between experiment and calculation represented by M1 prompted the need of a higher level calculation, which further revealed the problem of the B3LYP functional in calculating the interlayer distance. The resulting correction in interlayer distance, on the order of 4% corresponding to 0.14 Å, is also indicative of our experimental resolution. In our previous work of neutral and cationic pyrene clusters,10,14,16 we were able to resolve interlayer distances of 0.5 Å. The current work reaffirms the subÅngstrom resolution of this experiment. However, as shown in Fig. 5, the fitting with the revised interlayer distance results in a slightly different contribution of helium, and the improvement in the final fitting quality is a combined result of helium contribution and cluster structure. Further improvements in the signal-to-noise ratio of the experimental data or more experiments under different cluster concentrations are needed for a definitive statement on the experimental resolution. We also acknowledge that the bond length may change in the helium environment,43 but given the limited resolution, this change is not a concern at this stage of the experiment.
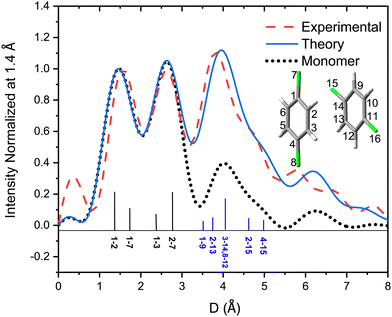
Fig. 6 shows the pair-distance distribution obtained from inverse Fourier transform of the diffraction profiles of Fig. 5. For this purpose, the modified molecular scattering intensity sM(s) is calculated from the experimental result using
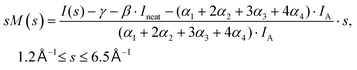 | (4) |
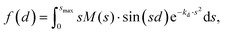 | (5) |
A few of the most intense pairs are labeled in the figure. The intramolecular pair distances are predominately in the region below 3 Å, while the inter-molecular pairs concentrate in the distance range longer than 4 Å due to the interlayer distance of ∼3.3 Å and the slip and rotation between the two molecules. The mismatch of the peak at 1.5 Å is opposite to the peak at 4 Å: the molecular frame of the monomer seems to be larger than expected in droplets, but the interlayer pair distances seem to be smaller. More experiments performed under different concentrations of the clusters need to be performed to confirm importance of these differences.
The conclusion from the above fitting results paints an intriguing evolution process for clusters formed in superfluid helium droplets. After the formation of a stacked dimer, the next 2ClB entering the droplet is oriented nearly perpendicular to the dimer, forming a 2+1 trimer. The most likely tetramer structure from the fitting, a stacked tetramer, cannot be easily obtained from the 2+1 trimer without a significant rearrangement of the third molecule in the trimer. The structure of neither the trimer nor the tetramer corresponds to its global minimum. We speculate that the kinetics of structure relaxation might play a role in the observed cluster structures. With the pickup of the third molecule together with its extra thermal energy, some slight tilts of the molecular planes of the dimer are possible, but to reach the global minimum of a triangular shape, a dramatic rearrangement is necessary. In the meantime, the surrounding helium quickly removes the internal energy of the cluster, freezing the cluster in its local minimum. Pickup of the fourth molecule is extremely puzzling, and attempts to find the transition state from the 2+1 trimer to a stacked trimer are limited by the available computational power. In our work on nanoclusters of I2,12 we also suspected that a large stable molecular cluster may result in evaporation of too many helium atoms, thereby reducing the probability of the resulting droplet traveling to the diffraction region. In this scenario, only metastable structures with the loss of fewer helium atoms can survive the doping process and be detected.
Similar observations of clusters stuck in structures of local minima have been reported in several previous works from superfluid helium droplets.44 For example, HCN forms a linear chain within superfluid helium droplets,44 different from the lowest energy folded structure. In our own work on CS2 embedded in superfluid helium droplets,13 although the dimer adopts the gas phase global minimum structure, the trimer adopts a crystal cut structure, different from the global minimum of a highly symmetric pinwheel structure. In another example, pyrene shows that a stacked trimer structure is preferred over the closely packed crystal structure.16 The helium environment is unique in its temperature and rate of energy removal, hence clusters formed in helium droplets may not be of identical structures as those of the gas phase or the solid state.
4. Conclusion
In this study we have shown the ease of forming molecular clusters inside superfluid helium droplets and demonstrated the possibility of determining the structure evolution of molecular clusters using electron diffraction. Without prior results on cluster structures of 2ClB, we relied on theoretical calculations and cuts from crystals for multiple linear regression fittings. The discrepancy between experiment and calculation prompted the need of a high level calculation using an extensive basis set, and the result revealed that B3LYP tends to overestimate the interlayer distance by 4% for dimers. This result further demonstrates that the precision of the diffraction experiment in determining this distance is on the order of subangstrom. We have also observed a unusual pattern of cluster structure evolution in superfluid helium droplets. While the trimer is of a 2+1 motif, the tetramer is stacked: the growth pattern of the cluster is inconsistent with the expectation of a simple addition of a newly absorbed molecule. Furthermore, the structures of trimer and tetramer are not the global minimum. This result is yet another example that the superfluid helium environment can trap the molecular cluster in a local minimum. This work has furthered the insight into how halogen substituted benzene structures form clusters within the superfluid helium environment and can hopefully lead to better understandings of these types of systems. Future work will focus on measurements of structures of larger 2ClB clusters in helium droplets, to determine if and when the structures of larger clusters converge to crystalline structures, as well as on measurements of structures of benzene clusters.Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This material is based upon work supported by National Institute of General Medical Sciences (1R01GM101392-01A1) from the National Institutes of Health.References
- R. Neutze, R. Wouts, D. van der Spoel, E. Weckert and J. Hajdu, Nature, 2000, 406, 752–757 CrossRef PubMed
.
- J. C. H. Spence, Struct. Dyn., 2017, 4, 044027 CrossRef PubMed
.
- I. V. Lundholm, J. A. Sellberg, T. Ekeberg, M. F. Hantke, K. Okamoto, G. van der Schot, J. Andreasson, A. Barty, J. Bielecki, P. Bruza, M. Bucher, S. Carron, B. J. Daurer, K. Ferguson, D. Hasse, J. Krzywinski, D. S. D. Larsson, A. Morgan, K. Muhlig, M. Muller, C. Nettelblad, A. Pietrini, H. K. N. Reddy, D. Rupp, M. Sauppe, M. Seibert, M. Svenda, M. Swiggers, N. Timneanu, A. Ulmer, D. Westphal, G. Williams, A. Zani, G. Faigel, H. N. Chapman, T. Moeller, C. Bostedt, J. Hajdu, T. Gorkhover and F. R. N. C. Maia, IUCrJ, 2018, 5, 531–541 CrossRef PubMed
.
- C. L. Lawson, A. Kryshtafovych, P. D. Adams, P. V. Afonine, M. L. Baker, B. A. Barad, P. Bond, T. Burnley, R. Cao, J. Cheng, G. Chojnowski, K. Cowtan, K. A. Dill, F. DiMaio, D. P. Farrell, J. S. Fraser, M. A. Herzik Jr, S. W. Hoh, J. Hou, L.-W. Hung, M. Igaev, A. P. Joseph, D. Kihara, D. Kumar, S. Mittal, B. Monastyrskyy, M. Olek, C. M. Palmer, A. Patwardhan, A. Perez, J. Pfab, G. D. Pintilie, J. S. Richardson, P. B. Rosenthal, D. Sarkar, L. U. Schafer, M. F. Schmid, G. F. Schroder, M. Shekhar, D. Si, A. Singharoy, G. Terashi, T. C. Terwilliger, A. Vaiana, L. Wang, Z. Wang, S. A. Wankowicz, C. J. Williams, M. Winn, T. Wu, X. Yu, K. Zhang, H. M. Berman and W. Chiu, Nat. Methods, 2021, 18, 156–164 CrossRef CAS PubMed
.
- M. L. Taheri, E. A. Stach, I. Arslan, P. A. Crozier, B. C. Kabius, T. LaGrange, A. M. Minor, S. Takeda, M. Tanase, J. B. Wagner and R. Sharma, Ultramicroscopy, 2016, 170, 86–95 CrossRef CAS PubMed
.
- D. Elmlund and H. Elmlund, Annu. Rev. Biochem., 2015, 84, 499–517 CrossRef CAS
.
-
J. Beckman, W. Kong, V. G. Voinov and W. M. Freund, USA Pat., Apparatus and method for determining molecular structure, US20150168318A1, 2016 Search PubMed
.
- J. Yang and M. Centurion, Struct. Chem., 2015, 26, 1513–1520 CrossRef CAS
.
- E. T. Karamatskos, S. Raabe, T. Mullins, A. Trabattoni, P. Stammer, G. Goldsztejn, R. R. Johansen, K. Długołecki, H. Stapelfeldt, M. J. J. Vrakking, S. Trippel, A. Rouzée and J. Küpper, Nat. Commun., 2019, 10, 3364 CrossRef PubMed
.
- J. Zhang and W. Kong, Phys. Chem. Chem. Phys., 2022, 24, 6349–6362 RSC
.
-
Molecules in Superfluid Helium Nanodroplets, in Topics in Applied Physics, ed. A. Slenczka and J. P. Toennies, Springer, Switzerland, 2022, vol. 145 Search PubMed
.
- Y. He, J. Zhang, L. Lei and W. Kong, Angew. Chem., Int. Ed., 2017, 56, 3541–3545 CrossRef CAS
.
- J. Zhang, S. Bradford and W. Kong, J. Chem. Phys., 2020, 152, 224306 CrossRef CAS PubMed
.
- L. Lei, J. Zhang, M. Trejo, S. Bradford and W. Kong, J. Chem. Phys., 2022, 156, 051101 CrossRef CAS PubMed
.
- J. Zhang, M. Trejo, S. Bradford and W. Kong, J. Phys. Chem. Lett., 2021, 12, 9644–9650 CrossRef CAS PubMed
.
- L. Lei, Y. Yao, J. Zhang, D. Tronrud, W. Kong, C. Zhang, L. Xue, L. Dontot and M. Rapacioli, J. Phys. Chem. Lett., 2020, 11, 724–729 CrossRef CAS
.
- T. Poerschke, D. Habig, G. Schwaab and M. Havenith, Z. Phys. Chem. (Muenchen, Ger.), 2011, 225, 1447–1456 CrossRef CAS
.
- M. J. Rusyniak, Y. M. Ibrahim, D. L. Wright, S. N. Khanna and M. S. El-Shall, J. Am. Chem. Soc., 2003, 125, 12001–12013 CrossRef CAS
.
- G. L. Wheeler and S. D. Colson, J. Chem. Phys., 1976, 65, 1227–1235 CrossRef
.
- S. Yang and A. M. Ellis, Chem. Soc. Rev., 2013, 42, 472–484 RSC
.
- E. García-Alfonso, M. Barranco, D. A. Bonhommeau, N. Halberstadt, M. Pi and F. Calvo, J. Chem. Phys., 2022, 157, 014106 CrossRef PubMed
.
- Y. He, J. Zhang and W. Kong, J. Chem. Phys., 2016, 145, 034307 CrossRef PubMed
.
- J. Zhang, Y. He and W. Kong, J. Chem. Phys., 2016, 144, 221101 CrossRef PubMed
.
- M. W. J. Chase, NIST-JANAF thermochemical tables, 4th Ed., J. Phys. Chem. Ref. Data, Monograph 9, NIST, 1998.
- N. B. Brauer, S. Smolarek, X. Zhang, W. J. Buma and M. Drabbels, J. Phys. Chem. Lett., 2011, 2, 1563–1566 CrossRef CAS
.
- G. I. Nemeth, H. L. Selzle and E. W. Schlag, Chem. Phys. Lett., 1993, 215, 151–155 CrossRef CAS
.
- P. R. van der Linde, J. C. van Miltenburg, G. J. K. van den Berg and H. A. J. Oonk, J. Chem. Eng. Data, 2005, 50, 164–172 CrossRef CAS
.
-
A. Slenczka and J. P. Toennies, in Low Temp. Cold Mol., ed. I. W. M. Smith, World Scientific Press, Singapore, 2008, pp. 345–392 Search PubMed
.
- M. Hartmann, R. E. Miller, J. P. Toennies and A. F. Vilesov, Science, 1996, 272, 1631–1634 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. A.03, Wallingford, CT, 2016 Search PubMed
.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS
.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS
.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef
.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef
.
- R. J. Bartlett and M. Musial, Rev. Mod. Phys., 2007, 79, 291–352 CrossRef
.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC
.
- J. A. Frey, S. Leutwyler, C. Holzer and W. Klopper, Chem. Rev., 2016, 116, 5614–5641 CrossRef CAS
.
- L. O. Brockway, Rev. Mod. Phys., 1936, 8, 231–266 CrossRef CAS
.
-
E. Prince, International Tables for Crystallography, Kluwer Academic Publishers, Dordrecht, 2004 Search PubMed
.
- Y. He, J. Zhang and W. Kong, J. Chem. Phys., 2016, 144, 084302 CrossRef PubMed
.
- H. Akaike, IEEE Trans. Autom. Control, 1974, 19, 716–723 CrossRef
.
- K. P. Burnham and D. R. Anderson, Sociol. Methods Res., 2004, 33, 261–304 CrossRef
.
- A. W. Hauser, A. Volk, P. Thaler and W. E. Ernst, Phys. Chem. Chem. Phys., 2015, 17, 10805–10812 RSC
.
- K. Nauta and R. E. Miller, Science, 1999, 283, 1895–1897 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available: Structures of all clusters used in fitting the experimental diffraction profile are tabulated, including cuts from crystals and from calculation. See DOI: https://doi.org/10.1039/d2cp04492g |
| This journal is © the Owner Societies 2022 |