Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revealing resonance effects and intramolecular dipole interactions in the positional isomers of benzonitrile-core thermally activated delayed fluorescence materials†
Nadzeya A.
Kukhta‡
 ab,
Heather F.
Higginbotham‡
c,
Tomas
Matulaitis
ab,
Heather F.
Higginbotham‡
c,
Tomas
Matulaitis
 bd,
Andrew
Danos
bd,
Andrew
Danos
 *c,
Aisha N.
Bismillah
*c,
Aisha N.
Bismillah
 a,
Nils
Haase
ef,
Marc K.
Etherington
a,
Nils
Haase
ef,
Marc K.
Etherington
 c,
Dmitry S.
Yufit
c,
Dmitry S.
Yufit
 a,
Paul R.
McGonigal
a,
Paul R.
McGonigal
 a,
Juozas Vidas
Gražulevičius
a,
Juozas Vidas
Gražulevičius
 b and
Andrew P.
Monkman
b and
Andrew P.
Monkman
 *c
*c
aDepartment of Chemistry, Durham University, South Road, Durham, DH1 3LE, UK
bDepartment of Polymer Chemistry and Technology, Kaunas University of Technology, Radvilenu pl. 19, LT-254 Kaunas, Lithuania
cDepartment of Physics, Durham University, South Road, Durham, DH1 3LE, UK. E-mail: andrew.danos@durham.ac.uk; a.p.monkman@durham.ac.uk
dOrganic Semiconductor Centre, EaStCHEM School of Chemistry, University of St Andrews, St Andrews, Fife KY16 9ST, UK
eMerck KGaA, Performance Materials—Display Solutions, Frankfurter Straße 250, 64293 Darmstadt, Germany
fInstitute of Physics, Experimental Physics IV, University of Augsburg, Universitätsstr. 1, 86135 Augsburg, Germany
First published on 12th July 2019
Abstract
We report on the properties of the three positional isomers of (2,7-di-tert-butyl-9,9-dimethylacridin-10(9H)-yl)benzonitrile, which are found to have comparable donor steric environments and donor–acceptor dihedral angles. An unexpected intramolecular dipole interaction imparts a unique molecular geometry to the ortho-linked isomer, while comparison of the meta- and para-isomers uncovers how positional differences in acceptor strengths (a consequence of differences in aromatic π-system electron density) lead to very different triplet harvesting and emission properties. These positional-isomer effects on TADF follow the well-known aromatic directing rules from organic synthesis, in keeping with their common origin arising from contributions of multiple electronic resonance structures. Understanding these positional effects and methods of dihedral control is critical to the future design of efficient TADF emitters.
Introduction
Recent commercial applications of organic light-emitting diodes (OLEDs) can largely be attributed to the development of triplet harvesting materials with internal quantum efficiencies up to 100%—a marked increase from the upper limit of 25% achievable through conventional fluorescence. In contrast to iridium- or platinum-based triplet harvesting phosphors, purely organic OLEDs based on thermally activated delayed fluorescence (TADF)1 hold the potential to yield high-efficiency and reduced-cost devices for lighting and displays, using materials that are readily available and of low toxicity.2–8Designing efficient TADF materials often requires delicate tuning of charge-transfer (CT) character in the molecular excited-state. Non-overlapping highest occupied molecular orbitals (HOMOs) and lowest unoccupied molecular orbitals (LUMOs) in donor–acceptor (D–A) or donor–acceptor–donor (D–A–D) structures reliably yield such CT states with low electron exchange energy, and thus minimal singlet–triplet energy gaps (ΔEST). More recently, through-space D–A interactions and non-overlapping single molecule resonance structures have also been shown to deliver outstanding TADF performance.9–12 Reducing this gap leads to exponentially faster reverse intersystem crossing (rISC), which enables triplets to be harvested for emission. The rISC is mediated by second order spin–vibronic coupling between the CT triplet (3CT) and a local triplet state (3LE) of either the donor or acceptor.13 While increasing CT character often reduces ΔEST, it also redshifts the emission colour and reduces the fluorescence rate constant through a lower oscillator strength (reduced HOMO/LUMO overlap). Therefore, in designing high-efficiency blue TADF materials the trade-off between emissive and triplet-harvesting properties must be carefully considered, as each puts competing constraints on the molecular design.
The maximum achievable CT character of D–A(–D) TADF materials is controlled by the choice of donor and acceptor, while the actual contribution to excited-state properties is modulated by the D–A dihedral angle. Perpendicular structures hinder π-system conjugation across the molecule, spatially separating the HOMO and LUMO to yield strong CT character in the lowest-energy excited-state from which emission originates (although this CT state sometimes requires stabilisation by a polar environment to actually be the lowest energy excited-state – see discussion of emission solvatochromism below and Fig. S9.2, ESI†). Coplanar structures instead stabilise whole-molecule π-system excited-states with locally excited (LE) character (and large ΔEST), as these permit the greatest electron delocalisation. Therefore, control of D–A angles has been identified as critical for effective TADF material design. This control is most commonly achieved by repulsive contact forces (i.e. steric effects) between the donor and acceptor units or between multiple donor units around the same acceptor. Indeed, well-designed studies of differently substituted or connected donor units – or of donor units in different conformations – demonstrate how both TADF and room temperature phosphorescence can be selectively activated by control of the D–A angle and CT character.14–18
While the behaviour of smaller donor units such as carbazole have been shown to be dominated by inter-donor and D–A steric interactions,19,20 this understanding cannot be a priori generalised to larger donor units or those with interrupted conjugation. Similarly, the conformational effects seen in phenothiazine and other flexible donors are not necessarily shared by more rigid donors.21 9,9-Dimethyl-9,10-dihydroacridine (DMAC) is an example of a large and rigid donor that has become popular for designing blue TADF materials22–25 due to its intermediate donor strength (higher than carbazole and diphenylamine, but lower than phenoxazine and phenothiazine according to HOMO energies26). It is therefore desirable to understand how this donor responds to different steric (and electronic) environments, so that it can be effectively incorporated into the design of advanced TADF emitters.
Initially with the aim of understanding these steric effects for DMAC, we here present synthesis and photophysical characterisation of the three positional isomers of DMAC coupled to benzonitrile (BZN) as acceptor (ortho-1, meta-2, and para-3, Scheme 1 and collectively DMAC–BZN). Time-resolved emission spectra show that these positional isomers display very different rISC rates and TADF performance, which has been loosely attributed to steric or conjugation differences for similar materials in the past.27–31 However, our detailed density functional theory analysis of these materials reveal that the meta- and para-isomers experience extremely similar steric environments relevant to the D–A dihedral angle, while the ortho-isomer shows an unexpected intramolecular dipole interaction that restricts its own D–A angle. We are therefore able to reattribute the differences in TADF performance to the differences in BZN electron withdrawing strength at the meta- and para-positions, consistent with the different resonance and inductive effects around the acceptor unit aromatic π-system. Previously examined in terms of “linear” and “angular” isomers,15,32–34 this newly understood feature of TADF design mirrors the directing rules from organic chemistry, making it a timely and highly appropriate inclusion in this themed collection celebrating the career achievements of Martin Bryce.
Results and discussion
Design, synthesis and chemical characterization
Scheme 1 presents the synthetic pathways used to isolate the target materials. DMAC and BZN were chosen as donor and acceptor due to their increasing popularity in the design of blue TADF emitters, again in the hope of understanding the different steric effects at different positions around the ring. The popularity of these units for blue TADF materials is due to their well-matched relative electron donating/accepting strengths, as well as their high triplet energies.26,35 Intermediate iodobenzonitriles were prepared by diazotization–iodination reactions from appropriate starting aminobenzonitriles. The target D–A compounds were then produced using a Buchwald–Hartwig palladium cross-coupling protocol. Full synthetic procedures are included in the ESI† (Section S2). All compounds were purified by column chromatography followed by recrystallisation. The identities and high purities of the target compounds were confirmed by 1H and 13C NMR spectroscopy, mass spectrometry and elemental analysis (ESI,† Sections S2 and S3). Additional characterisation of thermal (TGA and DSC) and electrochemical properties (CV) are included in ESI† Section S7.NMR analysis
As well as confirming the identities of the isolated target materials, analysis of the NMR chemical shifts reveals subtle differences in ground-state conjugation across the donor and acceptor units in the DMAC–BZN isomers (ESI,† Section S3). We select for comparison the H atoms and associated C atoms closest to the nitrogen of the DMAC units (equivalent pairs at the 4- and 5-positions, Scheme 1), as these positions are closest to the withdrawing BZN ring without directly participating in the acceptor unit π-system. The chemical shifts observed for ortho-1, meta-2, and para-3 are 5.98, 6.08, and 6.35 ppm for the 1H nuclei and 113.4, 114.4, and 115.8 ppm for the 13C nuclei, respectively. The nuclear environments at these positions are therefore shielded relative to benzene (7.36 ppm, 128.4 ppm), which we attribute to increased local electron density arising from the nearby DMAC nitrogen lone pair.The order of these chemical shifts then suggests that the nitrogen atom electron density is increasingly depleted in the order of ortho-1, meta-2, and para-3, presumably due to increased D–A conjugation in the same order. The overall level of conjugation depends on the D–A angle as well as acceptor strength, and so in many TADF systems it is difficult to attribute such differences to a unique cause. Nonetheless based on complementary X-ray and computational studies of these materials we later illustrate that the differences between meta-2 and (more conjugated) para-3 are due to different effective acceptor strengths only. For ortho-1 the D–A angle is restricted closer to perpendicular, preventing stronger D–A conjugation.
Variable temperature NMR was also performed to assess the heights of the barriers to donor unit rotation around the bridging DMAC–BZN C–N bond in these materials (ESI,† Section S4). The C–N bond rotation of ortho-1, which is hindered by the neighbouring CN group, reaches the slow exchange regime in an accessible temperature range, allowing us to measure a free energy barrier to rotation of approximately 45 kJ mol−1. The less hindered meta-2 isomer, on the other hand, does not reach slow exchange down to temperatures as low as −98 °C. We estimate (ESI,† Section S4), therefore, that its rotational barrier is <33 kJ mol−1. The additional plane of symmetry present in para-3 prevents measurement of its rotational barrier, but the steric environment around the DMAC–BZN bond is expected to be similar to meta-2, with a similarly low barrier to rotation.
X-ray crystallography analysis
X-ray crystallographic analysis of the three materials (ESI,† Section S5, CCDC 1917139–1917141†) reveals near-perpendicular D–A dihedral angles for each in the solid-state. This was unexpected, as with larger conjugation (as inferred from NMR and following optical results) para-3 was anticipated to possess a more coplanar geometry.Interestingly, we also note a folding of the DMAC unit unique to ortho-1. Hirshfeld surfaces were calculated for the crystal structures (ESI,† Section S6) to determine whether this folding is the result of packing effects brought about by the orientation of the nitrile group. However, no notable differences in the locations or sizes of close contact areas (where nearest neighbour molecular spacing is smaller than the sum of van der Waals radii) were observed between the three isomers. We note however that this analysis cannot discount the possibility that DMAC folding occurs to minimise molecular volume and eliminate strain that would be present in crystals of ortho-1 with otherwise planar DMAC units. We therefore cannot make definitive claims about the geometry of the DMAC unit of ortho-1 from these X-ray results alone, although DFT calculations presented further below support the observation of DMAC folding.
Photophysical properties
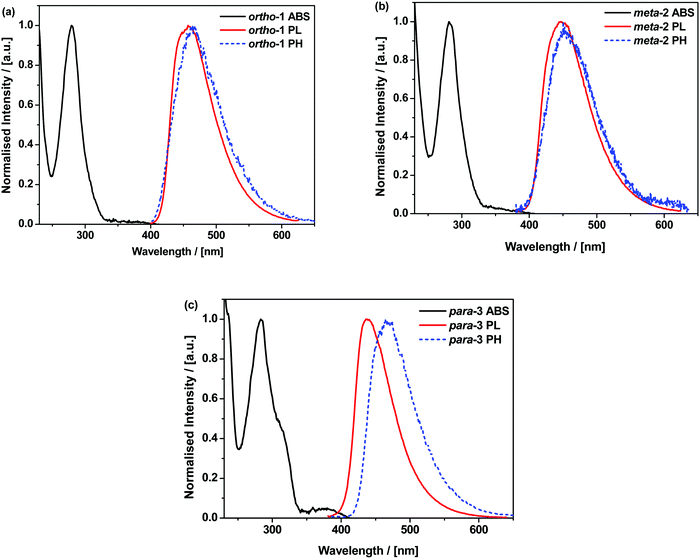
In cyclohexane (CH), chloroform, and dichloromethane (DCM) solutions, ortho-1 and meta-2 show strong absorption peaks at ∼280 nm extending out to 340 nm (Fig. 1 and Fig. S9.1, ESI†). Solutions of para-3 also possess additional absorption bands at 320 and 378 nm, redshifted due to increased conjugation in this material.36,37 The presence of such low intensity and low energy bands – presumably of n–π* or n–π*/π–π* origin, and none of which are shared with the individual donor or acceptor units – is widely observed in D–A systems.38–40 Similar absorption bands were attributed to direct CT transitions by Noda et al. for similar materials.27Photoluminescence (PL) spectra were recorded in solvents of increasing polarities, experimentally establishing the CT character of the emissive excited-state through the Gaussian line shape and increasing redshift (Fig. S9.2, ESI†). In non-polar CH, vibronically structured emission is observed for all three materials and attributed to an LE singlet state. In other solvents and in non-polar polymer host zeonex all materials exhibit only Gaussian emission from CT excited-states. The size of the solvatochromic shift is different in each molecule, a combined effect of the excited-state dipole moment and CT character. The emission in degassed toluene is also greatly enhanced for each DMAC–BZN isomer (Fig. S10, ESI†), confirming that they are all effective triplet harvesting materials.
The materials were further analysed using time-resolved spectroscopy in both zeonex and polar small molecule host bis[2-(diphenylphosphino)phenyl]ether oxide (DPEPO), and at temperatures between 80 and 300 K. DPEPO is a widely-used high triplet energy host for blue TADF OLEDs and was employed to emulate conditions relevant to device applications.41,42 The individual spectra (that make up the decay curves presented further below, Fig. 3) reveal information about the excited-state dynamics in the DMAC–BZN isomers. Fig. 2 shows the slight apparent redshift observed for ortho-1 in the early prompt fluorescence (PF) time region, as well as the surprising blueshifts observed for meta-2 and para-3 across similar time intervals. In contrast, Fig. S13 (ESI†) shows similar time-resolved spectra in DPEPO, where only apparent redshifts are observed. After these spectral shifts in the early PF time region the time-resolved spectra remain unchanged throughout the later delayed fluorescence (DF).
 | ||
| Fig. 2 Early PF time-resolved emission spectra of 1% w/w zeonex films of ortho-1 (a) meta-2 (b) and para-3 (c) at 300 K. | ||
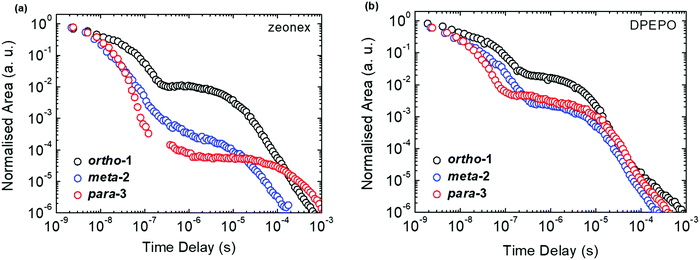
All materials were found to emit across two distinct time regimes, with PF occurring over nanoseconds as optically excited 1CT states emit, while DF extends over microseconds as triplet states undergo slower rISC and emit at later times. At low temperatures a third phosphorescence regime can be identified, from which the spectra in Fig. 1 are taken. The emission decay curves of the three DMAC–BZN isomers are presented in Fig. 3 (300 K), and in Fig. S11 (ESI†) for other temperatures.
The emission decay curves can be reasonably well fit with single exponentials in regions representing the PF and DF for ortho-1 and para-3, with lifetimes at 300 K included in Table 1. Similar fitting is more challenging for meta-2, especially in the intermediate time region spanning 100–1000 ns where signal to noise ratios were the lowest. Values of the rISC rate constant (krISC) were also determined by kinetic fitting of the decays as described elsewhere, with decay fits for kinetic and exponential fitting shown in ESI,† Section S15.43 Measurements of the power dependence of DF emission with excitation dose rule out bimolecular TTA as the DF mechanism (Fig. S12, ESI†). Photoluminescence quantum yields (PLQYs, 380 nm excitation) of the zeonex films were also measured in air (PF component) and after purging with nitrogen (PF + DF components) and are also included in Table 1; DPEPO films of suitable uniformity could not be obtained for PLQY measurements.
| Material | τ PF (ns) | τ DF (μs) | ΔESTa (meV) | k rISC (×105 s−1) | PLQYc (N2) | PLQYc (air) | k F (×106 s−1) |
|---|---|---|---|---|---|---|---|
| a ΔEST from difference in high energy onsets of steady state PL and phosphorescence spectra. b k rISC from combined kinetic fitting of PF and DF decay data.43 c PLQYs measured on drop cast films on sapphire substrates using 380 nm excitation. d Calculated using kF = (PLQYAIR)/τPF following Dias et al. eqn (8).39 | |||||||
| ortho-1 | 47 | 10 | <10 | 5.7 | 78 | 41 | 8.7 |
| meta-2 | 20 | 15 | <10 | 2.3 | 21 | 9 | 4.5 |
| para-3 | 11 | 181 | 110 | 0.13 | 47 | 20 | 18 |
Discussion and DFT calculations
The significant differences in the optical properties of these materials are difficult to reconcile with their similar structures. The results raise several questions:• Despite similar PF decay lifetimes, why are the PF components of the PLQYs for meta-2 and para-3 so different?
• Similarly, with comparable ΔEST, why are the DF PLQY components of ortho-1 and meta-2 (37% and 12% respectively) so different? How does para-3 have higher PLQY than meta-2 despite a larger ΔEST?
• Why do the early PF spectra blueshift in zeonex, when redshifts due to D–A angle relaxation or lifetime dispersion are more commonly observed?40,44 Why is this blueshift seen for meta-2 and para-3 to different extents, but not ortho-1?
• Despite showing stronger D–A conjugation from NMR, direct CT absorption, and lower triplet energy, how does para-3 still manage to possess a similarly orthogonal D–A angle to the other isomers as revealed by X-ray diffraction?
In order to better understand the behaviour of these materials and answer the questions above, we performed DFT calculations on both ground (S0) and excited (S1) state surfaces for the DMAC–BZN isomers.
Due to the proximity of the cyano-group to the DMAC in ortho-1, we expected this material to exhibit the greatest steric hindrance and a D–A angle most tightly restricted around 90°. This would then result in significantly higher CT character for ortho-1, in contrast to meta-2 and para-3 which were expected to more freely rotate.40 Similar differences in rotational freedom have been used to explain differences in photophysical properties for similar molecules featuring carbazole donors.17,20,26,42
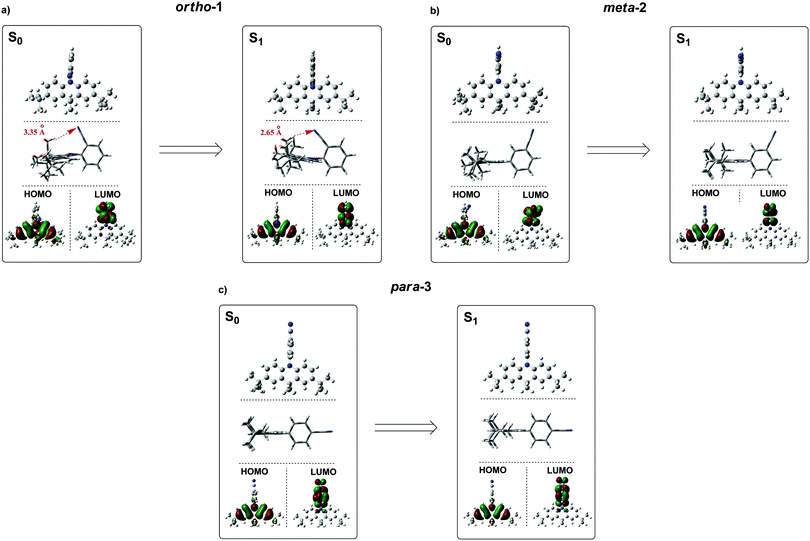
Instead – and in agreement with X-ray crystal structures – DFT calculations of the DMAC–BZN isomers (rBMK/6-31G(d) level of theory) reveal similar chromophore arrangements in the optimised ground-state geometry regardless of the substitution pattern. To examine the effects of structural reorganisation in the excited state, the S1 geometries were initially accessed using TD-DFT (Fig. S8.1, ESI†).45 Surprisingly, no dramatic change in the D–A torsional angle was observed upon excitation for any of the isomers. The BZN acceptor is attached perpendicularly to the DMAC donor in all cases, which we suggest is due to the innermost DMAC hydrogens (those at the 4- and 5-positions in Scheme 1) capturing the plane of the BZN ring from above and below and locking rotation of the D–A bond. A similar form of dihedral control using inwardly pointing methyl substituents was able to greatly improve the performance of TADF materials with carbazole donors, which are otherwise much freer to rotate.46 For DMAC the dihedral angle control afforded by the inner C–H bonds relies on the rigid and large 6-member central ring of the DMAC, and so is intrinsic to all three isomers and explains their shared D–A angles. This is in contrast to more common steric control strategies engineered using repulsive contact forces between neighbouring donors or acceptor substituents, as employed in other TADF materials.14,16–18,34,42,47 In any case, observation of uniformly orthogonal chromophore arrangements means that the differences in photophysical properties between the DMAC–BZN isomers cannot be attributed to different D–A angles.
For further and more detailed structural comparisons the experimentally obtained X-ray crystal structures were taken to represent the ground-state geometries. Additionally, the Tamm–Dancoff (TDA) approximation was employed for further excited-state calculations, using the X-ray structure as input geometries (Fig. 4). The TDA approach was previously shown to describe CT states more accurately than conventional TD-DFT, therefore giving more reliable excited-state geometry information for the DMAC–BZN isomer excited-states.48,49
While the converged geometries using this second computational approach are qualitatively similar to those of the first, there are some notable differences. Firstly, the D–A torsion angles in the ground- and excited-states no longer reach precisely 90° (Fig. 4 and 5). These geometrical differences then influence the electron wavefunction distribution: the increased HOMO/LUMO overlap in para-3 (Fig. 4c) is immediately visible compared to meta-2, consistent with the largest conjugation (giving rise to strongest LE character) inferred from NMR, lowest triplet energy, shortest ground-state D–A bond length (from the X-ray structures, Fig. 5b), and strongest direct CT absorption bands in this material (both experimental, Fig. 1, and simulated, Fig. S8.2, ESI†). These differences in calculated geometries clearly indicate that simpler TD-DFT approaches cannot fully describe the excited-state characteristics of D–A compounds with strong CT character. The degree of D–A conjugation was also assessed quantitatively for the excited-state geometries by calculating the charge separation index (q) in Multiwfn.50,51 The values obtained again confirm that para-3 (q = 0.900) is the most conjugated (least charge separation), with ortho-1 (0.916) and meta-2 (0.924) more similar to each other, although in reverse order to the ranking inferred from NMR chemical shifts.
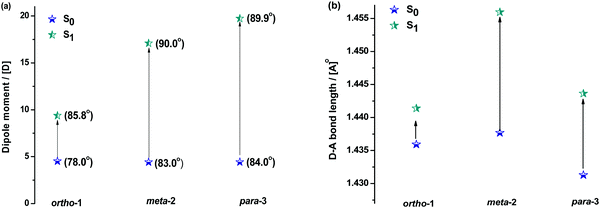
Fig. 5 shows how the D–A bond angles, D–A bond lengths, and (calculated) dipole moments change from the ground to excited-state. We note that these calculations reveal the gas phase properties of the DMAC–BZN isomers, and so are comparable only to measurements recorded in the fluid and non-polar zeonex host. Despite this limitation the structural insight provided by these calculations is what allows us to fully understand the puzzling photophysics arising from positional effects in the DMAC–BZN isomers.
It is immediately noteworthy that the changes in the D–A bond angles upon excitation are not extreme, making direct CT excitation in these materials a near-vertical transition as it concerns the D–A dihedral nuclear coordinate. The excited-state dipole moments increase in line with the charge separation distances, as would be expected for a classical electric dipole. That is, the larger the distance between the electron accepting cyano-group and electron donating DMAC nitrogen (with ortho-1 shortest and para-3 longest), the larger the dipole moment.
The changes in D–A bond lengths also explain the blueshift of the early time-resolved spectra in zeonex, in a manner that similarly appeals to classical intuition. As recently demonstrated in exciplex systems, increasing the CT state electron–hole separation reduces the magnitude of the coulombic binding energy, resulting in blue-shifted emission.52,53 We propose that the same mechanism causes the meta-2 isomer to blueshift significantly as its D–A bond relaxes by dynamic elongation. From the spectra in Fig. 2 we note this relaxation takes up to 50 ns, which is much longer than typical vibrational mode oscillation periods for this kind of D–A bond stretch. However, we note that any D–A bond stretching mode will be frustrated by the surrounding host. While zeonex provides a relatively fluid environment (compared to compact small molecule OLED hosts like DPEPO), meta-2 must still perform mechanical work to expand its molecular volume against the pressure of the surrounding host. As the polymer host reorganisation required to clear space for the expanding molecule takes time, both the bond length relaxation and associated spectral shift take longer than would be expected for an unhindered vibration. For para-3 the bond elongation and blueshift are both smaller and more rapid, while they are both negligible for ortho-1.
In contrast to zeonex, the time-resolved spectra do not blueshift in DPEPO. We suggest that the compact small molecule host cannot be so easily pushed aside as the D–A bond attempts to relax, preventing its elongation. As a result only an apparent redshift due to lifetime dispersion is observed, with the particularly long duration of this dispersion in meta-2 (∼250 ns, Fig. S13, ESI†) indicative of an extremely broad distribution of excited-state geometries.40
While bond lengthening explains the spectral evolution of these materials in zeonex, the differences in bond lengthening in turn demand some explanation. We first consider ortho-1; why does its D–A bond change so little compared to the others? The answer to this question can be found in the X-ray and TDA excited-state geometries of this material. Fig. 4 shows how the plane of the DMAC unit is tilted with respect to the BZN in the ground state of ortho-1 (X-ray geometry, with the vector normal to the plane of the DMAC unit non-perpendicular to the vector along the D–A bond). For meta-2 and para-3 there is no such tilting (DMAC normal vector completely perpendicular to the D–A bond vector). In the excited state this tilting increases as highlighted in Fig. 6a, with the H⋯N interatomic distance closing from 3.35 Å to 2.63 Å.
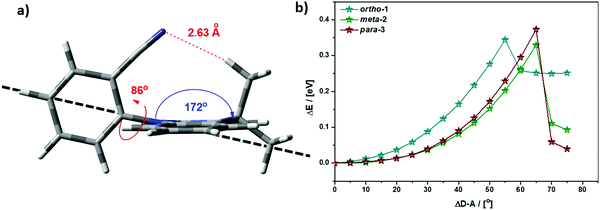 | ||
| Fig. 6 (a) Profile view of ortho-1 S1 optimised structure (TDA-DFT BMK/6-31G(d)) showing tilting of DMAC plane, with dashed line to guide the eye to the expected DMAC position. This tilting and the reduced H⋯N interatomic distance arise from an intramolecular dipole interaction. (b) Conformational analysis of DMAC–BZN isomers in the excited-state (rBMK/6-31G(d)): change in total energy plotted against displacement of D–A dihedral angle (away from optimised values given in Fig. 5a, upper value). | ||
The presence of this tilting in both the X-ray ground state (with crystal packing) and DFT excited-state (gas phase) leads us to conclude that it is indeed a real effect and not an artefact of either approach. We suggest that this tilting is a result of intramolecular dipole interactions between the slightly positive DMAC methyl hydrogen and the partially negative nitrogen of the cyano-group. While D–A bond weakening in the excited state causes it to simply lengthen for meta-2 and para-3, in ortho-1 this weakening instead allows the dipole interaction to draw the two moieties closer together through space, with little effect on the D–A covalent bond length.
This explanation of bond lengthening in ortho-1 immediately raises another important question: Does this intramolecular dipole interaction impact the D–A dihedral angle? To answer this question, we performed DFT calculations to map out the excited-state energy surfaces of the DMAC–BZN isomers along the nuclear coordinate of D–A bond rotation. The results are shown in Fig. 6b, extending out to angles at which the restricted geometry optimisation begins to seek alternative local minima (55° for ortho-1, and 65° for meta-2 and para-3). For angle displacements up to 50° these results demonstrate that while meta-2 and para-3 have identical rotational energy well shapes (controlled in both only by the DMAC hydrogens capturing the plane of the BZN ring), ortho-1 is more tightly constricted. This we believe is due to the intramolecular dipole interaction, which holds the D–A bond angle more closely around its equilibrium value. The use of attractive potentials to control bond dihedral angles is currently rare,54,55 but holds significant promise as a new tool for TADF molecular design, potentially allowing much finer control over torsion angles than the use of repulsive potentials. In the context of ortho-1 this additional dihedral control would be expected to increase the CT character of the material.
While the smaller bond elongation in ortho-1 is thus understood, there are no structural differences that can easily explain the differences in optical properties of meta-2 and para-3. As the excited-state D–A bond in meta-2 is significantly longer than in para-3, for otherwise equal donors and acceptors this greater decoupling of donor and acceptor would be expected to lead to greater CT character and larger rISC rates. We indeed observe this in optical measurements, but stress again that this difference in CT character cannot be attributed to different D–A angles, and that the donor strength of the DMAC should be the same for all three materials. We note however that the assumption of equal acceptor strengths at the different BZN positions is not yet justified.
Indeed, the results above suggest that this assumption cannot actually be justified. Instead, we infer that different accepting strengths exist in the different acceptor positions for BZN, which explains the differences between meta-2 and para-3. In ortho-1 the additional intramolecular dipole interaction affects the D–A rotational freedom, so we only compare it to para-3—which we expect to have a similar acceptor strength for reasons detailed immediately below.
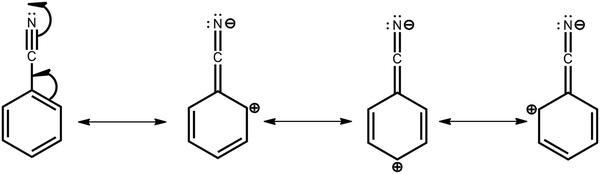
To justify the conclusion of different acceptor strengths for the DMAC–BZN isomers (and qualitatively predict their relative acceptor strengths), we recall the general substituent orientation rules from organic chemistry. As nitrile is a relatively strong meta-orienting and deactivating group for electrophilic substitution, the opposite rules (ortho- and para-activating) apply for nucleophilic substitution. Indeed, while a different synthetic strategy was used here (Scheme 1 and ESI,† Section S2), the D–A bonds in the DMAC–BZN materials could potentially be formed by nucleophilic attack of the BZN ring by the deprotonated DMAC unit (with an appropriate leaving group on the BZN). The activating effect towards ortho- and para-positions is due to reduced π-system electron density at these positions, due to the resonance and inductive effects of the cyano-group, as shown in Fig. 7.
Crucially, there is no reason to expect that these resonance and inductive effects should cease once the D–A bond has formed. The electron withdrawing effects of the cyano-group again result in depleted π-system electron density at ortho- and para-positions, leading to larger effective acceptor strengths. This leads to different levels of electronic communication between the donor and acceptor, with significant subsequent effects on conjugation and CT character for the isomers. Comparing only meta-2 and para-3, the weaker acceptor is the reason for meta-2 having reduced D–A conjugation, a weaker (longer) bond, and consequently a greater degree of CT character with low ΔEST. Thus, at the early times shown in Fig. 2b it has by far the most red-shifted CT emission peak. Indeed, excessive CT character greatly reduces the emission oscillator strength in this material, leading to its low PLQY. This is true even after the D–A bond length has relaxed and meta-2 gains a more LE excitonic character as evidenced by its blue-shifted emission.52,53 Despite this change, the LE character is still too low to promote efficient emission, and this relaxation also comes at a cost of slower rISC in the DF (compared to the early PF ISC occurring at the unrelaxed bond length, bestowing a temporarily increased CT character).
The relatively fast PF lifetime in meta-2 we suggest may be due to faster ISC, itself also a result of the larger CT character compared to the other isomers. Alternatively or additionally, there may be quenching modes associated with the D–A bond stretch, which are enhanced in meta-2 as its weaker bond (with smaller spring constant) makes these modes easier to populate. In contrast, restrictions of quenching vibrational modes have been used to explain the superior performance of TADF materials exhibiting intramolecular hydrogen bonding.55,56 In the delayed emission the electronic decoupling of donor and (weakest) acceptor in meta-2 results in a material with a low ΔEST and fast rISC, but one without the ability to effectively undergo radiative decay from the singlet state and thus inferior PLQYs. These changes in CT and LE character during the meta-2 emission decay (and associated ISC and rISC rates) also then explain the difficulty in fitting the decay to a single exponential, while similar fitting is straightforward for the other two isomers.
In contrast, para-3 has a larger ΔEST and longer (i.e., worse) DF lifetime, but conversely possesses much enhanced emission properties. Radiative rates for all materials in zeonex were calculated from the PF decay lifetime and the air PLQY, according to Dias et al.39 The radiative rate is fastest for para-3, followed by ortho-1 and then meta-2. This again reflects the differences in CT character between these materials, with para-3 possessing the most LE character and meta-2 the most CT character. Due to its increased LE character the radiative rate constant is large and PF lifetime is therefore fast for para-3, a similar outcome to meta-2 but for very different reasons. This interpretation is supported by the larger fraction of PF decays being emissive for para-3 (compare 20% vs. 9% PLQYs in air). This compound is not able to harvest triplets as quickly as meta-2, but the triplets that it does harvest to the singlet state are able to emit more readily, giving para-3 a larger DF PLQY component as well. The emission is also the most blue-shifted, indicating that this material possesses the most LE character, again in agreement with its fast PF rate.52,53
We expect similar resonance and inductive effects for ortho-1 compared to para-3, but the additional dipole interaction further restricts the D–A dihedral angle (and D–A bond elongation) in ortho-1 only. In this way ortho-1 enjoys better conjugation than meta-2 due to increased acceptor strength, while still retaining a higher CT character (and smaller ΔEST) than para-3. As a result, ortho-1 has a longer PF lifetime than para-3 but a shorter DF lifetime and overall the best PLQYs. In DPEPO the ΔEST gaps remain small for ortho-1 and meta-2 and is reduced for para-3 (88 meV, Fig. S15, ESI†), while any excited-state D–A bond lengthening is likely to be severely restricted by host packing. Hence, we observe much more similar kinetic behaviour for all three materials, as shown by the tighter clustering of decay curves in Fig. 3b (compared to the rapid divergence of emission decays in zeonex, Fig. 3a).
Similar arguments appear to explain the differences observed between “angular” and “linear” D–A–D isomers with DMAC donors and similar ΔEST values.34 We identify that the “angular” isomers are para-substituted with respect to the electron withdrawing moiety of the acceptor unit, while “linear” isomers are meta-substituted. As demonstrated in the DMAC–BZN isomers, resonance effects associated with para-connectivity result in increased effective acceptor strength which is needed to balance emissive and triplet harvesting properties. The trend seen here and elsewhere of para-substituted materials outperforming meta-substituted ones may be reversed with more exotic choices of acceptor. Electron accepting groups that are inductively withdrawing towards the meta-position (such as CH2NO2, NO, and CHCl2) might achieve this, although we are not aware of any reported examples. Similar performance trends comparing meta- and para-substituted TADF materials are also seen for other donors, although in those cases differences in D–A angles and donor conformation (and ΔEST values) appear to dominate.15,21,33
Finally, the use of physically attractive rather than repulsive potentials to engineer dihedral control is also simultaneously attractive for molecular design. As exhibited by the C–H⋯N–C– dipole interaction in ortho-1, this can be used to ‘nudge’ molecular structural parameters towards the desired values, and then keep them trapped there. This is in contrast to the use of repulsive potentials, where multiple substituents must be used to ‘bookend’ the target structural parameter at the edges of the desired range. The inner DMAC hydrogens unexpectedly trapping the BZN ring is revealed to be a fortuitous example of this second kind of dihedral control. Alternatively, complete locking of the D–A angle in a perpendicular conformation has been shown to reduce the dynamic rocking of chromophores necessary for rISC, hence resulting in room temperature phosphorescence.57
Conclusions
Detailed DFT calculations have been used to unravel the initially perplexing photophysics of three DMAC–BZN positional isomers. The D–A bond dihedral angles – often the critical factor in similar studies – are found to be much more alike than expected due to the inward pointing DMAC C–H bonds capturing the plane of the BZN acceptor ring. TD-DFT was f-state properties of the structural isomers beyond qualitative comparisons, while use of the Tamm–Dancoff approximation led to much more accurate results.With identical D–A dihedral environments, the large differences between meta- and para-isomers are instead attributed to different bond lengths and acceptor strengths associated with resonance and inductive effects in the BZN π-system. The para- and ortho-isomers are likely similar in acceptor strength, but an additional intramolecular dipole interaction further restricts ortho-D–A dihedral angle rotation, and results in improved performance. We also identify D–A bond length relaxation as an important factor in TADF performance, alongside D–A dihedral motion.
Finally, we identify an interesting and useful example of an attractive intramolecular dipole interaction that can be used to control dihedral angles by trapping at favourable angles instead of repelling from unfavourable ones. These kinds of dihedral control open new horizons in TADF rational design.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
NAK, HFH, MKE, and APM acknowledge the EU's Horizon 2020 for funding the PHEBE project under grant no. 641725. NAK, MKE, AD, NH and APM acknowledge the EU's Horizon 2020 for funding the HyperOLED project under grant no. 641725. APM thanks EPSRC grant EP/L02621X/1 for funding. ANB acknowledges an EPSRC Doctoral Training Grant. TOC image elements adapted from ref. 58, under Creative Commons BY 3.0 license.58References
- H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238 CrossRef CAS
.
- Z. Yang, Z. Mao, Z. Xie, Y. Zhang, S. Liu, J. Zhao, J. Xu, Z. Chi and M. P. Aldred, Chem. Soc. Rev., 2017, 46, 915–1016 RSC
.
-
W. Hu, Organic optoelectronics, Wiley-VCH, 2013 Search PubMed
.
- D. Volz, M. Wallesch, C. Flechon, M. Danz, A. Verma, J. M. Navarro, D. M. Zink, S. Brase and T. Baumann, Green Chem., 2015, 17, 1988–2011 RSC
.
- C. Adachi, Jpn. J. Appl. Phys., 2014, 53, 60101 CrossRef
.
- Y. Tao, K. Yuan, T. Chen, P. Xu, H. Li, R. Chen, C. Zheng, L. Zhang and W. Huang, Adv. Mater., 2014, 26, 7931–7958 CrossRef CAS
.
- M. Y. Wong and E. Zysman-Colman, Adv. Mater., 2017, 29, 1605444 CrossRef
.
- Q. Zhang, B. Li, S. Huang, H. Nomura, H. Tanaka and C. Adachi, Nat. Photonics, 2014, 8, 326–332 CrossRef CAS
.
- E. Spuling, N. Sharma, I. D. W. Samuel, E. Zysman-Colman and S. Bräse, Chem. Commun., 2018, 54, 9278–9281 RSC
.
- Y. Gao, Q.-Q. Pan, L. Zhao, Y. Geng, T. Su, T. Gao and Z.-M. Su, Chem. Phys. Lett., 2018, 701, 98–102 CrossRef CAS
.
- K.-L. Woon, C.-L. Yi, K.-C. Pan, M. K. Etherington, C.-C. Wu, K.-T. Wong and A. P. Monkman, J. Phys. Chem. C, 2019, 123, 12400–12410 CrossRef CAS
.
- X. Wang, S. Wang, J. Lv, S. Shao, L. Wang, X. Jing and F. Wang, Chem. Sci., 2019, 10, 2915–2923 RSC
.
- J. Gibson, A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961 CrossRef CAS
.
- C. Chen, R. Huang, A. S. Batsanov, P. Pander, Y.-T. Hsu, Z. Chi, F. B. Dias and M. R. Bryce, Angew. Chem., 2018, 130, 16645–16649 CrossRef
.
- M. K. Etherington, F. Franchello, J. Gibson, T. Northey, J. Santos, J. S. Ward, H. F. Higginbotham, P. Data, A. Kurowska, P. Lays, D. Santos, D. R. Graves, A. S. Batsanov, F. B. Dias, M. R. Bryce, T. J. Penfold and A. P. Monkman, Nat. Commun., 2017, 8, 14987 CrossRef
.
- R. Huang, J. S. Ward, N. A. Kukhta, J. Avó, J. Gibson, T. Penfold, J. C. Lima, A. S. Batsanov, M. N. Berberan-Santos, M. R. Bryce and F. B. Dias, J. Mater. Chem. C, 2018, 6, 9238–9247 RSC
.
- C. S. Oh, D. de, S. Pereira, S. H. Han, H.-J. Park, H. F. Higginbotham, A. P. Monkman and J. Y. Lee, ACS Appl. Mater. Interfaces, 2018, 10, 35420–35429 CrossRef CAS
.
- H. F. Higginbotham, C.-L. Yi, A. P. Monkman and K.-T. Wong, J. Phys. Chem. C, 2018, 122, 7627–7634 CrossRef CAS
.
- M. K. Etherington, N. A. Kukhta, H. F. Higginbotham, A. Danos, A. N. Bismillah, D. R. Graves, P. R. McGonigal, N. Haase, A. Morherr, A. S. Batsanov, C. Pflumm, V. Bhalla, M. R. Bryce and A. P. Monkman, J. Phys. Chem. C, 2019, 123, 11109–11117 CrossRef CAS
.
- C. S. Oh, H. L. Lee, S. H. Han and J. Y. Lee, Chem. – Eur. J., 2019, 25, 642–648 CrossRef CAS
.
- N. A. Kukhta, A. S. Batsanov, M. R. Bryce and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 28564–28575 CrossRef CAS
.
- P. L. dos Santos, J. S. Ward, M. R. Bryce and A. P. Monkman, J. Phys. Chem. Lett., 2016, 7, 3341–3346 CrossRef CAS
.
- G. Meng, X. Chen, X. Wang, N. Wang, T. Peng and S. Wang, Adv. Opt. Mater., 2019, 7, 1900130 CrossRef
.
- W. Song and J. Y. Lee, J. Phys. D: Appl. Phys., 2015, 48, 365106 CrossRef
.
- M. Godumala, S. Choi, M. J. Cho and D. H. Choi, J. Mater. Chem. C, 2019, 7, 2172–2198 RSC
.
- Y. Im, M. Kim, Y. J. Cho, J.-A. Seo, K. S. Yook and J. Y. Lee, Chem. Mater., 2017, 29, 1946–1963 CrossRef CAS
.
- H. Noda, R. Kabe and C. Adachi, Chem. Lett., 2016, 45, 1463–1466 CrossRef CAS
.
- Y. Zhang, D. Zhang, M. Cai, Y. Li, D. Zhang, Y. Qiu and L. Duan, Nanotechnology, 2016, 27, 94001 CrossRef PubMed
.
- K.-C. Pan, S.-W. Li, Y.-Y. Ho, Y.-J. Shiu, W.-L. Tsai, M. Jiao, W.-K. Lee, C.-C. Wu, C.-L. Chung, T. Chatterjee, Y.-S. Li, K.-T. Wong, H.-C. Hu, C.-C. Chen and M.-T. Lee, Adv. Funct. Mater., 2016, 26, 7560–7571 CrossRef CAS
.
- Y. Geng, L.-S. Cui, J. U. Kim, H. Nakanotani and C. Adachi, Chem. Lett., 2017, 46, 1490–1492 CrossRef CAS
.
- M. Kim, S.-J. Yoon, S. H. Han, R. Ansari, J. Kieffer, J. Y. Lee and J. Kim, Chem. – Eur. J., 2019, 25, 1829–1834 CrossRef CAS PubMed
.
- F. B. Dias, K. N. Bourdakos, V. Jankus, K. C. Moss, K. T. Kamtekar, V. Bhalla, J. Santos, M. R. Bryce and A. P. Monkman, Adv. Mater., 2013, 25, 3707–3714 CrossRef CAS
.
- R. Huang, J. Avó, T. Northey, E. Chaning-Pearce, P. L. dos Santos, J. S. Ward, P. Data, M. K. Etherington, M. A. Fox, T. J. Penfold, M. N. Berberan-Santos, J. C. Lima, M. R. Bryce and F. B. Dias, J. Mater. Chem. C, 2017, 5, 6269–6280 RSC
.
- P. Stachelek, J. S. Ward, P. L. dos Santos, A. Danos, M. Colella, N. Haase, S. J. Raynes, A. S. Batsanov, M. R. Bryce and A. P. Monkman, ACS Appl. Mater. Interfaces DOI:10.1021/acsami.9b06364
.
- T.-A. Lin, T. Chatterjee, W.-L. Tsai, W.-K. Lee, M.-J. Wu, M. Jiao, K.-C. Pan, C.-L. Yi, C.-L. Chung, K.-T. Wong and C.-C. Wu, Adv. Mater., 2016, 28, 6976–6983 CrossRef CAS
.
- C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203 CAS
.
- C. M. Marian, J. Phys. Chem. C, 2016, 120, 3715–3721 CrossRef CAS
.
- P. L. dos Santos, J. S. Ward, P. Data, A. S. Batsanov, M. R. Bryce, F. B. Dias and A. P. Monkman, J. Mater. Chem. C, 2016, 4, 3815–3824 RSC
.
- F. B. Dias, T. J. Penfold and A. P. Monkman, Methods Appl. Fluoresc., 2017, 5, 12001 CrossRef
.
- F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. Bryce and A. P. Monkman, Adv. Sci., 2016, 3, 1600080 CrossRef PubMed
.
- P. L. Dos Santos, J. S. Ward, M. R. Bryce and A. P. Monkman, J. Phys. Chem. Lett., 2016, 7, 3341–3346 CrossRef CAS
.
- D. R. Lee, M. Kim, S. K. Jeon, S.-H. Hwang, C. W. Lee and J. Y. Lee, Adv. Mater., 2015, 27, 5861–5867 CrossRef CAS
.
- N. Haase, A. Danos, C. Pflumm, A. Morherr, P. Stachelek, A. Mekic, W. Brütting and A. P. Monkman, J. Phys. Chem. C, 2018, 122, 29173–29179 CrossRef CAS
.
- T. Northey, J. Stacey and T. J. Penfold, J. Mater. Chem. C, 2017, 5, 11001–11009 RSC
.
- J.-M. Ku, D.-K. Kim, T.-H. Ryu, E.-H. Jung, Y. Lansac and Y.-H. Jang, Bull. Korean Chem. Soc., 2012, 33, 1029–1036 CrossRef CAS
.
- L.-S. Cui, H. Nomura, Y. Geng, J. U. Kim, H. Nakanotani and C. Adachi, Angew. Chem., Int. Ed., 2017, 56, 1571–1575 CrossRef CAS
.
- S.-J. Woo, Y. Kim, S.-K. Kwon, Y.-H. Kim and J.-J. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 7199–7207 CrossRef CAS
.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS
.
- A. Chantzis, A. D. Laurent, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 4517–4525 CrossRef CAS
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS
.
- S. Huang, Q. Zhang, Y. Shiota, T. Nakagawa, K. Kuwabara, K. Yoshizawa and C. Adachi, J. Chem. Theory Comput., 2013, 9, 3872–3877 CrossRef CAS
.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. Lett., 2019, 10, 793–798 CrossRef CAS
.
- M. Colella, A. Danos and A. P. Monkman, J. Phys. Chem. C DOI:10.1021/acs.jpcc.9b03538
.
- X.-K. Chen, Y. Tsuchiya, Y. Ishikawa, C. Zhong, C. Adachi and J.-L. Brédas, Adv. Mater., 2017, 29, 1702767 CrossRef
.
- X. Qiu, Y. Xu, C. Wang, M. Hanif, J. Zhou, C. Zeng, Y. Li, Q. Jiang, R. Zhao, D. Hu and Y. Ma, J. Mater. Chem. C, 2019, 7, 5461–5467 RSC
.
- V. Thangaraji, P. Rajamalli, J. Jayakumar, M.-J. Huang, Y.-W. Chen and C.-H. Cheng, ACS Appl. Mater. Interfaces, 2019, 11, 17128–17133 CrossRef CAS
.
- J. S. Ward, R. S. Nobuyasu, A. S. Batsanov, P. Data, A. P. Monkman, F. B. Dias and M. R. Bryce, Chem. Commun., 2016, 52, 2612–2615 RSC
.
- R. Mohapatra and S. Panda, Int. J. Zool., 2014, 2014, 1–7 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 1917139–1917141. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9tc02742d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |