A continuous-flow acoustofluidic cytometer for single-cell mechanotyping†
Han
Wang
 a,
Zhongzheng
Liu
a,
Zhongzheng
Liu
 b,
Dong M.
Shin
c,
Zhuo G.
Chen
c,
Younghak
Cho
b,
Dong M.
Shin
c,
Zhuo G.
Chen
c,
Younghak
Cho
 d,
Yong-Joe
Kim
b and
Arum
Han
d,
Yong-Joe
Kim
b and
Arum
Han
 *efg
*efg
aDepartment of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, 100084, China
bDepartment of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA
cDepartment of Hematology and Medical Oncology, Emory University School of Medicine, Atlanta, GA, USA
dDepartment of Mechanical System Design Engineering, Seoul National University of Science and Technology, Seoul, Republic of Korea
eDepartment of Electrical and Computer Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: arum.han@ece.tamu.edu; Fax: +1 979 845 6259; Tel: +1 979 845 9686
fDepartment of Biomedical Engineering, Texas A&M University, College Station, TX 77843, USA
gCenter for Remote Health Technologies & Systems, Texas A&M University, College Station, TX 77843, USA
First published on 10th January 2019
Abstract
The biophysical properties of cells such as their compressibility have been found to be closely related to disease progression such as cancer development and metastasis. As cancer cells are heterogeneous, rapid and high-throughput evaluation of cell biophysical properties at single-cell resolution is needed to assess their potential as biomarkers for cancer staging and prognosis. Acoustofluidics has shown promise as a contactless method for accurately measuring cell biophysical properties; however, previously reported methods had relatively low throughput due to their requirement of no-flow conditions. This work presents a high-throughput continuous flow-based acoustofluidic cell mechanotyping method at single-cell resolution that retains the advantage of simplicity and low-cost.
Clinical cancer diagnosis and prognosis have largely relied on imaging-based tissue-level analysis, such as positron emission tomography (PET) and computed tomography (CT), or biopsy-based examination using histopathological methods.1 Recent advances in the molecular diagnostics and liquid biopsy of circulating tumor cells (CTCs) and cell-free DNA are allowing researchers and clinicians to identify cancer cells and secreted biomarkers (e.g., extracellular vesicles, ctDNA, and microRNA) by performing genomic/transcriptomic analysis and/or surface biomarker-based cell phenotyping.2,3 However tissue-level diagnosis lacks information regarding intratumoral heterogeneity, and molecular-level analysis needs to be coupled with phenotypic characterization due to the heterogeneous nature of tumors. In contrast, cellular-level analysis can provide insights into both phenotypic heterogeneity and disease progression dynamics.4 Therefore, developing cellular-level phenotyping methods, which can be eventually coupled with other diagnostic technologies such as molecular-level analysis to allow multi-modal analysis, is of high interest.
Traditionally, cellular-level phenotyping methods have largely relied on surface biomarkers, as in the case of detecting CTCs.5 However surface biomarker-based cell phenotyping alone has been insufficient to accurately identify various high-risk cancer cells and tumor heterogeneity.6 Other technologies such as size-based CTC isolation also have shortcomings in capture efficiency and purity.7 Thus, identifying the highly aggressive subpopulation in solid tumors remains to be a major challenge in understanding tumorigenesis, reducing drug resistance, and improving cancer therapy.8,9 The biophysical properties of cells have been reported to be associated with cancer cell differentiation and disease progression.10–13 It was found that many malignant tumor cells, especially those that have the potential to metastasize to other locations, go through a series of phenotypic changes such as epithelial–mesenchymal transition (EMT), which results in changes in the biophysical properties of cells. Thus, there is significant interest in methods that can quantify their biophysical properties and identify various subpopulations of cells. Although many single-cell analysis methods for cell mechanotyping have been developed in the past decade, high-throughput and accurate measurement of such properties remains a major challenge.
Using a variety of forces directly applied to cells, such as mechanical force in atomic force microscopy and micropipette aspiration, optical force in optical tweezers, and magnetic force in magnetic twisting cytometry, researchers were able to measure deformation of cellular shapes and extract cell compressibility with single-cell resolution.14–19 However, these conventional methods have intrinsically low throughput and typically need expensive or complex instruments as well as advanced operator skills.
Microfluidic systems have been extensively developed in the past decade and have been used in many studies related to cell mechanotyping.20 Among them, constricting microchannels have been widely adopted to quantify cell deformability due to their simple design and multi-factorial output signals such as cell deformation, impedance change, and cell transit time through the constricting microchannels.21–23 Nyberg et al. presented a high-throughput cell mechanotyping system with a constricting microchannel using power-law rheology and determined deformability of human breast cancer cells based on their shape changes.24 However in general, since these methods rely on physical contact between cells and constricting geometries, they can easily result in measurement inaccuracy due to device variations as well as difficulties in decoupling the effect coming from cell size variations. Also, cells may be damaged while they pass through such constricting geometries. The second category of microfluidic approaches relies on cell deformation in a flow stream, such as a narrowing channel (but without physical contact with channel walls)25 or a cross-junction channel that applies colliding fluids to cells and measures cell deformation in response to those forces.26 This deformation can be imaged and analyzed using an ultra-high-speed camera and image processing module and has shown a throughput of up to 1000 cells per second. However this method requires an extremely high-speed camera that is costly, as well as complex image processing, limiting its wide-spread use. Inertial microfluidics, where cells of different sizes and compressibilities can be separated based on the margination phenomena under inertial force, has been also employed to separate cancer cells from normal blood cells based on their compressibility differences.27,28 However, these devices typically require high flow speed, and the separation resolution is relatively poor compared to that of other methods.
Overall, a major drawback of many systems developed so far is the incapability of decoupling cell size-dependent effects from cell compressibility-dependent effects. Those that can distinguish the two effects require an ultra-high-speed camera that has to very accurately record the deformation process of single cells. Therefore, a high-throughput single-cell resolution cell mechanotyping system that can decouple the cell compressibility-dependent effect from the cell size-dependent effect is essential in adopting the biophysical properties of cells as potential biomarkers in cancer biology research and clinical applications. Affordability in terms of cost and expertise is another important factor that needs to be resolved before any of these methods can be widely adopted.
Microfluidic acoustophoresis techniques have been utilized in many applications involving contactless cell and particle manipulation, separation, and concentration.29,30 There are mainly two types of microfluidic acoustic cell manipulation approaches, the ones using bulk acoustic wave resonators and the ones using surface acoustic wave (SAW) resonators. Although SAW-based acoustofluidic devices have been extensively utilized for cell and particle separation, so far SAW resonators have not been readily applied for direct single-cell mechanotyping studies. In addition this method requires expensive specialty substrates and more complex fabrication procedures.31 Thus here our main focus and motivation are in the context of bulk acoustofluidic devices that require only a simple microfluidic channel with a piezoelectric transducer attached to the bottom.
Several studies have reported the measurement of cell biophysical properties using bulk acoustic wave resonators.32–35 Hartono et al. analyzed the trajectories of cells moving in the Y-direction of the acoustic field (with the X-direction being the microchannel flow direction) and extracted their compressibility using referenced densities from the literature (not from the samples themselves).34 Barnkob et al. extracted the densities and compressibilities of particles and cells simultaneously using calibration microbeads.33 To reduce measurement errors stemming from different starting positions or varying Z-locations of cells during the cell trajectory analysis, Wang et al. incorporated acoustophoretic control of the three dimensional positions of cells in a microchannel to improve the accuracy and robustness of cell biophysical property measurement.35 However, in all of the above acoustophoretic cell trajectory-based measurement methods, the experimental procedure is tedious and consists of the following steps: introduce cells into the microchannel, stop the flow, actuate the transducer to generate an acoustic resonance field, record and analyze the trajectories of cells, flush the cells and repeat the process. Therefore the throughout is extremely low (less than 10 cells per min), as during the cell trajectory measurement cells have to be stationary in the X-direction (i.e., no flow).
In this work, to decouple the cell size-dependent effect from the compressibility-dependent effect and achieve higher throughput using acoustophoresis, a continuous-flow acoustofluidic cytometer was constructed for cell mechanotyping, where cells could be introduced into the acoustic field at a constant position and then move under the influence of acoustophoretic force, and have their exit positions recorded and analyzed. This facilitates highly robust and accurate single-cell resolution mechanotyping at high throughput without the need for calculating the exact values of cell compressibility, where decoupling the cell size-dependent effect can also be easily conducted. The primary acoustic radiation force is given in the following equation.36
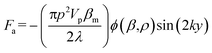 | (1) |
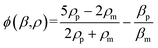 | (2) |
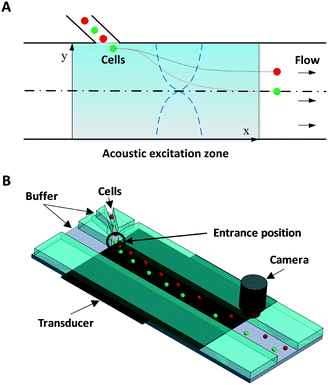
Fig. 1 illustrates the system and working principle. The straight flow channel has a piezoelectric transducer attached to the bottom to form an acoustic resonance field inside the channel for cell manipulation and a downstream imaging camera for recording the exit positions of cells. When cells enter the main channel they can move in the transverse Y-direction by the acoustophoretic force, where this movement is used for cell mechanotyping. To use the cells' exit position (in the Y-direction) for determining the cell compressibility-dependent movement under acoustophoretic force, it is important that the cells always enter the exact same location into the acoustic resonance field. To improve the consistency in the cell entrance point, a three-inlet hydrodynamic flow focusing system was used in the side channel. Thus cells are first aligned to the center of the side channel before entering the main channel, allowing cells to be consistently introduced into the same position in the acoustic resonance field. Also several studies have revealed the importance of Z-locations of cells during acoustophoretic actuation, since the cells would experience different acoustophoretic forces and acoustic streaming depending on their Z-locations, and also there could be increased friction as cells become close to the channel wall. Therefore in this study we reduced the channel height and introduced sheath flow to improve the consistency of the Z-location of the cells.38–40
The device was fabricated in glass/silicon using a similar procedure as described previously.41 In short, an aluminium layer (thickness: 500 nm) was patterned on a silicon substrate to form the etch mask. The microchannel was then etched in silicon by deep reactive ion etching (Oxford Plasmalab 100 ICP RIE) to a depth of 30 μm. The fabricated silicon microchip was then anodically bonded to a glass substrate with inlet/outlet holes pre-drilled. The fluidic connection was provided by flat-bottom ferrules (P-200N, Upchurch Scientific, WA) and Tygon® tubing (Saint-Gobain Performance Plastics, OH).
The first set of fabricated microdevices (set 1) had a main microchannel width of 370 μm and a side channel width of 30 μm. The second set of fabricated microdevices (set 2) had a main microchannel width of 390 μm and a side channel width of 38 μm. The flow rates in each stream were set to: center main inlet 100 μl h−1, side inlet 10 μl h−1, and side sheath flow inlet 10 μl h−1. The acoustic resonance field was generated using a piezoelectric ceramic plate (PZ26, Ferroperm Piezoceramics A/S, Denmark) attached to the bottom, which was stimulated with a sinusoidal wave of 2.17 MHz/1.835 MHz for set 1/set 2, respectively, amplified using a 50 dB power amplifier (E&I 2100 L, Electronics & Innovation, Ltd.).
To calibrate the acoustic resonance field, polystyrene beads (diameter: 11 μm, Polysciences, Inc) with known density and compressibility were first introduced and used to calculate the acoustic pressure field. Following this calibration, cancer cells were tested for mechanotyping.
In our experiment we evaluated the continuous-flow acoustofluidic cytometer for single-cell mechanotyping of two different types of cancer cells. For the set 1 microdevice we tested three different breast cancer cell lines, BT474, MDA-MB-231, and MCF-7, as well as immortalized breast epithelial cell line MCF-10A. BT474 is a ductal carcinoma cell line with primary tumor origins, while MCF-7 and MDA-MB-231 are also ductal carcinoma cell lines but derived from metastatic sites by pleural effusion. For the set 2 microdevice we evaluated the compressibility of three head and neck cancer cell lines 37B, M4e, and Tu686. These cell lines were obtained from our collaborator's laboratory at the Emory University School of Medicine.
The initial entrance position has a significant impact on the acoustophoretic force-actuated cell movement, since the acoustic pressure field differs depending on the Y-locations. Thus without flow focusing, cells enter the acoustic resonance field at random positions within the width of the side channel (even when using a relatively narrow channel), as can be seen in Fig. 2A. In this case the acoustophoretic force they experience is significantly different, resulting in large variations in their trajectories, essentially making the cell trajectory analysis meaningless. On the other hand when using the hydrodynamic flow focusing scheme in the side channel, cells were aligned in a single flow streamline (Fig. 2B), greatly reducing the variations in entrance position differences.
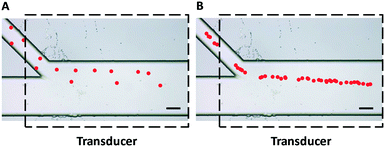 | ||
| Fig. 2 Trajectories of polystyrene beads (pseudocolor for better visualization) passing through an acoustic standing wave field (A) without and (B) with hydrodynamic flow focusing using sheath flow in the side channel. The uniformity of particle trajectories was greatly improved and the entrance positions were more precise and repeatable with the flow focusing scheme shown in Fig. 2B. Dashed lines indicate the position of the piezoelectric transducer attached to the bottom of the device. Scale bar = 100 μm. | ||
The first-order resonance frequency corresponding to the channel width was applied to generate a transversal (Y-direction) acoustic resonance field in the microchannel. As cells entered the acoustic field, they were subject to the acoustophoretic force, which moved them to the transversal first harmonics pressure node in the channel center, as well as to the size-dependent viscous drag force that was applied in the opposite direction. By tuning the acoustic pressure field (adjusted by the applied power) and cell transit time (adjusted by the flow rate), the transversal positions of cells when exiting the acoustic field could be controlled in the range between the channel sidewall and channel center. In this way only cells with a higher acoustic contrast factor move closer to the center pressure node, while cells with a lower contrast factor do not have enough time to move to the center pressure node. This allows relating the cells' transversal position differences to the acoustophoretic force differences caused by their size, density, and compressibility differences.
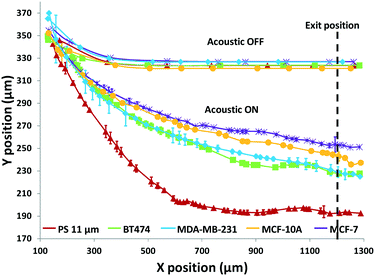
Using the set 1 microdevice, we first analyzed and compared the trajectories of the breast cancer cell lines, BT474, MDA-MB-231, and MCF-7, as well as immortalized breast epithelial cell line MCF-10A as control, while using polystyrene beads for calibration. The cell's exit position and size were recorded with a CCD camera (Hamamatsu ORCA-Flash4.0, Hamamatsu Photonics K.K.) at 30 fps and then analyzed using a custom-built MATLAB® (MathWorks, Inc.) program. The coordinate conversion scheme for the raw image data is illustrated in Fig. S1.† As shown in Fig. 3, a simple comparison of the trajectories of cells provides some useful information, but only in a limited way. When no acoustophoretic force was applied, all cells showed the same exit position as expected. When the acoustophoretic force was applied, a simple exit position-based classification showed the order BT474/MDA-MB-231 > MCF10A > MCF-7, with no obvious differences between BT474 and MDA-MB-231. From eqn (1), if the cell size is the same, the cells with a higher acoustic contrast factor would experience a higher acoustophoretic force, while the drag force remains the same, thus their exit positions will be more towards the center of the microchannel. MDA-MB-231 has been reported to be significantly more invasive than MCF-7, which translates to a higher compressibility and acoustic contrast factor,42,43 and indeed move more towards the channel center compared to MCF-7. However previous studies have reported that the compressibility of MCF-7 is higher than MCF-10A,18,34 which is not consistent with the result shown in Fig. 3. This is an indicator that trajectory analysis alone cannot accurately determine cell compressibility-dependent movement, as other parameters such as cell size also play a role. Therefore it is necessary to decouple the cell size-dependent effect from the cell compressibility-dependent effect.
Thus next, we included the cell size in our analysis, as all cell types measured here had slightly different average sizes. The averaged diameter and standard deviation of the different cell lines as well as those of polystyrene beads are shown in Table 1. The cell areas were calculated using a custom-made MATLAB® program to analyze time-lapse images of passing cells. Also, to facilitate faster and simpler data processing, instead of trajectory-based whole image analysis (as used in Fig. 3), an exit position-based image acquisition and analysis method was utilized. In this method, rather than imaging and plotting the entire trajectories, only the transversal positions where cells leave the acoustic field are captured with a small imaging window, so that the image acquisition speed and flow rate can be further increased to improve the throughput while still using a low-cost low-speed CCD camera. Also this small image window allows faster image processing to obtain the size of cells and their exit positions to achieve increased measurement speed. In our test, the image acquisition speed with the same 30 fps camera could reach 100 fps (using a smaller region-of-interest (ROI) window) while the highest flow rate tested was 375 μl h−1, making the throughput in the range of 10 cells per second, which was 60-fold improvement as compared to previously reported no-flow acoustic cell compressibility analysis methods.32–34,44
| Item | Average area (μm2) | Standard deviation (μm2) |
|---|---|---|
| PS | 100.4 | 4.4 |
| BT474 | 211.8 | 12.4 |
| MDA-MB-231 | 164.9 | 16.1 |
| MCF-7 | 165.1 | 19.5 |
| MCF-10A | 199.4 | 19.2 |
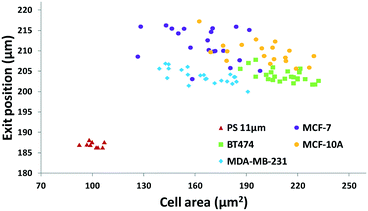
The results in Fig. 3 are plotted in Fig. 4 based on the cell sizes vs. exit positions (i.e., transversal positions in the Y-direction at X = 1200 μm, shown as the dashed line in Fig. 3), which can help to easily visualize differences in cell biophysical properties, and thus can be used for cell mechanotyping.32 As can be seen in Fig. 4, MCF-7 and MDA-MB-231 have similar size distributions, while MDA-MB-231 shows longer travelling distance in the transversal direction, which can be interpreted as MDA-MB-231 experiencing a stronger acoustophoretic force and similar drag force, an indicator of a higher acoustic contrast factor. This is similar to the result from the trajectory analysis in Fig. 3. Based on the results in Fig. 4, the acoustic contrast factors of these cell lines were calculated and shown in Fig. 5, after taking into account all forces (i.e., acoustophoretic force, viscous drag force, gravitational force, and buoyancy force) the cells were subjected to.26,45 The numerical model used polystyrene beads with known mechanical properties (i.e. the acoustic contrast factor of polystyrene beads is 0.67) to calibrate the acoustic pressure field, and then the acoustic contrast factors of cells were extracted.35 From Fig. 5, it can be clearly seen that MDA-MB-231 has the highest acoustic contrast factor, while MCF-10A has the lowest acoustic contrast factor. The order of the acoustic contrast factors of these cell lines is: MDA-MB-231 (0.175 ± 0.012) > BT474 (0.135 ± 0.007) > MCF-7 (0.132 ± 0.023) > MCF-10A (0.116 ± 0.011). This was not obvious from the simple trajectory analysis shown in Fig. 3, which did not account for the differences in the cell size, but clearly distinguishable in Fig. 4 and 5 when the cell size was also considered.
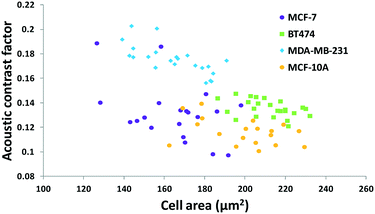 | ||
| Fig. 5 Scatter plot of the cell size (in the form of cross-sectional cell area) and cell acoustic contrast factor of breast cancer cell lines for single-cell mechanotyping. (n = 94). | ||
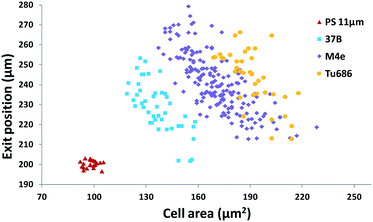
Furthermore, we applied the set 2 microdevice to evaluate the compressibility of the head and neck cancer cell lines 37B, M4e, and Tu686 along with the polystyrene beads as a reference. The exit Y-positions of particles per cells at a particular X-location (5 mm downstream of the main microchannel) were recorded using a small ROI window and plotted against the cell areas analyzed by using the time-lapse images (Fig. 6). These cell lines could be successfully distinguished using this scatter plot as shown in Fig. 6. The order of the acoustic contrast factors of the head and neck cancer cell lines was 37B (0.235 ± 0.048) > M4e (0.153 ± 0.026) > Tu686 (0.133 ± 0.025), which were in line with previous cell mechanotyping studies under no-flow conditions, as well as live cell studies, indicating that the invasiveness of 37B and M4e is significantly higher than Tu686.35,46 These results demonstrate the potential of the presented method in cell mechanotyping of not only cancer cells versus normal cells, but also cancer cells with different metastatic potential.
These results confirm that the presented measurement and analysis method that account for both the cell size and the cell compressibility can be an accurate cell mechanotyping method. Also, as only the exit position has to be recorded instead of the entire cell trajectory, achieving higher throughput is possible without the need for an expensive high-speed camera, allowing low-cost high-throughput analysis. Having to only record the exit position rather than the entire cell trajectory also significantly simplifies the image processing need, which has the potential to provide real-time cell mechanotyping.
As shown in the acoustofluidic cytometer scatter plot in Fig. 4 and 6, there is about 10–20% overlap in the experimental data between the different cell lines. However this overlap most likely comes from the heterogeneity of the compressibility of cells even within the same cell population, not due to any inherent limitation of the method itself. This is well-supported from other cell mechanotyping studies in the literature. For example, Hou et al. compared the deformability of MCF-7 and MCF-10A using constricting microchannels and showed about 20–30% population similarity in the deformability between these cells.21 Lee et al. evaluated the deformability characteristics of normal blood cells and cancerous blood cells using optical pressure and showed about 35% population similarity.19 Nyberg et al. studied the deformability of MCF-7 and MDA-MB-231 by quantitative analysis of the cells passing through constricting microchannels and showed 20–40% population similarity.24 Therefore, in many of these studies, the deformability profiles of each cell line were instead plotted in separate columns, due to significant overlapping of data points from different cell lines. This also clearly indicates that such similarity is not the limitation of our method or other reported methods, but rather the inherent heterogeneity in compressibility characteristics of cells in a given population.
In conclusion, a label-free and non-invasive acoustofluidic cytometer was developed for the mechanotyping of different cancer cell lines based on their intrinsic biophysical properties in continuous flow using a simple device and a simple and low-cost experimental setup. The acoustophoretic force was utilized to translocate cells in the transversal direction under continuous flow, and such movement could be analyzed for mechanotyping of cells. The presented method significantly improves upon previous acoustophoresis-based cell compressibility phenotyping methods that are accurate but have low throughput. The throughput of the presented method can be further increased by modifying the system design to allow sufficient transit time of cells in the acoustic resonance field or applying alternative impedance spectroscopy-based cell sizing methods.47,48 We expect that the developed system can be used in a variety of applications, such as phenotyping of cancer cells with different metastatic potential based on their biophysical properties, studying EMT for the change in their biophysical properties, and even for analyzing erythrocytes with regard to malaria infection.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the grant ECCS-1232251 from the Division of Electrical, Communications and Cyber Systems of National Science Foundation (NSF).References
- J. R. Galvin and T. J. Franks, Radiology, 2013, 268, 9–11 CrossRef PubMed.
- C. L. Sawyers, Nature, 2008, 452, 548 CrossRef CAS PubMed.
- M. J. Duffy, Med. Princ. Pract., 2012, 22, 4–11 CrossRef PubMed.
- K. Pantel, R. H. Brakenhoff and B. Brandt, Nat. Rev. Cancer, 2008, 8, 329–340 CrossRef CAS PubMed.
- M. G. Krebs, R. L. Metcalf, L. Carter, G. Brady, F. H. Blackhall and C. Dive, Nat. Rev. Clin. Oncol., 2014, 11, 129–144 CrossRef CAS PubMed.
- P. K. Grover, A. G. Cummins, T. J. Price, I. C. Roberts-Thomson and J. E. Hardingham, Ann. Oncol., 2014, 25, 1506–1516 CrossRef CAS PubMed.
- M. T. Gabriel, L. R. Calleja, A. Chalopin, B. Ory and D. Heymann, Clin. Chem., 2016, 62, 571–581 CrossRef CAS PubMed.
- A. Marusyk, V. Almendro and K. Polyak, Nat. Rev. Cancer, 2012, 12, 323 CrossRef CAS PubMed.
- I. Dagogo-Jack and A. T. Shaw, Nat. Rev. Clin. Oncol., 2018, 15, 81–94 CrossRef CAS PubMed.
- S. Suresh, Acta Biomater., 2007, 3, 413–438 CrossRef PubMed.
- G. Y. H. Lee and C. T. Lim, Trends Biotechnol., 2007, 25, 111–118 CrossRef CAS PubMed.
- D. Wirtz, K. Konstantopoulos and P. C. Searson, Nat. Rev. Cancer, 2011, 11, 512–522 CrossRef CAS PubMed.
- D. A. Fletcher and R. D. Mullins, Nature, 2010, 463, 485 CrossRef CAS PubMed.
- F. J. Alenghat, B. Fabry, K. Y. Tsai, W. H. Goldmann and D. E. Ingber, Biochem. Biophys. Res. Commun., 2000, 277, 93–99 CrossRef CAS PubMed.
- R. M. Hochmuth, J. Biomech., 2000, 33, 15–22 CrossRef CAS PubMed.
- V. r. M. Laurent, S. Hénon, E. Planus, M. Balland, D. Isabey, F. o. Gallet and R. Fodil, J. Biomech. Eng., 2002, 124, 408–421 CrossRef PubMed.
- S. E. Cross, Y. S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS PubMed.
- Q. S. Li, G. Y. H. Lee, C. N. Ong and C. T. Lim, Biochem. Biophys. Res. Commun., 2008, 374, 609–613 CrossRef CAS PubMed.
- W. G. Lee, H. Bang, H. Yun, J. Lee, J. Park, J. K. Kim, S. Chung, K. Cho, C. Chung, D. C. Han and J. K. Chang, Lab Chip, 2007, 7, 516–519 RSC.
- J. El-Ali, P. K. Sorger and K. F. Jensen, Nature, 2006, 442, 403 CrossRef CAS PubMed.
- H. W. Hou, Q. S. Li, G. Y. H. Lee, A. P. Kumar, C. N. Ong and C. T. Lim, Biomed. Microdevices, 2009, 11, 557–564 CrossRef CAS PubMed.
- A. Adamo, A. Sharei, L. Adamo, B. Lee, S. Mao and K. F. Jensen, Anal. Chem., 2012, 84, 6438–6443 CrossRef CAS PubMed.
- M. Mak, C. A. Reinhart-King and D. Erickson, Lab Chip, 2013, 13, 340–348 RSC.
- K. D. Nyberg, K. H. Hu, S. H. Kleinman, D. B. Khismatullin, M. J. Butte and A. C. Rowat, Biophys. J., 2017, 113, 1574–1584 CrossRef CAS PubMed.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Topfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- H. T. K. Tse, D. R. Gossett, Y. S. Moon, M. Masaeli, M. Sohsman, Y. Ying, K. Mislick, R. P. Adams, J. Rao and D. Di Carlo, Sci. Transl. Med., 2013, 5, 212ra163 CrossRef PubMed.
- H. W. Hou, A. A. S. Bhagat, A. G. Lin Chong, P. Mao, K. S. Wei Tan, J. Han and C. T. Lim, Lab Chip, 2010, 10, 2605–2613 RSC.
- S. C. Hur, N. K. Henderson-MacLennan, E. R. B. McCabe and D. Di Carlo, Lab Chip, 2011, 11, 912–920 RSC.
- T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506 RSC.
- T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. A. Weitz, Lab Chip, 2010, 10, 789–794 RSC.
- X. Ding, Z. Peng, S.-C. S. Lin, M. Geri, S. Li, P. Li, Y. Chen, M. Dao, S. Suresh and T. J. Huang, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12992–12997 CrossRef CAS PubMed.
- P. Augustsson, R. Barnkob, C. Grenvall, T. Deierborg, P. Brundin, H. Bruus and T. Laurell, in Proceedings of the 14. International Conference on Miniaturized Systems for Chemistry and Life Sciences, 2010, pp. 1337–1339 Search PubMed.
- R. Barnkob, P. Augustsson, C. Magnusson, H. Lilja, T. Laurell and H. Bruus, in Proceedings of the 15th International Conference on Miniaturized Systems for Chemistry and Life Sciences, 2011, pp. 127–129 Search PubMed.
- D. Hartono, Y. Liu, P. L. Tan, X. Y. S. Then, L.-Y. L. Yung and K.-M. Lim, Lab Chip, 2011, 11, 4072–4080 RSC.
- H. Wang, Z. Liu, D. M. Shin, Z. G. Chen, Y. Cho, Y.-J. Kim and A. Han, Microfluid. Nanofluid., 2018, 22, 68 CrossRef.
- L. P. Gorkov, Phys.-Dokl., 1962, 6, 773 Search PubMed.
- Z. Liu, H. Wang, A. Han and Y.-J. Kim, Proc. Meetings Acoust., 2013, 19, 045015 Search PubMed.
- D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef CAS PubMed.
- L. Ren, S. Yang, P. Zhang, Z. Qu, Z. Mao, P.-H. Huang, Y. Chen, M. Wu, L. Wang, P. Li and T. J. Huang, Small, 2018, 14, 1801996 CrossRef PubMed.
- M. Wu, K. Chen, S. Yang, Z. Wang, P.-H. Huang, J. Mai, Z.-Y. Li and T. J. Huang, Lab Chip, 2018, 18, 3003–3010 RSC.
- H. Wang, Z. Liu, S. Kim, C. Koo, Y. Cho, D.-Y. Jang, Y.-J. Kim and A. Han, Lab Chip, 2014, 14, 947–956 RSC.
- C. Sheridan, H. Kishimoto, R. K. Fuchs, S. Mehrotra, P. Bhat-Nakshatri, C. H. Turner, R. Goulet, S. Badve and H. Nakshatri, Breast Cancer Res., 2006, 8, R59 CrossRef PubMed.
- L. Hughes, C. Malone, S. Chumsri, A. M. Burger and S. McDonnell, Clin. Exp. Metastasis, 2008, 25, 549–557 CrossRef PubMed.
- H. Wang, Z. Liu, D. M. Shin, G. Chen, Y. Cho, Y.-J. Kim and A. Han, J. Acoust. Soc. Am., 2013, 133, 3280–3280 Search PubMed.
- P. Augustsson, J. T. Karlsen, H.-W. Su, H. Bruus and J. Voldman, Nat. Commun., 2016, 7, 11556 CrossRef CAS PubMed.
- S. Kang, S. Elf, K. Lythgoe, T. Hitosugi, J. Taunton, W. Zhou, L. Xiong, D. Wang, S. Muller, S. Fan, S. Y. Sun, A. I. Marcus, T. L. Gu, R. D. Polakiewicz, Z. G. Chen, F. R. Khuri, D. M. Shin and J. Chen, J. Clin. Invest., 2010, 120, 1165–1177 CrossRef CAS PubMed.
- A. Pierzchalski, M. Hebeisen, A. Mittag, M. D. Berardino and A. Tarnok, in SPIE BiOS, SPIE, 2010, p. 11 Search PubMed.
- K. C. Cheung, M. Di Berardino, G. Schade-Kampmann, M. Hebeisen, A. Pierzchalski, J. Bocsi, A. Mittag and A. Tárnok, Cytometry, Part A, 2010, 77A, 648–666 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc00711j |
| This journal is © The Royal Society of Chemistry 2019 |