Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single-layer metal halides MX2 (X = Cl, Br, I): stability and tunable magnetism from first principles and Monte Carlo simulations†
Vadym V.
Kulish
 *a and
Wei
Huang
*b
*a and
Wei
Huang
*b
aDepartment of Mechanical Engineering, National University of Singapore, 21 Lower Kent Ridge Rd, 119077, Singapore. E-mail: kulishvadym@gmail.com
bInstitute of Systems Science, National University of Singapore, 25 Heng Mui Keng Terrace, 119615, Singapore. E-mail: huangwei860921@gmail.com
First published on 26th July 2017
Abstract
Based on first-principles calculations, we investigate a novel class of 2D materials – MX2 metal dihalides (X = Cl, Br, I). Our results show that single-layer dihalides are energetically and dynamically stable and can be potentially exfoliated from their bulk layered forms. We found that 2D FeX2, NiX2, CoCl2 and CoBr2 monolayers are ferromagnetic (FM), while VX2, CrX2, MnX2 and CoI2 are antiferromagnetic (AFM). The magnetic properties of 2D dihalides originate from the competition between AFM direct nearest-neighbor d–d exchange and FM superexchange via halogen p states, which leads to a variety of magnetic states. The thermal dependence of magnetic properties and the Curie temperature of magnetic transition are evaluated using statistical Monte Carlo simulations based on the Ising model with classical Heisenberg Hamiltonian. The magnetic properties of single-layer dihalides can be further tuned by strain and carrier doping. Our study broadens the family of existing 2D materials with promising applications in nanospintronics.
1. Introduction
Tremendous research attention is currently focused on two-dimensional (2D) nanomaterials due to their rich physical properties and diverse technological applications.1–3 The possibility of designing magnetic 2D nanostructures is particularly intriguing and can be useful for spintronics and nanoscale magnetic memory devices.4 Most 2D nanomaterials, however, do not show any intrinsic magnetism with only rare exceptions.5–13 The strategies to induce magnetic moments in otherwise non-magnetic 2D materials include defect engineering,14 strain,15 adatom adsorption,16–22 and substitutional doping.23,24 However, the resulting materials lack experimental controllability and stability. Moreover, metal dopants tend to form clusters due to strong d–d interactions resulting in non-homogenous magnetization and low Curie temperature values. Identifying magnetic 2D nanomaterials thus has been a challenge.Here, we examine a novel class of 2D nanostructures – single-layer metal dihalides (MX2, where X = Cl, Br, I). Surprisingly, this class of nanomaterials is relatively unexplored despite the presence of stable layered structures in the bulk. However, halides start to attract research attention now, including the layered ones.25–28 For instance, the experimentally synthesized layered BiI3 has a bandgap of 1.8 eV and demonstrates room-temperature band-edge photoluminescence.29–31 Layered ternary bismuth iodides show good photovoltaic performance with an extra advantage of the significantly reduced toxicity of Bi when compared with Pb.32 Theoretical calculations demonstrate that single-layer PbI2 is stable and exhibits interesting exciton and spin–orbit coupling effects.33,34 Monolayer GaBiCl2, ZrBr and HfCl were identified as room-temperature quantum spin Hall insulators with large nontrivial band gaps.35,36 FeCl2 displays a half-metallic ferromagnetic ground state.37,38 Recent experimental studies demonstrated that single crystals of CrI3 can be cleaved very easily, possess a ferromagnetic order even in the monolayer form, and are stable in air/water, in the absence of CrI2 contamination.39–41 The above studies show a high potential of 2D halides from both fundamental and applied perspectives.
In this work, we demonstrate that single-layer metal dihalides are energetically stable and possess intrinsic ferromagnetism. Their magnetic properties originate from the competition between antiferromagnetic (AFM) direct nearest-neighbor d–d exchange and ferromagnetic (FM) superexchange via halogen p states, leading to a variety of magnetic states. By using density functional theory (DFT) methods, we determine the ground-state magnetic ordering and calculate the exchange coupling constants in 2D dihalides. The thermal dependence of magnetic properties and the Curie temperature of magnetic transition are estimated using statistical Monte Carlo (MC) simulations based on the Ising model. We find that single-layer dihalides exhibit comparable or even slightly higher Curie temperatures than single-layer dichalcogenides. This can be attributed to the profound ionic bonding in halides, which enhances the superexchange coupling between the magnetic metal ions via the halogen atoms, consistent with the Goodenough–Kanamori–Anderson rules.
2. Computational methods
Spin-polarized first-principles calculations were performed within the density functional theory (DFT) framework, as implemented in the Quantum Espresso package.42 The core electrons were treated within the projector augmented wave (PAW) method.43 Exchange–correlation effects were described through the generalized gradient approximation (GGA) and the PBEsol exchange–correlation functional.44 PBEsol is a revision of the PBE functional, specifically tailored for solids, and has been shown to produce better agreement with experimental data.44 For accurate electronic structure prediction, we used the HSE06 hybrid functional including 25% non-local Hartree–Fock exchange.45 The total energy of monolayers was calculated using a Γ-centered 15 × 15 × 1 Monkhorst–Pack k-point grid for a primitive cell. The plane-wave cutoff is 50 Ryd (680 eV). Test calculations with a larger number of k points and higher cutoff energies produced the same results. The optimized structures were obtained by relaxing all atomic positions and lattice parameters using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) quasi-Newton algorithm until all forces are smaller than 0.01 eV Å−1. To account for the on-site Coulomb interactions between the 3d electrons, we performed DFT+U calculations by adding an effective parameter, Ueff.46 We have used Ueff values for transition metals suggested by Ceder et al.47 We have also performed additional tests using other Ueff values from 1.0 to 6.0 eV, and found that the use of different Ueff values leads to qualitatively similar results.3. Results and discussion
3.1. Crystal structure and stability
First, we examine the atomic structure of dihalides MX2 (M = V, Cr, Mn, Fe, Co, Ni, and X = Cl, Br, I). As shown by experimental studies, bulk metal dihalides have a natural layered structure as shown in Fig. 1a. Therefore, similar to graphene and MoS2, individual layers of dihalides can be potentially extracted from the bulk using exfoliation techniques. For each monolayer, we have determined the minimum-energy structure by optimizing all atomic positions and lattice constants. The typical crystal structure of single-layer MX2 is shown in Fig. 1b and c. The atomic geometry of monolayer dihalides is conceptually similar to the well-known transition-metal dichalcogenides (TMDCs). Namely, each metal dihalide is composed of three atomic planes: a layer of transition-metal (TM) atoms sandwiched between two layers of halogen atoms. Interestingly, we find that all studied single-layer dihalides prefer the 1-T crystal structure (C3v symmetry). Each metal atom is surrounded by 6 neighboring halogen atoms forming an octahedral [MX6]4− unit. The 1-T crystal phase is also found in NbS2 and TiSe2, in contrast to the H phase in MoS2 and WSe2.48 To assess the possibility of T–H phase transition, we computed the energy difference between these phases (E = EH − ET) for each monolayer (Fig. 2). We find that all relative energies are positive, indicating that 1-T is a ground-state structure. The energy associated with the T–H transition is considerable: several tenths of an eV per MX2 formula unit. The computed absolute values are comparable to those in dichalcogenides, such as MoS2, WSe2 and VS2.48,49 The smallest H–T energy difference is found in Fe dihalides and the largest in V and Ni dihalides.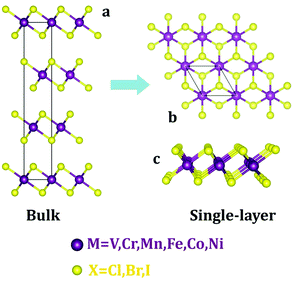 | ||
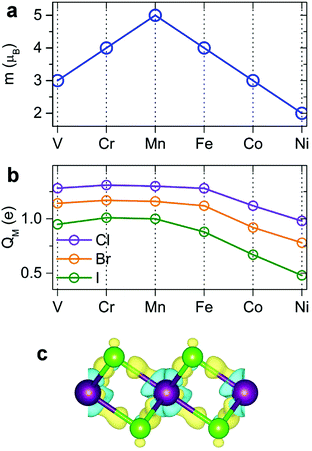
| Fig. 1 Crystal structures of metal dihalides (MX2) in the 1-T phase: (a) bulk and (b and c) single-layer. Top (b) and side (c) views are shown. | ||
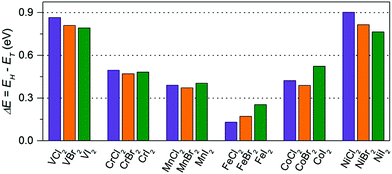 | ||
| Fig. 2 The energy difference (per MX2 formula unit) between H and T phases for all studied monolayers. The energies are computed at the equilibrium lattice parameters for each phase. | ||
The calculated structural parameters of MX2 are summarized in Table 1. The obtained lattice constants are in good agreement with experimental data on bulk structures.50,51 The M–X bond lengths increase as M changes from V to Mn and then decrease to Ni. Both lattice parameters and M–X bond lengths increase with the element number of X (Cl → Br → I). These trends are consistent with the variations of the radii of the TM atoms in their +2 valence states, as well as increasing the atomic radius of halogen. All M–X–M bond angles are ∼90°. The stability of single-layer dihalides can be evaluated from their formation energy as Eform = E(MX2) − μM − 2μX. Here, μM and μX correspond to the energy per atom of the stable bulk (bcc-V, bcc-Cr, bcc-Mn, bcc-Fe, hcp-Co, fcc-Ni) and gas (Cl2, Br2, I2) phases, respectively. We found that all calculated formation energies are negative in the range from −0.83 to −4.66 eV per M atom. These values are very close to the calculated formation energies of MoS2, VS2 and WSe2 (−2.49, −2.79 and 1.86 eV per M atom, respectively).48 Therefore, metal halide monolayers are energetically stable and could be potentially obtained by exfoliation.
| E form | a (DFT) | a (Exp.) | d M–X | C | |
|---|---|---|---|---|---|
| VCl2 | −3.46 | 3.58 | 3.60 | 2.45 | 25.63 |
| VBr2 | −2.77 | 3.76 | 3.77 | 2.60 | 26.32 |
| VI2 | −1.93 | 4.04 | 4.06 | 2.80 | 30.86 |
| CrCl2 | −2.57 | 3.55 | 3.59 | 2.49 | 26.15 |
| CrBr2 | −2.00 | 3.74 | 3.81 | 2.61 | 24.95 |
| CrI2 | −1.28 | 3.99 | 4.08 | 2.81 | 22.01 |
| MnCl2 | −3.23 | 3.64 | 3.68 | 2.51 | 33.08 |
| MnBr2 | −2.65 | 3.80 | 3.82 | 2.66 | 29.77 |
| MnI2 | −1.83 | 4.06 | 4.16 | 2.86 | 28.73 |
| FeCl2 | −2.22 | 3.43 | 3.57 | 2.42 | 41.49 |
| FeBr2 | −1.61 | 3.63 | 3.74 | 2.57 | 39.41 |
| FeI2 | −0.83 | 3.91 | 4.04 | 2.77 | 37.92 |
| CoCl2 | −1.71 | 3.42 | 3.54 | 2.38 | 20.19 |
| CoBr2 | −1.15 | 3.62 | 3.68 | 2.53 | 21.74 |
| CoI2 | −0.67 | 3.80 | 3.96 | 2.62 | 27.14 |
| NiCl2 | −1.98 | 3.42 | 3.48 | 2.36 | 53.30 |
| NiBr2 | −1.50 | 3.61 | 3.70 | 2.50 | 49.42 |
| NiI2 | −0.96 | 3.88 | 3.89 | 2.69 | 46.64 |
To access the dynamical stability of single-layer dihalides, we calculated their phonon band structure using density functional perturbation theory (DFPT). The force constants were calculated for a 4 × 4 × 1 supercell by using Phonopy package.52 Fig. S1 in the ESI† shows the phonon dispersions of all monolayers. We observe no imaginary (negative) frequencies, confirming the dynamical stability of single-layer dihalides.
We then determine the mechanical properties of halide monolayers by calculating their in-plane stiffness – the analogue of Young's modulus for 2D materials. This can be done by applying a series of small deformations on the material and monitoring its mechanical response. Starting with the fully relaxed structure of MX2, its lattice constants are imposed to small strains εx and εy within the harmonic range of ±0.02. For each (εx, εy) pair, we fully optimize the structure and calculate the strain energy Es. In the harmonic regime, the strain energy can be fitted to a two-dimensional quadratic polynomial expressed by
| Es(εx, εy) = a1εx2 + a2εy2 + a3εxεy | (1) |
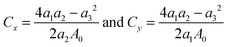 | (2) |
3.2. Electronic properties
Our spin-polarized calculations demonstrate that most transition-metal (TM) dihalides possess a large magnetic moment. The total magnetic moment forms a “volcano” curve (Fig. 3a) starting with V-halides (3 μB per TM atom), increasing to Mn-halides (5 μB), and then gradually decreasing to 2 μB for Ni-halides, in good agreement with the magnetic moments of free metal atoms, described by Hund's rules. The calculated magnetic moments in 2D dihalides are higher than those in magnetic 2D dichalcogenides (e.g. VS2, NbS2).5,15,57 The majority of the total magnetic moment comes from the TM atoms, while the halogens have a small magnetic moment of only 0.16–0.40 μB. The detailed analysis indicates that the local magnetic moment on TM atoms increases with the atomic number of the X atom (Cl → Br → I). This trend is opposite to the amount of electron transfer between TM and X atoms. The Cl atom has the largest electronegativity and withdraws the most valence electron charge from TM atoms, decreasing their magnetization.The bonding mechanism is examined by plotting the electron density distribution. The distinctive feature of 2D metal halides is a significant charge transfer. The bonding has a profound ionic character. Halogen atoms have strong affinity for acquiring an extra electron to fill its outer shell, and the Bader charge analysis shows that 0.48–0.65 e is transferred from M to each Cl, 0.39–0.58 e from M to each Br, and 0.24–0.50 e from M to each I atom (Fig. 3b). The direction of charge transfer can be rationalized by much larger electronegativity of Cl, Br and I atoms versus metal atoms. The amount of charge transfer decreases going as Cl → Br → I. The charge distribution in dihalides was visualized by calculating the charge density difference (Δρ) plots as shown in Fig. 3c. Here, Δρ is obtained as the difference between the charge density of the MX2 monolayer and the superposition of the charge densities of the constituent atoms. The blue and yellow isosurfaces represent charge depletion and accumulation regions, respectively. There is noticeable electron depletion in the region of M atoms, consistent with electron affinities and Bader analysis.
We compare the densities of states (DOSs) calculated using GGA, GGA+U and HSE methods on the example of NiCl2. The GGA spin-polarized DOS of monolayer NiCl2 is shown in Fig. 4a. The electronic structures of different dihalides share several common features. The valence band is formed by halogen p bands, while the bottom of the conduction band mainly originates from metal s states. The TM atoms transfer their 4s electrons to halogens and have a +2 oxidation state; therefore, TM 4s states are completely unoccupied. The spin-polarized 3d states of TM atoms are located within the band gap. We can observe significant hybridization between TM 3d and halogen p orbitals. Each TM atom is surrounded by six halogen neighbors (“ligands”) which form a nearly spherical octahedral coordination. The octahedral crystal field splits the 3d orbitals of TM atoms into upper eg (dx2−y2, dz2) and lower t2g (dxy, dxz, dyz) states. The eg orbitals point directly at the six negatively charged halogens, which increases their energy due to the electrostatic repulsion with halogens. In contrast, t2g orbitals lie between the halogens, making them relatively more stable and lowering their energy. Halogens are weak ligands from the spectroscopic series; therefore, 3d TM atoms in the octahedral field are expected to prefer the high spin state. This is consistent with the large exchange splitting of the TM 3d states, as observed in Fig. 4.
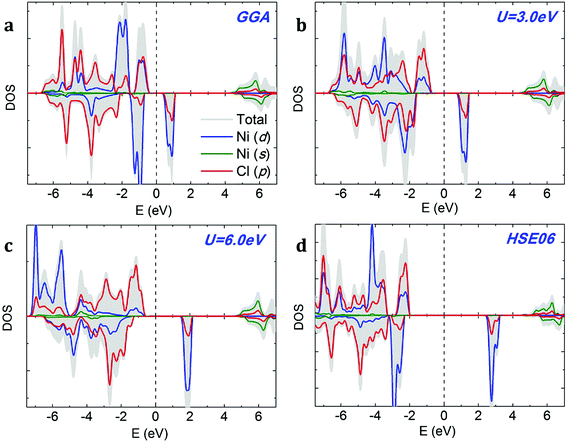 | ||
| Fig. 4 Density of states (DOS) of monolayer NiCl2 calculated using (a) GGA, (b and c) GGA+U, and (d) HSE06 methods. The Fermi level is indicated by a dashed vertical line. | ||
The addition of on-site Coulomb repulsion (GGA+U, Fig. 4b and c) increases the exchange splitting between filled and empty orbitals in the TM 3d manifold. Consequently, the occupied spin-up TM 3d states now move towards the valence band and hybridize more strongly with the halogen p states. The unoccupied spin-down TM 3d states shift towards the CBM. GGA+U reduces the width of the TM 3d peak inside the band gap, suggesting stronger localization. As shown in Fig. 4c, the above-mentioned effects become even more pronounced as the on-site Coulomb repulsion (Ueff) increases from 3.0 to 6.0 eV. The DOS calculated using the high-accuracy HSE06 functional (Fig. 4d) confirms that NiCl2 is a semiconductor. In agreement with GGA/GGA+U calculations, the VBM is formed by halogen p bands and the CBM originates from metal s states. There is a single spin-polarized peak in the middle of the band gap, formed by metal 3d states.
3.3. Magnetic ordering
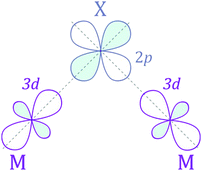
The next step is to identify the preferable magnetic ordering in 2D dihalides. We have constructed a larger (2 × 2) supercell, and set the spin ordering to either ferromagnetic (FM) or antiferromagnetic (AFM), as shown in Fig. 5a. The exchange energy (Eex) is calculated as Eex = EAFM − EFM. Positive exchange energy indicates that the ground state of the system is ferromagnetic. From our calculations, we have found that FeX2, CoX2 and NiX2 prefer the FM ground state, while VX2, CrX2 and MnX2 are AFM. The observed preference for either FM or AFM ordering can be rationalized using the Goodenough–Kanamori–Anderson (GKA) formalism.58–60 The magnetic properties of single-layer dihalides are governed by the competition between two distinct mechanisms (Fig. 5b): (i) the direct exchange between two TM atoms, and (ii) the halogen-mediated M–X–M superexchange interaction. In Mn dihalides, the direct exchange is robustly AFM as the Mn ions are in the half-filled high-spin d5 state. In contrast, for the Fe, Co and Ni dihalides, the AFM direct exchange is weakened by a FM component as these ions have a nearly filled d-shell.61 The sign of M–X–M superexchange can be predicted from the local crystal symmetry (M–X–M bond angles) and d electron configurations of TM atoms. In 2D dihalides, all calculated metal-halogen-metal (M–X–M) bond angles are ∼90°. In such a case, the d-orbitals on neighboring TM atoms overlap different halogen-p orbitals (Fig. 6) and are, therefore, orthogonal to one another. According to the GKA rules, in systems with 90° bond angles the superexchange interaction between TM atoms is deduced only from a potential exchange which is always FM. The competition between FM and AFM components may lead to different magnetic states, depending on the TM atoms involved. For instance, Mn dihalides exhibit AFM properties because of the relatively large AFM direct exchange. However, in Fe, Co and Ni dihalides, the FM superexchange is dominating leading to the FM ground state. Overall, the 1-T crystal structure of Fe, Co and Ni dihalides containing 90° M–X–M bond angles represents a promising platform for stable and robust ferromagnetism.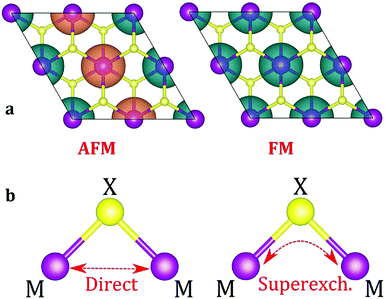 | ||
| Fig. 5 (a) Spin density isosurface plots for AFM and FM spin arrangements. (b) Schematic mechanism of direct (M–M) and superexchange (M–X–M) interactions. | ||
3.4. Curie temperature
One of the critical properties of ferromagnetic materials is the Curie temperature (TC) of a FM–AFM transition. It is possible to estimate TC from the mean-field theory (MFT); however, such a value is often overestimated.62 The more accurate prediction can be made using statistical Monte Carlo (MC) simulations based on the Ising model. This method has been successfully used to predict the TC in other 2D materials producing values close to the experimental data.6 Consider a set of magnetic spins located at the sites on a regular lattice of 2D halides. Neighboring spins interact though an exchange constant J. The system is described by the classical Heisenberg Hamiltonian: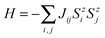 | (3) |
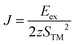 | (4) |
| E ex | J | T MCC | MS | m | |
|---|---|---|---|---|---|
| VCl2 | −81.80 | −3.03 | — | AFM | 3.0 |
| VBr2 | −41.25 | −1.53 | — | AFM | 3.0 |
| VI2 | −14.85 | −0.55 | — | AFM | 3.0 |
| CrCl2 | −63.30 | −1.32 | — | AFM | 4.0 |
| CrBr2 | −32.09 | −0.67 | — | AFM | 4.0 |
| CrI2 | — | AFM | 4.0 | ||
| MnCl2 | −18.63 | −0.25 | — | AFM | 5.0 |
| MnBr2 | −15.65 | −0.21 | — | AFM | 5.0 |
| MnI2 | −15.43 | −0.21 | — | AFM | 5.0 |
| FeCl2 | 122.58 | 2.55 | 109 | FM | 4.0 |
| FeBr2 | 90.05 | 1.88 | 81 | FM | 4.0 |
| FeI2 | 47.48 | 0.99 | 42 | FM | 4.0 |
| CoCl2 | 53.05 | 1.96 | 85 | FM | 3.0 |
| CoBr2 | 14.35 | 0.53 | 23 | FM | 3.0 |
| CoI2 | −12.83 | −0.48 | — | AFM | 3.0 |
| NiCl2 | 38.55 | 3.21 | 138 | FM | 2.0 |
| NiBr2 | 37.33 | 3.11 | 132 | FM | 2.0 |
| NiI2 | 36.28 | 3.02 | 129 | FM | 2.0 |
Within the MC scheme, the magnetic system goes through a number of spin configurations with a probability of “spin flip” that depends exponentially on the change in energy as a result of the flip. We use a Metropolis algorithm and a 100 × 100 two-dimensional supercell with periodic boundary conditions. The MC simulation is run for 106 steps. Fig. 7a shows the calculated magnetization per TM atom as a function of temperature. At low temperatures, all spins are aligned parallel, producing a large net magnetic moment (FM state). At high temperatures, the spins are aligned randomly resulting in zero net magnetization (AFM state). The calculated Curie temperatures of FM/AFM phase transitions are summarized in Table 2. The calculated TC values are comparable with those in the state-of-the-art 2D magnetic materials, such as CrSiTe3 (36–90 K), CrGeTe3 (57–130 K) and CrSnTe3 (170 K).6,63 The TC values for all dihalides are decreasing from Cl to Br to I, consistent with the trends in exchange energies. Remarkably, single-layer dihalides exhibit comparable or even slightly higher Curie temperatures than single-layer dichalcogenides (for example, 90 K in VS2).57 This can be attributed to the profound ionic bonding in halides, which enhances the superexchange coupling between the magnetic metal ions via halogen p states, consistent with the GKA rules.6
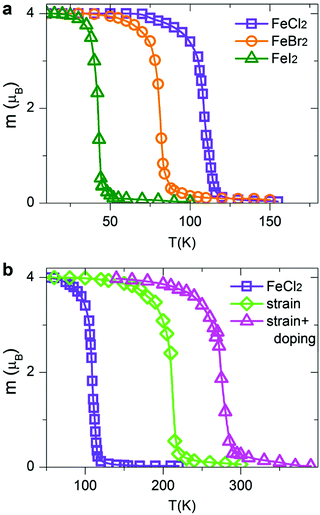 | ||
| Fig. 7 Variation of the calculated magnetization per TM atom versus temperature for (a) pristine FeCl2, FeBr2 and FeI2, and (b) strained and hole-doped FeCl2 monolayers. | ||
The Curie temperature can be further increased by applying strain and/or carrier doping.7,15,64–70 The outstanding elastic behaviour and stretchability of 2D crystals can potentially lead to novel tunability levels which are not accessible in conventional bulk semiconductors. For example, MoS2 can sustain in-plane strain levels as large as 11% and has a high Young's modulus of ∼270 GPa.71 In contrast, bulk silicon can be strained to only ∼1.5% before breaking.72 On the other hand, hole doping has been shown to promote ferromagnetism and half-metallicity in single-layer materials, such as GaSe, CrI3 and phosphorene.27,40,73,74 Taking FeCl2 as a prototype, we first apply biaxial in-plane strain ranging from −10% to +10%. To simulate the effect of carrier doping, we add/remove electrons from FeCl2 and use a compensating jellium background to maintain charge neutrality. Note that high doping carrier densities of up to 1014 cm−2 have been achieved by electrostatic gating in graphene and MoS2.75,76 We therefore expect that hole doping levels, described in this work, are experimentally feasible. Remarkably, we find that both biaxial strain and carrier doping can enhance the magnetic properties of FeCl2. At a strain level of 10%, the calculated exchange energy increases from 122.57 meV per unit cell in pristine FeCl2 to 234.52 meV in the strained one. It is possible to further increase the exchange energy to 307.85 meV using a combination of strain and carrier doping. Fig. 7b shows the magnetization versus temperature for pristine, stained and hole-doped FeCl2. The corresponding Curie temperatures are found to be 109, 212 and 273 K, respectively, suggesting a high degree of tunability and promising potential of single-layer dihalides for room-temperature spintronic devices.
4. Conclusions
In summary, we have investigated the structural, electronic and magnetic properties of single-layer metal dihalides using first-principles calculations with the GGA, GGA+U and hybrid HSE06 functionals. We found that single-layer dihalides prefer the 1-T crystal phase and are energetically stable. The magnetic properties of 2D dihalides are governed by the competition between AFM direct nearest-neighbor d–d exchange and FM superexchange via halogen p states, which leads to different magnetic states. Thus we found that 2D FeX2, NiX2, CoCl2 and CoBr2 monolayers are ferromagnetic (FM), while VX2, CrX2 and MnX2 are antiferromagnetic (AFM). Using the DFT derived spin exchange parameters, we estimated the Curie temperature of magnetic transition from the Monte Carlo simulations based on the Ising model and Heisenberg Hamiltonian. We find that single-layer dihalides exhibit comparable or even slightly higher Curie temperatures than single-layer dichalcogenides. This can be attributed to the profound ionic bonding in halides, which enhances the superexchange coupling between the magnetic metal ions via the halogen atoms. Overall, single-layer dihalides represent a new addition to the family of 2D materials with promising applications in nanoscale devices. We expect that our theoretical results will inspire further experimental studies.Acknowledgements
We appreciate the computational support received from the Institute of Systems Science (NUS) and Institute of High Performance Computing (A*STAR) of Singapore.References
- K. F. Mak and J. Shan, Nat. Photonics, 2016, 10, 216–226 CrossRef CAS.
- L. Shi and T. S. Zhao, J. Mater. Chem. A, 2017, 5, 3735–3758 CAS.
- B. Luo, G. Liu and L. Wang, Nanoscale, 2016, 8, 6904–6920 RSC.
- W. Han, R. K. Kawakami, M. Gmitra and J. Fabian, Nat. Nanotechnol., 2014, 9, 794–807 CrossRef CAS PubMed.
- Y. Ma, Y. Dai and M. Guo, et al. , ACS Nano, 2012, 6, 1695–1701 CrossRef CAS PubMed.
- H. L. Zhuang, Y. Xie, P. R. C. Kent and P. Ganesh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035407 CrossRef.
- Y. Wang, S.-S. Wang, Y. Lu, J. Jiang and S. A. Yang, Nano Lett., 2016, 16, 4576–4582 CrossRef CAS PubMed.
- L. Hu, X. Wu and J. Yang, Nanoscale, 2016, 8, 12939–12945 RSC.
- H. L. Zhuang, P. R. C. Kent and R. G. Hennig, Phys. Rev. B, 2016, 93, 134407 CrossRef.
- H. Y. Lv, W. J. Lu, D. F. Shao, Y. Liu and Y. P. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214419 CrossRef.
- J. Liu, Z. Liu, T. Song and X. Cui, J. Mater. Chem. C, 2017, 5, 727–732 RSC.
- Y. Sun, Z. Zhuo, X. Wu and J. Yang, Nano Lett., 2017, 17, 2771–2777 CrossRef CAS PubMed.
- E. Kan, W. Hu and C. Xiao, et al. , J. Am. Chem. Soc., 2012, 134, 5718–5721 CrossRef CAS PubMed.
- H. Wang, J. Zhang and X. Hang, et al. , Angew. Chem., Int. Ed., 2015, 54, 1195–1199 CrossRef CAS PubMed.
- Y. Zhou, Z. Wang and P. Yang, et al. , ACS Nano, 2012, 6, 9727–9736 CrossRef CAS PubMed.
- E. J. Duplock, M. Scheffler and P. J. D. Lindan, Phys. Rev. Lett., 2004, 92, 225502 CrossRef PubMed.
- O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408 CrossRef.
- V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 992–1000 RSC.
- V. V. Kulish, Phys. Chem. Chem. Phys., 2017, 19, 11273–11281 RSC.
- H. Sevincli, M. Topsakal, E. Durgun and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195434 CrossRef.
- Z. Li, W. Xu and Y. Yu, et al. , J. Mater. Chem. C, 2016, 4, 362–370 RSC.
- B. Onat, L. Hallioglu, S. pek and E. Durgun, J. Phys. Chem. C, 2017, 121, 4583–4592 CAS.
- M. Sun, Q. Ren and Y. Zhao, et al. , Carbon, 2017, 120, 265–273 CrossRef CAS.
- M. Sun, Q. Ren and Y. Zhao, et al. , J. Appl. Phys., 2016, 119, 143904 CrossRef.
- W.-B. Zhang, Q. Qu, P. Zhu and C.-H. Lam, J. Mater. Chem. C, 2015, 3, 12457–12468 RSC.
- Y. Zhou, H. Lu, X. Zu and F. Gao, Sci. Rep., 2016, 6, 19407 CrossRef CAS PubMed.
- J. Liu, Q. Sun, Y. Kawazoe and P. Jena, Phys. Chem. Chem. Phys., 2016, 18, 8777–8784 RSC.
- J. He, S. Ma, P. Lyu and P. Nachtigall, J. Mater. Chem. C, 2016, 4, 2518–2526 RSC.
- R. E. Brandt, R. C. Kurchin and R. L. Z. Hoye, et al. , J. Phys. Chem. Lett., 2015, 6, 4297–4302 CrossRef CAS PubMed.
- A. J. Lehner, H. Wang and D. H. Fabini, et al. , Appl. Phys. Lett., 2015, 107, 131109 CrossRef.
- F. Ma, M. Zhou and Y. Jiao, et al. , Sci. Rep., 2015, 5, 17558 CrossRef CAS PubMed.
- A. J. Lehner, D. H. Fabini and H. A. Evans, et al. , Chem. Mater., 2015, 27, 7137–7148 CrossRef CAS.
- M. Zhou, W. Duan, Y. Chen and A. Du, Nanoscale, 2015, 7, 15168–15174 RSC.
- A. S. Toulouse, B. P. Isaacoff and G. Shi, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 165308 CrossRef.
- L. Li, O. Leenaerts and X. Kong, et al. , Nano Res., 2017, 10, 2168–2180 CrossRef CAS.
- L. Zhou, L. Kou and Y. Sun, et al. , Nano Lett., 2015, 15, 7867–7872 CrossRef CAS PubMed.
- E. Torun, H. Sahin, S. K. Singh and F. M. Peeters, Appl. Phys. Lett., 2015, 106, 192404 CrossRef.
- E. Torun, H. Sahin, C. Bacaksiz, R. T. Senger and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 104407 CrossRef.
- M. A. McGuire, H. Dixit, V. R. Cooper and B. C. Sales, Chem. Mater., 2015, 27, 612–620 CrossRef CAS.
- W. Hongbo, F. Fengren, Z. Shasha and W. Hua, EPL, 2016, 114, 47001 CrossRef.
- B. Huang, G. Clark and E. Navarro-Moratalla, et al. , Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni and N. Bonini, et al. , J. Phys.: Condens. Matter, 2009, 21, 19 CrossRef PubMed.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, A. Ruzsinszky and G. I. Csonka, et al. , Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef CAS.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- C. Ataca, H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 8983–8999 CAS.
- K.-A. N. Duerloo, Y. Li and E. J. Reed, Nat. Commun., 2014, 5, 4214 CAS.
- R. W. G. Wyckoff, Crystal structures, Interscience Publishers, New York, 1963 Search PubMed.
- S. R. Kuindersma, C. Haas, J. P. Sanchez and R. Al, Solid State Commun., 1979, 30, 403–408 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- H. Sahin, S. Cahangirov and M. Topsakal, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- V. V. Kulish, O. I. Malyi, C. Persson and P. Wu, Phys. Chem. Chem. Phys., 2015, 17, 13921–13928 RSC.
- X. Li, X. Wu and J. Yang, J. Am. Chem. Soc., 2014, 136, 11065–11069 CrossRef CAS PubMed.
- D. Kecik, E. Durgun and S. Ciraci, Phys. Rev. B, 2016, 94, 205409 CrossRef.
- H. L. Zhuang and R. G. Hennig, Phys. Rev. B, 2016, 93, 054429 CrossRef.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23 CrossRef.
- P. W. Anderson, Phys. Rev., 1959, 115, 2–13 CrossRef CAS.
- N. Sivadas, M. W. Daniels, R. H. Swendsen, S. Okamoto and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 235425 CrossRef.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston, 1976 Search PubMed.
- X. Li and J. Yang, J. Mater. Chem. C, 2014, 2, 7071–7076 RSC.
- R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, J. Phys.: Condens. Matter, 2015, 27, 313201 CrossRef PubMed.
- S. Manzeli, A. Allain, A. Ghadimi and A. Kis, Nano Lett., 2015, 15, 5330–5335 CrossRef CAS PubMed.
- A. S. Rodin, A. Carvalho and A. H. Castro Neto, Phys. Rev. Lett., 2014, 112, 176801 CrossRef CAS PubMed.
- A. Castellanos-Gomez, R. Roldán and E. Cappelluti, et al. , Nano Lett., 2013, 13, 5361–5366 CrossRef CAS PubMed.
- L. C. Gomes, A. Carvalho and A. C. Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 214103 CrossRef.
- S. Guan, Y. Cheng and C. Liu, et al. , Appl. Phys. Lett., 2015, 107, 231904 CrossRef.
- L. Zhu, S.-S. Wang and S. Guan, et al. , Nano Lett., 2016, 16, 6548–6554 CrossRef CAS PubMed.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS PubMed.
- J. Munguia, G. Bremond, J. M. Bluet, J. M. Hartmann and M. Mermoux, Appl. Phys. Lett., 2008, 93, 102101 CrossRef.
- T. Cao, Z. Li and S. G. Louie, Phys. Rev. Lett., 2015, 114, 236602 CrossRef PubMed.
- B. Fu, W. Feng, X. Zhou and Y. Yao, 2D Mater., 2017, 4, 025107 CrossRef.
- J. Ye, M. F. Craciun and M. Koshino, et al. , Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13002–13006 CrossRef CAS PubMed.
- K. F. Mak, K. He and C. Lee, et al. , Nat. Mater., 2013, 12, 207–211 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Phonon dispersions, stability and density of states for all dihalides. See DOI: 10.1039/c7tc02664a |
| This journal is © The Royal Society of Chemistry 2017 |