A DFT investigation of photocatalytic water splitting properties of the InS/GaTe heterostructure: direct Z-scheme vs. traditional type-II
Redi Kristian
Pingak
 *ab,
Oliver J.
Conquest
*ab,
Oliver J.
Conquest
 a and
Catherine
Stampfl
a and
Catherine
Stampfl
 *a
*a
aThe School of Physics, The University of Sydney, 2006, NSW, Australia. E-mail: catherine.stampfl@sydney.edu.au; rpin0929@uni.sydney.edu.au
bDepartment of Physics, Faculty of Science and Engineering, University of Nusa Cendana, 85001, Kupang, Indonesia
First published on 2nd October 2025
Abstract
Density Functional Theory is used to predict the structural, electronic, and optical properties, as well as the reaction energetics, of the InS/GaTe heterostructure. The system is stable and found to have an ideal band gap of 1.34 eV, significantly lower than its monolayer counterparts. This makes it more effective in absorbing light in the visible region, as confirmed by our analysis of its optical properties. The oxygen evolution reaction (OER) was investigated for both the direct Z-scheme and the type-II mechanisms. The photogenerated hole potential for the Z-scheme ranges from 2.37 eV for pH = 0 to 4.02 eV for pH = 14, while that for the type-II mechanism is from 1.44 eV (pH = 0) to 3.09 eV (pH = 14). Based on the analysis of the electronic properties of the InS/GaTe heterostructure, and its Gibbs free energy reaction pathway for OER when the light is turned on, the transfer mechanism of the photogenerated electrons and holes in InS/GaTe is predicted to follow the direct Z-scheme mechanism. Notably, the OER reaction is predicted to be spontaneous for a wide pH range: 2 ≤ pH ≤ 14 (Z-scheme) and 3 ≤ pH ≤ 14 (type-II). This makes the InS/GaTe heterostructure more promising for OER compared to many other catalysts. While the type-II mechanism cannot facilitate HER, the Z-scheme mode of InS/GaTe is predicted to have good performance for HER, with an ideal Gibbs free energy of −0.02 eV at pH = 7. The solar-to-hydrogen efficiency is predicted to be 44.8%, which is higher than that of many other photocatalysts, and is far higher than the 10% threshold for commercial applications. These results strongly indicate that the InS/GaTe heterostructure, in its Z-scheme mode, holds high potential as a photocatalyst to facilitate both OER and HER for water splitting applications.
1 Introduction
Due to its environmentally friendly and renewable nature, solar energy along with other renewable technologies, is expected to replace fossil fuels in the future.1 Photocatalytic water splitting devices using semiconductors as photocatalysts have shown to be promising candidates to generate hydrogen, which is a green and renewable energy source.2 Currently, commercially available H2 is mostly derived from fossil fuels which also produce CO2 emissions.3 Therefore, use of clean and renewable solar energy to generate H2 through water splitting is a major research focus. Water-splitting devices include photovoltaic-powered electrolysis, photoelectrochemical (PEC) water splitting, and photocatalysis (PC). It is expected that PC is the least expensive method although the additional cost is anticipated from subsequent gas separation.4 Despite being intensively investigated, the low photocatalytic efficiency is still a major problem.5One of the major causes for the low photocatalytic efficiency is the rapid photogenerated electron–hole recombination in photocatalysts,6 which limits the efficiency of the energy conversion. We need to develop photocatalytic materials that can inhibit the electron–hole recombination while still being able to perform the photoreduction and oxidation reactions.7 Post-modification engineering can also be applied to increase the utilization of the photogenerated electrons and holes and inhibit the electron–hole recombination.8 As an example, Zhang et al.8 modified pristine cerium metal–organic frameworks (Ce-MOFs) by adopting the one-step partial oxidation strategy. The modification includes adjusting the valence states of metal nodes in a Ce-MOF, namely the [Ce(1,3,5-BTC) (H2O)6] (1,3,5-BTC = 1,3,5-benzene-tricarboxylate) MOF. The authors showed that after mild oxidation, hetero-valence metals nodes with abundant Ce3+/Ce4+ redox couple are formed. This inhibits the electron–hole recombination and extends the optical harvesting to the visible region, which leads to a higher photocatalytic activity. Two-dimensional (2D) materials have also emerged as promising photocatalysts as they are more effective in inhibiting such a recombination by promoting the separation of electrons and holes.9 The significant difference between the magnitude of the mobility of the electrons and holes in these materials was shown as an important factor.10–12 However, an ideal photocatalyst should also exhibit a wide absorption range and strong redox ability. This cannot be achieved simultaneously by a single photocatalyst because to have a broad absorption range means that the photocatalyst should have a narrow band gap, while to have an excellent redox ability, it should possess a high conduction band minimum (CBM) and a shallow valence band maximum (VBM), meaning that it should have a larger band gap. To address these limitations, heterostructures consisting of two or more photocatalysts have emerged.13 Among different types of heterostructures, the direct Z-scheme heterostructures have great potential as they not only improve the separation efficiency but also retain strong redox ability of the catalyst.13,14 The charge transfer mechanism in Z-scheme heterostructures is more suitable for water splitting compared to the conventional type-II heterostructures although they possess a similar staggered band structure.15 Although type-II heterostructures can inhibit the electron–hole recombination to some extent, their reduction and oxidation ability is weakened by their charge transfer mode. By contrast, Z-scheme heterostructures not only effectively enhance the separation of photogenerated electron–holes but also retain their reduction and oxidation ability, improving their photocatalytic performance.15,16 Hence, it is crucial to determine the type of charge transfer in a staggered band heterostructure before investigating their photocatalytic performance.
Among 2D materials, group III monochalcogenide based monolayers MX (M = Ga and In, X = S, Se, and Te) were predicted to be suitable for photocatalytic water splitting.17 As a result, a number of heterostructures are formed from these monolayers to achieve better performance in various applications including in the water splitting mechanism.18–28 For instance, GaTe-based heterostructures such as GaTe/AsP29 and GaTe/ZnI2 (ref. 30) have recently been reported to have outstanding optical absorption and photocatalytic activity for water splitting, based on DFT calculations. This is due to their narrow band gap, suitable band edge position for redox reactions, and staggered band nature. However, the solar to hydrogen efficiency of GaTe/AsP is still relatively low (14.10%),29 even though it is predicted to be a direct Z-scheme heterostructure. Despite having a staggered band structure, GaTe/ZnI2 follows the traditional type-II charge transfer mechanism and has an indirect band gap,30 which might limit its efficiency as a photocatalyst. Similarly, recent theoretical studies suggest that heterostructures based on InS monolayers are promising as catalysts for water splitting. The systems include Al2SeTe/InS31 and GeC/InS.32 In those studies,29–32 GaTe and InS were reported to possess good reduction and oxidation ability. Therefore, it is expected that the GaTe/InS heterostructure would be a highly promising photocatalyst for water splitting applications. In fact, the InS/GaTe heterostructure has been studied before,18,19,22 but interestingly, the studies reported different finding to each other related to the type of the charge transfer mechanism at its interface. It was assumed that the H2 and O2 evolution occurs at the surface of InS and GaTe, respectively,18,19 implying the traditional type-II transfer mechanism. As a result, Rawat and co-workers18 reported that InS/GaTe could be promising for water splitting but only for a very limited pH range while Chen et al.19 claimed that it is not suitable for water splitting applications. By contrast, a recent study22 claimed that InS/GaTe exhibits a direct Z-scheme charge transfer mode and is therefore a promising photocatalyst for overall water splitting. The contradiction in the studies18,19,22 is believed to arise because the authors only analyze the charge density at the heterojunction to determine the type of the charge transfer in InS/GaTe. The analysis of the charge density difference alone is insufficient to accurately draw a conclusion regarding the type of charge transfer.33 This was demonstrated in the case of the staggered band phosphorus/BiVO4 heterostructure, in which charge transfer was experimentally found to follow the Z-scheme mode but theoretically predicted to possess the type-II mode.33–35
A more in-depth analysis is required to accurately predict the type of charge transfer within band staggered heterostructures from the computational perspective. Currently, the theoretical and computational methods used are not well-established, meaning that new approaches should be developed.36,37 The nonadiabatic molecular dynamics (NAMD) approach,38–41 which investigates the dynamics of the photogenerated electrons and holes, is an example. If the transport of photogenerated electrons and holes is much slower than electron–hole recombination in a staggered band heterostructure, the heterostructure follows the Z-scheme while the reverse corresponds to the type-II mechanism.42 In the Z-scheme mechanism, the recombination of the photogenerated electrons at the CBM of the oxidizing catalyst and the photogenerated holes at the VBM of the reducing catalyst occurs much faster than the rate of transfer of the photogenerated electrons (holes) from the CBM (VBM) of the oxidizing (reducing) catalysts to the CBM (VBM) of the reducing (oxidizing) catalysts. As a result, the electrons (holes) remain at the CBM (VBM) of the catalysts with the strongest reduction (oxidation) ability. The reverse is true for the type-II charge transfer mechanism. The NAMD technique is, however, computationally expensive especially for large systems.43,44 Furthermore, it also has some shortcomings such as the lack of spin–orbit coupling and highly accurate exciton wave functions to describe the exciton dynamics, which might lead to inaccurate dynamic calculations.37 Alternatively, a new strategy based on the principle of minimum energy barrier was recently implemented by Liu and co-workers45 to determine the charge transfer mechanisms in staggered band heterostructures. However, the new proposed method45 is only based on the free energy diagram of the OER and HER when the light is off. As the charge transfer mechanism describes the movement of photogenerated electrons and holes, it would be more appropriate if the analysis of the charge transfer mode is performed when the light is on.
Environmental conditions also play an important role in the HER and OER mechanisms in photocatalytic water splitting.46,47 In principle, the water splitting reactions can be performed in acidic and alkaline media. While many computational investigations were carried out to study the performance of monolayers and heterostructures for water oxidation in acidic media, very few studies investigated the water oxidation in alkaline media.47 Interestingly, most experimental studies on photocatalytic water splitting are performed in alkaline media.47 Hence, it is of great importance to investigate the photocatalytic water splitting mechanisms not only in the acidic media but also in the alkaline media.
The present study utilizes density functional theory (DFT) calculations to comprehensively investigate the photocatalytic water splitting mechanism of the InS/GaTe heterostructure in acidic and alkaline media. To determine the most favorable charge transfer mechanism in InS/GaTe, we propose a new alternative approach by examining the Gibbs free energy differences of the OER between the two schemes when the light is on. Unlike the most commonly used approach of using the charge density difference and the built-in electric field, the proposed approach in this study performs the adsorption of intermediates on different surfaces of the catalysts under illumination, for both possible charge transfer mechanisms. The OER will be performed at the surface of the oxidation (reduction) catalyst for Z-scheme (type-II). By evaluating their Gibbs free energy difference under light illumination, the most favorable charge transfer mechanism can be predicted. As adsorption of intermediates is dependent on the surface, this is expected to give more reliable results compared to depending just on the built-in electric field and charge density. In addition, this approach is also expected to be less expensive than NAMD since it does not require molecular dynamics simulation. The results indicate that the Z-scheme consistently exhibits the lowest Gibbs free energy for all the OER intermediates and for the whole pH range (0 ≤ pH ≤ 14). It can therefore be inferred that the Z-scheme transfer mode is more favorable for the InS/GaTe heterostructure, which is also consistent with the built-in electric field. Equally important, the Z-scheme of InS/GaTe is also predicted to facilitate HER while the type-II does not. The proposed method can be used to predict the charge transfer mechanism in other staggered band heterostructures.
2 Computational methods
In this study, we perform Density Functional Theory (DFT) calculations as implemented in Quantum Espresso (QE)48 to investigate the InS/GaTe heterostructure. The projector augmented wave (PAW) pseudopotential49 was used in the structure optimization and the calculation of the electronic properties. The Optimized Norm-Conserving Vanderbilt Pseudopotential (ONCVPSP)50 was employed to calculate the optical properties of the heterostructure. This is because the PAW and ultrasoft pseudopotentials (USPP) are not supported by the epsilon.x program of the QE to calculate the optical properties of materials. The Generalized Gradient Approximation (GGA) of Perdew–Burke–Ernzerhof (PBE)51 was utilized to treat the exchange–correlation functional. The hybrid functional of Heyd–Scuseria–Ernzerhof (HSE06)52 was also implemented to obtain a more reliable electronic band structure of the studied material. The interpolation of the electronic band structure from the HSE06 functional was performed using the Wannier code.53 The DFT-D3 method of Grimme et al.54,55 was used to describe the long range vdW interactions for all calculations in this study. The ab initio molecular dynamics (AIMD) simulation was performed using the Vienna Ab initio Simulation Package (VASP)56–58 with the projector augmented-wave method.49 In addition, the effect of the spin–orbit coupling (SOC) on the properties of the material was also investigated.The GGA-PBE was used to optimize the structure of InS, GaTe, and InS/GaTe and to calculate their phonon dispersion. The electronic structure of InS and GaTe was first calculated using the PBE and PBE + SOC to investigate the effect of spin–orbit coupling on the electronic band structure of the monolayers. As the spin–orbit coupling was found to have a small effect on their band structure, further calculations on the band structure of InS, GaTe, and InS/GaTe were performed using the HSE06 functional without applying the SOC. All the other calculations, including the work functions, the charge carrier mobility, and the optical properties were performed using the HSE06.
A vacuum region of 20 Å was used in the perpendicular direction to the InS and GaTe monolayers to avoid interlayer interaction, while a larger vacuum region of 35 Å was employed for the calculation of the properties of the InS/GaTe heterostructure. The energy cut-off was set to be 60 Ry. The k-point mesh used for all systems in this study was 12 × 12 × 1. The results of the convergence test are shown in Fig. S1 and S2. The total energy convergence threshold was set to be 10−10 Ry.
3 Results and discussion
3.1 Structural properties
InS and GaTe monolayers possess the same structure as other group III monochalcogenides MX (M = Ga, In; X = S, Se, Te) with space group p![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2, illustrated in Fig. 1.17
m2, illustrated in Fig. 1.17
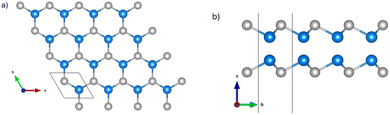 | ||
| Fig. 1 The top (a) and side (b) views of the atomic structure of InS and GaTe monolayers: blue balls represent Ga or In and grey ones are S or Te. The unit cell is indicated by the black lines. | ||
The InS and GaTe monolayers were optimized and their in-plane equilibrium lattice parameters are found to be 3.92 Å and 4.12 Å, respectively. These are in excellent agreement with previous findings of 3.94 Å (ref. 17) and 3.93 Å (ref. 22) for InS and of 4.14 Å (ref. 17) and 4.12 Å (ref. 22) for the GaTe monolayer. The thickness of InS was found to be 5.27 Å while that of GaTe is slightly smaller (4.95 Å).
The combined lattice parameter for the InS/GaTe heterostructure was initially taken as the average of the lattice parameters of InS and GaTe, namely 4.02 Å. To investigate the most favorable stacking type of the InS/GaTe heterostructure, four possible stacking positions are investigated as shown in Fig. 2. The first is the AA (top) stacking configuration, where InS was placed directly on top of GaTe (Fig. S3), i.e. In over Ga atoms and S over the Te atoms. Then, the AB (bridge) configuration was considered, which was obtained by placing In over the Ga–Te bridge site (Fig. S4). The last two stacking types are termed AC1 (Fig. S5) and AC2 (Fig. S6), obtained by placing GaTe over the hollow position of InS (AC1) and InS over the hollow position of GaTe (AC2).
The total energy as a function of the interlayer distance for the four stacking configurations is presented in Fig. 3. It can be seen that AC2 stacking possesses the lowest energy, meaning that it is the most favorable configuration. Therefore, all calculations of the properties of the InS/GaTe heterostructure in the present work are performed using this hollow type stacking structure AC2. In this configuration, the InS monolayer is placed over the hollow position of GaTe such that the S atoms fill the hollow sites of GaTe (as seen from top). Furthermore, the binding energy (Eb) of the four stacking configurations was calculated using eqn (1).
| Eb = EGaTe/InS − (EGaTe − EInS) | (1) |
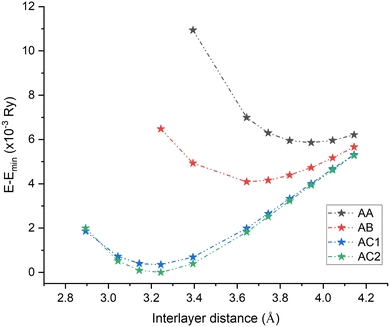 | ||
| Fig. 3 The energy difference versus interlayer distance of the four different stacking configurations of the InS/GaTe heterostructure. E is the total energy while Emin is the lowest energy. | ||
The obtained values of the AA, AB, AC1, and AC2 stacking geometries are: −0.07 eV, −0.12 eV, −0.21 eV, and −0.22 eV, respectively. Interestingly, the AA configuration, which was investigated in ref. 22, is the least favorable stacking configuration of InS/GaTe heterostructure. In their study, Li and co-workers22 investigated electronic and optical properties of the InS/GaTe heterostructure. However, as they used the PBE functional for most of their calculations, it is highly likely that the results they reported severely underestimate the band gap of the heterostructure. Moreover, the authors did not investigate the stability of different stacking configurations and just studied the top–top stacking configuration (AA). In the present study, we investigated the stability of different stacking configurations of InS/GaTe and found out that the hollow configuration (AC2) is the most stable configuration, much more stable than the AA configuration. In addition, we used the HSE06 functional to obtain more reliable electronic and optical properties of the InS/GaTe heterostructure.
The AC2 configuration was fully optimized and it was found that its equilibrium lattice parameter and interlayer distance are 4.02 Å and 3.38 Å, respectively. This interlayer distance is consistent with interlayer spacings of other van der Waals heterostructures, which are generally between 3 Å and 4 Å.59
Based on the calculated lattice parameters, the lattice mismatch of the InS/GaTe heterostructure is 4.85%. In general, the lattice mismatch of a stable van der Waals heterostructure is smaller than 5%.60,61 This indicates that InS/GaTe could possess stability. To investigate the dynamical stability of the InS and GaTe monolayers, and the InS/GaTe heterostructure, the phonon dispersion was calculated using the Phonopy code.62 The calculation was performed using a (4 × 4 × 1) supercell for the InS and InS/GaTe heterostructure, while a (2 × 2 × 1) supercell was employed for the GaTe monolayer. When using a (2 × 2 × 1) supercell for InS and InS/GaTe, imaginary phonon modes were still present in their phonon dispersion curves. As a result, a larger supercell of size (4 × 4 × 1) was used for InS and InS/GaTe. The results are shown in Fig. S7, it can be seen that the three materials are dynamically stable as evidenced by the absence of imaginary phonon modes. The phonon dispersion curves for the InS and GaTe monolayers agree with a previous ab initio study for the monolayer systems,63 implying the accuracy of our calculations.
Furthermore, we performed AIMD calculations to evaluate the thermodynamic stability of the InS/GaTe heterostructure. The simulation was performed using a (4 × 4 × 1) supercell of InS/GaTe, containing 128 atoms. The NVT ensemble was considered and the Nose–Hoover thermostat64,65 was used. Fig. 4 shows the change in temperature and energy for 5 ps. The initial and final structure is also displayed in the figure. It can be seen that the system is predicted to be thermodynamically stable at 300 K. This is a good indication that the system will be thermodynamically stable in aqueous solution for practical applications at room temperature (300 K).
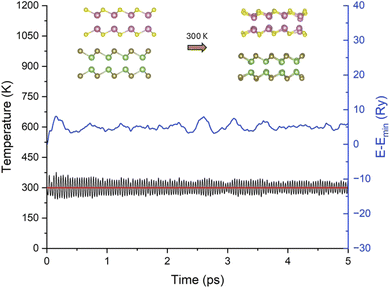 | ||
| Fig. 4 AIMD simulation performed at 300 K; inset: the optimized structure and the structure after 5 ps. | ||
3.2 Electronic properties
To obtain a more reliable band gap energy, the band structures of the monolayers were also calculated using the hybrid HSE06 functional. The results are presented in Fig. S9. The calculated band gap for InS is 2.61 eV, which is in good agreement with 2.71 eV (ref. 17) and 2.66 eV (ref. 22) which also used the HSE06 functional. The obtained band gap of the GaTe monolayer is 2.16 eV, also aligning well with previously reported values of 2.22 eV (ref. 17) and 2.15 eV (ref. 22).
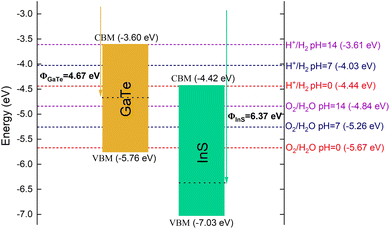
The position of conduction band minimum (CBM) and valence band maximum (VBM) of the two monolayers is an important factor for their potential application as catalysts for water splitting. The CBM and VBM of InS are located at −4.42 eV and −7.03 eV with respect to the vacuum level, while those of GaTe are −3.60 eV and −5.76 eV, respectively. The position of the CBM and VBM values is plotted along with the water reduction and oxidation potential in Fig. 5. As the CBM of GaTe is considerably more positive than the reduction potential of water for the whole pH range (0 ≤ pH ≤ 14), it is predicted to have a strong reduction ability. On the other hand, InS has potential as an oxidation catalyst since its VBM is significantly more negative than the water oxidation potential (Fig. 5). Hence, it is expected that the InS/GaTe heterostructure could be a promising system to realize efficient reduction and oxidation performance for the overall water splitting mechanism.
The reduction and the oxidation potential of water, as indicated in Fig. 5, were calculated using eqn (2) and (3).10 In these equations, −4.44 eV and −5.67 eV are the standard reduction potential for H+/H2 and oxidation potential for O2/H2O, respectively, at pH = 0 and at the room temperature.17 It is important to note that the difference between the two potential values is 1.23 eV, which is the free energy of water splitting.17 Based on the Nernst equation, the reduction and oxidation potential vary with pH by 0.059 eV at room temperature.66
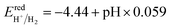 | (2) |
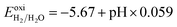 | (3) |
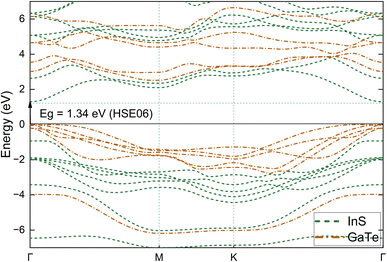 | ||
| Fig. 6 Electronic band structure of the InS/GaTe heterostructure as obtained using the HSE06 functional. | ||
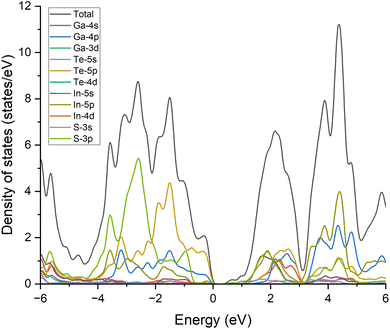
In addition, it is worthy to note that the VBM of the InS/GaTe heterostructure is formed by GaTe while the CBM is constructed by the InS orbitals. To further verify this, the total and projected density of states of the heterostructure are calculated and shown in Fig. 7. The figure demonstrates that the top of the valence band of the system is formed by the Te-5p state, followed by the Ga-4p state with slightly lower contributions. On the other hand, the bottom of the conduction band is formed by the In-5s and S-3p states with approximately the same contributions. This confirms the staggered band nature of the InS/GaTe heterostructure, important for its potential applications as a photocatalyst for the overall water splitting mechanism.
The work functions of the InS monolayer and the InS/GaTe heterojunction were found to be 6.37 eV and 5.01 eV, respectively. These values are in reasonable agreement with those reported in a previous study,22 with respective values being 6.17 eV and 5.13 eV. Meanwhile, the work function of GaTe was calculated to be 4.67 eV in the present work, slightly higher than 4.58 eV (ref. 18) and lower than 5.08 reported in ref. 21 and 22 which used the PBE. Another study using the HSE06 functional reported a value of 4.98 eV for the work function of GaTe.19
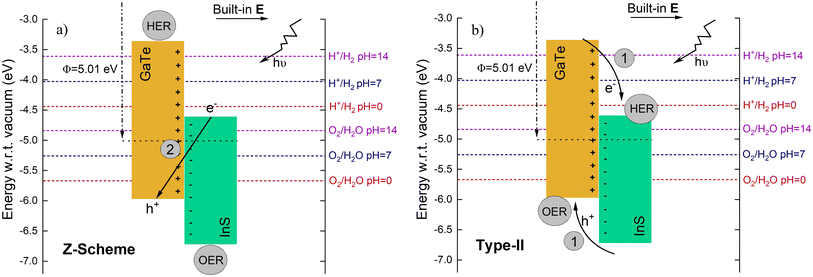
As GaTe possesses higher Fermi energy (lower work function) than InS, electrons diffuse from GaTe to InS when the heterojunction is formed, until their Fermi levels align. This is illustrated in Fig. 9. As a result, there will be a built-in electric field with direction from GaTe to InS. To confirm this, the charge density difference (CDD) of the InS/GaTe heterostructure is calculated using eqn (4) and the result is visualized in Fig. 8.
| Δρ(r) = ρGaTe/InS(r) − (ρGaTe(r) + ρInS(r)) | (4) |
The CDD clearly indicates that there is a charge redistribution along the junction between InS and GaTe. In particular, an apparent charge depletion is seen in the GaTe surface and charge accumulation along the InS side. The Bader charge analysis67 was further conducted to estimate the electron transfer between the surface of the two monolayers in the heterostructure. The results are summarized in Table 1, from which it can be inferred that GaTe loses 0.02 electrons while at the same time InS gains 0.02 electrons. This verifies the electron transfer from the GaTe monolayer to the InS monolayer, as predicted from the analysis of Fermi energy and charge density difference distribution.
| Atom | Number of electrons | Valence electrons | Δe |
|---|---|---|---|
| Ga | 12.520 | 13 | −0.479 |
| Ga | 12.586 | 13 | −0.414 |
| Te | 16.448 | 16 | 0.448 |
| Te | 16.426 | 16 | 0.426 |
| Total | 57.981 | 58 | −0.019 |
| In | 12.216 | 13 | −0.784 |
| In | 12.133 | 13 | −0.868 |
| S | 6.841 | 6 | 0.841 |
| S | 6.830 | 6 | 0.830 |
| Total | 38.019 | 38 | 0.019 |
Regarding the potential of the InS/GaTe heterostructure for water splitting applications, its band alignment (Fig. 5) indicates that it straddles the water redox potential for the whole pH range (pH = 0 to pH = 14). In other words, the water redox potential for the whole acid pH range lies between the CBM and the VBM of the heterostructure. This implies that InS/GaTe heterostructure could potentially show remarkable photocatalytic performance.
As it has a staggered band, the transfer mechanism of photogenerated electrons and holes along the junction could follow two paths. The first path is the type-II mode, in which the photogenerated electrons move from the conduction band (CB) of photocatalyst GaTe to that of InS whereas the photogenerated holes move from the valence band (VB) of InS to that of GaTe. This separation of charge is expected to reduce the intralayer electron–hole recombination at each photocatalyst, but such a charge transfer mechanism is not very favorable for water splitting as the electrons gather at InS with weak reduction potential and similarly, the holes are accumulated at GaTe with weak oxidation potential. In fact, HER can not take place at the surface of InS since its CBM is lower than the water reduction potential for the whole pH range. In addition, the repulsion from the existing electrons at InS (holes at GaTe) will hinder a continuous transfer of electrons from GaTe (holes from InS). On the other hand, Z-scheme heterostructures not only improve the separation efficiency but also retain strong redox ability of the catalyst. This is because the electrons (holes) with strong reduction (oxidation) ability stay in the CB of GaTe (VB of InS) whereas electrons (holes) with lower redox ability recombine (shown as path 2 in Fig. 9).
The presence of the built-in electric field, E, from GaTe to InS will prevent photogenerated electrons moving from the CBM of GaTe to that of InS. It will also prevent the movement of photogenerated holes from the VBM of InS to that of GaTe. Therefore, it is highly unlikely that the heterostructure possesses the type-II charge transfer mechanism (path 1 in Fig. 9). On the other hand, the built-in E will promote the interlayer recombination of the photogenerated electrons at the CBM of the InS and the photogenerated holes at the VBM of the GaTe monolayer. This increases the possibility of the presence of the Z-scheme transfer mechanism (path 2 in Fig. 9). However, this analysis alone is not sufficient to come to the conclusion of the charge transfer mechanism as some previous studies fail to reproduce such a prediction in the experimental results just by using this procedure. Therefore, a further analysis is performed in the next sections to support this finding. This analysis involves calculating the reaction free energy diagram of the oxygen evolution reaction (OER) on the InS/GaTe heterostructure for both type-II and direct Z-scheme charge transfer paths. The Gibbs free energies are then calculated for each reaction pathway. The hydrogen evolution reaction (HER) will also be investigated on the direct Z-scheme path but not on the type-II, as the CBM of InS is more negative than the reduction potential for all pH range, as mentioned above. In other words, type-II scheme of the InS/GaTe heterostructure cannot facilitate HER.
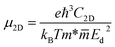 | (5) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) is the average effective mass defined to be
is the average effective mass defined to be 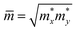 . C2D and Ed are the 2D elastic constant and the deformation potential, which are calculated using eqn (6) and (7), respectively.
. C2D and Ed are the 2D elastic constant and the deformation potential, which are calculated using eqn (6) and (7), respectively.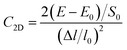 | (6) |
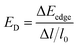 | (7) |
To calculate the carrier mobility in the zig–zag (x) and armchair (y) directions, the hexagonal unit cell of the heterostructure was first transformed into an orthorhombic cell as visualized in Fig. S11. The optimized lattice parameters of the new unit cell are a = 4.04 Å and b = 6.99 Å. The uniaxial strain was applied to both lattice parameters and each strained system was fully relaxed while keeping the lattice constant fixed, to obtain newly relaxed electronic configurations for the calculation of the electronic band structure.
Fig. S12 demonstrates the change in the total energy and the band edges of the InS/GaTe heterostructure due to the uniaxial strain along the x and y directions. The general pattern of the total energy is similar for both directions although the total energy of the system under strain along the x direction is slightly lower than that along the y direction. The variation in the band edge, both CBM and VBM, is similar along x and y directions.
The calculated carrier mobility, along with the effective mass, elastic modulus, and deformation potential are summarized in Table 2.
| Carrier | m*/m0 | C 2D (N m−1) | E d (eV) | μ 2D (cm2 V−1 s−1) |
|---|---|---|---|---|
| Electron (x) | 0.77 | 294.02 | −6.00 | 285.20 |
| Electron (y) | 0.81 | 267.57 | −6.29 | 224.50 |
| Hole (x) | 3.75 | 294.02 | 1.00 | 680.83 |
| Hole (y) | 2.82 | 267.57 | 0.86 | 629.97 |
The calculated carrier mobility for electrons along x and y directions are 285.20 cm2 V−1 s−1 and 224.50 cm2 V−1 s−1, respectively. These values are higher than reported mobility of about 200 cm2 V−1 s−1 for some 2D systems including single layer MoS2 (ref. 68) and graphene nanoribons,69 which is also comparable to that of thin strained silicon films (250 cm2 V−1 s−1).70 Nevertheless, these values are still lower than the mobility of other systems including Ge2Se2P4 (7396.35 cm2 V−1 s−1 and 375.35 cm2 V−1 s−1 along x and y directions, respectively),10 ScSeI (933.83 cm2 V−1 s−1 along y direction),11 and the AlN/PtSSe heterostructure (1320.49 cm2 V−1 s−1 and 3998.32 cm2 V−1 s−1 along x and y directions, respectively).45
Interestingly, the calculated values of the hole mobility in x and y directions are 680.83 cm2 V−1 s−1 and 629.97 cm2 V−1 s−1, respectively, around 2 times higher than those of electron. Similar behaviour was also observed for other heterostructures such as the MoS2/MoSe2-Janus XMoSiZ2 (X = S, Se, Te; Z = N, P) heterostructure,71 where the hole mobility (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 219.42 cm2 V−1 s−1 and 4750.80 cm2 V−1 s−1 along x and y directions, respectively) is significantly higher than the electron mobility (256.64 cm2 V−1 s−1 and 196.01 cm2 V−1 s−1 along x and y directions, respectively) for the MoSe2/SeMoSiP2 heterostructure. This implies that electrons and holes can be more effectively separated.71 These values are higher than the hole mobility of many systems including ScSeI (225.98 cm2 V−1 s−1 and 146.47 cm2 V−1 s−1 along x and y directions, respectively),11 Ge2Se2P4 (155.95 cm2 V−1 s−1 along x direction),10 and AlN/PtSSe (252.79 cm2 V−1 s−1 along y direction).45 The results suggest that the InS/GaTe heterostructure exhibits high electron and hole mobility, which is crucial for its potential applications including as a photocatalyst for water splitting.
219.42 cm2 V−1 s−1 and 4750.80 cm2 V−1 s−1 along x and y directions, respectively) is significantly higher than the electron mobility (256.64 cm2 V−1 s−1 and 196.01 cm2 V−1 s−1 along x and y directions, respectively) for the MoSe2/SeMoSiP2 heterostructure. This implies that electrons and holes can be more effectively separated.71 These values are higher than the hole mobility of many systems including ScSeI (225.98 cm2 V−1 s−1 and 146.47 cm2 V−1 s−1 along x and y directions, respectively),11 Ge2Se2P4 (155.95 cm2 V−1 s−1 along x direction),10 and AlN/PtSSe (252.79 cm2 V−1 s−1 along y direction).45 The results suggest that the InS/GaTe heterostructure exhibits high electron and hole mobility, which is crucial for its potential applications including as a photocatalyst for water splitting.
3.3 Photocatalytic properties of the InS/GaTe heterostructure
To investigate the photocatalytic performance of the heterostructure, the OER and HER mechanisms were studied on the surfaces of the heterostructure for both the Z-scheme and type-II charge transfer mechanisms. We first consider acidic conditions. The overall water oxidation reaction, under acidic conditions at p = 1 bar and T = 298.15 K, is shown in eqn (8).72–74| 2H2O(l) → O2 + 4H+ + 4e−; ΔG0 = 4.92 eV | (8) |
which consists of four steps as follows:
| 2H2O(l) + * → OH* + H+ + e− | (9) |
| OH* → O* + H+ + e− | (10) |
| H2O(l) + O* → OOH* + H+ + e− | (11) |
| OOH* → * + O2(g) + H+ + e− | (12) |
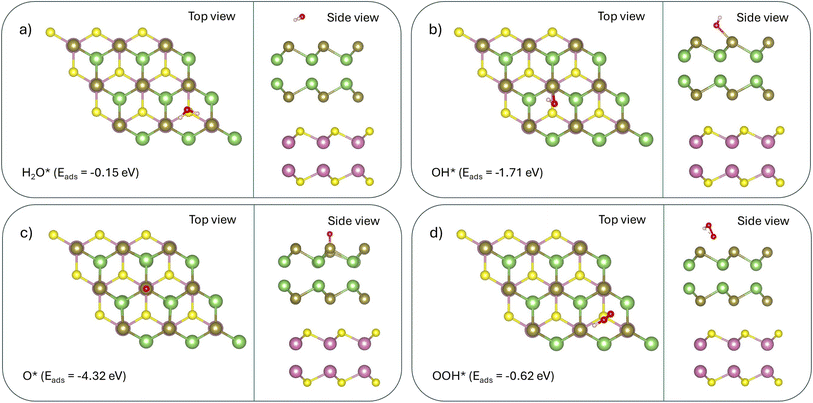
The theoretical Gibbs free energy differences of each reaction step are calculated using eqn (13),10
| ΔG = ΔE + ΔZPE − TΔS + GU − GpH | (13) |
| GU = −eUSHE | (14) |
| GpH = kBT × ln(10) × pH | (15) |
| Ue = Ue(pH = 0) − pH × 0.059 V | (16) |
| Uh = Uh(pH = 0) + pH × 0.059 V | (17) |
Based on eqn (8) and (13), the following equations were used to calculate the Gibbs free energy difference for the four reaction steps as shown in eqn (9)–(12). Each of the ΔG values is evaluated relative to the preceding steps as illustrated in Fig. 14(a). The data used to calculate these quantities are provided in the SI (Table S10).
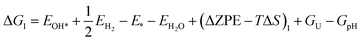 | (18) |
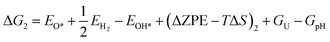 | (19) |
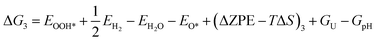 | (20) |
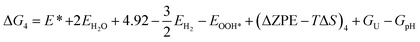 | (21) |
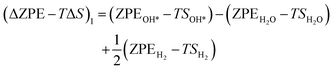 | (22) |
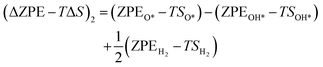 | (23) |
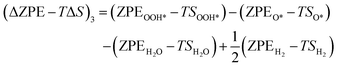 | (24) |
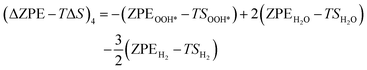 | (25) |
The zero-point energy ZPE and the entropy of the adsorbed intermediates in this study were calculated using eqn (26) and (27), respectively.77
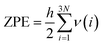 | (26) |
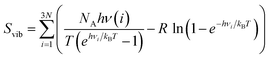 | (27) |
The HER mechanism is characterized by the following reactions.39
| * + H+ + e− → H* | (28) |
| H* + H+ + e− → * + H2 | (29) |
Eqn (28) and (29) are referred to as the Volmer–Heyrovsky mechanism. Moreover, the HER mechanism can also follow the Volmer–Tafel route (eqn (28) and (30)).81
| 2H* → H2 + 2* | (30) |
It is noted that the terminology of the Volmer, Heyrovsky, and Tafel steps originate in electrochemical splitting of water, but analogous steps also occur in photochemical water splitting. Which of the steps of eqn (29) or (30) occur will depend on the particular system. The Gibbs free energy is calculated using eqn (31) and (32)
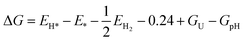 | (31) |
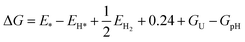 | (32) |
Table S1 of the SI shows all H2O adsorption configurations with their adsorption energy while Fig. 10 presents the most favorable adsorption configuration of H2O on the InS surface. Overall, the water molecule is weakly adsorbed with the most favorable configuration having an adsorption energy of −0.19 eV. The distance between the adsorbed H2O and the InS surface for the most stable state is 2.48 Å. The adsorption of intermediates OH, O, and OOH on the InS surface was investigated, with stable adsorption sites and associated adsorption energies presented in Tables S2–S4 of the SI, respectively.
 | ||
| Fig. 10 The most favorable adsorption configurations of H2O (a), OH (b), O (c), and OOH (d) on the InS surface, for the Z-scheme mode. | ||
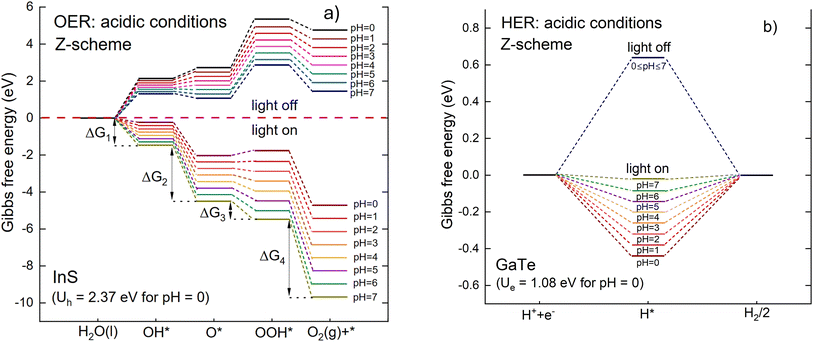
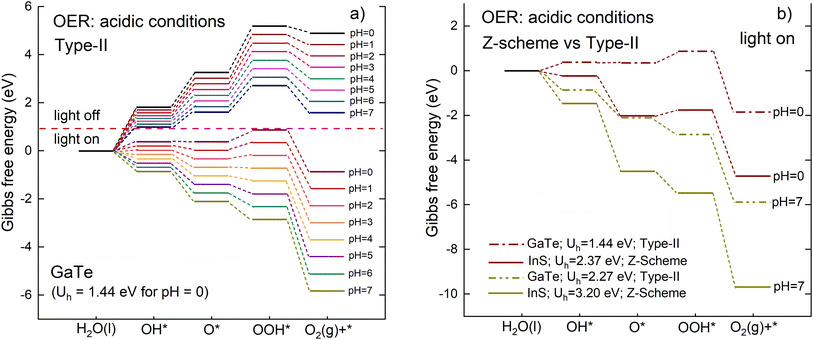
The most favorable adsorption configurations of the species on the InS surface are visualized in Fig. 10. The adsorption energies of OH, O, and OOH for the most favorable adsorption configurations are −1.38 eV, −4.60 eV, and −0.33 eV, respectively. Overall, OH and O were found to be strongly adsorbed on the InS surface, with O forming a chemical bond with the S atom with O–S bond lengths of 1.764 Å and 1.521 Å, respectively. On the other hand, OOH is physisorbed on the surface, which agrees with the results of other studies on the surface of other monolayers.76,82 The Gibbs free energies of the intermediates are illustrated in Fig. 11(a), for pH = 0 to pH = 7, with and without photogenerated hole potential, Uh. In this study, the term “light on” means the potential Ue > 0 or Uh > 0 while “light off” means the conditions for which the potential is zero Ue = 0 or Uh = 0. As shown by the figure, the reaction is upward (endothermic) when the light is off for all pH values, and under this condition, the influence of pH is not very significant on the reaction steps, i.e. only leads to a slight decrease in the Gibbs free energies. The GpH value for pH = 1 is 0.059 eV, steadily increasing to 0.413 eV for pH = 7. On the other hand, when the light is on, the photogenerated hole potential leads to a downward trend of the reactions. For pH = 0 and pH = 1, there is still an endothermic reaction for OOH* while for 2 ≤ pH ≤ 7, the OER is spontaneous for all the reaction steps.
For the HER mechanism, a H atom was adsorbed on the GaTe surface where various adsorption sites were considered, as shown in Table S5. The hydrogen atom was found to have an adsorption energy of −1.93 eV and a H–Te bond length of 1.685 Å. The Gibbs free energy diagram for the HER mechanism is presented in Fig. 11(b), for pH = 0 to pH = 7. When the light is off, it can be seen that adsorption of a H atom on the surface is not favorable compared to being in a free H2 molecule. Further, the effect of pH on the Gibbs free energy is negligible as it varies with pH by only 0.059 eV. On the other hand, with light on, pH and the photogenerated electron potential have a notable effect on the Gibbs free energy. More importantly, the ΔG (adsorbed H atom) is found to be −0.02 eV at pH = 7 under light illumination. This highlights the promising property of the InS/GaTe heterostructure as a photocatalyst to facilitate HER.
It is interesting to note that the rate limiting reaction (the most endothermic step) is the formation of the OOH* intermediate. This agrees well with other studies on heterostructures including GeH/InSe,83 GaTe/AsP,84 and CdS/C6N7,39 as well as monolayers such as ScSeI,11 and SnSe monolayers.85 This is because O is strongly bonded to the surface, meaning that more energy is required to form the OOH intermediate.
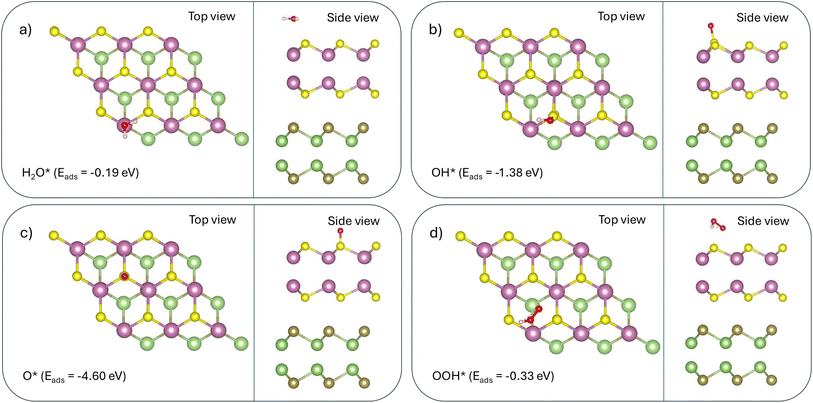
Similar to the results of the Z-scheme mechanism, H2O and OOH were found to be physically absorbed on the surface of GaTe, while the OH and O are chemisorbed with O forming a bond with Te atom. The O–Te bond lengths for the adsorption of OH and O are 2.183 Å and 1.872 Å, respectively.
The adsorption energies of the most favorable configurations for H2O, OH, O, and OOH adsorbed on the surface are −0.15 eV, −1.71 eV, −4.32 eV, and −0.62 eV, respectively. All adsorption sites considered with associated adsorption energies are presented in Tables S6–S10. The most favorable adsorption configurations are shown in Fig. 12.
 | ||
| Fig. 12 The most favorable adsorption configurations of H2O (a), OH (b), O (c), and OOH (d) on GaTe surface, for the type-II mode. | ||
The Gibbs free energy diagram for the OER is shown in Fig. 13(a) for the type-II scheme. In general, the overall trends observed in the calculated free energy differences for the Z-scheme are also found for the type-II mechanism, with the main difference being the magnitude of the Gibbs energy. In particular, the reaction is predicted to be spontaneous when the light is on for 3 ≤ pH ≤ 7.
For the present system of InS/GaTe, comparing the OER pathways when the light is off, shows that the Z-scheme exhibits a larger energy barrier compared to the type-II. Therefore, based on the proposed method of Liu et al.45 the InS/GaTe heterostructure should have the traditional type-II charge transfer mode. However, this analysis is only based on the “dark condition”, which is not completely appropriate as the photogenerated charge transfer occurs after light illumination. Moreover, the type-II mode predicted for InS/GaTe using the method of ref. 45 in the present study contradicts with the analysis of the electronic properties of InS/GaTe discussed in the previous section, especially related to the direction of the built-in electric field.
In this study, we propose that a more appropriate way to determine the charge transfer mechanism in band staggered heterostructures is by examining the Gibbs free energy differences when the light is on. As the Z-scheme and type-II mechanisms describe the charge transfer mechanism of photogenerated charges (electrons and holes), the analysis of the reaction steps to determine which mechanism is favorable for a particular heterostructure should be performed when the light is on. The scheme with the lowest Gibbs free energy change when the light is on is the most favorable scheme.
Fig. 13(b) presents the Gibbs free energy diagram of the OER for the Z-scheme and type-II mechanisms when the light is on. For clarity, the figure only shows the diagram for pH = 0 and pH = 7. The figure illustrates that both Z-scheme and type-II scheme possess the same general trend of Gibbs free energy for all reaction steps for a given pH. The OER reactions are spontaneous only when the light is on and for 2 ≤ pH ≤ 7 for the Z-scheme and for 3 ≤ pH ≤ 7 for the type-II. This means that the InS/GaTe heterostructure is a promising photocatalyst to realize spontaneous OER reactions, irrespective of the type of the photogenerated charge transfer. However, it can be clearly seen that for all reaction steps, the Z-scheme mechanism exhibits lower (more negative) Gibbs free energy difference than the type-II mechanism. This is because it has a larger value of photo-induced potential with only a slight difference in the relative free energies with “light-off” for Z-scheme and type-II. Although the maximum increase in Gibbs free energy for the Z-scheme (2.57 eV at pH = 0, cf.Fig. 11) is slightly higher than type-II (1.93 eV at pH = 0, cf.Fig. 13), the hole potential for Z-scheme (2.37 eV at pH = 0) is considerably larger than type-II (1.44 eV at pH = 0). This leads to more greatly lower Gibbs free energy for the Z-scheme when the light is turned on, implying that the Z-scheme mechanism is more favorable for the InS/GaTe heterostructure.
The Z-scheme nature predicted for the InS/GaTe using this method is also supported by the direction of the built-in electric field as shown in Fig. 9, which is also true for the AA stacking configuration of InS/GaTe reported in ref. 22. It is also worth noting that the spontaneous reaction of OER for 2 ≤ pH ≤ 7 makes InS/GaTe more promising for a wider range of media compared to other heterostructures such as AlN/PtSSe,45 for which the OER was predicted to be spontaneous only at pH = 7.
The oxygen evolution reaction performance of InS/GaTe in the present work is compared with that of two of the most efficient OER catalysts, namely RuO2 and IrO2 (ref. 86) in Table S15 of the SI. The comparison of the OER Gibbs free energy and overpotential between InS/GaTe, RuO2 and IrO2, shows the four steps of the OER reactions are similar for the three materials. In particular, the potential determining step is the *OOH formation step (step 3) for all three materials. The most striking difference is found for the Gibbs free energy for the O2 formation step (step 4 of the reaction) which for our system is spontaneous but is not spontaneous for RuO2 and IrO2. Our results also showed that as pH increases, the Gibbs free energy for all reactions decreases and leads to oxygen formation becoming spontaneous at high pH. The overpotential of InS/GaTe is found to increase for increasing pH, higher than that of RuO2 and IrO2 for neutral-basic pH. However, InS/GaTe is better than IrO2 at pH = 0 with overpotential of 1.14 eV and 1.19 eV, respectively. The overpotential of InS/GaTe is also comparable with that of IrO2, especially under acidic conditions, where the overpotential of InS/GaTe is below 1.5 eV. Therefore, this strongly suggests the high potential of InS/GaTe as an OER photocatalyst.
InS/GaTe is also promising as a HER catalyst. This can be seen from its Gibbs free energy for the H2 formation reaction at pH = 6 and pH = 7 with values of −0.08 eV and −0.02 eV, respectively. This is comparable to the Gibbs free energy of the most efficient HER catalyst, namely Pt with Gibbs free energy of −0.09 eV.87 However, the HER potential determining step of InS/GaTe becomes larger for other pH values, making it less suitable as a HER catalyst.
| 4OH− → O2(g) + 2H2O(l) + 4e− | (33) |
which is generally assumed to proceed in four steps as follows:
| * + OH− → OH+ + e− | (34) |
| OH* + OH− → O* + H2O(l) + e− | (35) |
| O* + OH− → OOH* + e− | (36) |
| OOH* + OH− → * + O2(g) + H2O(l) + e− | (37) |
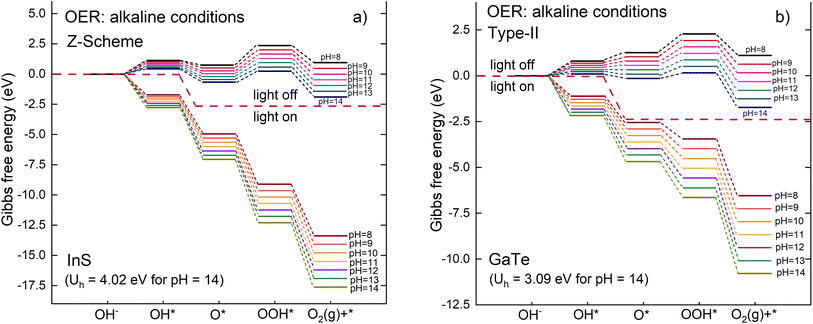
Although the reactions are different, the equations to calculate the Gibbs free energy of each reaction step in alkaline conditions are the same as those in acidic conditions i.e.eqn (18)–(21). The full derivation can be found in ref. 74. Fig. 14 shows the Gibbs free energy diagram for the OER mechanism under alkaline conditions for Z-scheme and type-II modes.
Overall, the general pattern is similar to the OER mechanism under acidic medium. It can be seen that the energy barrier is lower in alkaline media although OOH* is still the rate limiting reaction (the most endothermic step). As for the acidic medium, the OER reaction is not spontaneous when the light is off. On the other hand, the reaction is predicted to be spontaneous for the whole pH range from pH = 8 to 14. Consistent with the results for acidic medium, it can also be inferred from Fig. 14 that Z-scheme is more favorable for the OER reaction in alkaline medium compared to the traditional type-II scheme as it has a more negative Gibbs free energy for all reaction steps.
Regarding the HER mechanism, it is found that in general, catalysts display substantially lower HER rate in alkaline medium than in acidic medium.88,89 This is due to the additional energy barrier introduced by the water dissociation step in the Volmer step in the alkaline HER.90–92 The additional step of water dissociation provides more protons for the subsequent reactions, which is not the case in the acidic media.76 This is clearly demonstrated in the case of Pt catalyst, where the HER rate in alkaline medium was found to be two or three orders of magnitude lower than that under acidic condition.93 This is also true in the present study, where it is predicted that HER performance is decreasing in alkaline medium as the electron potential decreases when pH increases (Table S10). This may lead to the reduction in its ability to overcome the energy barrier in alkaline media.
3.4 The water splitting efficiency of the InS/GaTe heterostructure
Solar-to-hydrogen efficiency (ηsth) is generally used to evaluate the water splitting efficiency of a photocatalyst. It can be calculated using eqn (38), where ηabs and ηcu are the efficiency of light absorption and carrier utilization, respectively.94ηabs and ηcu are presented in eqn (39) and (40), respectively.| ηsth = ηabs × ηcu | (38) |
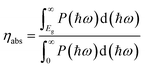 | (39) |
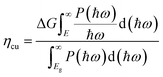 | (40) |
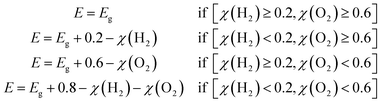 | (41) |
The calculated solar-to-hydrogen efficiency (ηsth) for the Z-scheme InS/GaTe heterostructure is 44.8% for the pH range considered (2 ≤ pH ≤ 14). It is the combination of the overpotential and the energy gap of the heterostructure which plays the vital role in obtaining a high solar-to-hydrogen efficiency. This predicted value is higher than the efficiency of many photocatalysts investigated for water splitting applications. For instance, the indium gallium nitride photocatalyst was recently synthesized and the solar-to-hydrogen efficiency was reported to be 9.2%.96 The water splitting efficiency of 44.8% for InS/GaTe is also higher than theoretically predicted efficiency for other photocatalysts including heterostructures: MoSe2/Ti2CO2 (12%),9 GaTe/AsP (14.1%),84 and PtSSe/γ-phosphorene 24.86%,42 and monolayers: Ge2Se2P4 (17.05%)10 and ScSeI (17%).11 More importantly, this value is also significantly higher than the threshold of 10% based on the technoeconomic analysis.97 Hence, it is apparent that the InS/GaTe heterostructure is a promising photocatalyst for water splitting although its efficiency is still lower than that theoretically predicted for MoTe2/BAs (56.32%).94
A sensitivity analysis is provided to estimate how ηsth changes if the band gap is inaccurate by −0.1 eV and +0.1 eV. Table S14 summarizes the changes in the HER and OER over-potentials as well as the water splitting efficiency (ηsth) for inaccuracy in the band gap by −0.1 eV and +0.1 eV. The details of the calculations are presented in the SI, just under Table S14. The results show that ηsth increases (decreases) when the band gap of InS/GaTe is narrower (broader), with pH = 14 (for a decrease in the band gap by 0.1 eV) being the only exception. It is predicted that the maximum increase (decrease) in the efficiency for the case where the band gap is inaccurate by −0.1 eV (+0.1 eV) is 48.6% (39.9%), from the estimated efficiency of 44.8% (Eg = 1.34 eV). This has been anticipated as the narrower the band gap of a material, the broader its light absorption range.
Eqn (38), (40) and (41) indicate that the HER and OER overpotentials have a direct impact on ηsth. The largest contribution of the overpotentials to the efficiency is when χ(H2) ≥ 0.2 and χ(O2) ≥ 0.6. Efficiency is expected to decline for overpotentials below these thresholds. This is clearly demonstrated for the case of the band gap being inaccurate by −0.1 eV (for pH = 14), where χ(H2) = 0.154, which leads to a slight decline in the efficiency from 44.8% to 42.6% (Table S14). For other cases where χ(H2) ≥ 0.2 and χ(O2) ≥ 0.6, the obtained ηsth values are the same: a more detailed explanation is provided in the SI (just below Table S14).
Charge recombination is another important factor which can reduce ηsth. The recombination will cause smaller number of electrons and holes reaching reaction sites, leading to lower photocatalytic performance. In the present work, the Z-scheme is predicted to be the most favorable charge transfer mechanism for InS/GaTe. Therefore, it is expected that photogenerated electrons (holes) will stay at the surface of GaTe (InS) and participate in the HER (OER) reactions. Meanwhile, less useful photogenerated electrons at the CBM of InS will recombine with photogenerated holes at the VBM of GaTe.
For practical applications, it is expected that the solar-to-hydrogen efficiency of InS/GaTe is lower than 44.8%. This is because our DFT model cannot capture some real-world losses such as defects, surface states, catalyst overpotential and non-radiative recombination. However, such phenomena can be experimentally minimized to obtain an optimal solar to hydrogen conversion efficiency. For instance, Zhang and co-workers98 recently observed that surface Ti vacancies around positively polarized facets in PbTiO3 lower its photocatalytic performance by trapping electrons and inducing their recombination. The authors then modified the system by growing SrTiO3 nanolayers on the polarized facets PbTiO3. The modification successfully mitigated the interface Ti defects and as a result, the electron lifetime significantly increases. This leads to increasing participation of electrons in the water splitting reactions and a significant increase in the quantum yield for overall water splitting. Moreover, doping99 and the optimization of some key characteristics of catalysts including the conductivity, crystal size, microstructure, and assembly can significantly reduce the overpotential of the catalysts.100 Furthermore, many catalysts still suffer from high non-radiative recombination. Such recombination can be suppressed by structural modification including optimal doping of 2D materials101 and other crystalline engineering techniques to reduce the number of recombination centers.102
It should also be mentioned that the effect of solvation is not considered in the present work. This might lead to an underestimation or overestimation of the adsorption energy and the Gibbs free energy of the studied material. However, it is expected that the qualitative trend for the free energy reaction pathway is the same so that the overall conclusion regarding the type of charge transfer remains unchanged. This was demonstrated by a recent study103 using an implicit solvent model to study the OER at the MoS2 surface. The authors observed that the inclusion of the implicit water model only slightly alters the adsorption geometry and OER reaction mechanics. It was also reported that the presence of the solvent reduces the adsorption energy of all the intermediates (OH*, O* and OOH*) with comparable magnitude.
3.5 Optical properties
The optical properties of materials are of great significance as they provide information on how they interact with incoming photons. For optoelectronic applications including photocatalytic water splitting, the materials should exhibit strong light absorption ability, which can be inferred from the optical characteristics such as their absorption capability.The complex dielectric functions of the InS and GaTe monolayers, as well as the InS/GaTe heterostructure, are calculated using the HSE06 functional and are presented in Fig. S13 and S14. Once the imaginary dielectric function ε1 (Fig. S13) and the real part ε2 (Fig. S14) are determined using eqn (42) and (43),104–106 all the other optical characteristics can be derived.107
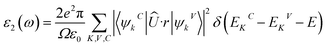 | (42) |
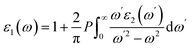 | (43) |
It is important to note that the calculated dielectric function is for the unit cell of the 2D structures including the vacuum region. Therefore, to obtain the intrinsic dielectric function of the structures, the calculated dielectric functions need to be renormalized. This was performed using eqn (44) and (45), respectively.108 In these equations, (εi)MX and (εi)SC (i = 1, 2; M = Ga, In; X = S, Te) are the dielectric functions of the studied MX monolayers without the influence of the vacuum region and for the whole supercell, respectively; dSC is the thickness of the monolayer plus the vacuum while dMX is the effective thickness of the monolayers. In this study, the vacuum thickness used was 20 Å for each monolayer and 35 Å for the heterostructure, while the thicknesses of InS, GaTe, and the InS/GaTe heterostructure were 5.27 Å, 4.95 Å, and 13.60 Å, respectively.
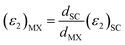 | (44) |
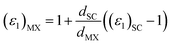 | (45) |
The intrinsic dielectric function of the InS and GaTe monolayers after the renormalization is shown in Fig. S13 and S14. Comparison with the uncorrected dielectric function including the vacuum region is presented in Fig. S15 and S16 of the SI. The figures clearly demonstrate that without renormalization the magnitudes are significantly smaller, as expected.
We note that in the literature, this correction is often ignored in studies on 2D materials, which leads to errors in the reported dielectric functions and therefore the optical properties of the 2D materials. This was clearly demonstrated by Yang and Gao,108 who applied the corrections to some 2D materials including well-known h–BN and MoS2 and found that their calculated optical properties of the materials are in better agreement with the measured values compared to previous calculations. The authors also observed strong anisotropy in the optical properties of the h–BN and MoS2, which differs from their bulk counterparts.108 A practice of ignoring the volume correction in the calculation of the dielectric function of 2D materials is a common mistake in the field and therefore needs reconsideration, as it may lead to unphysical conclusions.109 It was demonstrated that the imaginary dielectric function of the 2D MoS2 is significantly higher than that of the 3D MoS2.109 Hüser et al.110 also studied the dielectric functions of the monolayer MoS2 and presented discussions on the difference between 2D and 3D screening. Hence, to obtain more accurate optical properties of 2D materials, this correction should be included.
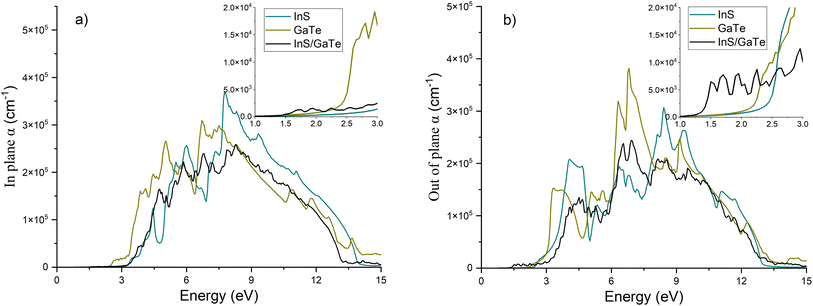
The imaginary part of the dielectric function (Fig. S13) represents the absorption behaviour of the InS/GaTe heterostructure. Despite having lower imaginary dielectric functions in higher energy (E > 3 eV), it is apparent that in the visible region, especially between 1.5 and 2.5 eV, the InS/GaTe heterostructure possesses the highest values. This is consistent with the finding that the InS/GaTe heterostructure exhibits a band gap of 1.34 eV, significantly lower than that of the InS and GaTe monolayers with band gaps of 2.61 eV and 2.12 eV, respectively. The strong light absorption of the InS/GaTe heterostructure, especially in the visible region of the solar spectrum, further supports its promising photocatalytic properties for overall water splitting. Fig. S14 shows that the real part of the dielectric function of InS, GaTe, and InS/GaTe have some negative values between 4.5 eV and 13.5 eV (in plane) and between 4 eV and 13.5 eV (out of plane). This indicates that the systems can facilitate plasmonic phenomena around this energy range.
To further evaluate the ability of the InS/GaTe heterostructure to absorb any incoming light, its optical absorption was calculated using eqn (46),108 where ε1 and ε2 were obtained using eqn (44) and (45), respectively.
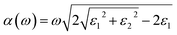 | (46) |
The absorption coefficient of the InS/GaTe heterostructure is illustrated in Fig. 15, along with that of the InS and GaTe monolayers. It is apparent from the figure that the materials possess a high absorption coefficient, reaching 105 cm−1. Materials with high absorption coefficient (104 cm−1–105 cm−1) are promising for various optoelectronic applications.111 This suggests the strong light absorption ability of the materials, making them of huge interest for optoelectronic applications, including for water splitting112,113 as the absorption coefficient in the visible region is predicted to reach 104 cm−1. In particular, the InS/GaTe is predicted to exhibit higher absorption coefficients, both in-plane and out-of-plane, than InS and GaTe monolayers in the visible region of the solar spectrum, as shown in the inset of Fig. 15.
4 Conclusions
The structural, electronic, photocatalytic, and optical properties of the InS/GaTe heterostructure and its constituent monolayers have been investigated using density functional theory calculations. The structural optimization shows that InS is preferentially positioned over GaTe with the S atom over the hollow site of GaTe. The system has a direct band gap of 1.34 eV, ideal as an absorber for photocatalytic applications. The analysis of the calculated work functions and the Bader analysis along the junction suggested that there is electron transfer from the GaTe monolayer to the InS monolayer, resulting in an built-in electric field. This is consistent with the electronegativity of the S and Te atoms which are the closest atoms to the heterojunction. The InS/GaTe heterostructure was also found to possess high charge carrier mobility with significant difference in the electron and hole mobility, implying its possibility to effectively separate electrons and holes. The oxygen evolution reaction (OER) mechanism was analyzed for both the Z-scheme and type-II mechanisms to determine the most favorable photogenerated electron and hole transfer mechanisms. Based on the Gibbs free energy diagrams of OER reactions when the light is turned on, the InS/GaTe heterostructure is predicted to possess the direct Z-scheme charge transfer, consistent with the direction of the built-in electric potential. The heterostructure was found to facilitate spontaneous OER for 2 ≤ pH ≤ 14 (Z-scheme) and 3 ≤ pH ≤ 14 (type-II). It was found that the type-II scheme of InS/GaTe cannot facilitate HER, while the Z-scheme is predicted to be promising for HER with ΔG = −0.02 eV at pH = 7. The water splitting efficiency of InS/GaTe was calculated to be 44.8%, significantly higher than the commercial threshold of 10%. The promising photocatalytic properties of InS/GaTe are also supported by its optical properties, where the heterostructure is predicted to show stronger light absorption in the visible spectrum, compared to the individual InS and GaTe monolayers. Hence, these results strongly indicated that the heterostructure is a promising photocatalyst for overall water splitting.Author contributions
All authors contributed to the writing of this manuscript. All authors have approved the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
Data supporting this article have been included as part of the supplementary information (SI).Supplementary information: convergence study results, different stacking configurations of InS/GaTe, phonon dispersion, electrostatic potential, band structure of the InS and GaTe monolayers, energy and band edges for different uniaxial strain values along x and y directions, dielectric functions, adsorption sites and numerical data used in the calculations. See DOI: https://doi.org/10.1039/d5ta04464b.
Acknowledgements
R. K. P. acknowledges the Indonesia Endowment Fund for Education (LPDP) for providing his PhD scholarship. C. S. acknowledges financial support from the Australian Research Council (FL 230100176). We acknowledge the supercomputing facilities provided by the National Computational Infrastructure (NCI), the Pawsey Supercomputing Centre, and the School of Physics Supercomputing Centre at the University of Sydney.References
- M. D. Bhatt and J. S. Lee, J. Mater. Chem. A, 2015, 3, 10632–10659 RSC.
- K. Maeda and K. Domen, J. Phys. Chem. Lett., 2010, 1, 2655–2661 CrossRef CAS.
- S. Nishioka, F. E. Osterloh, X. Wang, T. E. Mallouk and K. Maeda, Nat. Rev. Methods Primers, 2023, 3, 42 CrossRef CAS.
- L. Pan, N. Vlachopoulos and A. Hagfeldt, ChemSusChem, 2019, 12, 4337–4352 CrossRef CAS PubMed.
- Q. Xu, L. Zhang, B. Cheng, J. Fan and J. Yu, Chem, 2020, 6, 1543–1559 CAS.
- A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278 RSC.
- L.-J. Sun, H.-W. Su, Q.-Q. Liu, J. Hu, L.-L. Wang and H. Tang, Rare Met., 2022, 41, 2387–2404 CrossRef CAS.
- L.-Z. Zhang, L. Chen, G.-Y. Yan, R.-W. Liang and H.-H. Ou, Rare Met., 2024, 43, 5802–5812 CrossRef CAS.
- C.-F. Fu, X. Li and J. Yang, Chem. Sci., 2021, 12, 2863–2869 RSC.
- T. V. Vu, N. N. Hieu, D. D. Vo, A. I. Kartamyshev, H. D. Tong, T. T. Trinh, V. Khuong Dien, Z. Haman, P. Dey and N. Khossossi, J. Phys. Chem. C, 2024, 128, 4245–4257 CrossRef CAS.
- J. Yang, R. Wan, Z. Zhang, G. Tian, S. Ju, H. Luo, B. Peng and Y. Qiu, ACS Appl. Mater. Interfaces, 2024, 16, 49454–49464 CrossRef CAS PubMed.
- F. Hu, R. Wan, Z. Zhang, G. Tian, S. Ju, H. Luo, B. Peng and Y. Qiu, Mater. Sci. Semicond. Process., 2024, 171, 108051 CrossRef CAS.
- B.-J. Ng, L. K. Putri, X. Y. Kong, Y. W. Teh, P. Pasbakhsh and S.-P. Chai, Adv. Sci., 2020, 7, 1903171 CrossRef CAS PubMed.
- Y. Wang, H. Suzuki, J. Xie, O. Tomita, D. J. Martin, M. Higashi, D. Kong, R. Abe and J. Tang, Chem. Rev., 2018, 118, 5201–5241 CrossRef CAS PubMed.
- J. Li, H. Yuan, W. Zhang, B. Jin, Q. Feng, J. Huang and Z. Jiao, Carbon Energy, 2022, 4, 294–331 CrossRef CAS.
- G. Ding, Z. Wang, J. Zhang, P. Wang, L. Chen and G. Liao, EcoEnergy, 2024, 2, 22–44 CrossRef CAS.
- H. L. Zhuang and R. G. Hennig, Chem. Mater., 2013, 25, 3232–3238 CrossRef CAS.
- A. Rawat, R. Ahammed, D. Dimple, N. Jena, M. K. Mohanta and A. De Sarkar, J. Phys. Chem. C, 2019, 123, 12666–12675 CrossRef CAS.
- J. Chen, X. He, B. Sa, J. Zhou, C. Xu, C. Wen and Z. Sun, Nanoscale, 2019, 11, 6431–6444 RSC.
- C. Wen, Z. Zhang, Z. Guo, J. Shen, B. Sa, P. Lin, J. Zhou and Z. Sun, J. Phys.:Condens. Matter, 2019, 32, 065501 CrossRef PubMed.
- T. Li, Z. Gao, W. Ju, D. Wang, Y. Zhang, Y. Xu and H. Li, Comput. Mater. Sci., 2021, 188, 110153 CrossRef CAS.
- M. Li, K. Liang, W. Xing, Y. Zhang, H. Chen, Y. Yang, J. Liu, Y. Tian, Z. Li and L. Duan, New J. Chem., 2024, 48, 14970–14983 RSC.
- Q. An, B. Wang, J. Yang, X. Zhang and J. Ni, Int. J. Hydrogen Energy, 2024, 89, 84–89 CrossRef CAS.
- T. Qi, Y. Gong, A. Li, X. Ma, P. Wang, R. Huang, C. Liu, R. Sakidja, J. Z. Wu, R. Chen and L. Zhang, Adv. Funct. Mater., 2020, 30, 1905687 CrossRef CAS.
- W. Feng, Z. Jin, J. Yuan, J. Zhang, S. Jia, L. Dong, J. Yoon, L. Zhou, R. Vajtai, J. M. Tour, P. M. Ajayan, P. Hu and J. Lou, 2D Materials, 2018, 5, 025008 CrossRef.
- Y. Fan, X. Ma, X. Liu, J. Wang, H. Ai and M. Zhao, J. Phys. Chem. C, 2018, 122, 27803–27810 CrossRef CAS.
- W. Wei, Y. Dai, C. Niu, X. Li, Y. Ma and B. Huang, J. Mater. Chem. C, 2015, 3, 11548–11554 RSC.
- H. R. Jappor and M. A. Habeeb, Curr. Appl. Phys., 2018, 18, 673–680 CrossRef.
- S.-Z. Sun, Y. Zhang, Y.-F. Luo, Y.-S. Yang, J.-H. Li, L. Duan, J. Xie and T.-T. Guo, Surf. Sci., 2024, 749, 122553 CrossRef CAS.
- A. O. M. Almayyali, H. R. Jappor and H. O. Muhsen, J. Phys. Chem. Solids, 2023, 178, 111317 CrossRef CAS.
- S. Guo, Z. Cui, Y. Zou and B. Sa, Phys. Chem. Chem. Phys., 2024, 26, 5368–5376 RSC.
- J. Wang, K. Liang, X. Wei, Y. Zhang, H. Chen, Y. Yang, J. Liu, Y. Tian and L. Duan, J. Phys.: Condens. Matter, 2023, 36, 115702 CrossRef PubMed.
- J. Abdul Nasir, A. Munir, N. Ahmad, T. u. Haq, Z. Khan and Z. Rehman, Adv. Mater., 2021, 33, 2105195 CrossRef CAS PubMed.
- Y. Chen, T. Shi, P. Liu, X. Ma, L. Shui, C. Shang, Z. Chen, X. Wang, K. Kempa and G. Zhou, J. Mater. Chem. A, 2018, 6, 19167–19175 RSC.
- M. Zhu, Z. Sun, M. Fujitsuka and T. Majima, Angew. Chem., Int. Ed. Engl., 2018, 57, 2160–2164 CrossRef CAS PubMed.
- D. Salazar-Marín, G. Oza, J. D. Real, A. Cervantes-Uribe, H. Pérez-Vidal, M. Kesarla, J. T. Torres and S. Godavarthi, Appl. Surf. Sci. Adv., 2024, 19, 100536 CrossRef.
- Z. Zhou, S. Yuan and J. Wang, Front. Phys., 2021, 16, 43203 CrossRef.
- Q. Zheng, W. Chu, C. Zhao, L. Zhang, H. Guo, Y. Wang, X. Jiang and J. Zhao, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2019, 9, e1411 CAS.
- C. biao Lin, F. li Sun, J. Wen, W. xian Chen and G. lin Zhuang, Fuel, 2023, 341, 127682 CrossRef.
- D. Li, R. Li, F. Zeng, W. Yan, M. Deng and S. Cai, Appl. Surf. Sci., 2023, 614, 156104 CrossRef CAS.
- Y. Zhang and R. Long, J. Phys. Chem. Lett., 2024, 15, 6002–6009 CrossRef CAS PubMed.
- P. Chauhan and A. Kumar, Sci. Rep., 2024, 14, 21618 CrossRef CAS PubMed.
- H. Uratani and H. Nakai, J. Chem. Phys., 2020, 152, 224109 CrossRef CAS PubMed.
- S. Axelrod, E. Shakhnovich and R. Gómez-Bombarelli, Nat. Commun., 2022, 13, 3440 CrossRef CAS PubMed.
- Y. Liu, Y. Yao, Z. Liang, Z. Gong, J. Li, Z. Tang and X. Wei, J. Phys. Chem. C, 2024, 128, 9894–9903 CrossRef CAS.
- C. Hu, L. Zhang and J. Gong, Energy Environ. Sci., 2019, 12, 2620–2645 RSC.
- M. Jakhar and A. Kumar, Catal. Sci. Technol., 2021, 11, 6445–6454 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- D. R. Hamann, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 085117 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- D. L. Duong, S. J. Yun and Y. H. Lee, ACS Nano, 2017, 11, 11803–11830 CrossRef CAS PubMed.
- H. Zheng, X.-B. Li, N.-K. Chen, S.-Y. Xie, W. Q. Tian, Y. Chen, H. Xia, S. B. Zhang and H.-B. Sun, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 115307 CrossRef.
- A. Koma, J. Cryst. Growth, 1999, 201–202, 236–241 CrossRef.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001 CrossRef CAS PubMed.
- S. Demirci, N. Avazl ı, E. Durgun and S. Cahangirov, Phys. Rev. B, 2017, 95, 115409 CrossRef.
- N. Shuichi, Prog. Theor. Phys. Suppl., 1991, 103, 1–46 CrossRef.
- W. G. Hoover, Phys. Rev. A:At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- J. Joe, H. Yang, C. Bae and H. Shin, Catalysts, 2019, 9, 149 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147 CrossRef CAS PubMed.
- X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229–1232 CrossRef CAS PubMed.
- L. Gomez, I. Aberg and J. L. Hoyt, IEEE Electron Device Lett., 2007, 28, 285–287 CAS.
- Y. Zhao, Z. Dai, X. Jia and L. Bai, ACS Appl. Nano Mater., 2025, 8, 6563–6574 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef PubMed.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- Q. Liang, G. Brocks and A. Bieberle-Hütter, J. Phys.: Energy, 2021, 3, 026001 CAS.
- H. Yang, Y. Ma, S. Zhang, H. Jin, B. Huang and Y. Dai, J. Mater. Chem. A, 2019, 7, 12060–12067 RSC.
- X. Chen, W. Han, Z. Tian, Q. Yue, C. Peng, C. Wang, B. Wang, H. Yin and Q. Gu, J. Phys. Chem. C, 2023, 127, 6347–6355 CrossRef CAS.
- G. Ding, Y. Gao, H. Zhang, N. Yang, X. Niu and J. Wang, Phys. Chem. Chem. Phys., 2025, 27, 577–588 RSC.
- NIST Computational Chemistry Comparison and Benchmark Database, ed. R. D. Johnson, The National Institute of Standards and Technology (NIST), 2022, http://cccbdb.nist.gov/ Search PubMed.
- A. Tiwari, C. Honingh and B. Ensing, J. Chem. Phys., 2019, 151, 244124 CrossRef CAS PubMed.
- B. Bagchi, in The Entropy of Water, Cambridge University Press, 2013, pp. 287–304 Search PubMed.
- J. D. Parkinson and N. V. Rees, J. Solid State Electrochem., 2025, 29, 2075–2088 CrossRef CAS.
- K. Ren, W. Tang, M. Sun, Y. Cai, Y. Cheng and G. Zhang, Nanoscale, 2020, 12, 17281–17289 RSC.
- R. Li, S. Zhu and J. Ding, Chem. Phys. Lett., 2024, 840, 141160 CrossRef CAS.
- S.-Z. Sun, Y. Zhang, Y.-F. Luo, Y.-S. Yang, J.-H. Li, L. Duan, J. Xie and T.-T. Guo, Surf. Sci., 2024, 749, 122553 CrossRef CAS.
- Y. Xu, K. Xu, C. Ma, Y. Chen, H. Zhang, Y. Liu and Y. Ji, J. Mater. Chem. A, 2020, 8, 19612–19622 RSC.
- A. Zagalskaya and V. Alexandrov, ACS Catal., 2020, 10, 3650–3657 CrossRef CAS.
- Y. Cheng, X. Fan, F. Liao, S. Lu, Y. Li, L. Liu, Y. Li, H. Lin, M. Shao and S.-T. Lee, Nano Energy, 2017, 39, 284–290 CrossRef CAS.
- J. AU Wei, M. Zhou, A. Long, Y. Xue, H. Liao, C. Wei and Z. J. Xu, Nano-Micro Lett., 2018, 10, 75 CrossRef PubMed.
- M. Lao, P. Li, Y. Jiang, H. Pan, S. X. Dou and W. Sun, Nano Energy, 2022, 98, 107231 CrossRef CAS.
- J. Huang, P. Li and S. Chen, J. Phys. Chem. C, 2019, 123, 17325–17334 CrossRef CAS.
- P. S. Lamoureux, A. R. Singh and K. Chan, ACS Catal., 2019, 9, 6194–6201 CrossRef CAS.
- L. Liu, Y. Liu and C. Liu, J. Am. Chem. Soc., 2020, 142, 4985–4989 CrossRef CAS PubMed.
- Y. Zheng, Y. Jiao, A. Vasileff and S.-Z. Qiao, Angew. Chem., Int. Ed., 2018, 57, 7568–7579 CrossRef CAS PubMed.
- M. Cao, L. Ni, Z. Wang, J. Liu, Y. Tian, Y. Zhang, X. Wei, T. Guo, J. Fan and L. Duan, Appl. Surf. Sci., 2021, 551, 149364 CrossRef CAS.
- C. A. Gueymard, Sol. Energy, 2004, 76, 423–453 CrossRef.
- P. Zhou, I. A. Navid, Y. Ma, Y. Xiao, P. Wang, Z. Ye, B. Zhou, K. Sun and Z. Mi, Nature, 2023, 613, 66–70 CrossRef CAS PubMed.
- B. A. Pinaud, J. D. Benck, L. C. Seitz, A. J. Forman, Z. Chen, T. G. Deutsch, B. D. James, K. N. Baum, G. N. Baum, S. Ardo, H. Wang, E. Miller and T. F. Jaramillo, Energy Environ. Sci., 2013, 6, 1983–2002 RSC.
- J. Zhang, Y. Liu, T. Dittrich, Z. Wang, P. Ji, M. Li, N. Ta, H. Zhang, C. Zhen, Y. Xu, D. Li, Z. Feng, Z. Li, Y. Luo, J. Cui, D. Su, Y. Weng, G. Liu, X. Wang, F. Fan and C. Li, Nat. Commun., 2025, 16, 1515 CrossRef CAS PubMed.
- N. Artrith, W. Sailuam, S. Limpijumnong and A. M. Kolpak, Phys. Chem. Chem. Phys., 2016, 18, 29561–29570 RSC.
- W. Li, Y. Liu, A. Azam, Y. Liu, J. Yang, D. Wang, C. C. Sorrell, C. Zhao and S. Li, Adv. Mater., 2024, 36, 2404658 CrossRef CAS PubMed.
- T. Das, F. Farooq, P. Garg, S. Singla, A. Guchhait and A. Bera, Sustainable Energy Fuels, 2025, 9, 269–279 RSC.
- A. Dai, Z. Huang, L. Tian, Z. Zhang, X. Guan and L. Guo, Chin. J. Struct. Chem., 2025, 44, 100630 Search PubMed.
- E. German and R. Gebauer, Molecules, 2023, 28, 5182 CrossRef CAS PubMed.
- R. K. Pingak, S. Bouhmaidi, A. Harbi, L. Setti, F. Nitti, M. Moutaabbid, A. Z. Johannes, N. U. J. Hauwali and M. Z. Ndii, RSC Adv., 2023, 13, 33875–33886 RSC.
- C. Ambrosch-Draxl and J. O. Sofo, Comput. Phys. Commun., 2006, 175, 1–14 CrossRef CAS.
- M. A. Green, Y. Jiang, A. M. Soufiani and A. Ho-Baillie, J. Phys. Chem. Lett., 2015, 6, 4774–4785 CrossRef CAS PubMed.
- L. Niu, O. J. Conquest, C. Verdi and C. Stampfl, Nanomaterials, 2024, 14, 1659 CrossRef CAS PubMed.
- G. Yang and S.-P. Gao, Nanoscale, 2021, 13, 17057–17067 RSC.
- A. Yadav, C. M. Acosta, G. M. Dalpian and O. I. Malyi, Matter, 2023, 6, 2711–2734 CrossRef.
- F. Hüser, T. Olsen and K. S. Thygesen, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 245309 CrossRef.
- X. Du, J. Li, G. Niu, J.-H. Yuan, K.-H. Xue, M. Xia, W. Pan, X. Yang, B. Zhu and J. Tang, Nat. Commun., 2021, 12, 3348 CrossRef CAS PubMed.
- M. R. Islam, M. S. Islam, A. F. Mitul, M. R. H. Mojumder, A. S. M. J. Islam, C. Stampfl and J. Park, Sci. Rep., 2021, 11, 17739 CrossRef CAS PubMed.
- M. R. Islam, M. S. Islam, M. Y. Zamil, N. Ferdous, C. Stampfl, J. Park and M. K. Hossain, J. Phys. Chem. Solids, 2023, 176, 111263 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |