Modulation of CO2 adsorption thermodynamics and selectivity in alkali-carbonate activated N-rich porous carbons†‡
J. Ehren
Eichler
 a,
James N.
Burrow
a,
James N.
Burrow
 b,
Naman
Katyal
a,
Graeme
Henkelman
b,
Naman
Katyal
a,
Graeme
Henkelman
 a and
C. Buddie
Mullins
a and
C. Buddie
Mullins
 *ab
*ab
aDepartment of Chemistry, The University of Texas at Austin, Austin, Texas 78712-1224, USA. E-mail: mullins@che.utexas.edu
bJohn J. McKetta Department of Chemical Engineering, The University of Texas at Austin, Austin, Texas 78712-1224, USA
First published on 7th February 2023
Abstract
Here we analyze how changes in the charge density of activating alkali cations (lithium, sodium, and potassium) alters the synthesis and resulting physicochemical properties of N-rich activated carbons. In general, the synthesis reagents had significant influence on the total nitrogen content (2–24 at%), the chemical environment of the nitrogen species, the specific surface area (∼600–4300 m2 g−1), and the types of pores that formed in the activated materials. Each sample was screened for carbon dioxide (CO2) and nitrogen (N2) gas adsorption. From application of the ideal adsorbed solution theory, the predicted CO2/N2 selectivity spanned a large range from ∼8 to ∼150 at 15% CO2 and was dependent on d-spacing, surface N content, and porosity. Finally, the materials were analyzed with a simplified temperature swing adsorption model to estimate the optimal working capacity and regeneration energy of the materials in a cyclic process. Overall, this study demonstrates that while the precursor nitrogen content drives significant changes in the isotherm shape, a careful choice of activating cation during synthesis of advanced porous carbons can strongly influence physicochemical properties and the resulting thermodynamics and selectivity of CO2 adsorption.
1 Introduction
To avoid the most detrimental impacts of climate change, rapid implementation of decarbonization technologies such as carbon capture and storage (CCS) is critical.1 Among a variety of candidate processes for CCS, separation via swing adsorption with solid-state porous adsorbents incurs relatively low intrinsic energy cost.2 Activated carbons, one promising class of solid-state adsorbents, can be produced cheaply and sustainably, exhibit good thermochemical stability, and require only modest energy for regeneration in a cyclic separation process.3 However, activated carbons frequently show poor selectivity for CO2 adsorption, especially at the low concentrations encountered in post-combustion flue gas.2,4 In addition, convoluted structure–function relationships arising from challenges in the synthesis of porous carbons have hindered attempts at identifying and optimizing the most important material properties.5 Nonetheless, tuning surface chemistry via dopants like nitrogen, phosphorus, or sulfur and decreasing pore size can greatly improve the CO2/N2 selectivity of a carbon-based adsorbent.6 As such, controlling these material properties is essential when designing advanced carbon materials for selective CO2 adsorption.Many synthetic schemes exist for activating carbons. Among the most common include the reaction of alkali oxysalts with carbonaceous material via high temperature (>700 °C) pyrolysis.7 In our previous work we explored how porosity depends on the nitrogen (N) content in the precursor and the amount of activating salt.8 In brief, with low N-content and relatively large amounts of activating agent, redox-type reactions between the carbon and the K+ cation occur, resulting in porosity as the metal intercalates between and exfoliates carbon sheets. As the N-content increases, these redox interactions between graphitic carbon and the cation are limited. Instead, “chemical etching” processes dominate, where the cation reacts with surface N-functionalities to form cyanide and/or cyanate adducts. In this case, porosity is mostly created in the form of void spaces left behind from the sequestration of N-containing groups by the cation. At excessively large precursor N-content relative to the activating agent, another process occurs after chemical etching. With an abundance of N-content after etching by cations, N-functionalities are volatized and significant mass is lost. If enough mass is lost in this manner, the formed alkali cyanide salts can then solvate the carbon, resulting in porosity induced by molten salt templating.8 In this work, we seek to understand how the charge density of the cation employed during activation of porous carbons alters material properties and resulting CO2 adsorption performance.
Several previous studies investigating the role of different alkali salts in modulating the pore architecture and CO2 adsorption performance of activated carbons have been limited to precursors with only sparse N content (<5 at%).9,10 These studies implicate the size of the cation as a functional handle to fine-tune the diameter of small micropores. To expand on these previous works, we synthesized and chemically activated a suite of carbon precursors with N-content tunable up to 45 at% with M-carbonate salts, where “M” = Li, Na, or K. The physicochemical properties of the resulting materials covered a broad range, with BET surface areas and final N contents spanning ∼600–4300 m2 g−1 and ∼2–24 at%, respectively. In general, bulkier cations tended to produce more N2-accessible surface area, while the charge density of the cation influenced the stratification of different surface N-functionalities. The largest CO2 capacities and CO2/N2 selectivities, as well as lowest calculated energy costs, were observed for carbons with large quantities of pyridinic and pyrrolic N-functionalities and critical pore dimensions small enough to exclude N2 but not CO2 adsorption. This study aims to provide useful insights into the design of carbon adsorbents for selective CO2 uptake through the lenses of both adsorption thermodynamics and material property engineering.
2 Experimental
2.1 Semi-carbonization of sucrose and melamine
Informed by our previous works, carbon foams were produced via semi-carbonization of mixtures of sucrose (Alfa Aesar) and melamine (Aldrich).8,11 These foams were designated “SMX-Carb”, where X refers to the mass percent of melamine added to sucrose and “Carb” indicates the sample was semi-carbonized. In this work, mass percentages corresponding to 20, 40, 60, and 80% melamine were studied, and the precursor N-content was found to influence the mechanisms of porosity generation as described in our previous work.8 Samples with N-content less than SM20-Carb were excluded from this study to avoid systems with significant oxygen content. For the synthesis of each semi-carbonized sample, a total of 20 grams of the sucrose/melamine mixture (either 20, 40, 60, or 80 wt% melamine) were ground in a mortar and pestle, divided equally into four 250 mL covered alumina crucibles, and heated in air at 410 °C for 2.5 hours at a ramp rate of 5 °C min−1. After semi-carbonization, the foams were collected from the crucibles and ground in a mortar and pestle into a powder prior to activation.2.2 Activation of semi-carbonized samples
Before activation, 1.5 g of semi-carbonized precursor was impregnated with either 13.35 mL of 1 M K2CO3 or Na2CO3. In case of the significantly less soluble Li2CO3, the appropriate amount of powdered Li2CO3 was mixed with the precursor and then 13.35 mL of DI water was added. In this way each sample was activated with the same molar quantity of Li, Na, or K. Samples were dried in air at 120 °C overnight. For activation, each dried mixture was added to covered 20 mL alumina crucibles, placed inside a tube furnace under Ar flowing at 150 sccm, heated to 800 °C at 3 °C min−1, held at 800 °C for 60 min, and then allowed to cool naturally to room temperature. After activation, the samples were washed with 50 mL of 1 M HCl for 1 hour and 2 liters of DI water to ensure the removal of all inorganic salts. A small portion (∼15 mg) of the unwashed material was collected for XRD analysis. Samples were named “M–X” where “M” refers to the corresponding cation (Li, Na, or K) in the activating agent while “X” again refers to the weight percent of melamine in the precursor.2.3 Characterization
To track the gaseous products formed during activation, evolved gas analysis (EGA) was studied using a home-built fixed bed reactor described previously.12 In brief, 18 mg of impregnated precursor was placed into a 70 μL alumina crucible and carefully lowered into a quartz reactor tube under 20 sccm of Ar flow. The sample was heated at 3 °C min−1 and held at 800 °C in line with the activation procedure. An Extorr XT100 quadrupole mass spectrometer (QMS) was used to continuously monitor the effluent during activation. A helium internal standard with a flow rate of 9 sccm was added before the QMS but after the sample bed to correct signal fluctuations as a result of changes in the total flow rate during activation.Solid-state byproducts of activation were identified by powder X-ray diffraction (XRD) performed ex situ at temperatures informed by decomposition features in the EGA spectra. Specifically, evolution of CO or CO2 likely indicates a reaction of the carbonate salt, as such measurements were taken after each of these features resolved. XRD after acid washing was also employed to measure semi-crystalline parameters of the resulting carbons. XRD patterns were collected with a Rigaku Miniflex 600 Diffractometer in continuous scan mode at 2.5° min−1 from 5–50° 2θ with a step size of 0.02 using a single crystal Si zero-background diffraction holder (MTI). In order to prevent the oxidation of lithium salts formed during activation upon exposure to air, aliquots were sealed in the MTI holder with Kapton tape immediately after removing the sample from the furnace.
Quantitative information of the surface chemistry of the activated carbons was obtained via X-ray photoelectron spectroscopy (XPS) using a Kratos Axis Ultra DLD spectrometer. A charge neutralizer was used to mitigate surface charging effects, and the resulting spectra were shifted such that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C component of the C 1s spectra was centered at 284.7 eV. XPS spectra were analyzed using CasaXPS™ software and fit with Shirley backgrounds. For the high-resolution scans of the C 1s region, four Gaussian–Lorentzian peaks were used to fit the total response, centered at 284.7 eV for sp2 carbon (C
C component of the C 1s spectra was centered at 284.7 eV. XPS spectra were analyzed using CasaXPS™ software and fit with Shirley backgrounds. For the high-resolution scans of the C 1s region, four Gaussian–Lorentzian peaks were used to fit the total response, centered at 284.7 eV for sp2 carbon (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); 286 ± 0.1 eV for sp3 carbon (C–C or C–N); 288.3 ± 0.3 eV for melem-type carbons (CN3); and 290 ± 0.3 eV for oxidized (C
C); 286 ± 0.1 eV for sp3 carbon (C–C or C–N); 288.3 ± 0.3 eV for melem-type carbons (CN3); and 290 ± 0.3 eV for oxidized (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) functionalities. For the N 1s region, four Gaussian–Lorentzian peaks were used for deconvolution, centered at 398.3 ± 0.1 eV for pyridinic (C–N
O) functionalities. For the N 1s region, four Gaussian–Lorentzian peaks were used for deconvolution, centered at 398.3 ± 0.1 eV for pyridinic (C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C); 399.8 ± 0.2 eV for pyrrolic (C2NH); 400.9 eV ± 0.3 for graphitic (NC3); and 402.7 ± 0.4 eV for oxidized nitrogen (NOx). Finally, for the O 1s regions, two Gaussian–Lorentzian peaks were employed at 530 ± 0.3 eV for hydroxyl (OH) and 532 ± 0.6 eV for oxidized carbons or nitrogen (CO/NO).
C); 399.8 ± 0.2 eV for pyrrolic (C2NH); 400.9 eV ± 0.3 for graphitic (NC3); and 402.7 ± 0.4 eV for oxidized nitrogen (NOx). Finally, for the O 1s regions, two Gaussian–Lorentzian peaks were employed at 530 ± 0.3 eV for hydroxyl (OH) and 532 ± 0.6 eV for oxidized carbons or nitrogen (CO/NO).
Flash combustion analysis was performed in oxygen via an ECS 4010 (Costech Analytical Technologies, Valencia CA, USA) to gain information about the bulk composition of the material. For analysis, ∼5 mg of sample was loaded into a tin crucible and the molecular nitrogen, carbon dioxide, and water vapors generated after combustion were separated through a 3 meter chromatography column before detection with a thermal conductivity detector. A calibration curve created with analytical standards of atropine and urea was used for quantification of the evolved species.
The resulting textural properties of the activated carbons were studied with N2 adsorption at 77 K using a Quantachrome Autosorb iQ-MP (Anton Parr). Using ASiQ Win™ software, surface areas were quantified with multi-point BET analysis with optimized point selection to account for the microporous nature of these materials. Pore size distributions were derived from the adsorption branch of the isotherm with quenched-solid density functional theory assuming a convolution of spherical, cylindrical, and slit-shaped pores. Total pore volume (up to 200 nm) was quantified using the total quantity adsorbed at a P/P0 = 0.99.
Adsorption of N2 and CO2 were measured on a NOVA 2200e from ∼1 Torr to ∼760 Torr with a float sensor paired with a temperature-controlled water bath (Isotemp refrigerated circulator, Fischer Scientific). Prior to analysis, samples were outgassed overnight under vacuum at 200 °C. CO2 isotherms were measured at four temperatures: 10, 20, 30, and 40 °C. Nitrogen isotherms were measured at 30 °C for selectivity calculations.
2.4 Modeling and calculations
Density functional theory (DFT) calculations were performed to model the reaction between the activating agent and N-containing carbons. All DFT calculations were carried out using the Vienna ab initio simulations package (VASP) with a generalized gradient approximation functional.13 For geometry optimizations, the energy and force convergence criteria was 10−6 eV and −0.01 eV Å−1. Core electrons were modeled using the projector augmented wave method (PAW) method and electron-correlation effects were incorporated using the Perdew–Burke–Ernzerhof (PBE) functional.14 For electronic convergence, a plane-wave cutoff of 300 eV and a Monkhorst–Pack 2 × 2 × 1 k-point mesh was chosen for all calculations.15,16 The effect of the metal cation on N-containing carbons was modelled by calculating the change in Gibbs free energy using the following reaction (eqn (1)):| M2CO3(s) + X(s) → MCN(s) + MOCN(s) + CO2(g) | (1) |
The reaction between different N-functionalities and activating agents was also modelled with DFT to understand the relationship between different N-groups and metal cations. From XPS, different N-groups (viz., pyridinic nitrogen, trimethyl amine and pyrrolic nitrogen) were observed, and the reaction of each group was modelled using the formulae given below (eqn (2)–(4)).
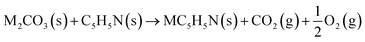 | (2) |
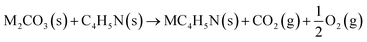 | (3) |
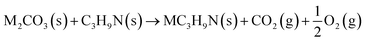 | (4) |
Each CO2 isotherm was fit to a temperature dependent dual-site Langmuir (DSL) model (eqn (5) & (6)) with nonlinear regression in OriginPro™. For each sample's set of CO2 isotherms, the saturation capacity of independent sites (qi,sat) was held constant with temperature while the site affinity (bi) was allowed to vary with temperature. Site-specific adsorption enthalpies and entropies were extracted with a van't Hoff relation (eqn (6)).17 The primary site of adsorption (qA) was assigned to the higher affinity site with stronger energetics of adsorption than the secondary site (qB). Isotherms of N2 were fit to a linear model to extract the Henry's law constant (kN2) (eqn (7)).
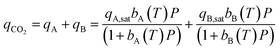 | (5) |
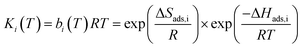 | (6) |
| qN2 = kN2P | (7) |
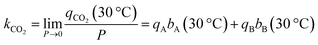 | (8) |
Isosteric heats of adsorption (Qst) for CO2 were calculated using the Clausius–Clapeyron equation (eqn (9)).18 The ASiQ Win software performs analysis of the raw data, while a procedure defined by Long et al. was used to derive values from the dual-site Langmuir model.19
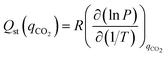 | (9) |
The thermodynamics of CO2 adsorption were calculated from the DSL fit parameters, their associated uncertainties, and a range of fractional coverages. In brief, eqn (1) was algebraically rearranged to solve for the pressure required to achieve a certain uptake (q) at a specific temperature. At each uptake, the slope and intercept of a linear fit between the natural log of the pressure against inverse temperature were related to enthalpy and entropy of adsorption, respectively. Eqn (10) (below) was then used to determine the Gibbs energy of adsorption at 303 K. The uncertainty for each term was propagated for each step. The uncertainty in the linear fit parameters was then determined from a weighted least squares regression with the weighting shown in eqn (11), where δ is the determined uncertainty in natural log of pressure. In this way, points with significant uncertainties were weighted less in the determination of the uncertainty in the linear fit parameters.
| ΔGads = ΔHads − TΔSads | (10) |
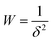 | (11) |
The adsorption selectivity for CO2/N2 was calculated from ideal adsorbed solution theory (IAST) with an open-source Python package (pyIAST) developed by Simon et al.20 In brief, the non-linear system of equations defined in eqn (12)–(18) was solved iteratively for equality of spreading pressure (πi) as a function of partial pressure of CO2 and N2 in the vapor phase. The only necessary inputs for the calculation are the fitted pure-component isotherm parameters for both CO2 and N2 at the same temperatures. Selectivity (SIAST,i) at a given feed composition is given by eqn (19), while purity was quantified as the mole fraction of CO2 (xCO2) in the adsorbed phase (eqn (20)).
| yCO2 + yN2 = 1 | (12) |
| Pi = xiP0i = yiPtotal | (13) |
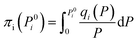 | (14) |
| πCO2 = πN2 | (15) |
| xCO2 + xN2 = 1 | (16) |
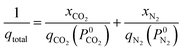 | (17) |
| qi = xiqtotal | (18) |
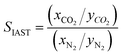 | (19) |
| Purity = 100% × xCO2 | (20) |
To estimate the performance of the samples in a temperature swing adsorption (TSA) process, a model was adapted from Sculley et al. and modified in our previous work.21,22 This model uses the fit parameters derived from the dual-site Langmuir model to determine the regeneration energy (Qregen) and working capacity (qworking) as functions of desorption temperature. The working capacity, defined in eqn (21), is determined as the difference in CO2 adsorption at 40 °C at a range of partial pressures (0–1 bar) of CO2 (qads) and the desorption in a pure feed of CO2 (qdes) at an elevated desorption temperature (Tdes). The regeneration energy (eqn (22)) was calculated as the sum of the energy required for desorption and the energy required to increase the sorbent temperature (Qtemp). This model is significantly oversimplified, and to a significant extent underestimates the work requirements of real systems. Despite this systematic underestimation, relative comparisons within the sample set are useful to screen for material properties that are desirable for a TSA process.
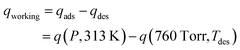 | (21) |
| Qregen = Qsorption + Qtemp | (22) |
| Qsorption = Qads − Qdes | (23) |
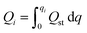 | (24) |
| Qtemp = mCpΔT = mCp(Tdes − 313 K) | (25) |
3 Results & discussion
3.1 Synthesis and investigation of activating process
The synthesis of N-containing foams resulting from the semi-carbonization of sucrose and melamine mixtures at 410 °C has been previously studied in detail.8 Details on the synthesis and material properties of these carbon foams with tunable N/C ratios can be found in the following references and in the Table S1.‡8,11 These specific weight percents of melamine were selected because the chemical activation method is dependent on precursor N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C
C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K ratios. Specifically, for SM20-Carb samples, porosity was generated mostly by reduction–intercalation mechanisms. Some redox reactions occurred with SM40-Carb precursors, but porosity was mostly attributed to chemical etching. For SM60-Carb, porosity was almost exclusively generated by etching processes. Finally, while chemical etching occurred with SM80-Carb, the observed porosity is attributed most significantly to molten salt templating.
K ratios. Specifically, for SM20-Carb samples, porosity was generated mostly by reduction–intercalation mechanisms. Some redox reactions occurred with SM40-Carb precursors, but porosity was mostly attributed to chemical etching. For SM60-Carb, porosity was almost exclusively generated by etching processes. Finally, while chemical etching occurred with SM80-Carb, the observed porosity is attributed most significantly to molten salt templating.
Although different activating salts were used in the present study, analogous gas species and solid-state products formed during activation imply that similar reaction schemes occurred regardless of activating salt. This section serves to summarize the chemical activation reactions and analyze the nuanced temperature-dependent changes in reactivity and gas evolution which occurred from changing the activating salt identity or the N-content of the precursor. The gaseous products were analyzed in situ with evolved gas analysis (EGA) during activation. The complete temperature-dependent spectra of each impregnated sample (with and without activating agents) and a detailed discussion of m/z signal assignments and data interpretation is available in the ESI Fig. S1–S6 and Discussion S1.‡ In addition to solid state by-products produced at the ultimate synthetic temperature of 800 °C, crystalline intermediates formed during the course of activation were identified with powder X-ray diffraction (XRD) ex situ by truncating the synthesis process at various temperatures (below 800 °C) (Fig. S7–S10‡).
The chemical reactions likely to occur are summarized in the equations below (eqn (26)–(33)). Eqn (26)–(30) describe the series of surface-mediated reactions occurring when the activating cation interacts with graphitic, heteroatom-free motifs, resulting in the carbothermal reduction of the cation “M” to an intercalated metallic species.23 Our previous work implicates this reductive exfoliation mechanism as critical for porosity development in low N-content precursors (i.e., SM20-Carb). However, as the N-content in the precursors increased, chemical etching mechanisms dominated the generation of porosity (eqn (31)–(33)).8,24
| M2CO3 + (–C) → –CO2M + –COM | (26) |
| –CO2M + (–C) → –CM + CO2 | (27) |
| –CO2M + (–C) → –COM + CO | (28) |
| –COM + (–C) → –CM + CO | (29) |
| –CM(s) → C(s) + M(g) | (30) |
| M2CO3 + 2(–CN) → 2MOCN + CO | (31) |
| M2CO3 + 2(–CN) → MOCN + MCN + CO2 | (32) |
| MOCN + (–C) → MCN + CO | (33) |
In general, identical gas species were observed in each of the carbonate systems, but the evolution profiles showed distinct trends in temperature-dependence. During activation, gas evolution corresponding to CO2 (Fig. 1) and CO (Fig. S5‡) was observed. Of all gas species observed, the CO2 evolution profiles were the most intense and varied as both the salt and precursor N-content changed.
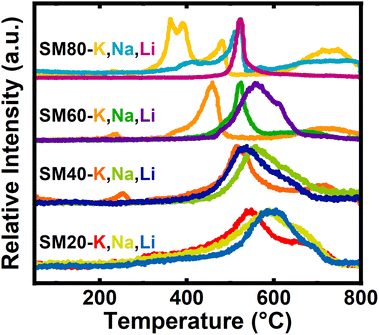 | ||
| Fig. 1 Normalized CO2 evolved gas analysis spectra for each of the impregnated samples, grouped by precursor. | ||
As the precursor N-content increased (from SM20 to SM80 derived samples), CO2 evolution shifted to lower temperatures and the features narrow. By increasing surface polarity, increased precursor N-content ostensibly strengthens interactions between the carbon surface and the alkali cation. As cations interact more strongly with the precursor surface, the cation–carbonate ionic bond is weakened, and carbonate decomposition (i.e., CO2 evolution) occurs at lower temperatures. Additionally, with a larger quantity of N-functionalities available for chemical attack, the probability of the physical processes represented by eqn (31)–(33) occurring increases, restricting the cations' participation in the surface-mediated pathways described in eqn (26)–(30). The broadness of the CO2 features in low N-containing samples originates from volatilization of oxygen functionalities native to the carbon.
Interestingly, in addition to sensitivity to precursor N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio, the reaction temperature was also dependent on cation identity. For example, the K+-activated series exhibited a shift in the most prominent peak from a temperature of ∼550 °C to ∼375 °C for K20 and K80, respectively. In comparison, the temperature of this gas evolution feature for the corresponding Na+- and Li+-activated samples both showed a less-pronounced shift, with peak temperatures ranging instead from ∼600 °C to ∼525 °C. Absolute Gibbs energy calculations support this observed reactivity. A large variety of systems were used to model both the N-rich carbon precursor and individual types of N-containing motifs, all of which suggested potassium would react at the lowest temperatures and lithium the greatest. Perhaps this reactivity, observed both experimentally and computationally, reflects hard–soft acid–base theory. In short, it may be expected that the individual nitrogen motifs may act as soft Lewis bases, while all cations are hard Lewis acids. Despite the hardness of all the alkali cations, potassium should be significantly softer when compared to sodium and especially lithium. Thus, as softer acids tend to react both faster and more strongly with soft bases, potassium would react at the lowest temperature and lithium at the highest.
C ratio, the reaction temperature was also dependent on cation identity. For example, the K+-activated series exhibited a shift in the most prominent peak from a temperature of ∼550 °C to ∼375 °C for K20 and K80, respectively. In comparison, the temperature of this gas evolution feature for the corresponding Na+- and Li+-activated samples both showed a less-pronounced shift, with peak temperatures ranging instead from ∼600 °C to ∼525 °C. Absolute Gibbs energy calculations support this observed reactivity. A large variety of systems were used to model both the N-rich carbon precursor and individual types of N-containing motifs, all of which suggested potassium would react at the lowest temperatures and lithium the greatest. Perhaps this reactivity, observed both experimentally and computationally, reflects hard–soft acid–base theory. In short, it may be expected that the individual nitrogen motifs may act as soft Lewis bases, while all cations are hard Lewis acids. Despite the hardness of all the alkali cations, potassium should be significantly softer when compared to sodium and especially lithium. Thus, as softer acids tend to react both faster and more strongly with soft bases, potassium would react at the lowest temperature and lithium at the highest.
Finally, for both the Na80 and K80 activated samples, multiple distinct features of CO2 evolution were observed between 300–775 °C. In contrast, Li80 shows a single defined feature at 575 °C. Due to changes in Lewis acidity, different cations may react more selectively with different surface N groups, which could alter the distributions of N functionalities in the activated materials. Because K+-activation yields many overlaying CO2 evolution features over a broad range of temperatures and Li+ only yields one sharp well-defined feature, it would be expected that K+ would react with different N-motifs in the least selective way, with Li+ being the most selective activator. DFT calculations agree with this trend, as the Gibbs energy of reactions between K2CO3 and the different analogs for N-motifs are nearly identical while those of Li2CO3 are significantly different (Fig. S12–S19‡). Interestingly, as all reactions expected to occur during activation maintain the same stoichiometry, this may suggest that changing the cation during activation may be a tool for keeping total nitrogen content in the activated material constant while varying the type of nitrogen. Indeed, this seems to be the case and we detail these properties later in the manuscript.
The activation of SM80-Carb using K2CO3 in the present work can be directly compared with our previous study on activation with potassium oxalate (K2C2O4), which employed the same carbon precursor and molar quantity of K+ (Fig. S20‡).8 During activation with K2C2O4, CO2 evolves a single sharp peak at ∼475 °C at a temperature about 100 °C higher than observed for K2CO3. Often, K2CO3 is implicated as the reactive intermediate formed during K2C2O4 activation.5 Under these assumptions, the oxalate anion seemingly acts as a “protecting group” that prevents activation until its eventual thermal decomposition into the more reactive carbonate at higher temperatures. Via such an oxalate-mediated mechanism, preventing reactivity at intermediate temperatures during synthesis results in the formation of kinetic, instead of thermodynamic, carbon products. In contrast, when carbonate is used, peaks corresponding to multiple discrete reactions, likely with different surface functionalities, results in the thermodynamic carbon product at high temperatures. Thus, oxalate activation and carbonate activation may provide a handle for material property control. For example, in SM80-Carb samples molten salt templating via KCN largely controls textural properties. However, the differing reaction pathways may once again alter the surface chemistry of a material but could feasibly maintain similar textural properties.
In summary, activation of N-rich precursors with alkali carbonates proceeds largely through the same reaction mechanisms, regardless of cation identity; however, the charge density and reactivity of each unique cation can impart significant differences to the synthesis of N-rich porous carbons. Precursor N-content plays the primary role in determining which method of porogenesis dominates during synthesis, but differences in a salt's reactivity results in unique temperature dependent activation.
3.2 Physicochemical property analysis
A variety of chemical and structural factors are known to affect the adsorption of CO2 in activated carbons. In this section, these various properties (Table 1) are analyzed with XPS, CHN analysis, XRD, and N2 porosimetry to better understand their role in facilitating selective CO2 capture.| Sample | C (at%) | N (at%) | O (at%) | N/Ca | d 002 (Å) | BET surface area (m2 g−1) | Pore volume <1 nm (cm3 g−1) | Pore volume 1–2 nm (cm3 g−1) | Pore volume 2–50 nm (cm3 g−1) | Porosity generation modeb |
|---|---|---|---|---|---|---|---|---|---|---|
| a Calculated molar quantities via CHN analysis. b Defines the primary porosity generation pathway (viz., intercalation exfoliation, chemical etching, or molten salt templating). | ||||||||||
| K20 | 92.9 | 2.65 | 4.47 | 0.017 | 4.44 | 4363 | 0.53 | 0.59 | 1.04 | Exfoliation |
| K40 | 84.1 | 12.4 | 3.45 | 0.197 | 3.80 | 3164 | 0.40 | 0.41 | 0.93 | Etching |
| K60 | 75.4 | 21.7 | 2.92 | 0.326 | 3.39 | 1234 | 0.15 | 0.18 | 0.49 | Etching |
| K80 | 73.0 | 23.5 | 3.46 | 0.446 | 3.32 | 579 | 0.09 | 0.07 | 0.24 | Templating |
| Na20 | 94.5 | 2.22 | 3.25 | 0.017 | 4.33 | 2242 | 0.39 | 0.18 | 0.48 | Exfoliation |
| Na40 | 81.1 | 14.4 | 4.52 | 0.180 | 3.55 | 1268 | 0.22 | 0.10 | 0.31 | Etching |
| Na60 | 74.2 | 22.7 | 3.03 | 0.352 | 3.40 | 1004 | 0.19 | 0.10 | 0.22 | Etching |
| Na80 | 72.7 | 23.5 | 3.83 | 0.429 | 3.32 | 655 | 0.10 | 0.07 | 0.32 | Templating |
| Li20 | 87.9 | 7.15 | 4.95 | 0.086 | 3.66 | 1574 | 0.30 | 0.12 | 0.33 | Exfoliation |
| Li40 | 84.0 | 10.3 | 5.74 | 0.137 | 3.51 | 1304 | 0.20 | 0.11 | 0.41 | Etching |
| Li60 | 76.6 | 20.4 | 3.04 | 0.317 | 3.44 | 896 | 0.14 | 0.10 | 0.29 | Etching |
| Li80 | 75.9 | 20.5 | 3.62 | 0.351 | 3.40 | 797 | 0.08 | 0.08 | 0.43 | Templating |
Quantification of the total N-content largely agreed between the XPS and CHN analysis, except for samples with small surface areas (Fig. S21‡). The surface N-content of the resulting materials increased with precursor N-content until N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratios of at least 0.8 in the precursor (viz., SM60- and SM80-Carb), when surface N-content instead plateaued towards a thermodynamic saturation limit (around 24 at% at 800 °C). On the other hand, instead of approaching saturation, the bulk N
C ratios of at least 0.8 in the precursor (viz., SM60- and SM80-Carb), when surface N-content instead plateaued towards a thermodynamic saturation limit (around 24 at% at 800 °C). On the other hand, instead of approaching saturation, the bulk N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio of the activated carbons determined from CHN analysis monotonically increased with precursor N-content. It is possible the difference in surface and bulk N-content arises from a stabilizing van der Waals interaction between sheets in the bulk that are lacking in the surface, thus hindering thermal degradation of bulk N-motifs. Additionally, while the final N-content was strongly dependent on the precursor N
C ratio of the activated carbons determined from CHN analysis monotonically increased with precursor N-content. It is possible the difference in surface and bulk N-content arises from a stabilizing van der Waals interaction between sheets in the bulk that are lacking in the surface, thus hindering thermal degradation of bulk N-motifs. Additionally, while the final N-content was strongly dependent on the precursor N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
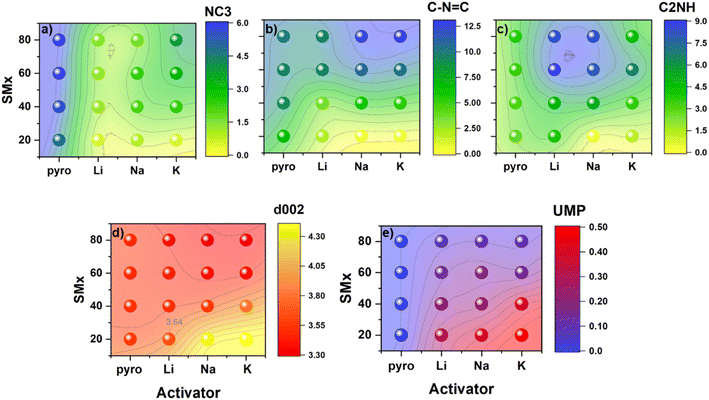
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio, the resulting N-content in the activated carbons was much less sensitive to the identity of the activating alkali cation. In all cases (except for Na80 and K80), alkali-activated carbons exhibited decreased surface N content relative to analogous control samples pyrolyzed in the absence of an activating agent (PyroX). Rather than modulating total N-content, the cation identity instead seemed to strongly influence the stratification of this N-species into different chemical environments on the surface. This fine-tuning of the N-rich surface chemistry likely arises from differing reactivity and/or stabilizing interactions between discrete types of N motifs (differing in basicity) and alkali cations of different sizes (i.e., charge densities/Lewis acidities). The influence of cation identity on the distribution of N-functionalities into different binding motifs is directly visualized in Fig. 2. Comparing the carbons activated with the various alkali carbonates against analogous control samples (i.e., pyrolyzed without activating agents) emphasizes how Li+-, Na+-, and K+-activation each uniquely affect the resulting surface chemistry.
C ratio, the resulting N-content in the activated carbons was much less sensitive to the identity of the activating alkali cation. In all cases (except for Na80 and K80), alkali-activated carbons exhibited decreased surface N content relative to analogous control samples pyrolyzed in the absence of an activating agent (PyroX). Rather than modulating total N-content, the cation identity instead seemed to strongly influence the stratification of this N-species into different chemical environments on the surface. This fine-tuning of the N-rich surface chemistry likely arises from differing reactivity and/or stabilizing interactions between discrete types of N motifs (differing in basicity) and alkali cations of different sizes (i.e., charge densities/Lewis acidities). The influence of cation identity on the distribution of N-functionalities into different binding motifs is directly visualized in Fig. 2. Comparing the carbons activated with the various alkali carbonates against analogous control samples (i.e., pyrolyzed without activating agents) emphasizes how Li+-, Na+-, and K+-activation each uniquely affect the resulting surface chemistry.
For example, all activated carbons show decreased tertiary NC3 content relative to the control, regardless of precursor N-content (Fig. 2a). Interestingly, the quantity of NC3 species removed from the carbons increased monotonically as the charge density of the alkali cation increased from K+ to Na+ to Li+. Similar chemical etching reactivity between Li+ and NC3 motifs has been demonstrated in the Li+-ion battery literature, where post-mortem analysis of N-doped carbon anodes revealed the selective removal of NC3 motifs.25 Though the exact mechanism of this process is currently under debate, the observation is in agreement with the trends established in the present study.26,27
At the same time, increased charge density of the activating cation was also associated with increased incorporation of C2NH species in the resulting carbons (Fig. 2c). In particular, samples derived from Li+-activation showed enhanced C2NH content compared to the pyrolyzed controls, regardless of precursor N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio. The same was true for Na+-activated samples, except for the carbon derived from the precursor with the smallest N
C ratio. The same was true for Na+-activated samples, except for the carbon derived from the precursor with the smallest N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio (viz., SM20-Carb). In contrast, only carbons derived from the most N-rich precursors exhibited enhanced C2NH content relative to the control when K2CO3 was employed for activation.
C ratio (viz., SM20-Carb). In contrast, only carbons derived from the most N-rich precursors exhibited enhanced C2NH content relative to the control when K2CO3 was employed for activation.
Though the concentration of NC3 and C2NH functionalities both exhibited clear dependence on the charge density of activating cations, C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C functionalities do not show such a straightforward trend with cation size. All samples derived from activation of precursors with N
C functionalities do not show such a straightforward trend with cation size. All samples derived from activation of precursors with N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio less than 0.6 (viz., SM20-Carb and SM40-Carb) exhibited smaller quantities of C–N
C ratio less than 0.6 (viz., SM20-Carb and SM40-Carb) exhibited smaller quantities of C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C motifs than the control samples (Fig. 2b). However, when the precursor N-content was increased, the C–N
C motifs than the control samples (Fig. 2b). However, when the precursor N-content was increased, the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C content observed after activation was enhanced relative to the control for both Na+ and K+-activated samples. These results point towards stabilizing interactions of these softer Lewis acids (viz., Na+ and K+) with C–N
C content observed after activation was enhanced relative to the control for both Na+ and K+-activated samples. These results point towards stabilizing interactions of these softer Lewis acids (viz., Na+ and K+) with C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C species that inhibit thermal decomposition and/or conversion to other surface N motifs.28 On the other hand, Li+-activated carbons exhibited C–N
C species that inhibit thermal decomposition and/or conversion to other surface N motifs.28 On the other hand, Li+-activated carbons exhibited C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C content very similar to the pyrolyzed control, suggesting weaker interactions between Li+ and C–N
C content very similar to the pyrolyzed control, suggesting weaker interactions between Li+ and C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C species.
C species.
Altogether, the choice of activating cation has small effects on total N-content but can significantly alter the product distribution of the resulting N species on the carbon surface. Li+-activation strongly diminishes NC3 while enhancing C2NH contents, with a smaller relative effect on C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C species. As a result, carbons derived from Li+-activation exhibit surfaces particularly rich in C2NH and poor in NC3 species. In addition, Na+-activation also decreases NC3 and bolsters C2NH species, albeit to a smaller extent than Li+. On the other hand, surface concentrations of C–N
C species. As a result, carbons derived from Li+-activation exhibit surfaces particularly rich in C2NH and poor in NC3 species. In addition, Na+-activation also decreases NC3 and bolsters C2NH species, albeit to a smaller extent than Li+. On the other hand, surface concentrations of C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C are larger after Na+-activation compared to the pyrolyzed control, ostensibly through stabilizing ionic interactions. Accordingly, Na+-activated carbons exhibit surfaces rich in both C2NH and C–N
C are larger after Na+-activation compared to the pyrolyzed control, ostensibly through stabilizing ionic interactions. Accordingly, Na+-activated carbons exhibit surfaces rich in both C2NH and C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C species. Finally, K+-activation impacts the resulting quantity of NC3 and C2NH motifs less than Li+- or Na+-activation. However, as in the case of Na+-activation, the C–N
C species. Finally, K+-activation impacts the resulting quantity of NC3 and C2NH motifs less than Li+- or Na+-activation. However, as in the case of Na+-activation, the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C content in carbons derived from N-rich precursors is enhanced after K+-activation. Consequently, K+-activated carbons display surfaces rich primarily in these C–N
C content in carbons derived from N-rich precursors is enhanced after K+-activation. Consequently, K+-activated carbons display surfaces rich primarily in these C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C species. In this way, the charge density of cations employed during chemical activation templates unique surface chemistries into the resulting porous carbons.
C species. In this way, the charge density of cations employed during chemical activation templates unique surface chemistries into the resulting porous carbons.
In addition to fine-tuning the N-rich surface chemistry, the identity of alkali cation also strongly affected the resulting porosity of the activated carbons as quantified by cryogenic N2 porosimetry. The N2 isotherms acquired at 77 K displayed both type I and type IV characteristics, consistent with the formation of mixed micro- and mesoporous materials (Fig. S26–S28‡). Pore size distributions and surface areas obtained via BET and QSDFT analysis of these isotherms are summarized in Table 1 and Fig. 2d and 3. It should be noted that because this technique relies on N2 gas molecules as a probe, porosity smaller than N2 would be underestimated by this technique. In general, carbons derived from N-poor precursors and activated with larger, less charge-dense cations exhibited increased porosity. For example, of all the studied samples, K20 exhibited the largest BET surface area (∼4400 m2 g−1) and volume of micropores (∼1.1 cm3 g−1). In all samples, seemingly three groups of pores formed: small micropores with diameters <1 nm, large micropores about 1.5 nm in diameter, and small mesopores with diameters of approximately 3 nm (Fig. 3).
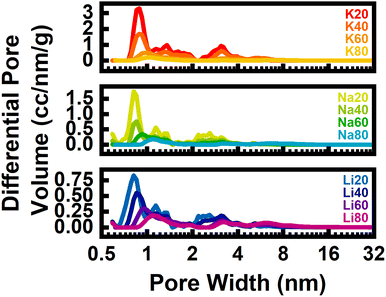 | ||
| Fig. 3 Pore size distributions for each sample derived from N2 isotherms at 77 K, grouped by activating cation. | ||
Regardless of the activating agent, increasing the precursor N-content resulted in a shift of the small micropores to slightly larger micropores and mesopores (Fig. 3). This result, in line with our previous work focused on K2C2O4-activation, suggests that the precursor N-content – and not the identity of the activating cation – predominantly determined the mechanism of porogenesis (and the resulting types of pores that formed during synthesis). For precursors with low N-content, porosity is developed mainly through intercalative-exfoliation which results in an abundance of small micropores. As the N-content in precursors increases, chemical etching and molten salt templating mechanisms play dominant roles in porosity formation, leading to the creation of semi-crystalline, turbostratic carbons with an overall smaller quantity of larger micro- and mesopores.
However, as apparent by comparing carbons derived from activation of identical precursors with different alkali cations, cation identity did exhibit a subtle effect on the pore characteristics. For activation of SM20-Carb where porosity was induced mainly through the intercalative-exfoliation mechanism, the diameter of small micropores increased with cation size. For example, the pore size of K20 (0.889 nm) was slightly larger than the pore size of Li20 (0.818 nm) (Fig. S31‡). Previous studies focused on activation of N-poor precursors with various alkali cations revealed similar results; pore size increased with cation radius, likely because larger species intercalate and exfoliate carbon sheets more than smaller intercalants.9,10 Additionally, the total pore volume was a strong function of the cation, with bulkier K+-species inducing nearly triple the cumulative microporosity of the smaller Li+-species (1.12 vs. 0.42 cm3 g−1).
As the N-content in precursors increased (viz., SM40- and SM60-Carb), this intercalative-exfoliation mechanism waned and the chemical etching reactions began to dominate. For these samples, the magnitude and types of porosities were much less dependent on cation identity (Fig. 3 and S31‡). At a given precursor N![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C ratio, the cumulative pore volume distributions were extremely similar for samples derived from chemical etching when compared to those from intercalative-exfoliation (Fig. S30‡). These similarities are particularly noticeable for samples activated from SM60-Carb. The porosity of Na60 and Li60 were nearly identical, but K60 exhibited a slightly larger volume of small micropores, perhaps suggesting enhanced reactivity of K+-species towards intercalative-exfoliation even in the presence of significant N-content. Despite these rather subtle differences, the geometry of void spaces (i.e., pore size and volume) generated from formation of chemical adducts seems largely insensitive to alkali cation size/charge density.
C ratio, the cumulative pore volume distributions were extremely similar for samples derived from chemical etching when compared to those from intercalative-exfoliation (Fig. S30‡). These similarities are particularly noticeable for samples activated from SM60-Carb. The porosity of Na60 and Li60 were nearly identical, but K60 exhibited a slightly larger volume of small micropores, perhaps suggesting enhanced reactivity of K+-species towards intercalative-exfoliation even in the presence of significant N-content. Despite these rather subtle differences, the geometry of void spaces (i.e., pore size and volume) generated from formation of chemical adducts seems largely insensitive to alkali cation size/charge density.
Further, when precursors were rich in N-content (viz., SM80-Carb), molten salt templating dominated the activation. Interestingly, in this case the volume of micropores was very similar, ranging between 0.14–0.18 cm3 g−1, respectively. However, the mesopore volume steadily increased with charge density from 0.24 to 0.43 cm3 g−1 from K+ to Li+. Moderately sized mesopores between 5 and 8 nm in diameter comprised a large proportion of total porosity in SM80-Carb activated samples when compared to any other samples made from a fixed precursor composition. The size of mesopores in carbons derived from Li+-activation and templating were more tightly distributed around a smaller value (6.16 nm) than either those made from Na+ (6.38 nm) or K+ (6.60 nm). As a result, changing charge density and/or volume of the molten salt template tailors the mesoporosity and distribution of N-content in the resulting carbons without significantly altering total nitrogen content or microporosity.
The strong effects of precursor N-content on the generated porosity was also observed in the (semi)-crystallinity of the resulting carbons, summarized as the d-spacing and average crystalline domain size from Scherrer analysis in Tables 1 and S2,‡ and Fig. 2d. In agreement with our previous study, we found a strong correlation between the final N-content and the d-spacing of the resulting carbon, ostensibly through enhanced van der Waals interactions between stacked carbon domains (Fig. S33‡). When intercalative-exfoliation mechanisms occurred, large and varied d-spacings from 3.66 to 4.44 Å were induced in Li20 and K20, respectively. The d-spacing increased with cation radius, likely due to enhanced exfoliation from the intercalation of a bulky cation as observed in cumulative pore size distributions (Table S2‡). In contrast, samples that exclusively underwent chemical etching processes displayed more similar d-spacings, deviating at most by 0.6 Å. During molten salt templating, semi-crystallinity of the carbons was enhanced during synthesis relative to pyrolyzed controls, with smaller d-spacings and larger crystallite domain sizes observed in the salt-treated materials. In contrast to the materials activated via intercalative-exfoliation, the Li+-activated carbon exhibited a notably larger d-spacing than the K+- or Na+-activated carbons after molten salt templating, likely due to the slight disparity in final N-content in the resulting carbons. While the mechanism of porogenesis in carbons derived from molten salt synthesis are poorly understood, charge density of the molten cation and/or effective volumetric concentration of the carbon precursors in the melt are critical components for consideration. We speculate that, upon cooling, the templating MCN crystallites tended to be smaller and more uniform when the cation charge density was higher and acted as hard templates which the carbon formed around. Smaller templating crystals resulted in carbons that had a larger volume of smaller mesopores, greater surface area, and larger d-spacing.
3.3 CO2 adsorption and thermodynamic analysis
For the separation of CO2 from flue gas, an adsorbent must exhibit both high capacity for CO2 and sufficient selectivity for CO2/N2 at a given concentration, temperature, and pressure. In this section, CO2 isotherms at variable temperatures (10–40 °C) are analyzed to quantify the thermodynamics of CO2 adsorption for each sample. Each set of CO2 isotherms (Fig. S34–S36‡) was fit to a temperature-dependent dual-site Langmuir model, and the thermodynamic parameters of adsorption were determined as a function of coverage or loading as described in Section 2.3. The raw CO2 data was with well-fit by the dual-site model for all samples (Table S3‡R2 and chi values). K20 was better fit by a single-site Langmuir model. As a result, thermodynamic calculations of the K20 sample are less reliable especially in the lower pressure region as visualized in Fig. 4d. The raw data and model fits for the CO2 isotherms at 30 °C are shown in Fig. 4a–c.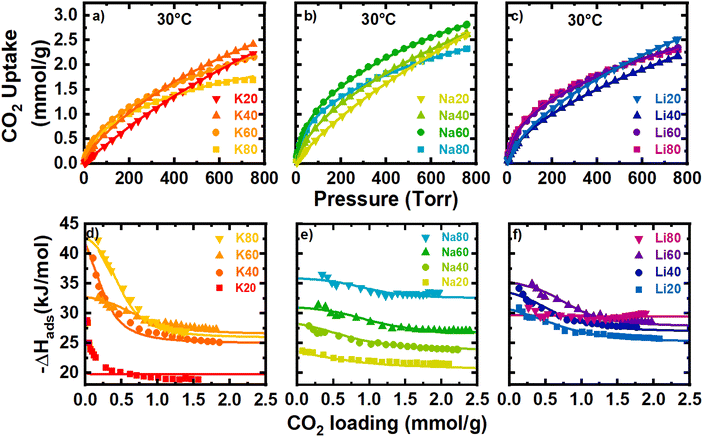 | ||
| Fig. 4 Panels (a)–(c) show CO2 isotherms at 30 °C for K, Na, and Li activated materials respectively. Panels (d)–(f) show the isosteric heats of adsorption (points) and the calculated −ΔHads. | ||
Generally, carbons with more N-rich surfaces exhibited larger uptakes of CO2 at low pressures (<200 Torr), resulting in isotherms with more curvature as the N-content increased. The theoretical saturation capacities of the strong site (qA,sat) and the weak site (qB,sat) determined from the DSL fits capture this general trend. As N-content increased, qA,sat tended to increase strongly while qB,sat tended to decrease significantly. Thus, the incorporation of surface N-content tends to increase uptake at low-pressure at the expense of some high-pressure uptake. As the activator was varied, Na+-activated samples tended to exhibit the largest qA,sat and qB,sat, and interestingly, the largest qA,sat of the sample set was found for Na60. This is surprising because Na60 has less N-content than both K80 and Na80 yet has more than double the qA site capacity of K80, and a qA,sat only 3.5% larger than Na80. Furthermore, microporosity was negatively correlated with the observed low-pressure CO2 uptake (Fig. S37‡). Generally, large volumes of small pores and N-dopants are correlated with increased uptake for CO2. While Na60 does have a large N-content, its exceptional capacity at any pressure remains enigmatic; thus, we propose that the porosity essential for low-pressure uptake of CO2 may be smaller than that probed by N2 porosimetry. As such, the propensity for Na+-activated samples, especially Na60, to uptake more CO2 than other activated samples at low pressures is likely a cumulative effect of relatively large amount of N-content and a population of pores too small to be probed by N2 porosimetry (but still large enough to be accessible to CO2).
Variable temperature CO2 isotherms (10–40 °C) were analyzed to quantify the thermodynamics of adsorption. The isosteric heats of adsorption (Qst), which gauges adsorption affinity for CO2 as a function of adsorbent coverage, were determined numerically from raw analysis data and overlaid with the model-derived −ΔHads for all samples (Fig. 4d–f). In general, agreement was excellent between the analytical Qst data and the −ΔHads calculated from the dual site Langmuir fit parameters despite significant uncertainty in −ΔHads (Fig. 4d–f and S38–S49‡). Increases in the heats of adsorption, especially at large CO2 loadings, were loosely correlated with the absolute N-content. This trend is most easily visualized with the Na+-activated samples, which shows a clear upward shift in the heat of adsorption at all loadings as the N-content increased from 2–24 at%.
However, clear outliers to this general trend of increasing heat of adsorption with total N-content were observed, especially at near-zero surface coverage. For example, K40 with 12 at% N displayed an exceptionally large initial heat of adsorption (∼−42 kJ mol−1) while K60 (22 at% N) and Li80 (21 at% N) exhibited unexpectedly low initial heats of adsorption (∼−32.5 and −31 kJ mol−1, respectively). Besides N-content, pore geometry also influences a porous material's affinity for CO2 adsorption. For example, particularly small nanopores can exhibit synergistic increases to adsorption affinity as the adsorption potentials of two opposing pore walls overlap.29,30 In general, decreases in the mode pore size measured by N2 porosimetry were found to have a slight correlation with increased heats of adsorption at the weak adsorption site (qB). This effect is most clearly observed when N-content was low (i.e., SM20 samples). Here, the mode pore size decreased in the order K20 > Na20 > Li20, and as the pore size decreased the CO2 adsorption affinity increased. At the strong site, any correlations between micropore size and the heats of adsorption were limited, likely because these high-affinity pores are expected to be smaller than can be probed by N2 and complicated by changes in surface chemistry. To aid in deconvoluting the effects of surface chemistry and pore geometry on the observed adsorption affinity, analyzing the differential −ΔSads helps to gain further insight into the fundamentals of CO2 adsorption. Previously, a linear exchange relation between −ΔHads and −ΔSads has been found that is rationalized by nanoconfinement effects.22,31–33 In addition to boosting −ΔHads due to net increases in adsorption potential, nanopores also induce confinement that restricts the translational and rotational motion of adsorbed gas molecules. This process incurs an energetic penalty which is directly reflected in the magnitude of −ΔSads. As the pore dimension decreases, more configurational degrees of freedom are lost, and the magnitude of −ΔSads increases.34,35
For the samples analyzed here, a large majority of the observed entropy loss likely occurs from this restriction in motion of adsorbed CO2. This contrasts with other adsorbents, especially amine-appended chemisorbents, where CO2 adsorption can cause structural changes and incur entropic penalties of the total system.33,36 Because the physisorbents under present consideration are rigid and avoid significant structural or chemical change upon adsorption, the −ΔSads serves as a useful qualitative probe for the extent of confinement of the adsorbed phase and, as a result, the nanopore dimension of the adsorption site. This is particularly important for the study of CO2 adsorbents. As previously stated, due to the smaller relative kinetic diameter of CO2 than either N2 or Ar (which are routinely used to quantify porosity), the smallest CO2-accessible porosity in these samples are poorly defined by traditional porosimetry methods. In this context, the magnitude of −ΔSads at a given loading of CO2 can aid in demystifying these undercounted pores.
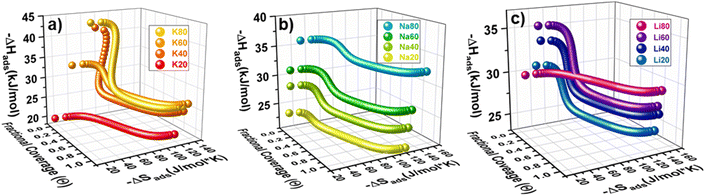
Holistically, adsorption is an interplay between enthalpic and temperature dependent entropic contributions. At the relevant temperatures for this study (∼30 °C), any relative change in −ΔHads is approximately three times as significant as a change in −ΔSads. However, during adsorption there are clear regions when −ΔSads interactions dominate contributions to −ΔGads, easily visualized in the 3D plots shown above in Fig. 5. For example, K20 has a constant −ΔHads of adsorption, and so all changes in −ΔGads are derived from entropic contributions. For this sample, entropy is a monotonically increasing function with respect to coverage (Fig. 5a and S38‡) and −ΔSads increases quickly at very low coverages. This significant increase in −ΔSads relative to −ΔHads at the smallest coverages is consistent across all samples. The rapid rise in entropy at these low coverages likely results from crowding at the highest affinity site that further hinders rotational and translational degrees of freedom and dominates effects to ΔGads. In contrast to the entropy curve for K20, samples modeled with the DSL parameters frequently showed a local maximum at moderate coverages (Fig. S38–S49‡). This feature may develop as the magnitude of −ΔGads becomes comparable between two sites with dissimilar −ΔHads, for instance as a result of entropic penalties from crowding at a strong site. In this case, CO2 may begin to occupy a weak site before saturation of the strong site, effectively partitioning between the sites. Such site intermixing and the associated additive thermodynamics would result in the local maximum observed in some plots. Significantly, this observation suggests that stratifying the site-specific −ΔGads could enable isolation of an adsorbate in a specific pore by avoiding partitioning between two dissimilar adsorption sites, which could have benefits for size-sieving separations or selective catalysis. This could be achieved by increasing the affinity and capacity of the strong site, or by decreasing the affinity and capacity of the weak site.
In addition to analyzing how thermodynamics vary as a function of coverage for an individual sample, comparisons of the thermodynamics of CO2 adsorption at a fixed coverage for the sample set as a whole are also useful in identifying structure–function relations. As with −ΔHads, increasing the N-content in the activated materials was generally associated with increased −ΔSads. In fact, when −ΔSads and −ΔHads are plotted at a constant coverage, a linear exchange relationship is observed (Fig. 6a). This phenomenon has previously been observed for many adsorption systems and indicates that when adsorption to a site is strong, the degrees of freedom of the adsorbate are more significantly restricted.33,36,37 When comparing samples that have fixed confinement (similar −ΔSads) the addition of N-content increases the magnitude of −ΔHads. These observations suggest that, while confinement in nanopores plays a dominant role in determining the local −ΔHads (which varies nearly 20 kJ mol−1 with −ΔSads), N-content exerts a fine-tuning secondary effect on the magnitude of −ΔHads (here, up to ∼5 kJ mol−1).
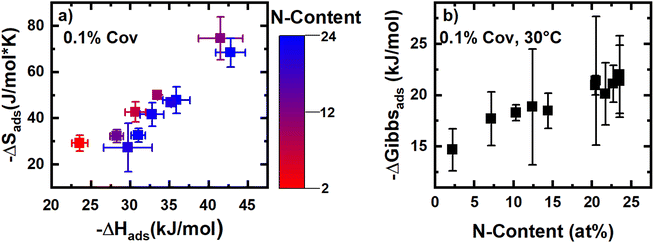 | ||
| Fig. 6 Panel (a) shows the exchange relationship between the enthalpy and entropy of adsorption, while panel (b) shows the relationship between N-content and the Gibbs energy of adsorption at 30 °C. | ||
Nevertheless, at a given fixed coverage of CO2 and temperature of 303 K, N-content was strongly correlated with the Gibbs energy of adsorption (Fig. 6b). Interestingly, the Gibbs energy increases most significantly with the C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH motifs and is poorly correlated with NC3 content (Fig. S62 and S67‡). Computational studies have suggested that C–N
C and C2NH motifs and is poorly correlated with NC3 content (Fig. S62 and S67‡). Computational studies have suggested that C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C functionalities are beneficial for CO2 adsorption, as the lone electron pair can act as a Lewis base; pyrrolic motifs, which resemble secondary amines, are thought to interact with CO2 through hydrogen-bonding.38–40 Regardless, this trend in free energy at low coverage suggests that the entropic penalties associated with stronger adsorption (i.e., more confinement) is outweighed by a proportionally larger increase in enthalpy due to surface chemistry. However, deviations can occur if the volume/capacity of the site is small, causing the entropy to quickly rise from local crowding effects. As such, in optimizing a carbon for CO2 adsorption, incorporation of N-content, especially C–N
C functionalities are beneficial for CO2 adsorption, as the lone electron pair can act as a Lewis base; pyrrolic motifs, which resemble secondary amines, are thought to interact with CO2 through hydrogen-bonding.38–40 Regardless, this trend in free energy at low coverage suggests that the entropic penalties associated with stronger adsorption (i.e., more confinement) is outweighed by a proportionally larger increase in enthalpy due to surface chemistry. However, deviations can occur if the volume/capacity of the site is small, causing the entropy to quickly rise from local crowding effects. As such, in optimizing a carbon for CO2 adsorption, incorporation of N-content, especially C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH motifs, while preserving large volumes of small pores is critical to maximizing the capacity achieved at the necessary gas feed conditions.
C and C2NH motifs, while preserving large volumes of small pores is critical to maximizing the capacity achieved at the necessary gas feed conditions.
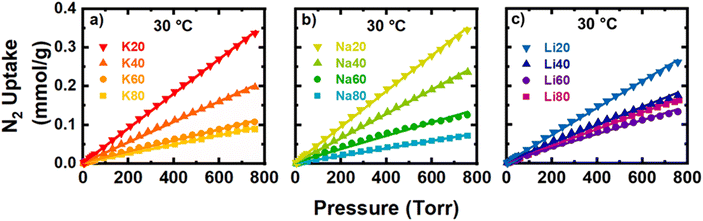
3.4 N2 adsorption and selectivity
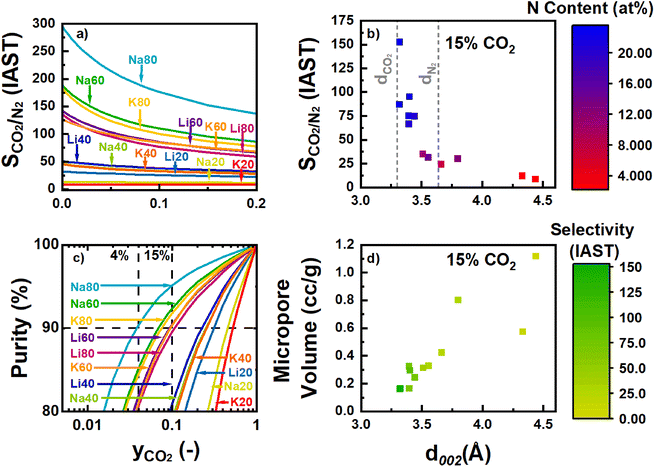
Poor selectivity for CO2 over N2 and resultingly low purity of the adsorbed phase are some of the most significant hurdles for the implementation of porous carbons in adsorptive CCS processes. Under industrially relevant pressures and temperatures for post-combustion flue gas separations (1 bar, 4–15% CO2, and 30 °C), an ideal adsorbent would exhibit large uptakes for CO2 and negligible uptakes for N2, the primary component of flue gas. Accordingly, in this section the adsorption of N2 at 30 °C is analyzed to determine the CO2/N2 adsorption selectivity via the IAST. Interestingly, by changing synthetic parameters and, as a result, carbon adsorbent material properties, the magnitude of N2 adsorption was much more tunable as compared to CO2 adsorption, especially at the partial pressures relevant for CCS (0.04–0.15 bar and 0.85–0.96 bar for CO2 and N2, respectively) (Fig. 4 and 7). For example, the observed CO2 uptake at 0.15 bar and 30 °C increased nearly threefold from ∼0.4 to ∼1.2 mmol g−1 between the samples with smallest and the largest CO2 uptakes (K20 vs. Na60). In contrast, the N2 uptake at 0.85 bar and 30 °C spanned a range of 0.06 and 0.31 mmol g−1, slightly more than five times the uptake, between the samples with the smallest (Na80) and the largest (Na20) uptakes of N2.As visible in Fig. 7, the raw isotherm data was fit well with a linear model, and the Henry's constant (kH,N2) was determined from the slope (eqn (7)). In general, the N-content of the precursor played a much stronger role than the identity of the activating cation in tuning the resulting adsorption of molecular N2. The kH,N2 decreased significantly as N-content in the precursor increased. Further, the dominant physical property of the carbons associated with these trends in N2 adsorption is the ultramicroporosity, which we showed previously was dependent on both precursor N-content and cation identity (Fig. 2d). However, the final N-content of the resulting carbons also seems to have a parasitic effect on the observed N2 uptake. Interestingly, the same N-containing motifs associated with increased Gibbs energy of CO2 adsorption are generally associated with decreased kH,N2. At a given volume of ultramicropores accessible to N2, increases in the combined C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH content were associated with decreases in kH,N2 (Fig. S63 and S69‡). Future work will focus on further elucidating the effect of different N-motifs on the thermodynamics of N2 adsorption by N-rich carbons. The selectivity for each sample as calculated via the IAST as described in Section 2.4 is plotted in Fig. 8a. As discussed, increases in N-content, specifically C–N
C and C2NH content were associated with decreases in kH,N2 (Fig. S63 and S69‡). Future work will focus on further elucidating the effect of different N-motifs on the thermodynamics of N2 adsorption by N-rich carbons. The selectivity for each sample as calculated via the IAST as described in Section 2.4 is plotted in Fig. 8a. As discussed, increases in N-content, specifically C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH functionalities, were associated with increases and decreases in the uptakes of CO2 and N2, respectively. As a net result, the predicted CO2/N2 selectivity was a strong function of total N-content in the carbons (Fig. S63 and S70‡). Besides altering the surface chemistry of the adsorbent, varying N-content in the activated materials also has structural effects on the carbon during synthesis, as described in Section 3.3. In short, the retention of more N can decrease the interlayer spacing between different turbostratic carbon nanosheets, likely as a result of increasing the van der Waals interactions between the different layers as more polar species are incorporated. As shown in our previous work, selectivity was found to increase as this interlayer space decreased (Fig. 8b).22 A rapid rise in selectivity is observed when the d-spacing decreases below the kinetic diameter of N2. As the kinetic diameter of CO2 (3.30 Å) is smaller than the kinetic diameter of N2 (3.64 Å), the selectivity improvements likely arise due to a “size-sieving” mechanism where pores are simultaneously large enough for accessibility by CO2 but small enough for exclusion of N2 gas (Fig. 8b). This size-selective, intersheet site may be the same previously noted CO2-accessible porosity that is uncharacterized by N2 porosimetry. The volume of the site accessible to CO2 adsorption for samples like Na80 and K80 may be smaller than expected because the interlayer spacing approaches the same kinetic diameter as CO2, perhaps excluding it. However, as the d-spacing decreased, the total micropore volume also decreased, further limiting sites where competitive adsorption between N2 and CO2 could occur (Fig. 8d).
C and C2NH functionalities, were associated with increases and decreases in the uptakes of CO2 and N2, respectively. As a net result, the predicted CO2/N2 selectivity was a strong function of total N-content in the carbons (Fig. S63 and S70‡). Besides altering the surface chemistry of the adsorbent, varying N-content in the activated materials also has structural effects on the carbon during synthesis, as described in Section 3.3. In short, the retention of more N can decrease the interlayer spacing between different turbostratic carbon nanosheets, likely as a result of increasing the van der Waals interactions between the different layers as more polar species are incorporated. As shown in our previous work, selectivity was found to increase as this interlayer space decreased (Fig. 8b).22 A rapid rise in selectivity is observed when the d-spacing decreases below the kinetic diameter of N2. As the kinetic diameter of CO2 (3.30 Å) is smaller than the kinetic diameter of N2 (3.64 Å), the selectivity improvements likely arise due to a “size-sieving” mechanism where pores are simultaneously large enough for accessibility by CO2 but small enough for exclusion of N2 gas (Fig. 8b). This size-selective, intersheet site may be the same previously noted CO2-accessible porosity that is uncharacterized by N2 porosimetry. The volume of the site accessible to CO2 adsorption for samples like Na80 and K80 may be smaller than expected because the interlayer spacing approaches the same kinetic diameter as CO2, perhaps excluding it. However, as the d-spacing decreased, the total micropore volume also decreased, further limiting sites where competitive adsorption between N2 and CO2 could occur (Fig. 8d).
For the samples analyzed here, the materials derived from activation of SM80-Carb were the most selective due to their increased C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH contents, small surface area and porosity, and narrow d-spacing. Among these most selective samples, changing the activating cation caused a near two-fold change in the selectivity (86 vs. 153 at 15% CO2 for K+vs. Na+) even though changes in the resulting material properties (as quantified by XPS, XRD, and N2 porosimetry) were seemingly less significant. Similarly, while samples activated from SM60- and SM80-Carb achieved predicted adsorbed phase purities sufficient for viability in post-combustion capture, the minimum required concentration of CO2 varied greatly depending on which cation was used for activation (Fig. 9c). For example, Na80 achieved 90% purity at gas-phase concentrations of less than 4% CO2, nearly half of the concentration required for similar adsorbed phase purity on K80. In summary, increasing the total N-content of a carbon is critical for achieving the necessary purity requirements. In addition, significant further enhancements can be made by altering the cation employed during activation.
C and C2NH contents, small surface area and porosity, and narrow d-spacing. Among these most selective samples, changing the activating cation caused a near two-fold change in the selectivity (86 vs. 153 at 15% CO2 for K+vs. Na+) even though changes in the resulting material properties (as quantified by XPS, XRD, and N2 porosimetry) were seemingly less significant. Similarly, while samples activated from SM60- and SM80-Carb achieved predicted adsorbed phase purities sufficient for viability in post-combustion capture, the minimum required concentration of CO2 varied greatly depending on which cation was used for activation (Fig. 9c). For example, Na80 achieved 90% purity at gas-phase concentrations of less than 4% CO2, nearly half of the concentration required for similar adsorbed phase purity on K80. In summary, increasing the total N-content of a carbon is critical for achieving the necessary purity requirements. In addition, significant further enhancements can be made by altering the cation employed during activation.
3.5 TSA modelling
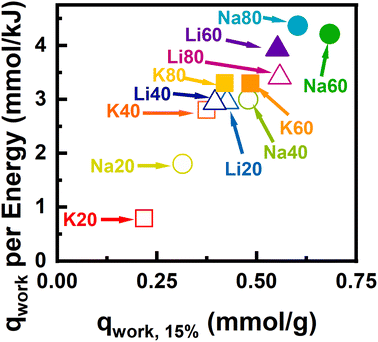
In addition to sufficient adsorption selectivity for capture of CO2 from N2-rich streams, enhanced performance in a swing adsorption process also requires large working capacity and low regeneration energy requirements per cycle. To better understand what properties may influence process efficiency and regeneration energy requirements, we used open-source code available in the ESI‡ to model a simplified TSA process. This process performance estimation method was described previously and is a modification of the work done by Sculley et al.21,41 In brief, the process regeneration energy is calculated from the heat required to raise the sorbent sample temperature and overcome the endothermic energy barrier for desorption. This is a highly idealized calculation and likely contains significant systematic error. For example, energy integration and ‘heat to work’ conversion efficiencies are not considered. While the relative importance of sensible vs. desorption heat may be inaccurate, insight into material properties of interest can be gleaned from the relative energy cost between the different adsorbents.In Fig. 9 the optimal working capacity is plotted against the regeneration energy. Samples which achieved adsorbed phase purities to be viable for CCS are shown as solid points, while samples with insufficient selectivity are shown as hollow points. In this representation, working capacity is maximized and parasitic energy cost is minimized in the upper right corner of the plot. The materials that fall within in this space were derived from SM60- and SM80-Carb and were activated with the smaller cations Li+ and Na+, while samples derived from SM20- and SM40-Carb fell in the bottom left corner. The best-performing materials exhibited large amounts of N-content rich in C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or C2NH motifs; large high-affinity saturation capacities for CO2; and large free energy gains upon CO2 adsorption in the Henry's law regime. Samples which performed poorly had low N-content and CO2 capacities. In general, at a fixed desorption temperature of 425 K (∼150 °C) and feed of 15% CO2, increasing the N-content required slightly higher regeneration energies from ∼115–132 J g−1 for Na20 and Na80, respectively. This increase in regeneration energy is related to enhanced heats of adsorption for the N-rich carbons. In contrast, under the same conditions, the working capacity increased from ∼0.15–0.58 mmol g−1 for Na20 and Na80, respectively. Therefore, the energetic penalty associated with stronger adsorption – ∼13% increase – is significantly outweighed by the increase in achievable working capacity – ∼285% increase.
C or C2NH motifs; large high-affinity saturation capacities for CO2; and large free energy gains upon CO2 adsorption in the Henry's law regime. Samples which performed poorly had low N-content and CO2 capacities. In general, at a fixed desorption temperature of 425 K (∼150 °C) and feed of 15% CO2, increasing the N-content required slightly higher regeneration energies from ∼115–132 J g−1 for Na20 and Na80, respectively. This increase in regeneration energy is related to enhanced heats of adsorption for the N-rich carbons. In contrast, under the same conditions, the working capacity increased from ∼0.15–0.58 mmol g−1 for Na20 and Na80, respectively. Therefore, the energetic penalty associated with stronger adsorption – ∼13% increase – is significantly outweighed by the increase in achievable working capacity – ∼285% increase.
While these observations explain the general trends in the regeneration energy and working capacity plots (Fig. S71 and S72‡) significant changes can also occur for samples activated from different cations but a fixed N-content. For the samples derived from SM80-Carb, and assuming regeneration at 425 K and a theoretical feed stream of 15% CO2, the regeneration energies ranged from 124–132 J g−1 (∼6% increase) while the working capacities range from 0.39–0.58 mmol g−1 (∼50% increase) for K80 and Na80 respectively, simply by changing the activating cation. Comparisons under optimal regeneration conditions revealed that the Na60 and Na80 activated materials performed best, followed by Li60. Interestingly, Li20 with approximately a third of the N-content of K60 or K80 performed only slightly worse under optimized conditions. This indicates that total N-content, while critical for selective CO2 capture, is not always a good predictor for energy-efficient CO2 adsorption in a cyclic process. Instead, ideal process performance arises from the cumulative impact of several physicochemical properties: the amount and chemical environment of N-content, the pore geometry and volume, and the (semi)-crystalline structure. Of the samples studied here, samples activated with Na+ and from precursor compositions of high nitrogen content (viz., SM60 & SM80-Carb) achieved both necessary selectivities and the most efficient process performances.
4 Conclusions
In this work, porous carbons were produced from precursors with tunable N-content and activated from different alkali carbonate salts (Li, Na, and K). In agreement with our previous work, increasing the total precursor N-content in these carbons was the single most important factor for improving selectivity for CO2 over N2. However, this work highlights that, even for samples with the highest precursor N-content (i.e., SM80-Carb), simply changing the activator from Li2CO3 to Na2CO3 enabled a 129% increase in CO2/N2 selectivity for a feed of 15% CO2 at 1 bar. By varying both the precursor N-content and the activating agent, the activated carbons in this work had highly varied physicochemical properties with surface N-contents ranging between 2–24 at% and microporosities ranging between 0.16–1.12 cm3 g−1. The impact of the cation identity on the synthesis process and resulting physicochemical properties of activated materials was thoroughly investigated and was found to have a nuanced effect that was dependent on the N-content of the precursor.In general, the total N-content in the resulting carbons was a function primarily of N-content in the precursor and was less dependent on cation identity. However, increasing the charge density of the cation increased the amount of C2NH while decreasing the amount of NC3 surface functionalities. When porosity was produced via intercalative-exfoliation pathways, larger cations yielded larger pores with more N2-accessible cumulative porosity. In contrast, during activation via chemical etching (i.e., for precursors with larger N-content), the N2-accessible porosity deviated very little between different activating cations. However, significant differences in the CO2 capacity and adsorption thermodynamics suggest that CO2-accessible porosity exists that is inaccessible to N2 probe molecules. In agreement with our previous work, this size-selective porosity is seemingly associated with the carbon intersheet distance, as a dramatic increase in CO2/N2 selectivity is achieved when the d-spacing decreases below the kinetic diameter of N2 (3.64 Å). Quantification of CO2 adsorption thermodynamics helped to elucidate that increased N-content (especially C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C2NH motifs) induces additional enthalpic contributions via favorable adsorbent–adsorbate interactions. This effectively causes deviation from a linear exchange (i.e., compensation) relationship between the enthalpy and the entropy of adsorption, which stems from synergy in nanoconfinement. Thus, at temperatures near 30 °C, the Gibbs energy for adsorption (and low-pressure CO2 uptake) was generally well-correlated with increases in N-content. These same types of N-motifs were implicated in inhibiting N2 adsorption, perhaps indirectly by reducing the number of sites available for competitive adsorption. The introduction of N-content is correlated to decreases in the N2-accessible micro- and mesoporosity and narrowed d-spacing to sizes exclusive to CO2. As such, N-content was found to be critical for selective adsorption.
C and C2NH motifs) induces additional enthalpic contributions via favorable adsorbent–adsorbate interactions. This effectively causes deviation from a linear exchange (i.e., compensation) relationship between the enthalpy and the entropy of adsorption, which stems from synergy in nanoconfinement. Thus, at temperatures near 30 °C, the Gibbs energy for adsorption (and low-pressure CO2 uptake) was generally well-correlated with increases in N-content. These same types of N-motifs were implicated in inhibiting N2 adsorption, perhaps indirectly by reducing the number of sites available for competitive adsorption. The introduction of N-content is correlated to decreases in the N2-accessible micro- and mesoporosity and narrowed d-spacing to sizes exclusive to CO2. As such, N-content was found to be critical for selective adsorption.
Despite this, large amounts N-content was not always associated with the best process efficiency under TSA modeling. In this work, sufficiently high selectivity and optimal process performance were both achieved when N-content exceeded 20 at% and was rich in C2NH and C–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C motifs; porosity was small enough to exclude N2 while not inhibiting CO2 adsorption; and micro- and mesopores that seemed to facilitate competitive N2 adsorption were limited.
C motifs; porosity was small enough to exclude N2 while not inhibiting CO2 adsorption; and micro- and mesopores that seemed to facilitate competitive N2 adsorption were limited.
These conditions were best achieved with Li2CO3 and Na2CO3 activation. While activation via these salts yielded superior materials for selective CO2 capture and efficient regeneration, it is worthwhile to consider external factors which could influence the practicality of using the different salts studied. It was observed in this work that the LiCN byproduct reacts rapidly in air when compared to KCN or NaCN. It is known that the alkali cyanides degrade in air in a process which may evolve HCN, which may occur more abruptly for LiCN, posing considerable health concerns if precautions are not enacted.42 Furthermore, each of these salts sees use in the rapidly-growing battery industry, and in 2019 the price of Li2CO3 was reported to be nearly six times more expensive than K2CO3 and thirty times more expensive than Na2CO3 on a USD per ton basis.43 Thus, for the systems studied in this work, Na2CO3 has the most significant advantages from both performance and practical considerations.
In summary, this work outlines opportunities for future studies by providing a better understanding of the effect of activator and precursor on the material properties of the resulting nanoporous carbons. For example, by using similar N-rich carbon precursors and eutectic molten salts of varying charge density, structural reorganization mediated via molten salt templating is likely a promising avenue for tuning the chemical environment of the N-content while inducing porosity that is size exclusive to CO2. This could greatly improve capture for CO2, especially from more dilute feed concentrations. While many samples in this study achieved theoretical selectivity performance required for viability in post-combustion flue gas separation, larger scale and more realistic testing, such as the inclusion of humidity effects and transport/kinetics, would be required to demonstrate the applicability of this adsorbent class for carbon capture. Nevertheless, this work suggests that with more rigorous testing and optimization, porous carbons are a sustainable, stable, and tunable materials class that hold potential for practical and economical carbon capture.
Author contributions
J. Ehren Eichler: conceptualization; validation; formal analysis; investigation; software, writing – original draft. James N. Burrow: conceptualization; investigation; writing – reviewing & editing. Naman Katyal: software, writing – reviewing & editing. Greame Henkelman: resources, writing – reviewing & editing. C. Buddie Mullins: project administration; funding acquisition; writing – reviewing and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Robert A. Welch Foundation (C. B. M, grant no. F-1436 and G. H., grant no. F-1841) for their generous support of this research. J. N. B. also thanks the Sellers family and the Cockrell School of Engineering for providing graduate research fellowships. Computational support was provided by the Texas Advanced Computing Center.References
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- S. Y. Lee and S. J. Park, J. Ind. Eng. Chem., 2015, 23, 1–11 CrossRef CAS.
- A. E. Creamer and B. Gao, Environ. Sci. Technol., 2016, 50, 7276–7289 CrossRef CAS.
- R. L. Siegelman, E. J. Kim and J. R. Long, Nat. Mater., 2021, 20, 1060–1072 CrossRef CAS PubMed.
- M. Sevilla, A. S. M. Al-Jumialy, A. B. Fuertes and R. Mokaya, ACS Appl. Mater. Interfaces, 2018, 10, 1623–1633 CrossRef CAS PubMed.
- M. Oschatz and M. Antonietti, Energy Environ. Sci., 2018, 11, 57–70 RSC.
- M. Sevilla, N. Díez and A. B. Fuertes, ChemSusChem, 2021, 14, 94–117 CrossRef CAS PubMed.
- J. E. Eichler, J. N. Burrow, Y. Wang, D. C. Calabro and C. B. Mullins, Carbon, 2022, 186, 711–723 CrossRef CAS.
- J. Fujiki and K. Yogo, Chem. Commun., 2016, 52, 186–189 RSC.
- J. Zhou, Z. Li, W. Xing, H. Shen, X. Bi, T. Zhu, Z. Qiu and S. Zhuo, Adv. Funct. Mater., 2016, 26, 7955–7964 CrossRef CAS.
- J. V. Guerrera, J. N. Burrow, J. Ehren Eichler, M. Z. Rahman, M. V. Namireddy, K. A. Friedman, S. S. Coffman, D. C. Calabro and C. Buddie Mullins, Energy Fuels, 2020, 34, 6101–6112 CrossRef CAS.
- A. Brush, S. McDonald, R. Dupré, S. Kota, G. M. Mullen and C. Buddie Mullins, React. Chem. Eng., 2017, 2, 512–520 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 1–4 CrossRef.
- Y. Liu, J. Chem. Eng. Data, 2009, 54, 1981–1985 CrossRef CAS.
- A. Nuhnen and C. Janiak, Dalton Trans., 2020, 49, 10295–10307 RSC.
- J. A. Mason, K. Sumida, Z. R. Herm, R. Krishna and J. R. Long, Energy Environ. Sci., 2011, 4, 3030–3040 RSC.
- C. M. Simon, B. Smit and M. Haranczyk, Comput. Phys. Commun., 2016, 200, 364–380 CrossRef CAS.
- J. P. Sculley, W. M. Verdegaal, W. Lu, M. Wriedt and H. C. Zhou, Adv. Mater., 2013, 25, 3957–3961 CrossRef CAS PubMed.
- J. N. Burrow, J. E. Eichler, Y. Wang, D. C. Calabro and C. B. Mullins, J. Mater. Chem. A, 2022, 10, 24649–24661 RSC.
- D. A. Sams and F. Shadman, AIChE J., 1986, 32, 1132–1137 CrossRef CAS.
- M. Sevilla, G. A. Ferrero, N. Diez and A. B. Fuertes, Carbon, 2018, 131, 193–200 CrossRef CAS.
- G. M. Veith, L. Baggetto, L. A. Adamczyk, B. Guo, S. S. Brown, X.-G. Sun, A. A. Albert, J. R. Humble, C. E. Barnes, M. J. Bojdys, S. Dai and N. J. Dudney, Chem. Mater., 2013, 25, 503–508 CrossRef CAS.
- J. P. Pender, J. V. Guerrera, B. R. Wygant, J. A. Weeks, R. A. Ciufo, J. N. Burrow, M. F. Walk, M. Z. Rahman, A. Heller and C. B. Mullins, ACS Nano, 2019, 13, 9279–9291 CrossRef CAS PubMed.
- M. Hankel, D. Ye, L. Wang and D. J. Searles, J. Phys. Chem. C, 2015, 119, 21921–21927 CrossRef CAS.
- J. N. Burrow, J. P. Pender, J. V. Guerrera, B. R. Wygant, J. Ehren Eichler, D. C. Calabro and C. Buddie Mullins, ACS Appl. Nano Mater., 2020, 3, 5965–5977 CrossRef CAS.
- C. Lastoskie, K. E. Gubbins and N. Quirke, J. Phys. Chem., 1993, 97, 4786–4796 CrossRef CAS.
- S. Samios, A. K. Stubos, N. K. Kanellopoulos, R. F. Cracknell, G. K. Papadopoulos and D. Nicholson, Langmuir, 1997, 13, 2795–2802 CrossRef CAS.
- R. Gounder and E. Iglesia, J. Am. Chem. Soc., 2009, 131, 1958–1971 CrossRef CAS PubMed.
- R. L. Siegelman, T. M. McDonald, M. I. Gonzalez, J. D. Martell, P. J. Milner, J. A. Mason, A. H. Berger, A. S. Bhown and J. R. Long, J. Am. Chem. Soc., 2017, 139, 10526–10538 CrossRef CAS PubMed.
- M. E. Zick, S. M. Pugh, J.-H. Lee, A. C. Forse and P. J. Milner, Angew. Chem., Int. Ed., 2022, 61, e202206718 ( Angew. Chem. , 2022 , 134 , e202206718 ) CrossRef CAS PubMed.
- C. T. Campbell and J. R. V. Sellers, J. Am. Chem. Soc., 2012, 134, 18109–18115 CrossRef CAS PubMed.
- P. J. Dauenhauer and O. A. Abdelrahman, ACS Cent. Sci., 2018, 4, 1235–1243 CrossRef CAS PubMed.
- P. J. Milner, R. L. Siegelman, A. C. Forse, M. I. Gonzalez, T. Runčevski, J. D. Martell, J. A. Reimer and J. R. Long, J. Am. Chem. Soc., 2017, 139, 13541–13553 CrossRef CAS PubMed.
- R. R. Krug, W. G. Hunter and R. A. Grieger, Nature, 1976, 261, 566–567 CrossRef CAS.
- G. Lim, K. B. Lee and H. C. Ham, J. Phys. Chem. C, 2016, 120, 8087–8095 CrossRef CAS.
- D. Saha and M. J. Kienbaum, Microporous Mesoporous Mater., 2019, 287, 29–55 CrossRef CAS.
- X. Ma, L. Li, R. Chen, C. Wang, H. Li and S. Wang, Appl. Surf. Sci., 2018, 435, 494–502 CrossRef CAS.
- J. N. Burrow, R. A. Ciufo, L. A. Smith, Y. Wang, D. C. Calabro, G. Henkelman and C. B. Mullins, ACS Nano, 2022, 16(4), 5393–5403 CrossRef CAS PubMed.
- E. Gail, S. Gos, R. Kulzer, J. Lorösch, A. Rubo, M. Sauer, R. Kellens, J. Reddy, N. Steier and W. Hasenpusch, Ullmann’s Encycl. Ind. Chem., 2011, 10, 679–681 Search PubMed.
- J. Zhang, T. Liu, X. Cheng, M. Xia, R. Zheng, N. Peng, H. Yu, M. Shui and J. Shu, Nano Energy, 2019, 60, 340–361 CrossRef CAS.
Footnotes |
| † 10th Anniversary Statement: I am so pleased and thankful to be able to contribute to the special 10th Anniversary issue of the Journal of Materials Chemistry A. I have read and learned from papers published in JMCA, I have refereed papers for JMCA, I have authored papers in JMCA and I have served on the Editorial Advisory Board for JMCA… All of these experiences have been enjoyable and enlightening. I hope to continue to be able to contribute and serve this wonderful journal and community. |
| ‡ Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09376f |
| This journal is © The Royal Society of Chemistry 2023 |