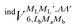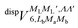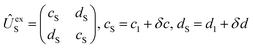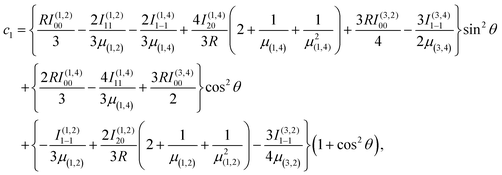Open Access Article
Open Access ArticleStatistical theory for the reaction N + OH → NO + H: thermal low-temperature rate constants
A. I.
Maergoiz
 ab,
E. E.
Nikitin
ac and
J.
Troe
ab,
E. E.
Nikitin
ac and
J.
Troe
 *ab
*ab
aMax-Planck-Institut für Multidisziplinäre Naturwissenschaften, Am Fassberg 11, D-37077 Göttingen, Germany. E-mail: juergen.troe@mpinat.mpg.de
bInstitut für Physikalische Chemie, Universität Göttingen, Tammannstr. 6, D-37077 Göttingen, Germany
cSchulich Faculty of Chemistry, Technion-Israel Institute of Technology, Haifa 32000, Israel
First published on 22nd February 2022
Abstract
The reaction N + OH → NO + H involves the intermediate formation of NOH adducts which in part rearrange to HNO conformers. A statistical treatment of the process is developed in which an initial adiabatic channel capture of the reactants is accompanied by partial primary redissociation of the N⋯OH collision pairs. A criterion for the extent of this primary redissociation in competition to the formation of randomized, long-lived, complex of NOH is proposed. The NOH adducts then may decompose to NO + H, rearrange in a unimolecular process to HNO, or undergo secondary redissociation back to the reactants N + OH, while HNO may also decompose to NO + H. As the reactants N(4S) + OH(2Π) have open electronic shells, non-Born–Oppenheimer effects have to be considered. Their influence on thermal rate constants of the reaction at low temperatures is illustrated and compared with such effects in other reactions such as C(3P) + OH(2Π).
1. Introduction
The mechanism of complex-forming bimolecular reactions can be understood in terms of an initial capture of the reactants, the formation of long-lived adducts, and the subsequent decay of these adducts. While adiabatic capture theory often characterizes the initial stage of the reaction, statistical unimolecular rate theory is frequently used to quantify the intramolecular evolution of the adducts. The described concept has successfully rationalized a large number of experimental results. Simplified versions of the treatment have been proposed, for instance, in ref. 1. Looking into the finer details of the reaction, however, a number of aspects deserve further attention.(i) Obviously, the potential energy surface (PES) of the system plays a central role. The identification and proper representation of the rate-determining parts of the PES, therefore, is of high priority.
(ii) The reactants may have open electronic shells and the interaction between the arising PESs has to be taken into account. This complicates the analysis on the Born–Oppenheimer (BO) level of the interaction between individual adiabatic channel potential energy curves, see, for instance, the capture of C(3P) by OH(2Π) elaborated in ref. 2, or the capture of H(2S) by O2(3Σ) and of O(3P) by OH(2Π) discussed in ref. 3. It is common practice to consider reaction on a single PES, which correlates with a single state of the reactants, and to multiply the resulting thermal rate constants by electronic factors fel(T) which account for the thermal population of the reactants in their relevant fine-structure levels.4 Because of the interaction of the PESs at large intermolecular distances, this may not be sufficient for low-temperature conditions; but as the consequences may reach up to temperatures of several tens of K, they may be important for astrochemical applications, for instance, see ref. 5 and 6.
(iii) Reaction cross sections and thermal rate constants for capture from the statistical adiabatic channel model (SACM, ref. 7 and 8), have been compared with results from quasi-classical trajectory (CT) calculations in ref. 9–13. The extent of dynamical non-adiabaticity was inspected and simplified representations of the SACM/CT results were proposed. While quantum effects of the internal reactant states are accounted for in SACM/CT approaches from the beginning, comparisons with detailed quantum scattering (CS) calculations are also required, in particular when capture of light particles like electrons are considered, for instance, see ref. 14.
(iv) The connection of the initial capture of the reactants with the subsequent evolution of the adduct may be of importance and has to be understood on a state-specific level. There may be “primary redissociation” of the “collision pair”, before a long-lived complex is formed. At a later stage of the process, a “secondary (unimolecular) redissociation” of the randomized adduct may take place in competition to other decay channels. Both types of redissociation lead to a reduction of the reaction rate in comparison to the capture rate.
It is the aim of the present work to illustrate the described details of an analysis within an extended SACM approach. The complex-forming, exothermic, bimolecular reaction
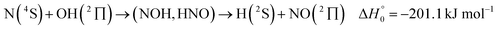 | (1) |
The comparison of experimental and modelled rate constants for reaction (1) leads to interesting conclusions. Like in ref. 23 one realizes that modelled capture rate constants are markedly higher than the experimental low-temperature values of the reaction rate constants from ref. 6 and 33, corresponding to probabilities for reaction after capture of only about 1/2. Similar values in ref. 23 were found for the reactions of O, S, and N atoms with OH. As ACCSA and SACM calculations for the same PES are essentially equivalent (for instance, see ref. 34), the present work is in agreement with this result. On the other hand, ACCSA, SACM, and CT calculations led to practically identical rate constants for the reaction of C with OH which corresponds to probabilities for reaction after capture near unity. Likewise, ACCSA and SACM calculations of capture rate constants were found to agree with experimental data for reactions of N+ ions with H2O or NH3.35
The conclusion on probabilities smaller than unity for reaction after capture calls for an explanation. This may be found in CT calculations, such as those performed for reaction (1) in ref. 24, or for the reaction of O with OH in ref. 36–38. “Recrossing effects” then may be distinguished in terms of “primary redissociation” and/or “secondary redissociation” mechanisms of the initial collision pairs of reactants and of the adducts being formed, respectively. In the present work, we propose to characterize the redissociation processes by a state-specific criterion. We consider various factors possibly leading to primary redissociation, such as the number of atoms in the reactants, the distribution of masses between the reactants, the properties of the PES, and NBO effects under low-temperature conditions. Tests for the validity of the proposed approach are made by comparing modelled and experimental reaction rate constants. When the latter are not available, comparisons of rate constants for reaction from the present approach and from CT calculations are also useful. Finally, comparisons of product state distributions from the present approach and from CT calculations are helpful. This will be demonstrated for reaction (1) in the present article as well as in the more detailed publications of ref. 39 and 40.
2. Potential energy surfaces for the capture/redissociation process N(4S) + OH(2Π) ↔ N⋯OH
An energy diagram for the intermediates of reaction (1) on the attractive 3A′′ PES of the reaction system is shown in Fig. 1 (adapted from ref. 19, scaled with energies for N + OH, NOH, HNO, and H + NO from ref. 41; the species NOH, HNO, and the various transition states correspond to different structures on the same PES). Instead of the ab initio characterization of the PES performed in ref. 15–20, the present work determined part of the PES by the asymptotic method described in ref. 2, 3, 23 and 42. Furthermore, it focuses attention on the entrance side of the PES, i.e. on the side of the reactants N + OH, while the remaining parts, relevant for the transformation NOH ↔ HNO and the subsequent dissociation (NOH, HNO) → H(2S) + NO(2Π), will be elaborated in ref. 39 and 40. An asymptotic long-range potential between N(4S) and OH(2Π), considering dispersion and induction interactions, but neglecting exchange interaction, has been constructed before,23 the present work in this respect goes beyond this. In addition, we also go beyond the BO approximation. The treatment closely follows the procedure described in more detail in ref. 2. It also uses the nomenclature from that article.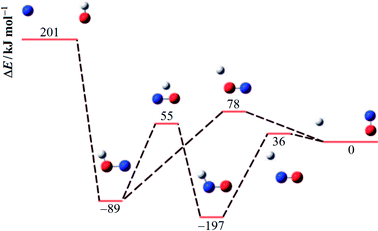 | ||
| Fig. 1 Energy diagram for reaction (1) and its intermediates (blue, red, and white spheres symbolize N, O, and H atoms, respectively; the energies ΔE relative to H + NO are adapted from ref. 19 and 41). | ||
In order to construct asymptotic PESs within the BO approximation, following ref. 2 we use a basis of electronic functions of the system with total spin S = 1, 2 in the form
| ψel± = 〈L, ML, Λ, S, MS| = 〈L= 0,ML = 0|〈Λ = ±1|〈S, MS| | (2) |
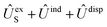 generates four PESs (the SO interaction originating from OH(2Π) is neglected here; we note that there is no SO structure in N(4S)). The four PESs correspond to 3A′,3A′′,5A′,5A′′ classification, of which only the 3A′′ PES is attractive and eventually reactive, while the other PESs are repulsive and considered nonreactive in the energy range of interest. On the basis of the electronic wave functions of eqn (2), the matrix elements of the sum of the induction and dispersion interactions are
generates four PESs (the SO interaction originating from OH(2Π) is neglected here; we note that there is no SO structure in N(4S)). The four PESs correspond to 3A′,3A′′,5A′,5A′′ classification, of which only the 3A′′ PES is attractive and eventually reactive, while the other PESs are repulsive and considered nonreactive in the energy range of interest. On the basis of the electronic wave functions of eqn (2), the matrix elements of the sum of the induction and dispersion interactions are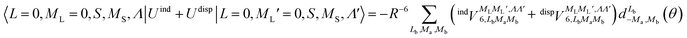 | (3) |
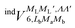 and
and 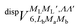 , are induction and dispersion coefficients, respectively, and are given in Table 1, in agreement with those from ref. 23. Composed from these elements, one has the matrix
, are induction and dispersion coefficients, respectively, and are given in Table 1, in agreement with those from ref. 23. Composed from these elements, one has the matrix 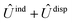 in the form
in the form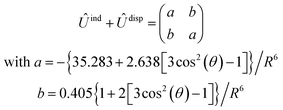 | (4) |
Using the same basis as eqn (2), the exchange interaction matrix is given by
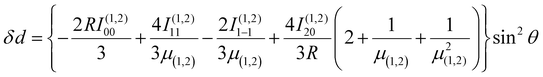 | (5) |
| ln(I(q,q′)kn) = a(q,q′)knR3 + b(q,q′)knR2 + c(q,q′)knR + d(q,q′)kn | (6) |
| q | Orbitals | γ q | A q |
|---|---|---|---|
| 1 | N,2p | 1.0336 | 1.6 |
| 2 | OH,1π | 0.9775 | 1.6 |
| 3 | N,2s | 1.2225 | 2.0 |
| 4 | OH,3σ | 1.1012 | 2.0 |
| q | q′ | k | n | 100a(q,q′)kn | 10b(q,q′)kn | c (q,q′)kn | d (q,q′)kn |
|---|---|---|---|---|---|---|---|
| 1 | 2 | 0 | 0 | 0.1463 | −0.4572 | −1.3693 | 1.2581 |
| 1 | 2 | 1 | 0 | 0.1463 | −0.4572 | −1.3695 | 0.5592 |
| 1 | 2 | 1 | 1 | 0.1462 | −0.4578 | −1.3455 | 1.1455 |
| 1 | 2 | 1 | −1 | 0.1464 | −0.4578 | −1.3934 | 1.0879 |
| 1 | 2 | 2 | 0 | 0.1463 | −0.4572 | −1.3698 | −0.1396 |
| 1 | 4 | 0 | 0 | 0.1264 | −0.3934 | −1.5797 | 1.7100 |
| 1 | 4 | 1 | 0 | 0.1264 | −0.3934 | −1.5801 | 0.9513 |
| 1 | 4 | 1 | 1 | 0.1267 | −0.3944 | −1.6097 | 1.5027 |
| 1 | 4 | 1 | −1 | 0.1263 | −0.3944 | −1.5500 | 1.5636 |
| 1 | 4 | 2 | 0 | 0.1264 | −0.3934 | −1.5804 | 0.1928 |
| 3 | 2 | 0 | 0 | 0.1124 | −0.3195 | −1.6589 | 1.6961 |
| 3 | 2 | 1 | −1 | 0.1222 | −0.3254 | −1.7752 | 1.4014 |
| 3 | 4 | 0 | 0 | 0.1000 | −0.3021 | −1.8799 | 2.1609 |
| 3 | 4 | 1 | −1 | 0.1017 | −0.3056 | −1.9364 | 1.8899 |
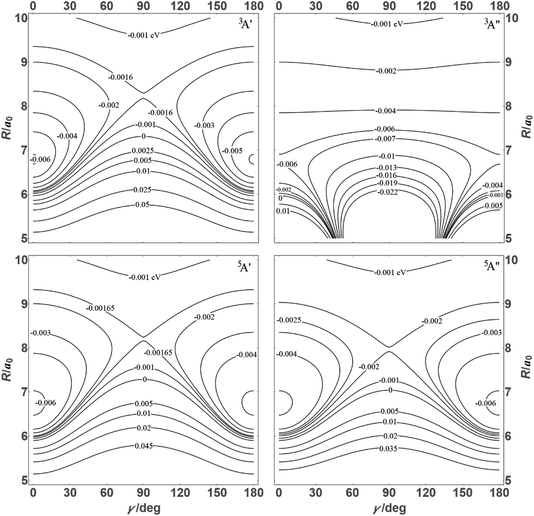
Combining the induction, dispersion, and exchange terms on the side of the reactants N + OH, for the 3A′,3A′′,5A′,5A′′ states one obtains
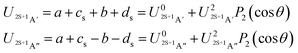 | (7) |
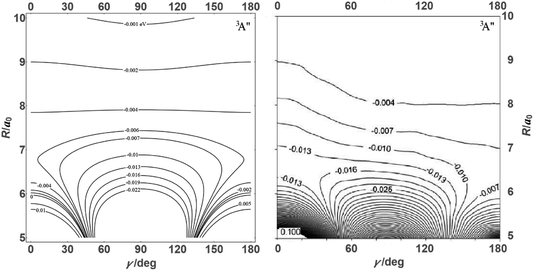
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) – anisotropies such as illustrated in the contour map of Fig. 2 for the 3A′′ PES (left-hand side of the figure). The present results from asymptotic theory in Fig. 2 are compared with the results from the ab initio calculations of ref. 19 (right-hand side of the figure). The general agreement looks satisfactory. Contour plots for the nonreactive 3A′,5A′, and 5A′′ states are compared with those for the reactive 3A′′ state in Fig. 3.
θ) – anisotropies such as illustrated in the contour map of Fig. 2 for the 3A′′ PES (left-hand side of the figure). The present results from asymptotic theory in Fig. 2 are compared with the results from the ab initio calculations of ref. 19 (right-hand side of the figure). The general agreement looks satisfactory. Contour plots for the nonreactive 3A′,5A′, and 5A′′ states are compared with those for the reactive 3A′′ state in Fig. 3.
 | ||
| Fig. 2 Energy contours (in eV) of the attractive 3A′′ PES of the N + OH system (Jacobi coordinates: N–OH distances R in atomic units, γ = θ in degrees). Comparison of results from the present asymptotic theory (left) with results from the ab initio calculations of ref. 19 (right). | ||
 | ||
| Fig. 3 Energy contours (in eV) of the 3A′,3A′′,5A′,5A′′ states of the N + OH system (coordinates as in Fig. 2). | ||
3. Adiabatic channel potential energy curves and good quantum numbers
Adiabatic channel (AC) potential energy curves Vi(R), for the 3A′′ electronic state of the N–OH system, are obtained by diagonalization of the Hamiltonian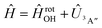 in the basis of rigid rotor functions, where
in the basis of rigid rotor functions, where 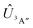 has the asymptotic P2-anisotropy (see eqn (7)). In an NBO approach, the asymptotic Hamiltonian
has the asymptotic P2-anisotropy (see eqn (7)). In an NBO approach, the asymptotic Hamiltonian 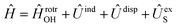 in
in 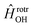 , in addition to the rotational Hamiltonian
, in addition to the rotational Hamiltonian 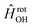 also includes the spin–orbit (SO) interaction. NBO AC potential energy curves Vi(R) then are obtained by diagonalization of the Hamiltonian in the basis of the functions from eqn (2), multiplied by rotronic functions with the projection Λ of the rotronic momentum K of OH onto its axis. Details of the diagonalization procedure have been described in ref. 2 and will be not repeated here.
also includes the spin–orbit (SO) interaction. NBO AC potential energy curves Vi(R) then are obtained by diagonalization of the Hamiltonian in the basis of the functions from eqn (2), multiplied by rotronic functions with the projection Λ of the rotronic momentum K of OH onto its axis. Details of the diagonalization procedure have been described in ref. 2 and will be not repeated here.
The ACs are characterized by sets of good quantum numbers and are specified by indices “i”. The ACs lead from those of the separated reactants N + OH into those of the adduct NOH. Conserving total angular momentum (exact quantum number J), and its projection onto the slowly rotating N⋯O collision axis (good quantum number k, with k ≤ J), in the BO approximation is of particular importance. Because of too short times for Coriolis mixing, k can be assumed to be conserved during the initial capture and the primary redissociation process. For the present distribution of atomic masses and not too high rotational states of the reactant OH, the orbital angular momentum of the collision pair (quantum number l), is close to the total angular momentum (i.e., J ≈ l). The states of the free reactant OH are characterized by rotational (neglecting SO) and vibrational quantum numbers jOH ≪ J and nOH, respectively. The adduct NOH is represented by a rigid symmetric top (characterized by the quantum numbers J and k) and by three separated Morse oscillators with the vibrational quantum numbers n1, n2, and n3 (spectroscopic parameters were taken from ref. 20 and 27).
In the framework of SACM, the quantum number nOH during the capture and primary redissociation stage of the encounter correlates with the quantum number n1 of the high-frequency vibration of NOH. Considering low-energy collisions with nOH = n1 = 0 only, we exclude OH stretching transitions during this stage of the process. The quantum number jOH then correlate with the quantum number n2 of the deformation vibration of the nearly T-shaped adduct NOH, according to a relationship
| n2 = jOH − |k| | (8) |
In the NBO approach, the projection of the total momentum J (now including the total spin S of the system) onto the slowly rotating N–O axis is characterized by the good quantum number P (at large intermolecular distances, P = MK + MS, where MK and MS are the respective projections of K and S onto the mentioned axis, see ref. 2).
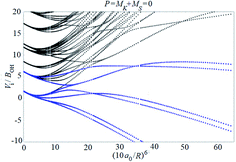
Examples of rotronic NBO AC potential energy curves are shown in Fig. 4 and 5. At small intermolecular distances R (right-hand side of the figures), the attractive curves (drawn in blue) correlate with the 3A′′ curves of NOH (with their given k and n2). At large R (left-hand side of the figures), the NBO curves approach the rotronic states of free OH (with the rotational constant of OH denoted by BOH). NBO AC potential energy curves correlating with BO curves from repulsive PESs (drawn in black) are included in Fig. 4 and 5. As only the attractive 3A′′ PES leads to reaction, only NBO curves correlating with the corresponding BO ACs are further considered.
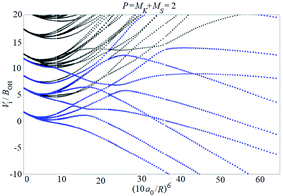 | ||
| Fig. 5 As Fig. 4, but for P = 2. | ||
The curves show a number of avoided crossings. The passing of the narrowest crossing (δV ≤ 0.1BOH) is considered as diabatic, see ref. 2 (otherwise it is considered as adiabatic). At short distances (R <5a0), the degeneracy gi of the attractive NBO curves correlating with the (3A′′,k,n2) BO level of NOH is equal to unity when both of P and k are equal to zero, otherwise one has gi = 2.
4. Low-energy cross sections and low-temperature rate constants
The maxima of the sum of the AC potential energy curves Vi(R) and the approximate orbital energies ℏ J(J + 1)/2 μR2 of the N⋯OH collision pair define the AC threshold energies E0,i (observing that l ≈ J). When the energy of the system is larger than E0,i, ACs are treated as “open” for capture; otherwise they are “closed”. The range of open and closed channels can be characterized by those values Jcl at which, for a given collision energy Ecol, channels with increasing J pass from open to closed. For example, at Ecol = 0.1 eV, nOH = 0, jOH = 10, and the possible projection quantum numbers k (with k ≤ J), values for Jcl as shown in Table 4 are obtained (line with bold numbers). Once the values of Jcl are known, the corresponding state-specific cross sections ICScap and rate constants kcap for capture follow as discussed in ref. 2. Fig. 6 shows examples of ICScap at two collision energies and a variety of jOH.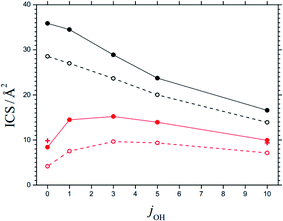 | ||
| Fig. 6 State-specific cross sections ICS for capture (black) and reaction (red), at Ecol = 0.1 eV (solid curves) and 0.2 eV (dashed curves) and for rotational quantum numbers jOH (curves = statistical theory for the 3A′′ PES from the present work, red crosses = results for reaction at Ecol = 0.1 eV from the CT calculations of ref. 28, omitting fel, NBO effects of SO interaction are neglected). | ||
| j OH | k = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 11 | 14 | 33 | 42 | 48 | 50 | 52 | 52 | |||||
| 10 | 25 | 40 | 50 | 57 | 61 | 64 | 66 | |||||
| 9 | 31 | 45 | 55 | 62 | 68 | 72 | 75 | |||||
| 8 | 34 | 48 | 58 | 66 | 72 | 77 | 81 | |||||
| 7 | 36 | 50 | 61 | 69 | 76 | 81 | 86 | |||||
| 6 | 37 | 52 | 63 | 71 | 79 | 84 | 89 | |||||
| 5 | 52 | 64 | 73 | 80 | 87 | 92 | ||||||
| 4 | 64 | 74 | 82 | 89 | 94 | |||||||
| 3 | 74 | 83 | 90 | 96 | ||||||||
| 2 | 83 | 90 | 97 | |||||||||
| 1 | 91 | 98 | ||||||||||
| 0 | 98 |
Overcoming the E0,i, however, is not sufficient for reaction. Instead, there may be redissociation of the adducts to the initial reactants, similar to what has been observed in the CT calculations of a reaction between OH and O, see ref. 36–38. One of the aims of the present work was the characterization of this effect by a specific criterion for the formation of randomized states of the adduct. We suggest that two types of redissociation can occur, one during the primary encounter between the reactants before such an adduct is formed, and the other after randomization has taken place. The former we term “primary redissociation”, while the latter is called “secondary redissociation”. The latter needs an application of unimolecular rate theory and will be elaborated in detail in ref. 39 and 40. Here, the condition for forming randomized adduct states is described in the following. We assume that only that part of the open ACs does not undergo primary redissociation, but succeeds to form long-lived NOH adducts capable for reaction, whose modeled energy levels ENOH(J, k, n1, n2, n3) meet the total energy of the system. Thus, the following conditions must be fulfilled
| Etot ≥ ENOH(J, k, n1, n2, n3) | (9a) |
| Etot ≤ ENOH(J, k + 1, n1, n2, n3) | (9b) |
| Etot ≤ ENOH(J, k, n1 + 1, n2, n3) | (9c) |
| Etot ≤ ENOH(J, k, n1, n2 + 1, n3) | (9d) |
| Etot ≤ ENOH(J, k, n1, n2, n3 + 1) | (9e) |
The total energy Etot, as measured from the bottom of the NOH potential well, is given here by the collision energy Ecol plus the internal energy of OH. n1, n2, and n3 are the quantum numbers of separated vibrations of NOH, approximated by Morse oscillators. The quantum numbers J and k, for overall angular momentum and its projection, respectively, define the rotational contribution to ENOH in rigid symmetric top approximations. During the approach of N and OH, the quantum numbers n2 of the adduct form according to the correlation of eqn (8). When the criterion for complex formation of eqn (9) is not fulfilled, there may be a statistical redistribution of n2 (under conservation of k and n1) over other ACs correlating with them. jOH then, in general will have changed. For separation of the reactants, the outgoing collision pair (with conserved J and k), however, then will also have to overcome its AC threshold. The corresponding Jcl will then differ from the value for the incoming collision pair. Table 4, therefore, includes values of Jcl for outgoing collision pairs (lines with light numbers). If the outgoing collision pair does not succeed to overcome its threshold, it tries again by changing n2 and so on. As the barriers on the way from N + OH to H + NO are considerably lower than the entrance energy in Fig. 1, there is only a limited extent of secondary redissociation under low-energy and low-temperature conditions (contributing to reaction probabilities by a factor of more than 0.9, see ref. 39 and 40). We, therefore, focus our attention here on the primary redissociation only.
In order to justify the use of the criterion in eqn (9), we have calculated state-specific cross sections ICS for the full reaction (1). For the moment, the results could not be compared with experimental product distributions. However, a comparison with the CT and QS calculations of ref. 24–29 on the 3A′′ PES showed satisfactory agreement. Fig. 6 illustrates this for an ICS on the 3A′′ PES as a function of jOH (for collision energies Ecol = 0.1 and 0.2 eV). The agreement of results from the present work and from the CT calculations of ref. 28 is taken as confirmation for the validity of the criterion of eqn (9). The agreement of the ICS for jOH = 0 and 10 deserves particular mention.
Accounting for the described primary (and secondary) redissociation, reaction rate constants kr and reaction probabilities kr/kcap were determined. This was done by inspecting individual AC potential energy curves and their E0,i values in the framework of BO and NBO treatments. Results from BO calculations were multiplied with the electronic factor fel(T), in the present case given by
fel(T) = 3/(8 + 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−205 K/T]) exp[−205 K/T]) | (10) |
Fig. 7 shows the results. Between 50 and 200 K, the BO rate constants practically agree with the experimental data and NBO effects do not yet play a major role. However, in contrast to the kcap(T), BO and NBO results for reaction rate constants kr below about 50 K differ markedly. NBO couplings, relevant for low-temperature conditions, here efficiently loosen the restrictions imposed by eqn (9) and in this way partly circumvent redissociation effects. On the one hand, this illustrates the importance of NBO effects under low-temperature conditions. On the other hand, the close agreement between calculations and experiments between 50 and 200 K also validates the criterion of eqn (9) for formation of randomized intermediate adducts capable of reaction.
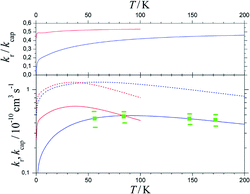 | ||
| Fig. 7 Reaction probabilities kr/kcap (upper panel), capture rate constants kcap (lower panel, dashed curves) and reaction rate constants kr (lower panel, solid curves), from fel(T)-corrected BO (blue curves) and NBO (red curves) calculations of the present work, in comparison to experimental results from ref. 33 (green symbols with error bars). | ||
Compared to the fel(T)-corrected BO results, the NBO calculations of capture rate constants kcap(T) led to only slightly larger limiting low-temperature values. The results obtained practically agreed with those from the ACCSA calculations of ref. 23. The low-temperature region accordingly is governed by the long-range dispersion and induction contributions only, while short-range exchange contributions will become relevant only at higher collision energies. The near-agreement of the present kcap(T) with the results from the ACCSA and SACM treatments of ref. 23 is not surprising. It has been shown in ref. 34 that the two approaches, as well as “adiabatic variance” or “perturbed rotational state” treatments such as employed in ref. 43 and 44, are equivalent and small differences arise from numerical differences only.
As the number of considered ACs for technical reasons was limited, only calculations for low temperatures were made in the present work. However, the comparison with the experimental rate constants kr from ref. 33 in Fig. 7 appears satisfactory. It leads to reaction probabilities kr/kcap of the order of 1/2, which are consistent with the values empirically suggested in ref. 23. Although the present study was limited to low temperatures, according to Fig. 7 it does not appear improbable to assume only a weak temperature dependence above 200 K. The results from the present work on the one hand illustrate the importance of NBO effects under low-temperature conditions. On the other hand, the close agreement between calculations and experiments validates the criterion of eqn (12) and (13) for formation of randomized intermediate adducts capable of reaction.
5. Discussion
A comparison of the results for reaction (1) with related information for other reactions leads to interesting conclusions. This appears most clear for the reaction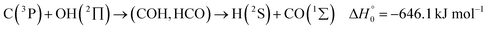 | (11) |
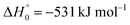 in contrast to N(4S) + OH(2Π) → NOH with
in contrast to N(4S) + OH(2Π) → NOH with 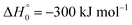 ). In contrast to that of reaction (1), the overall rate constant for reaction (11) was found to be close to the capture rate constant,47i.e. neither primary nor secondary redissociation were found to play a significant role. In view of the large endothermicity of a process (COH, HCO) → C + OH this is not surprising for secondary redissociation, but primary redissociation caused by the conditions in eqn (9) apparently is also not too important. As the vibrational frequencies of the adducts are not very different, the reason must be a much larger density of vibrational adduct states in reaction (11) which allow the condition of eqn (9) to be fulfilled more easily. The chance of hitting an adduct state by the capture process then is much larger in reaction (11) than in reaction (1) which reduces the probability for primary redissociation. The reactions
). In contrast to that of reaction (1), the overall rate constant for reaction (11) was found to be close to the capture rate constant,47i.e. neither primary nor secondary redissociation were found to play a significant role. In view of the large endothermicity of a process (COH, HCO) → C + OH this is not surprising for secondary redissociation, but primary redissociation caused by the conditions in eqn (9) apparently is also not too important. As the vibrational frequencies of the adducts are not very different, the reason must be a much larger density of vibrational adduct states in reaction (11) which allow the condition of eqn (9) to be fulfilled more easily. The chance of hitting an adduct state by the capture process then is much larger in reaction (11) than in reaction (1) which reduces the probability for primary redissociation. The reactions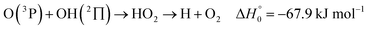 | (12) |
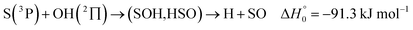 | (13) |
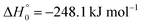 , or S + OH → HOS,
, or S + OH → HOS, 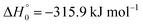 , respectively) like reaction (1) were found to have reaction probabilities as low as 1/2. As the exothermicities of these reactions are markedly different from that of reaction (11), the distinction between primary and secondary redissociation is more difficult. The situation may be comparable to that of reaction (1) with a primary redissociation characterized by the criterion of eqn (9), but secondary redissociation also has to be considered here.
, respectively) like reaction (1) were found to have reaction probabilities as low as 1/2. As the exothermicities of these reactions are markedly different from that of reaction (11), the distinction between primary and secondary redissociation is more difficult. The situation may be comparable to that of reaction (1) with a primary redissociation characterized by the criterion of eqn (9), but secondary redissociation also has to be considered here.
Adducts with larger vibrational densities of states have a larger chance to fulfill the criterion of eqn (9a)–(9e) during the capture process. Primary redissociation, therefore, appears to be a phenomenon encountered in reaction systems of limited complexity only. The reactions mentioned in the introduction, with experimental rate constants equal to the capture rate constants, apparently do not fall into this category. Obviously, for reactions without adduct formation, primary redissociation appears less probable.
A comparison of the present results with the work of ref. 2 on reaction (11) also sheds light on the role of NBO effects in low-temperature rate constants. With a single attractive PES contributing to product formation, reaction (1) shows only small NBO effects on the capture rate constants. On the other hand, CT and NBO calculations for reaction (11), where primary redissociation apparently can be neglected, have led to similar limiting low-temperature rate constants as long as only capture on the lowest PES was important (up to about 20 K, where kcap rises by about a factor of 2 from its low-temperature limiting value). Between 20 and 200 K, however, kcap in the lowest electronic state of the adduct was found to be successively replaced by capture into higher electronic states, with an overall rate constant not varying too much with temperature. Obviously, NBO effects play an important role there.
In summary, the comparison of the N + OH with the C + OH reaction identifies differences in the role of primary redissociation effects during adduct formation. Further differences arise from different numbers of attractive electronic states of the adducts. The present work highlights the application of statistical rate theories and their extension by the conditions of eqn (9) to reaction (1). In this way, we rationalize the results from CT and CS calculations.
Conflicts of interest
There are no conflicts to declare.References
- J. Troe, Simplified representation of partial and total rate constants of complex-forming bimolecular reactions, J. Phys. Chem. A, 2015, 119, 12159–12165 CrossRef CAS PubMed.
- A. I. Maergoiz, E. E. Nikitin and J. Troe, Electronic nonadiabatic effects in low temperature radical-radical reactions. I. C(3P) + OH(X2Π), J. Chem. Phys., 2014, 141, 044302 CrossRef CAS PubMed.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Asymptotic interaction between open shell partners operative in low-temperature complex formation: H(2S) + O2(X3Σg-) and O(3P) + OH(2Π) systems, in Theory of chemical reaction dynamics, NATO ASI Series, ed. G. Lendvay, Kluwer, Dordrecht, 2004, pp. 21 – 44 Search PubMed.
- M. M. Graff and A. F. Wagner, Theoretical studies of fine-structure effects and long-range forces: Potential energy surfaces and reactivity of O(3P) + OH(2Π), J. Chem. Phys., 1990, 92, 2423–2439 CrossRef CAS.
- A. Potapov, A. Canosa, E. Jiménez and B. Rowe, Uniform supersonic chemical reactors: 30 years of astrochemical history and future challenges, Angew. Chem., Int. Ed., 2017, 56, 8618–8640 CrossRef CAS PubMed.
- K. M. Hickson and A. Bergeat, Low temperature kinetics of unstable radical reactions, Phys. Chem. Chem. Phys., 2012, 14, 12057–12069 RSC.
- M. Quack and J. Troe, Specific rate constants of unimolecular processes II.Adiabatic channel model, Ber. Bunsen-Ges. Phys. Chem., 1974, 78, 240–252 CrossRef CAS.
- M. Quack and J. Troe, Complex formation in reactive and inelastic scattering: Statistical Adiabatic Channel Model of unimolecular processes III, Ber. Bunsen-Ges. Phys. Chem., 1975, 79, 170–183 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. I. Ion - dipole capture, J. Chem. Phys., 1996, 105, 6263–6269 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. II. Ion - quadrupole capture, J. Chem. Phys., 1996, 105, 6270–6276 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical trajectory and adiabatic channel study of the transition from adiabatic to sudden capture dynamics. III. Dipole - dipole capture, J. Chem. Phys., 1996, 105, 6263–6269 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical trajectory and statistical adiabatic channel study of the dynamics of capture and unimolecular bond fission. IV. Valence interactions between atoms and molecules, J. Chem. Phys., 1998, 108, 5265–5280 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin, J. Troe and V. G. Ushakov, Classical trajectory and statistical adiabatic channel study of the dynamics of capture and unimolecular bond fission. V. Valence interactions two linear rotors, J. Chem. Phys., 1998, 108, 9987–9998 CrossRef CAS.
- E. I. Dashevskaya, I. Litvin, E. E. Nikitin and J. Troe, Modelling low-energy electron-molecule capture processes, Phys. Chem. Chem. Phys., 2008, 10, 1270–1276 RSC.
- F. Pauzat, Y. Ellinger, G. Berthier, M. Gérin and Y. Viala, Theoretical study of a basic process in interstellar nitrogen chemistry: reaction of N with OH, Chem. Phys., 1993, 174, 71–79 CrossRef CAS.
- M. Stumpf, A. J. Dobbyn, D. H. Mordaunt, H.-M. Keller, H. Flöthmann, R. Schinke, H.-J. Werner and K. Yamashita, Unimolecular dissociations of HCO, HNO, and HO2: From regular to irregular dynamics, Faraday Discuss., 1995, 102, 192–213 RSC.
- R. Guadagnini, G. C. Schatz and S. P. Walch, Global potential energy surfaces for the lowest 1A′, 3A′′, and 1A′′ states of HNO, J. Chem. Phys., 1995, 102, 774–783 CrossRef CAS.
- D. H. Mordaunt, H. Flöthmann, M. Stumpf, H.-M. Keller, C. Beck, R. Schinke and K. Yamashita, The dissociation of HNO. I. Potential energysurfaces for the X 1A’, A 1A’’, and a 3A’’ states, J. Chem. Phys., 1997, 107, 6603–6615 CrossRef CAS.
- A. Li, C. Xie, D. Xie and H. Guo, A global ab initio potential energy surface for HNO (a3A′′) and quantum mechanical studies of vibrational states and reaction dynamics, J. Chem. Phys., 2011, 134, 194309 CrossRef PubMed.
- U. Bozkaya, J. M. Turney, Y. Yamaguchi and H. F. Schaefer, The lowest electronic singlet and triplet potential energy surfaces for the HNO – NOH system: Energetics, unimolecular rate constants, tunneling and kinetic isotope effects for the isomerization and dissociation reactions, J. Chem. Phys., 2012, 136, 164303 CrossRef PubMed.
- C. J. Cobos, Theoretical analysis of the rate constants for the interstellar reaction N + OH → NO + H, Int. J. Chem. Kinet., 1995, 27, 219–233 CrossRef CAS.
- D. Edvardsson, C. F. William and D. C. Clary, Rate constant calculations on the N(4S) + OH (X2Π)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) reaction, Chem. Phys. Lett., 2006, 431, 261–266 CrossRef CAS.
reaction, Chem. Phys. Lett., 2006, 431, 261–266 CrossRef CAS. - T. Stoecklin, B. Bussery-Honvault, P. Honvault and F. Dayou, Asymptotic potentials and rate constants in the adiabatic capture centrifugal sudden approximation for X + OH(X2Π) → OX + H(2S) reactions where X = O(3P), S(3P) or N(4S), Comput. Theor. Chem., 2012, 990, 39–46 CrossRef CAS.
- R. Guadagnini, G. C. Schatz and S. P. Walch, Quasiclassical trajectory studies of N + OH, O + NH, and H + NO collisions using global ab initio potential energy surfaces, J. Chem. Phys., 1995, 102, 784–791 CrossRef CAS.
- M. Jorfi, P. Honvault and P. Halvick, Quasi-classical determination of integral cross-sections and rate constants for the N + OH → NO + H reaction, Chem. Phys. Lett., 2009, 471, 65–70 CrossRef CAS.
- M. Jorfi, P. Honvault and P. Halvick, Quasiclassical trajectory calculations of differential cross sections and product energy distributions for the N + OH → NO + H reaction, J. Chem. Phys., 2009, 131, 094302 CrossRef PubMed.
- C. Xie, A. Li, D. Xie and H. Guo, State-to-state quantum dynamics of the N(4S) + OH (X2Π) → H(2S) + NO (X2Π) reaction, J. Chem. Phys., 2011, 135, 164312 CrossRef PubMed.
- N. Bulut, O. Roncero, M. Jorfi and P. Honvault, Accurate time dependent wave packet calculations for the N + OH reaction, J. Chem. Phys., 2011, 135, 104307 CrossRef PubMed.
- X. Hu, C. Xie and D. Xie, State-to-state reaction dynamics for the reaction of atom N with radicals, Int. J. Quantum Chem., 2015, 115, 596–606 CrossRef CAS.
- M. J. Howard and I. W. M. Smith, Direct rate measurements on the reactions N + OH →NO + H and O + OH →O2 + H from 250 to 515 K, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 997–1008 RSC.
- W. H. Brune, J. J. Schwab and J. G. Anderson, Laser magnetic resonance, resonance fluorescence, and resonance absorption studies of the reactions O + OH →O2 + H, O + HO2 →OH + O2, N + OH →NO + H, and N + HO2 → products at 300 K between 1 and 5 torr, J. Phys. Chem., 1983, 87, 4503–4514 CrossRef CAS.
- I. W. M. Smith and D. W. A. Stewart, Low-temperature kinetics and reactions between neutral free radicals. Rate constants for the reactions of OH radicals with N atoms (103 ≤T/K ≤294) and with O atoms (158 ≤T/K ≤294), J. Chem. Soc., Faraday Trans., 1994, 90, 3221–3227 RSC.
- J. Daranlot, M. Jorfi, C. Xie, A. Bergeat, M. Costes, P. Caubet, D. Xie, H. Guo, P. Honvault and K. M. Hickson, Revealing atom-radical reactivity at low temperature through the N + OH reaction, Science, 2011, 334, 1538–1541 CrossRef CAS PubMed.
- M. L. Dubernet and R. McCarroll, Rotational state dependence of ion-polar molecule reactions at very low temperature, Z. Phys. D: At., Mol. Clusters, 1989, 13, 255–258 CrossRef CAS.
- J. Troe, Statistical adiabatic channel model for ion-molecule capture processes. II. Analytical treatment of ion-dipole capture, J. Chem. Phys., 1996, 105, 6249–6262 CrossRef CAS.
- J. A. Miller, Nonstatistical effects and detailed balance in quasiclassical trajectory calculations of the thermal rate coefficient for O + OH →O2 + H, J. Chem. Phys., 1986, 84, 6170–6177 CrossRef CAS.
- G. Nyman and J. Davidsson, A low-energy quasiclassical trajectory study of O(3P) + OH(2Π) → O2(3Σg-)+ H(2S)”. II. Rate constants and recrossing, zero-point energy effects, J. Chem. Phys., 1990, 92, 2415–2422 CrossRef CAS.
- G. Nyman, Dynamical and statistical behaviour of O(3P) + OH(2Π) → H(2S) + O2(3Σg-), Chem. Phys., 1993, 173, 159–66 CrossRef CAS.
- A. I. Maergoiz, E. E. Nikitin and J. Troe, Statistical interpretation of rate constants for the reaction N + OH →NO + H. I. Thermal rate constants, J. Chem. Phys. Search PubMed , to be submitted..
- A. I. Maergoiz, E. E. Nikitin and J. Troe, Statistical interpretation of rate constants for the reaction N + OH →NO + H. II. Product energy distributions, J. Chem. Phys. Search PubMed , to be submitted..
- E. Goos, A. Burcat and B. Ruscic, Extended Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables, http://burcat.technion.ac.il/div September 2005, January 2015 Search PubMed.
- E. E. Nikitin and S. Ya. Umanskii, Theory of slow atomic collisions, Springer Series in Chemical Physics, Springer-Verlag Berlin, New York, 1984, vol. 30 Search PubMed.
- K. Sakimoto and K. Takayanagi, Influence of the dipole orientation on the low-energy ion-molecule reactions, J. Phys. Soc. Jpn., 1980, 48, 2076–2083 CrossRef CAS.
- D. R. Bates, Ion-polar molecule encounters, Proc. R. Soc. London, Ser. A, 1982, 384, 289–300 CAS.
- A. Zanchet, B. Bussery-Honvault, M. Jorfi and P. Honvault, C(3P) + OH(X2Π)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) → CO(a3Π) + H(2S) reaction: fully global ab initio energy surfaces of the 12A′′ and 14A′′ excited states and non adiabatic couplings, Phys. Chem. Chem. Phys., 2009, 11, 6182–6191 RSC.
→ CO(a3Π) + H(2S) reaction: fully global ab initio energy surfaces of the 12A′′ and 14A′′ excited states and non adiabatic couplings, Phys. Chem. Chem. Phys., 2009, 11, 6182–6191 RSC. - M. Jorfi, T. González-Lezana, A. Zanchet, P. Honvault and B. Bussery-Honvault, Quasiclassical trajectoryand statistical quantum calculations for the C + OH →CO + H reaction on the first excited 12A′′ potential energy surface, J. Phys. Chem. A, 2013, 117, 1872–1879 CrossRef CAS PubMed.
- M. Jorfi, B. Bussery-Honvault, P. Honvault, T. Stoecklin, P. Larrégaray and P. Halvick, Theoretical sensitivity of the C(3P) + OH(X2Π) → CO(X1Σ+) + H(2S) rate constant: The role of the long-range potential, J. Phys. Chem. A, 2010, 114, 7494–7499 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2022 |