Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hybrid scanning electrochemical cell microscopy-interference reflection microscopy (SECCM-IRM): tracking phase formation on surfaces in small volumes
Dimitrios
Valavanis†
 a,
Paolo
Ciocci†
b,
Gabriel N.
Meloni†
a,
Paolo
Ciocci†
b,
Gabriel N.
Meloni†
 a,
Peter
Morris
a,
Jean-François
Lemineur
b,
Ian J.
McPherson
a,
Peter
Morris
a,
Jean-François
Lemineur
b,
Ian J.
McPherson
 a,
Frédéric
Kanoufi
a,
Frédéric
Kanoufi
 *b and
Patrick R.
Unwin
*b and
Patrick R.
Unwin
 *a
*a
aDepartment of Chemistry, University of Warwick, Coventry CV4 7AL, UK. E-mail: p.r.unwin@warwick.ac.uk
bUniversité de Paris, ITODYS, CNRS, F-75006 Paris, France. E-mail: frederic.kanoufi@u-paris.fr
First published on 5th October 2021
Abstract
We describe the combination of scanning electrochemical cell microscopy (SECCM) and interference reflection microscopy (IRM) to produce a compelling technique for the study of interfacial processes and to track the SECCM meniscus status in real-time. SECCM allows reactions to be confined to well defined nm-to-μm-sized regions of a surface, and for experiments to be repeated quickly and easily at multiple locations. IRM is a highly surface-sensitive technique which reveals processes happening (very) close to a substrate with temporal and spatial resolution commensurate with typical electrochemical techniques. By using thin transparent conductive layers on glass as substrates, IRM can be coupled to SECCM, to allow real-time in situ optical monitoring of the SECCM meniscus and of processes that occur within it at the electrode/electrolyte interface. We first use the technique to assess the stability of the SECCM meniscus during voltammetry at an indium tin oxide (ITO) electrode at close to neutral pH, demonstrating that the meniscus contact area is rather stable over a large potential window and reproducible, varying by only ca. 5% over different SECCM approaches. At high cathodic potentials, subtle electrowetting is easily detected and quantified. We also look inside the meniscus to reveal surface changes at extreme cathodic potentials, assigned to the possible formation of indium nanoparticles. Finally, we examine the effect of meniscus size and driving potential on CaCO3 precipitation at the ITO electrode as a result of electrochemically-generated pH swings. We are able to track the number, spatial distribution and morphology of material with high spatiotemporal resolution and rationalise some of the observed deposition patterns with finite element method modelling of reactive-transport. Growth of solid phases on surfaces from solution is an important pathway to functional materials and SECCM-IRM provides a means for in situ or in operando visualisation and tracking of these processes with improved fidelity. We anticipate that this technique will be particularly powerful for the study of phase formation processes, especially as the high throughput nature of SECCM-IRM (where each spot is a separate experiment) will allow for the creation of large datasets, exploring a wide experimental parameter landscape.
Introduction
The ability to visualise and study phase formation and change is extremely important in materials science, to understand processes such as crystallisation, precipitation, and deposition. Practical applications include the development of new pharmaceuticals,1 crop protection agents,2 new energy storage materials,3 among others. Many techniques are available to track phase formation, including optical,4 fluorescence,5 and scanning electron and transmission electron microscopies (SEM/TEM),6 as well as Raman and infrared spectroscopy,7,8 or scanning probe techniques like scanning tunnelling microscopy or atomic force microscopy (STM/AFM).9,10 Application of microscopy with electrochemical control is particularly attractive as it provides a means to trigger, monitor and track (electro)chemical processes, ultimately at the single entity level.11,12 More generally, the use of co-located microscopy techniques that probe and correlate structure and activity in the same space have the power to reveal surface processes in quantitative microscopic detail,13 particularly when applied in operando.14–17Electrochemical techniques can be used to change solution composition in a controlled manner, by either consuming/producing reagents at the surface of an electrode immersed in a solution,18–20 or by precisely mixing reagents using migration and electroosmotic flow in a nanopipette.21–24 A particular advantage of electrochemistry is that the driving force can usually be controlled via the applied potential and mass transport can be varied over a wide range, and modelled with a high degree of accuracy,25–27 allowing spatiotemporal changes in solution composition to be predicted quantitatively.
Recently a hybrid approach, using interference reflection microscopy (IRM) coupled to electrochemistry, was used to visualise and study the growth of ensembles of nanoparticles at optically transparent electrodes, in situ, at different overpotentials.28–30 As a surface sensitive technique, IRM is particularly suited to the investigation of phenomena at the electrode/electrolyte interface.31–34 At optically transparent electrodes, such as indium tin oxide (ITO) immersed in solution, local phase formation and/or change at the electrode surface modify the refractive index, giving rise to a difference in contrast in the observed reflected light image. For example, this phase change can arise from the growth of nanoparticles or crystals at the electrode surface providing real-time in situ observation of the phase formation event.31 The sensitivity of IRM, or its analogue known as iSCAT, named for interferometric scattering microscope,35 can be pushed towards single molecule imaging, or in the context of electrochemistry to the imaging of the restructuring of the electrochemical double layer of nanoparticles.34 Although IRM is usually performed in large electrolyte volume, IRM can be coupled with spatially resolved electrochemical techniques to provide local electrochemical control and monitoring of phase formation events.
Scanning electrochemical cell microscopy (SECCM) provides a powerful platform to create very well defined and consistent microscale and nanoscale-sized electrochemical cells on various substrates.36,37 Since its inception,38,39 SECCM, and the scanning micropipette contact method (SMCM) as an earlier variant was named, has been widely employed to investigate electrochemical processes at the nanoscale, revealing heterogeneous properties of many features of materials including 2D materials,36,40–43 nanotubes,44,45 grain boundaries and crystallographic facets in electrodes and electrocatalysts,46–48 single particles,49–53 among a rapidly expanding range of applications.37 For phase formation and phase change processes, the ability to confine electrochemical reactions to small volumes allows the investigation of a few or even single events.54,55 In this context, the use of SECCM in hopping mode,56 where the SECCM meniscus is landed at a series of spots on a surface, is particularly powerful, as it is possible to build up large datasets with the same, or different, experimental conditions applied to each spot.
In this work, we combine SECCM with the surface sensitivity of IRM to investigate phase formation in tiny droplet cells at an ITO electrode surface. First, we employ this new hybrid technique to visualise and monitor the evolution of the SECCM meniscus dimension during electrochemical actuation. Subtle variations in the meniscus surface area are detected when faradaic current flows at the ITO/electrolyte interface. Meanwhile IRM can track, in situ with high temporal resolution (ms), changes to the electrode within the meniscus footprint, with the indication of indium (In) nanoparticle (NP) formation at potential regions associated with the solvent breakdown at the ITO electrode. Second, as proof of concept of the use of SECCM-IRM to track phase formation, we demonstrate the nucleation and growth of calcium carbonate (CaCO3), driven by a pH change caused primarily by the oxygen reduction reaction (ORR) at the ITO surface. We observe a dependence of the number of crystallisation sites on the electrochemical cell geometry and ORR driving potential. Supported by finite element method (FEM) simulations, we further demonstrate that the pattern of crystals formed within the SECCM meniscus is related to spatiotemporal variations in supersaturation within the meniscus, governed by the interplay between oxygen transport across the meniscus/air interface, and its reduction at ITO, mass transport from the SECCM pipette, coupled to carbonate buffer speciation.
The combination of SECCM and IRM opens up many new opportunities for the investigation of electro(chemical) dynamics at the nanoscale. The successful development and application of SECCM-IRM in this work serves as a foundation for future studies.
Experimental
Reagents and materials
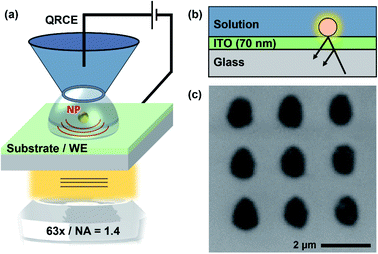
Potassium nitrate (KNO3, Sigma), hydrochloric acid (HCl, 37%, Honeywell Fluka), anhydrous calcium chloride (CaCl2, 96%, Acros Organics), and sodium bicarbonate (NaHCO3, 99+%, Acros Organics), were used as supplied by the manufacturer. Solutions were prepared with ultrapure deionised water (PURELAB Chorus, ELGA, UK).ITO coated coverslips (20 × 20 mm, 70 nm coating thickness, SPI Supplies, USA) served as the working electrode (WE)-IRM substrate. They were first cleaned by sonication in isopropanol and subsequently in deionised water. Electrical connection to the ITO was made by connecting a copper wire to the coverslip with silver conductive paint (RS Components, UK). To secure the wire, two-part epoxy adhesive was used (Araldite, UK). An Ag/AgCl quasi-reference counter electrode (QRCE) was prepared by anodizing 0.125 mm diameter annealed silver wire (99.99%, Goodfellow, UK) in a saturated KCl solution for 10 min. All potentials reported herein are versus this QRCE, which is stable over long experimental run times.57 All SECCM experiments were performed with a single barrel pipette, loaded with electrolyte solution, as the mobile probe.37 Three different sizes of pipettes (end aperture) were used in the experiments, all pulled from borosilicate capillary tubes: (i) 200 nm diameter pipettes from outer diameter (O.D.) 1.2 mm, inner diameter (I.D.) 0.69 mm tubes; (ii) 5 μm diameter pipettes from O.D. 1.0 mm, I.D. 0.5 mm tubes, both pulled using a laser pipette puller (P-2000, Sutter Instrument, USA). (iii) Pipettes with a diameter in the range of 20–30 μm were pulled from O.D. 1.0 mm, I.D. 0.5 mm tubes, using a vertical resistive heating pipette puller (PC-10, NARISHIGE, Japan). Micropipette diameters were measured using an optical microscope before the experiments, while nanopipettes were routinely visualised using SEM and TEM.58
SECCM-IRM instrumentation
An inverted fluorescence microscope (DMI4000B, Leica, Germany) was utilised as the base for the SECCM-IRM workstation. For the IRM measurements, 2 light sources were used to back-illuminate the ITO electrodes: either the blue channel LED (intensity peak at wavelength of 470 nm, full-width at half-maximum (FWHM) bandwidth of 19 nm) from a multi-LED light source (Niji, Bluebox Optics, UK); or a mercury metal halide white light source (EL6000, Leica) in conjunction with a bandpass filter (ET480/20x, intensity peak at 480 nm, FWHM bandwidth of 20 nm, Chroma, USA). Images were captured using a 20× objective (N Plan, numerical aperture (NA) 0.35, Leica) or a 63× oil immersion objective (HCX Plan Apochromatic, NA 1.4, Leica). An additional 1.6× tube lens was used, to achieve up to 100× effective magnification. IRM images were recorded with a CMOS camera (C11440-42U30, Hamamatsu Photonics, Japan) at acquisition rates ranging from 30 to 300 frames per second (FPS). The microscope, camera and light sources were controlled using MicroManager (release 1.4.22, open source).59A two-axis piezoelectric positioning stage (Nano-Bio300, with a Nano-Drive controller, Mad City Labs, USA) was mounted atop the microscope and used to move the ITO substrate (WE) in the XY plane. A single axis piezoelectric actuator (P-753.3, with an E-665 controller, Physik Instrumente, Germany) was used for moving the SECCM probe along the Z axis, perpendicular to the WE plane. For coarse SECCM probe positioning, XYZ micropositioners (M-461-XYZ-M, Newport, USA) were used in conjunction with a Z axis stepper motor (8303 Picomotor Actuator, Newport). All high resolution SECCM approaches were performed using the Z axis piezoelectric actuator.
Electrochemical measurements were performed using custom built current followers. Data acquisition and SECCM probe positioning control were performed by an FPGA card (USB-7856R OEM, National Instruments, USA), in turn governed by the Warwick Electrochemical Scanning Probe Microscopy (WEC-SPM) platform,60 controlled by LabVIEW software (release 2019, National Instruments). Image recording was triggered from the WEC-SPM platform, by outputting a TTL signal to the camera input trigger port. The camera output trigger’s pulse train was also fed to the FPGA card, and recorded concurrently with the electrochemical measurements, allowing synchronous analysis and presentation of SECCM and IRM data. The entire equipment (microscope, stage, positioners, and camera) was enclosed in a Faraday cage, lined with thermal isolation panels, and supported on an active optical table (CleanBench, TMC, USA).
Electrochemical data processing and plotting was carried out using the MATLAB (release R2019b, The MathWorks, Inc., USA) and OriginPro (release 2021, OriginLab, USA) software packages. Image analysis and treatment was performed with custom Python routines based on Skimage and Trackpy packages (release 2021, open source).
Raman spectroscopy
Raman spectra were recorded using a Raman microscope (Horiba LabRam HR Evolution) fitted with a charged couple device detector and a 660 nm OPSS laser. A 50× (0.5 NA) objective and 1800 lines mm−1 grating was used, with 10 × 1 s acquisitions averaged per spectrum.Reactive-transport modelling
The time-dependent speciation inside the meniscus and pipette were simulated by numerically solving the diffusion equation for the system using the FEM in COMSOL Multiphysics (version 5.6, COMSOL Inc., USA). A typical axisymmetric geometry consisting of the end of the pipette and the SECCM meniscus was based on optical images of the pipette and the wetted area observed by IRM. We applied the reactive-transport model we previously reported for time-dependent CaCO3(aq) speciation.21 Simulation details are further described in the FEM results section below.Results and discussion
SECCM-IRM principles
The SECCM-IRM setup is presented schematically in Fig. 1. It consists of an inverted optical microscope which focuses the light source, through an objective lens, onto the back of an ITO-coated glass coverslip. The top conductive side of the coverslip is used as the WE. The SECCM probe, loaded with electrolyte solution (50 mM KNO3, for the study of ITO; and 5 mM CaCl2 and 5 mM NaHCO3 (pH 2.7 HCl) for the crystallisation experiments) and containing a QRCE, was coarsely brought closer to the ITO substrate using the micromanipulators and the stepper motor. The SECCM QRCE potential was controlled during the experiments, while the ITO substrate (WE) was held at a virtual ground. The resulting current was measured at the WE with a custom-built current follower. For ease of interpretation, all potentials reported are for the WE electrode, which is the negative value of the SECCM QRCE potential. Final tip approach was performed by applying a small bias between the QRCE and WE (+0.2 V for ITO studies and −0.1 V for the crystallisation experiments). The probe movement stopped automatically as soon the current was above a threshold, set at the noise level (ranging between 100 fA and 30 pA, depending on the sensitivity of the current follower that was appropriate for each probe size). The event indicated contact between the electrolyte meniscus formed at the end of the probe and the WE, resulting in a small electrochemical cell, with dimensions related to the tip-end diameter used. This event could also be detected in the IRM images (vide infra).The optical detection principle has been detailed in previous works.28,31,32 It is based on the reflection of the light wave at the ITO–electrolyte interface and its possible interference with light wave scattered by objects present on the ITO surface, which disturb the local optical conditions and are highlighted within the background, with the camera acting as an interferometric detector. Optical features can show either a negative contrast, the feature appearing darker than the background, or a positive contrast, where the feature appears brighter than the background. The sign of the contrast depends on the dielectric properties of the object relative to its environment and its size.31,61
Once the meniscus had landed on the WE (no contact from the pipette itself), a short pause allowed monitoring of the meniscus stability and provided a background for later image treatment (vide infra). The potential was then swept or stepped to drive ORR (and water reduction) at the WE, with synchronous IRM visualisation of the meniscus footprint region. Once the potential sweep or step was finished, the potential was switched back to the approach value. The probe was then retracted, to detach the meniscus from the surface, and the WE shifted laterally and the approach recommenced. In this way, the experiment could be repeated on a fresh ITO region, allowing replicates of the experiment (Fig. 1). IRM images were acquired synchronously throughout the entire experiment.
Real-time imaging of the SECCM meniscus
The use of IRM opens up the possibility of real-time, in situ, tracking of the SECCM meniscus, allowing monitoring of its size and shape during experiments and the (electro)chemical phenomena occurring within. This opens the possibility of important phenomena such as the wetted area dependence on potential (electrowetting) to be studied. Although the wetted area may have little impact on the SECCM currents for steady-state transport-limited measurements,62 it is of great importance for new applications where current density is essential, such as in energy storage/conversion materials.63Previously, the meniscus contact area and size has been deduced or inferred from a variety of means, including: (i) scanning sharp electroactive features on surfaces, such as individual single walled nanotubes, the border between an electrode and insulator, or step edges, and tracking the resulting current–lateral distance profiles with nm-resolution;36,44,64–66 (ii) measuring droplet footprints or line tracks left on a surface, with SEM or AFM, after SECCM scanning under certain conditions;36,63,67 (iii) AFM analysis of surface patterns after SECCM molecular-grafting, polymerisation or adsorption;68–72 (iv) AFM analysis of SECCM etch features;73,74 (v) in situ visualisation of the meniscus and nanopipette with laser scanning fluorescence microscopy;62 (vi) analysis of dual-channel ion conductance tip approach curves.36,62,75 Nonetheless, as we show herein, IRM provides unprecedented views of the SECCM meniscus dynamics under operation.
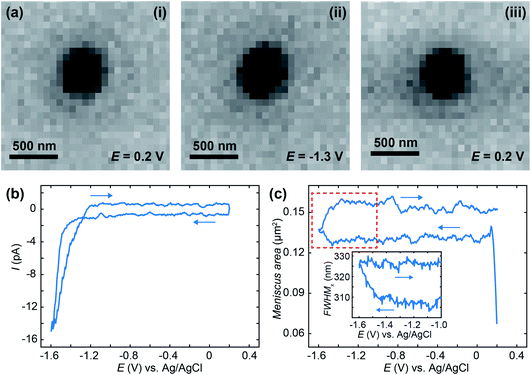
To demonstrate IRM SECCM-meniscus imaging in real-time, we repeatedly approached a 50 mM KNO3-loaded 200 nm diameter nanopipette to an ITO substrate and recorded cyclic voltammograms between +0.2 V and −1.6 V at 1.7 V s−1 while IRM images were synchronously recorded at a rate of 325 FPS. This procedure was repeated at 17 different locations over the ITO substrate. Fig. 2a shows IRM images of the meniscus (dark contrasted area), which has a diameter of ca. 400 nm, at selected potentials. The voltammograms (Fig. 2b) show no faradaic contribution before solvent breakdown at the extreme cathodic potential. The evolution of the dimension of the meniscus footprint was monitored during each voltammogram. The area of the meniscus was evaluated either from the surface area (in pixels) of the dark region in the centre of the images, or from the super-localization of its edges along two orthogonal directions.
The meniscus was rather reproducible among the 17 different experiments with an overall ±5% variation in area, measured during the short pause after meniscus landing. Fig. 2c gives the evolution of the ensemble-averaged surface area of 17 menisci during the potential cycle. The meniscus was rather stable during the forward potential scan from 0 V to −1.47 V, but its surface area increased when faradaic current flowed, in the solvent breakdown region. On the reverse scan, the meniscus did not retract to its original dimension. Note that the sudden increase in the meniscus size to a stable value at the start of the scan is associated with meniscus landing that we will analyse in detail elsewhere.
The inset of Fig. 2c shows the evolution (in a narrower potential region from −1 V to −1.6 V) of the width of an individual meniscus estimated from the FWHM of the intensity profile. If the surface area provides an estimate with a quantum pixel resolution, the edge localization procedure allows sub-pixel resolution, here the individual meniscus diameter increases by 0.31 pixel, 20 nm, above the usual 5 nm resolution of the procedure.76,77 The observed electrowetting is not attributed to double layer charging effects since it rather occurs in the solvent electrochemical decomposition. However, the observed phenomena are in general agreement with the Lippmann equation predicting a decrease of the droplet contact angle (and therefore increase in its footprint) with applied voltage.78–80
SECCM-IRM offers a non-invasive dynamic observation of the meniscus with unprecedented >300 FPS image acquisition rate of the whole meniscus and, through superlocalization strategy, with sub-10 nm relative size variation. Other high spatial resolution methods used to infer the SECCM meniscus size, such as SEM or AFM are performed ex situ on the meniscus footprint.
NP growth within a nanometre sized meniscus
The faradaic current flowing at the most cathodic potentials can be attributed to solvent breakdown, and there may also be the reduction of ITO producing surface confined In NPs. This process has been evidenced by ex situ SEM images of the electroreduced NPs for a variety of electrolyte composition and pH.81 The dynamics of the NP formation and its competition with H2 nanobubble electrogeneration during the hydrogen evolution reaction (HER) was more recently monitored in situ by IRM.32From the previously reported optical and SEM images, the density of In NPs is of the order of 108 cm−2.31 Thus, in principle, the confined region on the ITO WE accessed by SECCM facilitates the study of a single NP formation and growth event. For example, within a meniscus of diameter, d < 500 nm, such as the one monitored in Fig. 2a, the probability of finding one nucleation site is below 1 for an average nucleation site density lower than 4/πd2 = 5 × 108 cm−2.
Although previous studies of nucleation/growth of NPs with optical microscopy monitoring could optically isolate a single event, the electrochemical information (current) associated to such event was recorded for the entire electrode, averaged over the ensemble of NPs.28–30,82 In contrast, with SECCM-IRM, the current is confined to the small SECCM meniscus, allowing the synchronous electrochemical monitoring and optical imaging of a single event.83 Image background subtraction is then a helpful technique to improve analyses of noisy data sets and it is often used in image processing in IRM.28 The IRM image captured during the last instant before the potential cycle was switched on can be used as the background image, which is taken to be equivalent of the system baseline state. The individual pixel intensity values of the background are subtracted from the intensity values of all the subsequent IRM images. For periodic noise, created by fluctuations in the light source output, time domain filtering is also applied: images with sharp intensity changes repeated periodically are excluded from the image stack; and pixel-by-pixel sliding-window smoothing is applied.
A treated version of the IRM snapshots at 0.2, −1.3 and −1.5 V for the forward scan and 0.2 V for the reverse scan can be seen in Fig. 3a, with an indicative delimitation of the meniscus border (red dashed circle). These images can be compared to the raw images for 0.2, −1.3 (forward) and 0.2 V (reverse) in Fig. 2a. The image is featureless during the forward scan until the potential reaches −1.5 V, or until a significant cathodic current is flowing (Fig. 2b). Once cathodic current flows, an optical feature is clearly visible inside the meniscus perimeter, which was not visible in the untreated data (Fig. 2a(ii)), and this feature remains during the whole reverse scan (at 0.2 V in Fig. 3a). By inspecting the intensity (Fig. 3b) of the region of interest (ROI) within the meniscus (red dashed circle in Fig. 3a) throughout the entire image series, a decrease in the intensity was initiated at −1.5 V and is maintained over the cycle. Assigning t = 0 to the onset of the potential cycle, the intensity of the ROI is also plotted vs. time in Fig. 3c. These data show that the intensity decreases over time after the feature appears on the image, indicating that the feature is growing in size with time, alongside the electrode plane.31,32,61 Furthermore, by integrating the current over the cyclic voltammogram, one obtains the charge flowing through the ITO. The variation of the ROI intensity profile is remarkably similar to the morphology of the charge–time transient in Fig. 3c.
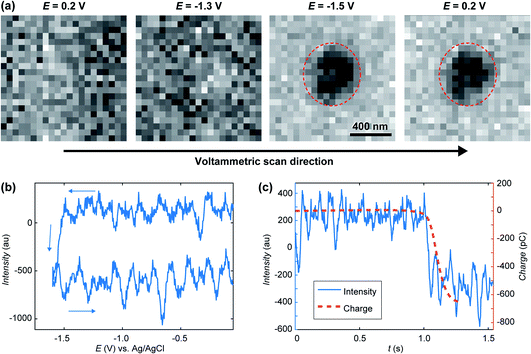 | ||
| Fig. 3 (a) Treated IRM images recorded during the cyclic voltammetry in Fig. 2a, showing the presence of a feature inside the SECCM meniscus after −1.5 V was reached on the forward scan. (b) Opto-voltammogram showing the intensity in the corresponding ROI (red circle in part a) over the applied potential range. (c) Charge transient (calculated from integrating the current in Fig. 2a) compared to the optical intensity transient (t = 0 at the onset of the cyclic voltammetry). | ||
The feature may have two possible chemical origins. It could be related to HER and nanobubble formation or the reduction of ITO into In NP. The formation of a nanobubble at such a small volume would likely block the pipette opening which would be detected by a sudden drop in electrochemical current.84 Also, once HER had stopped (in the reverse scan) the nanobubble would dissolve back into solution quickly, which would be discerned by the IRM intensity.85,86 The current magnitude increases along the forward potential cycle and a crossing of the forward trace is detected on the reverse. Such crossing is often observed during the electrodeposition of metals and is usually attributed to the formation of a material with increased electroactive area (and electroactivity). From the electrowetting analysis, in Fig. 2c, one could evaluate the variation in current density during voltammetry, knowing the dynamic meniscus surface area, obtained from Fig. 2c. When this is done, the same voltammetric shape presenting the crossing branches is observed, indicating that the crossing is not related to the change in meniscus surface area. It is then due to the formation of a material with higher electrochemical activity than the ITO, as would most likely be the metal In formed during ITO reduction. The ability to visualise, track and record the current flow for a single sub-diffraction limited event corresponding to ITO reduction into In NP with high temporal resolution of better than 5 ms, showcases the capabilities of SECCM-IRM for single entity opto-electrochemical dynamic measurements.
Moreover, from observations of both the meniscus surface area and surface degradation, we conclude that ITO is optically stable for IRM during electrochemical experiments (E > −1.5 V in KNO3 at neutral pH), enabling us to monitor the electrodeposition of various nanomaterials in a rather large potential window. However, any interference or influence from possible ITO instability has to be considered for each particular set of conditions, as illustrated in the next section.
Controlled CaCO3 crystallisation in a microscale meniscus
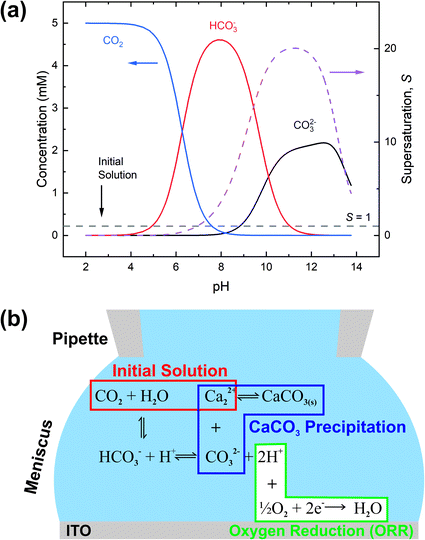
We now turn to the electrochemically-induced deposition of insulating materials on ITO. For this we take CaCO3 as our model system and use the slightly larger volumes provided by the meniscus of a few μm (1–8 μm) diameter SECCM probe. The use of a larger meniscus allows us to probe dynamics within a population of nano-entities within the electrolyte.CaCO3 is found throughout the natural world where it exists in a variety of structural forms (polymorphs) and morphologies. Many biological systems utilise CaCO3 in their structural, defensive and optical structures, and have the ability to control and even switch between different polymorphs.87 The product of crystallisation is also heavily dependent on the reaction volume, with small (micron-size) volumes stabilising early-stage, less stable forms (e.g. amorphous calcium carbonate, ACC).16 The early stages of CaCO3 precipitation remain hotly debated,88–90 although it is known to proceed via rapid formation of ACC at moderate supersaturations.
To control the precipitation of CaCO3 we modify the local supersaturation, S:
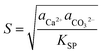 | (1) |
Electrochemically-induced CaCO3 precipitation was investigated across a series of applied potentials at the ITO electrode starting from the same initial solution. In each case a small potential (−0.1 V) was used to approach the SECCM probe to the surface. This potential was held for 1 s to allow the SECCM meniscus to stabilise before being switched to the potential of interest for 10 s, and then back to −0.1 V while the probe retracted, ensuring a constant reaction time in each case. To maintain the pipette solution conditions over the course of several depositions, on alternate approaches of the probe to the surface, the potential was not switched, so as to allow the solution to re-equilibrate and any precipitate within the tip to be removed by deposition via meniscus contact with the ITO surface. This procedure was repeated by means of successive approaches at different locations of the ITO surface to form an array of points, typically with 5–8 repeats at each potential.
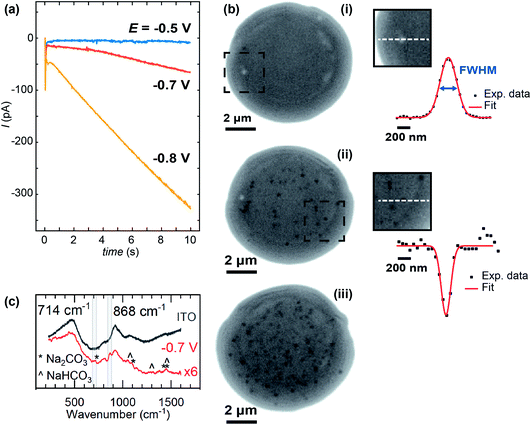
Whole, ca. 8 μm wide, meniscus IRM images, after 10 s of polarisation at three different potentials, are shown in Fig. 5, along with the current–time (I–t) traces recorded (Fig. 5a). The dark contrasted area delineates the meniscus region. At less negative potential (Fig. 5b(i)), the current was negligible and only a few bright spots are observed by IRM. At −0.7 V (Fig. 5b(ii)), however, a more significant current was recorded, and multiple spots, now dark, are observed in the images. This trend continues at −0.8 V (Fig. 5b(iii)), but at −0.85 V (not shown), although the current magnitude was still increasing, no clear spots inside the meniscus were seen. Feature detection was hampered by a general darkening of the spot area at this potential and below. The I–t traces in all cases where E < −0.5 V show non-monotonic behaviour. An initial spike to negative currents is followed by a rapid decay, and the onset of a sustained increase towards more negative currents. This is unexpected for an ORR pulse at ITO and could suggest that either the crystallisation events or a separate process at the ITO, possibly the formation of In NPs (vide infra), are increasing the surface activity.
The size of the optical features seen in the IRM images can be estimated by their FWHM intensity, which is calculated by fitting a Gaussian function to the intensity profiles. The smallest FWHM associated with the dark features in Fig. 5b(ii) and (iii) are 185 ± 25 nm (from 30 spots – with an example shown in Fig. 5b(ii)). Optical features characterized by this low limit value of FWHM can be considered as diffraction-limited, suggesting that nanometric particles (<200 nm) have been generated. The bright features observed at −0.5 V (Fig. 5) increase in intensity with time, in contrast to a decrease observed for the lower potentials. Such behaviour is attributed to the difference in size of the particles formed, as was demonstrated in earlier work for gas nanobubbles: bubbles larger than ca. 300 nm appeared lighter than the background, those smaller appeared darker.32 Despite a difference in the shape and refractive index of the CaCO3 deposits, we might expect a similar behaviour. Indeed, the bright features also show two-fold larger FWHM (365 nm – see example in Fig. 5b(i)), indicating a particle > 300 nm in size at E = −0.5 V, while the FWHM remains diffraction-limited during the whole course of experiments at the other potentials.
For E < −0.85 V, in addition to the formation of NPs, a homogeneous decrease of the optical intensity was observed over the entire meniscus area (no change detected for the outer ITO/air interface region). This can be explained if a homogeneous decrease of the reflective properties of the ITO/electrolyte interface is considered, and most likely results from the deposition of a homogeneous layer of CaCO3, or a highly dense array of nanoobjects separated by <500 nm such that they cannot be resolved by the optical visualisation, onto the ITO surface. These large negative driving potentials will lead to more rapid formation of the supersaturation condition,19 and faster nucleation generally results in more nuclei and hence particles. Dense layers of ACC are also known to form at interfaces at appropriately high supersaturations.91 At such negative potentials and low pH, the reductive degradation of ITO may also occur.32 The formation of CaCO3 crystals is supported by ITO background-subtracted Raman micro-spectroscopy of a dried meniscus deposited at −0.7 V, which reveals spectra with peaks consistent with the presence of CaCO3 particles (Fig. 5c). A broad peak at 868 cm−1 is consistent with either the ν3 mode of amorphous CaCO3 (863 cm−1) or calcite (873 cm−1), while a small feature at 714 cm−1 is also consistent with calcite.92
Controlled CaCO3 crystallisation at a larger meniscus
Using pipette probes of tens of μm in diameter allows investigation of even larger areas and the production of a population of hundreds or thousands of electrochemically-induced crystallisation events. At this length scale surface heterogeneities, concentration gradients over the meniscus volume and localized fluxes may contribute to the SECCM-IRM observations. Fig. 6 shows example IRM images taken after 8 s for two different applied potentials at the ITO electrode.When the applied potential is −0.8 V (Fig. 6a(ii)), a number of features, are observed. Most features show bright contrast and we observe a few aggregates, where neighbouring features coalesce. Experiments at −1.0 V (Fig. 6b) show no homogeneous drop in optical intensity over the meniscus: a much larger amount of nanometric features are observed at the beginning of the potential pulse (Fig. 6b(iii)) which quickly grow to form a variety of μm-sized crystals with different size and shape, formed from the aggregation of nanometric deposits. For both −0.8 V (Fig. 6a(ii)) and −1.0 V (Fig. 6b(ii)) dark contrasted features are also detected. This behaviour is similar to that in the small meniscus and, as suggested by the background experiments and cyclic voltammograms in acidic media (vide infra), the features could be associated with indium oxide (In2O3) reduction into metallic In.
Further spatiotemporal analysis of the crystallisation events show that the position of emerging new optical features in the meniscus, plotted as the radial position (dc) divided by the meniscus radius (r), as a function of time, has a non-stochastic trend with the onset time of crystallisation for −0.8 V (Fig. 6a(iii)) and −1.0 V (Fig. 6b(iii)). In the first 0.5 s after the potential was applied, a large percentage of the events initiate in a circular crown between 0.4 < dc/r < 0.9 for E = −0.8 V and between 0.5 < dc/r < 0.8 for E = −1.0 V. Other crystals start to be formed in areas closer to the meniscus centre only at longer times.
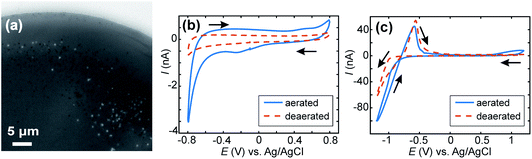
When the experiment was repeated without CaCl2 present in the solution (Fig. 7a) a few spots were observed in the IRM images for E ≤ −1.0 V. For more negative potential, and for the considered acidic pH, it is known that ITO is unstable (with respect to reduction of In to metallic NPs), which has been observed, along with H2 nanobubbles, by IRM previously.32 The features observed here (Fig. 7a) are different in shape and appear in much smaller numbers than those observed when Ca2+ is present. To assess the effect of possible ITO degradation to the overall intensity change seen in IRM, cyclic voltammetry in acid media (HCl solution, pH 2.7) was carried out for aerated and deaerated (with nitrogen) solutions and over 2 different potential windows. Fig. 7b shows the voltammograms recorded from 0.8 to −0.8 V. From this experiment it is clear the SECCM current is predominantly carried by ORR as a clear cathodic wave at around −0.4 V, present in aerated solution, is absent when the solution is deaerated. No other voltammetric feature alludes to ITO degradation, although the relatively large capacitive current might obscure some features. In contrast, for a larger potential window (Fig. 7c), from 1.2 V to −1.2 V, a clear anodic peak at around −0.55 V is observed in the reverse scan, for both the aerated and deaerated solutions. This suggests that under the pH conditions for the CaCO3 studies ITO reduction (leading to the re-oxidation peak at −0.55 V) only starts to become significant at potentials more negative than −0.8 V and that at less cathodic potentials, many (if not all) of the diffraction-limited optical spots can be attributed to CaCO3 particles.
FEM model of CaCO3 precipitation in the larger meniscus
To understand the differences observed when applying −0.8 V and −1.0 V to the larger menisci, reactive transport modelling of the pipette and meniscus was carried out. The model used an axisymmetric geometry based on microscopic characterisation of the pipette and the wetted area observed with IRM. Two approach distances (meniscus heights – dapp) corresponding to the outer radius of the micropipette (31 μm), and half of this value, were modelled. This is because the meniscus thickness impacts O2 transport at the air–water interface (and hence the current distribution).75 We did not measure the meniscus thickness in this work, but for this size pipette it should be achievable in the future through the use of laser scanning confocal microscopy and an appropriate fluorophore.62 Indeed, the use of a pH-sensitive fluorophore would also confirm the pH distribution in these types of experiments.93To achieve a realistic estimate of the supersaturation we consider the 12 most significant species in the solution (the ions Ca2+, Cl−, Na+, HCO3−, CO32−, H+ and OH−, the ion pairs NaCO3−, CaCO30, NaHCO3 and Ca(HCO3)+ and the gas phase species O2 and CO2) based on prior modelling with the PHREEQC speciation code.94 We solved the diffusion eqn (2) for the flux of the ith species, Ji, at concentration, ci, and time, t. Equilibria between the species was maintained by the continuity equation (eqn (3)), where Ri is the reaction flux necessary to maintain equilibrium (although deviations of up to 400% in equilibrium constants at long times were observed as there was a limitation on the rate of HCO3− dissociation that could be applied for reasonable computational efficiency, which would lead to an underestimate of supersaturation). Equilibrium constants were based on the local species activity ai (eqn (4)), calculated from the activity coefficient γi based on the local ionic strength, I (eqn (5)) using the Davies equation (eqn (6)) with A = 1.82 × 106 (εT)−3/2, where ε is the solution permittivity. For charged species b = 0.3, for uncharged species b = 0.1. Note that direct capture of CO2 by OH− to form HCO3− (as opposed to equilibration with H2O to form HCO3− and H+ based on the local pH) was not considered, based on modelling of similar systems where the rate was negligible on these timescales due to the low OH− concentrations.46
| ji = −Di∇ci | (2) |
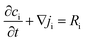 | (3) |
| ai = γici | (4) |
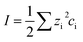 | (5) |
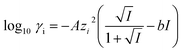 | (6) |
The equilibrium concentrations given by the PHREEQC code were applied as the boundary condition at a plane 3500 μm inside the micropipette. Given the apparent importance of spatial variation across the wetted area, we imposed atmospheric equilibrium concentrations of O2 and CO2 at the air/meniscus interface (273 μM and 13.6 μM, respectively). A consequence of this approximation is that the total concentration of carbon species in the meniscus is depleted relative to that in the micropipette. We note that the alternative limiting treatment of CO2 (no exchange with the atmosphere) would result in greater buffering and therefore longer timescales for the pH swing.
Using the simplifying assumptions that all current arises from the ORR, and that for a given potential, ORR is first order in O2, we imposed an inwards flux of O2 and an outwards flux of OH− at the ITO surface:
| JOH−,ITO = −4JO2,ITO = kORR[O2] | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dA) matched the experimental current. For all other boundaries and species not mentioned, a no flux boundary condition was used.
dA) matched the experimental current. For all other boundaries and species not mentioned, a no flux boundary condition was used.
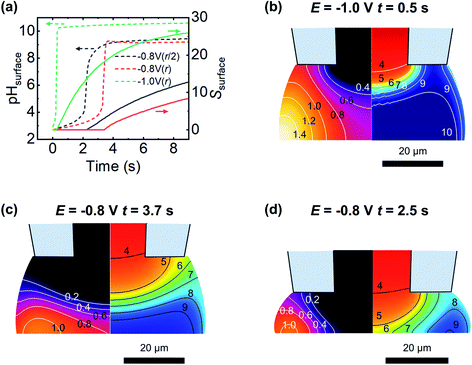
The expected evolution of pH and supersaturation, for fluxes corresponding to the current observed at −0.8 V and −1.0 V, are shown in Fig. 8a. At dapp = r, both pH and S change much earlier at −1.0 V than at −0.8 V, with the −1.0 V case reaching saturation (S = 1) in less than 0.5 s, while −0.8 V takes closer to 4 s. These timescales correspond well with appearance times of new features presented in Fig. 6a(iii) and b(iii), with a clustering of new features around 1 s in the −1.0 V case, and a similar clustering at 4 s in the −0.8 V case. The effect of a closer approach (dapp = r/2) was examined and found to shift the observed changes to earlier times, (ca. 2 s at −0.8 V, Fig. 8a, black line, and ca. 0.4 s at −1.0 V, data not shown for clarity) and corresponding lower values of S. Electroneutrality was also considered and found to be violated as OH− flux into the meniscus is not counter balanced by inward diffusion of cations; however, including electroneutrality (via the coupled Poisson–Nernst–Planck equations, data not shown) led only to minimal changes in timescale, with a slight increase in time taken to reach supersaturation.
The spatial distribution of pH and S at the first timepoint where saturation is observed for both −1.0 V and −0.8 V cases, at dapp = r, are shown in Fig. 8b and c, respectively. Both parameters have a strong spatial dependence, with change starting at the meniscus/air interface where the O2 flux is greatest. Combined with the buffering action at the centre of the droplet due to diffusion from inside the micropipette, this explains the experimentally observed preference for nucleation to occur around the edges of the meniscus rather than at its centre. The pH buffering by atmospheric CO2 may also contribute to the absence of particles at the very edge in the −1.0 V case (Fig. 6b(ii)). At longer times, at −1.0 V the pH of the meniscus rapidly equilibrates and the spatial variation in S and pH is lost, however at −0.8 V slight variation in S and pH across the surface is observed to persist. Closer approaches (to dapp = r/2, Fig. 8d) show a larger degree of spatial variation in pH and S. This simplified model is able to rationalise the timescale over which new features are observed and, to some extent, their spatial variation, emphasising the importance of FEM modelling in interpreting SECCM deposition experiments.
Conclusion
We have demonstrated the combination of SECCM and IRM to produce a new instrumental method for the investigation of electrochemically-driven phase formation phenomena with high spatial and temporal resolution. The already proven capabilities of SECCM to precisely and repeatedly position a small scale meniscus from a pipette tip on a substrate has been married to the IRM surface-sensitive imaging technique, enabling high spatiotemporal imaging of the SECCM footprint and processes occurring within it.Making use of an optically-transparent ITO electrode, we have been able to image and track the stability of the SECCM meniscus size during voltammetry, resolving an important question in SECCM, which has hitherto mainly been addressed with ex situ analysis of droplet footprints or the analysis of SECCM scanning droplet images at a fixed potential. The ability to view the meniscus in situ provides a more holistic view of meniscus contact. Moreover, careful analysis of the IRM images unambiguously showed the growth of diffraction-limited features within the meniscus, attributed to the reduction of ITO into In NP at the most extreme cathodic potentials.
To demonstrate new possibilities for SECCM-IRM, we studied the precipitation of CaCO3 by electrochemically changing the solution pH to create locally supersaturated solution. IRM in situ imaging provided evidence of the number and spatial distribution of crystallisation events over the SECCM meniscus in real-time, revealing striking patterns for different driving potentials and tip sizes. Smaller reaction volumes showed increased density of fairly evenly distributed nanoscale CaCO3 crystals (confirmed by Raman spectroscopy), with increased applied cathodic potential, which created high supersaturation. For larger reaction volumes (SECCM tips), the location of the crystallisation events become dependent on the driving potential hinting at the dynamic interplay between the pipette mass transport, ORR rates at the ITO surface, and CO2 and O2 transport across the air/meniscus interface. FEM simulations have highlighted the origins of the crystallisation patterns and we were able to predict the onset time and, to an extent, the location of the crystallisation events.
More generally, this work establishes a foundation for the use of SECCM-IRM in nanoscale (electro)chemistry. In future work we shall explore the landing and pull-off of the SECCM meniscus on (electrode) surfaces, during translation of the probe to and from the surface, also expanding the work on ITO to other transparent electrode materials. Particularly, we will investigate electrode materials resistant to the electrochemically generated corroding environment, e.g. in this work the CaCO3 electrocrystallisation and its visualisation are complicated by the electrochemical etching of ITO under some conditions. Transparent thin Au coated glass coverslips could be used, as previously demonstrated for the optical monitoring of the electrochemistry of single NPs.28,29,31,95 Coverslips coated with graphene-based materials are also possible electrode candidates, as shown in the IRM imaging of the electrochemistry of graphene oxide.33,95 Finally, reflectivity microscopy can also be operated at reflective and non-transparent electrodes96 and the combination with a modified SECCM setup (e.g., with an angled nanopipette, as used in some scanning ion conductance microscopy studies)97 could be explored. Among other applications, we shall also investigate direct electrodeposition (e.g. of metals), where we shall be able to tie together electrochemical signatures to an optical view of the entire meniscus. SECCM-IRM should reveal considerable new detail on the mechanisms of nanoscale electrodeposition.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge use of the Spectroscopy Research Technology Platform, University of Warwick. D. V., P. C., F. K. and P. R. U. acknowledge support from the European Union’s Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie MSCA-ITN Single-Entity Nanoelectrochemistry, SENTINEL [812398]. P. M., I. J. M. and P. R. U. acknowledge an EPSRC Programme Grant (grant EP/R018820/1) which funds the Crystallisation in the Real World consortium. P. R. U. thanks the Royal Society for a Wolfson Research Merit Award.References
- L. S. Taylor, D. E. Braun and J. W. Steed, Crystals and Crystallization in Drug Delivery Design, Cryst. Growth Des., 2021, 21(3), 1375–1377, DOI:10.1021/acs.cgd.0c01592.
- M. A. McDonald, H. Salami, P. R. Harris, C. E. Lagerman, X. Yang, A. S. Bommarius, M. A. Grover and R. W. Rousseau, Reactive Crystallization: A Review, React. Chem. Eng., 2021, 6(3), 364–400, 10.1039/d0re00272k.
- J. Zhou and B. Wang, Emerging Crystalline Porous Materials as a Multifunctional Platform for Electrochemical Energy Storage, Chem. Soc. Rev., 2017, 46(22), 6927–6945, 10.1039/c7cs00283a.
- E. R. Ravenhill, M. Adobes-Vidal and P. R. Unwin, Calcium Carbonate Crystallisation at Charged Graphite Surfaces, Chem. Commun., 2017, 53(93), 12552–12555, 10.1039/c7cc07441g.
- C. Zheng, Q. Zang, H. Nie, W. Huang, Z. Zhao, A. Qin, R. Hu and B. Z. Tang, Fluorescence Visualization of Crystal Formation and Transformation Processes of Organic Luminogens with Crystallization-Induced Emission Characteristics, Mater. Chem. Front., 2018, 2(1), 180–188, 10.1039/c7qm00435d.
- H. E. M. Hussein, R. J. Maurer, H. Amari, J. J. P. Peters, L. Meng, R. Beanland, M. E. Newton and J. V. Macpherson, Tracking Metal Electrodeposition Dynamics from Nucleation and Growth of a Single Atom to a Crystalline Nanoparticle, ACS Nano, 2018, 12(7), 7388–7396, DOI:10.1021/acsnano.8b04089.
- Y. Hu, J. K. Liang, A. S. Myerson and L. S. Taylor, Crystallization Monitoring by Raman Spectroscopy: Simultaneous Measurement of Desupersaturation Profile and Polymorphic Form in Flufenamic Acid Systems, Ind. Eng. Chem. Res., 2005, 44(5), 1233–1240, DOI:10.1021/ie049745u.
- V. Liotta and V. Sabesan, Monitoring and Feedback Control of Supersaturation Using ATR-FTIR to Produce an Active Pharmaceutical Ingredient of a Desired Crystal Size, Org. Process Res. Dev., 2004, 8(3), 488–494, DOI:10.1021/op049959n.
- R. M. Penner, Mesoscopic Metal Particles and Wires by Electrodeposition, J. Phys. Chem. B, 2002, 106(13), 3339–3353, DOI:10.1021/jp013219o.
- J. V. Zoval, R. M. Stiger, P. R. Biernacki and R. M. Penner, Electrochemical Deposition of Silver Nanocrystallites on the Atomically Smooth Graphite Basal Plane, J. Phys. Chem., 1996, 100(2), 837–844, DOI:10.1021/jp952291h.
- Y. Wang, X. Shan and N. Tao, Emerging Tools for Studying Single Entity Electrochemistry, Faraday Discuss., 2016, 193, 9–39, 10.1039/c6fd00180g.
- L. A. Baker, Perspective and Prospectus on Single-Entity Electrochemistry, J. Am. Chem. Soc., 2018, 140(46), 15549–15559, DOI:10.1021/jacs.8b09747.
- C. L. Bentley, M. Kang and P. R. Unwin, Nanoscale Surface Structure–Activity in Electrochemistry and Electrocatalysis, J. Am. Chem. Soc., 2019, 141(6), 2179–2193, DOI:10.1021/jacs.8b09828.
- J. T. Mefford, A. R. Akbashev, M. Kang, C. L. Bentley, W. E. Gent, H. D. Deng, D. H. Alsem, Y.-S. Yu, N. J. Salmon, D. A. Shapiro, P. R. Unwin and W. C. Chueh, Correlative Operando Microscopy of Oxygen Evolution Electrocatalysts, Nature, 2021, 593(7857), 67–73, DOI:10.1038/s41586-021-03454-x.
- Y. Yang, Y. Xiong, R. Zeng, X. Lu, M. Krumov, X. Huang, W. Xu, H. Wang, F. J. DiSalvo, J. D. Brock, D. A. Muller and H. D. Abruña, Operando Methods in Electrocatalysis, ACS Catal., 2021, 11(3), 1136–1178, DOI:10.1021/acscatal.0c04789.
- F. C. Meldrum and C. O’Shaughnessy, Crystallization in Confinement, Adv. Mater., 2020, 32(31), 2001068, DOI:10.1002/adma.202001068.
- S. Santesson, E. S. Cedergren-Zeppezauer, T. Johansson, T. Laurell, J. Nilsson and S. Nilsson, Screening of Nucleation Conditions Using Levitated Drops for Protein Crystallization, Anal. Chem., 2003, 75(7), 1733–1740, DOI:10.1021/ac020496y.
- C. Gabrielli, G. Maurin, G. Poindessous and R. Rosset, Nucleation and Growth of Calcium Carbonate by an Electrochemical Scaling Process, J. Cryst. Growth, 1999, 200(1–2), 236–250, DOI:10.1016/S0022-0248(98)01261-5.
- B. Blount, K. Kilner, H. Hu, D. Gohmann, E. Gordon, Y. Wang and H. Ren, Electrochemically Induced Nucleation of a Nanoscopic Ionic Solid, J. Phys. Chem. C, 2020, 124(31), 17413–17417, DOI:10.1021/acs.jpcc.0c05009.
- O. Oloye and A. P. O’Mullane, Electrochemical Capture and Storage of CO2 as Calcium Carbonate, ChemSusChem, 2021, 14(7), 1767–1775, DOI:10.1002/cssc.202100134.
- P. D. Morris, I. J. McPherson, G. N. Meloni and P. R. Unwin, Nanoscale Kinetics of Amorphous Calcium Carbonate Precipitation in H2O and D2O, Phys. Chem. Chem. Phys., 2020, 22(38), 22107–22115, 10.1039/d0cp03032e.
- P. D. Morris, I. J. McPherson, M. A. Edwards, R. J. Kashtiban, R. I. Walton and P. R. Unwin, Electric Field-Controlled Synthesis and Characterisation of Single Metal–Organic-Framework (MOF) Nanoparticles, Angew. Chem., Int. Ed., 2020, 59(44), 19696–19701, DOI:10.1002/anie.202007146.
- B. Babakinejad, P. Jönsson, A. López Córdoba, P. Actis, P. Novak, Y. Takahashi, A. Shevchuk, U. Anand, P. Anand, A. Drews, A. Ferrer-Montiel, D. Klenerman and Y. E. Korchev, Local Delivery of Molecules from a Nanopipette for Quantitative Receptor Mapping on Live Cells, Anal. Chem., 2013, 85(19), 9333–9342, DOI:10.1021/ac4021769.
- B. Chen, D. Perry, J. Teahan, I. J. McPherson, J. Edmondson, M. Kang, D. Valavanis, B. G. Frenguelli and P. R. Unwin, Artificial Synapse: Spatiotemporal Heterogeneities in Dopamine Electrochemistry at a Carbon Fiber Ultramicroelectrode, ACS Meas. Sci. Au, 2021, 1(1), 6–10, DOI:10.1021/acsmeasuresciau.1c00006.
- L. I. Stephens and J. Mauzeroll, Demystifying Mathematical Modeling of Electrochemical Systems, J. Chem. Educ., 2019, 96(10), 2217–2224, DOI:10.1021/acs.jchemed.9b00542.
- E. Kätelhön and R. G. Compton, Testing and Validating Electroanalytical Simulations, Analyst, 2015, 140(8), 2592–2598, 10.1039/c4an02276a.
- A. Molina, J. Gonzalez, E. O. Barnes and R. G. Compton, Simple Analytical Equations for the Current–Potential Curves at Microelectrodes: A Universal Approach, J. Phys. Chem. C, 2014, 118(1), 346–356, DOI:10.1021/jp409167m.
- J.-F. Lemineur, J.-M. Noël, C. Combellas and F. Kanoufi, Optical Monitoring of the Electrochemical Nucleation and Growth of Silver Nanoparticles on Electrode: From Single to Ensemble Nanoparticles Inspection, J. Electroanal. Chem., 2020, 872, 114043, DOI:10.1016/j.jelechem.2020.114043.
- J.-F. Lemineur, J.-M. Noël, D. Ausserré, C. Combellas and F. Kanoufi, Combining Electrodeposition and Optical Microscopy for Probing Size-Dependent Single-Nanoparticle Electrochemistry, Angew. Chem., Int. Ed., 2018, 57(37), 11998–12002, DOI:10.1002/anie.201807003.
- L. Godeffroy, P. Ciocci, A. Nsabimana, M. Miranda Vieira, J. M. Noël, C. Combellas, J. F. Lemineur and F. Kanoufi, Deciphering Competitive Routes for Nickel-Based Nanoparticle Electrodeposition by an Operando Optical Monitoring, Angew. Chem.,Int. Ed., 2021, 60(31), 16980–16983, DOI:10.1002/anie.202106420.
- J. F. Lemineur, J. M. Noël, A. Courty, D. Ausserré, C. Combellas and F. Kanoufi, In Situ Optical Monitoring of the Electrochemical Conversion of Dielectric Nanoparticles: From Multistep Charge Injection to Nanoparticle Motion, J. Am. Chem. Soc., 2020, 142(17), 7937–7946, DOI:10.1021/jacs.0c02071.
- P. Ciocci, J.-F. Lemineur, J.-M. Noël, C. Combellas and F. Kanoufi, Differentiating Electrochemically Active Regions of Indium Tin Oxide Electrodes for Hydrogen Evolution and Reductive Decomposition Reactions. An in Situ Optical Microscopy Approach, Electrochim. Acta, 2021, 386, 138498, DOI:10.1016/j.electacta.2021.138498.
- W. Li, M. Wojcik and K. Xu, Optical Microscopy Unveils Rapid, Reversible Electrochemical Oxidation and Reduction of Graphene, Nano Lett., 2019, 19(2), 983–989, DOI:10.1021/acs.nanolett.8b04216.
- K. Namink, X. Meng, M. T. M. Koper, P. Kukura and S. Faez, Electric-Double-Layer-Modulation Microscopy, Phys. Rev. Appl., 2020, 13(4), 044065, DOI:10.1103/physrevapplied.13.044065.
- R. W. Taylor and V. Sandoghdar, Interferometric Scattering Microscopy: Seeing Single Nanoparticles and Molecules via Rayleigh Scattering, Nano Lett., 2019, 19(8), 4827–4835, DOI:10.1021/acs.nanolett.9b01822.
- N. Ebejer, A. G. Güell, S. C. S. Lai, K. McKelvey, M. E. Snowden and P. R. Unwin, Scanning Electrochemical Cell Microscopy: A Versatile Technique for Nanoscale Electrochemistry and Functional Imaging, Annu. Rev. Anal. Chem., 2013, 6(1), 329–351, DOI:10.1146/annurev-anchem-062012-092650.
- O. J. Wahab, M. Kang and P. R. Unwin, Scanning Electrochemical Cell Microscopy: A Natural Technique for Single Entity Electrochemistry, Curr. Opin. Electrochem., 2020, 22, 120–128, DOI:10.1016/j.coelec.2020.04.018.
- C. G. Williams, M. A. Edwards, A. L. Colley, J. V. Macpherson and P. R. Unwin, Scanning Micropipet Contact Method for High-Resolution Imaging of Electrode Surface Redox Activity, Anal. Chem., 2009, 81(7), 2486–2495, DOI:10.1021/ac802114r.
- N. Ebejer, M. Schnippering, A. W. Colburn, M. A. Edwards and P. R. Unwin, Localized High Resolution Electrochemistry and Multifunctional Imaging: Scanning Electrochemical Cell Microscopy, Anal. Chem., 2010, 82(22), 9141–9145, DOI:10.1021/ac102191u.
- A. G. Güell, A. S. Cuharuc, Y. R. Kim, G. Zhang, S. Y. Tan, N. Ebejer and P. R. Unwin, Redox-Dependent Spatially Resolved Electrochemistry at Graphene and Graphite Step Edges, ACS Nano, 2015, 9(4), 3558–3571, DOI:10.1021/acsnano.5b00550.
- J. W. Hill and C. M. Hill, Directly Visualizing Carrier Transport and Recombination at Individual Defects within 2D Semiconductors, Chem. Sci., 2021, 12(14), 5102–5112, 10.1039/d0sc07033e.
- M. Brunet Cabré, A. E. Paiva, M. Velický, P. E. Colavita and K. McKelvey, Electrochemical Kinetics as a Function of Transition Metal Dichalcogenide Thickness, Electrochim. Acta, 2021, 393, 139027, DOI:10.1016/j.electacta.2021.139027.
- Y. Takahashi, Y. Kobayashi, Z. Wang, Y. Ito, M. Ota, H. Ida, A. Kumatani, K. Miyazawa, T. Fujita, H. Shiku, Y. E. Korchev, Y. Miyata, T. Fukuma, M. Chen and T. Matsue, High-Resolution Electrochemical Mapping of the Hydrogen Evolution Reaction on Transition-Metal Dichalcogenide Nanosheets, Angew. Chem., 2020, 132(9), 3629–3636, DOI:10.1002/ange.201912863.
- A. G. Güell, K. E. Meadows, P. V. Dudin, N. Ebejer, J. V. Macpherson and P. R. Unwin, Mapping Nanoscale Electrochemistry of Individual Single-Walled Carbon Nanotubes, Nano Lett., 2014, 14(1), 220–224, DOI:10.1021/nl403752e.
- J. C. Byers, A. G. Güell and P. R. Unwin, Nanoscale Electrocatalysis: Visualizing Oxygen Reduction at Pristine, Kinked, and Oxidized Sites on Individual Carbon Nanotubes, J. Am. Chem. Soc., 2014, 136(32), 11252–11255, DOI:10.1021/ja505708y.
- R. G. Mariano, M. Kang, O. J. Wahab, I. J. McPherson, J. A. Rabinowitz, P. R. Unwin and M. W. Kanan, Microstructural Origin of Locally Enhanced CO2 Electroreduction Activity on Gold, Nat. Mater., 2021, 20(7), 1000–1006, DOI:10.1038/s41563-021-00958-9.
- B. D. B. Aaronson, C.-H. Chen, H. Li, M. T. M. Koper, S. C. S. Lai and P. R. Unwin, Pseudo-Single-Crystal Electrochemistry on Polycrystalline Electrodes: Visualizing Activity at Grains and Grain Boundaries on Platinum for the Fe2+/Fe3+ Redox Reaction, J. Am. Chem. Soc., 2013, 135(10), 3873–3880, DOI:10.1021/ja310632k.
- Y. Wang, E. Gordon and H. Ren, Mapping the Potential of Zero Charge and Electrocatalytic Activity of Metal–Electrolyte Interface via a Grain-by-Grain Approach, Anal. Chem., 2020, 92, 2859–2865, DOI:10.1021/acs.analchem.9b05502.
- B. Tao, L. C. Yule, E. Daviddi, C. L. Bentley and P. R. Unwin, Correlative Electrochemical Microscopy of Li-Ion (De)Intercalation at a Series of Individual LiMn2O4 Particles, Angew. Chem., 2019, 131(14), 4654–4659, DOI:10.1002/ange.201814505.
- S. C. S. Lai, P. V. Dudin, J. V. Macpherson and P. R. Unwin, Visualizing Zeptomole (Electro)Catalysis at Single Nanoparticles within an Ensemble, J. Am. Chem. Soc., 2011, 133(28), 10744–10747, DOI:10.1021/ja203955b.
- M. Choi, N. P. Siepser, S. Jeong, Y. Wang, G. Jagdale, X. Ye and L. A. Baker, Probing Single-Particle Electrocatalytic Activity at Facet-Controlled Gold Nanocrystals, Nano Lett., 2020, 20(2), 1233–1239, DOI:10.1021/acs.nanolett.9b04640.
- C. L. Bentley, Scanning Electrochemical Cell Microscopy for the Study of (Nano)Particle Electrochemistry: From the Sub-particle to Ensemble Level, Electrochem. Sci. Adv., 2021, 1–18, DOI:10.1002/elsa.202100081.
- P. Saha, M. M. Rahman and C. M. Hill, Borohydride Oxidation Electrocatalysis at Individual, Shape-controlled Au Nanoparticles, Electrochem. Sci. Adv., 2021, 1–10, DOI:10.1002/elsa.202100120.
- J. Ustarroz, M. Kang, E. Bullions and P. R. Unwin, Impact and Oxidation of Single Silver Nanoparticles at Electrode Surfaces: One Shot versus Multiple Events, Chem. Sci., 2017, 8(3), 1841–1853, 10.1039/c6sc04483b.
- J. C. Byers, B. Paulose Nadappuram, D. Perry, K. McKelvey, A. W. Colburn and P. R. Unwin, Single Molecule Electrochemical Detection in Aqueous Solutions and Ionic Liquids, Anal. Chem., 2015, 87(20), 10450–10456, DOI:10.1021/acs.analchem.5b02569.
- C.-H. Chen, L. Jacobse, K. McKelvey, S. C. S. S. Lai, M. T. M. M. Koper and P. R. Unwin, Voltammetric Scanning Electrochemical Cell Microscopy: Dynamic Imaging of Hydrazine Electro-Oxidation on Platinum Electrodes, Anal. Chem., 2015, 87(11), 5782–5789, DOI:10.1021/acs.analchem.5b00988.
- C. L. Bentley, D. Perry and P. R. Unwin, Stability and Placement of Ag/AgCl Quasi-Reference Counter Electrodes in Confined Electrochemical Cells, Anal. Chem., 2018, 90(12), 7700–7707, DOI:10.1021/acs.analchem.8b01588.
- D. Perry, D. Momotenko, R. A. Lazenby, M. Kang and P. R. Unwin, Characterization of Nanopipettes, Anal. Chem., 2016, 88(10), 5523–5530, DOI:10.1021/acs.analchem.6b01095.
- A. D. Edelstein, M. A. Tsuchida, N. Amodaj, H. Pinkard, R. D. Vale and N. Stuurman, Advanced Methods of Microscope Control Using Manager Software, J. Biol. Methods, 2014, 1(2), e10, DOI:10.14440/jbm.2014.36.
- Warwick Electrochemisitry and Interfaces Group, WEC-SPM, https://warwick.ac.uk/fac/sci/chemistry/research/unwin/electrochemistry/wec-spm/, accessed Apr 21, 2021 Search PubMed.
- J.-F. Lemineur, P. Ciocci, J.-M. Noël, H. Ge, C. Combellas and F. Kanoufi, Imaging and Quantifying the Formation of Single Nanobubbles at Single Platinum Nanoparticles during the Hydrogen Evolution Reaction, ACS Nano, 2021, 15(2), 2643–2653, DOI:10.1021/acsnano.0c07674.
- M. E. Snowden, A. G. Güell, S. C. S. Lai, K. McKelvey, N. Ebejer, M. A. O’Connell, A. W. Colburn and P. R. Unwin, Scanning Electrochemical Cell Microscopy: Theory and Experiment for Quantitative High Resolution Spatially-Resolved Voltammetry and Simultaneous Ion-Conductance Measurements, Anal. Chem., 2012, 84(5), 2483–2491, DOI:10.1021/ac203195h.
- C. L. Bentley, M. Kang, F. M. Maddar, F. Li, M. Walker, J. Zhang and P. R. Unwin, Electrochemical Maps and Movies of the Hydrogen Evolution Reaction on Natural Crystals of Molybdenite (MoS2): Basal vs. Edge Plane Activity, Chem. Sci., 2017, 8(9), 6583–6593, 10.1039/c7sc02545a.
- A. G. Güell, N. Ebejer, M. E. Snowden, K. McKelvey, J. V. Macpherson and P. R. Unwin, Quantitative Nanoscale Visualization of Heterogeneous Electron Transfer Rates in 2D Carbon Nanotube Networks, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(29), 11487–11492, DOI:10.1073/pnas.1203671109.
- E. Daviddi, Z. Chen, B. Beam Massani, J. Lee, C. L. Bentley, P. R. Unwin and E. L. Ratcliff, Nanoscale Visualization and Multiscale Electrochemical Analysis of Conductive Polymer Electrodes, ACS Nano, 2019, 13(11), 13271–13284 CrossRef CAS PubMed.
- S. C. S. Lai, A. N. Patel, K. McKelvey and P. R. Unwin, Definitive Evidence for Fast Electron Transfer at Pristine Basal Plane Graphite from High-Resolution Electrochemical Imaging, Angew. Chem., Int. Ed., 2012, 51(22), 5405–5408, DOI:10.1002/anie.201200564.
- L. C. Yule, V. Shkirskiy, J. Aarons, G. West, C. L. Bentley, B. A. Shollock and P. R. Unwin, Nanoscale Active Sites for the Hydrogen Evolution Reaction on Low Carbon Steel, J. Phys. Chem. C, 2019, 123(39), 24146–24155, DOI:10.1021/acs.jpcc.9b07216.
- P. M. Kirkman, A. G. Güell, A. S. Cuharuc and P. R. Unwin, Spatial and Temporal Control of the Diazonium Modification of sp2 Carbon Surfaces, J. Am. Chem. Soc., 2014, 136(1), 36–39, DOI:10.1021/ja410467e.
- G. Zhang, P. M. Kirkman, A. N. Patel, A. S. Cuharuc, K. McKelvey and P. R. Unwin, Molecular Functionalization of Graphite Surfaces: Basal Plane versus Step Edge Electrochemical Activity, J. Am. Chem. Soc., 2014, 136(32), 11444–11451, DOI:10.1021/ja505266d.
- A. N. Patel, K. McKelvey and P. R. Unwin, Nanoscale Electrochemical Patterning Reveals the Active Sites for Catechol Oxidation at Graphite Surfaces, J. Am. Chem. Soc., 2012, 134(50), 20246–20249, DOI:10.1021/ja3095894.
- E. E. Oseland, Z. J. Ayres, A. Basile, D. M. Haddleton, P. Wilson and P. R. Unwin, Surface Patterning of Polyacrylamide Gel Using Scanning Electrochemical Cell Microscopy (SECCM), Chem. Commun., 2016, 52(64), 9929–9932, 10.1039/c6cc05153g.
- K. McKelvey, M. A. O’Connell and P. R. Unwin, Meniscus Confined Fabrication of Multidimensional Conducting Polymer Nanostructures with Scanning Electrochemical Cell Microscopy (SECCM), Chem. Commun., 2013, 49(29), 2986, 10.1039/c3cc00104k.
- A. S. Parker, R. Al Botros, S. L. Kinnear, M. E. Snowden, K. McKelvey, A. T. Ashcroft, M. Carvell, A. Joiner, M. Peruffo, C. Philpotts and P. R. Unwin, Combinatorial Localized Dissolution Analysis: Application to Acid-Induced Dissolution of Dental Enamel and the Effect of Surface Treatments, J. Colloid Interface Sci., 2016, 476, 94–102, DOI:10.1016/j.jcis.2016.05.018.
- S. L. Kinnear, K. McKelvey, M. E. Snowden, M. Peruffo, A. W. Colburn and P. R. Unwin, Dual-Barrel Conductance Micropipet as a New Approach to the Study of Ionic Crystal Dissolution Kinetics, Langmuir, 2013, 29(50), 15565–15572, DOI:10.1021/la403630u.
- C.-H. Chen, K. E. Meadows, A. Cuharuc, S. C. S. Lai and P. R. Unwin, High Resolution Mapping of Oxygen Reduction Reaction Kinetics at Polycrystalline Platinum Electrodes, Phys. Chem. Chem. Phys., 2014, 16(34), 18545, 10.1039/c4cp01511h.
- H. Wang, X. Shan, H.-Y. Chen and N. Tao, Pauli Repulsion-Induced Expansion and Electromechanical Properties of Graphene, Nano Lett., 2017, 17(1), 236–241, DOI:10.1021/acs.nanolett.6b03955.
- V. Brasiliense, J. Clausmeyer, P. Berto, G. Tessier, C. Combellas, W. Schuhmann and F. Kanoufi, Monitoring Cobalt-Oxide Single Particle Electrochemistry with Subdiffraction Accuracy, Anal. Chem., 2018, 90(12), 7341–7348, DOI:10.1021/acs.analchem.8b00649.
- G. Lippmann, Relations Entre Les Phénomènes Électriques et Capillaires, Ann. Chim. Phys., 1875, 5, 494–549 Search PubMed.
- A. Quinn, R. Sedev and J. Ralston, Influence of the Electrical Double Layer in Electrowetting, J. Phys. Chem. B, 2003, 107(5), 1163–1169, DOI:10.1021/jp0216326.
- A. Quinn, R. Sedev and J. Ralston, Contact Angle Saturation in Electrowetting, J. Phys. Chem. B, 2005, 109(13), 6268–6275, DOI:10.1021/jp040478f.
- L. Liu, S. Yellinek, I. Valdinger, A. Donval and D. Mandler, Important Implications of the Electrochemical Reduction of ITO, Electrochim. Acta, 2015, 176, 1374–1381, DOI:10.1016/j.electacta.2015.07.129.
- C. M. Hill and S. Pan, A Dark-Field Scattering Spectroelectrochemical Technique for Tracking the Electrodeposition of Single Silver Nanoparticles, J. Am. Chem. Soc., 2013, 135(46), 17250–17253, DOI:10.1021/ja4075387.
- P. Saha, J. W. Hill, J. D. Walmsley and C. M. Hill, Probing Electrocatalysis at Individual Au Nanorods via Correlated Optical and Electrochemical Measurements, Anal. Chem., 2018, 90(21), 12832–12839, DOI:10.1021/acs.analchem.8b03360.
- Y. Liu, C. Jin, Y. Liu, K. H. Ruiz, H. Ren, Y. Fan, H. S. White and Q. Chen, Visualization and Quantification of Electrochemical H2 Bubble Nucleation at Pt, Au, and MoS2 Substrates, ACS Sens., 2021, 6(2), 355–363, DOI:10.1021/acssensors.0c00913.
- Q. Chen, L. Luo, H. Faraji, S. W. Feldberg and H. S. White, Electrochemical Measurements of Single H2 Nanobubble Nucleation and Stability at Pt Nanoelectrodes, J. Phys. Chem. Lett., 2014, 5(20), 3539–3544, DOI:10.1021/jz501898r.
- Y. Qiu, H. Ren, M. A. Edwards, R. Gao, K. Barman and H. S. White, Electrochemical Generation of Individual Nanobubbles Comprising H2, D2 , and HD, Langmuir, 2020, 36(22), 6073–6078, DOI:10.1021/acs.langmuir.0c00232.
- J. W. Morse, R. S. Arvidson and A. Lüttge, Calcium Carbonate Formation and Dissolution, Chem. Rev., 2007, 107(2), 342–381, DOI:10.1021/cr050358j.
- D. Gebauer, A. Völkel and H. Cölfen, Stable Prenucleation Calcium Carbonate Clusters, Science, 2008, 322(5909), 1819–1822, DOI:10.1126/science.1164271.
- P. J. M. Smeets, A. R. Finney, W. J. E. M. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. J. M. Sommerdijk, A Classical View on Nonclassical Nucleation, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(38), E7882–E7890, DOI:10.1073/pnas.1700342114.
- F. Sebastiani, S. L. P. Wolf, B. Born, T. Q. Luong, H. Cölfen, D. Gebauer and M. Havenith, Water Dynamics from THz Spectroscopy Reveal the Locus of a Liquid-Liquid Binodal Limit in Aqueous CaCO3 Solutions, Angew. Chem., Int. Ed., 2017, 56(2), 490–495, DOI:10.1002/anie.201610554.
- F. H. Y. Lui, Y. Wang, Y. Yao, R. J. Mobbs, R. E. Pogson, P. Koshy, F. P. Lucien, D. Zhou and C. C. Sorrell, Quiescent Mineralisation for Free-Standing Mineral Microfilms with a Hybrid Structure, J. Colloid Interface Sci., 2021, 604, 327–339, DOI:10.1016/j.jcis.2021.06.171.
- M. Farhadi Khouzani, D. M. Chevrier, P. Güttlein, K. Hauser, P. Zhang, N. Hedin and D. Gebauer, Disordered Amorphous Calcium Carbonate from Direct Precipitation, CrystEngComm, 2015, 17(26), 4842–4849, 10.1039/c5ce00720h.
- N. C. Rudd, S. Cannan, E. Bitziou, I. Ciani, A. L. Whitworth and P. R. Unwin, Fluorescence Confocal Laser Scanning Microscopy as a Probe of pH Gradients in Electrode Reactions and Surface Activity, Anal. Chem., 2005, 77(19), 6205–6217, DOI:10.1021/ac050800y.
- D. L. Parkhurst and C. A. J. Appelo, Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations, in U.S. Geological Survey Techniques and Methods, Book 6, U.S. Geological Survey Techniques and Methods, 2013, ch. A43, p. 497 Search PubMed.
- S. Campidelli, R. Abou Khachfe, K. Jaouen, J. Monteiller, C. Amra, M. Zerrad, R. Cornut, V. Derycke and D. Ausserré, Backside Absorbing Layer Microscopy: Watching Graphene Chemistry, Sci. Adv., 2017, 3(5), e1601724, DOI:10.1126/sciadv.1601724.
- S. Chakri, A. N. Patel, I. Frateur, F. Kanoufi, E. M. M. Sutter, T. T. M. Tran, B. Tribollet and V. Vivier, Imaging of a Thin Oxide Film Formation from the Combination of Surface Reflectivity and Electrochemical Methods, Anal. Chem., 2017, 89(10), 5303–5310, DOI:10.1021/acs.analchem.6b04921.
- A. Shevchuk, S. Tokar, S. Gopal, J. L. Sanchez-Alonso, A. I. Tarasov, A. C. Vélez-Ortega, C. Chiappini, P. Rorsman, M. M. Stevens, J. Gorelik, G. I. Frolenkov, D. Klenerman and Y. E. Korchev, Angular Approach Scanning Ion Conductance Microscopy, Biophys. J., 2016, 110(10), 2252–2265, DOI:10.1016/j.bpj.2016.04.017.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |