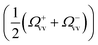Open Access Article
Open Access ArticleAddressing molecular optomechanical effects in nanocavity-enhanced Raman scattering beyond the single plasmonic mode†‡
Yuan
Zhang
*a,
Ruben
Esteban
*bc,
Roberto A.
Boto
b,
Mattin
Urbieta
b,
Xabier
Arrieta
c,
ChongXin
Shan
a,
Shuzhou
Li
 d,
Jeremy J.
Baumberg
e and
Javier
Aizpurua
d,
Jeremy J.
Baumberg
e and
Javier
Aizpurua
 *bc
*bc
aHenan Key Laboratory of Diamond Optoelectronic Materials and Devices, Key Laboratory of Material Physics, Ministry of Education, School of Physics and Microelectronics, Zhengzhou University, Zhengzhou 450052, China. E-mail: yzhuaudipc@zzu.edu.cn
bCenter for Material Physics (CSIC – UPV/EHU), Paseo Manuel de Lardizabal 5, Donostia-San Sebastian, Gipuzkoa 20018, Spain. E-mail: aizpurua@ehu.eus
cDonostia International Physics Center, Paseo Manuel de Lardizabal 4, Donostia-San Sebastian 20018, Spain. E-mail: ruben_esteban@ehu.eus
dSchool of Materials Science and Engineering, Nanyang Technological University, Nanyang Avenue 50, 639798 Singapore
eNanoPhotonics Centre, Cavendish Laboratory, University of Cambridge, Cambridge CB3 0HE, UK
First published on 26th November 2020
Abstract
The description of surface-enhanced Raman scattering (SERS) as a molecular optomechanical process has provided new insights into the vibrational dynamics and nonlinearities of this inelastic scattering process. In earlier studies, molecular vibrations have typically been assumed to couple with a single plasmonic mode of a metallic nanostructure, ignoring the complexity of the plasmonic response in many configurations of practical interest such as in metallic nanojunctions. By describing the plasmonic fields as a continuum, we demonstrate here the importance of considering the full plasmonic response to properly address the molecule-cavity optomechanical interaction. We apply the continuum-field model to calculate the Raman signal from a single molecule in a plasmonic nanocavity formed by a nanoparticle-on-a-mirror configuration, and compare the results of optomechanical parameters, vibrational populations, and Stokes and anti-Stokes signals of the continuum-field model with those obtained from the single-mode model. Our results reveal that high-order non-radiative plasmonic modes significantly modify the optomechanical behavior under strong laser illumination. Moreover, Raman linewidths, lineshifts, vibrational populations, and parametric instabilities are found to be sensitive to the energy of the molecular vibrational modes. The implications of adopting the continuum-field model to describe the plasmonic cavity response in molecular optomechanics are relevant in many other nanoantenna and nanocavity configurations commonly used to enhance SERS.
1. Introduction
Surface-enhanced Raman scattering (SERS) denotes the enhancement of the Raman signal emitted by molecules that are located near metallic nanostructures.1 The SERS enhancement, which can be of many orders of magnitude, is partially due to the molecule-metal chemical interaction,2 but the main mechanism is due to electromagnetic effects produced by metallic resonators that induce a tightly-confined and enhanced electromagnetic field.3 The latter is induced by the collective motion of conduction electrons in metallic nanostructures, known as localized surface plasmon-polaritons. The classical electromagnetic theory of SERS states simply that the SERS signal is approximately proportional to the fourth power of the enhancement of the electric near field acting on the molecules. On the other hand, a quantum theory of SERS4,5 recently put forward, has established an analogy of the SERS process with cavity optomechanics.6,7 This molecular optomechanics description allows the analysis of many intriguing phenomena, such as nonlinear effects4,8–10 (including diverging Raman intensities, known as parametric instability in quantum optomechanics), correlations of the emitted photons,5 frequency up-conversion,11 high-order Raman scattering,9,12 or heat transfer.13 Furthermore, this description also suggests that the molecular vibrations can couple with each other via their interaction with the surface plasmon polariton, and the resulting collective response10,14,15 leads, for example, to a reduction of the laser power required to reach parametric instability,4 and to a quadratic superradiant scaling of SERS with the number of molecules.15In most of previous studies, a model of molecular optomechanics based on a single optical mode has been adopted, which assumes that a single plasmonic mode dominates the electromagnetic response of the optical resonator, in close similarity with the typical situation in standard cavity optomechanics.6,7 In realistic SERS experiments, however, the molecules interact with multiple plasmonic modes. For example, any molecule close to a metallic surface interacts efficiently with a collection of high-order plasmonic resonances that behave as a pseudomode.16 Although the effect of these high-order modes on fluorescence has been studied in detail,17–19 their effect on SERS has not been fully explored in the context of molecular optomechanics.4,5,20,21 Nevertheless, we would like to point out that the classical SERS theory usually incorporates the influence of high-order plasmonic modes in typical calculations of the electromagnetic enhancement of SERS22 (through the standard 4th-power dependence of the local field enhancement), however such approach does not capture the non-linear evolution of the vibrational population and thus of the Raman spectrum, as predicted in the optomechanical model.
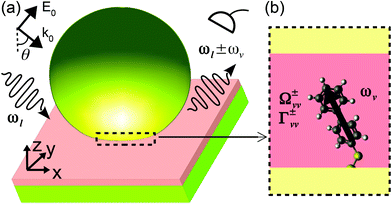
To understand the impact of the high-order plasmonic modes on the SERS signal, we apply a continuum-field model of molecular optomechanics, which treats the electromagnetic field of the optical (plasmonic) nanoresonator as a continuum, and accounts for its full response via the dyadic Green's function of the system.23 To show the practical importance of considering the full plasmonic response of a nanosystem, we use the continuum-field model to analyze the SERS signal of a single biphenyl-4-thiol (BPT) molecule located in the gap of a plasmonic nanocavity formed by a NanoParticle-on-a-Mirror (NPoM) structure, as shown in Fig. 1. This molecule has been shown to exhibit large optomechanical interaction in the NPoM system.8 Here, we assume the molecule to be located in the middle of the gap, as a representative position which can be experimentally realized by holding the molecule in a matrix formed by a self-assembled molecular layer, or by DNA origami-directed positioning.24 The central location of the molecule within the nanogap is an optimal one for optomechanical interaction via the relevant plasmonic modes, however our model can tackle any position of the molecule in the nanocavity, as far as the electromagnetic properties of that particular point (near field, Green's function and emission) are conveniently addressed, as described in the next section. The NPoM construct can be reliably fabricated and has been previously employed to explore charge transfer plasmons25 and single-molecule redox chemistry.26 This configuration has also been a key to reveal molecular-optomechanics effects in SERS.8,10
We compare the results obtained with a single optical mode and those obtained within the continuum-field model, and find that the consideration of the full plasmonic response of the NPoM configuration leads to substantial modification in the sign and magnitude of the key optomechanical parameters governing the dynamics of the molecular vibrations. For large laser intensity, these effects strongly influence the linewidth and spectral shifts of the Raman lines, as well as the vibrational population and the intensity of the emitted signal. Importantly, we find that the conditions to reach parametric instability in SERS become much more stringent because of the influence of the plasmonic pseudomode, with a strong dependence of the optomechanical dynamics on the energy of the vibrational modes considered. The influence of the full optical response of a lossy plasmonic resonator can thus substantially modify the properties of optomechanical effects in practical situations in SERS.
The paper is organized as follows. We first present the molecular optomechanical model in section 2, and afterwards analyze the properties of the molecular vibrations and those of the plasmonic nanocavity in sections 3 and 4, respectively. The combined effect of molecular and cavity properties on the optomechanical parameters is presented in sections 5 and 6. The consequences of considering the full plasmonic response in the dependence of the vibrational population and the Raman emission on the laser intensity is analyzed in detail in section 7. Last, we summarize and discuss the importance and implications of our findings.
2. Continuum-field model
We next describe briefly the molecular optomechanical model used in this paper, which is based on the approach addressed by M. K. Dezfouli and S. Hughes.23 This approach considers non-resonant Raman, and treats the molecule as infinitesimally small (point-like) with the vibrations as quantized harmonic oscillators. To model the optomechanical coupling between the molecular vibrations and the NPoM structure, the localized plasmonic electric field is quantized as a continuum of modes, according to the quantum theory of electromagnetic fields in dispersive and lossy media.27–29 The coupling is linearized within the rotating wave approximation by treating the laser-induced local field acting on the molecule as a classical field, and the remaining field degrees of freedom in the resulting Hamiltonian are eliminated adiabatically to obtain an effective master equation for the reduced density operator of the molecular vibrations. A more detailed discussion of the derivation and the approximations involved in this theoretical framework are presented in section S1 of the ESI.† There, we have also generalized this continuum-field formalism to the case of many vibrational modes, and verified that the correlations of the vibrational modes are very small when their frequencies are sufficiently different (as they are in our system) so that we can treat the molecular vibrations independently.
of the molecular vibrations. A more detailed discussion of the derivation and the approximations involved in this theoretical framework are presented in section S1 of the ESI.† There, we have also generalized this continuum-field formalism to the case of many vibrational modes, and verified that the correlations of the vibrational modes are very small when their frequencies are sufficiently different (as they are in our system) so that we can treat the molecular vibrations independently.
We present next the main results obtained by following this approach, for vibrational modes of frequency ωv and Raman tensor 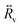 , labeled by the symbol “v”. First, we obtain the equations for the evolution of the vibrational population 〈
, labeled by the symbol “v”. First, we obtain the equations for the evolution of the vibrational population 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉:
v〉:
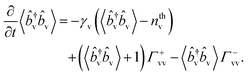 | (1) |
Here, ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v,
†v, ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v are the bosonic creation and annihilation operators of the molecular vibrations, and the trace
v are the bosonic creation and annihilation operators of the molecular vibrations, and the trace 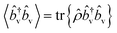 of the number operator
of the number operator ![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v describes the mean population of the vibrations. γv is the intrinsic vibrational decay rate and nthv = [eħωv/kBT − 1]−1 is the thermal vibrational population (with Boltzmann's constant kB and temperature T). The first term on the right-hand side of eqn (1) describes the vibrational decay at rate γv and the thermal pumping, and the second (third) term describes the vibrational pumping (damping) at rate Γ+vv (Γ−vv) due to the Stokes (anti-Stokes) scattering. The vibrational pumping Γ+vv and damping rate Γ−vv are a consequence of the optomechanical coupling, and are given by the expressions
v describes the mean population of the vibrations. γv is the intrinsic vibrational decay rate and nthv = [eħωv/kBT − 1]−1 is the thermal vibrational population (with Boltzmann's constant kB and temperature T). The first term on the right-hand side of eqn (1) describes the vibrational decay at rate γv and the thermal pumping, and the second (third) term describes the vibrational pumping (damping) at rate Γ+vv (Γ−vv) due to the Stokes (anti-Stokes) scattering. The vibrational pumping Γ+vv and damping rate Γ−vv are a consequence of the optomechanical coupling, and are given by the expressions
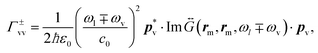 | (2) |
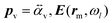 | (3) |
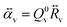 .
. 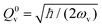 is the zero-point amplitude, and ωl is the angular frequency of the laser excitation. Last,
is the zero-point amplitude, and ωl is the angular frequency of the laser excitation. Last, 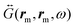 is the classical dyadic Green's function, denoting the dipole self-interaction, where the double argument on rm indicates that the field at position rm is induced by the point-like molecular Raman dipole located at the same position. We refer to
is the classical dyadic Green's function, denoting the dipole self-interaction, where the double argument on rm indicates that the field at position rm is induced by the point-like molecular Raman dipole located at the same position. We refer to 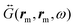 in the following as the near-field dyadic Green's function and, according to eqn (2), it needs to be evaluated at the Stokes ωl − ωv and anti-Stokes ωl + ωv frequencies.
in the following as the near-field dyadic Green's function and, according to eqn (2), it needs to be evaluated at the Stokes ωl − ωv and anti-Stokes ωl + ωv frequencies.
The factor −(γv + Γ−vv − Γ+vv) that multiplies the vibrational population 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 on the right side of eqn (1) indicates that the effective optomechanical damping rate, defined as Γoptv = Γ−vv − Γ+vv, modifies the total vibrational decay rate. In the steady-state, i.e.
v〉 on the right side of eqn (1) indicates that the effective optomechanical damping rate, defined as Γoptv = Γ−vv − Γ+vv, modifies the total vibrational decay rate. In the steady-state, i.e.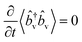 , a simple analytical expression for the vibrational population is obtained
, a simple analytical expression for the vibrational population is obtained
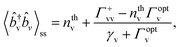 | (4) |
In typical Raman experiments, the magnitude of interest is the differential scattered power dP/dΩ in the direction of the detector (the differential Raman cross-section is simply the ratio of this scattered power to the laser intensity 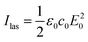 , where E0 is the amplitude of the laser field). dP/dΩ is obtained from the correlations of the electric field operator at position rd of the detector. These correlations can be related to the correlations of the creation and annihilation operators of the molecular vibrations via the classic dyadic Green's function
, where E0 is the amplitude of the laser field). dP/dΩ is obtained from the correlations of the electric field operator at position rd of the detector. These correlations can be related to the correlations of the creation and annihilation operators of the molecular vibrations via the classic dyadic Green's function 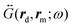 that connects the induced Raman dipole of the molecule at rm with the electromagnetic field at position rd of the detector (denoted as the far-field dyadic Green's function in the following).
that connects the induced Raman dipole of the molecule at rm with the electromagnetic field at position rd of the detector (denoted as the far-field dyadic Green's function in the following).
To obtain the equations for the correlations, we first derive the equations for the vibrational amplitude 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 (or 〈
v〉 (or 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v〉), which become:
†v〉), which become:
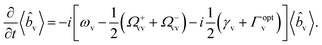 | (5) |
These equations indicate that the frequency of the vibrational modes are shifted by 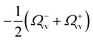 due to the optical spring effect,7 with Ω±vv defined as
due to the optical spring effect,7 with Ω±vv defined as
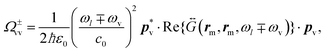 | (6) |
Finally, by applying the quantum regression theorem34 to eqn (5), we obtain the following expressions for the differential power of the Stokes (st) and anti-Stokes (as) scattering:
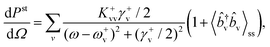 | (7) |
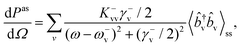 | (8) |
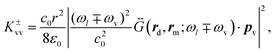 | (9) |
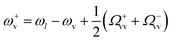 ,
, 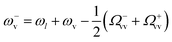 are shifted by
are shifted by 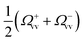 and
and 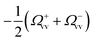 , respectively, and that their line-widths γ+v = γ−v = γv + Γoptv are modified by Γoptv.
, respectively, and that their line-widths γ+v = γ−v = γv + Γoptv are modified by Γoptv.
The differential scattering power integrated over frequency, 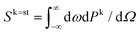 , follows
, follows
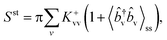 | (10) |
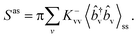 | (11) |
For simplicity, we call Sst and Sas the integrated Stokes and anti-Stokes intensity in the following. We note that a semi-classical approach allows one to reach similar results when the appropriate removal of the phonons due to the anti-Stokes processes is considered in the vibrational population equation rate.9,30,33 However, the vibrational frequency shift due to the optical spring effect is not captured even in that case.
3. Vibrational frequency and Raman tensor
The properties of the molecular vibrations can be computed with density functional theory (DFT). We consider the biphenyl-4-thiol (BPT) molecule (in vacuum) and the same molecule after binding the sulfur atom to a gold atom (insets in Fig. 2). The latter serves to partially account for chemical enhancements due to charge transfer.2,10,35 We carry out the DFT calculations with the Gaussian 16 package and utilize the B3LYP hybrid functional and 6-31G (d,p) basis set for the carbon, sulfur and hydrogen atoms, but the LANL2DZ basis set for the gold atom.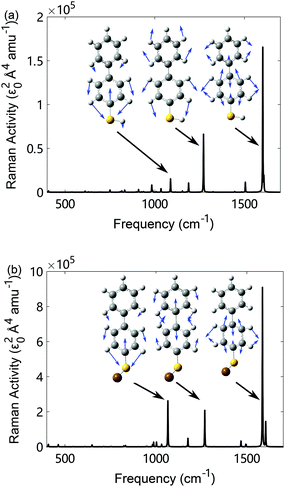 | ||
| Fig. 2 Raman activity of (a) biphenyl-4-thiol molecule and (b) the same molecule, except that the sulfur atom binds to a single gold atom. Insets show three main Raman-active vibrational modes (gray, white, yellow and brown spheres for carbon, hydrogen, sulfur and gold atoms, respectively). The vibrational frequencies are scaled by a factor of 0.967 to match with the experimental result,10 and the Raman activity of different modes is broadened by a Lorentzian function of width 2 cm−1. | ||
Fig. 2 shows the Raman activity for various vibrational modes in the wave-number range between 400 cm−1 and 1700 cm−1. The Raman activity is computed from the components of the Raman tensor  in such a way that the molecular orientations are averaged, and thus captures the Raman spectrum of randomly-oriented molecules measured in free-space.1 Here, we consider Raman activity only as an indicator for the overall strength of the Raman response and use the full Raman tensor (shown in Table 1) for the calculations. Fig. 2(a) shows that the isolated BPT molecule has three main Raman active vibrational modes at wave-numbers around 1066 cm−1, 1269 cm−1, and 1586 cm−1, which correspond to vibrational patterns with C–H rocking, and two in-plane stretches of the benzene rings, respectively (see insets). We note that the mode at 1066 cm−1 is the least active of the three modes according to these calculations, which differs from recent SERS experiments with NPoMs.10 On the other hand, Fig. 2(b) shows that the Raman activity of the 1066 cm−1 mode becomes larger than that of the 1269 cm−1 mode when the molecule binds to a gold atom, a result which agrees with these SERS experiments.10 The Raman activity of these modes at 1066 cm−1, 1269 cm−1 and 1586 cm−1 is enhanced by 16, 3.3, and 5.4 times, respectively. This chemical enhancement can be partially attributed to the change of molecular configuration, but mainly to the charge transfer induced by the gold–sulfur bond (see Fig. 13 of ref. 10). The largest chemical enhancement is produced for the least intense Raman active mode of the isolated molecule (of the three considered), in agreement with previous studies.35 In addition, we also find that the vibrational frequencies are slightly shifted for the isolated molecule without a gold atom. Since this shift is very small, we ignore it in the following for simplicity.
in such a way that the molecular orientations are averaged, and thus captures the Raman spectrum of randomly-oriented molecules measured in free-space.1 Here, we consider Raman activity only as an indicator for the overall strength of the Raman response and use the full Raman tensor (shown in Table 1) for the calculations. Fig. 2(a) shows that the isolated BPT molecule has three main Raman active vibrational modes at wave-numbers around 1066 cm−1, 1269 cm−1, and 1586 cm−1, which correspond to vibrational patterns with C–H rocking, and two in-plane stretches of the benzene rings, respectively (see insets). We note that the mode at 1066 cm−1 is the least active of the three modes according to these calculations, which differs from recent SERS experiments with NPoMs.10 On the other hand, Fig. 2(b) shows that the Raman activity of the 1066 cm−1 mode becomes larger than that of the 1269 cm−1 mode when the molecule binds to a gold atom, a result which agrees with these SERS experiments.10 The Raman activity of these modes at 1066 cm−1, 1269 cm−1 and 1586 cm−1 is enhanced by 16, 3.3, and 5.4 times, respectively. This chemical enhancement can be partially attributed to the change of molecular configuration, but mainly to the charge transfer induced by the gold–sulfur bond (see Fig. 13 of ref. 10). The largest chemical enhancement is produced for the least intense Raman active mode of the isolated molecule (of the three considered), in agreement with previous studies.35 In addition, we also find that the vibrational frequencies are slightly shifted for the isolated molecule without a gold atom. Since this shift is very small, we ignore it in the following for simplicity.
| ω v | R xx | R xy ,Ryx | R xz ,Rzx | R yy | R yz ,Rzy | R zz |
|---|---|---|---|---|---|---|
| 1066 cm−1 | 3.9 | −0.3 | 11.8 | 11.5 | 16.0 | 141.5 |
| 1269 cm−1 | 3.9 | −0.5 | −15.4 | 8.2 | 5.9 | 127.9 |
| 1586 cm−1 | 2.6 | 2.7 | −7.5 | −6.5 | 22.9 | 277.1 |
In Table 1 we collect the computed Raman tensor for the gold atom-bonded molecule. For the calculation of the different tensor elements, the orientation of the molecule becomes important. We assume that the molecule stands up at an angle of 15° with respect to the z-axis perpendicular to the substrate36 (Fig. 1(b)). The zz-component Rzz has the largest value for all three modes because the atomic displacement is mainly along the positive and negative z-direction for these vibrational modes (see the vibrational patterns in Fig. 2(b)). Comparing the Raman tensor components in Table 1 with the corresponding values for the isolated molecule (Table S1 in the ESI†), we find that the component Rzz is enhanced by about 4.4, 1.9, and 2.4 times due to the binding with a single gold atom. These values are consistent with the enhancement of the Raman activity since the latter is roughly proportional to the square of Rzz. The effect of such chemical enhancement, i.e. the modification of the Raman activity, can facilitate the appearance of optomechanical effects. All the calculations of optomechanical effects in this paper use the Raman tensor in Table 1 for the BPT molecule bonded to the gold atom, except in section 7.3 and section S4.7–S4.9 of the ESI,† where the Raman tensor of the isolated molecule is used (Table S1 of the ESI†) to normalize the SERS signal and compute its enhancement. In addition, we also provide the atomic coordinates of the BPT and the gold-bonded BPT molecule used in our DFT calculation in Table S2 of the ESI.†
4. Plasmonic response: local field and dyadic Green's function
The properties of the plasmonic nano-cavities in the absence of the molecule can be evaluated with classical electromagnetic simulations. We consider a NPoM plasmonic nanocavity formed by a truncated gold nano-sphere of radius 35 nm and a bottom facet of 5 nm radius, deposited over a gold substrate. The width of the gap between the bottom facet and the substrate is 1.3 nm, as set by a layer of relative dielectric permittivity εgap = 2.1 covering the whole gold substrate. A sketch of the system under study is shown in Fig. 1. We study such plasmonic nano-cavities here since they have been shown to be an effective configuration boosting the Raman signal in several SERS experiments.8,10,25,37–40 We carry out the simulations of the field enhancement and near-field Green's function with the use of the boundary element method41,42 as implemented in the MNPBEM toolkit43,44 and use the dielectric permittivity εAu of gold given by Johnson–Christy.45 For the calculation of the far-field Green's function, the COMSOL Multiphysics toolkit is used.46 The full NPoM system is placed in vacuum (or air).To mimic the experimental conditions,8,10,25,37 we illuminate the system with a plane-wave (laser) at an incident angle of 55° relative to the z-axis normal to the substrate (Fig. 1(a)). Fig. 3(a) shows that the far-field scattering spectrum (computed by integrating the real part of the Poynting vector of the fields scattered from the nano-particle over a closed surface in the far-field43), is dominated by two peaks (black solid line), which are often identified as the bonding dipolar plasmon (BDP) mode (at λBDP ≈ 720 nm) and the bonding quadrupole plasmon (BQP) mode (at λBQP ≈ 580 nm).8,10,47,48 We show the spatial near-field distribution of these modes in Fig. S3 of section S4.2 of the ESI,† which are consistent with those in previous work.49 The spectrum of the near-field enhancement along the z-axis calculated in the middle of the nanocavity (blue circles in Fig. 3(a)) shows also the same two modes, with enhancements as large as 400 for the BDP mode. In addition, the enhancement is 138 and 170 for illumination wavelengths of 633 nm and 785 nm, respectively, corresponding to lasers commonly used in SERS experiments.8,10
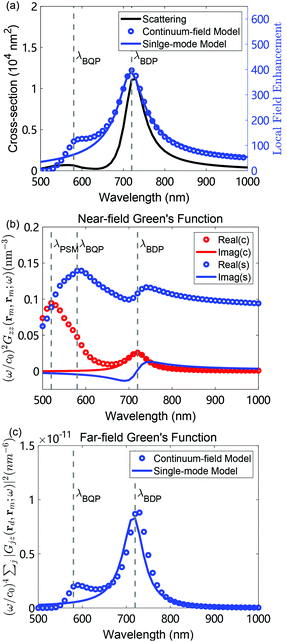 | ||
Fig. 3 Electromagnetic response of the plasmonic NPoM nanocavity. (a) Far-field scattering spectrum (black solid line), and near-field amplitude enhancement Ez(rm,ω)/|E0| as calculated within the continuum-field model considering the full optical response of the cavity (blue circles), and when only a single-mode is considered (solid blue line), at the molecular position (center of the plasmonic nanocavity). (b) Real (blue circles and line) and imaginary (red circles and line) parts of the dyadic Green's tensor component (ω/c0)2Gzz(rm,rm,ω) at the molecular position, within the continuum-field model (marked with c in the legend) and within the single-mode model (marked with s in the legend). (c) Sum of the tensor components 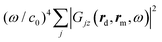 that describes the emission from the molecule to the detector within the continuum-field model (blue dots), and within the single-mode model (blue line). Dashed vertical grey lines indicate the bonding dipolar plasmon (BDP) mode (at λBDP ≈ 720 nm), the bonding quadrupole plasmon (BQP) mode (at λBQP ≈ 580 nm), and the plasmon pseudomode (PSM) (at λPSM ≈ 520 nm). The fitting of the BDP mode with the single Lorentzian mode is described in the text and in section S2 of the ESI.† that describes the emission from the molecule to the detector within the continuum-field model (blue dots), and within the single-mode model (blue line). Dashed vertical grey lines indicate the bonding dipolar plasmon (BDP) mode (at λBDP ≈ 720 nm), the bonding quadrupole plasmon (BQP) mode (at λBQP ≈ 580 nm), and the plasmon pseudomode (PSM) (at λPSM ≈ 520 nm). The fitting of the BDP mode with the single Lorentzian mode is described in the text and in section S2 of the ESI.† | ||
To compute the components of the dyadic Green's function Gij(r′, r, ω), we excite the system with a point dipole at position r of dipole moment μj along the j-axis with frequency ω, and compute the near-field component Ei(r′) along the i-axis at position r′. Then, we extract the Green's function according to the relationship Ei(r′) = (ω2/(ε0c02))Gij(r′, r, ω)μj. The dyadic Green's function can be decomposed into a contribution that corresponds to the radiation of an isolated dipole in a homogeneous bulk material of relative dielectric permittivity εgap, and the contribution of the scattering field from the NPoM. The real part of the former at the position of the dipole is infinite, and requires a careful regularization procedure.50,51 We thus focus on the scattering field contribution throughout the paper.
Fig. 3(b) shows the real (blue circles) and imaginary (red circles) parts of the zz-component of the near-field dyadic Green's function Gzz(rm,rm,ω) (multiplied by ω2/c20) for the molecular dipole located in the middle of the nanocavity. We focus on the zz-component because it dominates the optomechanical response, due to the strong polarization of the plasmonic fields along the z-axis and to the dominant zz-component of the Raman tensor in Table 1.
The real part of Gzz(rm,rm,ω) is associated with the parameters Ω±vv that describe the vibrational frequency shift and thus the spectral shift of the Raman lines (eqn 6). It is always positive for our system and, notably, it remains roughly constant for wavelengths larger than 600 nm, with a relatively shallow Fano-like feature near ≈720 nm. This spectral dependence can be understood as a consequence of the excitation of the BDP mode and the so-called plasmonic pseudomode16,52 (arising from the overlap of many high-order plasmonic modes49).
The imaginary part of Gzz(rm,rm,ω) governs the vibrational pumping Γ+vv and damping rate Γ−vv (eqn (2)). As observed from the red circles in Fig. 3(b), this imaginary part shows one spectral peak at around 720 nm corresponding to the BDP mode, and a small bump at around 580 nm due to the BQP mode. The latter is however superimposed with a strong peak around 520 nm due to the pseudomode. The near-field dyadic Green's function is thus strongly affected by the pseudomode, which is typically ignored in SERS studies. In section S3 of the ESI,† we discuss how this contribution from the pseudomode can be associated with the optical response for large k-vector of the metal–insulator–metal configuration.
To conclude the analysis of the plasmonic response, Fig. 3(c) shows the spectral sum of the squared absolute value of the far-field dyadic Green's tensor components 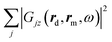 (blue circles, multiplied by ω4/c40). This response function is required to evaluate the propagation factor that describes the emission towards the detector, as given by eqn (9), from a point source polarized along the z direction (the dominant polarization of the induced Raman dipole pv of the molecule in the nanocavity). The calculated spectrum resembles that of the local field enhancement (squared) shown in Fig. 3(a), as expected from the optical reciprocity theorem.1,53
(blue circles, multiplied by ω4/c40). This response function is required to evaluate the propagation factor that describes the emission towards the detector, as given by eqn (9), from a point source polarized along the z direction (the dominant polarization of the induced Raman dipole pv of the molecule in the nanocavity). The calculated spectrum resembles that of the local field enhancement (squared) shown in Fig. 3(a), as expected from the optical reciprocity theorem.1,53
To illustrate the influence of the high-order plasmonic modes on SERS, we compare the results obtained within the continuum-field model which considers the full plasmonic response, with those obtained using a single optical reference mode. The latter is the treatment commonly used in descriptions of molecular optomechanics, where the field of a single optical mode is treated as a quantized harmonic oscillator and included in the optomechanical Hamiltonian. In particular, if one focuses on the near-field enhancement as typical in SERS studies, it might be expected from Fig. 3(a) that optomechanical phenomena will be dominated by the BDP mode near 720 nm. We thus focus on this resonance as a reference for the single-mode treatment, and fit the field enhancement and Green's function components to single Lorentzians (or modified Lorentzian) according to 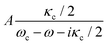 ,
, 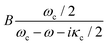 , and
, and 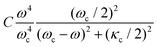 , respectively. Here, ωc, κc are the frequency and damping rate of the reference single plasmonic mode, and the values of A and B, and C determine the maximum value of each of the expressions above. These fits are implemented from careful comparison of the continuum-field and single-mode models (section S2 in the ESI† for a more detailed description of the procedure to obtain the fitting functions). We note that for the near-field dyadic Green's function, shown in Fig. 3(b), the real part differs dramatically from a Lorentzian, indicating the strong influence of the plasmonic pseudomode. Thus, we do not directly use this magnitude for the fitting.
, respectively. Here, ωc, κc are the frequency and damping rate of the reference single plasmonic mode, and the values of A and B, and C determine the maximum value of each of the expressions above. These fits are implemented from careful comparison of the continuum-field and single-mode models (section S2 in the ESI† for a more detailed description of the procedure to obtain the fitting functions). We note that for the near-field dyadic Green's function, shown in Fig. 3(b), the real part differs dramatically from a Lorentzian, indicating the strong influence of the plasmonic pseudomode. Thus, we do not directly use this magnitude for the fitting.
Once A and B are obtained from the fittings, they can be used to extract the physical properties of the reference single optical mode, such as its corresponding effective mode volume Veff, the plasmon-laser coupling ħΩexc and the optomechanical coupling gv. For our reference single mode, we obtain a value of Veff around ≈227.5 nm3, ħΩexc ≈ 2 meV for a laser intensity of 1 μW μm−2, and ħgv ≈ 0.032 meV, 0.027 meV, 0.052 meV for the 1066 cm−1, 1269 cm−1, 1586 cm−1 vibrational modes, respectively (see ref. 4 and 5 for a detailed discussion of these parameters). We discuss in section S2 of the ESI† the details about how the fitting is performed and how the expressions from the fittings are connected with the reference Lorentzian mode adopted in the single-mode model.
The blue and red solid lines in Fig. 3 correspond to the results of the reference single-mode model as obtained from the fitting for the amplitude of the near-field enhancement (a), the imaginary part of the dyadic Green's function (b) and the far-field dyadic Green's function (c). These were obtained with the plasmon energy ħωc = 1.726 eV (wavelength ≈718 nm), the plasmon damping rate ħκc = 0.136 eV, and the maximal local field enhancement K = 391. We observe that the fittings agree well with the exact results for longer wavelengths (except for the real part of the near-field dyadic Green's function, as discussed previously). For shorter wavelengths however, the differences can be more pronounced since the reference single-mode model does not take into account the high-order modes. We find a particularly large discrepancy for the imaginary part of the near-field dyadic Green's function, which is very strongly affected by the plasmonic pseudomode.16,52
5. Optomechanical parameters Γ±vv, Ω±vv and propagation factors K±vv
We can now determine the key magnitudes which govern the vibrational dynamics and thus the emission of the Raman process, namely the vibrational pumping (damping) rate Γ+vv (Γ−vv), and the vibrational frequency shift parameters Ω±vv, as well as the propagation factors K±vv, according to the prescriptions introduced in section 2. In Fig. 4, we show the dependence of these parameters on the incident laser wavelength λl for a laser intensity of Ilas = 1 μW μm−2, as an example, and for vibrational modes at 1066 cm−1 (upper panels a–c) and 1586 cm−1 (lower panels d–f). Since these parameters are linearly proportional to the laser intensity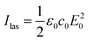 (viaeqn (3)) one can easily obtain their values for other laser intensities. We plot the results obtained within the continuum-field model (solid lines) and those within the reference single-mode model (dashed lines), which we label with the superscripts “c” and “s”, respectively, throughout the manuscript.
(viaeqn (3)) one can easily obtain their values for other laser intensities. We plot the results obtained within the continuum-field model (solid lines) and those within the reference single-mode model (dashed lines), which we label with the superscripts “c” and “s”, respectively, throughout the manuscript.
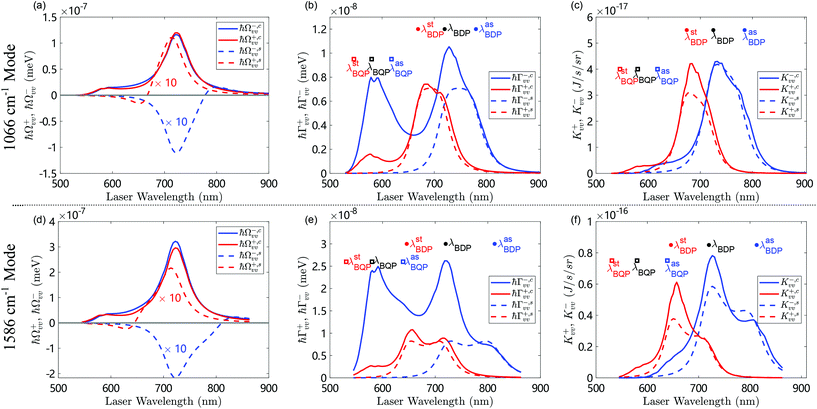 | ||
| Fig. 4 Dependence of (a and d) the vibrational frequency shift parameters Ω±,cvv, Ω±,svv, (b and e) the vibrational pumping Γ+,cvv, Γ+,svv and damping Γ−,cvv, Γ−,svv rates, and (c and f) the propagation factors K±,cvv, K±,svv, on the wavelength of the illuminating laser of intensity Ilas = 1 μW μm−2 and Raman-active vibrational mode of wave-number (a–c) 1066 cm−1 and (d–f) 1586 cm−1. The solid lines are computed with the continuum-field model (labeled by “c”) while the dashed lines are calculated with the single-mode model (labeled by “s”). In (b and c), the dots from right to left mark the laser wavelengths where the anti-Stokes emission (λasBDP = 780 nm), the excitation (λBDP = 720 nm), and the Stokes emission (λstBDP = 669 nm) are maximized due to the BDP mode. The squares mark the same information (λasBQP = 618 nm, λBQP = 580 nm, λstBQP = 546 nm) for the BQP mode. In (e and f), the dots and the squares mark the same information as in (b and c) for the high-energy vibrational mode with values of λasBDP = 813 nm, λBDP = 720 nm, and λstBDP = 646 nm for the BDP mode, and λasBQP = 639 nm, λBQP = 580 nm, and λstBQP = 531 nm for the BQP mode. The difference between the wavelengths marked in (b and c) and (e and f) are due to the difference in the vibrational energy, which affects the Stokes and anti-Stokes frequencies. The results for the 1269 cm−1 mode are shown in Fig. S4 of the ESI.† Other parameters are specified in the text. | ||
Fig. 4(a and d) show the spectral dependence of Ω±,cvv, Ω±,svv, as given by eqn (6). These results depend on the product of the local field at the laser frequency ωl (via the Raman-induced dipole, eqn (3)) and the real part of the near-field dyadic Green's tensor (with the zz-component dominating the response) at either the Stokes ωl − ωv or the anti-Stokes frequency ωl + ωv. For the continuum-field model, the dependence of Ω+,cvv and Ω−,cvv on λl resembles that of the near-field enhancement (circles in Fig. 3(a)), because the real part of the near-field dyadic Green's function depends relatively weakly on the wavelength. For the single-mode model, the absolute value |Ω±,svv| follows a similar λl-dependence as in the continuum-field model, but is about 10 times weaker. Furthermore, Ω−,svv near the resonant BDP peak at 720 nm, presents a negative minimum instead of the positive peak observed in the continuum-field model. We thus find a first remarkable difference between the continuum-field model and the reference single-mode model, which can be attributed to the large difference between the value of the real part of the near-field dyadic Green's function obtained within each of the models (compare the blue solid line with the blue circles in Fig. 3(b)). As discussed in the previous section, this discrepancy arises from the very large influence of the high-order plasmonic resonances, i.e. the pseudomode, in the continuum-field results, related to the local short-range response of the metal–insulator–metal configuration, (see section S3 in the ESI†), which adds a strong and nearly constant positive contribution to the real part of Gzz(rm,rm,ω). We discuss in section 7 the importance of this effect on the frequency shift of the Raman lines for strong laser illumination. We note finally that Ω±v is about two times larger for the vibrational mode at 1586 cm−1 (Fig. 4(d)) than for 1066 cm−1 (Fig. 4(a)) mostly because of the larger Raman tensor of the former.
Fig. 4(b and e) show the laser wavelength λl-dependence of Γ+,cvv and Γ+,svv (Γ−,cvv and Γ−,svv). These parameters are proportional to the product of the local field E(rm,ωl) (with z-component dominating) at the laser frequency ωl and the imaginary part of the near-field dyadic Green's functions, 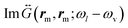 , or
, or 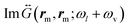 , evaluated at the Stokes ωl − ωv or anti-Stokes frequency ωl + ωv, respectively (eqn (2)) (with the zz-components dominating). The latter are shifted by −ωv or +ωv relative to the illumination frequency, and thus Γ−,cvv and Γ−,svv differ from Γ+,cvv and Γvv+,s because the dyadic Green function is evaluated at a different frequency, which changes the spectral dependence significantly, as observed in the figure. We again consider the vibrational modes at 1066 cm−1 (Fig. 4(b)) and 1586 cm−1 (Fig. 4(e)), and discuss first the continuum-field model (solid lines). To understand these results, we note that |E(rm,ωl)| presents a maximum for illumination wavelengths around λBDP = 2πc0/ωBDP ≈ 720 nm and a weaker one near λBQP = 2πc0/ωBQP = 580 nm due to the excitation of BDP and BQP modes, respectively. The imaginary part of the near-field Green's function
, evaluated at the Stokes ωl − ωv or anti-Stokes frequency ωl + ωv, respectively (eqn (2)) (with the zz-components dominating). The latter are shifted by −ωv or +ωv relative to the illumination frequency, and thus Γ−,cvv and Γ−,svv differ from Γ+,cvv and Γvv+,s because the dyadic Green function is evaluated at a different frequency, which changes the spectral dependence significantly, as observed in the figure. We again consider the vibrational modes at 1066 cm−1 (Fig. 4(b)) and 1586 cm−1 (Fig. 4(e)), and discuss first the continuum-field model (solid lines). To understand these results, we note that |E(rm,ωl)| presents a maximum for illumination wavelengths around λBDP = 2πc0/ωBDP ≈ 720 nm and a weaker one near λBQP = 2πc0/ωBQP = 580 nm due to the excitation of BDP and BQP modes, respectively. The imaginary part of the near-field Green's function 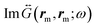 peaks also at approximately the same wavelength. Thus for the 1066 cm−1 vibrational mode
peaks also at approximately the same wavelength. Thus for the 1066 cm−1 vibrational mode 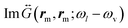 and
and 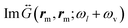 peak for illumination wavelength around λasBDP = 2πc0/(ωBDP − ωv) ≈ 780 nm and λstBDP = 2πc0/(ωBDP + ωv) ≈ 669 nm. The corresponding values for the BQP mode are λasBQP = 2πc0/(ωBQP − ωv) ≈ 618 nm, λstBQP = 2πc0/(ωBQP + ωv) ≈ 546 nm. These wavelengths are marked in Fig. 4(b) by dots and squares, respectively, allowing for a straightforward identification of the origin of the peaks and shoulders of the optomechanical pumping and damping rates in Fig. 4(b and e).
peak for illumination wavelength around λasBDP = 2πc0/(ωBDP − ωv) ≈ 780 nm and λstBDP = 2πc0/(ωBDP + ωv) ≈ 669 nm. The corresponding values for the BQP mode are λasBQP = 2πc0/(ωBQP − ωv) ≈ 618 nm, λstBQP = 2πc0/(ωBQP + ωv) ≈ 546 nm. These wavelengths are marked in Fig. 4(b) by dots and squares, respectively, allowing for a straightforward identification of the origin of the peaks and shoulders of the optomechanical pumping and damping rates in Fig. 4(b and e).
The maxima of Γ−,cvv near λBDP ≈ 720 nm and Γ+,cvv at λstBDP ≈ 669 nm for the low-energy vibrational mode at 1066 cm−1, occur when both the local field E(rm,ωl) and the near-field dyadic Green's function 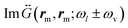 are significantly enhanced by the BDP mode. The peak of Γ−,cvv is red-shifted compared to the peak of Γ+,cvv because the latter depends on
are significantly enhanced by the BDP mode. The peak of Γ−,cvv is red-shifted compared to the peak of Γ+,cvv because the latter depends on 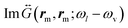 , which is increased for shorter laser wavelengths compared to
, which is increased for shorter laser wavelengths compared to 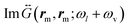 . On the other hand, the maxima of both Γ−,cvv and Γ+,cvv at λBQP = 580 nm occur mainly because the local field is strongly enhanced by the excitation of the BQP mode. Moreover, Γ−,cvv is significantly larger than Γ+,cvv at this wavelength because it depends on the near-field dyadic Green's function at shorter wavelengths, where the influence of the pseudomode is significantly stronger.
. On the other hand, the maxima of both Γ−,cvv and Γ+,cvv at λBQP = 580 nm occur mainly because the local field is strongly enhanced by the excitation of the BQP mode. Moreover, Γ−,cvv is significantly larger than Γ+,cvv at this wavelength because it depends on the near-field dyadic Green's function at shorter wavelengths, where the influence of the pseudomode is significantly stronger.
Furthermore, for the high-energy vibrational mode at 1586 cm−1, the difference between Γ−,cvv and Γ+,cvv becomes more pronounced, as shown in Fig. 4(e). In this case, the Stokes and anti-Stokes frequencies are more separated spectrally from each other. As a result, Γ−,cvv and Γ+,cvv reach maxima (or shoulders) for the laser wavelengths that optimize either the local field induced by the laser or the near-field dyadic Green's function. The features of Γ−,cvv and Γ+,cvv near λBDP = 720 nm and λBQP = 580 nm can thus be associated with the excitation of the BDP mode and the BQP mode. On the other hand, the signature of the BDP in the near-field dyadic Green's function explains the shoulder of Γ−,cvv at λasBDP = 813 nm and the peak of Γ+,cvv at λstBDP = 646 nm. The presence of the plasmonic pseudomode again affects the damping rate Γ−,cvv more strongly than the pumping rate Γ+,cvv, and this effect is even more pronounced than for the low-energy vibration (Fig. 4(b)) due to the larger separation between the Stokes and anti-Stokes frequencies. As a consequence, Γ−,cvv is larger than Γ+,cvv for all laser wavelengths considered here, which is in contrast with the behavior for the low-energy vibrational mode at 1066 cm−1, where Γ+,cvv is larger than Γ−,cvv in a small laser wavelength range [654.7 nm, 705.4 nm]. As discussed in section 7, this contrast leads to qualitatively different optomechanical behavior under strong illumination.
The results for the single-mode model (dashed lines) are different in key aspects. The parameters Γ±,svv are generally smaller than Γ±,cvv although the exact difference depends on the laser wavelength. The dashed lines in Fig. 4(b) show that the spectral dependence of Γ+,svv and Γ−,svv are mirror-symmetric with respect to the resonant wavelength 720 nm of the BDP mode. This behavior reflects the underlying symmetry of the single resonant peak considered, as well as the fact that the Stokes and anti-Stokes emission occur at ωl − ωv and ωl + ωv, respectively. Importantly for the upcoming analysis, Γ−,svv is larger than Γ+,svv only when ωl > 720 nm. More generally, the results for the single-mode model are only similar to those of the continuum-field model at long wavelengths where the BDP mode dominates the response. Crucially, the differences can be very pronounced at shorter wavelengths, where Γ−vv can be much larger within the continuum-field model than within the single-mode model. These differences are due to the importance of the high-order plasmonic modes (the pseudomode), which are completely ignored in the single-mode model.
Last, Fig. 4(c and f) show the dependence of the propagation factor K±,cvv on the laser wavelength λl. K+,cvv (K−,cvv) depend on the local field E(rm,ωl) at the laser frequency ωl and on the far-field dyadic Green's function 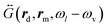
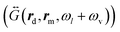 at the Stokes frequency ωl − ωv (anti-Stokes frequency ωl + ωv), as indicated by eqn (3) and (9). Importantly, both E(rm,ωl) and
at the Stokes frequency ωl − ωv (anti-Stokes frequency ωl + ωv), as indicated by eqn (3) and (9). Importantly, both E(rm,ωl) and 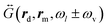 are not significantly affected by the plasmonic pseudomode. In this case, the main difference between the results of the continuum-field model (solid lines) and those of the single-mode model (dashed lines) is mostly associated with the influence of the BQP mode, which can make the former substantially larger.
are not significantly affected by the plasmonic pseudomode. In this case, the main difference between the results of the continuum-field model (solid lines) and those of the single-mode model (dashed lines) is mostly associated with the influence of the BQP mode, which can make the former substantially larger.
For completeness, we also show the results for the 1269 cm−1 vibrational mode in Fig. S4 in the ESI.† The dependence of this mode resembles that of the low-energy vibrational mode at 1066 cm−1 in Fig. 4(a–c), but the wavelength range where Γ+,cvv > Γ−,cvv narrows for the 1269 cm−1 mode. It appears that the wavelength window for Γ+,cvv > Γ−,cvv becomes narrower as the vibrational frequency ωv increases.
6. Vibrational frequency shift and effective optomechanical damping rate
After analyzing the individual contributions, here we address the wavelength-dependence of the effective optomechanical parameters, δωv = (Ω+vv + Ω−vv)/2 and Γoptv = Γ−vv − Γ+vv (Fig. 5). As shown in section 2, these parameters describe the shift and the broadening (or narrowing) of the Raman lines, respectively. The parameter Γoptv also plays a key role in the evolution of the vibrational population (and thus of the integrated Raman intensity) for sufficiently strong laser illumination (denominator in eqn (4)), as discussed in detail in the next section.Fig. 5(a) shows that within the single-mode model (dashed lines), the shift δωv changes sign several times because Ω+,svv and Ω−,svv possess similar spectral dependence with laser wavelength but with opposite sign (Fig. 4(a and d)). Hence the sign of δωv depends on which one is slightly larger. In contrast, in the continuum-field model (solid lines), Ω+,cvv and Ω−,cvv have the same positive sign in the wavelength range under study, so that δωv (solid lines) is always positive and reaches a maximum around 720 nm. These general trends hold for both the 1066 cm−1 (red lines) and the 1586 cm−1 (blue lines) vibrational modes. According to the single-mode model, the Stokes Raman lines are then blue- or red-shifted (due to the decrease or increase of the vibrational frequencies) depending on the detuning of the laser wavelength, while the continuum-field model predicts that these Raman lines are always blue-shifted due to the decrease of the vibrational frequency (i.e. lower emission wavelength). The anti-Stokes Raman lines always show a shift of opposite sign and equal absolute value compared to the Stokes lines. Also importantly, the shift in the continuum-field model is significantly larger than that given by the single-mode model, both because the individual Ω±vv terms are about 10 times larger, and because they have the same sign leading to shifts in the same direction, instead of largely cancelling each other as occurs in the single-mode model. As described in the previous section, the behavior of Ω±vv is related to the presence of the plasmon pseudo-mode, which contributes with large and positive values to the real part of the Green's function at all wavelengths (see Fig. 3(b)).
Furthermore, regarding the optomechanical broadening/narrowing, Fig. 5(b) shows that according to the single-mode model (dashed lines) the effective optomechanical damping rate Γoptv is (i) negative for illumination blue-detuned with respect to the BDP mode (laser wavelength smaller than the plasmonic resonant wavelength), (ii) zero when the laser is perfectly tuned to the resonant single optical mode and (iii) it becomes positive for red-detuned illumination. This relatively simple behavior of Γoptv occurs for all vibrational modes and has been much studied in standard cavity optomechanics6,7 and molecular optomechanics.4,5,8–10,15,17 However, Fig. 5(b) indicates that this behavior can change radically when the plasmonic cavity is more properly described within the continuum-field model (solid lines). For this more suitable description of the NPoM plasmonic response (or any similar plasmonic system), Γoptv for the 1066 cm−1 mode (red solid line) is positive for both short and long wavelengths, and only becomes negative in a narrow wavelength window [654.7 nm, 705.4 nm]. Thus, the single-mode model predicts that the Raman lines become narrower or broader for shorter or longer laser wavelengths, respectively, while according to the continuum-field model these lines become narrower only in a relatively small wavelength window. Moreover, for the 1586 cm−1 mode, Γoptv (blue solid line) is always positive in the continuum-model, and thus high-energy vibrational modes never get narrower. Overall, the larger value of Γoptv within the continuum-field model is mainly caused by the larger imaginary part of the Green's function at short wavelengths caused by the plasmonic pseudomode (see red circles in Fig. 3(b)), which enhances the vibrational damping rate, particularly at short laser wavelengths. The effect of the pseudomode can be combined with that from other modes of the system, for instance the BQP, giving rise to extra features, as observed with the emergence of a second peak in Γoptv at around 580 nm in Fig. 5(b) (solid red and blue lines).
The consequences of the behavior of Γoptv for the dependence of the vibrational population and the integrated SERS intensity on the incident laser intensity are explored in detail in the next section.
7. SERS versus incident laser wavelength and intensity
Once the optomechanical parameters and the propagation factors are obtained, the evolution of the vibrational population, the integrated intensity, the linewidth and the line-shift of the SERS lines can be studied as a function of the incident laser intensity. For this study, we focus on four laser wavelengths at 633 nm, 670 nm, 705.9 nm, and 785 nm (marked by vertical lines in Fig. 5 of the previous section). The first and last wavelengths are commonly used in SERS experiments8,10,39,40 and lead to a positive effective optomechanical damping rate Γoptv. The second and third wavelengths serve to illustrate the effect of negative and zero effective optomechanical damping rate (specifically for the 1066 cm−1 mode), as shown in Fig. 5(b).7.1 General trends within the single-mode model
To understand the evolution of the SERS signal with laser intensity, Ilas, it is worthwhile to summarize briefly the predictions of the single-mode model. According to earlier studies,5,6,9,15 there exist three distinct regimes of optomechanical interaction that correspond to different ranges of laser intensity. These regimes follow directly from eqn (4), (10) and (11) and can be appreciated in the evolution of the vibrational population and of the Stokes and anti-Stokes signal with increasing Ilas (dashed lines in Fig. 6(a and b) for the 1066 cm−1 vibrational mode and in Fig. 6(e and f) for the 1586 cm−1 vibrational mode).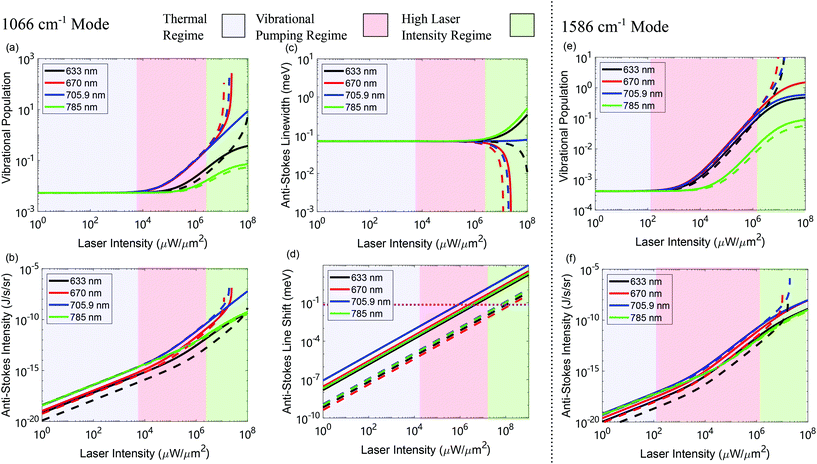 | ||
Fig. 6 Evolution of (a) the vibrational population 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v †v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 and (b) the frequency-integrated intensity Sas, (c) the line-width ħγ−v = ħ(γv + Γoptv), and (d) the line shift ħ[ω−v − (ωl + ωv)] = −ħ(Ω+vv + Ω−vv)/2 of the anti-Stokes lines for the 1066 cm−1 vibrational mode, as a function of the laser intensity Ilas and for wavelengths λlas = 633 nm (black lines), 670 nm (red lines), 705.9 nm (blue lines) and 785 nm (green lines). The solid and dashed lines are the results based on the continuum-field model and the single-mode model, respectively. In (d) all lines (except for the black and red dashed lines for laser wavelength 633 nm and 670 nm) are multiplied by minus one to be able to plot in logarithmic scale, while the horizontal dotted line indicates the intrinsic vibrational decay rate ħγv = 0.07 meV for reference. The light blue, red and green background colors indicate the laser intensity ranges corresponding to the thermal regime for weak Ilas, the vibrational pumping regime for moderate Ilas, and the regime with large Ilas, respectively (the exact boundaries between these regimes depend on the vibrational mode and laser wavelength under consideration). The temperature is T = 293 K resulting in thermal vibrational populations nthv = 5 × 10−3. The other parameters are specified in the text. We show the integrated intensity of the Stokes lines in Fig. S5 in the ESI† [the linewidth of the Stokes emission is the same as that of the anti-Stokes line because ħγ+v = ħγ−v, and the line-shift is also of equal amplitude but in the opposite direction ħ[ω+v − (ωl − ωv)] = ħ(Ω+vv + Ω−vv)/2]. (e) and (f) show equivalent results as in (a) and (b) but for the 1586 cm−1 vibrational mode. v〉 and (b) the frequency-integrated intensity Sas, (c) the line-width ħγ−v = ħ(γv + Γoptv), and (d) the line shift ħ[ω−v − (ωl + ωv)] = −ħ(Ω+vv + Ω−vv)/2 of the anti-Stokes lines for the 1066 cm−1 vibrational mode, as a function of the laser intensity Ilas and for wavelengths λlas = 633 nm (black lines), 670 nm (red lines), 705.9 nm (blue lines) and 785 nm (green lines). The solid and dashed lines are the results based on the continuum-field model and the single-mode model, respectively. In (d) all lines (except for the black and red dashed lines for laser wavelength 633 nm and 670 nm) are multiplied by minus one to be able to plot in logarithmic scale, while the horizontal dotted line indicates the intrinsic vibrational decay rate ħγv = 0.07 meV for reference. The light blue, red and green background colors indicate the laser intensity ranges corresponding to the thermal regime for weak Ilas, the vibrational pumping regime for moderate Ilas, and the regime with large Ilas, respectively (the exact boundaries between these regimes depend on the vibrational mode and laser wavelength under consideration). The temperature is T = 293 K resulting in thermal vibrational populations nthv = 5 × 10−3. The other parameters are specified in the text. We show the integrated intensity of the Stokes lines in Fig. S5 in the ESI† [the linewidth of the Stokes emission is the same as that of the anti-Stokes line because ħγ+v = ħγ−v, and the line-shift is also of equal amplitude but in the opposite direction ħ[ω+v − (ωl − ωv)] = ħ(Ω+vv + Ω−vv)/2]. (e) and (f) show equivalent results as in (a) and (b) but for the 1586 cm−1 vibrational mode. | ||
The thermal and vibrational-pumping regimes occur for weak and moderate laser intensities, where the intrinsic vibrational decay rate γv is larger than the optomechanical damping rate Γoptv, and thus Γoptv can be ignored in the denominator of eqn (4). In the thermal regime, for weak Ilas (light blue-shaded region in Fig. 6), the vibrational population is dominated by the thermal value, 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 ≈ nthv (dashed lines, hidden under the solid ones in Fig. 6(a and e)). In such a situation, the integrated anti-Stokes and Stokes SERS intensities scale linearly with laser intensity (dashed lines in Fig. 6(b and f) and Fig. S5 in the ESI†), according to Sas ≈ K−vvnthv and Sst ≈ K+vv(1 + nthv) (notice that K±vv ∝ Ilas).
v〉 ≈ nthv (dashed lines, hidden under the solid ones in Fig. 6(a and e)). In such a situation, the integrated anti-Stokes and Stokes SERS intensities scale linearly with laser intensity (dashed lines in Fig. 6(b and f) and Fig. S5 in the ESI†), according to Sas ≈ K−vvnthv and Sst ≈ K+vv(1 + nthv) (notice that K±vv ∝ Ilas).
As Ilas increases one reaches the vibrational pumping regime (red-shaded region in Fig. 6), where the vibrational population acquires an extra contribution due to creation of a vibration quantum by each Stokes-scattering event (vibrational pumping). As a consequence, the vibrational population (dashed lines in Fig. 6(a and e)) acquires a term proportional to the laser intensity 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 ≈ nthv + Γ+vv/γv (notice that Γ+vv ∝ Ilas) and the anti-Stokes intensity scales super-linearly and eventually quadratically with increasing Ilas (dashed lines in Fig. 6(b and f)), according to Sas ≈ K−vv(nthv + Γ+vv/γv). The Stokes signal (Fig. S5 in the ESI†) also acquires a quadratic component Sst ≈ K+vv(1 + nthv + Γ+vv/γv), but it only becomes significant when the increase of the vibrational population due to the vibrational pumping Γ+vv/γv reaches a value close to 1, which in our system occurs for laser intensities larger than those of the vibrational pumping regime. Furthermore, the modification of the Raman linewidth and spectral position remain negligible for moderate laser intensities (thermal and vibrational pumping regimes), where the intrinsic linewidth of the Raman line, given by the intrinsic vibrational decay rate γv, remains larger than the effective optomechanical damping rate Γoptv and the optomechanically-induced Raman line shift |(Ω+vv + Ω−vv)/2| (dashed lines in Fig. 6(c and d), some of them hidden by the solid lines).
v〉 ≈ nthv + Γ+vv/γv (notice that Γ+vv ∝ Ilas) and the anti-Stokes intensity scales super-linearly and eventually quadratically with increasing Ilas (dashed lines in Fig. 6(b and f)), according to Sas ≈ K−vv(nthv + Γ+vv/γv). The Stokes signal (Fig. S5 in the ESI†) also acquires a quadratic component Sst ≈ K+vv(1 + nthv + Γ+vv/γv), but it only becomes significant when the increase of the vibrational population due to the vibrational pumping Γ+vv/γv reaches a value close to 1, which in our system occurs for laser intensities larger than those of the vibrational pumping regime. Furthermore, the modification of the Raman linewidth and spectral position remain negligible for moderate laser intensities (thermal and vibrational pumping regimes), where the intrinsic linewidth of the Raman line, given by the intrinsic vibrational decay rate γv, remains larger than the effective optomechanical damping rate Γoptv and the optomechanically-induced Raman line shift |(Ω+vv + Ω−vv)/2| (dashed lines in Fig. 6(c and d), some of them hidden by the solid lines).
The vibrational pumping regime is achieved when the vibrational population induced by the Stokes scattering, which equals Γ+vv/γv (second term in eqn (4), with Γoptv ≪ γv in this regime), becomes larger than the thermal value nthv. Thus, we can define the laser threshold Ithr,1 to achieve this regime as the laser intensity satisfying Γ+vv/γv ≈ nthv. We estimate from Fig. 6(a and e) that Ithr,1 can be as low as 3 × 103 μW μm−2, which can be achieved with both pulsed and continuous-wave laser.10 These values are estimated at room temperature, but could be further reduced by increasing the vibrational frequency or by lowering the temperature, i.e. lowering nthv (see Fig. S6 in the ESI† for more details).
In the regime of large laser intensity Ilas (green-shaded region in Fig. 6) a qualitatively different behavior occurs for different laser wavelengths. In this regime, the effective optomechanical damping rate Γoptv becomes comparable to γv and thus it cannot be neglected in the denominator of eqn (4). Crucially, the laser wavelength determines the sign of Γoptv (see Fig. 5(b)). If the laser is blue-detuned with respect to the BDP mode (corresponding to the cases of λlas = 633 nm, 670 nm and 705.9 nm in Fig. 6), Γoptv is negative (red dashed line in Fig. 5(b)) and the denominator in eqn (4) approaches zero as Ilas increases. As a result, the vibrational population increases super-linearly and finally diverges (black, red, and blue dashed lines in Fig. 6(a and e)). This divergent behavior, which is also observed in the integrated anti-Stokes and Stokes scattering (black, red and blue dashed lines in Fig. 6(b and f) and Fig. S5 in the ESI†) due to their dependence on the vibrational population, is known as parametric instability in cavity-optomechanics.7 In this situation the SERS lines become narrower, as their linewidth is given by Γoptv + γv (Fig. 6(c)), and they also experience a relatively small frequency-shift (Ω+vv + Ω−vv)/2 with a sign that depends on the laser wavelength (the anti-Stokes lines shift towards larger frequencies at laser wavelengths of 633 nm and 670 nm, but towards smaller frequencies at 705.9 nm). The shifts are shown in Fig. 6(d). The Stokes lines show the same shift but with opposite signs.
If the laser is red-detuned from the BDP mode (λlas = 785 nm, green dashed line in Fig. 6), Γoptv is positive (red dashed line in Fig. 5(b)). The SERS lines then become broader (Fig. 6(c)) and the denominator in eqn (4) becomes larger as Ilas increases. Since the numerator in eqn (4) also grows with increasing Ilas, the vibrational population eventually saturates (green dashed line in Fig. 6(a)), leading to a linear scaling of the SERS signal with Ilas (green dashed line in Fig. 6(b) and Fig. S5 in the ESI†). Thus, as the laser intensity is increased, the integrated anti-Stokes signal (Fig. 6(b)) changes from linear (thermal regime) to quadratic (vibrational pumping regime) and again to linear (very large intensities) scaling with Ilas. The Raman lines also experience a frequency shift (Ω+vv + Ω−vv)/2 for this laser wavelength (Fig. 6(d)), but it is a factor 3 smaller than the optomechanicaly-induced broadening Γoptv.
Finally, if the laser is tuned to the exact frequency of the BDP mode (zero-detuned), Γoptv is precisely zero. As a result, the SERS lineshape does not change (neither in linewidth or frequency) and the trends discussed for the vibrational pumping regime continue to govern the response (not shown): the vibrational population increases linearly with increasing Ilas, i.e. 〈![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) †v
†v![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) v〉 ≈ Γ+vv/γv, and both the integrated Stokes and anti-Stokes SERS intensity scale quadratically with increasing Ilas, i.e. Sst(as) ≈ K+(-)vvΓ+vv/γv. Last, we note that the results of the single-mode model do not depend qualitatively on the actual vibrational frequency, and therefore the same trends are obtained in Fig. 6(a–f) for the 1066 cm−1 and 1586 cm−1 vibrational modes.
v〉 ≈ Γ+vv/γv, and both the integrated Stokes and anti-Stokes SERS intensity scale quadratically with increasing Ilas, i.e. Sst(as) ≈ K+(-)vvΓ+vv/γv. Last, we note that the results of the single-mode model do not depend qualitatively on the actual vibrational frequency, and therefore the same trends are obtained in Fig. 6(a–f) for the 1066 cm−1 and 1586 cm−1 vibrational modes.
The vibrational population saturation and the parametric instability are achieved when the absolute value of the effective optomechanical damping rate becomes comparable to the intrinsic vibrational decay rate, i.e. when |Γoptv| ≈ γv. By applying this condition, we can estimate the laser threshold Ithr,2 to achieve these two effects (we use here the subindex “2” to distinguish this threshold from the one established to reach the vibrational pumping regime, labeled by subindex “1”). We estimate from Fig. 6(a and f) that Ithr,2 could get values as low as 3 × 106 μW μm−2, which could be reached by using a pulsed laser.10
7.2 Trends within the continuum-field model
We demonstrate here the importance of using the continuum-field model to capture the influence of the full-plasmonic response on the SERS response. We first consider a low-energy vibrational mode at 1066 cm−1, and focus on the anti-Stokes Raman line for simplicity, but similar conclusions can be obtained for the Stokes scattering (shown in Fig. S5 in the ESI†). The dependence on the energy of the vibration will be considered at the end of the section (subsection 7.2.3).The difference between the results from both models (solid versus dashed lines in Fig. 6(a and b)) becomes more dramatic in the regime of large laser intensity Ilas (green-shaded area). This is the regime where the complex spectral structure of the effective optomechanical damping rate Γoptν becomes relevant in the continuum-field model, as compared to the simple negative and positive spectral oscillation of the single-mode model (compare the red dashed and solid lines in Fig. 5(b)). The influence of high-order plasmonic modes increases the values of Γoptν for shorter wavelengths, and even reverses its sign from negative to positive, thus turning situations of optomechanical pumping (blue-detuned) in the single-mode model into a situation of optomechanical damping (effective red-detuned case) in the continuum-field model. We can observe this situation, for instance, at a short laser wavelength of λlas = 633 nm in Fig. 6(a) (black lines). The reverse of sign of Γoptν at this wavelength turns the divergent behavior of the vibrational population with laser intensity within the single-mode model (black dashed line) into a saturated one (black solid line) within the continuum model. A similar difference can be observed for the anti-Stokes intensity (black solid and dashed lines) in Fig. 6(b) where the divergent behavior within the single-mode model turns into a linear dependency within the continuum-field model.
For large incident wavelengths, spectrally detuned from all the high-order cavity modes, where the BDP mode of the cavity is the main spectral feature, for instance for λlas = 785 nm (green lines in Fig. 6(a and b)), the values of Γoptv are very similar in both models, therefore the populations and Raman lines show the same qualitative and quantitative dependency with incident laser intensity (compare green dashed and solid lines). For intermediate incident wavelengths, which spectrally fall in the middle of the modal structure of the cavity, any behavior can be found when the continuum of electromagnetic field is properly accounted for. This can be observed, for instance, in the differences between the solid and dashed lines for λlas = 670 nm and λlas = 705.9 nm in Fig. 6(a and b): the tendency of the vibrational population and Raman signal with incident laser can remain unchanged sometimes when comparing the results from the single-mode and continuum-field models (red lines in Fig. 6(a and b)), or changed into a special dynamics if the condition Γoptν = 0 is fulfilled (blue lines in Fig. 6(a and b)).
Last, we note that the laser threshold intensity Ithr,2 needed to reach the vibrational population saturation and the parametric instability (which occur at similar intensity) is of the same order of magnitude in the single-mode model and in the continuum-field model for the laser wavelengths considered in Fig. 6 (except for the special case of λlas = 705.9 nm). However, this could vary significantly for other laser wavelengths, as detailed in Fig. S7 in the ESI.†
The linewidth of the Raman lines is given by the sum of the intrinsic losses and the effective optomechanical damping rate γv + Γoptv. Thus, the large difference in Fig. 6(c) between the broadening calculated with the continuum-field and with the single-mode models follows directly from the large difference in the values of Γoptv, as discussed in Fig. 5(b) (the values in this figure were calculated for Ilas = 1 μW μm−2 but they can be scaled to an arbitrary laser intensity).
Both models exhibit differences for the evolution of the linewidth of the Raman lines, which are consistent with those found for the vibrational population and the Raman intensities in Fig. 6(a and b). For large illumination wavelength (green lines) both models show similar quantitative broadening as a function of incident laser intensity (similar Γoptv). However, for small incident wavelength (black lines), the behavior is reversed from an increasing narrowing within the single-mode model to an increasing broadening within the continuum-field mode model, as a consequence of the reverse of sign of Γoptv discussed in the previous section. For intermediate illumination wavelengths (red and blue solid lines), in the middle of the spectral response of the cavity, the results from the continuum-field model, can show a quantitative softening of the narrowing (red lines), or an invariance for specific wavelengths (blue line, to be compared with the narrowing within the single-mode mode).
Significant spectral shifts can also be identified in the Raman lines for sufficiently large incident laser intensity. The shift of the Raman lines in Fig. 6(d) is directly given by |(Ω+vv + Ω−vv)/2| (Fig. 5(a)) (conveniently scaled for the particular value of Ilas considered). It follows from the results in section 6 that the continuum-field model predicts shifts of ≈2 orders of magnitude larger than those given by the single-mode model. According to the latter, the Raman line shifts are generally smaller than the optomechanically-modified linewidth γv + Γoptvv. However, the results from the continuum-field model (solid lines in Fig. 6(d)) suggest that spectral shifts significantly larger than γv + Γoptvv are feasible for large enough laser intensities. Furthermore, the sign of the spectral shifts depends on the laser wavelength when applying the single-mode model, but the continuum-field model indicates that the Stokes (anti-Stokes) lines always shift towards larger (smaller) emission frequencies (the sign of the shift cannot be directly read from Fig. 6(d), as it shows the absolute value, but it can be deduced from Fig. 5(a)).
All in all, our results suggest that the behavior of SERS in the regime of large illumination intensity depends on a delicate interplay between the plasmonic response of the nanocavity (BDP, BPQ and plasmonic pseudomode), and the frequency of the vibrational modes. The application of the reference single-mode model easily leads to wrong predictions, and therefore it is necessary to model the full plasmonic response of each particular system to describe the nonlinear response of SERS.
7.3 Spectral dependence of the SERS enhancement for different laser intensity regimes
We address next the enhancement of the Raman signal as a function of incident laser wavelength for the large-energy vibrational mode at 1586 cm−1, as it shows the strongest difference between the single-mode and the continuum-field model. In Fig. 7(a–c) we show the Stokes (red lines, left axis) and anti-Stokes (blue lines, right axis) SERS enhancement as a function of laser wavelength, for different illumination intensity regimes, and compare the predictions obtained from the continuum-field model (solid lines) with those from the single-mode model (dashed lines). We consider the enhancement with respect to the Raman signal obtained from an isolated BPT molecule with the same relative orientation in vacuum (see values of the Raman activity in Table S1 of the ESI†). In other words, our estimation of the SERS enhancement includes both the electromagnetic and the chemical enhancement.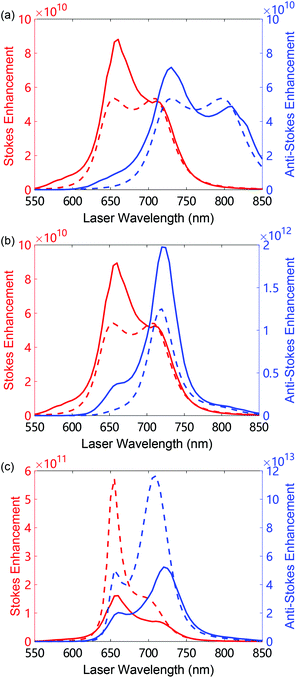 | ||
| Fig. 7 Enhancement of the Stokes (red lines, left axis) and anti-Stokes scattering (blue lines, right axis) as a function of incident wavelength for the BPT 1586 cm−1 vibrational mode at (a) weak (Ilas = 1 μW μm−2), (b) moderate (Ilas = 105 μW μm−2) and (c) large (Ilas = 8 × 106 μW μm−2) laser intensity. Solid and dashed lines show the results from the continuum-field model and from the single-mode model, respectively. All the other parameters are considered to be same as in Fig. 6. | ||
In the thermal regime, with weak laser intensity Ilas = 1 μW μm−2 (Fig. 7(a)), the enhancement of both the Stokes and anti-Stokes scattering predicted by the continuum-field and by the single-mode model reaches 11 orders of magnitude. The spectral shape and relative strength of the enhancement resemble that of the propagation factors K+vv, K−vv in both models (see Fig. 4(f)), because the SERS signal for weak Ilas is mainly determined by these factors.
In the vibrational pumping regime with moderate Ilas = 105 μW μm−2 (Fig. 7(b)), the enhancement of the Stokes scattering does not vary compared to that in the thermal regime, while the enhancement of the anti-Stokes scattering increases about 30 times with respect to the thermal regime for a laser wavelength of 720 nm, and shows a spectrally sharper shape. This extra enhancement can be explained by the increase of the vibrational population due to the vibrational pumping. The sharper spectral shape occurs because the vibrational pumping and the propagation of the anti-Stokes photons are optimized for a wavelength around 720 nm in this case, consistent with the results of the maxima of the optomechanical parameters displayed in Fig. 4(e).
In the large laser intensity regime, Ilas = 8 × 106 μW μm−2 (Fig. 7(c)), the enhancement of the anti-Stokes scattering increases further and reaches 14 orders of magnitude, while that of the Stokes scattering shows a 1.7 times extra enhancement with respect to the thermal and vibrational pumping regimes within the continuum-field model. As observed in Fig. 7(c), the single-mode model (dashed red line) can overestimate the Stokes enhancement by almost 4 times with respect to the result of the continuum-field model (red solid line).
Indeed, the SERS enhancement shows a sharp peak at around 650 nm in the single-mode model because the parametric instability is allowed at this wavelength within this model and thus the vibrational population increases dramatically before the parametric instability is reached. In contrast, in the continuum-field model, the SERS enhancement remains relatively broad (solid lines in Fig. 7(c)) since the vibrational population saturation is produced at all laser wavelengths, and thus the vibrational population stops increasing with laser intensity. For lower vibrational frequency, for instance for the 1066 cm−1 vibrational mode, the parametric instability is actually allowed for laser wavelengths slightly blue detuned from the BDP mode (here at 720 nm). An example of this can be observed in Fig. S9 of the ESI.†
We have also compared the results of the continuum-field model in Fig. 7 with those predicted by the classical SERS theory,1 as shown in Fig. S8 of the ESI.† We found that both frameworks show the same spectral shape and similar values of the SERS enhancement in the thermal regime. However, the classical description does not capture the spectral change produced in the vibrational pumping regime or in the high intensity regime because it does not incorporate the nonlinear behavior of the vibrational population, and thus of the Raman scattering, in those regimes. Nevertheless it is possible to capture the nonlinear behavior of the SERS enhancement in the vibrational pumping regime at large laser intensity with a semi-classical description of SERS if appropriate modified rate equations are used.9,20,30
In short, the SERS enhancement can vary orders of magnitude and show modified spectral shape for different incident laser intensities and frequencies of the vibrational modes. Therefore it is important to correctly identify the laser operation regime as well as the particular vibrational modes when interpreting the SERS enhancements obtained in an experiment.
8 Discussion and conclusion
We have applied a molecular optomechanical model of surface-enhanced Raman scattering (SERS) based on a continuum-field description of the plasmonic response to study SERS from a single biphenyl-4-thiol molecule located in the gap of a NanoParticle-on-a-Mirror (NPoM) plasmonic nanocavity. This approach goes beyond the single-mode model to describe the optical nanocavity,4,9,15 and accounts for the full response of the metallic nanostructure via the classical dyadic Green's function,23 and thus allows us to examine the influence of the high-order plasmonic modes on the optomechanical interaction of SERS. We focused on NPoMs as a particular system of current experimental interest, but many of our conclusions can be extended to other plasmonic configurations, including single nanoparticles, where the role of high-order modes is important.We compare the results from the continuum-field model with those obtained when only considering the bonding dipolar plasmon (BDP) mode that dominates the local field induced by the laser. We find that the vibrational population and SERS signal of our system are weakly affected by the high-order plasmonic modes in the thermal and vibrational pumping regime, corresponding to relatively weak and moderate laser intensity Ilas. However, in the regime of large laser intensity, we obtain that the optomechanical response is dramatically affected by the presence of the cavity bonding quadrupole plasmon (BQP) mode and, most notably, by the pseudomode that originates from the superposition of many high-order plasmonic modes. The latter can lead to a very efficient interaction with the molecule for short laser wavelengths, which can strongly increase the optomechanically-induced shift of the Raman lines.
The plasmonic pseudomode also affects the optomechanical damping rate Γoptv that governs the vibrational population, the intensity of the emitted Raman signal and the Raman linewidth in the regime of large laser intensity. The plasmonic pseudomode can change not only the value of Γoptv but also its sign, which leads to qualitative differences in the optomechanical interaction compared to a description based on a single cavity mode. For instance, it is possible to find a saturation of the vibrational population and a broadening of the Raman lines with increasing Ilas, for conditions where a single-mode model would indicate a divergence and narrowing, respectively. Furthermore, contrary to the prediction from the single-mode model, the sign of Γoptv within the continuum-field model depends on the vibrational energy, so that two different molecular vibrations can experience qualitatively different behaviors. As an example, for the BPT 1066 cm−1 vibrational mode, there is a laser wavelength window where it is possible to achieve the divergence of the Raman signal (parametric instability), but this is not possible for the larger-frequency vibrational mode at 1586 cm−1.
Furthermore, the implementation of the continuum-field model to describe the quantization of the electromagnetic field in a complex lossy plasmonic cavity as described here, allows for obtaining more accurate values of the laser intensity thresholds to observe optomechanical effects in molecular SERS (see sections S4.5 and S4.6 in the ESI†). The laser threshold intensity to achieve the vibrational pumping regime is estimated to be about 5.1 × 104 μW μm−2, and 2.7 × 103 μW μm−2 for the 1066 cm−1 and 1586 cm−1 BPT vibrational modes, respectively, at room temperature T = 293 K. These intensities can be experimentally achieved for instance with pulsed laser illumination,10 or even with continuous laser illumination,8 and can be further reduced by working at low temperature. In contrast, the laser threshold intensity to achieve the vibrational population saturation and the parametric instability is of the order of 3.17 × 106 μW μm−2 (considering a moderate chemical enhancement). To reduce this intensity threshold, one could optimize the molecular vibrational response or implement specially-designed plasmonic systems such as pico-cavities formed by atom-sized structures.8 Another possibility might rely on exploiting resonant SERS enhancement occurring for incident lasers in resonance with electronic excitations in the molecule,54,55 or to profit from the collective response in the optomechanical coupling of many molecules with the plasmonic structure.4,9,10,15 Some of these implementations could enable the observation of the characteristic optomechanical phenomena in SERS pointed out here for intense lasers, but at that point, further advances in the description of the interaction might require to consider the effect of vibrational anharmonities, the influence of the electronic structure of molecules, or to develop models beyond the rotating wave approximation.
Last, the continuum-field model allows us to straightforwardly examine how the SERS enhancement, which is usually discussed in the context of weak laser intensity, can be strongly modified for moderate or large laser intensity. Our calculation shows that the anti-Stokes SERS enhancement can increase by 10–103 times when the system goes from the thermal regime to the regime of large laser intensity, producing variations in the position and width of the spectral peaks of enhancement. In summary, our results unravel the importance of considering the full plasmonic response, which includes high-order modes (pseudomode), when addressing molecular-optomechanical effects, particularly for strong laser illumination, and provide accurate identification of unusual optomechanical nonlinear phenomena in SERS.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge project Nr. 12004344 from the National Science Foundation of China, joint project Nr. 21961132023 from the NSFC-DPG, project PID2019-107432GB-I00 from the Spanish Ministry of Science and Innovation, project KK-2019/00101 from Eusko Jaurlaritza, project H2020-FET Open “THOR” Nr. 829067 from the European Commission, UK EPSRC EP/L027151/1, and grant IT1164-19 for consolidated groups of the Basque University, through the Department of Education, Research and Universities of the Basque Government. The calculations with Matlab and Gaussian 16 were performed with the supercomputer at the Donostia International Physics Center and the Henan Supercomputer Center.References
- E. C. Le Ru and P. G. Etchegoin, Principles of Surface-Enhanced Raman Spectroscopy, Elsevier, Amsterdam, 2009 Search PubMed.
- J. R. Lombardi, R. L. Birke, T. Lu and J. Xu, J. Chem. Phys., 1986, 84, 4174–4180 CrossRef CAS.
- M. Moskovits, Rev. Mod. Phys., 1985, 57, 783–826 CrossRef CAS.
- P. Roelli, C. Galland, N. Piro and T. J. Kippenberg, Nat. Nanotechnol., 2016, 11, 164–169 CrossRef CAS.
- M. K. Schmidt, R. Esteban, A. González-Tudela, G. Giedke and J. Aizpurua, ACS Nano, 2016, 10, 6291–6298 CrossRef CAS.
- T. J. Kippenberg and K. J. Vahala, Science, 2008, 321, 1172–1176 CrossRef CAS.
- M. Aspelmeyer, T. J. Kippenberg and F. Marquardt, Rev. Mod. Phys., 2014, 86, 1391–1452 CrossRef.
- F. Benz, M. K. Schmidt, A. Dreismann, R. Chikkaraddy, Y. Zhang, A. Demetriadou, C. Carnegie, H. Ohadi, B. De Nijs, R. Esteban, J. Aizpurua and J. J. Baumberg, Science, 2016, 354, 726–729 CrossRef CAS.
- M. K. Schmidt, R. Esteban, F. Benz, J. J. Baumberg and J. Aizpurua, Faraday Discuss., 2017, 205, 31–65 RSC.
- A. Lombardi, M. K. Schmidt, L. Weller, W. M. Deacon, F. Benz, B. de Nijs, J. Aizpurua and J. J. Baumberg, Phys. Rev. X, 2018, 8, 11016 CAS.
- P. Roelli, D. Martin-Cano, T. J. Kippenberg and C. Galland, Phys. Rev. X, 2020, 10, 031057 CAS.
- M. K. Dezfouli, R. Gordon and S. Hughes, ACS Photonics, 2019, 6, 1400–1408 CrossRef CAS.
- S. M. Ashrafi, R. Malekfar, A. R. Bahrampour and J. Feist, Phys. Rev. A, 2019, 100, 013826 CrossRef CAS.
- E. Cortese, P. G. Lagoudakis and S. De Liberato, Phys. Rev. Lett., 2017, 119, 043604 CrossRef.
- Y. Zhang, J. Aizpurua and R. Esteban, ACS Photonics, 2020, 7, 1676–1688 CrossRef CAS.
- A. Delga, J. Feist, J. Bravo-Abad and F. J. Garcia-Vidal, Phys. Rev. Lett., 2014, 112, 253601 CrossRef CAS.
- P. Anger, P. Bharadwaj and L. Novotny, Phys. Rev. Lett., 2006, 96, 113002 CrossRef.
- S. Kühn, U. Håkanson, L. Rogobete and V. Sandoghdar, Phys. Rev. Lett., 2006, 97, 017402 CrossRef.
- N. Kongsuwan, A. Demetriadou, R. Chikkaraddy, F. Benz, V. A. Turek, U. F. Keyser, J. J. Baumberg and O. Hess, ACS Photonics, 2018, 5, 186–191 CrossRef CAS.
- C. M. Galloway, E. C. Le Ru and P. G. Etchegoin, Phys. Chem. Chem. Phys., 2009, 11, 7372 RSC.
- C. M. Galloway, P. G. Etchegoin and E. C. Le Ru, Phys. Rev. Lett., 2009, 103, 063003 CrossRef CAS.
- M. Yang, M. Mattei, C. Cherqui, X. Chen, R. P. Van Duyne and J. Schatz, Nano Lett., 2019, 19, 7309–7316 CrossRef CAS.
- M. K. Dezfouli and S. Hughes, ACS Photonics, 2017, 4, 1245–1256 CrossRef.
- R. Chikkaraddy, V. A. Turek, N. Kongsuwan, F. Benz, C. Carnegie, T. van de Goor, B. de Nijs, A. Demetriadou, O. Hess, U. F. Keyser and J. J. Baumberg, Nano Lett., 2018, 18, 405–411 CrossRef CAS.
- F. Benz, C. Tserkezis, L. O. Herrmann, B. De Nijs, A. Sanders, D. O. Sigle, L. Pukenas, S. D. Evans, J. Aizpurua and J. J. Baumberg, Nano Lett., 2015, 15, 669–674 CrossRef CAS.
- B. De Nijs, F. Benz, S. J. Barrow, D. O. Sigle, R. Chikkaraddy, A. Palma, C. Carnegie, M. Kamp, R. Sundararaman, P. Narang, O. A. Scherman and J. J. Baumberg, Nat. Commun., 2017, 8, 994 CrossRef.
- H. T. Dung, L. Knoell and D. G. Welsch, Phys. Rev. A, 1998, 57, 3931 CrossRef CAS.
- L. G. Suttorp and A. J. van Wonderen, EPL, 2004, 67, 766–772 CrossRef CAS.
- S. Y. Buhmann and D.-G. Welsch, Prog. Quantum. Electron., 2007, 31, 51–130 CrossRef.
- E. C. Le Ru and P. G. Etchegoin, Faraday Discuss., 2006, 132, 63–75 RSC.
- R. C. Maher, P. G. Etchegoin, E. C. Le Ru and L. F. Cohen, J. Phys. Chem. B, 2006, 110, 11757–11760 CrossRef CAS.
- R. C. Maher, C. M. Galloway, E. C. Le Ru, L. F. Cohen and P. G. Etchegoin, Chem. Soc. Rev., 2008, 37, 965–979 RSC.
- C. M. Galloway, E. C. Le Ru and P. G. Etchegoin, Phys. Chem. Chem. Phys., 2009, 11, 7372–7380 RSC.
- P. Meystre and M. Sargent, Elements of quantum optics, 2007 Search PubMed.
- Y. Fang, Y. Li, H. Xu and M. Sun, Langmuir, 2010, 26, 7737–7746 CrossRef CAS.
- H. Liu and B. Bhushan, Ultramicroscopy, 2002, 91, 177–183 CrossRef CAS.
- F. Benz, R. Chikkaraddy, A. Salmon, H. Ohadi, B. de Nijs, J. Mertens, C. Carnegie, R. W. Bowman and J. J. Baumberg, J. Phys. Chem. Lett., 2016, 7, 2264–2269 CrossRef CAS.
- H. H. Shin, G. J. Yeon, H. K. Choi, S. M. Park, K. S. Lee and Z. H. Kim, Nano Lett., 2018, 18, 262–271 CrossRef CAS.
- W. Chen, S. Zhang, M. Kang, W. Liu, Z. Ou, Y. Li, Y. Zhang, Z. Guan and H. Xu, Light: Sci. Appl., 2018, 7, 56 CrossRef.
- Y. Zhang, W. Chen, T. Fu, J. Sun, D. Zhang, Y. Li, S. Zhang and H. Xu, Nano Lett., 2019, 19, 6284–6291 CrossRef CAS.
- F. J. García de Abajo and A. Howie, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115418 CrossRef.
- F. J. García de Abajo, Rev. Mod. Phys., 2010, 82, 209 CrossRef.
- U. Hohenester and A. Trügler, Comput. Phys. Commun., 2012, 183, 370–381 CrossRef CAS.
- J. Waxenegger, A. Trügler and U. Hohenester, Comput. Phys. Commun., 2015, 193, 138–150 CrossRef CAS.
- P. B. Johnson and R. W. Christy, Phys. Rev. B: Solid State, 1972, 6, 4370 CrossRef CAS.
- COMSOL Multiphysics® v. 5.4. cn.comsol.com, COMSOL AB, Stockholm, Sweden.
- C. Tserkezis, R. Esteban, D. O. Sigle, J. Mertens, L. O. Herrmann, J. J. Baumberg and J. Aizpurua, Phys. Rev. A, 2015, 92, 053811 CrossRef.
- R. Esteban, G. Aguirregabiria, A. G. Borisov, Y. M. Wang, P. Nordlander, G. W. Bryant and J. Aizpurua, ACS Photonics, 2015, 2, 295–305 CrossRef CAS.
- N. Kongsuwan, A. Demetriadou, M. Horton, R. Chikkaraddy, J. J. Baumberg and O. Hess, ACS Photonics, 2020, 7, 463–471 CrossRef CAS.
- P. De Vries, D. V. Van Coevorden and A. Lagendijk, Rev. Mod. Phys., 1998, 70, 447 CrossRef.
- P. C. Chaumet, A. Sentenac and A. Rahmani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 036606 CrossRef.
- R.-Q. Li, D. Hernángomez-Pérez, F. J. García-Vidal and A. I. Fernández-Domínguez, Phys. Rev. Lett., 2016, 117, 107401 CrossRef.
- R. Carminati, J. J. Sáenz, J.-J. Greffet and M. Nieto-Vesperinas, Phys. Rev. A, 2000, 62, 012712 CrossRef.
- T. Neuman, R. Esteban, G. Giedke, M. K. Schmidt and J. Aizpurua, Phys. Rev. A, 2019, 100, 043422 CrossRef CAS.
- T. Neuman, J. Aizpurua and R. Esteban, Nanophotonics, 2020, 9, 295–308 CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Continuum-field model of molecular optomechanics, identification of the dipolar contribution in the plasmonic response for the single-mode model, dyadic Green's function of a metal–insulator–metal structure, and additional numerical results: Raman tensor of biphenyl-4-thiol molecule, identification of plasmonic modes based on the near-field maps, optomechanical parameters of the intermediate-frequency vibrational mode at 1269 cm−1, evolution of the integrated Stokes intensity for the low-frequency vibrational mode at 1066 cm−1, laser threshold to reach the vibrational pumping regime, laser threshold to reach parametric instability and saturation of the vibrational population, comparison with the classical SERS theory, SERS enhancement of the 1066 cm−1 vibrational mode, optomechanical parameters of the molecule in vacuum. See DOI: 10.1039/d0nr06649d |
| ‡ A metadata file with all the data of the figures in the manuscript is available in the public repository of CSIC: https://digital.csic.es/ |
| This journal is © The Royal Society of Chemistry 2021 |