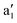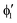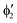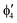Spin-state energetics of metallocenes: How do best wave function and density functional theory results compare with the experimental data?†
Gabriela
Drabik
 ,
Janusz
Szklarzewicz
,
Janusz
Szklarzewicz
 and
Mariusz
Radoń
and
Mariusz
Radoń
 *
*
Faculty of Chemistry, Jagiellonian University, ul. Gronostajowa 2, 30-387 Kraków, Poland. E-mail: mradon@chemia.uj.edu.pl
First published on 9th November 2020
Abstract
We benchmark the accuracy of quantum-chemical methods, including wave function theory methods [coupled cluster theory at the CCSD(T) level, multiconfigurational perturbation-theory (CASPT2, NEVPT2) and internally contracted multireference configuration interaction (MRCI)] and 30 density functional theory (DFT) approximations, in reproducing the spin-state splittings of metallocenes. The reference values of the electronic energy differences are derived from the experimental spin-crossover enthalpy for manganocene and the spectral data of singlet–triplet transitions for ruthenocene, ferrocene, and cobaltocenium. For ferrocene and cobaltocenium we revise the previous experimental interpretations regarding the lowest triplet energy; our argument is based on the comparison with the lowest singlet excitation energy and herein reported, carefully determined absorption spectrum of ferrocene. When deriving vertical energies from the experimental band maxima, we go beyond the routine vertical energy approximation by introducing vibronic corrections based on simulated vibrational envelopes. The benchmarking result confirms the high accuracy of the CCSD(T) method (in particular, for UCCSD(T) based on Hartree–Fock orbitals we find for our dataset: maximum error 0.12 eV, weighted mean absolute error 0.07 eV, weighted mean signed error 0.01 eV). The high accuracy of the single-reference method is corroborated by the analysis of a multiconfigurational character of the complete active space wave function for the triplet state of ferrocene. On the DFT side, our results confirm the non-universality problem with approximate functionals. The present study is an important step toward establishing an extensive and representative benchmark set of experiment-derived spin-state energetics for transition metal complexes.
1 Introduction
The ability to quantify the relative energies of different spin states (so called, spin-state energetics or spin-state splittings) of transition metal (TM) complexes is vital for computational studies in bioinorganic and organometallic chemistry: not only to identify the most stable spin state or a possibility of spin-crossover (SCO), but also to understand the reaction mechanisms involving a change in the reactant's spin state.1–4 However, it remains a grand challenge for quantum-chemistry methods to quantitatively and conclusively predict relative spin-state energetics.4–6 A notorious problem is when different methods lead to contradictory predictions. Such discrepancies are observed not only between different density functional theory (DFT) approximations,6–8 but in some cases also between different “high-level” wave function theory (WFT) methods. As an example, for the singlet-quintet splitting of model complex [Fe(NCH)6]2+, the best available diffusion Monte Carlo9,10 and single-reference coupled cluster CCSD(T)11–13 results differ from each other by as much as 1 eV or ca. 20 kcal mol−1, i.e., an order of magnitude larger than the desired “chemical accuracy” of 1–2 kcal mol−1. Comparable discrepancies exist between multireference CASPT2 and single-reference CCSD(T) predictions of singlet–triplet gaps for cobalt-nitrosyl complexes (with {CoNO}8 motif).14 The scarcity of credible reference values for spin-state energetics and the difficulty of obtaining them from theoretical calculations significantly impair the ability to carry out conclusive computational studies of open-shell TM complexes. We note that this pressure on increasing the computational accuracy is, clearly, not limited to TM chemistry, but is inline with the general trend in chemistry that electronic structure methods are nowadays more and more often perceived as the source of quantitative data.15There have been several attempts to create benchmark sets of spin-state energetics, using either high-level computed10,12,16,17 or experiment-derived18–22 reference data. Whereas the first approach, “theory vs. theory” benchmarks, has certainly many advantages,15 a practical problem with it in TM chemistry is the difficulty of finding undeniably accurate computational results (except for very small molecules, where full configuration interaction benchmark is obtainable). For the second approach, “theory vs. experiment” benchmarks, the main challenge is to find sufficiently reliable quantitative and representative experimental data and to account properly for vibrational corrections23 and condensed phase effects due to solvation24 or crystal packing22 when comparing the computed quantities with measured ones.
Recently, one of us has proposed5,13 a practical strategy of deriving quantitative measures of TM spin-state energetics by combining two sources of the appropriate experimental data: (i) the SCO enthalpies and (ii) the spin-forbidden d–d excitation energies. This approach was illustrated in ref. 13 with pilot application to four FeIII/FeII complexes with classical N- and O-donor ligands. The experimental data were corrected for condensed phase effects and the SCO enthalpies were also corrected for vibrational (zero-point and thermal) effects in order to derive quasi-experimental estimates of the electronic energy differences corresponding to isolated molecules. The choice of experimental data from the above two sources [(i), (ii)] is based on earlier important ideas developed by other authors,18,25 and we believe that combining the two sources is essential to create an unbiased benchmark set of spin-state energetics, which can be representative of diverse ligand field strengths and metal oxidation states occurring in bioinorganic and organometallic chemistry. In order to fulfill this requirement of molecular diversity, our group is presently interested in extending the benchmark set proposed in ref. 13 with more TM complexes for which the appropriate experimental data exist or could be obtained.
Looking for suitable TM complexes, we came across interesting experimental results for metallocene complexes: ferrocene FeCp2, ruthenocene RuCp2, cobaltocenium [CoCp2]+, and manganocene MnCp2 (where Cp− is the cyclopentadienyl anion). For MnCp2 (with MnII, d5 configuration) there is a thermal SCO equilibrium between the doublet (S = 1/2; low-spin) and the sextet (S = 5/2; high-spin) states, which is quantitatively documented by magnetic resonance in solution.26 For the other metallocenes (with FeII, RuII and CoIII; all having d6 configuration) there exist rich electronic spectroscopy data of spin-forbidden transitions between the closed-shell singlet ground state (S = 0; S0) and the lowest triplet excited state (S = 1; T1).27–33 In this paper we critically take a look at the above experimental data to derive from them the reference values of spin-state energetics, and employ the latter ones in the assessment of quantum-chemical methods.
Note that metallocenes feature a unique metal–π coordination mode and have a more covalent metal–ligand bond than classical octahedral complexes studied in ref. 13, making it interesting to compare the results for the two groups of TM complexes. Moreover, as we shall see below, the solvation effects hardly influence the spin-state energetics of metallocenes, in contrast to much larger solvation effects observed for some complexes studied in ref. 13. Since the computational treatment of solvation effects necessarily introduces some approximations and hence an additional element of uncertainty, it is an attractive opportunity to study a group of complexes for which these effects are eventually negligible. Finally, metallocenes are important organometallics, which not only have played a pivotal role in the development of organometallic chemistry, but are also of persisting interest even now in the context of spectroscopy, photochemistry, catalysis and materials science.34
Due to their importance and challenging electronic structures, metallocenes have been extensively studied by various theoretical methods, with a focus on either molecular geometry,35,36 metal–ligand bonding,36–40 or (last but not least) electronic excitation energies.41–52 In many of these studies, the experimental data, such as positions of band maxima in the absorption spectrum of ferrocene, were used with the aim of benchmarking computational results. It is clear that for such benchmarking to be meaningful, a good understanding and critical analysis of the underlying experimental data is necessary. Along this line we find that major experimental references employed in the previous theoretical studies41–49 considerably disagree on the S0 → T1 excitation energy of ferrocene. This issue will be discussed in depth below, but in a nutshell: although FeCp2 appears to be one of the most popular benchmarks, it is possible to find (at least) two “experimental” reference values for the S0 → T1 excitation energy. These values differ from each other by as much as 0.6 eV and different authors used either one41–45,49 or the other46–48 of these “experimental” values for comparison with their computational results. Moreover, it seems that some papers42,44 additionally compared one of these “experimental” estimates of the vertical energy with the calculated adiabatic energy; this is unjustified because for a closely related RuCp2 the Stokes shift (experimental) is about 1 eV.27,31,33 It thus becomes clear that a careful theoretical study of the singlet–triplet gap in FeCp2 and other metallocenes is mandatory, as well as critical analysis of the underlying experimental data, and we attempt to provide both in the present paper.
This paper is organized as follows. After summarizing our methods and models in Section 2, we give in Section 3.1 a detailed analysis of selected computational aspects which are critical for this benchmark study: the accuracy of molecular geometries, the role of solvation effects, and the reliability of the vertical energy approximation, so routinely applied in the analysis of electronic spectra. Herein, we develop the concept of vibronic correction to the position of band maximum, which plays in our approach the same role as well established zero-point and enthalpy corrections. We test the vibronic methodology on RuCp2, for which credible spectroscopic data exist. Armed with these tools, we derive in Section 3.2 the reference values of spin-state energetics, i.e., quasi-experimental estimates of the electronic energy differences (in the spirit of ref. 13), based on the experimental data of metallocenes. However, as mentioned above, we found that the existing data of FeCp2 and [CoCp2]+ need to be revised; we present a detailed analysis, including re-determination of the electronic absorption spectrum of ferrocene, in Section 3.3. The central point of this paper is Section 3.4, where we use the derived reference data for benchmarking the results of quantum-chemical calculations. One of the findings will be that the single-reference CCSD(T) method performs remarkably well and this is rationalized by the discussion of multireference character in Section 3.5. The conclusions are given in Section 4.
2 Methodology
2.1 Model and electronic structure
All calculations were performed for the eclipsed conformation of metallocenes (Fig. 1), with the exception of 6[MnCp2], where the staggered conformation was chosen due to its marginally lower energy at the DFT level (but in this case both conformations are degenerate to within <0.01 eV, making the actual choice irrelevant). For other metallocenes we also find a small energy difference between the two conformations, in agreement with Schaefer and coworkers.36 For FeCp2 we additionally checked that the singlet–triplet vertical excitation energies are similar for both conformations (ESI,† Table S59). As was also reported in ref. 36, we find that the staggered conformation of FeCp2 is not an energy minimum (DFT, gas), but a transition state joining two equivalent eclipsed conformations.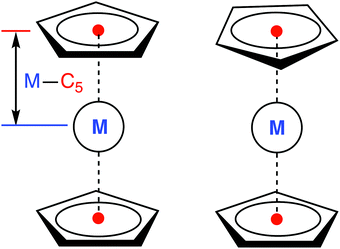 | ||
| Fig. 1 Eclipsed (D5h, left) and staggered (D5d, right) conformation of a metallocene molecule with defined metal–C5 distance. | ||
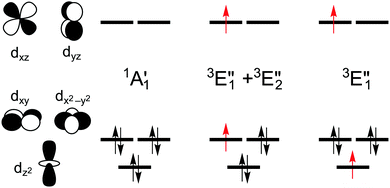
The splitting of the metal d energy levels in a metallocene molecule is qualitatively shown in Fig. 2. The orbitals dxz, dyz are most strongly destabilized by the ligand field. In fact, they acquire strongly antibonding metal–Cp character due to a covalent interaction with occupied Cp π orbitals. (Neither this antibonding character, nor the corresponding bonding orbitals are shown in a very schematic Fig. 2, but these features can be easily identified by looking at the CASSCF orbitals, Fig. S8, ESI†). The occupations to the left in Fig. 2 correspond to the singlet (S0) ground state of d6-metallocenes. Our interest is also in their singly excited states which arise from orbital occupancies shown to the right. From group theory, there are three singly excited configurations for total spin S = 1 or S = 0, resulting in three triplet (T1,T2,T3) and three singlet (S1,S2,S3) excited states. Our main interest is in the lowest triplet state (T1), but some calculations were also performed for the lowest singlet excited state (S1) or all six excited states.
The symmetry labels 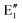 or
or 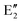 shown in Fig. 2 remind us that all these excited states are doubly degenerate for the D5h symmetry. For geometry optimization of the T1 state, Jahn–Teller (JT) distortion to C2v (or even lower) symmetry was taken into account. Actually, even for the fully symmetric structures, the computational symmetry was reduced (D5h to C2v or Cs; D5d to C2h or Cs) because the programs used for WFT calculations can only handle Abelian groups. Moreover, even if some other programs can handle non-Abelian groups, our calculations were always state-specific (SS) for one component of the degenerate state, which leads to the symmetry lowering. (The only exceptions are state-average CASSCF calculations discussed in Section 3.5.) Finally, as is also indicated in Fig. 2, for both the triplet and singlet states, there exist two configurations of
shown in Fig. 2 remind us that all these excited states are doubly degenerate for the D5h symmetry. For geometry optimization of the T1 state, Jahn–Teller (JT) distortion to C2v (or even lower) symmetry was taken into account. Actually, even for the fully symmetric structures, the computational symmetry was reduced (D5h to C2v or Cs; D5d to C2h or Cs) because the programs used for WFT calculations can only handle Abelian groups. Moreover, even if some other programs can handle non-Abelian groups, our calculations were always state-specific (SS) for one component of the degenerate state, which leads to the symmetry lowering. (The only exceptions are state-average CASSCF calculations discussed in Section 3.5.) Finally, as is also indicated in Fig. 2, for both the triplet and singlet states, there exist two configurations of 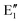 symmetry and one could predict that their mixing will bring some multireference character into the excited states, including T1. In practice, however, the consequences of this effect are greatly diminished in SS calculations, as will be discussed in Section 3.5.
symmetry and one could predict that their mixing will bring some multireference character into the excited states, including T1. In practice, however, the consequences of this effect are greatly diminished in SS calculations, as will be discussed in Section 3.5.
For MnCp2 the electronic states of our interest are sextet and doublet. For the sextet, all d orbitals of Mn are singly occupied leading to the non-degenerate ground state (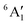 /6A1g in D5h/D5d). For the doublet, the lower degenerate orbital level in Fig. 2 (dxy, dx2−y2) is occupied by three electrons, leading to the degenerate state (
/6A1g in D5h/D5d). For the doublet, the lower degenerate orbital level in Fig. 2 (dxy, dx2−y2) is occupied by three electrons, leading to the degenerate state (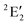 in D5h), whose equilibrium geometry is JT-distorted to C2v.
in D5h), whose equilibrium geometry is JT-distorted to C2v.
2.2 Geometry optimizations
All DFT geometry optimizations, followed by harmonic frequencies calculations, were performed with Turbomole53 at the BP86 and PBE0 levels, using the basis set def2-TZVP, the integration grid m5, and tight convergence criteria (SCF 10−8, Cartesian gradient max 10−4, a.u.). The calculations for open-shell states were spin-unrestricted. The geometries were optimized in the gas phase, except for additional COSMO calculations54 discussed in Section 3.1.3. Additional optimization at the UHF-CCSD(T)/cT(D)-PP level (cf. Section 2.4) was performed for the T1 state of RuCp2 using CFour.55 The optimized geometries are reported in Tables S2–S20, ESI.†2.3 DFT calculations
After the step of geometry optimization (see above), single-point DFT calculations were performed with the 30 exchange–correlation functionals used in ref. 13. (See Table 4 for the list of functionals and ESI† for the references.) Depending on the availability of a given functional, the calculations were performed either with Turbomole,53 ADF,56 or Gaussian57 (see ESI†). All calculations employed basis sets of quadruple-ζ quality, reduced to triplet-ζ on H atoms (see ESI† for details). Scalar relativistic effects for Ru were incorporated using the pseudopotential (Turbomole, Gaussian) or the ZORA Hamiltonian58 (ADF). For 3d-electron complexes, the relativistic effects were estimated at the second-order DKH59 and additively corrected for. It was carefully cross-checked that consistent results are obtained for representative functionals (PBE, PBE0, M06) in different programs (ESI,† Tables S32–S36). Calculations for open-shell states were spin-unrestricted, but without significant spin contamination. The maximum deviation of the 〈S2〉 expectation value from the S(S + 1) eigenvalue was observed for 3[CoCp2]+: 0.3 using B2PLYP or 0.2 using MVSh; for all other cases the analogous deviation was 0.1 or less. All 〈S2〉 values and total energies can be found in the ESI,† Tables S25–S31.2.4 WFT calculations
The coupled cluster CCSD(T), partially contracted NEVPT260 and internally contracted MRCISD+Q42 calculations were performed with Molpro;61 CASPT262 calculations were performed with Molcas v8 and OpenMolcas.63The CCSD(T) calculations for open-shell states were either partially spin-adapted RCCSD(T) or unadapted UCCSD(T), both based on an ROHF-type reference.64 As an alternative to the canonical HF orbitals, the Kohn–Sham orbitals (B3LYP) were used in calculations prefixed with “KS-”. In order to efficiently approach the complete basis set (CBS) limit in coupled cluster (CC) calculations for TM complexes,13,24,65–67 we used the explicitly correlated (R/U)CCSD(T*)-F12a method of Werner and coworkers.68 Because in Molpro it is not possible to use F12 methods in combination with the DKH Hamiltonian, the final (R/U)CCSD(T) relative energies reported below for MnCp2, FeCp2 and [CoCp2]+ were computed as
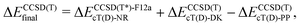 | (1) |
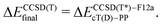 | (1a) |
The calculations with other WFT methods were performed with the basis set b = cT(D)-DK (Mn, Fe, Co) or cT(D)-PP (Ru), and the CBS limit was approximated by using the additive correction for basis set incompleteness obtained from CC calculations13,24
| ΔEmethodfinal = ΔEmethodb + δCBS, | (2) |
| δCBS = ΔEUCCSD(T)final − ΔEUCCSD(T)b. | (3) |
Unless mentioned otherwise, all CASSCF calculations were state-specific (SS); see below for the choice of active space. In the CASPT2 calculations, the standard IPEA shift of 0.25 a.u. and the imaginary shift of 0.1 a.u. were used. Size-inconsistency of the MRCISD method was additively corrected for69,7069,70 using the renormalized Davidson [+Q(D)], Davidson-Silver-Siegbahn [+Q(DSS)], or Pople [+Q(P)] corrections. All valence electrons were correlated, including the metal outer-core: 3s3p (first-row) or 4s4p (Ru), except for CASPT2/CC calculations,17 where the CASPT2 part was calculated with the frozen outer-core and the outer-core contribution to the correlation energy was recovered at the UCCSD(T) level.
As noted by Pierloot and coworkers,39 the virtual orbitals with 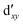 and
and 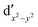 character (cf.Fig. 2) serve in this active space to describe not only the double-shell effect, but also correlation effects accompanying the metal to Cp π* back-donation. Treating these two effects separately in the larger (10,14) active space does not change the S0 → T1 excitation energy of FeCp2 appreciably, at either the PT2 or MRCI level (Table 1). The same holds true for augmenting the (10,14) active space with additional Cp π and π* orbitals to better describe intra-Cp correlation effects and thus to obtain the most extensive active space (14,18) considered in ref. 39. As can be seen in Table 1, the difference between CASPT2 excitation energies S0 → T1 for FeCp2 obtained with the (14,18) and the more economic (10,12) is only 0.03 eV. With the 5 × 107 (singlet) or 1 × 108 (triplet) CASSCF configurations for FeCp2 in C2v symmetry, the (14,18) active space is too large for the NEVPT2 and MRCI calculations, making the choice of the (10,12) a very reasonable compromise.
character (cf.Fig. 2) serve in this active space to describe not only the double-shell effect, but also correlation effects accompanying the metal to Cp π* back-donation. Treating these two effects separately in the larger (10,14) active space does not change the S0 → T1 excitation energy of FeCp2 appreciably, at either the PT2 or MRCI level (Table 1). The same holds true for augmenting the (10,14) active space with additional Cp π and π* orbitals to better describe intra-Cp correlation effects and thus to obtain the most extensive active space (14,18) considered in ref. 39. As can be seen in Table 1, the difference between CASPT2 excitation energies S0 → T1 for FeCp2 obtained with the (14,18) and the more economic (10,12) is only 0.03 eV. With the 5 × 107 (singlet) or 1 × 108 (triplet) CASSCF configurations for FeCp2 in C2v symmetry, the (14,18) active space is too large for the NEVPT2 and MRCI calculations, making the choice of the (10,12) a very reasonable compromise.
| (10,10) | (10,12) | (10,14) | (14,16) | (18,15) | (14,18) | |
|---|---|---|---|---|---|---|
| a All values in eV. b See ESI for the relations between different active spaces (Table S44 and Fig. S8 and S9). c Calculations not feasible. | ||||||
| CASSCF | 2.45 | 1.91 | 1.96 | 2.38 | 1.88 | 1.93 |
| CASPT2 | 1.91 | 2.02 | 2.02 | 1.89 | 1.77 | 2.05 |
| NEVPT2 | 2.08 | 2.37 | 2.27 | |||
| MRCISD+Q(D) | 2.18 | 2.02 | 2.02 | |||
We also compared the (10,12) active space with a smaller one, (10,10), that lacks the double-shell orbitals 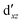 ,
, 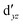 (cf. Fig. 2). The (10,10) active space was proposed in the seminal study of ferrocene by Pierloot et al.38 and was later used by Shamasundar et al.42 We find, however, that the excitation energies (both PT2 and MRCI) obtained from the (10,10) are underestimated by 0.1 eV as compared with those from the (10,12) active space (cf.Table 1). The same holds true for other active spaces proposed in the literature for the ground state of FeCp2: the (14,16) active space of Stein et al.77 (a subset of (14,18)) and the (18,15) active space of Sayfutyarova et al.45 Although these active spaces quite extensively treat the intra-Cp correlation effects, they both exclude the mentioned double-shell orbitals (
(cf. Fig. 2). The (10,10) active space was proposed in the seminal study of ferrocene by Pierloot et al.38 and was later used by Shamasundar et al.42 We find, however, that the excitation energies (both PT2 and MRCI) obtained from the (10,10) are underestimated by 0.1 eV as compared with those from the (10,12) active space (cf.Table 1). The same holds true for other active spaces proposed in the literature for the ground state of FeCp2: the (14,16) active space of Stein et al.77 (a subset of (14,18)) and the (18,15) active space of Sayfutyarova et al.45 Although these active spaces quite extensively treat the intra-Cp correlation effects, they both exclude the mentioned double-shell orbitals (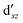 ,
, 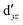 ) and hence give the excitation energies which are inferior to the (10,12) or (14,18) ones (cf.Table 1).
) and hence give the excitation energies which are inferior to the (10,12) or (14,18) ones (cf.Table 1).
Although the 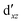 ,
, 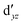 double-shell orbitals are generally important for the relative energies in our study, we noticed their tendency to rotate out of the active space when genuine (10,12) calculations were attempted for RuCp2. We therefore used the approximation, called in the ESI† “(10,12)fix,” in which the problematic two orbitals were obtained from preceding state-average CASSCF(10,12) calculations for six lowest triplet roots (i.e., T1, T2, and T3 states calculated together), and not optimized any further. The excellent accuracy of this approximation was confirmed for other d6 metallocenes (Tables S54–S58, ESI†).
double-shell orbitals are generally important for the relative energies in our study, we noticed their tendency to rotate out of the active space when genuine (10,12) calculations were attempted for RuCp2. We therefore used the approximation, called in the ESI† “(10,12)fix,” in which the problematic two orbitals were obtained from preceding state-average CASSCF(10,12) calculations for six lowest triplet roots (i.e., T1, T2, and T3 states calculated together), and not optimized any further. The excellent accuracy of this approximation was confirmed for other d6 metallocenes (Tables S54–S58, ESI†).
2.5 Vibronic simulations
In order to quantify the difference between the vertical energy and the band maximum for absorption (S0 → T1) or emission (T1 → S0) spectra of RuCp2, FeCp2, and [CoCp2]+, vibronic simulations of the spectral envelopes were performed at the Franck–Condon level, taking into account the Duschinsky effect and the change of vibrational frequencies, within the adiabatic hessian formulation,78 as implemented in FCclasses v3.79 We mainly used the time-dependent (TD) formalism,80,81 but also compared with time-independent (TI) one82 (see ESI† for details). The spectra were convoluted with Gaussian broadening (HWHM 0.025 eV or 0.005 eV). The thermal effects (300 vs. 0 K) were modeled assuming the Boltzmann distribution of initial vibronic states within the TD approach. The underlying geometries and vibrational modes of the singlet (S0) and the triplet (T1; one component) states were taken from the DFT (BP86 or PBE0/def2-TZVP) calculations and aligned to common orientation under the C2v symmetry.2.6 Experimental
The UV-Vis spectra of ferrocene in benzene were recorded in the 200–900 nm range at 25 °C on a Shimadzu 2101 PC spectrophotometer equipped with a long dimension cell holder in the slow scan mode. Spectra were measured in 1 cm or 5 cm quartz cells (with tight stoppers to avoid benzene evaporation). As a reference pure benzene was used in cells of the same dimension. Ferrocene (98%) and benzene (99.9%) were used as supplied by Sigma-Aldrich. Ferrocene weights were used to prepare solutions of molar concentration 0.8029 and 0.5595 M (in 10 mL measuring flask) and 0.08136 M (25 mL). Two further most diluted solutions were prepared by taking 2.500 mL of the 0.08136 M solution and diluting it with benzene in a 25 mL measuring flask.Measured absorbances can be found in the ESI,† Fig. S12. The spectrum shown in Fig. 9 was obtained by averaging the available data points. After excluding very small (A < 0.05) or very large (A > 2) absorbances (in order to avoid artifacts due to the spectral noise or “band flattening”, respectively), there remained 2–6 reliable measurements for every wavelength in the interesting spectral range of 400 to 800 nm. Based on these data, we determined the mean value, the standard deviation, and the 95%-confidence interval of ε(λ). The baselines of different measurements were adjusted to minimize the sum of squared deviations in the resulting ε values between all pairs of (reliable) measurements in the interesting wavelength range. The details of this extended baseline correction procedure are described in the ESI,† where it is also shown (Fig. S13–S15) that it has no effect on the shape of the spectrum, but it is helpful to reduce random uncertainties.
Gaussian analysis of the spectrum was performed on the energy scale using the least-squares Levenberg–Marquardt method as implemented in Fityk 1.3.83 The (averaged) experimental points were weighted by factor wt = 1/(σtλt)2, where σt is the standard deviation of εt and the 1/λt2 factor serves to compensate for non-uniform distribution of experimental points on the energy scale (the spectrophotometer acquires them uniformly on the λ scale with the density of 2 nm−1).
3 Results and discussion
3.1 Preliminary considerations
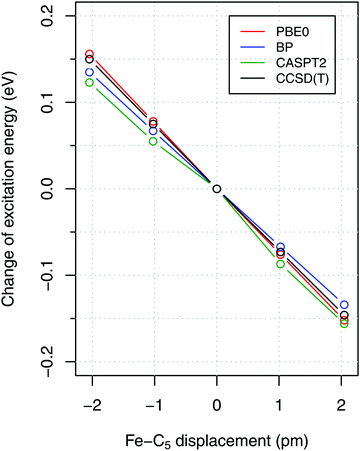
To estimate the sensitivity of vertical energies to the accuracy of molecular geometry, Fig. 3 shows (as a representative example) the variation of excitation energy S0 → T1 for FeCp2 with respect to the displacement of the Fe–C5 distance (i.e., metal to ring centroid, cf. Fig. 1) from the ground-state equilibrium value. It is not surprising that the Fe–C5 distance is the key parameter affecting the excitation energy, because the S0 → T1 excitation comes down to one-electron promotion from a mostly nonbonding d orbital into an antibonding Fe–Cp orbital (cf. Section 2.1). Thus, as might be expected, the elongation of the Fe–C5 distance decreases the excitation energy (cf.Fig. 3). The effect turns out to be almost linear, with the negative slope of 0.06–0.08 eV per picometer (1 pm = 0.01 Å). From this it becomes clear that the metal–C5 distance should be reproduced to within 1 pm or better in order to keep reasonably small the resulting error on calculated vertical energies.
Fortunately, accurate ground-state geometries of FeCp2 and RuCp2 are available from gas-phase electron diffraction (GED) data of Haaland's group,85 making it possible to independently benchmark the quality of computed geometries. The GED data of FeCp2 were already used for the same purpose by other authors.35a,b In particular, Coriani et al. have shown that their CCSD(T)-optimized bond lengths for FeCp2 agree with the GED values to within 0.2–0.5 pm.35b (Also Harding et al. discuss high-quality CCSD(T) geometries of FeCp2,35c but they do not compare them with the GED ones.) Although CCSD(T) geometry optimizations are certainly possible for molecules sized as metallocenes, we prefer sticking to DFT geometries, to be more compatible with the methodology widely used in bioinorganic chemistry. For a number of larger TM complexes within our interest, the geometry optimization could be still done, in practice, only at the DFT level, even if single-point CCSD(T) calculations are affordable.13
Fig. 4 shows deviations in the bond lengths of FeCp2 and RuCp2 calculated by several DFT methods with respect to the GED data. As explained in ref. 35b and references therein, before comparing the GED bond distances with the calculated ones (from energy minima), the GED data should be corrected for thermal motion; we use the same corrections as Coriani et al.35b‡ It is clear from Fig. 4 that the best agreement with the reference geometries is obtained for the BP86 functional, which reproduces the most critical distances (metal–C5, metal–C) with sub-picometer accuracy. The PBE0 functional also predicts rather similar (and very good) geometric parameters for FeCp2, but not so for RuCp2. By contrast, the B3LYP functional leads to a systematic and significant (2–4 pm) overestimation of the metal–ligand distance and underestimation of the C–C distance, particularly for FeCp2. Somewhat interestingly, inclusion of the dispersion correction (-D3) does not improve the BP86 and PBE0 geometries, although it improves slightly the B3LYP geometries. We also tested TPSS and TPSSh functionals and their dispersion-corrected versions (data not shown) to find out that these methods perform somewhat better than B3LYP, but do not outperform BP86. Thus, it is clear from this comparison that BP86 is the method of choice for geometry optimization of these d6-electron metallocenes in their S0 ground state. We assume this also holds true for isoelectronic [CoCp2]+ (no GED data to compare with).
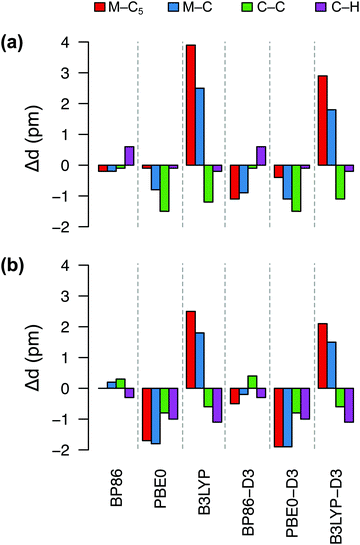 | ||
| Fig. 4 Deviations (in pm) of bond distances for (a) FeCp2, (b) RuCp2 predicted by six DFT methods from the corresponding experimental values: (a) Fe–C5 1.652, Fe–C 2.054, C–C 1.435, C–H 1.080 Å; (b) Ru–C5 1.816, Ru–C 2.187, C–C 1.433, C–H 1.089 Å (from GED,92 corrected for thermal motion). | ||
On the other hand, we found that the BP86 functional predicts the geometry of 6[MnCp2] with a bent Cp–Mn–Cp unit and irregularly rotated Cp rings (Fig. S1, ESI†), so that the resulting highly distorted structure has only C2 symmetry, rather than the expected D5d or D5h symmetry. A slightly bent Cp–Mn–Cp unit is also found (with all functionals) for 2[MnCp2], but this is the expected JT distortion due to the incomplete filling of the degenerate shell (dx2−y2, dxy; cf. Section 2.1). No similar JT distortion is expected to occur for the non-degenerate sextet state and, in fact, no distortion is suggested by the GED data of Haaland.86 For this reason we believe that the asymmetric distortion of 6[MnCp2] predicted by BP86 is unphysical, possibly caused by the DFT delocalization error (as was suggested by Zhang,87 who also observed a similar distortion). As the 6[MnCp2] molecule maintains its expected high symmetry with the PBE0 functional, which also performs good for FeCp2, we choose the PBE0 geometries for further single-point calculations of MnCp2.
In Table 2 we compare the relative energies computed (with three typical energy methods of our interest: BP86, PBE0, CCSD(T)) for the choice of either BP86 or PBE0 geometries. It turns out that for MnCp2 the actual choice of geometry does not really matter: even if the BP86 and PBE0 geometries differ so much from each other (see above and Fig. S1, ESI†), the adiabatic energies (calculated using a given method) differ by no more than 0.04 eV. This is a manifestation of the above rule of thumb that adiabatic energies are not particularly sensitive to the accuracy of molecular geometries. By contrast, the spin-state energetics of MnCp2 are very sensitive to the choice of method for energy calculation, with a difference between the BP86 and PBE0 results as large as 1.2 eV (this is typical of first-row TM complexes6,88,89). Comparable, yet slightly smaller variation of results with the choice of energy-calculation method is observed for FeCp2. In this case the difference caused by the use of either BP86 or PBE0 geometry is comparably smaller than for MnCp2, because for FeCp2 both geometries are similar (cf.Fig. 4(a)).
| System | ΔE type | Geometry | Calculated ΔE (eV) | ||
|---|---|---|---|---|---|
| BP86 | PBE0 | CCSD(T)a | |||
| a UCCSD(T), estimated CBS limit. b UHF-CCSD(T)/cT(D)-PP. | |||||
| 2,6[MnCp2] | Adiab | BP86 | 0.97 | −0.24 | 0.20 |
| PBE0 | 0.99 | −0.26 | 0.16 | ||
| 1,3[FeCp2] | Vert abs | BP86 | 2.17 | 1.56 | 2.16 |
| PBE0 | 2.12 | 1.62 | 2.16 | ||
| 1,3[RuCp2] | Adiab | BP86 | 2.65 | 2.67 | 2.88 |
| PBE0 | 2.76 | 2.67 | 2.89 | ||
| Vert abs | BP86 | 3.41 | 3.28 | 3.52 | |
| PBE0 | 3.59 | 3.43 | 3.68 | ||
| Vert emi | BP86 | 1.21 | 1.06 | 1.33 | |
| PBE0 | 1.98 | 1.75 | 2.00 | ||
| CCSD(T)b | 2.05 | 1.81 | 2.05 | ||
The situation is more interesting for RuCp2 (in the lower part of Table 2). Considering the available experimental data of RuCp2, which will be interpreted later, we analyzed separately the behavior of the adiabatic energy and the two vertical energies. First of all, we notice that all of them are almost insensitive to the choice of method for energy calculation (for fixed set of geometries). This will be also confirmed for other WFT and DFT methods below. Second, in contrast to FeCp2, we find that switching from BP86 to PBE0 geometry has an effect of 0.1–0.2 eV on the calculated vertical excitation (absorption) energy. This is fully understandable because PBE0 underestimates the critical Ru–C5 distance in the ground state of RuCp2 by almost 2 pm with respect to BP86 or experiment (cf.Fig. 4(b)). Going now to the adiabatic and vertical emission energies, we need to consider also the geometry of RuCp2 in the T1 excited state. Somewhat parallel to the earlier experience with 6[MnCp2], we found that the BP86 and PBE0 geometries of 3[RuCp2] differ remarkably, with the BP86 geometry being significantly more distorted (concerning the Cp–Ru–Cp angle and mutual orientation of the rings) than the PBE0 one; see Fig. S2, ESI.† As for MnCp2, this effect is modest for the adiabatic energy (within 0.1 eV), but it is of critical importance for the emission energy (0.7 eV!). This is reminiscent of large sensitivity of emission energies to the accuracy of excited-state geometries for singlet–singlet transitions in organic compounds.84
Since there are no GED (or any other) experimental data directly probing the excited-state 3[RuCp2] geometry, we decided to optimize it at the CCSD(T) level. The CCSD(T) geometry resembles the PBE0 one (Fig. S2, ESI†) and leads to a comparable emission energy (last row of Table 2). It is clear from this comparison that the BP86 geometry of the excited state is inferior to the PBE0 or CCSD(T) geometry, whereas the latter one appears to be the best possible choice, not only because it is optimized at a high-level of theory, but also because it leads to the vertical emission energy which is closest to the experimental one.33
Given the above, we made the following choice of geometries for further single-point calculations in this benchmark study: the CCSD(T) geometry of 3[RuCp2] for vertical emission energy; the PBE0 geometry for 2,6[MnCp2] adiabatic energy; and the BP86 geometry for all other cases.
Under the limit of a large HR parameter, which appears reasonable for typical d–d transitions in TM complexes, one may expect that the vertical energy should be close to the band maximum (as predicted by the classical Franck rule). On the other hand, differences between the two quantities as large as 0.3 eV occur for organic molecules.92 The situation is less clear for TM complexes because there are relatively few studies addressing the problem of vibronic effects in these systems (for some examples see ref. 93–97). Moreover, such studies are usually limited to small molecules or involve additional simplifying approximations (e.g., only selected vibrations are considered), and they do not explicitly address our main question: what is the difference between the position of a d–d band maximum and the corresponding vertical energy?
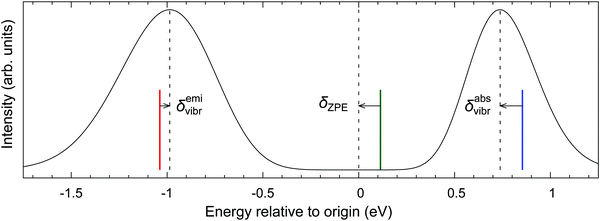
To challenge the vertical energy approximation, we decided to approximately simulate the vibrational envelopes for the bands of our interest using the methodology detailed in Section 2.5. It should be stressed that our purpose is by no means to quantitatively reproduce the experimental spectra, but rather to quantify the energy difference between the band maximum and the vertical energy,
| δvibr = ΔEmax − ΔEvert | (4) |
The absorption and emission spectra in Fig. 5 were obtained with significant Gaussian broadening; hence no vibrational fine structure can be seen. The red and blue vertical lines give the position of the vertical absorption and emission energies corresponding to these simulations, and vibronic corrections are represented by the arrows. For better context, the adiabatic energy is also shown as the green line and it is similarly compared with the position of the electronic origin (i.e., the 0–0 transition); the latter is marked by the central dashed line and obviously cannot be seen on this intensity scale.33 As shown in the figure, the simulated absorption maximum is observed at ∼0.1 eV below the vertical absorption energy, i.e., the vibronic correction for absorption is δabsvibr ≈ −0.1 eV. This resembles the difference between the adiabatic energy and the electronic origin, which is due to different vibrational zero-point energies (ZPEs) of both states, and the same is observed for other d6-metallocenes (ESI,† Table S22), suggesting that the predominant physical effect contributing to δvibr is the lowering of vibrational frequencies in the T1 state with respect to the S0 state. This interpretation also agrees with the recent study of Bai et al., who considered photoabsorption spectra of organic molecules within a nuclear ensemble approach.98 However, for the emission T1 → S0 band maximum, our simulations yield the vibronic correction which is twice smaller and has opposite sign to that for absorption, δemivibr ≈ +0.05 eV (cf.Fig. 5). This shows that there are clearly other physical effects related to vibrational progression (i.e., not only the differential ZPE correction), which also contribute to δvibr.
As can be seen from Table S22 (ESI†), the vibronic corrections for absorption maxima are very similar, around −0.1 eV, for all the d6-metallocenes. These corrections are also reasonably insensitive to the choice of functional (PBE0 vs. BP86) used to provide the equilibrium geometries and harmonic frequencies. We also estimated the effect of temperature (T = 300 vs. 0 K) on the positions of band maxima, and found it to be very small (Table S22, except for the T1 → S0 emission of RuCp2, for which the maximum is predicted to red-shift on increasing the temperature (qualitatively in agreement with the experimental data32).
It is important to stress at this point that our simulations are performed within the harmonic oscillator approximation. For consistency, we thus input to eqn (4) the vertical energy also within the harmonic approximation, i.e., the vertical energy computed from the adiabatic energy assuming a quadratic dependence of energy on the nuclear displacements between both states. We find for all these d6-electron metallocenes that the difference between such defined “harmonic vertical energy” and “true vertical energy” (computed at a given DFT level) is generally too large to be neglected. On the other hand, we believe that subtracting both harmonic terms in eqn (4) should result in a good cancellation of errors caused by the harmonic approximation. In other words, harmonic approximation is only used to compute the small correction δvibr, which is itself on the order of 0.05–0.1 eV (see above). Obviously, performing vibronic simulations using fully or partly anharmonic potential energy surfaces99 would be more elegant, but such calculations are currently out of reach for metallocenes and other TM complexes within our interest.
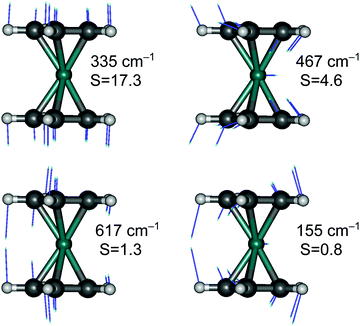
Finally, although we are generally not interested in studying detailed vibrational features of the d–d bands in TM complexes, we cannot refrain from making an exception for RuCp2, for which high-quality spectroscopic data are available for the T1 → S0 emission (complete vibrational progression31–33) and S0 → T1 absorption (traces of progression near the spectroscopic origin33). The observed progressions are mainly caused by the Ru–Cp symmetric stretching mode, which has the largest value of the HR parameter (for T1 → S0 emission: exptl estimated in ref. 33: S = 15, PBE0 computed here: S = 17.3; see Fig. 6).
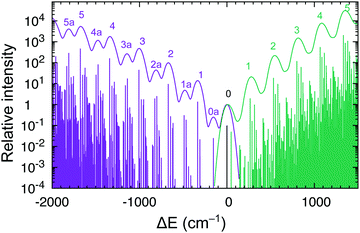
Interestingly, the experiment shows a doubling of the vibrational progression in the emission spectrum compared with that in the absorption spectrum. Riesen et al. ascribed this effect to the participation of a Cp–Ru–Cp skeletal bending mode in the case of the emission spectrum.33 Our vibronic simulations can reproduce this doubling effect at least qualitatively correct and essentially confirm their interpretation (Fig. 7).
As our simulations take into account all vibrations, the number of computed vibronic states is too large to directly compare the stick spectrum with the experimental one (also note that our simulations obviously do not account for coupling with the crystal environment, responsible for the appearance of phonon wings in the experimental spectrum). Introducing a small Gaussian broadening (HWHM 0.005 eV) leaves out only the dominant progressions. When this is done, it turns out that the emission spectrum (to the left in Fig. 7) has indeed a different morphology than the absorption spectrum (to the right). In accordance with the experiment, the emission spectrum is developed in the form of two shifted progressions: the main (0-1-2-…) starting from the true origin, and the secondary one (0a-1a-2a-…) starting from the false origin. In agreement with Riesen et al., we find that the false origin is caused by exciting one vibrational quantum in the Cp–Ru–Cp bending mode 155 cm−1 (PBE0), whose computed HR parameter is about one (cf.Fig. 6). Our simulations suggest, however, that also other deformational modes (shown in the same figure), whose computed HR parameters are 4.6 and 1.3, may contribute to the unusual morphology of the emission band observed in the experiment.
It seems that the second progression can be observed in the emission spectrum owing to rather special arithmetic relations between vibrational frequencies of these three bending modes and the Ru–Cp stretching mode, which by coincidence occur in the S0 state. In particular, the 155 cm−1 Cp–Ru–Cp bending frequency is approximately 1/2 of the stretching frequency (![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0 = 335 cm−1); the 467 cm−1 Cp tilting frequency is ≈3/2 ×
0 = 335 cm−1); the 467 cm−1 Cp tilting frequency is ≈3/2 × ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0; and the 617 cm−1 out-of-plane Cp deformation frequency is ≈2 ×
0; and the 617 cm−1 out-of-plane Cp deformation frequency is ≈2 × ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0. In the T1 state, the corresponding vibrational frequencies and arithmetic relations between them are very different, and the HR parameters of the deformational modes are also smaller (ESI,† Fig. S7). Consequently, only the main progression can efficiently develop in the absorption spectrum.
0. In the T1 state, the corresponding vibrational frequencies and arithmetic relations between them are very different, and the HR parameters of the deformational modes are also smaller (ESI,† Fig. S7). Consequently, only the main progression can efficiently develop in the absorption spectrum.
The smallness of solvation effects for metallocenes is corroborated by the experimental data of FeCp2, which show that the main d–d bands are practically independent of solvent and found at essentially the same positions in solution as in the vapor.28 Although the low polarity of some solvents (benzene, toluene, hexane) certainly contributes to this, one should note that negligibly small solvation effects are also predicted in ethanol and water (Tables S60, S61 and S63, ESI†). This is in marked contrast to significant (up to 0.5 eV) solvation effects for aqua complexes24,100 and other TM complexes whose ligands engage in hydrogen bonding with the solvent.5,13 This certainly cannot happen for the Cp ligands, and also a high covalency, viz. low ionicity, of the metal–Cp bond may be relevant for the observed behavior.
Relative energies reported in this work include scalar relativistic effects, but not the spin–orbit coupling (SOC). To justify this approximation we estimated the SOC effect for interpretation of vertical and adiabatic energies of RuCp2 using the state-interaction approach based on CASSCF/CASPT2 wave functions/energies of the S0, S1,2,3 and T1,2,3 states (ESI,† Tables S64 and S65). For vertical excitations (Table S64, ESI†), the energy levels are computed for the highly symmetric S0 structure and, when the SOC is included, each of the doubly degenerate triplet states splits into three sub-levels within ∼0.1 eV (each of these SOC sub-levels remains doubly degenerate). However, the splitting into sub-levels is well below the resolution of the available experimental data (broad and featureless absorption band). Moreover, the average energy of the three SOC sub-levels of common electronic parentage is identical to the energy of the parent state computed without the SOC (cf. Table S64, ESI†). Thus, the SOC is not expected to change the position of the S0 → T1 band maximum to any appreciable amount. The same holds true for the SOC effect on the adiabatic energy and vertical emission energy. Here, the analogous calculations were performed for the T1 equilibrium geometry, which is less symmetric than the S0 geometry and hence the T1 and other triplet states are no longer degenerate, leading to considerable reduction of their SOC splittings (see Table S65, ESI†). In fact, the three SOC sublevels resulting from the lowest component of the T1 state have almost identical energy (to within 0.01 eV) as their parent state.
3.2 Back-corrected experimental data
As previously in ref. 13, we use the available experimental data to derive the spin-state splitting in the form of purely electronic energy differences (either adiabatic or vertical ones). In the present case the solvation effects turned out to be negligible (Section 3.1.3). However, the experimental data still need to be back-corrected by subtracting relevant contributions of the vibrational origin, as will be detailed below. Table 3 gives the summary of experimental data, the corrections, and the resulting estimates of electronic energy differences (ΔErefe), i.e., the reference data for our benchmark set to be later discussed in Section 3.4.| Complex | ΔEb type | Exptl | Correction | ΔErefe |
|---|---|---|---|---|
| a All values in eV; energy/enthalpy differences defined as E(higher spin) − E(lower spin). b Type of energy difference: adiabatic or vertical absorption (S0 → T1) or vertical emission (T1 → S0). c SCO enthalpy 12.8 kJ mol−1 in toluene, ref. 26. d Electronic origin 21.4 × 103 cm−1 (crystal at T = 1.5 K), ref. 33. e Estimated S0 → T1 absorption max 26.5 × 103 cm−1 in the EPA mixture at T = 77 K from ref. 31 (see also values 26 and 27 × 103 cm−1 from ref. 27 and 101). f Estimated T1 → S0 emission max 16.9 × 103 cm−1 (crystal at T = 1.5 K), ref. 33. g Estimated S0 → T1 absorption max 17.1 × 103 cm−1 measured in this work (Section 3.3.2). h Roughly estimated S0 → T1 absorption max 19.1 × 103 cm−1 based on the estimated experimental S0 → S1 band max 24.3 × 103 cm−1 (ref. 27, perchlorate salt in water) and calculated T1–S1 splitting 5.2 × 103 cm−1 (mean of CBS-extrapolated CASPT2 and NEVPT2 results; see Section 3.3.3). i Enthalpy correction (PBE0/def2-TZVP, T = 212 K). j ZPE correction (BP86/def2-TZVP). k Vibronic correction from the simulated S0 → T1 band (BP86/def2-TZVP); ESI, Table S22. l Vibronic correction from the simulated T1 → S0 band (PBE0/def2-TZVP). | ||||
| 2,6[MnCp2] | Adiabatic | 0.13c | −0.06i | 0.19 |
| 1,3[RuCp2] | Adiabatic | 2.65d | −0.11j | 2.76 |
| Vert abs | 3.29e | −0.13k | 3.42 | |
| Vert emi | 2.10f | 0.04l | 2.06 | |
| 1,3[FeCp2] | Vert abs | 2.12g | −0.10c | 2.22 |
| 1,3[CoCp2]+ | Vert abs | 2.37h | −0.11k | 2.48 |
For MnCp2 the doublet–sextet adiabatic energy is derived from the SCO enthalpy difference from the magnetic resonance study of Köhler and Schlesinger.26 The raw experimental value is back-corrected by subtracting the enthalpy correction calculated using the standard statistical thermodynamics expression, based on the DFT harmonic frequencies. A very similar approach is used for the singlet–triplet adiabatic energy of RuCp2; in this case the raw experimental value is the 0–0 energy measured by Riesen et al.,33 from which we subtract the ZPE (zero-point energy) correction calculated at the DFT level. For all other cases, we use the experimental positions of the band maxima (see Table 3 for references) to derive the corresponding vertical energies by subtracting the appropriate vibronic corrections. These corrections are calculated using the approach discussed in Section 3.1.2 and play in our approach the same role as the enthalpy or ZPE corrections for adiabatic energies. To the best of our knowledge, no such vibronic corrections have been used before for d–d bands of TM complexes. However, the underlying vibronic methodology is similar to the state-of-the-art for organic molecules (see ref. 92 and references therein) and it can reproduce, at least qualitatively correct, the vibrational features of the S0 ↔ T1 band known from high-resolution spectroscopy of RuCp2 (cf. Section 3.1.2).
Uncertainties of the reference (back-corrected) energies originate from uncertainties of the input experimental data and uncertainties of the calculated corrections. The latter ones, in turn, originate from the use of DFT data (frequencies, geometries) and the harmonic oscillator model, neither of which is exact. In view of some but minor dependence of the computed corrections on the choice of functional (ESI,† Tables S21 and S22) and based on the experience with harmonic approximation in thermodynamics of TM complexes,102 we believe that 0.05 eV is a fair estimate of the total uncertainty in the case of adiabatic energies (2,6[MnCp2], 1,3[RuCp2]). In the case of vertical energies, however, we believe that it is reasonable to assume a twice larger uncertainty, i.e. 0.1 eV. One reason is that the presently introduced methodology of vibronic corrections is brand new and hence cannot be as thoroughly tested as the methodology of ZPE correction has been. Another reason is that even the procedure of reading the position of a weak singlet–triplet band maximum from the experimental spectrum is subject to some uncertainty and arbitrariness, possibly on the order of 500 cm−1 (0.06 eV). For instance, although we believe that the spectral data for RuCp2 are reliable, we find slightly divergent values for the S0 → T1 band maximum, like 26 × 10 cm−1 (ref. 27) or 27 × 10 cm−1 (ref. 101 based on data from ref. 31). These discrepancies are most probably related to different methodologies of reading the band position from the spectrum (unfortunately, such details are rarely documented). The value assumed by us for the S0 → T1 band maximum, 26.5 × 105 cm−1, is right in between the two literature values (and, in our opinion, it matches best the Gaussian analysis of the spectrum in EPA, 77 K, digitalized from Fig. 2 of ref. 31).
As was mentioned in the Introduction and will be discussed in Section 3.3, the existing literature data for FeCp2 and [CoCp2]+ are controversial. We were able to carefully revise the experimental value for FeCp2 (included in Table 3), but the corresponding value for [CoCp2]+ is merely an estimate which includes a computational ingredient (Section 3.3). Thus, the reference value for [CoCp2]+ has a larger uncertainty, possibly 0.2 eV (which is based on a plausible assumption that the computed ingredient is accurate to within 0.1 eV).
3.3 On experimental data of ferrocene and cobaltocenium
Based on the available data, at least two conflicting interpretations can be made regarding the S0 → T1 excitation energy for FeCp2. The first interpretation is due to Gray and coworkers,27 who assigned the T1 excited state to the shoulder they observed near 19 × 103 cm−1. The second interpretation is due to McGlynn and coworkers28a and Scott and Becker.28b Both groups also mentioned the ∼19 × 103 cm−1 shoulder, but they additionally reported the 14–16 × 103 cm−1 low-intensity absorption feature. Based on the Gaussian analysis they claimed that it consists of two bands, at ∼14 × 103 cm−1 and 16 × 103 cm−1, respectively, and they assigned the first band to the T1 state. This interpretation was criticized by Gray et al., who believed that only the band ∼19 × 103 cm−1 is unambiguously observed for ferrocene, whereas the existence of the two lower-energy bands is doubtful.27 The two discussed interpretations of the spectral data thus considerably differ on the S0 → T1 excitation energy: either ∼19 × 103 cm−1 (ref. 27) or ∼14 × 103 cm−1 (ref. 28), which makes a difference of 0.6 eV! Somewhat remarkably, both interpretations were supported by (differently parametrized) ligand-field calculations.27,28b
In another related work, Iogansen and Uvarov29 reinvestigated the absorption spectrum of FeCp2 and found no evidence for the earlier reported shoulder near 19 × 103 cm−1. In the lower energy region they reported a single weak band (shoulder) near 16 × 103 cm−1. Although not stated explicitly in ref. 29, their results are consistent with the S0 → T1 band at ∼16 × 103 cm−1, being the third possible interpretation of the spectral data of FeCp2!
The most recent work, intracavity laser photoacoustic spectroscopy study of Blackburn et al.,30 may be treated as providing support to both the second and the third interpretation. Blackburn et al. reported a weak band at about 13.3 × 103 cm−1 and attributed it to the T1 state (adhering to interpretation #2) although “the peak maximum was difficult to determine since the absorption is so broad and weak”. It cannot be excluded that their assignment was influenced by the calculations of Rohmer et al.108 predicting identical excitation energy.¶ This 13.3 × 103 cm−1 band is only mentioned in the text. The only band for which the appropriate part of the photoacoustic spectrum was reproduced in ref. 30 is the band with maximum at 16.25 × 103 cm−1, reminiscent of interpretation #3.
In Fig. 8(b) we summarize the energy of the S0 → T1 band for FeCp2 according to the three possible interpretations: 19 × 103 cm−1 from interpretation #1 (ref. 27); 14 or 13.3 × 103 cm−1 from interpretation #2 (ref. 28 and 30); or 16–17 × 103 cm−1 from interpretation #3 (based on data from ref. 29 and our new spectrum to be discussed below). Panels (a) and (c) of the same figure show analogous experimental data for RuCp2 and [CoCp2]+. For the reasons that will become clear, the figure also contains the experimental band positions corresponding to the S1 excited state of each metallocene.27
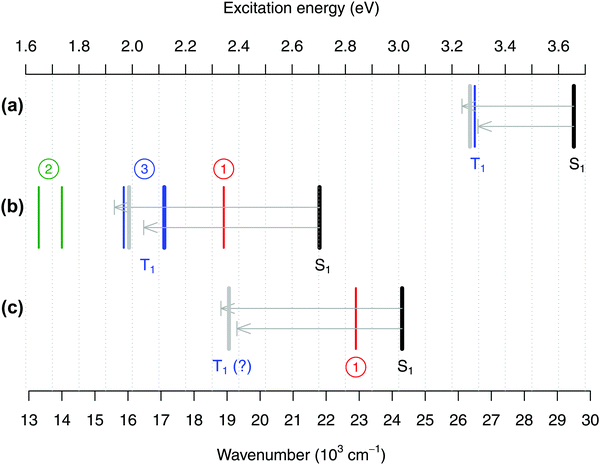 | ||
| Fig. 8 Positions of the absorption band maxima corresponding to excited states S1 (black lines) and T1 (colored lines) for (a) RuCp2, (b) FeCp2, and (c) [CoCp2]+ summarized from the literature or measured in this work, and theoretical estimates of the T1–S1 splittings obtained from CASPT2/NEVPT2 calculations (represented as arrows, upper CASPT2, lower NEVPT2, pointing from the experimental position of the S1 band downward in energy to predict the position of the T1 band; the gray bar is the predicted position based on the mean value of the CASPT2 and NEVPT2 splittings). See Tables S51–S53, ESI,† for details. As discussed in the text, for FeCp2 the actual position of the T1 state is very controversial with three possible interpretations of the literature data (circled numbers). Experimental values (in 103 cm−1): (a) For RuCp2 S1 at 29.5, T1 at 26.5 (from ref. 31 and 27). (b) For FeCp2 S1 at 21.8; (interpretation #1) T1 at 18.9 (from ref. 27) or (interpretation #2) T1 at 14.0 (ref. 28) or 13.3 (ref. 30) or (interpretation #3) T1 at 15.9 (shoulder from ref. 29) or 17.1 (band maximum from this work, thick blue line). (c) For [CoCp2]+ S0 at 24.3, T1 at 22.9 (ref. 27), which corresponds to interpretation #1 and is probably wrong. | ||
Indeed, it is very instructive to compare the alleged band positions corresponding to the T1 state with those corresponding to the S1 excited state. Not only the latter band position is more credibly known from the experiments, but also the T1 and S1 excited states arise from the same electronic configurations and differ merely in the magnetic coupling of the two unpaired electrons. For a pair of such spin–flip states, the energy difference (i.e., the T1–S1 splitting) should be easier to compute reliably than are the energies of both excited states with respect to the ground state. For this reason, Fig. 8 also includes the estimates of the T1–S1 splitting computed at the CASPT2 and NEVPT2 level. The computed values are graphically represented as arrows pointing from the experimental position of the S0 → S1 band maximum toward the expected position of the S0 → T1 band maximum. Note that in our previous study of TM aqua complexes,100 the two methods chosen here turned out to be very reliable in predicting the spin–flip energy differences.||
As shown in Fig. 8, the CASPT2 and NEVPT2 estimates of the T1–S1 splitting agree with each other to within 0.15 eV and, for each metallocene, their mean value is used to predict the expected position of the T1 maximum based on the experimental S1 maximum. For RuCp2 (panel a) we find that such predicted position of the T1 maximum is in good agreement with the actual experimental value, confirming that the latter one is reasonable. However, for FeCp2 (panel b) the predicted T1 position is only consistent with interpretation #3, whereas the alternative interpretations #1 and #2 point to the T1 band maximum being either too high (by 0.3–0.4 eV) or too low (by about 0.2–0.3 eV) in energy. In fact, if interpretation #1 was correct, the T1–S1 splitting – which is a measure of the on-site exchange interaction between unpaired electrons – would be about the same for Fe and Ru. This is unreasonable in view of not only the present CASPT2/NEVPT2 estimates, but also a recent computational study comparing exchange effects in 3d and 4d metal complexes with identical ligands.109
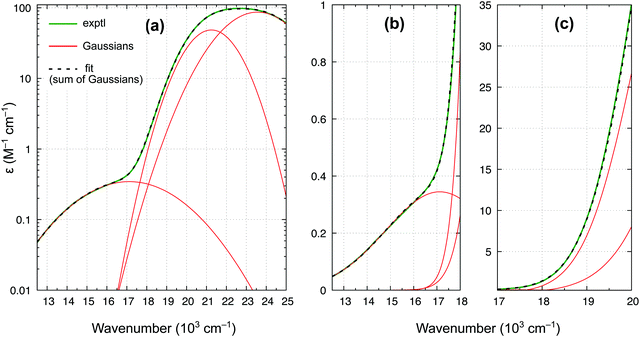
In accordance with all previous studies, ferrocene has an intense band εmax = 100 M−1 cm−1 at 22.6 × 103 cm−1, which is broad and asymmetric due to unresolved S1 and S2 excited states. In the lower energy region, the spectrum has only one shoulder, indicative of the presence of only one weak band. The spectrum in Fig. 9 can be almost perfectly reproduced by the sum of three Gaussian functions of which the first two represent the broad singlet peak, whereas the third one with εmax = 0.34 M−1 cm−1 is responsible for the shoulder. The width of this band (HWHM of 2.7 × 103 cm−1) is reasonable for it to be a d–d transition, whereas the low intensity is consistent with a spin-forbidden transition. The maximum from the Gaussian analysis is at 17.1 × 103 cm−1 and this is the number included above in Table 3 (to determine the reference energy for FeCp2) and in Fig. 8(b) (to show that it remains in a reasonably good agreement with the computed T1–S1 splitting).
Our revised spectrum is similar to that reported by Iogansen and Uvarov29 (see comparison in Fig. S15, ESI†). Like them, but in variance to others,27,28 we do not find the ∼19 × 103 cm−1 shoulder (cf.Fig. 9(c)).** Analogously, based on the spectrum in Fig. 9 and its nearly perfect Gaussian resolution, we find no evidence of any other spin-forbidden d–d bands at lower energies; in particular, we believe that there is no band with max at ∼14 × 103 cm−1 (such a band was tentatively proposed in ref. 28). As shown in the ESI,† Fig. S16, the weak band with max at 17.1 × 103 cm−1 continues downward in energy to somewhere around 11.8–12.1 × 103 cm−1, where the band origin is probably located. This would correspond to the T1 relaxation energy of 0.62–0.66 eV, almost identical to 0.64 eV for RuCp2 (cf. Table 3).
3.4 Assessment of WFT and DFT methods
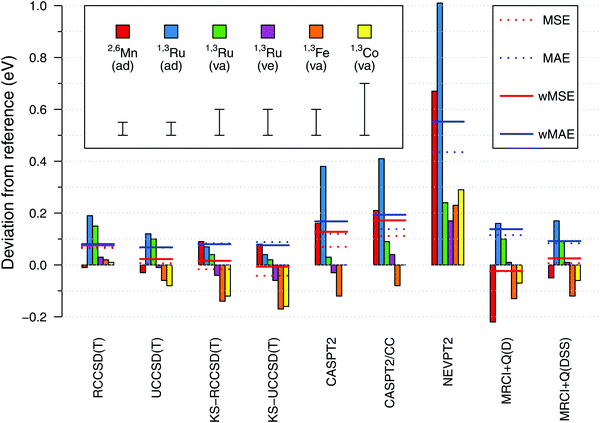
Having established the reference values of electronic spin-state splittings for metallocenes, we now come back to the central motif of this paper: assessing the accuracy of approximate WFT and DFT methods in reproducing these values. The results will be presented in a similar form as in our previous benchmark study of four octahedral iron complexes13 (but mind different energy units, 0.1 eV = 2.3 kcal mol−1).From Fig. 10, we find a very good agreement with the reference data for coupled cluster calculations at the CCSD(T) level. Four variations of the CCSD(T) method were compared: they are all based on an ROHF-type wave function, but differ in the spin-adaptation procedure (R vs. U) and the use of either canonical Hartree–Fock (HF, default) or Kohn–Sham (KS) orbitals. In general all four variants perform comparably good, yielding the maximum error below 0.2 eV and the wMAE below 0.1 eV. The wMSE values are close to zero (except RCCSD(T)), suggesting that these coupled cluster calculations do not have a systematic bias towards either lower- or higher-spin states when looking at our data globally. At the general level, all these observations are similar to those for the octahedral complexes in ref. 13.
Looking into the details, we pay particular attention to adiabatic energies for 2,6[MnCp2] and 1,3[RuCp2], for which the reference data have smallest uncertainties. For the 2,6[MnCp2] adiabatic energy, we find it somewhat remarkable that the use of KS orbitals in CCSD(T) calculations does not improve the agreement with the reference value; this is just the opposite to the behavior observed for 1,3[RuCp2] adiabatic energy and to what was observed for the SCO complex 1,5[Fe(tacn)2]2+ in ref. 13. For the 1,3[FeCp2] vertical energy, the KS-CCSD(T) calculations again produce a deviation exceeding the assumed uncertainty. Interestingly also, the effect on relative energy caused by switching from HF to KS orbitals is of opposite sign for 2,6[MnCp2] compared with that for other metallocenes studied. Looking also at the results in ref. 13, this may be a general pattern when comparing d5 with d6-electron complexes. The discussed differences between the CCSD(T) and KS-CCSD(T) results are generally subtle compared with much larger deviations observed for other methods and even (in some cases) with the uncertainties of the reference data. While we certainly agree that the use of KS orbitals is a valuable strategy (in particular, it allows in some cases to avoid problems with the convergence or wrong reference state110,111), the present data do not support the conjecture that switching from the HF to the KS orbitals uniformly improves the accuracy of CCSD(T) results. It is certainly true that the use of KS orbitals reduces the T1 and D1 diagnostics of multireference character (ESI,† Table S66), but there is only weak correlation, if any, between the values of these diagnostics and the accuracy achieved in CCSD(T) calculations.111a,112,113
Proceeding now to the results of multireference methods, we first remind that all of them were obtained for the same choice of active space based on 12 orbitals (cf. Section 2.4.1), which is the standard choice in the context of TM spin-state energetics.13 Judging from the obtained wMAE and wMSE values, we find that the MRCISD+Q calculations with the size-consistency correction DSS (Davidson–Silver–Siegbahn) are accurate on par with the CCSD(T) results, whereas other methods give larger deviations. The MRCI accuracy degrades when the standard Davidson correction (D) is used (as also found in ref. 13), but here this effect is significant only for the 2,6[MnCp2] adiabatic energy. The Pople correction gives almost the same results as the DSS correction (ESI†).
Among all the WFT methods studied by us, it is NEVPT2 that gives the largest deviations with respect to the reference data, like it was also found for octahedral complexes in ref. 13. The CASPT2 method performs better than NEVPT2, but worse than MRCI + Q(DSS), particularly for 2,6[MnCp2] and 1,3[RuCp2] adiabatic energies. It is of some importance that for these two outliers, our CASPT2 calculations tend to overestimate the energy of a higher-spin with respect to a lower-spin state (i.e., yield positive error in the sign convention of Fig. 10). This is just the opposite to the usual trend that CASPT2 underestimates such energy differences (i.e., this method is believed to have a systematic bias in favor of higher-spin states).11,74,76,114 The results obtained for octahedral complexes in ref. 13 also fit the usual trend, and this also seems to happen here for the 1,3[FeCp2] vertical energy. We note that spin-state gaps of metallocene complexes were only scarcely represented in the earlier studies, from which the above trend was deduced. In particular, we are not aware of any prior CASPT2 studies targeting the singlet–triplet gap in RuCp2. However, MnCp2 was studied before by Pierloot and coworkers,39,76 and they also found the doublet–sextet splitting to be overestimated at the CASPT2 level, i.e., their results are in agreement with our present findings.
Interestingly enough, the largest CASPT2 errors observed for 2,6[MnCp2] and 1,3[RuCp2] adiabatic energies are not reduced by using the CASPT2/CC approach (where the metal outer-core correlation effects are taken from CCSD(T) rather than being directly computed by CASPT2). This shows that the observed errors are due to imperfect description of not only the core, but also the valence correlation effects. For other (vertical) energies the agreement with the reference data is fair for both CASPT2 and CASPT2/CC results. An almost exact agreement with the 1,3[CoCp2]+ reference value should be put, however, into perspective by considering the large uncertainty of the latter value (see above). On the other hand, we notice that the CASPT2 and CASPT2/CC errors are not uniform when comparing them for the adiabatic energy and two vertical energies of 1,3[RuCp2], with relative deviations of ∼0.3 eV. This may be a sign of non-parallelity between the CASPT2 or CASPT2/CC potential energy surfaces and the exact ones. An analogous problem, in fact even more severe, is found at the NEVPT2 level. By contrast, these non-parallelity issues appear to be less pronounced for the CCSD(T) results.
The discussed practical problems will be smaller, perhaps negligible, in a hypothetical case of a much larger active space, ideally including all valence orbitals. The DMRG or stochastic-CASSCF techniques could be used to make such calculations feasible.115–117 However, our purpose in this work was to examine the performance of these methods for the “standard” active space, which is reasonably small, but still physically valid, and resembles the active spaces typically used in the literature for mononuclear TM complexes.
Finally, one should recall that CASPT2 and CASPT2/CC spin-state energetics are sensitive to the form of zero-order Hamiltonian. Here, the IPEA-shifted Hamiltonian was used with the default (0.25 a.u.) shift value, which is normally recommended and widely used also for TM complexes.16,17,39,75 As observed for other complexes,11,40,74,76 the spin-state splittings tend to increase with the increasing IPEA shift value (ESI,† Fig. S10). The effect is slightly larger for 1,3[RuCp2] than for 1,3[FeCp2] and 2,6[MnCp2]. In principle, the shift value could be optimized semi-empirically to best match the reference values, but any such modifications are beyond the scope of this work. Moreover, it seems that the optimal shift value is system-specific, e.g., the agreement with the reference would improve if the shift value is reduced for 2,6[MnCp2], but increased for 1,3[FeCp2] (cf. Fig. S10, ESI†).
| # | Method | 2,6[MnCp2] | 1,3[RuCp2] | 1,3[FeCp2] | 1,3[CoCp2]+ | wMSE | wMAE | ||
|---|---|---|---|---|---|---|---|---|---|
| (adiab) | (adiab) | (vert abs) | (vert emi) | (vert abs) | (vert abs) | ||||
| 1 | OLYP | 0.15 | −0.07 | −0.06 | −0.07 | −0.18 | −0.03 | −0.02 | 0.10 |
| 2 | B97D | 0.08 | −0.18 | −0.08 | −0.05 | −0.23 | −0.04 | −0.08 | 0.12 |
| 3 | M06L-D3 | −0.06 | 0.02 | −0.03 | −0.17 | −0.39 | −0.36 | −0.11 | 0.12 |
| 4 | LH14t-calPBE-D3 | −0.01 | 0.04 | −0.24 | −0.08 | −0.37 | −0.32 | −0.11 | 0.13 |
| 5 | BR | 0.13 | −0.28 | 0.07 | 0.08 | −0.03 | 0.07 | −0.02 | 0.14 |
| 6 | MN15 | −0.03 | −0.00 | −0.04 | −0.05 | −0.66 | −0.49 | −0.14 | 0.14 |
| 7 | wB97XD | 0.04 | −0.04 | −0.08 | −0.18 | −0.53 | −0.54 | −0.14 | 0.16 |
| 8 | B2PLYP-D3 | 0.13 | 0.13 | 0.16 | 0.05 | 0.14 | 0.86 | 0.17 | 0.17 |
| 9 | B3LYP*-D3 | 0.05 | −0.24 | −0.07 | −0.11 | −0.37 | −0.32 | −0.15 | 0.17 |
| 10 | OPBE | 0.31 | 0.20 | −0.03 | −0.10 | −0.19 | −0.05 | 0.09 | 0.18 |
| 11 | LC-wPBE-D3 | 0.12 | 0.00 | −0.18 | −0.35 | −0.49 | −0.44 | −0.13 | 0.20 |
| 12 | LC-BLYP | 0.00 | −0.06 | −0.20 | −0.35 | −0.58 | −0.52 | −0.20 | 0.20 |
| 13 | TPSSh-D3 | 0.48 | −0.01 | 0.01 | −0.13 | −0.30 | −0.29 | 0.05 | 0.21 |
| 14 | S12g | 0.52 | −0.06 | −0.14 | −0.10 | −0.17 | −0.07 | 0.06 | 0.21 |
| 15 | PW6B95-D3 | −0.22 | −0.04 | −0.08 | −0.17 | −0.61 | −0.64 | −0.23 | 0.23 |
| 16 | SSB-D | 0.46 | 0.04 | −0.19 | −0.17 | −0.28 | −0.20 | 0.03 | 0.23 |
| 17 | O3LYP | −0.37 | −0.09 | −0.11 | −0.16 | −0.43 | −0.34 | −0.24 | 0.24 |
| 18 | PBE-D3 | 0.89 | −0.04 | −0.01 | 0.00 | −0.05 | 0.06 | 0.22 | 0.26 |
| 19 | B3LYP-D3 | −0.26 | −0.29 | −0.11 | −0.17 | −0.50 | −0.48 | −0.28 | 0.28 |
| 20 | BLYP-D3 | 0.69 | −0.32 | −0.02 | 0.02 | −0.03 | 0.07 | 0.10 | 0.28 |
| 21 | TPSS-D3 | 1.02 | 0.01 | 0.08 | −0.02 | −0.04 | 0.00 | 0.28 | 0.29 |
| 22 | CAM-B3LYP-D3 | −0.32 | −0.21 | −0.15 | −0.27 | −0.60 | −0.59 | −0.32 | 0.32 |
| 23 | PBE0-D3 | −0.44 | −0.08 | −0.14 | −0.25 | −0.66 | −0.67 | −0.32 | 0.32 |
| 24 | MVS | −0.59 | −0.12 | −0.24 | −0.30 | −0.50 | −0.38 | −0.35 | 0.35 |
| 25 | MN15L | −1.08 | −0.01 | −0.02 | −0.17 | −0.52 | −0.35 | −0.41 | 0.41 |
| 26 | S12h | −0.66 | −0.20 | −0.23 | −0.33 | −0.70 | −0.74 | −0.45 | 0.45 |
| 27 | M06-D3 | −0.82 | −0.20 | −0.18 | −0.12 | −0.74 | −0.59 | −0.45 | 0.45 |
| 28 | M11 | −0.78 | −0.19 | −0.17 | −0.29 | −0.77 | −0.86 | −0.48 | 0.48 |
| 29 | M11L | 1.36 | −0.34 | −0.39 | −0.40 | −0.36 | −0.46 | 0.09 | 0.64 |
| 30 | MVSh | −1.66 | −0.22 | −0.35 | −0.51 | −1.01 | −1.10 | −0.83 | 0.83 |
In Table 4, the DFT methods are ranked based on the wMAE value and (if not discriminating) by the maximum error. It is clear that the precise position of a given functional in this ranking has rather limited meaning because the best performing functionals do not significantly differ in terms of their wMAE values. The same holds true for the group of functionals ranked in the middle. The maximum error is most frequently seen for 2,6[MnCp2] adiabatic energy, followed by 1,3[FeCp2] and 1,3[CoCp2]+ vertical energies. (If the maximum error occurs for [CoCp2]+, it is several times larger than the rather generous uncertainty of 0.2 eV assumed for the reference value.) The deviations observed for the 1,3[RuCp2] data are much smaller, with most DFT methods giving rather comparable results. This is manifestation of a generally smaller sensitivity of spin-state energetics to the choice of functional for 4d than for 3d TM complexes.109 In view of that, the spin-state splittings of RuCp2 may seem an “easier target” for computation than analogous splittings of 3d-electron complexes. However, even for 1,3[RuCp2] (adiabatic) rather significant errors of ∼0.2 eV are obtained in some cases (e.g., BR, B3LYP*-D3, B97D).
A general conclusion from our results in Table 4 is similar to that in ref. 13: it is very difficult to find a DFT method correctly reproducing all the reference values, although many functionals can reproduce a subset of them remarkably well. For instance, Truhlar's MN15 functional gives excellent results for MnCp2 and RuCp2, but it gives deviations larger than 0.5 eV for FeCp2 and [CoCp2]+. Similarly, PBE-D3 excellently reproduces the reference values for all d6-electron metallocenes (which is a remarkable achievement, anyway, for such a simple, non-empirical functional!). However, with a maximum error of almost 0.9 eV, the PBE-D3 fails miserably for MnCp2. These issues are manifestations of the non-universality problem with approximate density functionals when applied to TM complexes.13,23b,119
It is clear that due to the very special metal–π coordination mode in metallocenes (with η5-Cp ligand), the performance of DFT methods in Table 4 will not be transferable to other complexes, in particular to typical SCO complexes with quasi-octahedral architectures. Comparison with the previous similar assessment of functionals for octahedral complexes (ref. 13) fully confirms this presumption. The B2PLYP-D3 functional, previously ranked #1, is now in the 8th position only. The wMAE of this functional is still fair (below 0.2 eV), but the problem is with an almost 0.9 eV error for [CoCp2]+ (i.e., more than four times larger than estimated uncertainty of this reference value). For comparison, the maximum error of this functional based on the data of four octahedral complexes13 was only 0.14 eV (3.2 kcal mol−1). The OPBE, another leading functional of ref. 13, is now ranked 10th, mainly due to the significant error of 0.3 eV on the 2,6[MnCp2] adiabatic energy. On the other hand, the functional presently ranked #1 is OLYP: with a wMAE of 0.1 eV, negligibly small wMSE, and a maximum error of 0.18 (for 1,3[FeCp2]). Such error statistics are comparably good as for the best CCSD(T) methods (see above). However, looking into the benchmark set of ref. 13, it is evident that OLYP may easily give larger errors, up to 0.36 eV for 4,6[Fe(H2O)6]3+, and OLYP's MAE for octahedral complexes was about twice larger than found here for metallocenes.
3.5 Multireference character
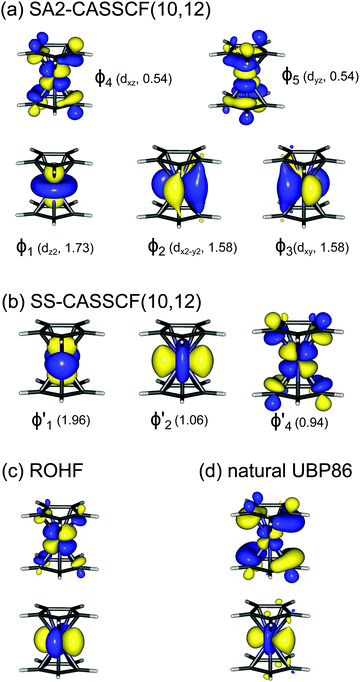
A motif rather frequently recurring in the literature is the question of multireference character for TM complexes and its supposed influence on the quality of single-reference correlated results. This issue may be also relevant for the understanding of our results for metallocenes. In particular, there are suggestions in the literature43,45 that “lowest excited states of ferrocene have significant multiconfigurational character” (ref. 45). Indeed, already based on a qualitative understanding of the electronic structure, one may expect a mixing between two singly excited triplet configurations (of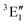 symmetry in D5h; cf. Fig. 2) and this effect should contribute a multireference character to the lowest triplet state, T1. If this is true, how can we rationalize the apparently good performance of single-reference CCSD(T) calculations, including also the S0 → T1 excitation energy for FeCp2 and other d6-electron metallocenes?
symmetry in D5h; cf. Fig. 2) and this effect should contribute a multireference character to the lowest triplet state, T1. If this is true, how can we rationalize the apparently good performance of single-reference CCSD(T) calculations, including also the S0 → T1 excitation energy for FeCp2 and other d6-electron metallocenes?
To understand this problem we take under scrutiny the T1 state of FeCp2 computed for the ground-state equilibrium geometry of the D5h symmetry (i.e., like for computation of the vertical excitation energy), for which the T1 state is two-fold degenerate. We take a look at the composition of a multiconfigurational (CASSCF) wave function for one component of this degenerate state.††Fig. 11 gives percentage weights of the leading configurations contributing to the CASSCF(10,12) wave function depending on the treatment of active orbitals (see below). The participating configurations are described in terms of occupancies of five orbitals with the Fe 3d character, shown in Fig. 12(a) and (b).
 | ||
| Fig. 11 Percentage weights of leading configurations contributing to the CASSCF(10,12) wave function for one component of the degenerate T1 state of FeCp2 depending on the treatment of active orbitals. The participating configurations are distinguished by occupancies of five orbitals with predominant Fe 3d character, shown in Fig. 12. For instance, the label “2a2a0” stands for |(ϕ1)2(ϕ2)1(ϕ3)2(ϕ4)1(ϕ5)0〉. | ||
If the active orbitals are obtained from state-average (SA2) calculations, i.e., a common set of orbitals (so called, average orbitals) is used to represent both components of the T1 state, the wave function indeed appears as strongly multiconfigurational (to the left in Fig. 11). However, if state-specific (SS) calculations are performed for one component of the T1 state, allowing the active orbitals to optimize accordingly, the character of wave function changes to being dominated by one configuration (83%) (to the right in Fig. 11). The contribution of the principal configuration is actually close to that in the S0 ground state (87%), which is believed to be dominated by dynamical correlation. In between the two extremes there is a situation when SA2 calculations are performed for both components of T1, but the wave function of a given component is expressed in terms of its own natural orbitals (in the middle of Fig. 11). We stress that while the SS calculations produce a lower variational energy than the SA2 calculations, the transformation from average to natural orbitals within the SA2 calculations does not change the energy, nor even the CASSCF wave function. These possibly counterintuitive observations of how the character of a CASSCF wave function can fluctuate for one and the same electronic state can be explained by considering changes in the active orbitals corresponding to the three discussed cases.
The average orbitals, shown in Fig. 12(a), maintain the full D5h symmetry, i.e., orbitals ϕ2, ϕ3 as well as ϕ4, ϕ5 appear in degenerate pairs (corresponding to degenerate irreps of D5h). The full symmetry is maintained because these orbitals are eigenvectors of the density matrix being a half-and-half mixture of density matrices for the two T1 components. However, the density matrix of a single component has lower symmetry (C2v). The same holds true for its eigenvectors, i.e. the natural orbitals, which then also transform as irreps of the C2v symmetry only. We would like to stress that this is a completely physical effect related to any degenerate state and it will be still present even for a hypothetical full CI wave function. (Thus, it should not be confused with broken-symmetry solutions appearing due to unphysical limitations of a single-determinant wave function.)
The symmetry lowering of the active orbitals is clearly shown in Fig. 12(b), where the natural orbitals from SS calculations are depicted (but they look qualitatively identical to natural orbitals of a specific component obtained from the SA2 calculations). Due to this symmetry lowering, the orbitals ϕ1 and ϕ2 (which belong now to the same irrep A1 in C2v) mix with each other and produce two new (“rehybridized”) orbitals 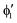 and
and 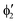 . Such mixing at the level of orbitals eliminates the need of mixing the configurations in which the two orbitals ϕ1 and ϕ2 were occupied differently (i.e., 2a2a0 and a22a0). In other words, the mix of configurations 2a2a0 and a22a0 expressed in terms of the average orbitals can be replaced by the single configuration 2a2a0 expressed in terms of the natural orbitals, which is easily seen in the middle of Fig. 11, when comparing the SA2(average) and SA2(natural) results.
. Such mixing at the level of orbitals eliminates the need of mixing the configurations in which the two orbitals ϕ1 and ϕ2 were occupied differently (i.e., 2a2a0 and a22a0). In other words, the mix of configurations 2a2a0 and a22a0 expressed in terms of the average orbitals can be replaced by the single configuration 2a2a0 expressed in terms of the natural orbitals, which is easily seen in the middle of Fig. 11, when comparing the SA2(average) and SA2(natural) results.
The mixing with the third important configuration (22a0a) appearing in the SA2 calculations cannot be eliminated in this way; therefore the contribution of this configuration is unaffected by the average-to-natural transformation of active orbitals. However, in SS calculations the role of this configuration is reduced too (cf.Fig. 11). This is possible because other orbitals also change when comparing them between the SA2 and SS calculations, although these changes are too subtle to be seen qualitatively. In Fig. S11, ESI,† we compared more quantitatively the changes occurring in the shapes of ϕ4 and ϕ5 orbitals, which have antibonding Fe–Cp character, and of their corresponding bonding orbitals. It follows that for the orbital ϕ4 (singly occupied in the chosen component of T1), the contribution of Fe 3dxz increases and the contribution of Cp πx decreases when comparing the SS with the SA2 calculations. Opposite changes are observed in the corresponding bonding orbital. This is consistent with reduced covalency for the xz-component of the Fe–Cp bond in SS calculations. Conversely, for the orbital ϕ5 (unoccupied in the chosen component of T1), the contribution of Cp πy increases and the contribution of Fe 3dyz decreases when comparing the SS with the SA2 calculations. Opposite changes are observed in the corresponding bonding orbital. This is consistent with increased covalency for the yz-component of the Fe–Cp bond in SS calculations. Thus, the different composition of the Fe–Cp antibonding orbitals in the SS than in the SA2 calculations is responsible for reducing the mixing between configurations in which these orbitals are occupied differently (2a2a0 and 22a0a).
It is also instructive to compare the SS-CASSCF orbitals 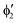 and
and 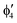 , which are singly occupied in the leading configuration, with the singly occupied orbitals of ROHF or unrestricted DFT calculations – see Fig. 12(c) and (d). All three sets of singly occupied orbitals are qualitatively identical, showing that HF and DFT can reasonably represent the degenerate T1 state (actually, one component of it, but this is enough to establish the energy because the state is degenerate anyway).
, which are singly occupied in the leading configuration, with the singly occupied orbitals of ROHF or unrestricted DFT calculations – see Fig. 12(c) and (d). All three sets of singly occupied orbitals are qualitatively identical, showing that HF and DFT can reasonably represent the degenerate T1 state (actually, one component of it, but this is enough to establish the energy because the state is degenerate anyway).
4 Conclusions and outlook
In this work we established experiment-derived reference values for relative spin-state energetics of four important metallocenes, of which one is a SCO complex, while the remaining ones feature spin-forbidden (singlet–triplet) optical transitions. Successful completion of this task required clarifying the controversies over the experimental data of FeCp2 and [CoCp2]+. In addition to extensive analysis of the previous data, a new experimental spectrum of FeCp2 was recorded to falsify earlier conjectures on the location of the S0 → T1 band maximum. The discovery of problems with the earlier reported spectra (and their interpretations) suggests that further experimental investigations of metallocenes may be worthwhile, in particular revising their MCD spectra, which were so far interpreted only in terms of the spin-allowed transitions.104When estimating vertical energies from the experimental band positions, we developed a practical scheme of vibronic corrections, which can (and probably should) be used in the future for similar analyses. The availability of rich experimental data for RuCp2 was helpful to put our vibronic simulations on firm grounds, by showing their ability to reproduce rather fine details of the electronic progressions seen in laser-excitation experiments.33
The results of our benchmarking based on the quasi-experimental reference data for metallocenes confirm the high accuracy of the CCSD(T) method. This was rationalized for the example of FeCp2 in the triplet excited state (sometimes claimed in the literature to have multireference character) by analyzing how the composition of the CASSCF wave function is dependent on the treatment of active orbitals. Our analysis showed that state-average calculations may significantly overestimate the multireference character compared with state-specific calculations, and this effect (possibly general) should be borne in mind when judging the multireference character of TM complexes on the basis of state-average calculations, which are natural in the context of spectroscopy.
The benchmarking results also supported the high accuracy of the MRCISD + Q method (with the DSS or P size-consistency correction). Other methods revealed moderate to significant deviations for at least one item in the present benchmark set. In particular, the investigation of 30 functionals confirmed the non-universality problem with approximate DFT methods. The functionals best performing for metallocenes were identified, but it is clear that due to the distinct metal–π coordination mode in metallocenes and high covalency of their Fe–C bonds, the performance of DFT methods for these systems is remarkably different from that for classical octahedral complexes, such as those with Fe–N and Fe–O bonds studied earlier (ref. 13). Thus, the non-universality problem was even more sharply demonstrated by comparing the DFT performance for these two groups of TM complexes. From this point of view, neither the present benchmark set (metallocenes), nor the previous one (classical octahedral complexes), or even both of them together, is yet to be considered as definite and fully representative in statistical terms. The studies should be continued to establish an even more extensive benchmark set of TM spin-state energetics, where experiment-derived data of classical and organometallic complexes are put together to represent the diversity of bonding types and ligand field strengths.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by the National Science Centre, Poland (grant no. 2017/26/D/ST4/00774), and by PLGrid Infrastructure (part of computations have been performed on resources provided by ACC Cyfronet AGH/UST). Dr Fabrizio Santoro (ICCOM, Pisa) and Dr Javier Cerezo (UAM, Madrid) are thanked for kindly sharing the development version 3 of FCclasses code and for helpful comments.References
- M. Costas and J. N. Harvey, Nat. Chem., 2013, 5, 7–9 CrossRef CAS.
- M. Swart and M. Gruden, Acc. Chem. Res., 2016, 49, 2690–2697 CrossRef CAS.
- S. Shaik, H. Chen and D. Janardanan, Nat. Chem., 2011, 3, 19–27 CrossRef CAS.
- M. Swart, New Directions in the Modeling of Organometallic Reactions, in Topics in Organometallic Chemistry, ed. A. Lledós and G. Ujaque, Springer, Cham, 2020, vol. 67, pp. 191–226 Search PubMed.
- M. Radoń, Advances in Inorganic Chemistry, Academic Press, 2019, vol. 73, pp. 221–226 Search PubMed.
- J. N. Harvey, Annu. Rep. Prog. Chem., Sect. C: Phys. Chem., 2006, 102, 203–226 RSC.
- A. Fouqueau, S. Mer, M. E. Casida, L. M. L. Daku, A. Hauser, T. Mineva and F. Neese, J. Chem. Phys., 2004, 120, 9473–9486 CrossRef CAS.
- A. Ghosh, JBIC, J. Biol. Inorg. Chem., 2006, 11, 712–724 CrossRef CAS.
- M. Fumanal, L. K. Wagner, S. Sanvito and A. Droghetti, J. Chem. Theory Comput., 2016, 12, 4233–4241 CrossRef CAS.
- S. Song, M.-C. Kim, E. Sim, A. Benali, O. Heinonen and K. Burke, J. Chem. Theory Comput., 2018, 14, 2304–2311 CrossRef CAS.
- L. M. Lawson Daku, F. Aquilante, T. W. Robinson and A. Hauser, J. Chem. Theory Comput., 2012, 8, 4216–4231 CrossRef CAS.
- B. M. Flöser, Y. Guo, C. Riplinger, F. Tuczek and F. Neese, J. Chem. Theory Comput., 2020, 16, 2224–2235 CrossRef.
- M. Radoń, Phys. Chem. Chem. Phys., 2019, 21, 4854–4870 RSC.
- A. Stępniewski, M. Radoń, K. Góra-Marek and E. Broclawik, Phys. Chem. Chem. Phys., 2016, 18, 3716–3729 RSC.
- R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018 CrossRef CAS.
- L. Wilbraham, P. Verma, D. G. Truhlar, L. Gagliardi and I. Ciofini, J. Phys. Chem. Lett., 2017, 8, 2026–2030 CrossRef CAS.
- Q. M. Phung, M. Feldt, J. N. Harvey and K. Pierloot, J. Chem. Theory Comput., 2018, 14, 2446–2455 CrossRef CAS.
- (a) K. P. Kepp, Inorg. Chem., 2016, 55, 2717–2727 CrossRef CAS; (b) K. P. Jensen and J. Cirera, J. Phys. Chem. A, 2009, 113, 10033–10039 CrossRef CAS.
- J. Cirera, M. Via-Nadal and E. Ruiz, Inorg. Chem., 2018, 57, 14097–14105 CrossRef CAS.
- D. Zhang and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 4416–4428 CrossRef CAS.
- S. E. Neale, D. A. Pantazis and S. A. Macgregor, Dalton Trans., 2020, 49, 6478–6487 RSC.
- S. Vela, M. Fumanal, J. Cirera and J. Ribas-Arino, Phys. Chem. Chem. Phys., 2020, 22, 4938–4945 RSC.
- (a) K. P. Kepp, Coord. Chem. Rev., 2013, 257, 196–209 CrossRef CAS; (b) K. P. Kepp, Transition Metals in Coordination Environments, in Challenges and Advances in Computational Chemistry and Physics, ed. E. Broclawik, T. Borowski and M. Radoń, Springer, Cham, 2019, vol. 29, pp. 1–33 Search PubMed.
- M. Radoń, K. Gąssowska, J. Szklarzewicz and E. Broclawik, J. Chem. Theory Comput., 2016, 12, 1592–1605 CrossRef.
- T. F. Hughes and R. A. Friesner, J. Chem. Theory Comput., 2011, 7, 19–32 CrossRef CAS.
- F. H. Koehler and B. Schlesinger, Inorg. Chem., 1992, 31, 2853–2859 CrossRef CAS.
- Y. S. Sohn, H. B. Gray and N. Hendrickson, J. Am. Chem. Soc., 1971, 93, 3603–3612 CrossRef CAS.
- (a) A. T. Armstrong, F. Smith, E. Elder and S. P. McGlynn, J. Chem. Phys., 1967, 46, 4321–4328 CrossRef CAS; (b) D. R. Scott and R. S. Becker, J. Organomet. Chem., 1965, 4, 409–411 CrossRef CAS.
- L. Iogansen and F. Uvarov, Z. Fiz. Khim., 1975, 49, 587–590 CAS.
- F. Blackburn, D. Snavely and I. Oref, Chem. Phys. Lett., 1991, 178, 538–542 CrossRef CAS.
- M. S. Wrighton, L. Pdungsap and D. L. Morse, J. Phys. Chem., 1975, 79, 66–71 CrossRef CAS.
- G. Crosby, G. Hager, K. Hipps and M. Stone, Chem. Phys. Lett., 1974, 28, 497–500 CrossRef CAS.
- H. Riesen, E. Krausz, W. Luginbühl, M. Biner, H. U. Güdel and A. Ludi, J. Chem. Phys., 1992, 96, 4131–4135 CrossRef CAS.
- Y. Yamaguchi, W. Ding, C. T. Sanderson, M. L. Borden, M. J. Morgan and C. Kutal, Coord. Chem. Rev., 2007, 251, 515–524 CrossRef CAS.
- (a) H. Koch, P. Jørgensen and T. Helgaker, J. Chem. Phys., 1996, 104, 9528–9530 CrossRef CAS; (b) S. Coriani, A. Haaland, T. Helgaker and P. Jørgensen, ChemPhysChem, 2006, 7, 245–249 CrossRef CAS; (c) M. E. Harding, T. Metzroth, J. Gauss and A. A. Auer, J. Chem. Theory Comput., 2008, 4, 64–74 CrossRef CAS.
- Z.-F. Xu, Y. Xie, W.-L. Feng and H. F. Schaefer, III, J. Phys. Chem. A, 2003, 107, 2716–2729 CrossRef CAS.
- M. Swart, Inorg. Chim. Acta, 2007, 360, 179–189 CrossRef CAS.
- K. Pierloot, B. J. Persson and B. O. Roos, J. Chem. Phys., 1995, 99, 3465–3472 CrossRef CAS.
- Q. M. Phung, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2012, 8, 883–892 CrossRef CAS.
- C. J. Stein, V. von Burg and M. Reiher, J. Chem. Theory Comput., 2016, 12, 3764–3773 CrossRef CAS.
- K. Ishimura, M. Hada and H. Nakatsuji, J. Chem. Phys., 2002, 117, 6533–6537 CrossRef CAS.
- K. R. Shamasundar, G. Knizia and H.-J. Werner, J. Chem. Phys., 2011, 135, 054101 CrossRef CAS.
- L. M. J. Huntington and M. Nooijen, J. Chem. Phys., 2015, 142, 194111 CrossRef.
- Y. Lei, W. Liu and M. R. Hoffmann, Mol. Phys., 2017, 115, 2696–2707 CrossRef CAS.
- E. R. Sayfutyarova, Q. Sun, G. K.-L. Chan and G. Knizia, J. Chem. Theory Comput., 2017, 13, 4063–4078 CrossRef CAS.
- P. Boulet, H. Chermette, C. Daul, F. Gilardoni, F. Rogemond, J. Weber and G. Zuber, J. Phys. Chem. A, 2001, 105, 885–894 CrossRef CAS.
- A. Rosa, G. Ricciardi, O. Gritsenko and E. J. Baerends, Principles and Applications of Density Functional Theory in Inorganic Chemistry I, in Structure and Bonding, ed. N. Kaltsoyannis, Springer, Berlin, Heidelberg, 2004, vol. 112, pp. 49–116 Search PubMed.
- A. Heil, M. Kleinschmidt and C. M. Marian, J. Chem. Phys., 2018, 149, 164106 CrossRef.
- T. Tsuchimochi and S. L. Ten-no, J. Chem. Theory Comput., 2019, 15, 6688–6702 CrossRef CAS.
- S. Grimme and M. Waletzke, J. Chem. Phys., 1999, 111, 5645–5655 CrossRef CAS.
- U. Salzner, J. Chem. Theory Comput., 2013, 9, 4064–4073 CrossRef CAS.
- E. Fromager, S. Knecht and H. J. A. Jensen, J. Chem. Phys., 2013, 138, 084101 CrossRef.
- TURBOMOLE V7.0-7.4 2015-2019, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com.
- A. Klamt and G. Schürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799 RSC.
- J. F. Stanton, J. Gauss, L. Cheng, M. E. Harding, D. A. Matthews and P. G. Szalay, CFOUR v2, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package.
- E. J. Baerends, et al., ADF2017, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2017, https://www.scm.com Search PubMed.
- M. J. Frisch, et al., Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS.
- (a) M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956 CrossRef CAS; (b) M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 2037–2047 CrossRef CAS.
- C. Angeli, M. Pastore and R. Cimiraglia, Theor. Chem. Acc., 2007, 117, 743–754 Search PubMed.
- H.-J. Werner, et al., MOLPRO, version 2015.1, a package of ab initio programs, 2015, see http://www.molpro.net Search PubMed.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1991, 96, 1218–1226 CrossRef.
- F. Aquilante, et al. , J. Chem. Phys., 2020, 152, 214117 CrossRef CAS.
- P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 1993, 99, 5219–5227 CrossRef CAS.
- M. Radoń, J. Chem. Theory Comput., 2014, 10, 2306–2321 CrossRef.
- T. F. Hughes, J. N. Harvey and R. A. Friesner, Phys. Chem. Chem. Phys., 2012, 14, 7724–7738 RSC.
- A. S. Petit, R. C. R. Pennifold and J. N. Harvey, Inorg. Chem., 2014, 53, 6473–6481 CrossRef CAS.
- (a) T. B. Adler, G. Knizia and H.-J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef; (b) G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef.
- P. G. Szalay, T. Müller, G. Gidofalvi, H. Lischka and R. Shepard, Chem. Rev., 2012, 112, 108–181 CrossRef CAS.
- D. B. Krisiloff and E. A. Carter, Phys. Chem. Chem. Phys., 2012, 14, 7710–7717 RSC.
- K. Pierloot, in Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker, Inc., New York, 2001, ch. 5, pp. 123–158 Search PubMed.
- K. Pierloot, Mol. Phys., 2003, 101, 2083–2094 CrossRef CAS.
- V. Veryazov, P. Å. Malmqvist and B. O. Roos, Int. J. Quantum Chem., 2011, 111, 3329–3338 CrossRef CAS.
- M. Kepenekian, V. Robert and B. Le Guennic, J. Chem. Phys., 2009, 131, 114702 CrossRef.
- M. Pápai, G. Vankø, C. de Graaf and T. Rozgonyi, J. Chem. Theory Comput., 2013, 9, 509–519 CrossRef.
- K. Pierloot, Q. M. Phung and A. Domingo, J. Chem. Theory Comput., 2017, 13, 537–553 CrossRef CAS.
- C. J. Stein and M. Reiher, J. Chem. Theory Comput., 2016, 12, 1760–1771 CrossRef CAS.
- F. J. Avila Ferrer and F. Santoro, Phys. Chem. Chem. Phys., 2012, 14, 13549–13563 RSC.
- F. Santoro and J. Cerezo, FCclasses3, a code to simulate electronic spectra, v3.0.1, 2020. Visit http://www.pi.iccom.cnr.it/fcclasses Search PubMed.
- A. Lami and F. Santoro, in Computational Strategies for Spectroscopy, ed. V. Barone, John Wiley & Sons, Ltd, 2011, ch. 10, pp. 475–516 Search PubMed.
- F. J. Avila Ferrer, J. Cerezo, J. Soto, R. Improta and F. Santoro, Comput. Theor. Chem., 2014, 1040–1041, 328–337 CrossRef CAS.
- F. Santoro, R. Improta, A. Lami, J. Bloino and V. Barone, J. Chem. Phys., 2007, 126, 084509 CrossRef.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- P.-F. Loos and D. Jacquemin, J. Chem. Theory Comput., 2019, 15, 2481–2491 CrossRef CAS.
- A. Haaland and J. E. Nilsson, Acta Chem. Scand., 1968, 22, 2653–2670 CrossRef CAS.
- A. Haaland, Inorg. Nucl. Chem. Lett., 1979, 15, 267–269 CrossRef CAS.
- Y. Zhang, J. Chem. Phys., 2018, 148, 044706 CrossRef.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48–55 Search PubMed.
- M. Radoń, Phys. Chem. Chem. Phys., 2014, 16, 14479–14488 RSC.
- (a) A. L. B. Formiga, S. Vancoillie and K. Pierloot, Inorg. Chem., 2013, 52, 10653–10663 CrossRef CAS; (b) S. Saureu and C. de Graaf, Chem. Phys., 2014, 428, 59–66 CrossRef CAS; (c) L. Freitag and L. González, Inorg. Chem., 2014, 53, 6415–6426 CrossRef CAS; (d) M. Fumanal and C. Daniel, J. Comput. Chem., 2016, 37, 2454–2466 CrossRef CAS.
- (a) C. Daniel, Coord. Chem. Rev., 2015, 282-283, 19–32 CrossRef CAS; (b) C. Daniel, Density-Functional Methods for Excited States, in Topics in Current Chemistry, ed. N. Ferré, M. Filatov and M. Huix-Rotllant, Springer, Cham, 2015, vol. 368, pp. 377–413 Search PubMed.
- F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, J. Chem. Theory Comput., 2013, 9, 2072–2082 CrossRef CAS.
- J. Landry-Hum, G. Bussière, C. Daniel and C. Reber, Inorg. Chem., 2001, 40, 2595–2601 CrossRef CAS.
- J. Neugebauer, E. J. Baerends and M. Nooijen, J. Phys. Chem. A, 2005, 109, 1168–1179 CrossRef CAS.
- C. Reber and J. I. Zink, Comments Inorg. Chem., 1992, 13, 177–220 CrossRef CAS.
- (a) P. Mondal, D. Opalka, L. V. Poluyanov and W. Domcke, J. Chem. Phys., 2012, 136, 084308 CrossRef; (b) P. Mondal, D. Opalka, L. V. Poluyanov and W. Domcke, Chem. Phys., 2011, 387, 56–65 CrossRef CAS.
- G. Capano, T. Penfold, U. Röthlisberger and I. Tavernelli, Chimia, 2014, 227–230 CrossRef CAS.
- S. Bai, R. Mansour, L. Stojanović, J. M. Toldo and M. Barbatti, J. Mol. Model., 2020, 26, 107 CrossRef CAS.
- A. Hazra and M. Nooijen, Phys. Chem. Chem. Phys., 2005, 7, 1759–1771 RSC.
- M. Radoń and G. Drabik, J. Chem. Theory Comput., 2018, 14, 4010–4027 CrossRef.
- C. Daul, H. Güdel and J. Weber, J. Chem. Phys., 1993, 98, 4023–4029 CrossRef CAS.
- J. Wu, C. Sousa and C. de Graaf, Magnetochemistry, 2019, 5, 49 CrossRef CAS.
- (a) M. L. Ceccarani, P. Sassi and R. S. Cataliotti, J. Chem. Soc., Faraday Trans., 1994, 90, 1397–1403 RSC; (b) S. Scuppa, L. Orian, D. Dini, S. Santi and M. Meneghetti, J. Phys. Chem. A, 2009, 113, 9286–9294 CrossRef CAS.
- D. Nielson, M. Farmer and H. Eyring, J. Phys. Chem., 1976, 80, 717–721 CrossRef CAS.
- (a) D. R. Scott and R. S. Becker, J. Chem. Phys., 1961, 35, 516–531 CrossRef CAS; (b) J. J. Smith and B. Meyer, J. Chem. Phys., 1968, 48, 5436–5439 CrossRef CAS.
- A. Müller-Goldegg and J. Voitländer, Z. Naturforsch., A: Astrophys., Phys. Phys. Chem., 1968, 23, 1236 Search PubMed.
- (a) M. Kikuchi, K. Kikuchi and H. Kokubun, Bull. Chem. Soc. Jpn., 1974, 47, 1331–1333 CrossRef CAS; (b) W. G. Herkstroeter, J. Am. Chem. Soc., 1975, 97, 4161–4167 CrossRef CAS; (c) A. Farmilo and F. Wilkinson, Chem. Phys. Lett., 1975, 34, 575–580 CrossRef CAS; (d) V. Balzani, F. Bolletta and F. Scandola, J. Am. Chem. Soc., 1980, 102, 2152–2163 CrossRef CAS.
- M.-M. Rohmer, A. Veillard and M. H. Wood, Chem. Phys. Lett., 1974, 29, 466–468 CrossRef CAS.
- A. Nandy, D. B. K. Chu, D. R. Harper, C. Duan, N. Arunachalam, Y. Cytter and H. J. Kulik, Phys. Chem. Chem. Phys., 2020, 22, 19326–19341 RSC.
- F. Neese, D. Liakos and S. Ye, JBIC, J. Biol. Inorg. Chem., 2011, 16, 821–829 CrossRef CAS.
- (a) J. N. Harvey, JBIC, J. Biol. Inorg. Chem., 2011, 16, 831–839 CrossRef CAS; (b) J. N. Harvey, in General Discussion, Faraday Discuss, 2003, 124, 145–153 RSC.
- M. K. Sprague and K. K. Irikura, Theor. Chem. Acc., 2014, 133, 1544 Search PubMed.
- X. Xu, W. Zhang, M. Tang and D. G. Truhlar, J. Chem. Theory Comput., 2015, 11, 2036–2052 CrossRef CAS.
- S. Vancoillie, H. Zhao, M. Radoń and K. Pierloot, J. Chem. Theory Comput., 2010, 6, 576–582 CrossRef CAS.
- Q. M. Phung and K. Pierloot, J. Chem. Theory Comput., 2019, 15, 3033–3043 CrossRef CAS.
- M. Roemelt and D. A. Pantazis, Adv. Theory Simul., 2019, 2, 1800201 CrossRef.
- G. Li Manni, D. Kats, D. P. Tew and A. Alavi, J. Chem. Theory Comput., 2019, 15, 1492–1497 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- O. Siig and K. P. Kepp, J. Phys. Chem. A, 2018, 122, 4208–4217 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04727a |
| ‡ The equilibrium bond distance re is derived from the GED averaged distance ra based on the equation re = ra + l2/ra − 3al2/2 (note that this equation has typographic error in ref. 35b), where l is the root-mean-square amplitude of vibration (available from the GED data) and a is the anharmonicity constant. We assume a = 0.025 pm−1 for the C–H bond and a = 0.02 pm−1 for C–C, Fe–C, and Ru–C bonds (ref. 35b and references therein). As an example, for the Fe–C distance in FeCp2 we have ra = 2.064 and re = 2.054 Å; for the C–C bond distance ra = 1.440 and re = 1.435 Å; the resulting change of the Fe–C5 distance is from 1.661 to 1.652 Å, i.e., by approximately 1 pm. |
| § Note that the S0 → S1 and S0 → S2 excitations of metallocenes are so close in energy that they are normally observed as a single broad band (ref. 28) and can be resolved into separate bands only at cryogenic temperatures (ref. 27). Other than that, there is no significant discrepancy concerning the singlet–singlet excitation energies given in different papers. |
| ¶ Analogous general remark could be made with respect to other mentioned experimental studies, where ligand-field theory calculations might be guiding the experimentalists to look in their spectra for features whose existence was not evident. |
| || For the most similar case of CoIIIaq6 (also d6 configuration), the splittings between open-shell excited states 3T2g and 1T1g or 1T2g at the CASPT2 and NEVPT2 level all agree up to 0.07 eV with the experimental values, even though the discrepancies in the excitation energies with respect to the closed-shell ground state are much larger, up to 0.56 eV. Moreover, the CASPT2 and NEVPT2 results agree with the experiment to within 0.2 eV for the 6A1g → 4Eg,4Ag spin-flip excitations of FeIII and MnIIaq6, and to within 0.07 eV for the 4A2g → 2Eg spin-flip excitation of CrIIIaq6. |
| ** We would like to note that our measured data are particularly rich in this region and none of the elementary spectra recorded by us show any sign of shoulder, except those where measured absorbance was too high to be treated as reliable (the “band flattening” artifact, i.e. almost 100% of light being absorbed). Possible failure to avoid such problems in the earlier studies might result in occurrence of an artificial shoulder. In particular, the transmittance spectrum shown in Fig. 1 of ref. 28a looks like a result of a single measurement in the spectral range of 12.5–20 103 cm−1 on which the ε and hence also the absorbance vary by a factor of ∼400 from left to right (cf.Fig. 9b and c). From our experience, it is not possible to reliably measure the spectrum with such rapidly varying absorbance in a single measurement, even on a modern two-beam spectrophotometer. Thus, artifacts are expected to appear in a spectrum like Fig. 1 of ref. 28a due to the absorbance being too high (in the higher energy part) and/or too low (in the lower energy part). Alternatively, it is possible that the shoulder was previously observed due to impurities which are not present in our samples. This is, however, less likely, because we also investigated the spectra of less pure (reagent-grade) ferrocene, and they are essentially identical in this region. |
| †† Consideration of the wave function for the second (orthogonal) component of the T1 state would lead to identical results and conclusions, but in a differently oriented coordinate system. |
| This journal is © the Owner Societies 2021 |