Open Access Article
Open Access ArticleOrigin of pressure-induced band gap tuning in tin halide perovskites†
Mauro
Coduri
 a,
Thomas B.
Shiell
b,
Timothy A.
Strobel
a,
Thomas B.
Shiell
b,
Timothy A.
Strobel
 b,
Arup
Mahata
b,
Arup
Mahata
 *cd,
Federico
Cova
e,
Edoardo
Mosconi
d,
Filippo
De Angelis
*cdfg and
Lorenzo
Malavasi
*cd,
Federico
Cova
e,
Edoardo
Mosconi
d,
Filippo
De Angelis
*cdfg and
Lorenzo
Malavasi
 *a
*a
aDepartment of Chemistry and INSTM, Viale Taramelli 16, 27100, Pavia, Italy. E-mail: lorenzo.malavasi@unipv.it
bEarth and Planets Laboratory, Carnegie Institution for Science, Washington, DC 20015, USA
cCompuNet, Istituto Italiano di Tecnologia, Via Morego 30, 16163 Genova, Italy. E-mail: arup.mahata@iit.it; filippo@thch.unipg.it
dComputational Laboratory for Hybrid/Organic Photovoltaics (CLHYO), CNR-SCITEC, via Elce di Sotto 8, I-06123 Perugia, Italy
eESRF – The European Synchrotron, 81, Avenue des Martyrs, 38000, Grenoble, France
fDepartment of Chemistry, Biology and Biotechnology, University of Perugia, Via Elce di Sotto 8, 06123 Perugia, Italy
gChemistry Department, College of Science, King Saud University, Riyadh, Saudi Arabia
First published on 6th October 2020
Abstract
Structural and optical high-pressure study of FASnBr3 (FA = formamidinium) revealed a cubic to orthorhombic phase transition near 1.4 GPa accompanied by a huge band gap red-shift from 2.4 to 1.6 eV, which is followed by a blue-shift of ∼0.2 eV upon further pressure increase. DFT calculations indicate that the variation in band gap is related to changes in Sn–Br bond length alternation, with an equalization of such difference predicted at high pressure. Extending the calculations to analogous lead-free systems provides a unifying mechanistic picture of pressure-induced band gap tuning in tin halide perovskites, which is correlated to the variation of specific structural parameters. These results represent a solid guide to predict and modulate the pressure-response of metal halide perovskites based on the knowledge of their structural properties at ambient pressure.
Introduction
Metal halide perovskites (MHPs) possess unique electronic and optical properties and have been the subject of tremendous experimental and computational efforts focused on understanding the mechanisms that dominate their functionalities. This huge work had unveiled relevant correlations between phase composition and structural features affecting optical properties and charge carrier dynamics.1,2 Despite these efforts, challenges still exist in the fundamental understanding of structure–property relationships that govern the wide tunability of MHPs. Due to their soft lattice, MHPs are highly sensitive to mechanical deformation, resulting in changes of their electronic structure and physical properties. In this regard, in situ high-pressure (HP) research has proven to be a powerful tool with great potential for the engineering of MHPs.3–73D perovskites have been the subject of intense HP study with strong focus on lead-based systems, namely MAPbX3 (MA = methylammonium) compounds (where X = Cl, Br and I), as well as FAPbI3, FAPbBr3 (FA = formamidinium) and CsPbBr3.8–18 Numerous experimental and computational results have revealed the existence of some common pressure-induced features. These features include band gap (Eg) red-shift upon initial compression, which is followed by a blue-shift that correlates to the occurrence of a structural phase transition to a more distorted crystal structure.3,4 Concerning the microscopic mechanisms proposed for lead halide perovskites, it appears that the first red-shift is typically correlated to a shortening of the Pb–X bond length, resulting in increased orbital coupling. The subsequent blue-shift is related to local deformations in the crystal structure, connected with the bending of the Pb–X–Pb bond angles, which tend to reduce orbital coupling.7 Moreover, all of the lead halide perovskites investigated under pressure have shown that significant amorphization of the lattice occurs within the blue-shift regime of the band gap.3,4 However, systematic studies that couple HP experiments with computational modelling tools are still scarce, and additional insights into the mechanistic features of HP effects are still required.
We recently conducted HP investigations of Sn-based systems, which have been much less extensively investigated with respect to their lead counterpart, despite the huge interest toward lead-free perovskites.19,20 In particular, we reported the structural and optical properties of MASnBr3 and CsSnBr3, where large red shifts of 0.4 eV for MASnBr3 and 0.2 eV for CsSnBr3 were observed by ∼1.5 GPa, followed by large blue shifts of 0.3 and 0.5 eV, respectively.20 Using density functional theory (DFT) calculations, it was then possible to determine the underlying mechanism affecting the band gap evolution with pressure, the key role of metal–halide bond lengths for CsSnBr3 and of cation orientation for MASnBr3. These results highlight the impact of different A-cations on the pressure response.20 Triggered by these results, clearly correlating the observed trends to local lattice properties, we extended the HP study to FASnBr3 by virtue of its peculiar structural features, and also to confirm the mechanistic picture we obtained on MASnBr3 and CsSnBr3.20,21 Previously, we reported that FASnBr3 is characterized by a distorted structure with partly uncoupled SnBr3 units, and that its 3D structure originates from a dynamical averaging of quasi-0D structures.21 Such structural characteristics make FASnBr3 a useful system to probe the extent of pressure effects on the electronic structure and to correlate these effects to local metal–halide bond distances.
In view of the above considerations, in this paper we present the results of a high-pressure structural and optical properties investigation of FASnBr3. The high-pressure experiments are carried out using diamond anvil cells (DAC), and are readily comparable with our previous results on MASnBr3 and CsSnBr3. This systematic experimental and computational work provides the first unifying mechanistic picture of pressure induced effects on lead-free MHPs.
Results and discussion
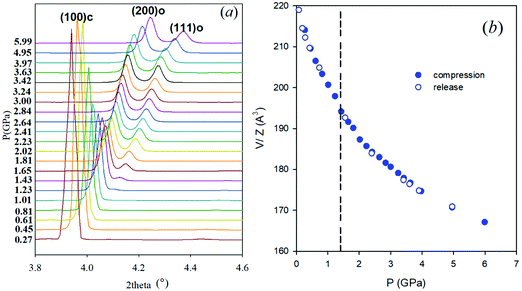
Synchrotron X-ray powder diffraction data were collected in a DAC using helium as pressure transmitting medium up to 6 GPa. Fig. 1a reports the evolution with pressure of the cubic (100) reflection. Full patterns are reported in the ESI,† Fig. S1. FASnBr3 is cubic (space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) at ambient conditions as previously reported, and this structure is retained up to ∼1.4 GPa. The pressure increase induces splitting of some of the main reflections (see for example the peaks around 4° in Fig. 1a), consistent with the formation of an orthorhombic phase, with metric
m) at ambient conditions as previously reported, and this structure is retained up to ∼1.4 GPa. The pressure increase induces splitting of some of the main reflections (see for example the peaks around 4° in Fig. 1a), consistent with the formation of an orthorhombic phase, with metric 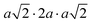 , and space group Pnma. Examples of refinements are reported in Fig. S2 (ESI†). No further phase transition nor evidence of amorphization was observed with pressure.
, and space group Pnma. Examples of refinements are reported in Fig. S2 (ESI†). No further phase transition nor evidence of amorphization was observed with pressure.
Surprisingly, no temperature or pressure resolved studies have been performed so far on this compound. It follows that comparisons are available only with analogous compounds replacing one of the elements involved, e.g. MA for FA, Sn with Pb, or Br with I.
The same Pnma orthorhombic phase was observed in FAPbBr3 at pressures above 2 GPa and cooling below 100 K.18,22 Similarly, Schueller et al. showed that the orthorhombic Pnma phase is stable at low temperature for FASnI3.22 However, both studies reported intermediate phases (tetragonal P4/mbm at low temperature, and cubic Immm at high pressure), which are not observed here. FASnBr3 exhibits similar behaviour to MASnBr3, though the phase transformation involves a less distorted high-pressure phase. Indeed, the orthorhombic phase of MASnBr3 shows a doubling of all cell axis to produce the metric 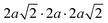 . Other than that, the structural high-pressure behaviour of FA and MA compounds is very similar.20 Another peculiarity of the ASnBr3 (A = MA, FA) system is the important splitting of the a and c axes, leading to a much more pronounced orthorhombic distortion than in the Pb and I counterparts, where the distortion is generally within 0.1 Å.18,22
. Other than that, the structural high-pressure behaviour of FA and MA compounds is very similar.20 Another peculiarity of the ASnBr3 (A = MA, FA) system is the important splitting of the a and c axes, leading to a much more pronounced orthorhombic distortion than in the Pb and I counterparts, where the distortion is generally within 0.1 Å.18,22
The unit cell volume trend was determined from XRD pattern refinements, both during compression and pressure release, as shown in Fig. 1b. The phase transition process is fully reversible and no discontinuity in unit cell volume was observed. Details on data refinement together with lattice parameters and volume as a function of P are reported in the ESI,† Fig. S3 and S4. No evidence of amorphization was found in the XRD patterns, in analogy with other Sn-based MHPs, differing from the behavior of all the lead-containing phases.3,4,20 After pressure release, the XRD pattern of FASnBr3 is cubic and clearly crystalline (see Fig. S5 and S6, ESI† for raw data and refinement).
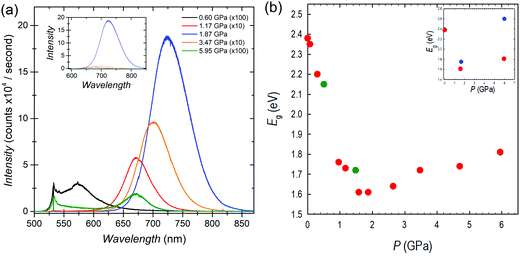
The optical properties of FASnBr3 under pressure were measured using both photoluminescence (PL) and optical absorption spectroscopy. The high-pressure PL spectra and the band gap extracted from absorption spectroscopy for FASnBr3 are reported in Fig. 2a and b, respectively. Selected optical absorption spectra are reported in Fig. S7–S9 (ESI†).
No detectable PL emission was observed at room temperature from ambient pressure up to about 0.3 GPa, even using a 405 nm laser for excitation. This is not unusual since many tin-based MHPs have very low emissions at ambient conditions due to the possible presence of defects. Above this pressure, a weak PL signal becomes evident in the spectra. With further pressure increase, the PL intensity increases exponentially, and as in other systems under pressure, the PL peak shifts to the red.20 Above 1.9 GPa, the PL trend reverses and a blue-shift coupled to a rapid decrease in PL intensity is observed. This pressure range of PL-trend change is consistent with the interval where the cubic to orthorhombic phase transition is observed. Above the transition pressure, the PL intensity diminishes significantly and is no longer detectable between 6–11 GPa. All PL trends are reversible with decreasing pressure.
The optical band gap extracted from absorption measurements confirms the ambient pressure value of about 2.4 eV for FASnBr3.21 With increasing pressure there is continuous red-shift of the band gap, which drops to ∼1.6 eV at 1.87 GPa. Above this pressure, the trend reverses, as observed in the PL, and the optical gap increases with pressure. These results are consistent with the XRD data indicating a phase transition in this pressure range, i.e. between 1.58 and 1.87 GPa, where the maximum wavelength of the absorption should be present. Above 1.87 GPa, the Eg continues to increase until 6.5–7.4 GPa, with band gap decreasing to approximately ∼2.2 eV. Finally, absorption data collected under decompression confirm the observed trends are reversible with slight hysteresis (see ESI†).
As shown in Fig. 2b, the overall variation of Eg (ΔEg) from ambient pressure to the phase transition is close to 0.8 eV, passing from about 2.4 to 1.6 eV. Such a high jump in the band gap as a function of pressure has never been observed in any 3D metal halide perovskite under pressure. In Pb-based MHPs, the first red-shift, coupled to the structural phase transitions, is generally of the order of 0.03 eV, while we demonstrated that passing to Sn-containing perovskites such ΔEg value tends to increase to about ∼0.2 eV and ∼0.4 eV for CsSnBr3 and MASnBr3, respectively.20 In both these last cases, the lowest value of the Eg was around 1.6 eV and occurred within about 2 GPa and in correspondence of the first structural phase transition. Therefore, the present data shows a record red-shift achieved in less than 2 GPa for FASnBr3, but even more important, a very interesting evidence is that in these three systems, irrespective to the value of the ambient pressure band gap, the lowest value reached during compression is always around 1.6 eV (before band gap reversing or to blue-shift).20
In order to gain further insights into this peculiar behavior of FASnBr3, and to provide a unifying mechanistic picture correlating the Eg variation across the three systems (i.e., including CsSnBr3 and MASnBr3), we investigated the band gap evolution of FASnBr3 with pressure using density functional theory (DFT) calculations.
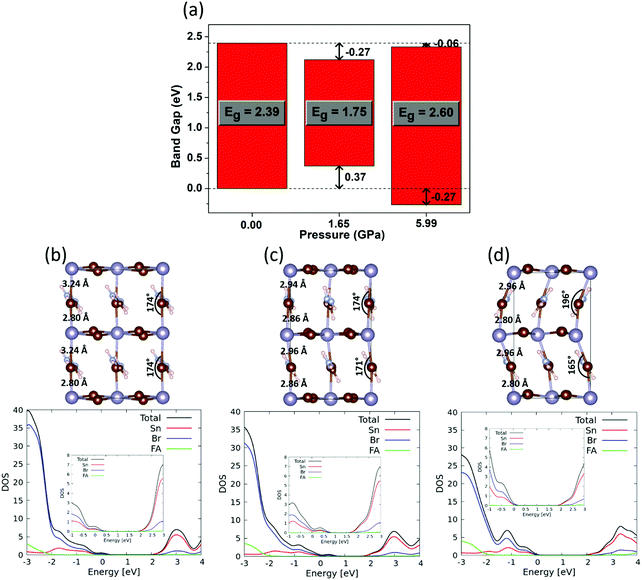
We started by optimizing the structures of FASnBr3 at ambient pressure and at the pressure with the lowest and the highest band gap, i.e. 0, 1.65 and 5.99 GPa. For the ambient pressure, we have considered tetragonal lattice by rotating the experimental cubic lattice parameters. The optimized tetragonal and cubic structures show similar structural parameters (see Fig. S10 in the ESI†). Such structural adaptation has been done for better comparison of structural properties (bond lengths, bond angles and organic cation's rotation) at ambient pressure with that of the high pressure orthorhombic structure. The band gap evolution matches nicely with the experimental trends (see inset of Fig. 2b), showing a substantial band gap narrowing with increasing pressure followed by a band gap opening with further pressure increase, in close agreement with optical measurements. To understand the shifting of band edges with pressure, we have aligned the density of states (DOS) as shown in Fig. 3a and in the bottom panel of Fig. 3b–d.
Optimized structure of FASnBr3 at ambient pressure (Fig. 3b) shows that the Sn–Br bond distances alternate between short and long, at 2.80 and 3.24 Å, respectively. As mentioned above, we previously described that FASnBr3 possesses a dynamical average of a short-long Sn–Br bond distance at shorter time scale and behaves as a quasi 0D perovskite, resulting in a high band gap of 2.39 eV.21 Since the band gap is the result of the metal halide connectivity, a more equalized pattern of Sn–Br bond distances, i.e. a more continuous 3D-connected perovskite, should result in a lower the band gap compared to a partly decoupled network of SnBr3 units. With increasing pressure (Fig. 3c), the alternating short-long nature of Sn–Br bond length tends to equalize (2.86 vs. 2.94 Å) and the overlap between Sn and Br increases, resulting in a band gap reduction to 1.75 eV with a concomitant destabilization of the valence band (VB). It is interesting to notice from Table 1 that lowest band gap under moderate pressure is almost identical for FASnBr3 (1.61 eV), MASnBr3 (1.62 eV) and CsSnBr3 (1.59 eV), however, the magnitude of the band gap lowering (ΔEg) from ambient pressure gradually decreases from FASnBr3 to CsSnBr3. Since the Sn–Br bond distances are almost equivalent for FASnBr3, MASnBr3 and CsSnBr3 at moderate pressure, the band gap values are similar for all three cases. However, the highest band gap variation from ambient pressure (∼0.8 eV) is found for FASnBr3 due to its greatest variation in short-long Sn–Br distances (0.45 Å). Such short-long bond distance variation decreases moving from MASnBr3 (0.25 Å) to CsSnBr3 (0.01Å), resulting in smaller ΔEg values for MASnBr3 (∼0.4 eV) and CsSnBr3 (∼0.2 eV) under pressure, as confirmed experimentally.20 Therefore, ∼1.6 eV represents a lower bound for the band gap of Sn-based cubic perovskites under pressure, irrespective of the organic or inorganic cation.
| Pressure domain | Systems | Sn–Br bond distance (Å) | Exp. band gap (eV) |
|---|---|---|---|
| Ambient | FASnBr3 | 2.80, 3.24 | 2.39 |
| MASnBr3 | 2.83, 3.08 | 2.00 | |
| CsSnBr3 | 2.90, 2.91 | 1.79 | |
| Moderate (0.9–1.6 GPa) | FASnBr3 | 2.86, 2.94 | 1.61 |
| MASnBr3 | 2.85, 2.95 | 1.62 | |
| CsSnBr3 | 2.87, 2.87 | 1.59 | |
With a further increase of pressure, one would expect that all Sn–Br lengths in FASnBr3 will eventually equalize, leading to a further reduction of band gap. This trend, however, is different from experimental observations. High pressure induces a significant alteration of the FA cation orientation, which in turn causes tilting of the metal–halide bond (Fig. 3d) along with the reappearance of alternating short-long Sn–Br bond lengths (2.80 and 2.96 Å). As a result, the metal halide orbital mixing is reduced, and the VB shifts toward lower energy by 0.64 eV with a concomitant increase of Eg. Notably, the higher absolute band gap in DFT compared with the experimental value at 5.99 GPa (see inset of Fig. 2b) is due to the presence of substantial structural flexibility of this kind of material. For such a distorted orthorhombic geometry, there could be a sizeable difference in the instantaneous structure from the time scale and experimental XRD structures (i.e., thermal averaged structure). Moreover, the dynamic disorder of the organic cation strongly influences the inorganic lattice and has important consequences on the electronic properties.23 Since the motivation of this work is to investigate the band gap evolution and its origin under pressure, the matching of the absolute values of the band gap with the experiment is not worth considering.
Therefore, in the moderate pressure domain, bond length shortening and the equalization of non-equivalent Sn–Br bond lengths, play the key roles in band gap reduction. At higher pressure, octahedral tilting and cation displacement start to play the central role leading to band gap increase upon further compression. While we previously described the relative weights of the two mechanisms in driving the red- and blue-shifts as a function of pressure, the overall picture drawn from these new data nicely and reliably correlates the ΔEg changes of the red-shift to the relative bond length changes with pressure, and provide a unifying mechanistic picture for understanding pressure-induced phenomena in tin-halide perovskites.20
Conclusions
In this study we report the first structural and optical high-pressure experiments on FASnBr3 halide perovskite coupled with DFT calculations. Measurements up to ∼6 GPa in DACs under hydrostatic conditions reveal an impressive 0.8 eV red-shift of the band gap from ambient pressure to the cubic to orthorhombic phase transition (i.e., within ∼1.8 GPa). This trend is followed by a blue-shift of the band gap up to 6 GPa. While analogous trends have been observed in some related systems, the overall band gap changes in those cases are about one order of magnitude lower.3,4 The mechanism of this unprecedented change in the optical properties of FASnBr3 halide perovskite is explained by local structural changes by means of DFT calculations, which also provides a comparison with MASnBr3 and CsSnBr3. These last two lead-free MHPs show similar pressure-induced variations with a common value of about 1.6 eV for the lowest Eg reported, corresponding to the first structural phase transition. However, the extent of band gap tuning from ambient conditions to the common value of 1.6 eV, changes for the three systems and scales with the magnitude of short-long Sn–Br bond distances, as determined by computational modelling. At the lowest common band gap of about 1.6 eV, the Sn–Br short-long bond distances are almost equivalent for FASnBr3, MASnBr3 and CsSnBr3, and the variation in these distances from the ambient pressure values is what governs the magnitude band gap reduction.The present experimental and computational data allow us to define a unifying mechanistic picture that governs the optical properties in a series of lead-free MHPs under pressure, and reveal a common lower boundary for the band gap under pressure, irrespective of the organic or inorganic cation. Such results enable predictions of which MHPs are most sensitive to pressure-induced tuning of optical properties through the knowledge of ambient-pressure structural features. We believe that the approach reported in this paper may become a guide to further experimental and modelling work in high-pressure research on MHPs.
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
The authors acknowledge the ESRF for provision of beam T. A. S. acknowledges support from the National Science Foundation, Division of Material Research (NSF-DMR) under award number 1809756. A. M., E. M. and F. D. A. acknowledge support from the European 531 Union's Horizon 2020 research and innovation programme under Grant Agreement No. 764047 of the Espresso project. F. D. A. thanks the from the Ministero Istruzione dell’Università e della Ricerca (MIUR) and the University of Perugia through the program “Dipartimenti di Eccellenza 2018–2022” (grant AMIS); and Distinguished Scientist Fellowship Program (DSFP) of King Saud University, Riyadh, Saudi Arabia.References
- J. Huang, Y. Yuan, Y. Shao and Y. Yan, Nat. Rev. Mater., 2017, 2, 17042 CrossRef CAS.
- L. M. Herz, Annu. Rev. Phys. Chem., 2016, 67, 65–89 CrossRef CAS.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 2496–2506 CrossRef.
- P. Postorino and L. Malavasi, J. Phys. Chem. Lett., 2017, 8, 2613–2622 CrossRef CAS.
- M. Li, T. Liu, Y. Wang, W. Yang and X. Lu, Matter Radiat. Extremes, 2020, 5, 018201 CrossRef CAS.
- A. Jaffe, Y. Lin and H. I. Karunadasa, ACS Energy Lett., 2017, 2, 1549–1555 CrossRef CAS.
- X. Lu, W. Yang, Q. Jia and H. Xu, Chem. Sci., 2017, 8, 6764–6776 RSC.
- K. Wang, R. Liu, Y. Qiao, J. Cui, B. Song, B. Liu and B. Zou, 2015, arXiv:1509.03717.
- A. Jaffe, Y. Lin, C. M. Beavers, J. Voss and W. L. Mao, ACS Cent. Sci., 2016, 2, 201–209 CrossRef CAS.
- S. Jiang, Y. Fang, R. Li, H. Xiao, J. Crowley, C. Wang, T. J. White, W. A. Goddard, Z. Wang and T. Baikie, Angew. Chem., Int. Ed., 2016, 55, 6540–6544 CrossRef CAS.
- F. Capitani, C. Marini, S. Caramazza, P. Postorino, G. Garbarino, M. Hanfland, A. Pisanu, P. Quadrelli and L. Malavasi, J. Appl. Phys., 2016, 119, 185901 CrossRef.
- M. Szafranski and A. Katrusiak, J. Phys. Chem. Lett., 2016, 7, 3458–3466 CrossRef CAS.
- I. P. Swainson, M. G. Tucker, D. J. Wilson, B. Winkler and V. Milman, Chem. Mater., 2007, 19, 2401–2405 CrossRef CAS.
- Y. Wang, X. Lu, W. Yang, T. Wen, L. Yang, X. Ren, L. Wang, Z. Lin and Y. Zhao, J. Am. Chem. Soc., 2015, 137, 11144–11149 CrossRef CAS.
- L. Wang, K. Wang, G. Xiao, Q. Zeng and B. Zou, J. Phys. Chem. Lett., 2016, 7, 5273–5279 CrossRef CAS.
- P. Wang, J. Guan, T. K. Galeschuk, Y. Yao, C. F. He, S. Jiang, S. Zhang, Y. Liu, M. Jin, C. Kin and Y. Song, J. Phys. Chem. Lett., 2017, 8, 2119–2125 CrossRef CAS.
- L. Zhang, Q. Zeng and K. Wang, J. Phys. Chem. Lett., 2017, 8, 3752–3758 CrossRef CAS.
- L. Wang, K. Wang and B. Zou, J. Phys. Chem. Lett., 2016, 7, 2556–2562 CrossRef CAS.
- W. Ke and M. G. Kanatzidis, Nat. Commun., 2019, 10, 965 CrossRef.
- M. Coduri, T. A. Strobel, M. Szafranski, A. Katrusiak, A. Mahata, F. Cova, S. Bonomi, E. Mosconi, F. De Angelis and L. Malavasi, J. Phys. Chem. Lett., 2019, 10, 7398–7405 CrossRef CAS.
- A. Pisanu, A. Mahata, E. Mosconi, M. Patrini, P. Quadrelli, C. Milanese, F. De Angelis and L. Malavasi, ACS Energy Lett., 2018, 3, 1353–1359 CrossRef CAS.
- E. C. Schueller, G. Laurita, D. H. Fabini, C. C. Stoumpos, M. G. Kanatzidis and R. Seshadri, Inorg. Chem., 2018, 57, 695–701 CrossRef CAS.
- C. Quarti, E. Mosconi and F. De Angelis, Phys. Chem. Chem. Phys., 2015, 17, 9394 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental and computational details. See DOI: 10.1039/d0ma00731e |
| This journal is © The Royal Society of Chemistry 2020 |