Open Access Article
Open Access ArticleA kinetic model for redox-active film based biophotoelectrodes†
D.
Buesen
 ,
T.
Hoefer
,
T.
Hoefer
 ,
H.
Zhang
,
H.
Zhang
 and
N.
Plumeré
and
N.
Plumeré
 *
*
Center for Electrochemical Sciences (CES), Faculty of Chemistry and Biochemistry, Ruhr University Bochum, Universitätsstr. 150, D-44780 Bochum, Germany. E-mail: nicolas.plumere@rub.de
First published on 30th January 2019
Abstract
Redox-active films are advantageous matrices for the immobilization of photosynthetic proteins, due to their ability to mediate electron transfer as well as to achieve high catalyst loading on an electrode for efficient generation of electricity or solar fuels. A general challenge arises from various charge recombination pathways along the light-induced electron transfer chain from the electrode to the charge carriers for electricity production or to the final electron acceptors for solar fuel formation. Experimental methods based on current measurement or product quantification are often unable to discern between the contributions from the photocatalytic process and the detrimental effect of the short-circuiting reactions. Here we report on a general electrochemical model of the reaction–diffusion processes to identify and quantify the “bottlenecks” present in the fuel or current generation. The model is able to predict photocurrent–time curves including deconvolution of the recombination contributions, and to visualize the corresponding time dependent concentration profiles of the product. Dimensionless groups are developed for straightforward identification of the limiting processes. The importance of the model for quantitative understanding of biophotoelectrochemical processes is highlighted with an example of simulation results predicting the effect of the diffusion coefficient of the charge carrier on photocurrent generation for different charge recombination kinetics.
1 Introduction
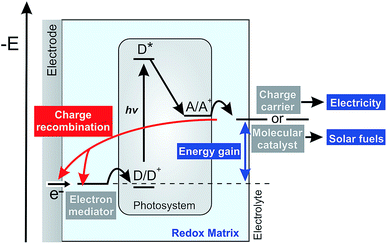
Photosynthetic proteins have evolved toward having near perfect light harvesting and charge separation properties, which makes them potentially valuable as photoactive components in devices for conversion of sunlight into electricity or solar fuels.1–3 A variety of biophotocathodes has been reported which typically follow the same general design. A natural or artificial electron mediator is used to shuttle electrons between the electrodes and the donor side (D/D+) of the photosynthetic protein. An electron acceptor then recovers the electron at the acceptor site (A/A+) of the protein which can subsequently act either (i) as a charge carrier that diffuses to the collector electrode to close the electrical circuit and generate electricity or (ii) as a redox catalyst that generates chemical energy in the form of a solar fuel in a follow up coupled reaction (Fig. 1).In both cases, the overall energy conversion efficiency is closely related to the rates of electron transport defining the photocurrent and to the redox potential of the various components defining the light-induced potential difference within the electrochemical half-cell and thus the potential energy gain. From a practical perspective, it is advantageous to immobilize the electron mediator and the photosynthetic proteins within thin redox films on the electrode surface to allow for efficient electrical wiring and for high catalyst loading and thus obtain high photocurrent generation.4,5
However, besides the photocatalytic process, possible competitive pathways may have a detrimental impact on the performance of such biophotocathodes. One of the general challenges in photoelectrochemical systems is related to charge recombination processes.6 Light-induced charge separation at the photosystem produces a high energy electron that is ideally transferred to the charge carriers or to the redox catalyst with minimal energy loss. However, the large driving force imposed by the light-induced potential difference favors recombination of these reduced electron acceptors with oxidized components of the redox matrix or with the electrode surface (Fig. 1, red pathway).7,8 These short-circuiting processes lower the photocurrents and hence the overall power output or solar fuel generation of the devices. Therefore, in-depth understanding of the processes involved in photocurrent generation, including such short circuit pathways, is an essential pre-requisite for the rational design and optimization of biophotoelectrochemical systems.
The short-circuiting processes are often invisible to electroanalytical methods since their contribution do not provide any net photocurrent. Therefore, it is paramount to establish theoretical models for biophotoelectrochemical systems which consider both the processes generating the photocurrent and the processes competing with photocurrent generation. The ability to simulate and deconvolute the various contributions, including photocathodic processes and recombination processes, would enable the pinpointing of bottlenecks in the power generation process. Ideally, such a model would not only include simulations for the entire observed signal, but would also contain the development of dimensionless groups which are useful for summarizing the rates of the major processes in the system, and in particular, predict how a given parameter may impact photocurrents and thus how it could be modulated to achieve energy conversion enhancement.
Several models have been previously developed for biophotoelectrochemical systems, which considered photosynthetic proteins9–12 or whole photosynthetic cells immobilized on electrodes or in solution.13,14 In these previous reports, electronic communication between the photosystems and the electrode were modelled based on freely diffusing electron mediators. Here, we establish a model for biophotoelectrodes with both the photosystems and the electron mediators confined in redox films on the electrode surface based on a reaction scheme that is generally applicable and relevant for multiple experimental cases.1,4,15,16 In particular, we consider both an outer-sphere electron transfer between the photosystem and the electron acceptor (which is typically relevant for photosystem 1 based biophotocathodes) as well as photoenzymatic reactions (which are typically relevant for biophotocathodes based on purple bacterial reaction centers). Moreover, we include the possibility for either electron transfer to a charge carrier that subsequently diffuses to the bulk of the solution or for electron transfer to a redox catalyst followed by subsequent catalytic reduction of a final electron acceptor generating solar fuels. The model is built upon previous models for bioelectrochemical systems17,18 in which we integrate the effect of light induction of electron transfer and the associated charge recombination processes to predict the time dependent photocurrent generation and the associated concentration profile. Dimensionless groups are developed for understanding the limiting processes. We highlight the usefulness of this modeling tool with an example of simulation results predicting the effect of the diffusion coefficient of the charge carrier on photocurrent generation with different charge recombination kinetics.
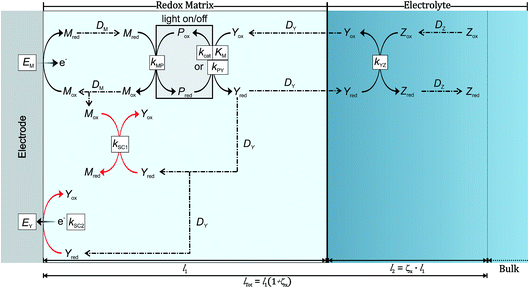
2 System schematic and reactions
The process generating the photocurrent (Fig. 2, in black) includes the redox mediator Mred|Mox and the photosystem Pred|Pox which are immobilized in the redox film, as well as the electron acceptors Yox and Zox and their respective reduced forms Yred and Zred which are freely diffusing within the film and in the bulk of the solution. The charge hopping between the redox mediators is assumed to follow the rules of diffusion and is described by an apparent diffusion coefficient DM. The partition of both substrate–product pairs Yred|Yox and Zred|Zox is neglected and their diffusion coefficients (DY and DZ, respectively) remain unchanged whether they are in or out of the redox matrix. Furthermore, we assume a steady state between the oxidized and reduced form of the photosystems while catalysis is taking place. The model considers only one electrochemical half-cell in which a constant potential is applied at the electrode. The heterogeneous electron transfer kinetics of Mred|Mox are modeled according to Butler–Volmer kinetics. Mred and Pox react in a bimolecular reaction with a rate constant kMP in single one-electron steps. This reaction is followed by a light-induced reaction between the reduced form of the photosystem with Yox, which is either modeled according to Michaelis–Menten kinetics (kcat and KM) or by a simple bimolecular reaction (kPY). This reaction leads to Yred which may serve as a charge carrier that diffuses in the bulk of the solution or as a redox catalyst that reduces another electron acceptor Zox in a subsequent reaction cascade leading to Zred. In the latter case Yred reacts in a bimolecular reaction with Zox with a kinetic constant kYZ. Because both Yred and Zox are free to diffuse in and out of the film this reaction can take place either in the redox matrix or in the surrounding electrolyte solution. The produced solar fuel Zred can then diffuse into the bulk of the system.In order to consider the possibility for charge recombination we consider two short-circuiting reactions involving Yred (Fig. 2, in red). The redox potential of Yred|Yox (E0Y) is more negative than the redox potential of Mred|Mox (E0M). Therefore, the potential difference favors the reduction of Mox by Yred. We model this first short-circuiting pathway (SC1) as a bimolecular reaction with a kinetic constant kSC1. The second possible short-circuiting pathway (SC2) takes place at the electrode and leads to the reoxidation of Yred. The heterogeneous (multi-) electron transfer is also modeled according to Butler–Volmer kinetics with a heterogeneous rate constant k0SC2 and an apparent electron transfer coefficient αY.
The reaction stoichiometry between Yox and Pred is fixed as one-to-one, but the number of electrons transferred in the reaction (νY) is variable. Additionally, the number of electrons that are transferred from Pox to Mred (νM) is flexible depending on the properties of the mediator. The number of electrons transferred between Yred and Mox in the SC1 process depends on the ratio of νY and νM.
3 Modeling equations
3.1 Space and time domains
The total space (ltot) is divided into two space domains: (1) the redox film, and (2) the stationary surrounding solution. As shown in eqn (1), the length of the film domain is l1, and the length of the second domain has a length which is set as a multiple of the film thickness (ζx).| ltot = l1 + l1ζx = l1(1 + ζx) | (1) |
As shown in eqn (2), the total time (ttot) is divided into three time domains: (1) when the light is initially off (teq), (2) when the film is under photoillumination (texp), and (3) when the light is off once again (trec).
| ttot = teq + texp + trec = τtottexp | (2) |
By means of the factor τtot, the total time is expressed as a multiple of the exposure time, which is the primary time related variable of interest. Information regarding the calculation of τtot is given in the ESI.†
3.2 Main equations
The main modeling equations were derived from material balances on the reduced form of the mediator (Mred), on the oxidized form of the first electron acceptor (Yox), and on the oxidized form of the final electron acceptor (Zox). Equations for these species in the film domain are shown in eqn (3)–(5) respectively. They constitute a system of coupled partial differential equations (PDEs) with time, space, and concentration as the primary variables. The equations account for transient behavior by the presence of first order time derivatives. They also account for 1-dimensional spatial variation related to diffusion by the presence of second order spatial derivatives. These are considered within the context of several interrelated chemical and electron transfer reactions. The equations were scaled with respect to their maximum possible values, so that the range of the major dimensionless variables (time, space, and concentrations) is between 0 and 1.Reaction stoichiometry is explicitly included in the model, and allows for flexibility with regards to the number of electrons that can be transferred to the electrode by the mediator, and by the first electron acceptor (Yred|Yox), which appear as zM and as zY in the modeling equations, respectively. The stoichiometry between the first electron acceptor and the second electron acceptor (Zred|Zox) is fixed as one-to-one.
These modeling equations shown for the film domain represent the most complex form of these equations, and the corresponding equations for simpler reaction schemes, or for the main equations in the solution domain can be deduced by setting the relevant kinetic terms or concentrations to zero. For example, the main equation for Yox in the solution domain can be deduced by setting κYCAT and κYSC1 in eqn (4) to zero.
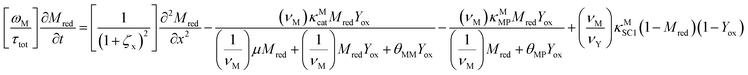 | (3) |
 | (4) |
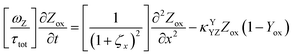 | (5) |
3.3 Contributions to current
The total current is the sum of two contributions, as shown in eqn (6). The photocatalytic contribution to the current (ιcat) is calculated based on the concentration gradient of the reduced form of the mediator at the electrode surface as shown in eqn (7). The SC2 contribution to the current (ιSC2) is calculated based on the concentration gradient of the oxidized form of the first electron acceptor Yox at the electrode surface, as shown in eqn (8).| ιtot = ιcat + ιSC2 | (6) |
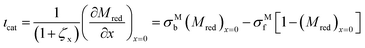 | (7) |
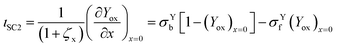 | (8) |
In contrast to the SC2 recombination process, current loss due to the SC1 recombination process is manifested indirectly as a reduction in the main current. In order to isolate the effect of SC1 recombination, each simulation is run twice: one time with the SC1 kinetic constant set to zero, and a second time with the SC1 kinetic constant set to its nominal value, where the corresponding catalytic currents are subtracted.
3.4 Boundary conditions
The boundary conditions for Mred and Yox at the electrode surface are shown in eqn (7) and (8). Zox cannot undergo electron transfer at the electrode surface; therefore, it has a “no-flux” boundary condition.The boundary condition at the film/electrolyte interface is different depending on the species involved. Since the mediator is immobilized in the film, the intermediate boundary condition for Mred is “no-flux”, which requires that the concentration gradient be equal to zero at the film/electrolyte interface when approaching the film boundary from domain I on the left side (l1−), as shown in eqn (9). The boundary condition for Mred in the bulk is that its concentration is zero, the same value that it has in the surrounding solution domain.
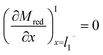 | (9) |
Since Yred|Yox is freely diffusing throughout the system, in particular, between the film and the surrounding solution, and without mass transfer resistance, the intermediate boundary condition for Yox is “perfect-flux”, where the concentration gradients just before and just after the film/solution interface are equal, as shown in eqn (10).
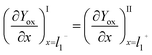 | (10) |
The bulk semi-infinite boundary condition holds for Yox and Zox, therefore, their concentrations at the bulk must remain undisturbed at their initial values, and with a slope of zero. At the end of each simulation, the concentration profiles at the end time are inspected, and if necessary, the simulation is repeated with a greater distance.
4 Dimensionless groups
After scaling of the major variables with respect to their maximum possible values, the dimensional parameters were formed into dimensionless groups. Two steps were deliberately taken in an effort to simplify and to unify the treatment of the dimensionless groups: (1) classification of the groups into “types”, where the respective rate ratios are as transparent as possible, and (2) the use of double script notation, where it is easily seen which rates are being compared.Inspection of the scaled main equations and the scaled electrode surface boundary conditions shows three main kinds of dimensionless groups: “κ” type groups, “ω” type groups, and “σ” type groups. As was done in a reference model,19 various κ type groups are used related to the various reaction–diffusion processes, which occur within the volume of the film or in the surrounding solution. In the model, single script notation was used to denote the particular chemical process of interest. The use of ω groups was inspired from another reference model,20 which focuses on transient electron transfer within redox-active films. Finally, σ type groups denote electron transfer processes at an electrode surface. One example of each of these group types is described in detail in the following sections. A summary of the dimensionless groups in the model is included in the ESI.†
4.1 κ YSC1 as an example of a κ type group
The κYSC1 group is shown in its most simplified form in eqn (11). The similarity of this expression to λ/σ2 in a reference model,17 and to κ in another reference model18 were helpful for interpreting this new dimensionless group as the ratio of the rate of SC1 to the rate of diffusion of Y.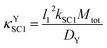 | (11) |
This ratio can be more clearly demonstrated after multiplication of the numerator and denominator by Ytot and rearrangement; the result is shown in eqn (12). In this equation, the units of the numerator and the denominator are mol cm−3 s−1; the numerator therefore represents the maximum possible rate of SC1 (when both reaction species are at their maximum possible concentrations), and the denominator represents the maximum molar diffusion rate of SC1 in a basis area of l12.
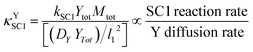 | (12) |
The inverse square root of κYSC1, which is shown in eqn (13), is also of interest because it allows for one to think of the same process in terms of the SC1 reaction layer.
 | (13) |
The reaction layer concept, which was introduced and emphasized in a foundational reference model,17 and was also used in a later reference model18 was useful for the interpretation of this dimensionless group as the fractional distance in the film that a formed Yred molecule will be able to travel within the film before undergoing SC1, ignoring all other processes in the system.
4.2 ω Y as an example of a ω type group
The ωY group is shown in its simplest form in eqn (14). It can be rearranged as a ratio of two time scales, as shown in eqn (15). In this form, ωY can be interpreted as the ratio of the minimum time needed for a film of a basis area of l12 to be fully saturated with Y by diffusion versus the exposure time. As such, ωY is an indicator of how much of the film is accessible to Y by diffusion at the given experimental time scale.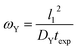 | (14) |
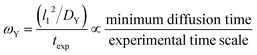 | (15) |
The inverse square root of ωY, which is shown in eqn (16), is also of interest because it allows for one to think of the same process in terms of the Y diffusion layer.
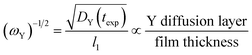 | (16) |
Comparison to the w dimensionless group in a reference model20 was helpful for the interpretation of this new dimensionless group as the fractional distance in the film that a Yox molecule will be able to travel within the film in the time given, ignoring all other processes in the system.
4.3 σ YSC2 as an example of a σ type group
The σYSC2 group arises from the non-dimensionalization of the Butler–Volmer equation, and therefore is composed of dimensionless groups related to k0Y (υY, shown in eqn (17)), the overpotential (εY, shown in eqn (18)), and to αY (the apparent electron transfer coefficient).υ Y is the only factor in σYSC2 that is outside of an exponent in eqn (19), therefore the units of this term will determine the overall units of σYSC2. Multiplication of the numerator and denominator of υY by Ytot and rearrangement results in units of mol cm−2 s−1 in the numerator and the denominator. This allows for the interpretation of this dimensionless group as the rate of heterogeneous electron transfer of Y at the electrode surface versus the rate of diffusion of a surface plane of Y, without considerations related to overpotential and the apparent electron transfer coefficient.
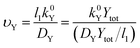 | (17) |
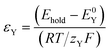 | (18) |
In keeping with the notation from a reference textbook,21 a reduction at the electrode surface is considered as a “forward” reaction, and oxidation is conversely regarded as a “backwards” reaction. Since SC2 occurs through oxidation of Yred, the “backwards” reaction is SC2; therefore σYb can be regarded as σYSC2 for this case as shown in eqn (19), and can be interpreted as the rate of SC2 versus the diffusion rate of Y, which includes the effects of the applied overpotential and of the apparent electron transfer coefficient on the electron transfer rate.
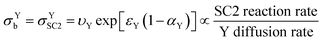 | (19) |
4.4 Secondary dimensionless groups: μ and θMM
A secondary group, μ, is shown in eqn (20). As the ratio of the Michaelis–Menten constant and the maximum substrate concentration, it denotes the fractional degree of enzyme saturation.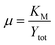 | (20) |
θ MM is a secondary group because it can be represented as a ratio of two individual κ groups. Starting from its simplified form, shown in eqn (21), multiplication of the numerator and the denominator by Ptot demonstrates how θMM can be interpreted as a ratio of the catalysis and electron transfer rates, as shown in eqn (22).
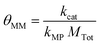 | (21) |
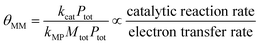 | (22) |
Since κ groups are ratios of reaction and diffusion rates, κYcat and κYMP can be defined by eqn (23) and (24).
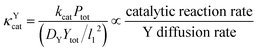 | (23) |
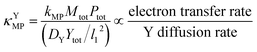 | (24) |
Similarly, κMPcat denotes the ratio of the catalytic reaction and electron transfer rates as shown in eqn (25).
 | (25) |
κ MPcat can then be expressed as the ratio of κYcat and κYMP, which is equal to θMM, as shown in eqn (26).
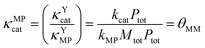 | (26) |
4.5 The SC1/SC2 ratio by the use of groups with double notation
Double script notation can be useful for deriving expressions for rate comparisons of interest. For example, a dimensionless expression which is indicative of the relative rates of SC1 in the film and SC2 at the electrode surface can be derived, for the case where the oxidation of Yred is strongly favored. This can be calculated from the ratio of κYSC1 (eqn (12)) and σYSC2 (eqn (19)), in which the Y diffusion rate cancels out; the final result is shown in eqn (27).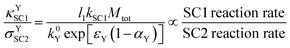 | (27) |
The appearance of l1 in the numerator of eqn (27) implies that for an extremely high value of l1 (extremely thick films), recombination is much more likely to be by SC1 than by SC2; this is physically reasonable since for very thick films, most of the Yred would be generated further away from the electrode. However, the likelihood of SC1 versus SC2 also depends on the relative kinetic parameters, as well as on the apparent electron transfer coefficient. For example, extremely high SC2 kinetics together with extremely low SC1 kinetics can therefore result in a higher likelihood for SC2 over SC1, even in a very thick film.
The derivation of expressions such as eqn (27) are useful because they are order of magnitude estimates of the individual rate ratios of interest. However, such expressions do not negate the need for full simulations, which include simultaneous considerations of all competing rates in the system, and which therefore generate exact results regarding the behavior of the system under a given set of conditions.
5 Numerical solution of the modeling equations
Because of the “no-flux” film/solution boundary condition for the reduced form of the mediator (eqn (9)), it was not possible to use built-in Matlab PDE solver functions, which ignore no-flux internal boundary conditions. Therefore, the space variable of the PDE system was discretized, resulting in a series of simultaneous first-order ordinary differential equations (ODEs) in time according to the method of lines.22 The discretization of the space variable was performed using a vertex-centered finite volume scheme with variable x-spacing.22–24 Custom functions for single and double exponentially expanding grids were constructed, according to a method suitable for electrochemical simulations.25 The finite volume method was chosen due to its strengths related to spatial discontinuities (since it is an integral-based method), and to its strengths related to adherence to the conservation equations (since the governing equation is solved in “conservative” form). The finite volume method schematic and the finite difference equations are included in the ESI.†The system of ODEs was then solved using a Matlab built-in ordinary differential equation solver (ode15s), which is designed specifically for systems in which concentration profiles increase steeply over short distances (i.e. numerically “stiff”22,26). The time discontinuities within the system (i.e. light on and off) were managed within ode15s by time-dependent coefficients which were changed by steep linear on/off ramps. Numerical solution of the system allowed for the calculation of a “deconvoluted” current–time curve, which shows all contributions (direct and indirect) to the observed total current, for calculated concentration profiles at specified times, and for the generation of concentration profile animations at all time points of the simulation.
After implementation of the simulation was completed, a series of calculations were performed in order to verify the correctness of the model. As much as possible, this verification was performed in a “piecewise” way, in which the model was simplified for direct and quantitative comparison to the results from relevant reference models. For example, for verification of the correct implementation of the heterogeneous electron transfer at the electrode by SC2, the kinetics for all chemical processes was set to zero, and the resulting current–time curve was compared to expected results from an analytical expression for quasi- and irreversible electron transfer in a potential step experiment.21 For verification of the SC1 process, reduction of the model was not possible. Therefore, in this case, a general material balance which simultaneously considers the initial and final concentration profiles as well as the corresponding current–time curve was used. More details and examples related to the piecewise verification are given in the ESI.†
6 Applications of the model
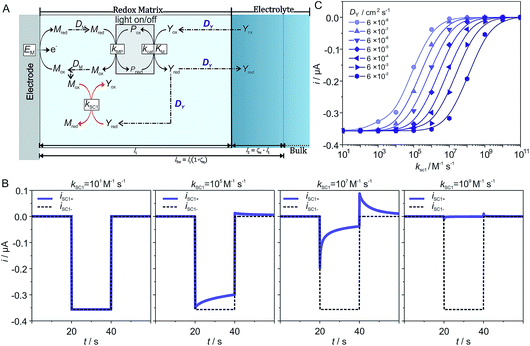
Such a model is useful for its predictive power, especially for situations or conditions where the outcome is unclear with qualitative estimation. Due to the large number of parameters, as well as the uniqueness of each individual experimental system, it is useful if simulations can be run to explore how parameters affect the photocurrent generation. In order to facilitate this, a standalone app was developed (see ESI,† Standalone App for Simulations).As a case study we performed simulations to predict the effect of the diffusion coefficient of the charge carrier (DY) on photocurrent generation as a function of the kinetic constant for the recombination (kSC1) of the reduced charge carrier Yred with the electron mediator Mox. The schematic illustration of the reactions is shown in Fig. 3A. In this particular example, we model the reaction between the photosynthetic protein and the charge carrier by means of Michaelis–Menten kinetics. The recombination of Yred at the electrode (SC2) is set as zero to unambiguously reveal the effect of DY and kSC1 on photocurrent generation. As highlighted in Fig. 3A, DY is involved in two competing processes. In the photocatalytic portion of the scheme, DY defines the flux of Yox to the photocatalytic reaction layer and thus an increase in DY would be expected to be beneficial to the photocatalytic process. However, DY also defines the flux of Yred to the reaction layer for recombination of Yred with Mox, so an increase in DY leads to a faster recombination rate. Since the rate of the photocatalytic process and the rate of recombination have opposite effects on photocurrent generation, the impact of DY on the system cannot be predicted based on a qualitative comparison of the two processes. Instead, simulations are required in order to quantitatively predict the effect of DY on the photocurrent generation.
The simulations were performed for a set of parameters (see the ESI†) that ensure that mass transport of Yox is limiting the photocatalytic process. 77 current–time curves were generated for 7 different values of DY and 11 different values of kSC1 while all other parameters where kept constant. Examples of deconvoluted current–time curves for increasing kSC1 values are shown in Fig. 3B for DY = 6 × 10−6 cm2 s−1. For the lowest value of kSC1 (below 102 M−1 s−1), a steady state photocurrent is obtained which is mostly overlaying with the predicted current for the one corresponding to kSC1 set to 101 M−1 s−1. As kSC1 is increased, the photocurrent–time curves increasingly deviate from the pure photocatalytic curve. At transition values for kSC1 (for instance 105 M−1 s−1 and 107 M−1 s−1) the photocathodic current is lower and decreases over time during illumination while an anodic current appears in the following dark phase. These features are characteristic for recombination processes. At the highest kSC1 values (above 109 M−1 s−1), both the photocurrent and the dark current completely vanish. The same qualitative trend of photocurrent decrease with increasing kSC1 is observed for all investigated values of DY.
Quantitative analysis of the impact of the diffusion coefficient is performed by plotting the photocurrent values (before the dark phase) against the kSC1 values for each value of DY (Fig. 3C). The i vs. kSC1 plots confirm the current cancelling effect of the charge recombination process irrespective of the value of DY. However, the most important feature is that the transition in photocurrent loss in the i vs. kSC1 curves is shifted to higher kSC1 values as DY is increased. For a 10-fold increase in kSC1, a given value for the photocurrent can be maintained if DY is increased by a factor of 100. These results demonstrate the ability to accommodate for increasing kSC1 by increasing DY according to the relationship shown in eqn (28).
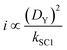 | (28) |
7 Conclusions
A model was developed for biophotoelectrodes based on photosynthetic proteins, in which the photocurrent can be simulated for the entire experiment, together with a deconvolution of the individual contributions to the total observed current, either by the catalytic process, or its loss through recombination processes within the redox film or at the electrode surface. Because of its strengths related to discontinuities in space (i.e. at the film/solution interface) and the balance of flux, the finite volume method within the context of the method of lines was used to solve the system of partial differential equations. The balance of flux is especially important for this problem because under stationary conditions, the substrate can diffuse in and out of the film. Besides photocurrents, time dependent concentration profiles were also predicted. Additionally, dimensionless groups which summarize the major processes in the system were developed and presented. The model is flexible and is therefore relevant for several possible systems with respect to the reaction between catalysts and the electron acceptor (modeled either as a bimolecular reaction, which is relevant for photosystem 1, or as a Michaelis–Menten enzymatic process, which is relevant for purple bacterial reaction centers). Similarly, the model can be adjusted either for direct generation of a charge carrier relevant for biophotovoltaic cells, or for an additional redox catalyst for the generation of a solar fuel as a final product.The simulations were compiled into a stand-alone app, which can be used to investigate the effects of different parameters on photocurrent generation. The example given here, in which the effect of increasing charge carrier diffusion coefficient on the ability of the system to withstand increasing mediator–charge carrier recombination kinetics was investigated, shows the ability of the simulation to predict the performance of the system for complex situations where it is not possible by means of qualitative reasoning. The same simulation approach can be carried out for predicting the effects of any other parameters described in the model. Therefore, the model developed in this work will be helpful for the rational design and further optimization of biophotoelectrodes for maximal energy conversion efficiency.
Author contributions
All authors contributed in conceiving the research. D. B. supervised all modeling activities and developed the model on “charge carrier” generation. T. H. developed the model on “solar fuel” generation and the stand-alone app. H. Z. performed the electrochemical simulations. All authors contributed to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the European Research Council (ERC Starting Grant 715900), by the DFG within the framework of the Cluster of Excellence RESOLV (EXC 1069), by the DFG/ANR within the projects SHIELD PL746/2-1 and No. ANR-15-CE05-0020. H. Z. is grateful for the support by the China Scholarship Council (CSC) (No. 201306950049). The authors thank Dierk Gruhn for helping with the simulations.Notes and references
- V. M. Friebe and R. N. Frese, Curr. Opin. Electrochem., 2017, 5, 126–134 CrossRef CAS.
- P. J. D. Janssen, M. D. Lambreva, N. Plumeré, C. Bartolucci, A. Antonacci, K. Buonasera, R. N. Frese, V. Scognamiglio and G. Rea, Front. Chem., 2014, 2, 36 CrossRef PubMed.
- K. Nguyen and B. D. Bruce, Biochim. Biophys. Acta, Bioenerg., 2014, 1837, 1553–1566 CrossRef CAS PubMed.
- T. Kothe, S. Pöller, F. Zhao, P. Fortgang, M. Rögner, W. Schuhmann and N. Plumeré, Chem.–Eur. J., 2014, 20, 11029–11034 CrossRef CAS PubMed.
- K. P. Sokol, D. Mersch, V. Hartmann, J. Z. Zhang, M. M. Nowaczyk, M. Rögner, A. Ruff, W. Schuhmann, N. Plumeré and E. Reisner, Energy Environ. Sci., 2016, 9, 3698–3709 RSC.
- N. Plumeré and M. M. Nowaczyk, Biophotoelectrochemistry of Photosynthetic Proteins, in Biophotoelectrochemistry: From Bioelectrochemistry to Biophotovoltaics. Advances in Biochemical Engineering/Biotechnology, ed. L. Jeuken, Springer, Cham, 2016, 158, pp. 111–136 Search PubMed.
- V. Proux-Delrouyre, C. Demaille, W. Leibl, P. Sétif, H. Bottin and C. Bourdillon, J. Am. Chem. Soc., 2003, 125, 13686–13692 CrossRef CAS PubMed.
- A. F. Janzen and M. Seibert, Nature, 1980, 286, 584–585 CrossRef CAS.
- M. T. Robinson, D. E. Cliffel and G. K. Jennings, J. Phys. Chem. B, 2018, 122, 117–125 CrossRef CAS PubMed.
- P. N. Ciesielski, D. E. Cliffel and G. K. Jennings, J. Phys. Chem. A, 2011, 115, 3326–3334 CrossRef CAS PubMed.
- R. Caterino, R. Csiki, A. Lyuleeva, J. Pfisterer, M. Wiesinger, S. D. Janssens, K. Haenen, A. Cattani-Scholz, M. Stutzmann and J. A. Garrido, ACS Appl. Mater. Interfaces, 2015, 7, 8099–8107 CrossRef CAS PubMed.
- F. Milano, F. Ciriaco, M. Trotta, D. Chirizzi, V. de Leo, A. Agostiano, L. Valli, L. Giotta and M. R. Guascito, Electrochim. Acta, 2019, 293, 105–115 CrossRef CAS.
- G. Longatte, M. Guille-Collignon and F. Lemaître, ChemPhysChem, 2017, 18, 2643–2650 CrossRef CAS PubMed.
- G. Longatte, A. Sayegh, J. Delacotte, F. Rappaport, F. Wollman, M. Guille-Collignon and F. Lemaître, Chem. Sci., 2018, 9, 8271–8281 RSC.
- O. Yehezkeli, R. Tel-Vered, J. Wasserman, A. Trifonov, D. Michaeli, R. Nechushtai and I. Willner, Nat. Commun., 2012, 3, 742 CrossRef PubMed.
- K. R. Stieger, S. C. Feifel, H. Lokstein and F. Lisdat, Phys. Chem. Chem. Phys., 2014, 16, 15667–15674 RSC.
- C. P. Andrieux, J. M. Dumas-Bouchiat and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1982, 131, 1–35 CrossRef CAS.
- P. N. Bartlett and K. Pratt, J. Electroanal. Chem., 1995, 397, 61–78 CrossRef.
- V. Fourmond, S. Stapf, H. Li, D. Buesen, J. Birrell, O. Rüdiger, W. Lubitz, W. Schuhmann, N. Plumeré and C. Léger, J. Am. Chem. Soc., 2015, 137, 5494–5505 CrossRef CAS PubMed.
- K. Aoki, K. Tokuda and H. Matsuda, J. Electroanal. Chem. Interfacial Electrochem., 1983, 146, 417–424 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, Wiley, New York, 2nd edn, 2001 Search PubMed.
- M. E. Davis, Numerical Methods and Modeling for Chemical Engineers, Wiley, New York and Chichester, 1984 Search PubMed.
- V. Ruas, Numerical Methods for Partial Differential Equations: An Introduction Finite Differences, Finite Elements and Finite Volumes, John Wiley & Sons, Chichester, West Sussex, United Kingdom, 2016 Search PubMed.
- W. J. Lick, Difference Equations From Differential Equations: Volume 41 of Lecture Notes in Engineering, Springer Verlag, 1989 Search PubMed.
- M. Rudolph, D. P. Reddy and S. W. Feldberg, Anal. Chem., 1994, 66, 589A–600A CrossRef CAS.
- L. F. Shampine and M. W. Reichelt, SIAM J. Sci. Comput., 1997, 18, 1–22 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8fd00168e |
| This journal is © The Royal Society of Chemistry 2019 |