 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-invasive force measurement reveals the number of active kinesins on a synaptic vesicle precursor in axonal transport regulated by ARL-8†
Kumiko
Hayashi
 *a,
Shin
Hasegawa
a,
Takashi
Sagawa
b,
Sohei
Tasaki
*a,
Shin
Hasegawa
a,
Takashi
Sagawa
b,
Sohei
Tasaki
 c and
Shinsuke
Niwa
*d
c and
Shinsuke
Niwa
*d
aDepartment of Applied Physics, Graduate School of Engineering, Tohoku University, Sendai, Japan. E-mail: kumiko@camp.apph.tohoku.ac.jp
bAdvanced ICT Research Institute, National Institute of Information and Communications Technology, Kobe, Japan
cFrontier Research Institute for Interdisciplinary Sciences (FRIS) and Graduate School of Science, Tohoku University, Sendai, Japan
dFrontier Research Institute for Interdisciplinary Sciences (FRIS) and Graduate School of Life Sciences, Tohoku University, Sendai, Japan. E-mail: shinsuke.niwa.c8@tohoku.ac.jp
First published on 19th January 2018
Abstract
Kinesin superfamily protein UNC-104, a member of the kinesin-3 family, transports synaptic vesicle precursors (SVPs). In this study, the number of active UNC-104 molecules hauling a single SVP in axons in the worm Caenorhabditis elegans was counted by applying a newly developed non-invasive force measurement technique. The distribution of the force acting on a SVP transported by UNC-104 was spread out over several clusters, implying the presence of several force-producing units (FPUs). We then compared the number of FPUs in the wild-type worms with that in arl-8 gene-deletion mutant worms. ARL-8 is a SVP-bound arf-like small guanosine triphosphatase, and is known to promote unlocking of the autoinhibition of the motor, which is critical for avoiding unnecessary consumption of adenosine triphosphate when the motor does not bind to a SVP. There were fewer FPUs in the arl-8 mutant worms. This finding indicates that a lack of ARL-8 decreased the number of active UNC-104 motors, which then led to a decrease in the number of motors responsible for SVP transport.
Introduction
Due to the morphology of neurons, efficient communication between the cell body and distal processes requires fast cargo vesicle transport in the axon.1,2 Kinesin superfamily proteins and cytoplasmic dynein, which are adenosine triphosphate (ATP)-dependent molecular motors, haul cargo vesicles anterogradely toward the terminal, and retrogradely toward the cell body.3–5 Neuronal communication largely depends on the delivery and receipt of synaptic vesicles in particular. The components of the synaptic vesicles are synthesized in the cell body and are then parcelled in synaptic vesicle precursors (SVPs). The SVPs are transported to the synapses, which are located around the axon terminal, by the kinesin superfamily protein UNC-104/KIF1A, which belongs to the kinesin-3 family.6–8UNC-104/KIF1A was originally identified in the worm Caenorhabditis elegans (C. elegans).7,8 ARL-8, a molecule related to UNC-104, which is a SVP-bound arf-like small guanosine triphosphatase (GTPase), has recently been reported to activate the motor by releasing its autoinhibition.9–11 The auto-inhibitory mechanism, which is a common mechanism for the regulation of molecular motors, is thought to be required to avoid both unnecessary cargo transport and futile ATP hydrolysis in cells when the motors do not bind to cargos. A lack of the regulatory protein ARL-8 leads to defects in axon-specific sorting of synaptic materials, decreased synapse density, and impaired cargo vesicle transport in vivo.10
In this paper, we investigated the physical mechanism underlying the finding that the absence of ARL-8 leads to decreased ability of UNC-104 to transport SVPs, as reported in a previous study.10 Our hypothesis regarding this issue is summarized in Fig. 1. In our model, more motors can bind to a SVP in the presence of ARL-8 than in its absence (Fig. 1(b)), because ARL-8 promotes the activation of UNC-104 (Fig. 1(c)). This model is consistent with the observation that a basal level of axonal transport is observed even in loss-of-function mutants of arl-8.10,11 Note that only the activated form of UNC-104 can bind to a SVP, as has been shown previously.10 The decreased number of motors hauling a SVP is thought to be the physical factor that lowers the SVP transport ability. For example, the run length of transported SVPs may become shorter as the number of motors decreases.
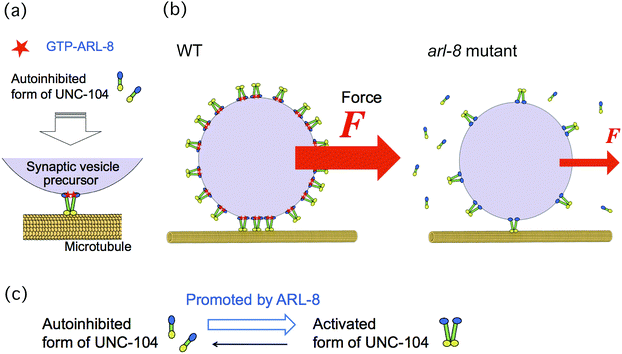 | ||
| Fig. 1 Schematics of our model. (a) Mechanism of auto-inhibition of UNC-104 released by ARL-8 binding, as suggested in a previous paper.10 Activation of UNC-104 motors is promoted by ARL-8 (red), and these then bind to a synaptic vesicle precursor (SVP). UNC-104 motors (yellow) carry the SVP (violet) along a microtubule (orange). (b) This model suggests that the lack of ARL-8 reduces the number of UNC-104 motors attached to a SVP. Consequently, the number of UNC-104 motors in charge of SVP transport is also reduced. Because the force (F) generated by the motors acting on a SVP increases directly with the number of motors, the force can be used for estimating the motor number. (c) The transition from the auto-inhibited state of UNC-104 to its activated state is promoted by ARL-8. | ||
In order to verify our model, we investigated the number of motors hauling a single SVP by measuring the force, exerted by the motors, acting on a SVP. This force is thought to be a good indicator of the number of motors that carry a SVP, because a larger force acts on the SVP when it is transported by more motors (Fig. 1(b)). We then compared the results of wild-type worms with those of the arl-8 mutant worms, in which arl-8 was deleted.10
We have developed an approach for non-invasive force measurement based on the fluctuation theorem, which describes the relationship of non-equilibrium statistical mechanics regarding entropy production in non-equilibrium states.12,13 For the membrane vesicles transported by kinesin and dynein in in vitro cultured neurons, the force acting on a single vesicle has been estimated using this measurement method.14 In this study, we also investigated the force acting on SVPs using the same force measurement method. First, we observed the directional motion of a GFP-labelled SVP in the axon of a C. elegans worm by using fluorescence microscopy, and obtained the center position of the SVP. The center position fluctuates due to thermal noise, collisions with other intercellular organelles, stochastic stepping motion of the motors caused by ATP hydrolysis, and other factors, while exhibiting the directional motion specified by the motors.
Second, we calculated the force indicator χ (eqn (1)) from the fluctuating center position, which describes a quantity that is constructed based on the fluctuation theorem (see Methods section). The measurement was repeated many times for a large number of SVPs, to obtain the distribution of χ. The distribution of χ was found to form several clusters, indicating the existence of multiple force-producing units (FPUs). From the calibrated force value of 1 FPU (about 5 pN), it was estimated that 1 FPU corresponds to a UNC-104 dimer.
Finally, we compared the distribution of the force indicator χ for the wild-type C. elegans with that for the arl-8-deleted mutant. As was expected from the model depicted in Fig. 1(b), we found that the number of FPUs was decreased in the mutant worm. The number of motors on a SVP remains poorly understood, yet this parameter is one of the important factors in understanding the physics of axonal transport; thus, our results are of general significance for the field of neuroscience.
Materials and methods
Sample preparation
C. elegans stains, wyIs251[Pmig-13::gfp::rab-3; Podr-1::gfp] and arl-8(wy271); wyIs251 have been described in previous studies.10,11Culture
C. elegans was maintained on OP50 feeder bacteria on nematode agar plates (NGM) agar plates, as per the standard protocol.15 Strains were maintained at 20 °C.Observation by fluorescence microscopy
A cover glass (32 mm × 24 mm, Matsunami Glass Ind., Ltd, Tokyo, Japan) was coated with 2% agar (Wako, Osaka, Japan). A volume of 20 μl of 25 mM levamisole mixed with 5 μl 200 nm-sized polystyrene beads (Polysciences Inc., Warrington, PA, USA) was dropped onto the cover glass. The polystyrene beads increased the friction, inhibiting the worms' movement16 and levamisole paralyzed worms. Ten to 20 worms were moved from a culture dish to the medium on the cover glass. Another cover glass was placed over the first cover glass to confine the worms (forming a chamber) (Fig. 2(a)). The worms in the chamber were observed under a fluorescence microscope (IX83, Olympus, Tokyo, Japan) at room temperature (Fig. 2(b)). The images of a GFP-labelled SVP in a worm's neuron were obtained using a 150× objective lens (UApoN 150×/1.45, Olympus) and a sCMOS camera (OLCA-Flash4.0 V2, Hamamastu Photonics, Hamamatsu, Japan) at 100 frames per second. The center position of each SVP was determined from the recorded images using the custom-made software, Tyrant (see below). We focused on the displacement along the direction of the SVP's motion X(t) (Fig. 2(c)). Data were collected from 40 vesicles from 33 individual wild-type worms in 21 different chambers, and from 40 vesicles from 36 individual arl-8 mutant worms in 22 different chambers. The worms for observations were chosen randomly after visual inspection, and the trajectories that lasted about 0.5–1 s constant velocity runs were selected for analysis, as described in the main text. Note that although there were many SVPs in an axon, there were time intervals (rare events) in which single SVPs were tracked (Fig. S1, ESI†). We collected all of the rare events that we could observe (n = 40 both for the wild-type and the mutant worms).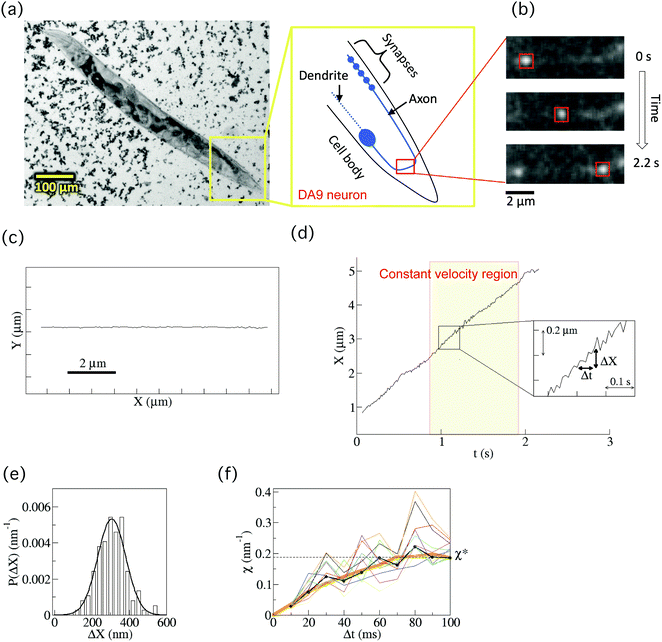 | ||
| Fig. 2 Fluorescence observation of a synaptic vesicle precursor (SVP) and calculation of the force indicator χ. (a) A bright-field micrograph of a C. elegans worm whose body was fixed in a chamber by the high viscosity medium (high-density 200 nm-sized polystyrene beads) and anaesthesia (see Methods section). SVPs were observed in the axon of the DA9 neuron. (b) Time-series fluorescence images of a SVP. The motion was tracked by in-house software (see Methods section). (c) An example of a 2D-trajectory of the movement of a SVP. The direction of the movement was set to be the x-direction. (d) Center position (X) of a SVP for anterograde transport as a function of time. Our analysis target was a constant velocity region that lasted longer than 0.5 s. When the recorded speed was high enough (100 frames per second), the fluctuation of X was observed (inset). Here, ΔX = X(t + Δt) – X(t). (e) Probability distribution (P(ΔX)) of ΔX for the cases of 100 ms. The distribution was well fitted by a Gaussian function (thick curve). (f) An example of the force indicator χ (eqn (1)) calculated for each P(ΔX) at a different Δt (10 ms ≤ Δt ≤ 100 ms) (black). After a relaxation time, χ reached a constant value χ* (see Supplementary material of ref. 14 for the relaxation time). The thin curves (n = 10) represent χ calculated based on the boot-strapping method for the error estimation (see Methods section). The estimated error of χ was 10%, which was consistent with the systematic error of the experimental system. The thick orange curve represents χ after the smoothing filtering (see Methods section). | ||
The accuracy of the position measurement was verified using beads (300 nm latex bead, Polysciences). The standard deviation (s.d.) of the position of the bead tightly attached to the glass surface was 8.3 ± 1.2 (s.d.) nm (based on four different beads). Because the standard deviation of the several-micron-sized synapses, which were fixed in worms, was 4.6 ± 1.7 nm (based on five different worms), the worms' bodies were considered to be tightly fixed during observations.
Image analysis by Tyrant
Tyrant is a custom-developed software written in LabVIEW 2013 (National Instruments, Austin, TX, USA); this software analyses the trajectory of the center position of a SVP from the captured fluorescent images. To obtain the one-dimensional displacement of the SVP, all captured images were rotated so that the moving direction of SVP was parallel to the x-axis in the images. First, noise in a fluorescent image was removed using a 3 × 3 median filter. Next, the fluorescent spot of a SVP in the filtered image was cropped by an appropriately sized box (red boxes in Fig. 2(b)). The fluorescent intensity of the spot in the cropped image was fitted with a two-dimensional Gaussian function to calculate the center position of the spot. This procedure was repeated for each selected SVP for a specified time interval.Analysis of fluctuation using the fluctuation theorem
The force indicator χ, which was first introduced in our previous study,14 is defined by| χ = ln[P(ΔX)/P(−ΔX)]/ΔX | (1) |
| P(ΔX) = exp(−(ΔX − b)2/2a)/(2πa)0.5 | (2) |
| χ = 2b/a | (3) |
| F = kBTeffχ* | (4) |
| F ∝ χ* | (5) |
The error of χ was estimated based on the idea of the bootstrapping method. For the 10 different randomly selected segments in the constant velocity segments of X(t) (the segments were half the length of the original), we calculated the values of χ (e.g., 10 thin curves in Fig. 2(f)). The standard deviation of χ* was estimated to be 10%.
Smoothing filtering and affinity propagation
A smoothing filter was applied to the values of χ to reduce variation in the raw data of χ as a function of Δt (Fig. 2(f)). Here, we used the averaging filter χf(Δt) = (χ(Δt − 10 ms) + χ(Δt) + χ(Δt + 10 ms))/3, which is one of the simplest filters. Note that, in this paper, the converged value χ* was defined as χ* = χf(Δt = 80 ms).Affinity propagation,17,18 an exemplar-based clustering method that does not require the number of clusters, was then adopted for clustering the smoothing-filtered two-dimensional data (χ*, χm) where χm is the mean value of χ from Δt = 10 ms to Δt = 100 ms. The method was applied by using “APCluster” implemented in the R software.18 The clustering was stable for the wide range of parameters used in the method (Fig. S2, ESI†).
Force calibration
In order to obtain the force value (F) from χ* through the relation (eqn (4)), we estimated the conversion factor| kBTeff = Γv/χ* | (6) |
Results
Non-invasive force measurement using the force indicator
We observed the axonal transport of SVPs in wild-type worms by fluorescence microscopy (Fig. 2(a) and ESI,† Movies). The worms were anaesthetized and fixed between cover glasses with highly viscous media (high density 200 nm-sized polystyrene beads) in order to fix the worms’ bodies and to minimize the fluctuation resulting from their body movements (see Methods section). Many studies have characterized the morphology and properties of the DA9 neuron and have investigated axonal transport mechanisms using this system.9–11,19,20 We therefore used the DA9 neuron as a model in this study. SVPs in the DA9 neuron were labelled with GFP::RAB-3 using a mig-13 promoter. The motion of each vesicle transported by the motors was tracked by using in-house software (Fig. 2(b), Methods). Transport continued without pauses for a few seconds. The direction of motion was set to be the x-direction (Fig. 2(c)). Then, the center position (X(t)) of a vesicle along an axon was obtained as a function of time (t) for anterograde transport (Fig. 2(d)). Note that we only focused on anterograde transport to investigate UNC-104, given that retrograde transport was a rare event and we could therefore not obtain enough data for this type of transport.Our analysis target was the constant velocity segment of a transported SVP that lasted about 0.5–1 s (Fig. 2(d)). It was difficult to track the same vesicle in the DA9 axon for longer than 1 s, because the axoplasm was crowded with SVPs that were moving fast (ca. 3 μm s−1) and disappeared from the screen within several seconds. When the recording rate was high enough (100 frames per second), fluctuating behaviour of the vesicle was observed even while it exhibited directional motion (inset of Fig. 2(d)). The origin of the fluctuation in the transported SVPs was considered to be mainly thermal noise, stochastic ATP hydrolysis of motors, and collision of the SVP with other vesicles and cytoskeletons. The fluctuation resulting from the worm's body movement was not regarded as a major factor, because we only observed the vesicles for the worms whose movements were highly suppressed by the high viscosity media as well as the anaesthesia (see Methods section).
The fluctuating behaviour of a SVP was represented by ΔX, which is defined by ΔX = X(t + Δt) − X(t) (inset of Fig. 2(d)). Fig. 2(e) shows the probability distribution (P(ΔX)) of ΔX for the case Δt = 100 ms. It was fitted well by a Gaussian function. Using P(ΔX), which was calculated for each Δt (0 ≤ Δt ≤ 100 ms), we then calculated the force indicator χ (eqn (1) in the Methods section) (thick black line in Fig. 2(f)). Applying the smoothing filter (the orange curve in Fig. 2(f), Method), it can be clearly seen that χ reaches a constant value χ* for a large Δt after a certain amount of relaxation time (see Supplementary theory section in ref. 14 regarding the relaxation time). This converged value χ* is found to be proportional to the force (F) acting on a single vesicle, exerted by the motors during constant velocity motion (eqn (5)). Practically, χ* was determined by χ* = (χ(Δt = 70 ms) + χ(Δt = 80 ms) + χ(Δt = 90 ms))/3 in this paper. Note that the error in χ was estimated to be 10% based on a bootstrapping method (thin lines in Fig. 2(f), (n = 10), see Methods section), which was consistent with the systematic error of the experimental system.
Distribution of the force indicator χ for anterograde transport of a SVP
For anterograde transport of SVPs, we investigated 40 vesicles from 33 individual wild-type worms (Fig. 3(a)). After applying the smoothing filter (Fig. 3(b)) and the affinity propagation analysis (Fig. 3(c)), we found that the data were distributed into four clusters (see Methods section for the filtering and analysis). Because the converged value χ* is proportional to the force (F) acting on a vesicle (eqn (5)), this discrete behaviour of χ indicates the existence of four FPUs in SVP anterograde transport.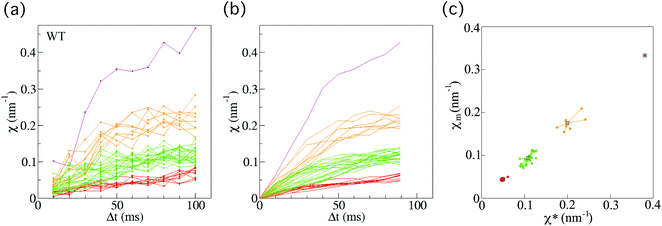 | ||
| Fig. 3 Force indicator χ for anterograde synaptic vesicle precursor (SVP) transport in wild-type C. elegans. (a) χ (eqn (1)) as a function of Δt for SVP anterograde runs for wild-type (WT) C. elegans worms (n = 40 SVPs from 33 different worms). (b) Results of applying the smoothing filter (see Methods section) to the data in (a). (c) The affinity propagation analysis (see Methods section) applied to the data in (b). There are four clusters in the case of wild-type worms. Each color denotes a cluster, representing different force-producing units. | ||
Next, we also investigated 40 vesicles from 36 different arl-8-deleted mutant worms (Fig. 4(a)). Similarly, after applying the smoothing filter (Fig. 4(b)) and the affinity propagation analysis (Fig. 4(c)), we found that the data were distributed into three clusters. The numbers of FPUs are summarized in Fig. 5. Compared with the case of the wild-type (Fig. 5(a)), the proportion of 3 FPUs was decreased, while the proportion of 1 FPUs was increased in the arl-8-deleted mutants (Fig. 5(b)). These evaluations thus indicated that the number of FPUs that hauled a SVP was reduced by 20% in the absence of ARL-8, as compared to the number of motors in wild-type worms.
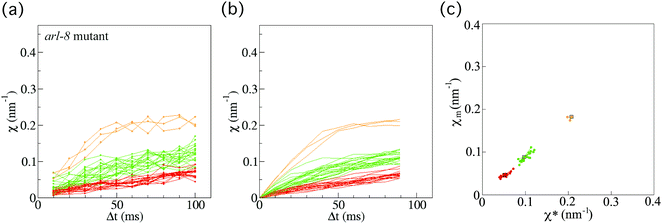 | ||
| Fig. 4 Force indicator χ for synaptic vesicle precursor (SVP) anterograde transport for the arl-8-deleted mutant. (a) χ (eqn (1)) as a function of Δt for SVP anterograde runs for the arl-8-deleted mutant C. elegans worms (n = 40 SVPs from 36 different worms). (b) Results of applying the smoothing filter (see Method section) to the data in (a). (c) The affinity propagation analysis (see Method section) applied to the data in (b). There are three clusters in the case of the arl-8-deleted mutant worms. Each color denotes a cluster, representing different force-producing units (FPUs). | ||
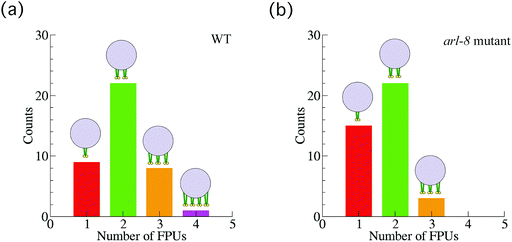 | ||
| Fig. 5 Number of force-producing units (FPUs). The number of FPUs involved in Fig. 3 and 4, in the case of the wild-type (WT) worms (a), and in the case of the arl-8-deleted mutant worms (b). | ||
Force–velocity relation for the SVP anterograde transport
The force–velocity relation for anterograde transport of SVPs was also investigated. By using the relation F ∝ χ*, instead of force (F), χ* was plotted as a function of velocity (v) for the wild-type worms (Fig. 6(a), filled symbols) and the arl-8 mutant worms (Fig. 6(a), open symbols). Here, v was measured as the slope of the constant velocity region used to calculate χ (e.g., Fig. 2(d)). It is seen that the mean velocity slightly increases as the number of FPUs increases in Fig. 6(a). The increase resulted from the reduction in load for a single motor when transport involved multiple motors.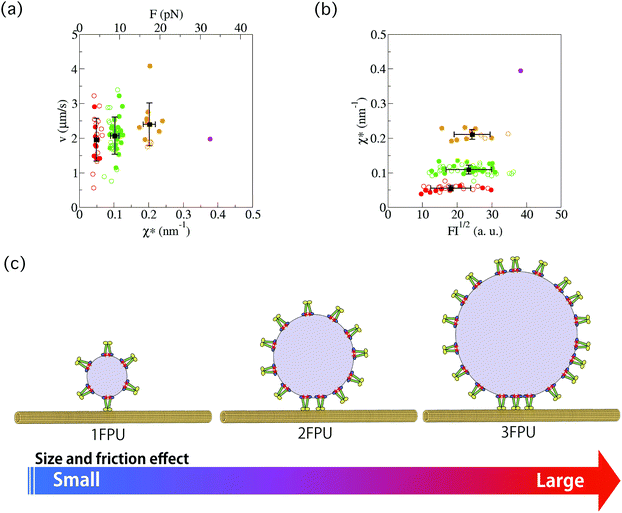 | ||
| Fig. 6 (a) Force–velocity relation for anterograde synaptic vesicle precursor (SVP) transport. By using the relation F ∝ χ*, instead of force (F), χ* was investigated as a function of velocity (v) for the wild-type (WT) worms (filled circles) and the arl-8 mutant worms (open circles). Here, v was measured as the slope of the constant velocity region used to calculate χ (e.g., Fig. 2(d)). Each color corresponds to a group shown in Fig. 3 and 4. In the superior axis, the calibrated force value is represented (see Methods). The error bars represents the standard deviations. (b) χ* as a function of the square root of the fluorescence intensity (FI) of a SVP. FI1/2 corresponds to the radius of a SVP. The error bars represents the standard deviations. There was a weak correlation between FI1/2 and χ* (R2 = 0.40). (c) Schematics explaining the graphs in (b). Each element of this schematics (e.g., UNC-104, microtubules, etc.) is explained in Fig. 1(a). | ||
The conversion factor (eqn (6)) from χ* to F was roughly estimated as Γava/χa* (the index “a” represents the averaged value of each quantity), where Γ is the friction coefficient of a SVP along microtubules. The calibrated force obtained from this rough estimation (see Method section) is shown in the superior axis in Fig. 6(a). Here, 1 FPU was considered to be a UNC-104 dimer, because the calibrated force value (about 5 pN) of 1 FPU was similar to the stall force value of the dimer measured in in vitro single-molecule experiments.23
Lastly, we compared the χ*–v relation of the wild-type worms (filled symbols) with that of the arl-8-deleted mutant worms (open symbols). Their similar χ*–v relation suggests that the force generation mechanism of UNC-104 motors was not largely affected by the lack of ARL-8.
Fluorescence intensity of SVPs
In Fig. 6(b), the fluorescence intensity (FI) of SVPs is plotted as a function of χ* for the wild-type worms (filled symbols) and the arl-8 mutant worms (open symbols). FI1/2 was considered to represent the radius of a SVP. Because the correlation coefficient (R2) was 0.40, there was a weak correlation between FI1/2 and χ*. This implies that a large SVP tends to be conveyed by multiple motors because many motors can be attached to a large SVP (Fig. 6(c)).Discussion
In a previous study 10, it was reported that absence of arl-8 causes mislocalization of synaptic vesicles in the DA9 neuron of C. elegans, implying that the lack of ARL-8 reduced the anterograde transport capability of SVPs. However, the physical parameters in the vesicle transport that are affected by the lack of ARL-8 remained elusive. In this study, we identified one of these physical parameters, i.e., the number of the motors carrying a SVP. We assumed that the binding of UNC-104 to a SVP is promoted by the presence of ARL-8, because ARL-8 promoted the chemical transition from the auto-inhibited state to the uninhibited state of UNC-104 (Fig. 1(c)), and only UNC-104 in the uninhibited state can bind to a SVP. Consequently, the number of motors carrying a single SVP was increased in the presence of ARL-8. In order to verify our assumption, we investigated the force acting on a SVP by counting the number of motors, because the force increases directly with the number of motors attached to the SVP (Fig. 1(b)). Then, using a non-invasive force measurement method based on the fluctuation theorem of non-equilibrium statistical mechanics,14 the force indicator χ (eqn (1)) was calculated for a transported SVP (Fig. 2(f)). The distribution of χ clustered into several groups (Fig. 3), implying the existence of multiple FPUs. In the case of the arl-8-deleted mutant, the number of clusters in the distribution of χ was decreased (Fig. 4). Thus, we concluded that the number of UNC-104 motors hauling a single SVP was decreased in the absence of ARL-8 (Fig. 5). Below, we discuss several issues related to these main findings.Quantal behaviour of force indicator χ
It was investigated by using optical tweezers in living cells that the stall force acting on a single cargo is quantal, reflecting the number of motors hauling the cargo.21,22 This quantal behaviour is one of typical properties of force in intracellular cargo transport systems. Similarly, in this paper, discrete behaviour was observed in the distribution of the force indicator χ in neuronal SVP transport (Fig. 3 and 4). The observation of the quantal behaviour of χ supported the relation F ∝ χ* proposed in our previous paper.14Run length
It has been shown by in vitro single-molecule experiments that the run length of kinesin motors increased with the number of motors, by controlling the number of DNA scaffolds.24 Using these reported values of the run length and the number of FPUs in Fig. 5, the averaged run length of a SVP for the arl-8-deleted mutant worms was calculated to be 70% shorter than that of the wild-type worms. Because it has been reported that the distance of synapses from the cell body was reduced by about 60% by the deletion of arl-8,10 the decreased run length in the mutant may contribute to induction of synapse misplacement in axons.Conclusions
The fluctuation theorem of non-equilibrium statistical mechanics12,13 has been experimentally applied to many non-equilibrium physical systems, such as colloidal particle systems,25 granular systems,26 and turbulence systems,27 as well as single-molecule experiments.28,29 In this paper, we applied the theorem to axonal transport in living worms. While in vitro single-molecule experiments on kinesin and dynein motors have revealed the basic dynamic properties of motors accompanied by ATP hydrolysis, their intracellular properties remain unknown. In particular, cooperative transport by multiple motors is one of the properties that differ from those observed in in vitro single-molecule experiments. Since physical measurements in vivo are difficult because of the complexity of the cell environments, non-invasive passive measurements using fluctuation properties are powerful tools for evaluating intracellular physical quantities. The non-invasive force measurement approach proposed here, which is based on the fluctuation theorem, is likely to find application in a wide range of complex biological in vivo systems.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Y. Okada for assistance with the initial planning of the study; Mr Y. Saito, and Ms S. Sato for help with the experiments; and the members belonging to the Innovative Areas “Soft Molecular Systems” and the young scientists of FRIS, Tohoku University for discussions about the study. This work was supported by PRIME (grant number JP17gm5810009h0003), AMED, MEXT KAKENHI (grant numbers 26104501, 26115702 and 16H00819), and JSPS KAKENHI (grant number 26310204) to K. H., as well as by the grant from Daiichi Sankyo Foundation of Life Science and JSPS KAKENHI (grant numbers 17H0510) to S. N.Notes and references
- E. L. Holzbaur, Trends Cell Biol., 2004, 14, 233–240 CrossRef CAS PubMed.
- N. Hirokawa, S. Niwa and Y. Tanaka, Neuron, 2010, 68, 610–638 CrossRef CAS PubMed.
- M. M. Fu and E. L. Holzbaur, Trends Cell Biol., 2014, 24, 564–574 CrossRef CAS PubMed.
- N. Hirokawa, Y. Noda, Y. Tanaka and S. Niwa, Nat. Rev. Mol. Cell Biol., 2009, 10, 682–696 CrossRef CAS PubMed.
- R. D. Vale, Cell, 2003, 112, 467–480 CrossRef CAS PubMed.
- Y. Okada, H. Yamazaki, Y. Sekine-Aizawa and N. Hirokawa, Cell, 1995, 81, 769–780 CrossRef CAS PubMed.
- D. H. Hall and E. M. Hedgecock, Cell, 1991, 65, 837–847 CrossRef CAS PubMed.
- A. J. Otsuka, A. Jeyaprakash, J. Garcia-Anoveros, L. Z. Tang, G. Fisk, T. Hartshorne, R. Franco and T. Born, Neuron, 1991, 6, 113–122 CrossRef CAS PubMed.
- M. P. Klassen, Y. E. Wu, C. I. Maeder, I. Nakae, J. G. Cueva, E. K. Lehrman, M. Tada, K. Gengyo-Ando, G. J. Wang, M. Goodman, S. Mitani, K. Kontani, T. Katada and K. Shen, Neuron, 2010, 66, 710–723 CrossRef CAS PubMed.
- S. Niwa, D. M. Lipton, M. Morikawa, C. Zhao, N. Hirokawa, H. Lu and K. Shen, Cell Rep., 2016, 16, 2129–2141 CrossRef CAS PubMed.
- Y. E. Wu, L. Huo, C. I. Maeder, W. Feng and K. Shen, Neuron, 2013, 78, 994–1011 CrossRef CAS PubMed.
- D. J. Evans, E. G. Cohen and G. P. Morriss, Phys. Rev. Lett., 1993, 71, 2401–2404 CrossRef CAS PubMed.
- S. Ciliberto, S. Joubaud and A. Petrosyan, J. Stat. Mech.: Theory Exp., 2010, P12003 CrossRef CAS.
- K. Hayashi and Y. Okada, bioRxiv, https://doi.org/10.1101/233064.
- S. Brenner, Genetics, 1974, 77, 71–94 CAS.
- S. W. C. Fang-Yen, P. Sengupta and A. D. T. Samuel, The Worm Breeder's Gazette, 2009, 18, 32 Search PubMed.
- B. J. Frey and D. Dueck, Science, 2007, 315, 972–976 CrossRef CAS PubMed.
- U. Bodenhofer, A. Kothmeier and S. Hochreiter, Bioinformatics, 2011, 27, 2463–2464 CrossRef CAS PubMed.
- C. I. Maeder, A. San-Miguel, E. Y. Wu, H. Lu and K. Shen, Traffic, 2014, 15, 273–291 CrossRef CAS PubMed.
- C. Y. Ou, V. Y. Poon, C. I. Maeder, S. Watanabe, E. K. Lehrman, A. K. Fu, M. Park, W. Y. Fu, E. M. Jorgensen, N. Y. Ip and K. Shen, Cell, 2010, 141, 846–858 CrossRef CAS PubMed.
- G. T. Shubeita, S. L. Tran, J. Xu, M. Vershinin, S. Cermelli, S. L. Cotton, M. A. Welte and S. P. Gross, Cell, 2008, 135, 1098–1107 CrossRef CAS PubMed.
- C. Leidel, R. A. Longoria, F. M. Gutierrez and G. T. Shubeita, Biophys. J., 2012, 103, 492–500 CrossRef CAS PubMed.
- M. Tomishige, D. R. Klopfenstein and R. D. Vale, Science, 2002, 297, 2263–2267 CrossRef CAS PubMed.
- K. Furuta, A. Furuta, Y. Y. Toyoshima, M. Amino, K. Oiwa and H. Kojima, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 501–506 CrossRef CAS PubMed.
- G. M. Wang, E. M. Sevick, E. Mittag, D. J. Searles and D. J. Evans, Phys. Rev. Lett., 2002, 89, 050601 CrossRef CAS PubMed.
- K. Feitosa and N. Menon, Phys. Rev. Lett., 2004, 92, 164301 CrossRef PubMed.
- S. Ciliberto, N. Garnier, S. Hernandez, C. Lacpatia, J. F. Pinton and G. R. Chavarria, Physica A, 2004, 340, 240–250 CrossRef.
- K. Hayashi, H. Ueno, R. Iino and H. Noji, Phys. Rev. Lett., 2010, 104, 218103 CrossRef PubMed.
- D. Collin, F. Ritort, C. Jarzynski, S. B. Smith, I. Tinoco, Jr. and C. Bustamante, Nature, 2005, 437, 231–234 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05890j |
| This journal is © the Owner Societies 2018 |
