Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
ENDOR characterization of an iron–alkene complex provides insight into a corresponding organometallic intermediate of nitrogenase†
Masaki
Horitani
 ab,
Katarzyna
Grubel
c,
Sean F.
McWilliams
c,
Bryan D.
Stubbert
ab,
Katarzyna
Grubel
c,
Sean F.
McWilliams
c,
Bryan D.
Stubbert
 d,
Brandon Q.
Mercado
c,
Ying
Yu
d,
Prabhuodeyara M.
Gurubasavaraj‡
d,
Nicholas S.
Lees
a,
Patrick L.
Holland
d,
Brandon Q.
Mercado
c,
Ying
Yu
d,
Prabhuodeyara M.
Gurubasavaraj‡
d,
Nicholas S.
Lees
a,
Patrick L.
Holland
 *c and
Brian M.
Hoffman
*c and
Brian M.
Hoffman
 *a
*a
aDepartment of Chemistry, Northwestern University, Evanston, Illinois 60208, USA. E-mail: bmh@northwestern.edu
bDepartment of Applied Biochemistry and Food Science, Saga University, Saga, 840-8502, Japan
cDepartment of Chemistry, Yale University, New Haven, CT 06520, USA. E-mail: patrick.holland@yale.edu
dDepartment of Chemistry, University of Rochester, Rochester, New York 14627, USA
First published on 30th June 2017
Abstract
A bio-organometallic intermediate, denoted PA, was previously trapped during the reduction of propargyl alcohol to allyl alcohol (AA) by nitrogenase, and a similar one was trapped during acetylene reduction, representing foundational examples of alkene binding to a metal center in biology. ENDOR spectroscopy led to the conclusion that these intermediates have η2 binding of the alkene, with the hydrogens on the terminal carbon structurally/magnetically equivalent and related by local mirror symmetry. However, our understanding of both the PA intermediate, and of the dependability of the ENDOR analysis on which this understanding was based, was constrained by the absence of reference iron–alkene complexes for EPR/ENDOR comparison. Here, we report an ENDOR study of the crystallographically characterized biomimetic iron(I) complex 1, which exhibits η2 coordination of styrene, thus connecting hyperfine and structural parameters of an Fe-bound alkene fragment for the first time. A tilt of the alkene plane of 1 from normal to the crystallographic Fe–C2–C1 plane causes substantial differences in the dipolar couplings of the two terminal vinylic protons. Comparison of the hyperfine couplings of 1 and PA confirms the proposed symmetry of PA, and that the η2 interaction forms a scalene Fe–C–C triangle, rather than an isosceles triangle. This spectroscopic study of a structurally characterized complex thus shows the exceptional sensitivity of ENDOR spectroscopy to structural details, while enhancing our understanding of the geometry of a key nitrogenase adduct.
Introduction
The binding of alkenes to transition metals is common in organometallic complexes,1 but in biological systems has rarely been observed. Copper-containing proteins bind ethylene in nature,2 and computations support the binding of acetylene to the metal in acetylene hydratase.3 A novel example of a bio-organometallic intermediate (denoted PA) was reported by one of us (B. M. H.), formed during the reduction of propargyl alcohol (PA) to allyl alcohol (AA) by the enzyme nitrogenase, with a similar state formed during the reduction of acetylene to ethylene.4 It is particularly interesting that this intermediate has Fe–C bonds to iron–sulfur clusters; since this report, there has also been spectroscopic evidence supporting ferraoxetane intermediates for catalytic [4Fe–4S] clusters.5 Most recently, ENDOR studies showed that a catalytically competent intermediate of radical-S-adenosylmethionine enzymes contains an Fe–C bond between a [4Fe–4S] cluster and the highly reactive 5′-deoxyadenosyl radical.6 The increased pace of discovery of compounds with metal–carbon bonds in biology further motivates the detailed spectroscopic characterization of biorelevant complexes with M–C interactions.The aforementioned intermediate in nitrogenase was shown to contain AA as a complex in which the double bond of AA undergoes η2 binding to a single Fe of the iron–molybdenum catalytic cofactor (FeMo-co) of nitrogenase (Fig. 1 (left)). This interpretation was later supported by EXAFS and NRVS studies of PA.7 This complex, in which the iron and two carbon atoms form a three-membered ring, can be described as a π-alkene or as a ferracyclopropane according to the Dewar–Chatt–Duncanson model.1
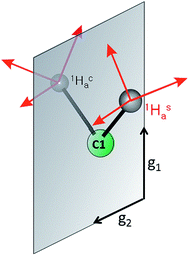
 | ||
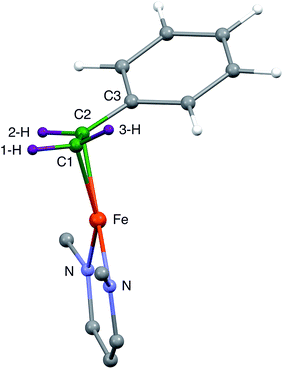
| Fig. 1 (Left) Proposed structure for bound AA in the PA intermediate of α-70Ala nitrogenase. The carbon atoms have been renumbered from the original report4 to correspond to those of 1. (Right) The core of 1, which has styrene bound to a high-spin iron(I) center. | ||
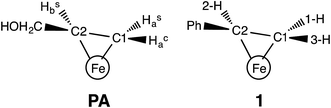
In our earlier work, a series of 1H/2H and 13C ENDOR experiments showed that the nitrogenase PA intermediate contains an adduct of AA.4 The binding site was assigned to the Fe 2, 3, 6, 7 face of FeMo-co, in part because PA is reduced only upon mutation of the α-70 residue from Val to Ala to create space for the large substrate. The bound species was assigned as the alkene product of alkyne reduction, rather than a singly-reduced intermediate, because isotopic labeling studies showed that two H atoms from solvent had been added to the alkyne reactant. The binding geometry (Fig. 1 (left)) was inferred from the surprisingly identical hyperfine parameters for the two H atoms (Hsa and Hca) on the terminal carbon. However, the coordination chemistry precedents for this proposal were relatively distant Os and Ta complexes, because there were no literature examples of EPR-active, structurally characterized iron–alkene complexes for comparison. Thus, an Fe–alkene complex that is both crystallographically characterized and paramagnetic would enable a comparison of the ENDOR parameters of a precisely known structure with those of the FeMo-co–allyl alcohol complex, thereby enhancing our understanding of the intriguing PA intermediate.
Here, we provide a detailed analysis of the iron(I) complex described below, LMeFe(styrene) (LMe = 2,4-bis(2,6-diisopropylphenylimido)-3-pentyl) (1; Fig. 1 (right)), which one of us (P. L. H.) reported earlier.8 This compound has a high-spin S = 3/2 ground state, and its η2 binding is midway between the π-alkene and ferracyclopropane resonance structures, as shown by crystallography and NMR spectroscopy. Strong backbonding was supported by computations for an analogous η2-alkyne complex.9 Most importantly, 1 has a monosubstituted alkene with three protons in the same η2 disposition as the FeMo-co-bound PA intermediate with bound allyl alcohol. Here, we show ENDOR studies of compound 1 and isotopologues that demonstrate the sensitivity of ENDOR to subtle structural features of such a complex, and give additional insight into the geometrical details of the PA intermediate.
Materials and methods
Sample preparation
Samples were synthesized, purified, and introduced into sample tubes in an MBraun glovebox in an N2 atmosphere maintained at or below 1 ppm of O2. Glassware and sample tubes were dried at 150 °C for at least 12 hours before use. Pentane, diethyl ether, benzene, and toluene were purified by passage through activated alumina and Q5 columns (Glass Contour Co., Laguna Beach, CA). All solvents were stored over activated 3 Å molecular sieves and passed through a plug of activated alumina before use. Deuterated cyclohexane was dried over potassium/benzophenone and vacuum transferred to a storage container before use. Graphite, Celite, and 3 Å molecular sieves were dried at 300 °C under vacuum for >12 h. Styrene-d3 and styrene-d5 were obtained from ICON Isotopes and vacuum distilled prior to use. Styrene-d1 and styrene-d2 were synthesized through published methods.10 α-13C-styrene and β-13C-styrene were obtained from Sigma-Aldrich (>98% 13C) purified by the freeze–pump–thaw degassing method. The iron complex 1 and its isotopologues were prepared according to the literature procedure, and characterized as described.81H NMR spectra of the isotopologues are shown in the ESI.† Samples for ENDOR spectroscopy were prepared by dissolving iron complexes in toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) benzene (3
benzene (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at a concentration of 2.1–2.5 mM in a quartz tube, and flash-freezing the solutions to 77 K.
1) at a concentration of 2.1–2.5 mM in a quartz tube, and flash-freezing the solutions to 77 K.
Crystallography of 1
Low-temperature diffraction data (ω-scans) were collected on a Rigaku SCX Mini diffractometer coupled to a Rigaku Mercury275R CCD with Mo Kα radiation (λ = 0.71073 Å). The diffraction images were processed and scaled using the Rigaku CrystalClear software.11 The data were solved with SHELXT and were refined against F2 on all data by full-matrix least squares with SHELXL.12 All non-hydrogen atoms were refined anisotropically. Unless stated otherwise, all hydrogen atoms were included in the model at geometrically calculated positions and refined using a riding model. (DFT was used to determine their positions for comparison to spectroscopic measurements, as described below.) The isotropic displacement parameters of all hydrogen atoms were fixed to 1.2 times the U value of the atoms to which they are linked (1.5 times for methyl groups). The terminal hydrogen atoms of the vinyl group in styrene were found in the difference map and freely refined. However, their atomic positions converged at chemically unreasonable values. Ultimately, geometrically restrained, riding atoms were used for H24 and H28. One of the two hexane solvent molecule was disordered near the crystallographic inversion center. The two positions were modeled with atoms {C10, C20, C30} as the major component set, where {C40, C50, C60} is the minor set. Numerous restraints were needed to maintain a chemically reasonable structure for the hexane solvent molecules. The site occupancies were freely refined and fixed at their converged values of 0.74(1) and 0.26(1), respectively. The full numbering scheme of complex 1 can be found in the ESI.† Full details of the X-ray structure determination are in the ESI.†EPR and ENDOR spectroscopy
X-band CW EPR measurements were performed on a Bruker ESP 300 spectrometer equipped with an Oxford Instruments ESR 910 continuous He flow cryostat. Q-band CW EPR and ENDOR spectra were collected at 2 K on a spectrometer with a helium immersion Dewar as previously reported.13 Stochastic field-modulation detected ENDOR technique, first reported by Brueggeman and Niklas,14 was utilized for 1H ENDOR measurement. In the stochastic ENDOR sequence, the RF is randomly hopped over the frequency range of the spectrum with the subtraction of a background signal (RF off) at each frequency. Pulsed ENDOR spectra were collected on a spectrometer described earlier,15 equipped with a helium immersion Dewar for measurements at a temperature of 2 K. ENDOR measurements employed the Mims pulse sequence (π/2–τ–π/2–T–π/2–τ-echo, RF applied during interval T).16For a nucleus with hyperfine coupling, A, Mims pulsed ENDOR has a response R which depends on the product, Aτ, according to eqn (1),
| R ∼ [1 − cos(2πAτ)] | (1) |
This function has zeros corresponding to minima in the ENDOR response (hyperfine “suppression holes”), at Aτ = n, with n = 0, 1,…, and maxima at Aτ = (2n+1)/2 with n = 0, 1,….17 The “holes” at A = n/τ with n = 1, 2, 3… can be adjusted by varying τ. However, the central n = 0 hole at ν = νN persists. This can be of significance in distinguishing a tensor that is dominated by anisotropic interactions from one that is dominated by isotropic ones. The latter would never lead to ENDOR intensity near νN; the former does so for certain orientations, but the ν = 0 Mims hole tends to diminish the differences between the two cases.
Density-functional theory calculation for hyperfine coupling constants of 1
DFT calculations used the ORCA program package, version 3.0.3.18 Calculations reported here employed the B3LYP functional.19 We used the Ahlrichs triple-ζ-quality basis set with one set of polarization functions, def2-TZVP,20 with ZORA relativistic corrections.21 SCF convergence was accelerated with the RI approximation using the def2-TZVP/J auxiliary basis set. An empirical van der Waals correction was applied to the DFT energy (D3BJ).22 The SCF calculations were tightly converged (TightSCF) with unrestricted spin (UKS). Geometry optimization used TightOpt criteria, and a numerical frequency calculation on the optimized geometry showed no negative frequencies. Hyperfine coupling constants were calculated in ORCA using this geometry but substituting the EPR-II basis set on C and H atoms.23Results
Structure of compound 1
The structure previously reported8 for 1 has anomalies that suggest unmodeled disorder in the core of the molecule. Re-refinement of the previous diffraction data showed that the best model for the published data has two positions of the Fe–diketiminate unit in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, and two positions of the styrene in a 4
1 ratio, and two positions of the styrene in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, in which the C
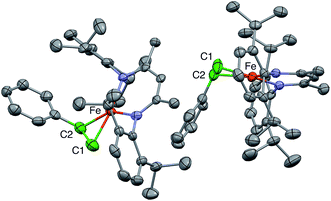
1 ratio, in which the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds are at right angles to one another. This physically unreasonable model is unsuitable for correlation with the ENDOR-derived parameters. Fortunately, we were able to grow a different crystal of a hexane solvate that gives a more reasonable model, with two molecules in the asymmetric unit (Fig. 2).
C bonds are at right angles to one another. This physically unreasonable model is unsuitable for correlation with the ENDOR-derived parameters. Fortunately, we were able to grow a different crystal of a hexane solvate that gives a more reasonable model, with two molecules in the asymmetric unit (Fig. 2).
In the new structure, the two independent molecules have very similar core structures (Table 1), each having the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond very close to the iron–diketiminate plane. The C
C double bond very close to the iron–diketiminate plane. The C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond lengths are equivalent at 1.384(8) and 1.380(8) Å, a distance that is significantly longer than that in free styrene (1.32 Å).24 This supports the description of this double bond as a π-complex with significant backbonding from the iron(I) ion into the π* orbitals of the alkene. Though one might imagine that the face-on binding mode of the alkene would make the C1–C2–C3 plane perpendicular to the Fe–C1–C2 plane (i.e. dihedral angle of 90° between the alkene plane and the iron–alkene plane), the phenyl substituent is tilted away from the metal to give a dihedral angle of 74 ± 1° between the C1–C2–C3 and Fe–C1–C2 planes. The distortion is presumably caused by steric interactions between the phenyl group and the supporting ligand, which twists the styrene around the axis formed by the C–C double bond (Fig. 3). The positions of the hydrogen atoms were not accurately obtained from the crystallographic analysis, because the electron density peaks for hydrogen atoms are small and diffuse from X-ray crystallography.
C bond lengths are equivalent at 1.384(8) and 1.380(8) Å, a distance that is significantly longer than that in free styrene (1.32 Å).24 This supports the description of this double bond as a π-complex with significant backbonding from the iron(I) ion into the π* orbitals of the alkene. Though one might imagine that the face-on binding mode of the alkene would make the C1–C2–C3 plane perpendicular to the Fe–C1–C2 plane (i.e. dihedral angle of 90° between the alkene plane and the iron–alkene plane), the phenyl substituent is tilted away from the metal to give a dihedral angle of 74 ± 1° between the C1–C2–C3 and Fe–C1–C2 planes. The distortion is presumably caused by steric interactions between the phenyl group and the supporting ligand, which twists the styrene around the axis formed by the C–C double bond (Fig. 3). The positions of the hydrogen atoms were not accurately obtained from the crystallographic analysis, because the electron density peaks for hydrogen atoms are small and diffuse from X-ray crystallography.
| Crystal molecule 1 | Crystal molecule 2 | DFT optimization | |
|---|---|---|---|
| Fe–N | 1.955, 1.977 | 1.963, 1.979 | 1.987, 1.993 |
| Fe–C1 | 1.996 | 2.015 | 2.001 |
| Fe–C2 | 2.020 | 2.033 | 2.062 |
| C–Fe–C | 40.2 | 39.4 | 41.0 |
| Dihedral (C–Fe–C to N–Fe–N) | 9.9 | 6.3 | 20.2 |
| Dihedral (C–Fe–C to C–C–C) | 74.8 | 74.1 | 61.2 |
| Fe–1-H | 2.568 | ||
| Fe–2-H | 2.604 | ||
| Fe–3-H | 2.632 | ||
| CCC plane – 1-H | 0.460 | ||
| CCC plane – 2-H | 0.416 | ||
| CCC plane – 3-H | 0.009 |
It is notable that the phenyl-bearing carbon C2 is further from the Fe atom than C1 by 0.020(7) Å in both independent molecules. Thus, the phenyl group on the alkene in 1 has two major influences on the geometry of alkene binding. (i) The Fe–C1–C2 triangle of 1 is scalene, not isosceles, with a longer distance to C2. (ii) The C1–C2–C3 plane tilts to place the phenyl group (and presumably the 3-H atom which is cis to the phenyl) further from the Fe atom.
Because the crystallographic analysis did not give the desired level of detail on the locations of the hydrogen atoms, we used density-functional calculations (B3LYP/def2-TZVP) to optimize a model of 1 with all atoms included. Fig. 3 shows the core of the optimized model, with the carbon and hydrogen atoms near the Fe colored green and purple, respectively, to highlight their positions. The DFT-optimized metrical parameters were in good agreement with the crystallographically determined structure (Table 1). There are some slight differences in the dihedral angles, which may result from the lack of crystal packing effects in the geometry optimized structure. The DFT model reproduces the crystallographically observed tilting of the phenyl group away from the iron as well as the difference between the two Fe–C bond distances. Importantly, the DFT model shows the hydrogen atom positions, and as expected the “tilt” of the alkene plane results in 3-H (cis to the phenyl) being furthest from the Fe center (see Table 1).
EPR spectra
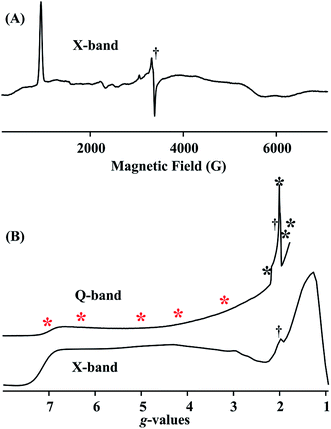
Fig. 4A and B (lower) show the derivative and absorption display X-band CW EPR spectrum of the S = 3/2 complex 1, whose highly anisotropic signal can be described in terms of a center with fictitious S′ = 1/2 spin that exhibits an effective g-tensor, g′ = [7.1, 1.3, 1.1]. This can be explained in terms of the transitions within the low-lying Kramers doublet of a true S = 3/2 (d7) system25 that exhibits a large and rhombic zero field splitting: |D| ≫ 0.3 cm−1, D < 0; rhombicity parameter, λ = |E/D| = 0.22; and intrinsic g-values for the true S = 3/2 spin state, g = [2.48, 2.00, 1.91]. The EPR spectrum also exhibits minor contributions at around g ∼4, ∼3 and ∼2, most likely from small amounts of decomposition and/or oxidized impurity. Fig. 4B (upper) displays the portion of the 2 K Q-band EPR absorption spectrum for compound 1 up to the highest magnetic field available. The asterisks in Fig. 4B show the fields at which ENDOR measurements were performed.1H/2H ENDOR spectra
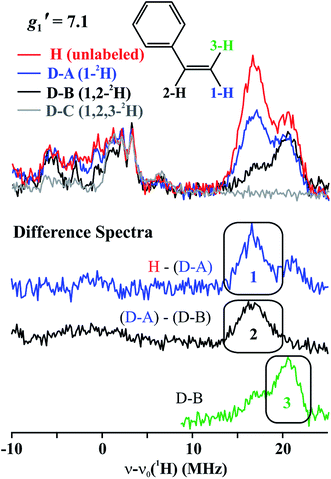
The top of Fig. 5 presents Q-band CW stochastic single-crystal-like 1H ENDOR spectra collected at g′1 = 7.1 from 1 prepared with the styrene H/D isotopologues illustrated in Fig. 5: H (unlabeled), D-A (1-2H), D-B (1,2-2H) and D-C (1,2,3-2H). The spectra show a strongly-coupled 1H ν+ pattern whose features are offset from the 1H Larmor frequency by one-half of their apparent hyperfine coupling, A′/2 = (g′1/ge)A/2 ∼ 17 MHz, which corresponds to an intrinsic hyperfine coupling to the S = 3/2 ion of A ∼10 MHz. This pattern contains contributions from all three vinyl protons as shown by the changes as the three protons of styrene (sample H) are replaced by deuterons in one (D-A), two (D-B) and all three (D-C) sites (Fig. 5, bottom). The feature contains no contributions from the aryl protons, as it disappears in the D-C spectrum, where all three vinyl protons are replaced with deuterium.The contribution from the 1-H proton is seen in the difference spectrum [H–(D-A)]; that of the 2-H proton likewise is provided by the [(D-A) − (D-B)] subtraction; that of 3-H is seen directly in the D-B spectrum. We assign the subsidiary signals of 1-1H and 3-1H to minor contamination (estimated as less than 30%) with unexchanged 3-H and 1-H and/or 2-H. From the frequencies of the peaks one obtains A′1(1-1H) ∼ A′1(2-1H) ∼33 MHz and A′1(3-1H) ∼42 MHz. Thus, these single-crystal-like spectra immediately reveal that the terminal hydrogens, (1-1H) and (3-1H), are not magnetically equivalent, indicative of deviations at the C1 terminal alkene carbon from idealized mirror symmetry through the Fe–C–C bonded triangle, in contrast to the identical couplings for the terminal H atoms and mirror symmetry for PA.
To estimate the full hyperfine coupling tensors26 and their orientations for the vinyl protons, a 2D field-frequency pattern of 1H CW stochastic/rf sweep ENDOR spectra was collected over the field range from g′1 to g ∼ 3; at higher fields (Fig. S1†) the extreme anisotropy of the effective g′ tensor of the S = 3/2 Fe(I) ion of 1 degrades both the intensity and the resolution of the 1H spectra. Although Mims 2H ENDOR signals for 1 could be collected at the higher fields (Fig. S2†), they were only of minimal use, as they were poorly resolved and distorted by Mims ‘holes’.27 We generated 2D patterns for the individual 1-H and 2-H vinyl protons, shown in Fig. 6 from the CW spectra collected at g > 3 by subtracting the sets of spectra as for Fig. 5; the pattern for 3-H in Fig. 6C was obtained directly from 1 with D-B (1,2-2H).
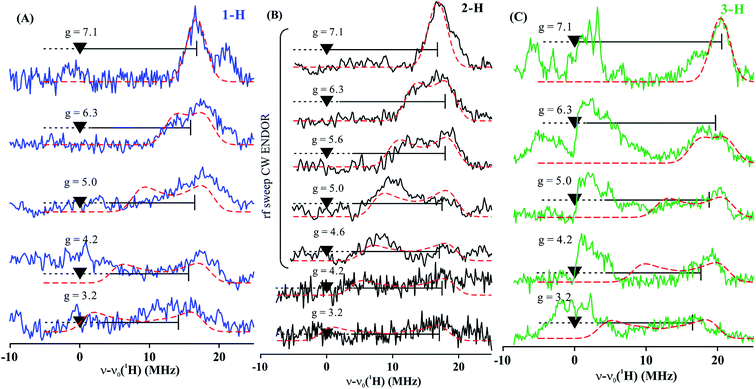 | ||
| Fig. 6 Two-dimensional frequency pattern of 1H CW stochastic/rf sweep ENDOR spectra for (A) 1-H, (B) 2-H, and (C) 3-H. Dashed red lines represent simulations with the GENDOR program26c using A and g′ tensors given in Table 2. | ||
The experimental 2D 1H/2H ENDOR patterns do not cover enough of the broad field range for this highly anisotropic S = 3/2 signal to achieve a unique fit to the 1H/2H hyperfine tensors, so we used the DFT model of 1 (see above) to calculate the intrinsic S = 3/2 hyperfine tensors for the vinyl protons and carbons of 1 (Table 2). The peak positions in the spectra taken at the single-crystal-like g′1 field value are well reproduced with the orientations of the tensors relative to the g tensor, to which the simulations are extremely sensitive. These values are listed in Table 2. Note that the DFT computations are not expected to give an accurate g tensor. Spectra at multiple fields were simulated using the calculated tensor components and fit orientations, and the resulting simulations are overlaid on the experimental 2D pattern in Fig. 6. Overall, this simulation procedure satisfactorily reproduces the experimental 2D pattern, supporting the synergistic use of ENDOR measurements and DFT computations to determine the proton hyperfine tensors of this high-spin iron(I) ion.
| A 1, A2, A3 (MHz) | A iso (MHz) | β (°) | ||
|---|---|---|---|---|
| a Hyperfine tensor components calculated by DFT; for 1H, values are supported by simulations using the Euler angle relating A to g derived from ENDOR simulation (see text). The uncertainty of the angles is ±1°. b From ref. 4; relative signs are experimentally determined, not absolute signs. | ||||
| 1 (styrene)a | 1-H | 13.9, −0.69, 0.89 | +4.7 | 41 |
| 2-H | 14.3, 2.4, −0.27 | +5.5 | 41 | |
| 3-H | 16.1, 4.7, 3.0 | +8.0 | 41 | |
| C1 | −12.8, −7.4, −5.2 | −8.5 | ND | |
| C2 | −12.5, −4.9, −3.0 | −6.8 | — | |
| Nitrogenase PA intermediateb | Ha[c,s] | 3, 16, 22.5 | 13.8 | |
| Hb | — | ∼4 | ||
| C1 | 5.1, 2.4, 3.5 | 3.7 | ||
| C2 | 0.55, 1.3, 1.4 | 1.1 | ||
In next making comparisons between the couplings for alkenes bound to 1 and PA, we take into account that the measured couplings for each nucleus of the alkene bound to the Fe of the PA intermediate (A) are modified from those for the alkene bound to an isolated Fe ion (Aint), such as 1, because the electron spins of the cluster Fe ions are coupled to give an total cluster spin of S = 1/2.28 As a result of this coupling the hyperfine interaction measured by ENDOR for each nucleus of the alkene bound to an Fe of the PA intermediate (A) is modified from that for the isolated Fe ion (Aint) through multiplication by a spin-coupling coefficient that is determined by nature of the spin coupling within the cluster, and may be greater or less than unity.
The principal components of the proton hyperfine interactions are the sum of an isotropic term, reflecting spin delocalization into the proton 1s orbital, and a traceless dipolar interaction with nearby spin density, Ai = Aiso + Ti (where i = 1–3). The Ti values are dominated by interaction with the spin on the bonded Fe, and vary inversely with the cube of the Fe–H distance. For comparisons, the dipolar coupling can be exemplified by the principal component of largest absolute value, Tmax. The different values of Tmax for the terminal vinylic protons of 1, with that for 1-H (9.2 MHz) being larger than that for 3-H (8.1 MHz), reflect the different calculated distances of these protons from Fe (2.568 Å vs. 2.632 Å, Table 1) caused by the tilt of the styrene. Correspondingly, Tmax for 2-H of 1 (8.8 MHz) lies between those for 1-H and 3-H, as does its distance from Fe (2.604 Å). These differences reflect the distorted geometry of 1, and contrast with the identical couplings for the terminal vinylic protons of PA.
The value of Tmax = 10.8 MHz for the two identical terminal protons of PA is reasonably similar to the values for the three vinylic protons of the styrene of 1 (8.1 to 9.2 MHz, Table 2). Likewise, the isotropic coupling, Aiso, for the terminal vinyl protons of the PA organometallic intermediate in nitrogenase, Table 2, is of similar magnitude to the average for those for the vinyl protons of 1, as shown in Table 2. Though the values are close, both Tmax and Aiso are somewhat greater for PA than 1, suggesting that the vector coupling coefficient of the alkene-coordinated Fe ion of PA may be greater than unity.
13C ENDOR spectra
To further characterize 1, we collected CW ENDOR spectra for 1 with individual 13C labels at the two vinyl carbons. Fig. S4† displays ENDOR spectra at g′1 for 13C1 labeled (red) and unlabeled (gray) 1, and their difference spectrum (black). The spectrum at this field exhibits ENDOR signals from 13C, weakly coupled 1H and strongly coupled 14N responses from the iron ligand of the diketiminate. As indicated in the figure, the difference spectrum at the g′1 single-crystal-like field shows a broad signal from 13C1 that arises from doublets split by the twice the 13C Larmor frequency and centered over a range of effective hyperfine coupling, A(13C)′/2 ∼ 10–15 MHz, corresponding to distributed intrinsic couplings A(13C)/2 = [A(13C)′/2] × (ge/g′1) ∼2.8–4.2 MHz. In the context of the DFT calculations, this suggests that the hyperfine tensor may be substantially rotated away from g′1. Unfortunately, the 13C difference signal (as well as the 14N signal) is lost as the field is raised, precluding any experimental determination of the full 13C1 hyperfine tensor.We also collected CW ENDOR spectra at g′1 for 13C2 labeled 1. However, the difference spectrum with unlabeled 1 failed to show any unambiguous 13C responses at g′1 or higher fields. We suggest this may reflect an even broader distribution in hyperfine couplings.
Discussion
This study shows that the 1H hyperfine couplings to the three vinyl protons of 1 reliably report the bonding and geometry of the alkene in this iron(I) complex, and they thus can be profitably compared to those of the AA protons of PA. Even though a number of factors reduce the precision for the vinyl 1H hyperfine couplings of 1 relative to those observed for the PA intermediate, comparison of the two systems yields structural information that was not previously available in the absence of the model complex.The key element in assigning the η2 structure of PA (Fig. 1) was the identical hyperfine coupling tensors for the two terminal 1H of the cluster-bound AA, one of which originated in the PA substrate (Hca) and one from solvent (Has) (Fig. 7).4 The S = 1/2 spin state of the PA intermediate, with its narrow g-spread, g = [2.123, 1.998, 1.986], allowed the 2D pattern of ENDOR spectra to be collected with high resolution across the entire EPR envelope of PA, and the ENDOR spectra from the two 1H overlay precisely at each field within the envelope. Likewise, the higher resolution of 2H spectra again yielded identical spectra for 2Hsa and 2Hca. These observations showed that Hca and Hsa exhibit magnetic equivalence, which in turn implies that these hydrogens are structurally equivalent and related by a local mirror symmetry, as illustrated by Fig. 7.
Analysis of the η2-alkene reference structures in the Cambridge Database at that time (M = Ta and Os, but not Fe) indicated that the only way for the vinylic protons of a bound alkene to be related in this way was through the π-alkene/metallacyclopropane structure.4 Specifically, these structures have high local symmetry at C1 that is consistent with the ENDOR measurements for the AA bound to FeMo-co in PA. In contrast, a binding mode in which the vinyl carbon atoms (C1 and C2) of the AA product each bind to a different Fe ion (dimetallacyclobutane) would be nonplanar (as in a known diosmium complex29), rendering the two C1 protons stereoelectronically and magnetically inequivalent.
Whereas the signals for Hca and Has of PA overlay at all fields, the spectra of 1 collected at the single-crystal-like field of g′1 = 7.1 (Fig. 5) show small but clear differences in the coupling to 1-H and 3-H. The largest 1H dipolar couplings (Tmax) are a good marker for the through-space distance from the Fe ion to the proton, and these values differ significantly for the terminal 1-H and 3-H of 1 (9.2 vs. 8.1 MHz, Table 2) as a consequence of the differing distances from Fe caused by the tilt of the alkene plane. Thus, the observation of inequivalent hyperfine couplings for the distorted structure of 1 supports the previous conclusion that a local mirror plane through the Fe–C–C unit is needed to observe equivalent couplings in PA. It is likely that the smaller size of the –CH2OH substituent of AA allows a more symmetric ‘face-on’ binding with no tilt, whereas the bulkier and more rigid phenyl substituent in 1 tilts the CH2 plane. Overall, it is evident that 1H ENDOR spectroscopy is an exceptionally sensitive reporter of distortions of the bound alkene.
The sensitivity of the ENDOR parameters of the two terminal 1H of a bound alkene to the small tilt in 1 supports the earlier rejection of a structural model in which the vinyl carbons (C1 and C2) of the AA each bind to a different Fe ion, because an alkene as part of a dimetallacyclobutane ring would be nonplanar, with an even larger tilt of the C1-Hca/Hsa fragment of bound AA. In short, the comparison of PA with 1 further substantiates the η2 binding in PA shown in Fig. 1A, with the C2–C1 (Hca/Hsa) plane of the AA alkene product perpendicular to the Fe–C2–C1 plane.
Additional key features of the PA analysis were that the C2 vinyl proton of PA (Hb) has a distinctly smaller isotropic coupling than the two Ha, and that C2 of AA has a much smaller hyperfine coupling than C3, which together were interpreted as implying that the Fe–C–C triangle is not equilateral, but scalene, with a longer bond to C2.4 The crystal structure of 1 shows a distortion in this direction, although with a difference in distances of only 0.02 Å. Correspondingly, although the estimated isotropic couplings for the C1 protons (1-H, 3-H) differ because of the structural distortion, their average is quite close to that for the C2 proton (2-H), again consistent with the small difference in Fe–C bond lengths. Thus, the data on the model complex support the conclusion that the Fe–C–C triangle in the enzyme environment is more distorted.
Conclusions
The ENDOR characterization of the crystallographically characterized biomimetic Fe complex 1, with its η2 coordination of styrene, provides an experimental connection between hyperfine and structural parameters of an alkene fragment on iron for the first time. The small tilt of the alkene plane in 1 away from normal to the Fe–C2–C1 plane causes a significant difference in the dipolar couplings of the two terminal vinylic H. This shows that the ENDOR measurements are highly sensitive to such structural details. The different couplings in the model contrast sharply with the identical couplings for the two terminal vinylic protons of AA in the PA intermediate, and this study thus shows that the AA vinylic fragment indeed binds face-on to Fe with negligible tilt of the alkene plane. In addition, the similar isotropic couplings of the protons on C1 and C2 of 1 correlate with a small difference in the Fe–C distances. The larger differences between the protons on C1 and C2 in the PA intermediate support the idea that the Fe–C distances to the alkene carbons of the PA nitrogenase intermediate differ significantly more than is observed for 1.Acknowledgements
The authors acknowledge support by the National Institutes of Health (GM065313 to P. L. H., GM111097 to B. M. H., GM116463 to S.·F. M.) We thank William Brennessel (University of Rochester) for re-analysis of the literature crystal structure of 1.Notes and references
- (a) R. H. Crabtree, The Organometallic Chemistry of the Transition Metals, Wiley-Interscience, New York, 6th edn, 2014 Search PubMed; (b) J. F. Hartwig, Organotransition Metal Chemistry, University Science Books, Sausalito, CA, 2010 Search PubMed.
- F. I. Rodriguez, J. J. Esch, A. E. Hall, B. M. Binder, G. E. Schaller and A. B. Bleecker, Science, 1999, 283, 996 CrossRef CAS PubMed.
- (a) M. A. Vincent, I. H. Hillier, G. Periyasamy and N. A. Burton, Dalton Trans., 2010, 3816 RSC; (b) R. Z. Liao, J. G. Yu and F. Himo, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22523 CrossRef CAS PubMed.
- H.-I. Lee, R. Y. Igarashi, M. Laryukhin, P. E. Doan, P. C. Dos Santos, D. R. Dean, L. C. Seefeldt and B. M. Hoffman, J. Am. Chem. Soc., 2004, 126, 9563 CrossRef CAS PubMed.
- G. E. Cutsail, J. Telser and B. M. Hoffman, Biochim. Biophys. Acta, Mol. Cell Res., 2015, 1853, 1370 CrossRef CAS PubMed.
- (a) M. Horitani, K. Shisler, W. E. Broderick, R. U. Hutcheson, K. S. Duschene, A. R. Marts, B. M. Hoffman and J. B. Broderick, Science, 2016, 352, 822 CrossRef CAS PubMed; (b) M. Dong, M. Horitani, B. Dzikovski, J. H. Freed, S. Ealick, B. M. Hoffman and H. Lin, J. Am. Chem. Soc., 2017, 139, 5680 CrossRef CAS PubMed.
- S. J. George, B. M. Barney, D. Mitra, R. Y. Igarashi, Y. Guo, D. R. Dean, S. P. Cramer and L. C. Seefeldt, J. Inorg. Biochem., 2012, 112, 85 CrossRef CAS PubMed.
- Y. Yu, J. M. Smith, C. J. Flaschenriem and P. L. Holland, Inorg. Chem., 2006, 45, 5742 CrossRef CAS PubMed.
- S. A. Stoian, Y. Yu, J. M. Smith, P. L. Holland, E. L. Bominaar and E. Münck, Inorg. Chem., 2005, 44, 4915 CrossRef CAS PubMed.
- E. J. Keliher, R. C. Burrell, H. R. Chobanian, K. L. Conkrite, R. Shukla and J. E. Baldwin, Org. Biomol. Chem., 2006, 4, 2777 CAS.
- CrystalClear-SM Expert, Rigaku Corporation, Tokyo, Japan, 2011 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- M. M. Werst, C. E. Davoust and B. M. Hoffman, J. Am. Chem. Soc., 1991, 113, 1533 CrossRef CAS.
- W. Brueggemann and J. R. Niklas, J. Magn. Reson., Ser. A, 1994, 108, 25 CrossRef CAS.
- C. E. Davoust, P. E. Doan and B. M. Hoffman, J. Magn. Reson., 1996, 119, 38 CrossRef CAS.
- P. E. Doan and B. M. Hoffman, Chem. Phys. Lett., 1997, 269, 208 CrossRef CAS.
- P. E. Doan, N. S. Lees, M. Shanmugam and B. M. Hoffman, Appl. Magn. Reson., 2010, 37, 763 CrossRef PubMed.
- (a) F. Neese, ORCA, MPI for Chemical Energy Conversion, Mülheim a.d. Ruhr, Germany, 2013, http://www.cec.mpg.de/forum/ Search PubMed; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2010, 2, 73 CrossRef.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908 CrossRef CAS PubMed.
- (a) S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- V. Barone, in Recent Advances in Density Functional Methods, Part I, ed. D. P. Chong, World Scientific, 1996 Search PubMed.
- A. D. Bond and J. E. Davies, Acta Crystallogr., Sect. A: Found. Crystallogr., 2001, 57, o1189–o1191 CrossRef.
- B. M. Hoffman, C. J. Weschler and F. Basolo, J. Am. Chem. Soc., 1976, 98, 5473 CrossRef CAS PubMed.
- (a) V. J. DeRose and B. M. Hoffman, Methods Enzymol., 1995, 246, 554 CAS; (b) B. M. Hoffman and R. J. Gurbiel, J. Magn. Reson., 1989, 82, 309 CAS; (c) P. E. Doan, The Past, Present, and Future of Orientation-Selected ENDOR Analysis: Solving the Challenges of Dipolar-Coupled Nuclei, in Paramagnetic Resonance of Metallobiomolecules, ed. J. Telser, American Chemical Society, 2003, pp. 55–81 Search PubMed.
- Spectra were also collected for a sample deuterated at the phenyl protons of styrene; see Fig. S3.†.
- J. M. Mouesca, L. Noodleman, D. A. Case and B. Lamotte, Inorg. Chem., 1995, 34, 4347 CrossRef CAS.
- M. R. Burke, J. Takats, F. W. Grevels and J. G. A. Reuvers, J. Am. Chem. Soc., 1983, 105, 4092 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional spectroscopic and crystallographic information. CCDC 1543306. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7sc01602f |
| ‡ Current address: School of Basic Science, Department of Chemistry, Rani Channamma University, Vidyasangama, PBNH-4, Belagavi, India. |
| This journal is © The Royal Society of Chemistry 2017 |