Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The road to nowhere: equilibrium partition coefficients for nanoparticles
Antonia
Praetorius
*a,
Nathalie
Tufenkji
b,
Kai-Uwe
Goss
c,
Martin
Scheringer
a,
Frank
von der Kammer
d and
Menachem
Elimelech
e
aInstitute for Chemical and Bioengineering, Swiss Federal Institute of Technology – ETH Zurich, Vladimir-Prelog-Weg 1, 8093 Zurich, Switzerland. E-mail: antonia.praetorius@chem.ethz.ch; Fax: +41 44 632 1189; Tel: +41 44 633 92 36
bDepartment of Chemical Engineering, McGill University, Montreal, Quebec H3A 0C5, Canada
cDepartment of Analytical Environmental Chemistry, Helmholtz-Centre for Environmental Research – UFZ, Leipzig, D-04318, Germany
dDepartment of Environmental Geosciences, University of Vienna, 1090 Vienna, Austria
eDepartment of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520, USA
First published on 10th June 2014
Abstract
Adequate fate descriptors are crucial input parameters in models used to predict the behaviour and transport of a contaminant in the environment and determine predicted environmental concentrations for risk assessment. When new fate models are being developed for emerging contaminants, such as engineered nanoparticles (ENPs), special care has to be applied in adjusting conventional approaches and fate descriptors to a new set of substances. The aim of this paper is to clarify misconceptions about the applicability of equilibrium partition coefficients, such as the octanol–water partition coefficient (Kow) or the soil–water distribution coefficient (Kd), whose application in the context of ENP fate assessment is frequently suggested despite lacking scientific justification. ENPs are present in the environment as thermodynamically unstable suspensions and their behaviour must be represented by kinetically controlled attachment and deposition processes as has been established by colloid science. Here, we illustrate the underlying theories of equilibrium partitioning and kinetically controlled attachment and discuss why the use of any coefficient based on equilibrium partitioning is inadequate for ENPs and can lead to significant errors in ENP fate predictions and risk assessment.
1. Introduction
Our ability to predict the behaviour of nanoparticles in natural aquatic systems is directly linked with our understanding of the processes governing the fate of nanoparticles in the environment and the adequate translation of these processes into conceptual models. Those models, while inherently being a simplified representation of the conceptualized system, require a solid mechanistic foundation based on the physico-chemical processes that govern the real system. For long, the environmental behaviour of organic chemicals and metals has been assessed using distribution coefficients such as the Henry's law constant or distribution functions of the Freundlich or Langmuir type.1,2 These coefficients are quantitative descriptors of how a substance distributes between certain phases (air/water, water/organic carbon, water/soil) and are derived from experiments which determine the ratio of e.g. dissolved and particle-bound fraction in the state of a thermodynamic equilibrium. Distribution coefficients have proven extremely powerful for the assessment and prediction of transport, retardation and accumulation of a wide range of substances, including metals and organic chemicals such as pesticides and polycyclic aromatic hydrocarbons (PAHs).1,2 The reason for the successful application of these distribution coefficients is that the underlying concept (distribution between two phases at equilibrium) describes well the processes taking place in the real system for a well-defined group of substances (typically non-ionizable organic chemicals).In recent years, growing concern about the fate of engineered nanoparticles (ENPs) in natural and engineered systems has led to a need to identify adequate fate descriptors to be used in ENP transport and fate models.3–5 Naturally, the straightforward determination and application of distribution coefficients in the field of environmental science resulted in the temptation to apply these established and relatively simple concepts to ENPs.3 However, when applying a concept well established for a specific group of substances to a fundamentally different type of material with distinctly different properties, caution needs to be used to ensure that the underlying concepts are still valid for the new material.4,6 Limitations of distribution coefficients to specific cases, such as polar and ionizable organic chemicals, have been widely discussed,1,7–9 but it seems that confusion exists regarding the question of how the distribution behaviour of ENPs should be described. Several recent publications report measured distribution coefficients for ENPs10–16 or propose their application in the context of ENP fate and risk assessment3,13,17 without acknowledging or sufficiently discussing the associated limitations.
Although ENPs are often treated as a fundamentally new class of materials, processes of colloidal particle aggregation and attachment to surfaces have been investigated for decades and the findings have been integrated into theories and models which have been demonstrated to accurately describe these processes in well controlled and relatively simple systems.18–20 Those models and theories are based on entirely kinetically controlled processes and have been used to describe aggregation, surface attachment (deposition) and transport processes of natural colloids and nanoparticles in the environment.21 To our knowledge, neither in traditional nor in environmental colloid science, the concept of an equilibrium distribution coefficient (Kd) has ever been successfully employed to describe colloidal particle behaviour.
The purpose of this paper is to clarify the fundamental differences between the two concepts of equilibrium partitioning and kinetically controlled attachment. We describe the underlying theories and discuss why the use of Kd or an analogous coefficient based on the same equilibrium distribution concept easily leads to erroneous interpretations and predictions of nanoparticle transport, distribution among environmental compartments and accumulation in the food chain.
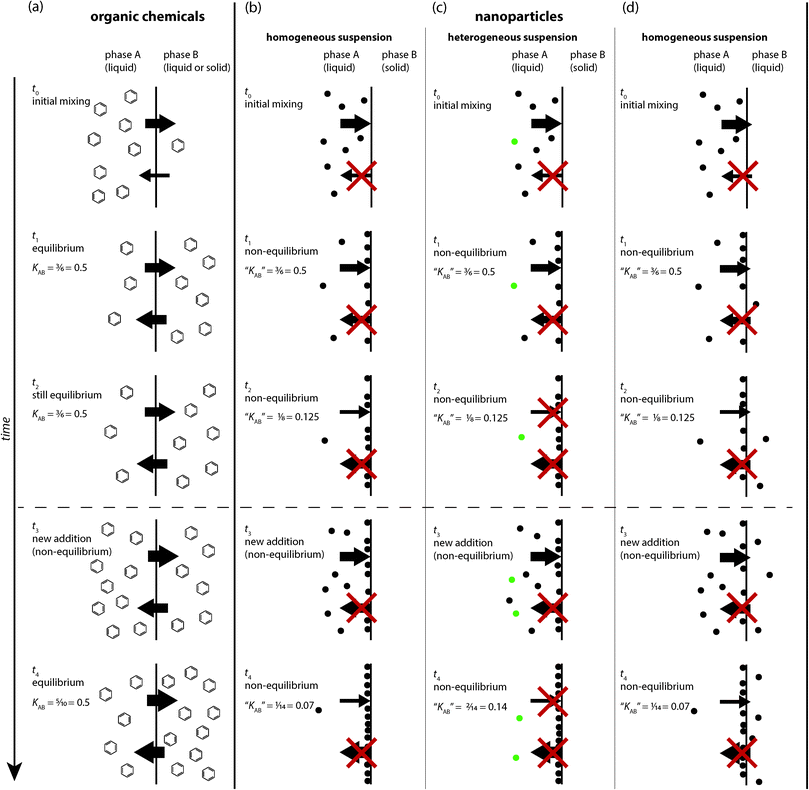
2. Theoretical bases of equilibrium partitioning and particle attachment
In this section, we summarize the theoretical concepts governing the behaviour of organic chemicals and ENPs in a two-phase system and highlight the most important differences between equilibrium partitioning of dissolved molecules and kinetically controlled attachment or deposition of particles. Fig. 1 illustrates the processes acting on organic chemicals (Fig. 1a) and ENPs (Fig. 1b–d) at a liquid–liquid and solid–liquid interface. Note that the focus of this paper is on the applicability of equilibrium partitioning to ENPs and not on general limitations or special cases of equilibrium partitioning, for example for ionized molecules, macromolecules or surfactants, which have been discussed elsewhere.1,7–9 Therefore, the discussion and depiction of equilibrium partitioning for organic chemicals in Fig. 1a is limited to the basic case of low-molecular-weight, uncharged organic molecules.It is important to note that the commonly used term “sorption” is a general term describing any kind of process through which a substance adsorbs on or absorbs into another substance. However, the terms sorption, adsorption, or absorption do not give any indication of the underlying processes driving the transfer of the sorbate, which can differ significantly for different substance types (as for example organic chemicals and ENPs). In some cases, adsorption or absorption are driven by thermodynamics and distribution isotherms (e.g. based on the Langmuir or Freundlich equations) can be used to describe adsorption, or distribution coefficients to describe absorption, based on the assumption that the system reaches a thermodynamic equilibrium. On the other hand, when adsorption or absorption are purely kinetically controlled, different mechanistic explanations are required to adequately describe the underlying processes as well as the quantitative macroscopic effect.
2.1. Equilibrium partitioning and partition coefficients
The equilibrium partitioning of organic chemicals (MW < 500 g mol−1) is mainly the result of two processes: molecular diffusion due to thermal motion and intermolecular interactions.2 Molecular diffusion alone would result in a uniform distribution of all molecules throughout space. However, in condensed phases (and non-ideal gas phases), neighbouring molecules interact with each other in various ways and this influences their partitioning. There are various types of interactions (e.g. non-specific van-der-Waals interactions, specific H-bond interactions, and ionic interactions). Depending on these interactions, molecules prefer to reside in one phase versus another. If the intermolecular interactions for molecule i are more attractive in phase B than in phase A, then the velocity or likelihood for a molecule i to diffuse out of phase A into phase B is increased. This leads to an enrichment of molecules i in phase B (Fig. 1a). Once the system reaches thermodynamic equilibrium, the number of molecules i in phase A times their likelihood to move from phase A to phase B is the same as the number of molecules i in phase B times their likelihood to move from phase B to phase A. That is, at equilibrium, the number of molecules moving back and forth between the two phases is the same. At equilibrium, the ratio of the equilibrium concentrations Ci,A/Ci,B equals the ratio of the rate constants ki,BA/ki,AB with which the molecules i move from phase B to phase A or vice versa (Fig. 1a). The ratio of Ci,A/Ci,B at equilibrium is referred to as the partition (or distribution) coefficient, Ki,AB.Typical equilibrium partition coefficients used in the context of chemical fate predictions and risk assessment are the octanol–water partition coefficient, Kow, and the distribution (or soil–water partition) coefficient, Kd. They are determined by mixing the chemical of interest in a system of octanol and water (Kow) or soil and water (Kd), allowing the system to reach thermodynamic equilibrium, separating the two phases and quantifying the concentration of the chemical in each phase using standard analytical techniques.22–24Kow and Kd are employed in environmental fate models and are very powerful input parameters to predict the distribution of organic chemicals between water and organic phases (e.g. soil, suspended sediments) in the environment.2 They are also used to predict bioconcentration factors (BCF) for aquatic organisms.1
The relationship between the equilibrium partition coefficient, Ki,AB = Ci,A/Ci,B, and the difference in standard Gibbs free energy, ΔGoi,AB, when i is distributed between phases A and B at equilibrium is given by:
ΔGoi,AB = − RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ki,AB Ki,AB | (1) |
The derivation of equilibrium partition coefficients is only valid because the solutions of substance i in solvents A and B are well-defined thermodynamic phases.† Moreover, the partition coefficient of substance i in the system of solvents A and B is not just the ratio of empirically determined concentrations of i in A and B, but is defined as the ratio of the concentrations of i in A and B at the point where the chemical potential, i.e. the molar free energy of i in the system of A and B is at its minimum (see eqn (1)). This means that the system is able to achieve the state of thermodynamic equilibrium by molecular diffusion of the molecules i, which enables them to overcome potential energy barriers to reach their most favourable (in terms of the Gibbs Free Energy) distribution between the two phases. This is an exact and non-empirical definition of the equilibrium partition coefficient.
2.2. Equilibrium partitioning does not apply to nanoparticles
In contrast to small organic molecules, nanoparticles do not form solutions, but colloidal dispersions,‡ which are multi-phase systems and thermodynamically unstable.25,26 Unlike small molecules, which can reach an energetically favourable state by dissolving in a solvent, colloidal particles are too large to dissolve, they form their own phase and require an energy input to be suspended throughout another phase. Nanoparticle dispersions can be kinetically stable for a long period of time (typically through electrostatic or steric stabilization) but they will never reach thermodynamic equilibrium and can consequently not be equilibrated with an additional phase. Therefore, empirically defined ratios of nanoparticle concentrations in two solvents A and B lack the fundamental definition of an equilibrium partition coefficient described above for organic molecules. They depend on many contingent factors such as the absolute amount of nanoparticles in the system, the initial conditions, and the time at which the concentrations are measured (Fig. 1b–d) (none of these factors affect equilibrium partition coefficients). Because the dispersions of nanoparticles in A and B are not thermodynamically stable, concentration ratios do not, by the very nature of the system, convey any general information about equilibrium partitioning properties of a type of nanoparticles, but are always limited to the conditions of their measurements.When nanoparticles are mixed in a two-phase system (Fig. 1b–d), they behave very differently from organic molecules (Fig. 1a). It is important to be aware of these differences to understand that any nanoparticle concentration ratio determined in such a system does not qualify as an equilibrium partition coefficient. Nanoparticles cannot reach thermodynamic equilibrium by distributing between the two phases A and B, but they can reduce their surface energy by attaching to each other (aggregation) or to the interface between A and B (deposition or attachment).
2.3. Kinetically controlled nanoparticle attachment and deposition
Particle–particle or particle–surface interactions that control nanoparticle attachment or deposition have traditionally been described by the Derjaguin–Landau–Verwey–Overbeek (DLVO) theory of colloidal stability,18,21 which considers the sum of electrical double-layer and van-der-Waals interactions. Additionally, non-DLVO forces such as steric, hydrophobic, and hydration forces can also play an important role in nanoparticle attachment.21 The profile of total interaction energy as a function of particle–particle or particle–surface distance is influenced by properties of the nanoparticles and the surrounding medium (i.e., particle size, zeta potential, Hamaker constant and electrolyte composition). Aggregation or deposition occurs if the particles can overcome the energy barrier and reach the deep primary energy minimum at short separation distances. If the conditions of the system are repulsive, e.g. due to a high zeta potential, the particle requires sufficient kinetic energy to overcome the energy barrier to reach the primary energy minimum. The energy provided by Brownian diffusion may be insufficient to overcome this repulsive energy barrier. In some cases, reversible deposition in a more shallow secondary energy minimum occurring at larger separation distances has been shown to contribute to the overall observed deposition.28 However, the importance of the secondary minimum for aggregation or deposition is directly related to the particle size and only significant for particles larger than ~0.5 μm, not for nanoparticles.21 Because of our inability to accurately quantify the physicochemical forces contributing to particle attachment, this step is typically described by an empirical parameter termed the particle attachment efficiency (α) that needs to be determined in aggregation or deposition experiments.Detachment of a nanoparticle deposited in the primary energy minimum does not occur spontaneously, i.e. by thermal motion, but only takes place if external forces (e.g. shear forces in turbulent waters or vigorous shaking in a laboratory experiment) are applied or the conditions of the system affecting the potential energy barrier, e.g. the ionic strength, are altered. Thus, the detachment of nanoparticles from a solid–liquid or liquid–liquid interface is a kinetically controlled process that relies on the nanoparticle overcoming the forces holding it in an energy minimum. This process is different from the spontaneous release of molecules sorbed at an interface. Therefore, the addition of more nanoparticles at a certain time point (t3) (Fig. 1b–d) does not result in an equivalent distribution of those particles (e.g. when compared to t2) as it is the case for dissolved organic molecules. Rather, the addition of new nanoparticles simply results in more particles attaching to the solid–liquid or liquid–liquid interface, yielding a new value of “KAB”. Thus, it is incorrect to describe nanoparticle attachment to a solid–liquid interface as an equilibrium process, because the apparent partition coefficient “KAB” changes with time.
Because the transfer of suspended nanoparticles from a liquid phase to a solid–liquid interface (Fig. 1b, c) is not a process reaching thermodynamic equilibrium, the mass transfer of nanoparticles from the fluid phase to the surface needs to be described in kinetic terms. The mass transfer of nanoparticles is described by the convective–diffusion equation, which can be solved for different well-defined geometries.29 For instance, the deposition of nanoparticles onto granular media is of importance in many environmental processes and is the subject of many theoretical and experimental studies.21 Often, an individual grain in a granular medium can be approximated as a sphere, in which case the mass transport of nanoparticles to the grain surface is described by the single-collector contact efficiency (η0).30,31 The single-collector contact efficiency considers the contributions of three major mechanisms for transport of particles to the solid surface; namely, gravitational sedimentation, interception and Brownian diffusion (the latter being the dominant mechanism for nano-sized particles). This kinetic parameter can readily be evaluated for different environmental systems by using a closed-form correlation equation or by numerically solving the steady-state convective–diffusion equation.30 In the context of nanoparticle deposition onto granular media, the particle attachment rate constant (katt) is related to η0 and α via
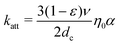 | (2) |
The quantitative analysis approach described above (including eqn (2)) is well suited for describing the kinetic deposition behavior of nanoparticles in relatively “ideal” conditions; namely, in homogeneous, well-defined granular media such as those used in controlled laboratory studies. However, in natural granular environments, it is not straightforward to evaluate katt (or η0) because of the inherent chemical and physical heterogeneities of the granular medium. In such environments, the kinetic deposition and release coefficients for nanoparticles must be determined from laboratory column studies with the natural granular material. For example, in the simplest case of irreversible nanoparticle deposition, the analytical solution to the one-dimensional advection–dispersion equation can be fitted to the measured nanoparticle breakthrough curves from columns packed with natural grains.32
Regardless of the system geometry, Fig. 1b and c describe the transfer of nanoparticles from a homogeneous or heterogeneous (in terms of nanoparticle population) suspension to the solid–liquid interface. In Fig. 1b and c, it is clear that the number of attached nanoparticles increases with time in this purely kinetically controlled process. Moreover, if the observed quantities of suspended versus attached nanoparticles are used to quantify an apparent partition coefficient, “KAB”, the value of this parameter will vary with time. Hence, the use of an equilibrium distribution concept is clearly inappropriate in these situations. Nanoparticles can readily attach at a liquid–liquid interface as this results in the reduction of their free energy (compared to a particle suspended in the bulk fluid) (Fig. 1d). However, a nanoparticle is much less likely to cross the liquid–liquid interface into another phase because this requires overcoming significant capillary and viscous forces (except in the case of a liquid–liquid interface having a very low interfacial tension).33 Nevertheless, the nanoparticles remain dispersed and do not truly dissolve in any of the liquid phases. Thus, as described above for the case where nanoparticles attach at a solid–liquid interface (and illustrated in Fig. 1d), the attachment of nanoparticles to a liquid–liquid interface cannot be described by an equilibrium partition coefficient “KAB”.
Another distinction to be made with regards to ENPs is their inherent heterogeneity. A dispersion of ENPs is an assembly of not fully similar entities, contrary to a solution of a chemical substance, where every molecule is identical to the other. Hence, ENP dispersions exhibit not only a distribution in particle size, shape and surface chemistry, but also a population heterogeneity in terms of their attachment behaviour.28,34Fig. 1c also shows how the apparent value of “KAB” will be different when the original nanoparticle dispersion consists of heterogeneous nanoparticle populations having distinct physicochemical properties that lead to different rates of attachment. This might be interpreted as the development of a dynamic equilibrium (Fig. 1c), but again would introduce a misrepresentation of the underlying processes.
3. The concept of partitioning is misused for nanoparticles
In summary, ENPs do not form solutions in environmental media but dispersions, which are thermodynamically unstable. Attachment of ENPs to other particles or surfaces is not driven by thermodynamically controlled equilibrium partitioning. Similar limitations have been discussed previously for microbial transport.35 It has been shown, for example, that attachment and detachment of bacteriophages (which are also of nanometric size) are kinetically controlled and it was suggested that the application of predictive models for microbial transport on the basis of equilibrium sorption could lead to significant errors.36Although the theories underlying partitioning behaviour and colloidal science are well-established concepts, there exists on-going confusion in the scientific community regarding ENP transfer between different environmental phases and compartments. Several experimental attempts have been made to determine partition coefficients for ENPs. In some cases, the inappropriateness of such measurements was recognized;37,38 however, in most instances, some type of partition coefficient was still derived and reported.10–16,39–43
Forouzangohar and Kookana37 clearly demonstrated that the partitioning concept is not even applicable to fullerenes (C60), which could in principle be viewed as a borderline case between organic molecules and nanoparticles. In an experiment measuring the interaction of C60 with soil in different ethanol–water mixtures, they found that C60 does not follow the behaviour expected for a dissolved hydrophobic molecule. Only a very small fraction of C60 is molecularly dissolved in water, whereas most is present as negatively charged nano-C60 clusters (nC60), whose interactions with soil particles are dominated by their surface characteristics and aggregation and deposition mechanisms rather than equilibrium partitioning. Forouzangohar and Kookana37 therefore warn against using the Kd term in the context of nC60 fate assessment, as the partitioning concept is not applicable to the environmentally relevant nC60 particles.
Several other experiments have shown that ENPs do not follow equilibrium partitioning.11,12,14,16 For example, different ENPs studied in a two-phase liquid system (to determine “Kow” values) did not dissolve and partition between the two phases but formed a third phase at the interface between octanol and water.14 In another study, the distribution behaviour of multi-walled carbon nanotubes (MWCNTs) between water and soil was shown to be heavily influenced by the aggregation and settling of the MWCNTs rather than by equilibrium partitioning.16 Elsewhere, it was recognized that the equilibrium assumption is not valid for the interaction of ENPs and soils and therefore Kd values should not be determined for ENPs.11,12 However, it appears that rather than accepting the inapplicability of the equilibrium partition concept to ENPs, many scientists are tempted to propose some operationally defined (partition) coefficients. Such operationally defined coefficients are, for example, “interface coefficients, KI”, to account for the ENP fraction that “partitions” to the interface14 (note that the interface coefficient proposed here is not related to the thermodynamic equilibrium partition coefficients for surfactants at liquid–liquid interfaces described elsewhere44,45), the “corrected soil sorption coefficients, Kcd”, to account for the effect of aggregative sedimentation16 and the “retention coefficients, Kr”, which are essentially measured like Kd values, but do not assume equilibrium.11,12 All these system-specific coefficients do not have a thermodynamic basis, but depend on contingent, system-specific factors; they do not replace the need for studying the system from a colloid science perspective and, most importantly, they can be strongly misleading when applied in the same manner as true equilibrium partition coefficients, for example, in environmental fate predictions.
There are also several studies that report measured partition coefficient values for ENPs without discussing any possible issues or limitations of this approach.10,13,15 In this context, it is important to remember that the fact that a value can be operationally defined and measured does not necessarily make it scientifically meaningful. The underlying equilibrium principles are still not applicable to ENPs and if this is ignored, inconsistencies in the results are easily overlooked or not apparent when the measurements are limited to a small set of conditions.
4. Implications
It is of great importance that scientists in the field of ENP fate and risk assessment gain a common understanding of, and agreement on, appropriate ENP fate descriptors. These fate descriptors must be based on established principles, theories and concepts and should not be driven by the idea that approaches established for organic chemicals can be directly applied to ENPs. While “partition coefficients” derived from batch experiments are often easier and faster to measure than attachment efficiencies (especially for heteroaggregation), their use is not justified, as they have no scientific meaning for ENPs. The determination and use of descriptors that either have been developed for an entirely different group of chemicals or that introduce new concepts must be preceded by a detailed examination of their applicability in controlled experiments. It is critical to ensure that defined fate descriptors have a well-founded physical or chemical meaning and are not simply artefacts of an experimental design.The use of “partition coefficients” instead of attachment efficiencies in predictive environmental fate or bioconcentration models for ENPs will very likely lead to erroneous results, thereby making risk assessment based on these results meaningless. The entirely kinetic nature of the processes that ENPs undergo in the environment and the heterogeneous nature of nanomaterials are in no way represented by equilibrium partition coefficients. It is imperative to recognize that time and resources invested in measuring and reporting “partition coefficients” for ENPs without substantiating their physico-chemical basis and proving their applicability would be better invested in the determination of adequate ENP fate descriptors, such as attachment efficiencies for aggregation and deposition.
References
- J. L. M. Hermens, J. H. M. de Bruijn and D. N. Brooke, Environ. Toxicol. Chem., 2013, 32, 732–733 CrossRef CAS PubMed.
- R. P. Schwarzenbach, P. M. Gschwend and D. M. Imboden, Environmental Organic Chemistry, John Wiley and Sons, Inc., 2nd edn, 2003 Search PubMed.
- P. Westerhoff and B. Nowack, Acc. Chem. Res., 2013, 46, 844–853 CrossRef CAS PubMed.
- G. V. Lowry, E. M. Hotze, E. S. Bernhardt, D. D. Dionysiou, J. A. Pedersen, M. R. Wiesner and B. Xing, J. Environ. Qual., 2010, 39, 1867–1874 CrossRef CAS.
- P. J. J. Alvarez, V. Colvin, J. Lead and V. Stone, ACS Nano, 2009, 3, 1616–1619 CrossRef CAS PubMed.
- A. Praetorius, M. Scheringer and K. Hungerbühler, Environ. Sci. Technol., 2012, 46, 6705–6713 CrossRef CAS PubMed.
- V. Burke, S. Treumann, U. Duennbier, J. Greskowiak and G. Massmann, J. Contam. Hydrol., 2013, 154, 29–41 CrossRef CAS PubMed.
- B. I. Escher and R. P. Schwarzenbach, Environ. Sci. Technol., 1996, 30, 260–270 CrossRef CAS.
- W. H. J. Vaes, E. U. Ramos, H. J. M. Verhaar and J. L. M. Hermens, Environ. Toxicol. Chem., 1998, 17, 1380–1384 CrossRef CAS.
- C.-Y. Chen and C. T. Jafvert, Environ. Sci. Technol., 2009, 43, 7370–7375 CrossRef CAS.
- G. Cornelis, J. K. Kirby, D. Beak, D. Chittleborough and M. J. McLaughlin, Environ. Chem., 2010, 7, 298–308 CrossRef CAS.
- G. Cornelis, B. Ryan, M. J. McLaughlin, J. K. Kirby, D. Beak and D. Chittleborough, Environ. Sci. Technol., 2011, 45, 2777–2782 CrossRef CAS PubMed.
- C. O. Hendren, A. R. Badireddy, E. Casman and M. R. Wiesner, Sci. Total Environ., 2013, 449, 418–425 CrossRef CAS PubMed.
- K. D. Hristovski, P. K. Westerhoff and J. D. Posner, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2011, 46, 636–647 CAS.
- C. T. Jafvert and P. P. Kulkarni, Environ. Sci. Technol., 2008, 42, 5945–5950 CrossRef CAS.
- M.-H. Jang, Y. S. Hwang, S.-K. Lee and Y.-J. Lee, Fullerenes, Nanotubes, Carbon Nanostruct., 2013, 21, 916–929 CrossRef CAS.
- A. A. Koelmans, B. Nowack and M. R. Wiesner, Environ. Pollut., 2009, 157, 1110–1116 CrossRef CAS PubMed.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, Particle Deposition & Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, Woburn, 1998 Search PubMed.
- R. Kretzschmar, M. Borkovec, D. Grolimund and M. Elimelech, in Advances in Agronomy, Academic Press, 1999, ch. Mobile Subsurface Colloids and Their Role in Contaminant Transport, vol. 66, pp. 121–193 Search PubMed.
- J. N. Ryan and M. Elimelech, Colloids Surf., A, 1996, 107, 1–56 CrossRef CAS.
- A. R. Petosa, D. P. Jaisi, I. R. Quevedo, M. Elimelech and N. Tufenkji, Environ. Sci. Technol., 2010, 44, 6532–6549 CrossRef CAS PubMed.
- OECD, Test No. 107: Partition Coefficient (n-octanol/water): Shake Flask Method, OECD Guidelines for the Testing of Chemicals, Section 1, OECD Publishing, 1995 Search PubMed.
- OECD, Test No. 117: Partition Coefficient (n-octanol/water), HPLC Method, OECD Guidelines for the Testing of Chemicals, Section 1, OECD Publishing, 2004 Search PubMed.
- OECD, Test No. 123: Partition Coefficient (1-Octanol/Water): Slow-Stirring Method, OECD Guidelines for the Testing of Chemicals, Section 1, OECD Publishing, 2006 Search PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, W. H. Freeman and Company, New York, 7th edn, 2002 Search PubMed.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, in Particle Deposition & Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, Woburn, 1998, ch. 1: Introduction Search PubMed.
- IUPAC, Compendium of Chemical Terminology, 2nd edn (the “Gold Book”), compiled by A. D. McNaught and A. Wilkinson, Blackwell Scientific Publications, Oxford, 1997. XML on-line corrected version: http://goldbook.iupac.org (2006–) created by M. Nic, J. Jirat, B. Kosata; updates compiled by A. Jenkins. ISBN 0-9678550-9-8 DOI:10.1351/goldbook.
- N. Tufenkji and M. Elimelech, Langmuir, 2005, 21, 841–852 CrossRef CAS PubMed.
- M. Elimelech, J. Gregory, X. Jia and R. A. Williams, in Particle Deposition & Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, Woburn, 1998, ch. 6: Modelling of Aggregation Processes Search PubMed.
- N. Tufenkji and M. Elimelech, Environ. Sci. Technol., 2004, 38, 529–536 CrossRef CAS.
- K.-M. Yao, M. T. Habibian and C. R. O'Melia, Environ. Sci. Technol., 1971, 5, 1105–1112 CrossRef CAS.
- D. Grolimund, M. Elimelech, M. Borkovec, K. Barmettler, R. Kretzschmar and H. Sticher, Environ. Sci. Technol., 1998, 32, 3562–3569 CrossRef CAS.
- A. Sinha, A. K. Mollah, S. Hardt and R. Ganguly, Soft Matter, 2013, 9, 5438–5447 RSC.
- N. Tufenkji and M. Elimelech, Langmuir, 2005, 21, 10896–10897 CrossRef CAS.
- N. Tufenkji, Adv. Water Resour., 2007, 30, 1455–1469 CrossRef PubMed.
- R. C. Bales, S. R. Hinkle, T. W. Kroeger, K. Stocking and C. P. Gerba, Environ. Sci. Technol., 1991, 25, 2088–2095 CrossRef CAS.
- M. Forouzangohar and R. S. Kookana, J. Environ. Monit., 2011, 13, 1190–1194 RSC.
- E. J. Petersen, Q. Huang and W. J. Weber Jr., Environ. Toxicol. Chem., 2010, 29, 1106–1112 CAS.
- W.-C. Hou, B. Y. Moghadam, P. Westerhoff and J. D. Posner, Langmuir, 2011, 27, 11899–11905 CrossRef CAS PubMed.
- W.-C. Hou, B. Y. Moghadam, C. Corredor, P. Westerhoff and J. D. Posner, Environ. Sci. Technol., 2012, 46, 1869–1876 CrossRef CAS PubMed.
- G. Cornelis, C. Doolette, M. Thomas, M. J. McLaughlin, J. K. Kirby, D. G. Beak and D. Chittleborough, Soil Sci. Soc. Am. J., 2012, 76, 891–902 CrossRef CAS.
- R. Avanasi, W. A. Jackson, B. Sherwin, J. F. Mudge and T. A. Anderson, Environ. Sci. Technol., 2014, 48, 2792–2797 CrossRef CAS PubMed.
- J. Rottman, L. C. Platt, R. Sierra-Alvarez and F. Shadman, Chem. Eng. J., 2013, 217, 212–220 CrossRef CAS PubMed.
- A. Graciaa, J. Lachaise, J. G. Sayous, P. Grenier, S. Yiv, R. S. Schechter and W. H. Wade, J. Colloid Interface Sci., 1983, 93, 474–486 CrossRef CAS.
- A. Graciaa, J. Andérez, C. Bracho, J. Lachaise, J.-L. Salager, L. Tolosa and F. Ysambertt, Adv. Colloid Interface Sci., 2006, 123–126, 63–73 CrossRef CAS PubMed.
Footnotes |
| † According to J. W. Gibbs, a phase is a state of matter that is uniform throughout, both in chemical composition and physical state. A solution is composed of only one phase and is uniform on a microscopic level.25 |
| ‡ A colloidal dispersion is a system of particles in the size range of approximately 1 nm to 1 μm dispersed in a continuous phase of a different composition or state. Unlike a solution, a dispersion is composed of more than one phase and is only uniform on a macroscopic scale, but not on a microscopic scale.26,27 |
| This journal is © The Royal Society of Chemistry 2014 |