Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electrocatalysis of hydrogen peroxide reactions on perovskite oxides: experiment versus kinetic modeling†
T.
Poux
a,
A.
Bonnefont
b,
A.
Ryabova
c,
G.
Kéranguéven
a,
G. A.
Tsirlina
c and
E. R.
Savinova
*a
aInstitut de Chimie et Procédés pour l'Energie, l'Environnement et la Santé, UMR 7515 CNRS-University of Strasbourg, 25 rue Becquerel, 67087 Strasbourg Cedex, France. E-mail: Elena.Savinova@unistra.fr; Fax: +33(0)3 68 85 27 61; Tel: +33(0)3 68 85 27 39
bInstitut de Chimie de Strasbourg, UMR 7177 CNRS-University of Strasbourg, 4 rue Blaise Pascal, 67070 Strasbourg, France
cFaculty of Chemistry, Lomonosov Moscow State University, 119991 Leninskie Gory, Moscow, Russia
First published on 28th February 2014
Abstract
Hydrogen peroxide has been identified as a stable intermediate of the electrochemical oxygen reduction reaction on various electrodes including metal, metal oxide and carbon materials. In this article we study the hydrogen peroxide oxidation and reduction reactions in alkaline medium using a rotating disc electrode (RDE) method on oxides of the perovskite family (LaCoO3, LaMnO3 and La0.8Sr0.2MnO3) which are considered as promising electrocatalytic materials for the cathode of liquid and solid alkaline fuel cells. The experimental findings, such as the higher activity of Mn-compared to that of Co-perovskites, the shape of RDE curves, and the influence of the H2O2 concentration, are rationalized with the help of a microkinetic model.
1. Introduction
Hydrogen peroxide has been identified as a stable intermediate of the electrochemical oxygen reduction reaction (ORR) on various electrodes including metal, metal oxide and carbon materials. In this article we study the hydrogen peroxide oxidation and reduction reactions (HPOR/HPRR) in alkaline medium on oxides of the perovskite family which are considered as promising electrocatalytic materials for the cathode of liquid and solid alkaline fuel cells. While several researchers studied the catalytic hydrogen peroxide decomposition kinetics on perovskite oxides, very few published results can be found for the study of the electrochemical HPOR/HPRR on perovskite oxides,1–3 and these are unfortunately not sufficiently detailed.Considering the value of pKa of H2O2 (11.74), in alkaline media it transforms into HO2−:
| H2O2 + OH− ⇆ HO2−+ H2O | (I) |
Four electrode reactions can theoretically occur in the presence of HO2−: HO2− reduction into OH− (II), HO2− oxidation into O2 (III), and the inverse reactions, OH− oxidation into HO2− (−II) and O2 reduction into HO2− (−III).
| HO2− + 2e− + H2O ⇆ 3OH−, E° = 1.71 VRHE at pH 14 | (II) |
| HO2− + OH− ⇆ O2 + H2O + 2e−, E° = 0.77 VRHE at pH 14 | (III) |
Given the standard potential of the HO2−/OH− couple, the OH− oxidation into HO2− (step −II) is unlikely in the potential range of interest for a cathode of an alkaline fuel cell, and will be neglected in this work. Thus, the current–potential curve over a perovskite electrode in a H2O2 containing electrolyte is essentially determined by reactions II, III, and −III.
In this work, the HPOR and HPRR are studied using the rotating disc electrode (RDE) method on two oxides of the perovskite family, LaCoO3 and La0.8Sr0.2MnO3, which demonstrated distinct behavior in the ORR (see our recent work in ref. 5), as well as on LaMnO3. The activity of the oxide materials is compared with that of Pt/C, a reference material in fuel cell electrocatalysis, and with carbon. The latter is an essential component of transition metal oxide-based cathodes improving their electronic conductivity, and thus the degree of the catalyst utilization. To better understand the mechanism of the HPOR and HPRR, and the ORR, on perovskite oxides, a kinetic model is proposed, and the experimental RDE curves are compared with the simulated ones. The study of the influence of the H2O2 concentration on the HPOR and HPRR allows one to shed light on the reaction kinetics and helps to validate the model assumptions.
2. Experimental
LaCoO3, LaMnO3 and La0.8Sr0.2MnO3 were synthesized at the Moscow State University using polyacrylamide gel by a soft chemistry method, which offers materials with higher surface areas than conventional high temperature approaches. For the synthesis procedure the reader is referred to ref. 5. Specific surface areas of LaCoO3, LaMnO3 and La0.8Sr0.2MnO3 measured by BET were 10, 14 and 17 m2 g−1, respectively. Oxides were mixed with carbon and deposited on a glassy carbon RDE (0.07 cm2 geometric area, Autolab) in the form of a thin layer.5 Carbon of the Sibunit family with a BET surface area of 65.7 m2 g−1 was chosen due to its high purity and high electron conductivity.6 In order to improve the adhesion of the perovskite and carbon particles onto the GC support, an alkaline ionomer (AS-4 from Tokuyama Company) was deposited on top of the dry catalyst layer to form a thin film (the ionomer loading was 2.4 μg cm−2). For further details on the electrode preparation the reader is referred to ref. 5. For all oxide/carbon loadings utilized in this work the catalytic layer thickness was smaller than the diffusion layer thickness.Pt/C electrodes were prepared by drop-casting a suspension containing Pt/C (40 wt% Pt on carbon black, Alfa Aesar) to obtain 20 μg cm−2 Pt loading. The roughness factor of Pt on the electrode estimated using the coulometry of the hydrogen underpotential deposition was equal to 6.
Electrochemical measurements were performed at 25 °C in a three electrode cell whose parts in contact with the electrolyte were made out of Teflon. The electrolyte was 1 M NaOH prepared from extra pure NaOH solution (50 wt% solution in water, Acros Organics) and ultrapure water (Purelab: 18.2 MΩ cm, <3 ppb TOC). The counter electrode was a platinum wire and the reference electrode was a Hg/HgO/1 M NaOH electrode (IJ Cambria Scientific). In what follows the electrode potentials are given in the RHE (reversible hydrogen electrode) scale. RDE curves were IR-corrected by using the value of the electrolyte resistance (15 Ohm) determined from the high frequency part of the electrochemical impedance spectra (measured in the 1 Hz to 100 kHz range). Electrochemical measurements were performed using an Autolab potentiostat with an analog scan generator at a scan rate of 10 mV s−1. H2O2 solutions were prepared from 30 wt% solution in water (SupraPur, Merck) titrated with standardized KMnO4.
3. Results and discussion
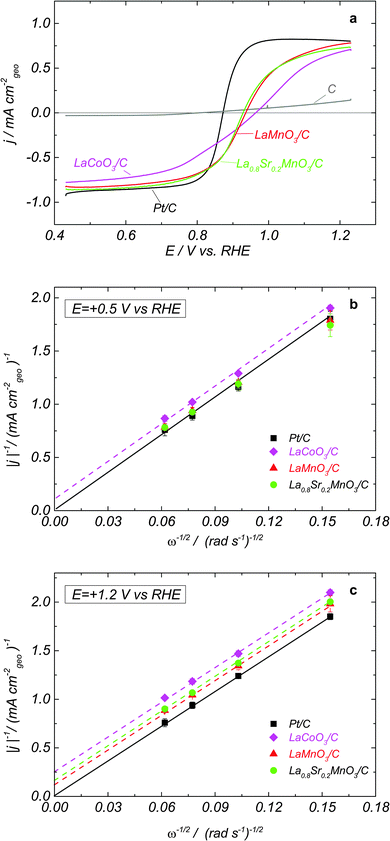
Fig. 1a shows positive scans of RDE voltammograms in N2-purged 1 M NaOH containing 0.84 mM H2O2 for LaCoO3/carbon, LaMnO3/carbon and La0.8Sr0.2MnO3/carbon composite electrodes, as well as for Pt/C and Sibunit carbon. Such H2O2 concentration was chosen since it corresponds to the O2 concentration in the O2 saturated electrolyte. For Pt/C in agreement with the literature data7–10 the voltammogram is reversible, suggesting fast hydrogen peroxide oxidation and reduction reactions, and the anodic and cathodic current plateaus correspond to the diffusion limited HPOR and HPRR, as confirmed by the Levich–Koutecky (LK) plots shown in Fig. 1b and c. For Sibunit carbon, the voltammogram is strongly irreversible, pointing to a very slow HPOR and an even slower HPRR (Fig. 1, grey curve). For oxide/carbon composites, both the anodic and the cathodic waves have smaller slopes compared to Pt, pointing out at slower electrocatalysis of hydrogen peroxide reactions on studied perovskite oxides. Furthermore, the mixed potential values, where the sum of currents of all electrode reactions (reactions II/−II and III/−III) is equal to zero, for perovskite oxides are shifted positive compared to those of Pt/C, suggesting a slower HO2− oxidation, notably for LaCoO3. In the absence of carbon, perovskite oxides show slower hydrogen peroxide oxidation/reduction kinetics (Fig. S1, ESI†). However, contrary to what has recently been demonstrated for the ORR on oxides of the perovskite family, where carbon plays a dual role, (i) improving the interparticle contact, and also (ii) participating in the ORR electrocatalysis, the enhancement of the rates of HPOR and HPRR is predominantly due to the first factor (improvement of the electronic conductivity of the catalytic layer). This is due to the low catalytic activity of carbon in HO2− reactions (cf.Fig. 1a, grey curve). Note also that for LaMnO3 the effect of addition of carbon on the RDE curves is stronger compared to that for the La0.8Sr0.2MnO3. This can be attributed to a higher intrinsic electron conductivity of the doped compared for the undoped Mn-based perovskite (for further details see ESI†).The Mn-based LaMnO3 and La0.8Sr0.2MnO3 perovskites display close mixed potentials (similar trends can be found in the literature for La1−xSrxMnO31), and very similar activities for HO2− reduction/oxidation, once sufficient amount of carbon is present in the catalytic layer (Fig. 1a). Moreover, their HO2− reduction and oxidation currents approach the diffusion plateau reached by the Pt/C electrode at low and high potentials, respectively (note however that at 1.2 V the intercepts of the LK plots are non-zero). This suggests that on Mn perovskite oxides at high overpotentials the HPOR and HPRR are diffusion-limited. For LaCoO3 electrodes, the currents do not reach the plateaus of Pt/C, due to a slower HO2− reduction and oxidation kinetics. The comparison of the current slope near the mixed potential for various perovskites (Fig. 1a) confirms that LaCoO3 is less catalytically active in HO2− reactions than either LaMnO3 or La0.8Sr0.2MnO3. Since the mixed potential of LaCoO3 is positively shifted compared to that of Mn perovskite oxides, we conclude that the HPOR is slower than the HPRR on the cobalt perovskite. The cathodic branch of the RDE voltammograms for LaCoO3 shows two slopes (Fig. 1a) suggesting that at least two steps are involved in the HO2− reduction reaction. In what follows this hypothesis will be corroborated with the help of a mathematical model.
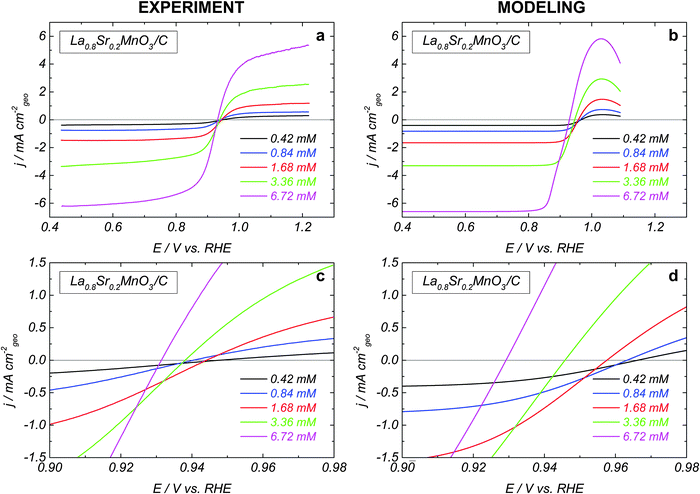
The influence of the H2O2 concentration on the HPOR and HPRR kinetics is shown in Fig. 2a for La0.8Sr0.2MnO3. While the absolute values of the limiting anodic and cathodic currents increase proportionally to the H2O2 concentration, the mixed potential is displaced towards the negative values (see close-up in Fig. 2c). The same behavior was observed for LaCoO3 (not shown). This indicates that the perovskite oxide-catalyzed HO2− reduction and the HO2− oxidation reactions have different concentration dependences.
In order to better understand the experimental findings, a microkinetic model was developed. Note that the mathematical model serves to understand the influence of the experimental parameters (potential and concentration), the differences between Mn and Co perovskites, and to verify the consistency of the proposed reaction mechanism with the experimental data, rather than to accurately determine the values of the rate constants. The elementary steps for the HO2− and O2 adsorption and reaction on perovskite oxides were inspired by the experimental studies of Goodenough11 and Suntivich et al.12 and the density functional theory (DFT) calculations of Wang and Cheng,13 and adapted in order to reproduce the experimental findings of this work.
Since the oxide surface in an alkaline electrolyte is supposed to be covered by OHad,11,14 displacement of OHad by either O2 or HO2− is likely to be the first step in the electrocatalysis of O211 and H2O2 reactions.
| HO2− + OHad ⇄ HO2,ad + OH− | (1) |
The adsorbed HO2,ad may be oxidized into oxygen in the reverse step of reaction (2):
| O2,ad + H2O + e− ⇆ HO2,ad + OH− | (2) |
The adsorbed oxygen molecule resulting from the backward step of reaction (2) may desorb in the reverse step of reaction (3). In agreement with the literature,11,13 we suppose that upon adsorption oxygen molecules displace hydroxo species on the oxide surface:
| O2 + OHad + e− ⇆ O2,ad + OH− | (3) |
The adsorbed HO2,ad can also undergo reduction. To account for the negative shift of the mixed potential with the increase of the H2O2 concentration, the HPOR and the HPRR must have different concentration dependence. In order to reproduce this, we assume that the HO2,ad reduction occurs in a sequence of chemical and electrochemical steps:
| HO2,ad + OHad ⇄ 2Oad + H2O | (4) |
| Oad + H2O + e− ⇆ OHad + OH− | (5) |
Note that steps (1)–(5) also account for the catalytic decomposition of H2O2 occurring under open circuit conditions.
Considering both the experimental and the literature data we suppose that Oad species are adsorbed on transition metal (B) cations in the high oxidation state B(m+1)+ (B![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), while OHad species – on B-cations in the low oxidation state Bm+ (B–OH). According to the DFT calculations of Wang and Cheng,13 these intermediates (OHad and Oad) are indeed strongly adsorbed on the surface of perovskite oxides.
O), while OHad species – on B-cations in the low oxidation state Bm+ (B–OH). According to the DFT calculations of Wang and Cheng,13 these intermediates (OHad and Oad) are indeed strongly adsorbed on the surface of perovskite oxides.
Assuming Langmuir-type adsorption isotherms and Butler–Volmer type of the electrochemical kinetics, the reaction rates may be expressed as follows:
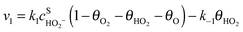 | (6) |
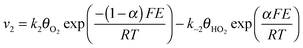 | (7) |
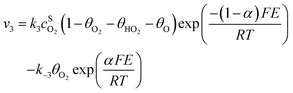 | (8) |
| v4 = k4θHO2(1 − θO2 − θHO2 − θO) | (9) |
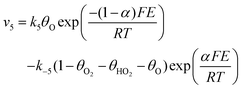 | (10) |
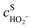 ,
, 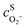 are the concentrations in front of the electrode at x = 0 (x is the distance along the normal to the electrode surface) and θHO2, θO2, θO the coverages of adsorbed intermediates, with θOH = 1 − θO2− θHO2− θO. α is the charge transfer coefficient, F = 96
are the concentrations in front of the electrode at x = 0 (x is the distance along the normal to the electrode surface) and θHO2, θO2, θO the coverages of adsorbed intermediates, with θOH = 1 − θO2− θHO2− θO. α is the charge transfer coefficient, F = 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 486 C mol−1 is the Faraday constant, R = 8.314 J K−1 mol−1 the ideal gas constant and T = 300 K the absolute temperature.
486 C mol−1 is the Faraday constant, R = 8.314 J K−1 mol−1 the ideal gas constant and T = 300 K the absolute temperature.
Under stationary conditions, this reaction scheme can be cast into a set of equations determining the concentrations of HO2− and O2 in front of the electrode surface, and the coverages of adsorbed intermediates, HO2,ad−, O2,ad, Oad, and OHad on perovskite sites:
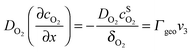 | (11) |
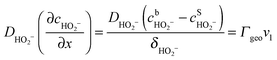 | (12) |
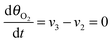 | (13) |
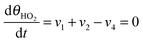 | (14) |
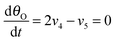 | (15) |
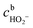 , the concentration of HO2− in the bulk of the electrolyte, and Γgeo stands for the number of active sites per geometric area of the electrode. The overall current density is given by eqn (16).
, the concentration of HO2− in the bulk of the electrolyte, and Γgeo stands for the number of active sites per geometric area of the electrode. The overall current density is given by eqn (16).| j = −FΓgeo(v2 + v3 + v5) | (16) |
A linear concentration profile for O2 and HO2− is assumed in front of the electrode surface. The electrode thickness is assumed to be sufficiently small to keep this linear concentration profile. The diffusion coefficients of O2 and HO2− in 1 M NaOH were determined as DO2 = 1.5 × 10−5 cm2 s−1 and DHO2− = 0.8 × 10−5 cm2 s−1, respectively, from the corresponding diffusion limited current plateaus for Pt/C electrodes. Thus, the diffusion layer thickness at 900 rpm is δO2 = 19 μm for O2 and δHO2− = 15 μm for HO2−.
Assuming that B cations act as active sites, the number of active sites per geometric surface area Γgeo was calculated from the catalyst loading and the number of B sites per unit of the real surface area, which was estimated from the crystalline structure of perovskite oxides as 4.14 × 10−10 mol cm−2oxide. The values of the reaction rate constants were adjusted in order to reproduce the main features of the experimental RDE voltammograms for HPOR and HPRR, as well as for the ORR,5 and are given in Table 1. Symmetry factors were all considered to be equal to 0.5, which is realistic for low and moderate overvoltages considered in this work. The adsorption–desorption rates of HO2− on perovskite sites directly depend on the values of k1 and k−1 which have to be considered sufficiently high for adsorption and low for desorption to account for the significant activity of perovskites in the HPRR. k2 and k3 were adjusted to reproduce both the onset potential and the Tafel slopes for the ORR on perovskite oxides,5 while the rate constants of the reverse reactions k−2, k−3 were chosen to account for the standard potential of the O2/HO2− at 0.77 V vs. RHE. Finally, the values of the mixed potential for the HPRR/HPOR and the potential of the B(m+1)+/B(m)+ redox peaks (see CVs in ref. 5) were used to adjust the values of k4, k5 and k−5.
| Rate constant | Units | Value | |
|---|---|---|---|
| LaCoO3 | La0.8Sr0.2MnO3 | ||
| k 1 | cm3 mol−1 s−1 | 5 × 107 | 5 × 107 |
| k −1 | s−1 | 50 | 50 |
| k 2 | s−1 | 5.1 × 108 | 5.1 × 109 |
| k −2 | s−1 | 4.9 × 10−8 | 4.9 × 10−7 |
| k 3 | cm3 mol−1 s−1 | 1.6 × 1011 | 1.6 × 1012 |
| k −3 | s−1 | 1.6 × 10−8 | 1.6 × 10−7 |
| k 4 | s−1 | 40 | 40 |
| k 5 | s−1 | 6 × 107 | 1.2 × 108 |
| k −5 | s−1 | 2.9 × 10−9 | 5.8 × 10−9 |
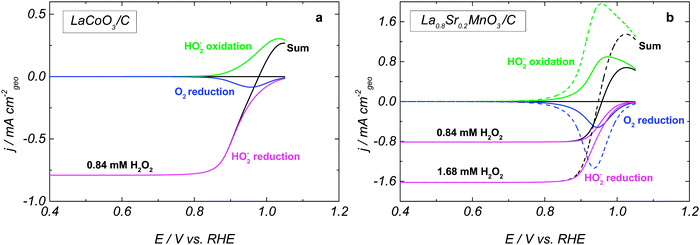
Fig. 3 shows simulated RDE voltammograms for LaCoO3 and La0.8Sr0.2MnO3 oxides. The rate constants are listed in Table 1, and an almost reversible voltammogram is obtained for La0.8Sr0.2MnO3 (Fig. 3b). By choosing smaller rate constants for steps 2, 3 and 5, we are able to reproduce a slower HPOR on LaCoO3 (cf.Fig. 3a and b) and a positive shift of the mixed potential compared to La0.8Sr0.2MnO3. Furthermore, the assumption of the HO2,ad reduction as a sequence of two elementary steps allows us to reproduce the observed change of the slope of the HPRR on LaCoO3. Fig. 3 also shows the splitting of the RDE voltammograms into a sum of three main contributions for two HO2− concentrations. The anodic branch corresponds to the HO2− oxidation into O2 (step III), while the cathodic branch consists of two contributions: the HO2− reduction into OH− (step II) and the O2 reduction (this oxygen is formed in the anodic branch) into HO2− (step −III). One may note that the differences between LaCoO3 and La0.8Sr0.2MnO3 are partly due to the lower ORR activity of LaCoO3 (cf. blue curves in Fig. 3a and b). For experimental ORR data on LaCoO3 and La0.8Sr0.2MnO3 the reader is referred to our earlier publication.5
The influence of the H2O2 concentration can be traced from simulated voltammograms shown in Fig. 2b, d and 3b. Increasing the concentration directly affects the reaction rate of the adsorption–desorption of HO2 (reaction (1)) and therefore the site coverage by HO2,ad species (θHO2). In the anodic direction, an increase of θHO2 causes an increase in the rate (step −2) of formation of O2,ad from HO2,ad (cf. dashed over solid green lines in Fig. 3b). On the other hand, in the cathodic branch, an increase of the HO2− concentration does not lead to a strong acceleration of reaction (4), since its rate depends on both θHO2 and θOH = (1 − θO2 − θHO2 − θO) (cf. dashed over solid magenta lines in Fig. 3b). A stronger concentration dependence of the HO2− oxidation compared to the reduction counterpart, and the potential dependence of the former result in the negative shift of the mixed potential with the HO2− concentration (Fig. 3b, black curves, and Fig. 2b and d).
The deconvolution of the whole current into individual contributions shows that the kinetic currents of the HO2− reduction/oxidation cannot be directly obtained from the total currents, contrary to what has been suggested in the literature.15
The main difference between the simulated and the experimental curves is the decrease of the HO2− oxidation current at high potentials for the former. It is caused by the oxidation of Bm+ cations (which in our model are required for the adsorption of HO2−) into B(m+1)+ cations at high potentials. Various possible explanations may be offered in order to account for the absence of such a current drop in the experiment, among these (i) surface heterogeneity resulting in a wide potential distribution of the Bm+/B(m+1)+ red-ox transitions, (ii) adsorption of HO2− on B(m+1)+ sites as well, (iii) carbon contribution to the HPOR at high electrode potentials (see grey curve in Fig. 1).
4. Conclusions
In this work, it is demonstrated that the LaCoO3, LaMnO3 and La0.8Sr0.2MnO3 perovskite oxides, when mixed with carbon, show significant activity towards hydrogen peroxide reduction/oxidation reactions, with LaCoO3 being less active than Mn perovskites. The kinetics of the hydrogen peroxide oxidation/reduction reactions on perovskite oxides can be reasonably described with a simple kinetic model. Modeling helps to rationalize the observed differences between Co and Mn perovskite oxides in H2O2 electrocatalysis, which are largely due to the lower electrocatalytic activity of Co perovskite for the H2O2 oxidation and O2 reduction. Furthermore, it allows one to explain the H2O2 concentration dependence (including the displacement of the mixed potential with the concentration) by the multistep mechanism of the hydrogen peroxide reduction. The conclusions obtained have far-reaching consequences for the understanding of the ORR electrocatalysis on oxides of the perovskite family and will be further corroborated in our forthcoming publication.Acknowledgements
The authors thank E.V. Antipov, S.Ya. Istomin and F.S. Napolskiy of the Moscow State University (Russia) for the synthesis and characterization of perovskite materials and for valuable discussions, P. Simonov of the Boreskov Institute of Catalysis (Novosibirsk, Russia) for supplying Sibunit Carbon, and Tokuyama Company for supplying alkaline ionomer. Financial support from CNRS (France), Region Alsace, Russian Foundation for Basic Research, and the French Ministry for the PhD scholarship of T.P. is gratefully appreciated.References
- G. Wang, Y. Bao, Y. Tian, J. Xia and D. Cao, Electrocatalytic activity of perovskite La1-xSrxMnO3 towards hydrogen peroxide reduction in alkaline medium, J. Power Sources, 2010, 195, 6463–6467 CrossRef CAS PubMed.
- S. Zhuang, S. Liu, C. Huang, F. Tu, J. Zhang and Y. Li, Electrocatalytic activity of nanoporous perovskite La1-xCaxCoO3 towards hydrogen peroxide reduction in alkaline medium, Int. J. Electrochem. Sci., 2012, 7, 338–344 CAS.
- Y. Matsumoto, H. Yoneyama and H. Tamura, The mechanism of oxygen reduction at a LaNiO3 electrode, Bull. Chem. Soc. Jpn., 1978, 51, 1927–1930 CrossRef CAS.
- D. Dobos, Electrochemical Data, Akademiai Kiado, Budapesht, 1978 Search PubMed.
- T. Poux, F. S. Napolskiy, T. Dintzer, G. Kéranguéven, S. Ya. Istomin, G. A. Tsirlina, E. V. Antipov and E. R. Savinova, Dual role of carbon in the catalytic layers of perovskite/carbon composites for the electrocatalytic oxygen reduction reaction, Catal. Today, 2012, 189, 83–92 CrossRef CAS PubMed.
- Y. I. Yermakov, V. F. Surovikin, G. V. Plaksin, V. A. Semikolenov, V. A. Likholobov, L. V. Chuvilin and S. V. Bogdanov, New carbon material as support for catalysts, React. Kinet. Catal. Lett., 1987, 33, 435–440 CrossRef CAS.
- V. G. Prabhu, L. R. Zarapkar and R. G. Dhaneshwar, Electrochemical studies of hydrogen peroxide at a platinum disc electrode, Electrochim. Acta, 1981, 26, 725–729 CrossRef CAS.
- I. Katsounaros, W. B. Schneider, J. C. Meier, U. Benedikt, P. U. Biedermann, A. A. Auer and J. J. Mayrhofer, Hydrogen peroxide electrochemistry on platinum: towards understanding the oxygen reduction reaction mechanism, Phys. Chem. Chem. Phys., 2012, 14, 7384–7391 RSC.
- A. M. Gomez-Marin, K. J. P. Schouten, M. T. M. Koper and J. M. Feliu, Interaction of hydrogen peroxide with a Pt(111) electrode, Electrochem. Commun., 2012, 22, 153–156 CrossRef CAS PubMed.
- S. Strbac, The effect of pH on oxygen and hydrogen peroxide reduction on polycrystalline Pt electrode, Electrochim. Acta, 2011, 56, 1597–1604 CrossRef CAS PubMed.
- J. B. Goodenough and B. L. Cushing, in Handbook of Fuel Cells—Fundamentals, Technology and Applications, ed. W. Vielstich, H. A. Gasteiger and H. Yokokawa, Wiley, 2003, vol. 2, pp. 520–533 Search PubMed.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Design principles for oxygen-reduction activity on perovskite oxide catalysts for fuel cells and metal-air batteries, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed.
- Y. Wang and H. P. Cheng, Oxygen reduction activity on perovskite oxide surfaces: a comparative first-principles study of LaMnO3, LaFeO3 and LaCrO3, J. Phys. Chem. C, 2013, 117, 2106–2112 CAS.
- J. O'M. Bockris and T. Otagawa, Mechanism of Oxygen Evolution on Perovskites, J. Phys. Chem., 1983, 87, 2960–2971 CrossRef.
- D. Cao, L. Sun, G. Wang, Y. Lv and M. Zhang, Kinetics of hydrogen peroxide electroreduction on Pd nanoparticles in acidic medium, J. Electroanal. Chem., 2008, 621, 31–37 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4cp00341a |
| This journal is © the Owner Societies 2014 |