Open Access Article
Open Access ArticleA transfer learning framework integrating molecular dynamics and group contribution methods for predicting polymer specific heat capacity
Sobin Alosious ab,
Jiaxin Xu
ab,
Jiaxin Xu b,
Meng Jiang
b,
Meng Jiang ac and
Tengfei Luo
ac and
Tengfei Luo *abd
*abd
aLucy Family Institute for Data and Society, University of Notre Dame, Notre Dame, IN 46556, USA. E-mail: tluo@nd.edu
bDepartment of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
cDepartment of Computer Science and Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
dDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, Notre Dame, IN 46556, USA
First published on 4th February 2026
Abstract
Heat capacity (Cp) of polymers is an essential property for diverse applications, such as energy storage systems, electronics thermal management, and thermal insulation. In this study, we explore a transfer learning framework to predict polymer Cp, where models are first pretrained on large datasets generated from molecular dynamics (MD) simulations and group contribution (GC) calculations, and then fine-tuned using experimental data. We evaluate multiple machine learning (ML) models, including multilayer perceptrons and graph neural networks, using various molecular fingerprints and structural descriptors. The trained models are applied to existing polymers and virtual polymers to enable large-scale Cp prediction and screening. We analyze structure–property relationships to identify key molecular features influencing Cp and propose an updated GC model through a data-driven regression for quick Cp evaluation. Using the predicted Cp, in combination with thermal conductivity and glass transition temperature, we search polymers for four functional categories relevant to thermal applications: thermal interface materials, insulators, buffers, and heat spreaders. Representative polymer candidates are identified for each category based on the combined thermal property thresholds, demonstrating the practical relevance of predicted values for real-world material selection. This integrated approach enables targeted selection of polymer materials for specific thermal applications.
Introduction
Efficient thermal energy management is increasingly critical across various sectors, including industry, electronics, and transportation, to enhance energy efficiency, reduce carbon emissions, and ensure system reliability.1–4 A significant portion of industrial energy input is typically lost as waste heat. Integrating waste heat recovery with thermal energy storage technologies offers the potential to capture and repurpose this otherwise wasted energy, contributing to more efficient energy practices.5 In electronics, overheating remains a primary cause of component failures, underscoring the importance of implementing robust thermal management strategies to maintain device performance and longevity.6 In electric vehicles, battery performance and safety are susceptible to temperature control.7 Latent heat thermal energy storage systems, which utilize phase change materials, offer an effective means of storing and releasing thermal energy.8For diverse applications, a comprehensive evaluation of thermal properties, particularly thermal conductivity (TC) and specific heat capacity (Cp), is therefore vital. While extensive research has focused on enhancing TC to improve heat transfer efficiency,9–13 Cp is equally important because it governs a material's ability to store thermal energy. Polymers have emerged as desirable candidates for thermal energy storage and management because of their unique combination of practical advantages, including low cost, lightweight, mechanical flexibility, and ease of processing into various shapes for scalable manufacturing and integration, while also offering high corrosion resistance and inherent electrical insulation.14–19
Various approaches exist for determining polymer Cp, including experimental methods, molecular dynamics (MD) simulations, group contribution (GC) techniques, and machine learning (ML) models. Experimental techniques, such as differential scanning calorimetry (DSC), provide direct and accurate measurements.20 However, they are time-consuming and require significant sample preparation and calibration. MD simulations provide atomistic insights and can handle a wide range of temperatures and polymer architectures,21 but classical MD tends to overpredict Cp as quantum effects are not accounted for.22 GC methods estimate Cp based on additive contributions of functional groups and are computationally efficient and suitable for large datasets, but their accuracy diminishes for complex polymers with intricate structures or interactions.23 Recently, ML models have shown great promise in predicting Cp by learning from experimental and simulation data, offering rapid predictions and the ability to generalize across diverse polymer chemistries.24 However, they require large, high-quality datasets, and careful feature engineering to avoid overfitting. Overall, integrating these methods may enable cross-validation and a balanced assessment of polymer Cp.
Recent advances in polymer informatics have further expanded the potential of ML in this field.19,25 For example, Bhowmik et al.24 applied Decision Tree (DT) and Principal Component Analysis (PCA) models to predict room-temperature Cp values for 68 polymers using experimentally derived molecular descriptors. Despite the limited dataset size, their optimized DT model achieved testing R2 values up to 0.83 under 5-fold cross-validation, demonstrating that physically meaningful polymer descriptors can capture key structure – Cp relationships. Their analysis further highlighted the dominant role of bonding, molecular-type, and atom-type descriptors in governing polymer heat capacity, illustrating the potential of ML for guiding polymer design even in data-scarce regimes. Building on this, Hayashi et al.26 applied a transfer learning (TL) strategy to bridge discrepancies between MD-calculated and experimental polymer properties, including Cp, linear expansion coefficient, and volume expansion coefficient. Using MD-derived data as a source domain and fine-tuning neural networks on limited experimental data from PoLyInfo, they substantially reduced systematic bias in Cp predictions. Specifically, while direct MD calculations exhibited large errors (RMSE ≈1972 J kg−1 K−1), transfer learning reduced the RMSE to approximately 279 J kg−1 K−1, corresponding to an error reduction of nearly 85% relative to raw MD predictions. These results demonstrate the effectiveness of TL in correcting MD-induced biases and highlight its utility for polymer thermophysical property prediction when experimental data are scarce. Furthermore, Malashin et al.27 explored a wide range of ML approaches for predicting various physical properties of polymers, including Cp. Utilizing a comprehensive polymer dataset, they compared ensemble, tree-based, regularization, and distance-based regression models. While their random forest models achieved R2 values up to 0.88 for certain thermal properties, the performance on Cp prediction was notably lower (R2 ≈ 0.13). This highlights both the potential of ML to capture complex polymer behaviors and the challenges of accurately modeling specific properties such as heat capacity, emphasizing the importance of careful model selection and the need for improved feature representations.
In this study, we present a comprehensive TL framework for accurate and scalable predictions of Cp in polymers. The TL strategy integrates multiple data fidelities, including (1) low-fidelity GC predictions derived from functional group analysis and MD simulations and (2) high-fidelity experimental data. We first develop extensive GC and MD datasets through automated workflows, including polymer system construction, equilibration, and Cp calculation. ML models such as Multilayer Perceptrons (MLP) and Graph Neural Networks (GNNs) are pretrained on GC or MD data and subsequently fine-tuned with limited experimental data using TL, leading to improved performance compared to models trained on experimental data alone. We also explore large language models (LLMs) with advanced prompting strategies to complement structure-based ML approaches. By leveraging the predictive power of TL-enhanced models, we identify polymers suitable for various thermal management applications by combining Cp predictions with thermal conductivity (TC) data from our previous studies. Finally, we develop a data-driven GC model and analyze key structural and physicochemical factors that govern Cp, providing both interpretability and physical insights. The primary novelty of this work lies in the unified multi-fidelity TL framework, large-scale Cp prediction across real and virtual polymer spaces, and systematic benchmarking of specialized ML and LLM-based approaches. The GC refitting and application-oriented categorization are presented as complementary, enabling components that enhance interpretability and demonstrate practical use of the predicted properties.
Methodology
Molecular dynamics simulations
To compute Cp of amorphous polymers, we employed a high-throughput MD pipeline consisting of polymer model generation, equilibration, and Cp calculation using both equilibrium and non-equilibrium approaches. The polymer generation and equilibration stages were adapted from our previous work.13,28 An overview of the MD workflow is illustrated schematically in Fig. 1. | ||
| Fig. 1 Schematic workflow illustrating the process from polymer SMILES input to Cp prediction via MD simulations and GC methods, followed by TL using experimental data. | ||
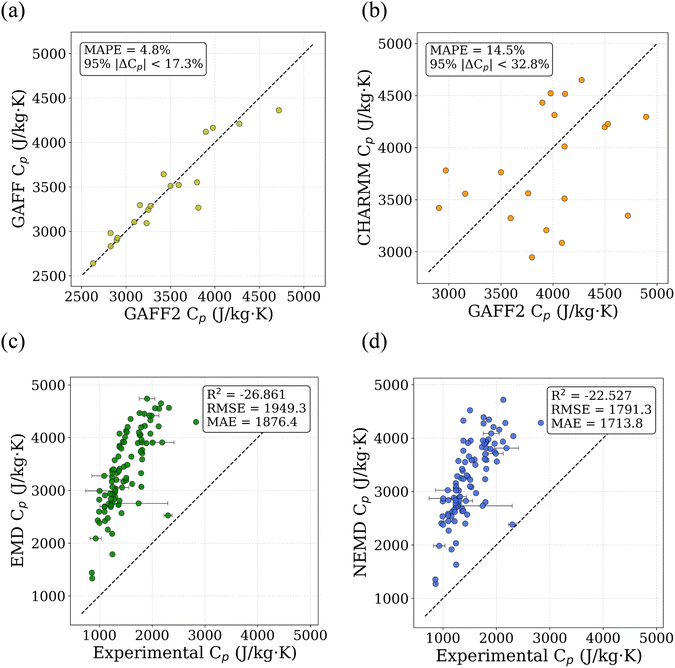
Polymer monomers were represented by simplified molecular input line entry system (SMILES) strings.29 A Python-based pipeline built on PYSIMM30 was used to create the initial structure of amorphous polymers. This process involves generating a polymer chain for each constituent polymer through polymerization, with each chain containing approximately 600 atoms. Force field parameters were assigned using the General AMBER Force Field 2 (GAFF2),31 with partial atomic charges assigned using the Gasteiger method. No quantum-chemical charge derivation (e.g., AM1-BCC or RESP) was performed, and charges were not refitted after polymerization; instead, Gasteiger charges were assigned automatically and consistently to all polymerized structures to enable scalable high-throughput simulations. GAFF2 is widely used for calculation of thermophysical properties in polymers due to its broad chemical coverage and established parameterization.26,32,33 To assess the sensitivity of MD-derived Cp to force-field choice, a targeted comparison was performed between GAFF2–GAFF and GAFF2–CHARMM using identical simulation protocols. The GAFF2–GAFF comparison yields a mean absolute percentage deviation (MAPE) of 4.8% (95% of deviations below 17.3%), while the GAFF2–CHARMM comparison exhibits a MAPE of 14.5% (95% of deviations below ∼32.8%), indicating bounded but force-field-dependent uncertainty. Parity plots illustrating these comparisons are shown in Fig. 2(a) and (b). These results support the use of GAFF2-based MD data as a low-fidelity input within the multi-fidelity learning framework rather than assuming force-field invariance. Each polymer chain was duplicated to form a six-chain system, which was placed in a simulation box with periodic boundary conditions in all spatial directions. Input scripts compatible with large-scale atomic-molecular massively parallel simulator (LAMMPS)34 were generated automatically by the python pipeline for subsequent simulations. After initialization, the system undergoes multiple optimization steps, which are broadly classified into two stages: initial relaxation and annealing.
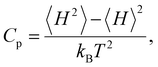 | (1) |
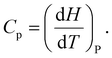 | (2) |
Group contribution method
The GC method is a well-established approach for estimating thermophysical properties of molecules by assuming that the total property is an additive function of the contributions from individual structural groups.39 For Cp calculations, the property of a polymer repeat unit is expressed as the weighted sum of predefined group contributions:
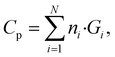 | (3) |
In this work, we used a set of 32 predefined functional groups, and their corresponding Cp contribution values adopted from the literature.39 A Python-based workflow was developed using RDKit40 to parse each SMILES string, identify all matching functional groups in the monomer, and count their occurrences. Once the group counts were determined, each polymer's Cp was calculated as a linear combination of the group contributions using eqn (3). This method provides a rapid, structure-based estimation of Cp and serves as a complementary baseline to MD simulations and ML models. An overview of the GC-based property prediction workflow is illustrated in Fig. 1.
Machine learning framework
Multilayer perceptron (MLP). MLP models were implemented using the Keras API with a TensorFlow backend.42 The architecture consisted of two hidden layers with ReLU activation and dropout regularization, followed by a linear output layer for Cp prediction. Models were trained using the MSE loss and the Adam optimizer. Key architectural and training hyperparameters, including hidden-layer size, dropout rate, and learning rate, were optimized using the Optuna framework43 to ensure fair comparison across representations.
Graph neural networks (GNNs). Graph-based models were implemented using the torch-molecule library.44 We evaluated two widely used architectures, Graph Isomorphism Networks (GIN)45 and Graph Convolutional Networks (GCN),46 which differ in expressive power and message-passing formulation. Hyperparameters related to network depth, embedding dimension, normalization strategy, learning rate, and regularization were optimized using Optuna. These choices were guided by dataset size and the requirements of the transfer-learning framework.
Graph rationalization with environment-based augmentations (GREA). The GREA model was also implemented using torch-molecule.44 Unlike conventional GNNs, GREA explicitly identifies graph rationales, i.e., subgraph structures most responsible for property prediction, and augments training with environment-based perturbations. This design improves interpretability and robustness by encouraging the model to focus on chemically meaningful substructures. Hyperparameters governing the graph encoders, embedding dimension, regularization, and rationale size were optimized using Optuna.
| Model | Fingerprint | MD | GC | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAE | R2 | RMSE | MAE | ||
| The results correspond exclusively to TL models. Metrics are reported as mean ± standard deviation across 5-fold nested cross-validation. | |||||||
| MLP | AtomPair | 0.12 ± 0.37 | 310.17 ± 26.93 | 230.56 ± 19.21 | 0.60 ± 0.18 | 215.01 ± 54.70 | 160.64 ± 29.31 |
| MACCS | 0.55 ± 0.12 | 235.04 ± 65.27 | 172.66 ± 41.10 | 0.50 ± 0.09 | 246.44 ± 64.87 | 177.73 ± 36.46 | |
| Morgan | 0.30 ± 0.10 | 290.90 ± 62.26 | 214.14 ± 44.42 | 0.54 ± 0.18 | 235.50 ± 80.50 | 177.30 ± 43.51 | |
| PE | 0.55 ± 0.09 | 236.75 ± 71.41 | 184.00 ± 42.65 | 0.56 ± 0.11 | 234.08 ± 72.59 | 183.25 ± 37.32 | |
| RDKit | 0.21 ± 0.28 | 298.53 ± 43.91 | 207.48 ± 35.73 | 0.57 ± 0.19 | 224.24 ± 73.76 | 164.34 ± 49.64 | |
| Topological torsion | 0.27 ± 0.36 | 289.03 ± 107.65 | 214.99 ± 72.13 | 0.46 ± 0.20 | 250.92 ± 80.41 | 183.30 ± 61.41 | |
| MLP + Desc | AtomPair | 0.29 ± 0.45 | 272.26 ± 47.93 | 222.03 ± 29.20 | 0.35 ± 0.39 | 262.28 ± 46.64 | 208.12 ± 30.26 |
| MACCS | 0.56 ± 0.09 | 233.29 ± 69.87 | 180.30 ± 46.80 | 0.52 ± 0.13 | 237.90 ± 54.74 | 179.61 ± 39.20 | |
| Morgan | 0.31 ± 0.19 | 288.05 ± 81.28 | 216.93 ± 53.45 | 0.39 ± 0.31 | 259.55 ± 53.00 | 183.91 ± 28.21 | |
| PE | 0.59 ± 0.17 | 222.39 ± 56.23 | 167.70 ± 31.74 | 0.60 ± 0.18 | 220.59 ± 87.10 | 159.85 ± 48.93 | |
| RDKit | 0.46 ± 0.22 | 258.29 ± 98.34 | 186.01 ± 52.88 | 0.53 ± 0.16 | 237.34 ± 67.53 | 170.17 ± 32.48 | |
| Topological torsion | 0.32 ± 0.11 | 284.02 ± 51.26 | 208.90 ± 40.43 | 0.43 ± 0.10 | 264.64 ± 75.43 | 184.42 ± 47.60 | |
| Polymer-family split | MLP(PE) | 0.47 ± 0.25 | 264.50 ± 57.84 | 207.60 ± 32.43 | 0.45 ± 0.29 | 269.42 ± 56.14 | 199.93 ± 34.16 |
| GREA | None | 0.36 ± 0.25 | 276.46 ± 60.37 | 199.08 ± 37.83 | 0.43 ± 0.16 | 280.52 ± 63.99 | 199.04 ± 26.70 |
| MACCS | 0.43 ± 0.15 | 267.75 ± 68.19 | 187.78 ± 40.93 | 0.40 ± 0.23 | 289.81 ± 97.46 | 188.82 ± 58.65 | |
| Morgan | 0.40 ± 0.13 | 274.88 ± 65.27 | 190.25 ± 42.92 | 0.39 ± 0.22 | 299.39 ± 77.13 | 208.49 ± 45.83 | |
| MACCS + Morgan | 0.36 ± 0.30 | 280.74 ± 78.37 | 192.48 ± 47.25 | 0.37 ± 0.19 | 275.89 ± 69.63 | 194.27 ± 42.57 | |
| GNN | None | 0.41 ± 0.22 | 284.32 ± 72.31 | 193.21 ± 33.40 | 0.32 ± 0.26 | 289.65 ± 71.84 | 187.17 ± 37.74 |
| MACCS | 0.44 ± 0.08 | 268.28 ± 69.56 | 187.09 ± 42.27 | 0.47 ± 0.22 | 271.54 ± 79.38 | 190.51 ± 37.52 | |
| Morgan | 0.41 ± 0.24 | 284.00 ± 79.09 | 192.69 ± 36.79 | 0.42 ± 0.23 | 284.16 ± 88.74 | 192.63 ± 37.19 | |
| MACCS + Morgan | 0.37 ± 0.19 | 282.84 ± 79.39 | 205.65 ± 53.59 | 0.43 ± 0.20 | 268.12 ± 84.31 | 191.60 ± 57.22 | |
| Combined (MD + GC) | |||||||
| Combined | Average | 0.65 ± 0.18, 202.1 ± 61.9, 147.4 ± 38.4 | |||||
| Best | 0.74 ± 0.08, 184.28 ± 60.3, 119.09 ± 46.4 | ||||||
Large language model-based prediction
To qualitatively explore the limits of general-purpose language models for polymer property prediction, we benchmarked several LLMs, including LLaMA 4, Qwen3, GPT-4o, Gemini 2.0 Flash, and Mistral Large, under zero-shot and few-shot in-context learning (ICL) settings. Unlike traditional ML models trained on structured molecular representations, LLMs rely on pretrained linguistic knowledge and contextual examples provided at inference time and do not involve model training or parameter optimization in this study.LLMs were prompted to predict polymer Cp values using different molecular representations, including SMILES strings, IUPAC names, and functional group counts. In the zero-shot setting, predictions were generated without examples, whereas in the few-shot setting, a small number of contextual examples with known Cp values were included in the prompt.
Few-shot examples were selected using a similarity-based strategy. Each query polymer was represented using a Morgan fingerprint, and Tanimoto similarity47 was used to identify structurally similar polymers with available experimental Cp data. The most similar entries were used as in-context examples. Standardized prompts were employed to ensure consistent numerical outputs across models. Because LLMs do not involve training or hyperparameter tuning, prediction accuracy was evaluated using standard 5-fold cross-validation, whereas nested cross-validation was reserved for trainable ML models to control hyperparameter optimization bias.
Datasets
We primarily make use of three types of datasets: experimental data, and data generated from MD simulations and GC calculations. The high-fidelity experimental Cp dataset used in this study was manually curated from the PolyInfo database and consists of approximately 120 unique amorphous polymers with Cp values reported near 300 ± 2 K. After removing duplicate entries and averaging repeated measurements for identical polymers, this dataset represents the full set of reliable experimental Cp data currently available under consistent thermodynamic conditions. Due to the limited availability of experimental Cp measurements for polymers, no larger or fully independent external experimental dataset exists at present. The MD dataset includes over 850 polymers whose Cp values were computed through high-throughput NEMD simulations conducted at 300 K. The details for system preparation, equilibration, and Cp extraction are provided in the Methodology section. The GC dataset consists of over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 polymers for which Cp values were estimated using a GC method based on the additive contributions of 32 functional groups, corresponding to 298.15 K. The procedure for GC-based calculation is also explained in the Methodology section. In addition to these Cp datasets, we collected SMILES strings for approximately 13
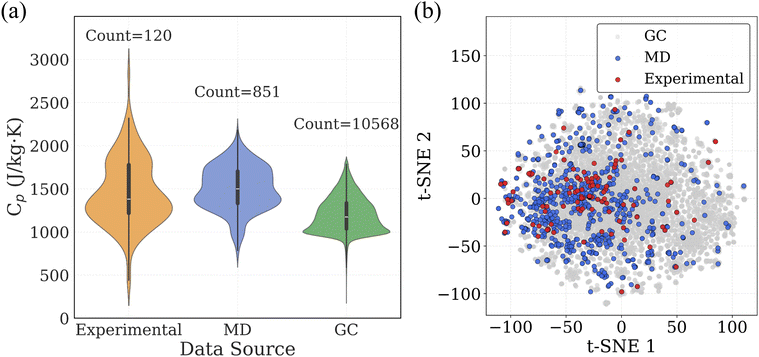
000 polymers for which Cp values were estimated using a GC method based on the additive contributions of 32 functional groups, corresponding to 298.15 K. The procedure for GC-based calculation is also explained in the Methodology section. In addition to these Cp datasets, we collected SMILES strings for approximately 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 real polymers from PolyInfo database48 and 1 million virtual polymers from the PI1M database,41 which was generated using a recurrent neural network (RNN) trained on real polymers from the PolyInfo database. These SMILES datasets provide a rich molecular representation of chemical space for virtual screening and prediction tasks. To visualize and compare the Cp distributions across the three datasets, we employed a violin plot (Fig. 3a), which combines a boxplot with a kernel density estimate to illustrate the full distribution of Cp values for each data source. The width of each violin indicates the density of data points at different Cp ranges, while central lines reflect the median and interquartile range. To understand how the molecular structures from each dataset occupy chemical space, we applied t-SNE (t-distributed stochastic neighbor embedding) dimensionality reduction on Morgan fingerprints derived from SMILES strings (Fig. 3b). Each point represents a polymer, and proximity in the 2D plot reflects structural similarity in the high-dimensional fingerprint space.
000 real polymers from PolyInfo database48 and 1 million virtual polymers from the PI1M database,41 which was generated using a recurrent neural network (RNN) trained on real polymers from the PolyInfo database. These SMILES datasets provide a rich molecular representation of chemical space for virtual screening and prediction tasks. To visualize and compare the Cp distributions across the three datasets, we employed a violin plot (Fig. 3a), which combines a boxplot with a kernel density estimate to illustrate the full distribution of Cp values for each data source. The width of each violin indicates the density of data points at different Cp ranges, while central lines reflect the median and interquartile range. To understand how the molecular structures from each dataset occupy chemical space, we applied t-SNE (t-distributed stochastic neighbor embedding) dimensionality reduction on Morgan fingerprints derived from SMILES strings (Fig. 3b). Each point represents a polymer, and proximity in the 2D plot reflects structural similarity in the high-dimensional fingerprint space.
Results and discussion
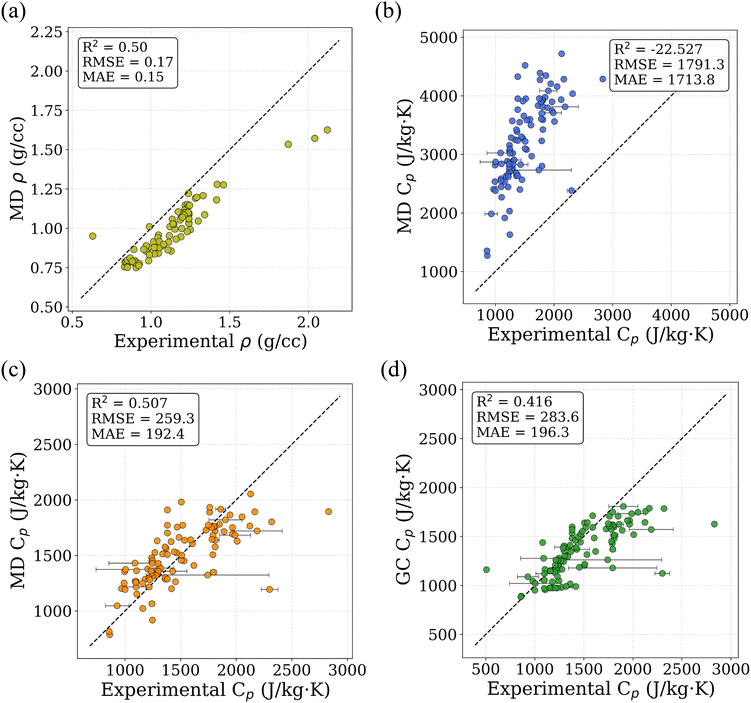
To assess the suitability of GAFF2 for large-scale polymer simulations, we performed an explicit validation by comparing MD-predicted polymer densities with available experimental values (Fig. 4a). The MD densities show good agreement with experiment, with an R2 of 0.50 and low absolute errors, indicating that GAFF2 reasonably captures equilibrium packing and structural properties across a chemically diverse polymer set. While this validation does not imply quantitative accuracy for all thermophysical properties, it supports the use of GAFF2 as a consistent and physically meaningful low-fidelity proxy within the proposed multi-fidelity and TL framework. To evaluate the accuracy of the MD-calculated Cp values, we compared them with the experimental dataset. Fig. 4b presents the parity plot between MD predictions and experimental values. The plot clearly shows that the MD-calculated (NEMD method) Cp values are consistently overestimated, as indicated by a high positive mean error (ME) of +1713.79 J (kg K)−1. Similar overpredictions by classical MD methods have been reported in previous studies.21,26 One fundamental reason for this overestimation lies in the inherent limitations of classical MD simulations, which do not account for quantum mechanical effects. Specifically, the vibrational energy in a classical harmonic oscillator is higher than that in its quantum mechanical counterpart at the same frequency. For high frequency vibrational modes, they are not fully excited at room temperature (300 K) according to the Bose–Einstein distribution. However, in MD simulations, which follows the classical Boltzmann distribution, all modes are fully excited despite the temperature. This discrepancy can be quantitatively described using the expressions for quantum and classical heat capacities.49 The quantum heat capacity for a harmonic oscillator is given by:
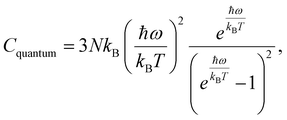 | (4) |
| Cclassical = 3NkB. | (5) |
From eqn (4) and (5), the ratio of the quantum to classical heat capacities can be expressed as:
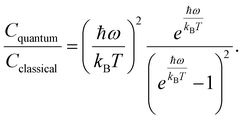 | (6) |
This ratio decreases monotonically with increasing vibrational frequency ω, which explains the systematic overestimation of Cp in classical MD simulations, particularly for polymers with stiff bonds. Previous studies have demonstrated that classical MD systematically overestimates thermophysical properties due to its neglect of quantum effects,50 and that the deviation between MD-predicted and experimental Cp values increases with the average bond-stretching and -bending force constants.26 Despite this systematic bias, the strong correlation between MD and experimental results suggests that the discrepancy may be addressed using data-driven correction strategies, such as TL or multi-fidelity modeling. We examined differences between MD-predicted and experimental Cp values across different polymer classes and structural motifs. However, only a small number of experimental polymers are available within most individual polymer families. This limited coverage prevents statistically reliable class-wise comparisons. Therefore, we focus on global trends and overall model behavior rather than drawing conclusions about family-specific MD discrepancies.
Motivated by the systematic and largely global overestimation observed in MD-calculated Cp values, we examined a simple empirical bias-correction as a diagnostic analysis. Specifically, MD-predicted Cp values were linearly mapped onto the experimental scale using polymers common to both datasets according to
| Cexpp = aCMDp + b, | (7) |
Similarly, the accuracy of the Cp values estimated using the GC method was evaluated by comparing them with experimental data. Fig. 4d presents the parity plot between GC predictions and experimental values. The GC method yields a moderately accurate estimation, with a coefficient of determination (R2) of 0.416. In contrast to the MD results, the GC predictions tend to slightly underestimate Cp, as indicated by a negative ME of −132.01 J (kgK)−1. This underestimation is likely due to the simplified additive nature of the GC method, which neglects long-range intermolecular interactions, conformational flexibility, and cooperative effects that are inherently present in experimental systems.51 These phenomena can contribute to enhanced heat capacity values, but are not captured in the GC framework. Despite these limitations, a notable advantage of the GC approach is its computational efficiency. It does not require expensive molecular simulations and allows for rapid estimation of Cp values directly from SMILES representations. This makes GC attractive for generating large-scale datasets for data-driven modeling.
To evaluate the utility of simulation-generated data, we employed a TL strategy using multiple ML models trained on MD- and GC-derived Cp values. In this work, experimentally measured Cp values are treated as the highest-fidelity data and serve as the sole reference for model evaluation and fine-tuning. Both MD-derived and GC-derived Cp values are used as lower-fidelity proxy data; however, they do not form a strict linear fidelity hierarchy. Instead, they represent distinct approximation pathways with different bias and noise characteristics. The models tested include MLP, vanilla GNN (GIN and GCN), and GREA. Fig. 1 illustrates the TL workflow, where models are first pretrained on either MD- or GC-derived Cp data and then fine-tuned using the experimental dataset. The detailed implementation of the TL framework is described in the Methodology section. A nested cross-validation scheme with 5 outer folds and 3 inner folds was employed to obtain an unbiased estimate of model performance while optimizing hyperparameters. In each outer iteration, one fold was held out for testing, while the remaining data were used in a 3-fold inner loop to tune MLP hyperparameters based on validation loss with early stopping. Final performance metrics were computed by pooling predictions from all outer test folds, with fold-wise mean and standard deviation reported to quantify variability across splits. Table 1 summarizes the performance of different TL models after pretraining on either MD or GC datasets and fine-tuning on experimental data. Multiple molecular fingerprints were used to represent polymer structures for MLP models, while graph-based models were trained on molecular graphs with or without fingerprint augmentation. The results in Table 1 correspond exclusively to TL models. Performance metrics are reported as mean ± standard deviation across the 5 folds.
Initially, we evaluated MLP models using six different molecular fingerprinting methods: Atom Pair, RDKit, Morgan, Polymer Embedding (PE), Topological Torsion, and MACCS fingerprints. In addition to the fingerprint vectors, a set of eight molecular descriptors was appended to the input features to improve model accuracy. These descriptors include Molecular Weight (MolWt), Topological Polar Surface Area (TPSA), Number of Hydrogen Bond Donors (NumHDonors), Number of Hydrogen Bond Acceptors (NumHAcceptors), Number of Rotatable Bonds, Ring Count, and Fraction of sp3 Carbon Atoms (FractionCSP3). We observed that the impact of incorporating molecular descriptors was fingerprint-dependent, with some representations improving model performance while others led to marginal degradation. Each fingerprint was tested independently, and the results are shown in Table 1. In parallel, we also developed graph-based models, specifically GNN and GREA, which were trained directly on molecular graph representations of the polymers. In addition to the intrinsic graph features, we augmented the input with pre-computed molecular fingerprints such as Morgan and MACCS, as well as their combined representation. This approach allows the models to exploit not only the atom- and bond-level information captured by the molecular graph, but also complementary global descriptors that encode connectivity patterns and functional group presence.
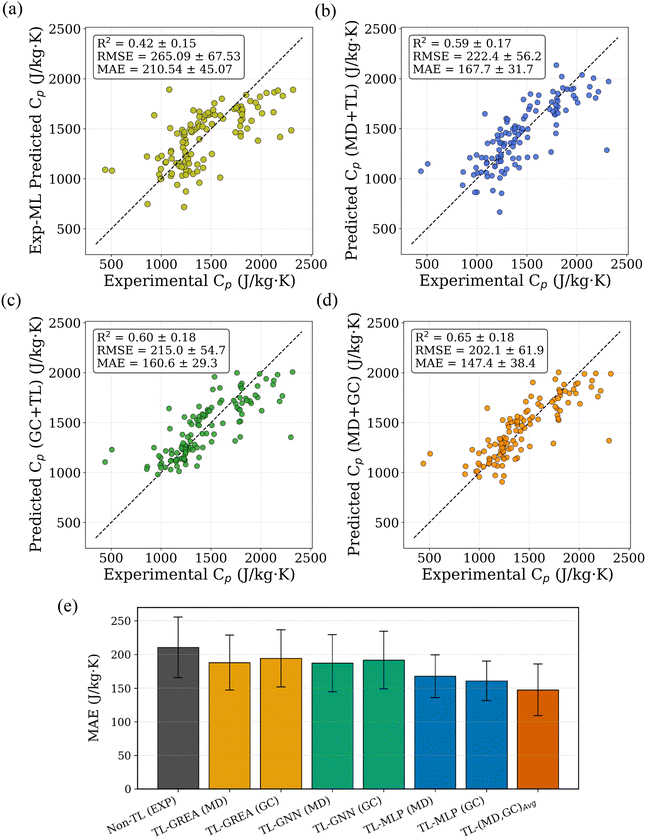
To establish a fair benchmark, we trained the same model architectures directly on the limited experimental dataset without any pretraining. As shown in Fig. 5a, these direct-training models exhibited lower performance and higher variance, likely due to overfitting caused by the small sample size. In contrast, TL models pretrained on either MD or GC data and fine-tuned with experimental data demonstrated significantly improved performance. TL models pretrained on either MD or GC data and fine-tuned with experimental data demonstrated clear performance gains. Based on reductions in mean absolute error (MAE), the MD-based TL model reduced prediction error by 20.5% relative to the experimental-only model, while the GC-based TL model achieved a larger reduction of 23.8%. Additionally, the variance across five folds was noticeably reduced, indicating improved model robustness. The parity plots for the best-performing TL models using MD and GC data are shown in Fig. 5b and c, respectively. Although the experimental dataset spans diverse polymer families, the number of samples per family is small and uneven, and several polymers belong to multiple classes. This limits the statistical reliability of family-resolved comparisons and prevents robust conclusions about class-specific advantages of MD- versus GC-based TL. Accordingly, this study focuses on global trends and model-level behavior rather than family-specific claims. Within this scope, neither proxy is universally superior: GC-based pretraining offers broader chemical coverage and lower noise, whereas MD-based pretraining incorporates richer physical information but exhibits systematic bias that must be corrected during fine-tuning.
To assess generalization beyond random splits, we performed an additional stress test using a polymer-family holdout strategy. The experimental dataset was grouped into five coarse classes based on backbone chemistry: (i) polyacrylics and polyvinyls, (ii) polyesters and thioesters, (iii) polyoxides, ethers, and acetals, (iv) polyamides, imides, imines, and urethane-based polymers, and (v) hydrocarbon and specialty polymers, including polyolefins, halogenated, sulfur-containing, and siloxane systems. Each group was held out in turn as an unseen test set, while the remaining groups were used for training and validation, with hyperparameters selected using a three-fold inner cross-validation loop. The resulting metrics, reported in Table 1, correspond exclusively to TL models pretrained on low-fidelity MD or GC data and fine-tuned on experimental data. Performance under polymer-family holdout is slightly lower than that obtained with random nested cross-validation, as expected for a chemically structured split, but remains stable across all folds. This indicates that the TL framework can generalize across distinct polymer families within the available experimental domain, while acknowledging that the evaluation remains within-domain rather than fully external.
To utilize the complementary strengths of the GC-based and MD-based predictive models, we examined simple ensemble strategies that combine their respective predictions. When evaluated individually, the GC-TL and MD-TL models exhibit comparable performance, with cross-validated R2 values of approximately 0.59 and 0.60, respectively. This indicates that neither model provides uniformly superior Cp predictions across the polymer chemical space. For each polymer in the experimental dataset, two independent Cp predictions were obtained, one from the GC-based model and one from the MD-based model. We then considered a simple arithmetic averaging of these predictions. Despite its simplicity, this ensemble approach consistently outperformed both individual models, achieving a pooled cross-validated R2 of 0.65. The observed improvement suggests that the GC and MD models capture partially complementary information and that averaging effectively mitigates model-specific bias and variance. The parity plot corresponding to the averaged GC and MD predictions is shown in Fig. 5d, where improved agreement with experimental Cp values is evident relative to the individual models. A comparison of prediction errors based on MAE for the experiment-only model, GC-TL, MD-TL, and the averaged ensemble is provided in Fig. 5e. For completeness, we also evaluated an idealized upper bound in which, for each polymer, the prediction closer to the experimental Cp value was selected between the GC and MD models. This oracle selection yields a higher R2 of 0.74, indicating that significant complementarity exists between the two models. While this approach is not deployable in practice due to its reliance on experimental values, it provides a useful reference for the maximum achievable performance attainable through optimal model combination.
Having established the performance of domain-specific ML models under the multi-fidelity TL framework, we next examine the applicability of recent general-purpose LLMs to polymer Cp prediction. This analysis is not intended to position LLMs as competitive quantitative predictors, but rather to assess their current limitations for numerical regression tasks in polymer science without task-specific training. The models evaluated include Llama 4, Qwen 3, GPT-4o, Gemini 2.0 Flash, and Mistral Large. These LLMs were used in an inference-only setting and were not fine-tuned on molecular property data, allowing us to probe whether implicit chemical knowledge alone is sufficient for quantitative prediction. A cross-validation-based data partitioning scheme was employed in which the experimental dataset was split into multiple folds. Few-shot prompts were constructed exclusively from polymers in the training portion of each split, while predictions were evaluated on the corresponding held-out data, preventing target information leakage and enabling fair comparison across models and prompting strategies. We examined multiple prompting configurations under both zero-shot and few-shot settings using 0, 5, 10, and 15 ICL examples, as well as different input representations, including SMILES strings, polymer IUPAC names, functional group descriptors, and their combinations. As summarized in Table 2, all tested LLM configurations perform substantially worse than traditional ML models, with several yielding negative R2 values. These results indicate that current LLM-based approaches lack the numerical accuracy required for quantitative polymer property prediction and should be interpreted strictly as exploratory or qualitative baselines.
| Model | # Shots | Identifier | R2 | RMSE | MAE |
|---|---|---|---|---|---|
| Metrics are reported as mean ± standard deviation. Best results in each column are highlighted in bold. | |||||
| Llama 4 | 5 | SMILES | 0.244 ± 0.24 | 346.44 ± 96.49 | 237.28 ± 68.99 |
| Qwen3 | 5 | SMILES | 0.296 ± 0.23 | 322.09 ± 7.43 | 206.36 ± 13.12 |
| GPT-4o | 5 | SMILES | −0.07 ± 0.35 | 399.11 ± 44.76 | 269.15 ± 28.59 |
| Gemini 2.0 Flash | 5 | SMILES | 0.264 ± 0.24 | 339.66 ± 80.08 | 241.95 ± 53.24 |
| Mistral Large | 5 | SMILES | 0.111 ± 0.23 | 372.83 ± 77.36 | 267.24 ± 50.76 |
| Qwen3 | 0 | SMILES | −0.622 ± 0.72 | 484.01 ± 109.79 | 396.47 ± 113.80 |
| 5 | SMILES | 0.296 ± 0.23 | 322.09 ± 7.43 | 206.36 ± 13.12 | |
| 10 | SMILES | 0.348 ± 0.15 | 321.99 ± 72.45 | 223.52 ± 49.86 | |
| 15 | SMILES | 0.397 ± 0.15 | 308.36 ± 64.69 | 204.99 ± 39.63 | |
| Qwen3 | 5 | SMILES | 0.296 ± 0.23 | 322.09 ± 7.43 | 206.36 ± 13.12 |
| 5 | SMILES + names | 0.337 ± 0.16 | 315.99 ± 24.75 | 207.87 ± 18.68 | |
| 5 | SMILES + group | 0.327 ± 0.13 | 321.24 ± 38.62 | 223.34 ± 36.08 | |
Among the LLMs tested, Qwen3 produced the most accurate predictions. Notably, the inclusion of few-shot examples in the prompt improved model performance compared to zero-shot settings, and accuracy generally increased with the number of examples provided. Furthermore, supplementing the SMILES input with corresponding IUPAC names consistently enhanced predictive performance. Across all evaluated LLMs and prompting settings, SMILES-only prompts consistently yielded lower predictive accuracy than prompts combining SMILES with IUPAC names, indicating that the absence of name-based contextual information degrades LLM performance.
Despite these relative improvements, the accuracy of LLM-based predictions remains substantially lower than that of the specialized ML models considered in this work. In several cases, certain LLMs (e.g., GPT-4o) yield negative R2 values, indicating performance worse than a simple mean predictor. Accordingly, LLMs are not intended to serve as competitive predictors of polymer Cp, but are included as an exploratory baseline to assess whether general-purpose language models can extract coarse structure–property signals directly from polymer representations. The limited performance of LLMs in this setting can be attributed to the possibility of lack of chemical inductive bias, the absence of explicit exposure to thermophysical property data such as Cp during pretraining, and their reliance on syntactic molecular encodings (e.g., SMILES) rather than physically informed molecular descriptors or graphs. As a result, their utility in the present context is qualitative and comparative rather than predictive. Overall, these results highlight the current limitations of LLMs for quantitative polymer property prediction and clarify their appropriate role relative to domain-specific ML models.
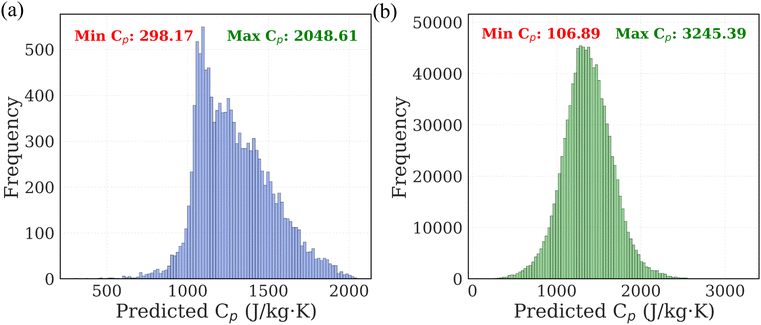
The next step in our study involved predicting Cp of polymers using the trained ML models. We predicted Cp values of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 real polymer from PolyInfo database. The distribution of these predictions is shown in Fig. 6a. The predicted Cp values range from 298.17 to 2048.61 J (kgK)−1, with the majority of polymers exhibiting values clustered within the 1000–1200 J (kg K)−1 range.
000 real polymer from PolyInfo database. The distribution of these predictions is shown in Fig. 6a. The predicted Cp values range from 298.17 to 2048.61 J (kgK)−1, with the majority of polymers exhibiting values clustered within the 1000–1200 J (kg K)−1 range.
To expand the chemical space, we further applied the ML models to the PI1M database, which contains 1 million virtual polymer SMILES. The distribution of the predicted Cp values for this dataset is shown in Fig. 6b. The predicted values range from 106.89 to 3245.39 J (kg K)−1, with the majority of polymers clustered within the 1200–1500 J (kg K)−1 range. Notably, the PI1M predictions span a broader Cp range compared to those from PolyInfo, suggesting the presence of novel structural motifs with potentially extreme thermal behaviors not captured in existing experimental databases. These large-scale predictions demonstrate the feasibility of using ML models to rapidly screen polymer candidates for desirable thermal properties, significantly accelerating the materials discovery process without the need for costly simulations or experimental measurements.
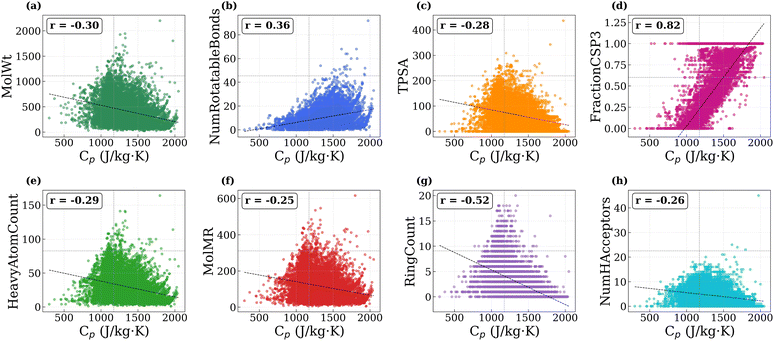
To better understand how molecular structure influences Cp in polymers, we analyzed the correlation between predicted Cp values and a set of structural and physicochemical descriptors. The descriptors considered include molecular weight, number of rotatable bonds, topological polar surface area, fraction of sp3 hybridized carbons (as a proxy for backbone flexibility), heavy atom count, molar refractivity, ring count, and the number of hydrogen bond acceptors. The scatter plots of Cp versus each descriptor, along with their respective Pearson correlation coefficients, are shown in Fig. 7a–h.
The Debye model provides a theoretical basis for estimating the volumetric heat capacity at constant volume:52
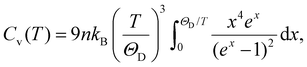 | (8) |
| Cv ≈ 3nkB, | (9) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching, are not excited at room temperature. The effective number of thermally active modes feff is therefore smaller than the classical limit of 3n.
O stretching, are not excited at room temperature. The effective number of thermally active modes feff is therefore smaller than the classical limit of 3n.
For condensed polymer solids, the difference between Cp and Cv is negligible because Cp − Cv = α2BVT ≪ Cp, where α is the thermal expansion coefficient, B the bulk modulus, V the molar volume, and T the temperature.52 Xie et al.53 proposed a modified form of the Debye expression for amorphous polymers by reducing the effective atomic density to exclude hydrogen atoms that contribute only to high-frequency modes:
| Cp ≈ 3nCkB = 2(n − nH)kB, | (10) |
Among all descriptors, the fraction of sp3 carbons shows the strongest positive correlation with Cp (r = +0.82), confirming that flexible single-bonded carbon frameworks enhance the density of low-frequency modes.55 The number of rotatable bonds also shows a positive correlation (r = +0.36), indicating that torsional flexibility contributes to higher Cp through low-frequency modes, whereas ring count exhibits a negative correlation (r = −0.52) because cyclic and aromatic structures restrict conformational motion and increase local stiffness.56 Other descriptors, such as molecular weight, TPSA, heavy atom count, molar refractivity, and hydrogen bond acceptors, show weaker negative correlations (r = −0.25 to −0.30). Although heavier atoms tend to lower individual bond vibrational frequencies, their incorporation is often accompanied by bulkier or more rigid substituents that suppress accessible low-frequency modes.56 Similarly, higher TPSA and larger numbers of hydrogen bond acceptors correspond to polar groups that form strong intermolecular interactions and further limit structural flexibility.56 These effects collectively reduce the number of thermally active degrees of freedom feff, leading to lower Cp. Therefore, polymers with greater conformational flexibility exhibit higher Cp values, whereas rigid frameworks have lower heat capacities due to fewer accessible vibrational modes.
While ML-based models provide accurate Cp predictions, classical GC methods remain attractive due to their simplicity and scalability. To improve the quantitative accuracy of GC-based Cp estimation, we next introduce a data-driven refitting strategy that leverages large-scale predicted datasets to update the GC parameters. The methodology leverages the predicted Cp values of 1 million polymers from the PI1M database, previously computed using our TL-based ML model. For each polymer, we extracted functional group counts from its molecular structure. These counts were then related to the corresponding predicted Cp (in J mol−1 K−1) using a non-negative least squares regression approach. The relation follows the standard additive GC framework:
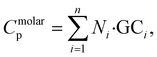 | (11) |
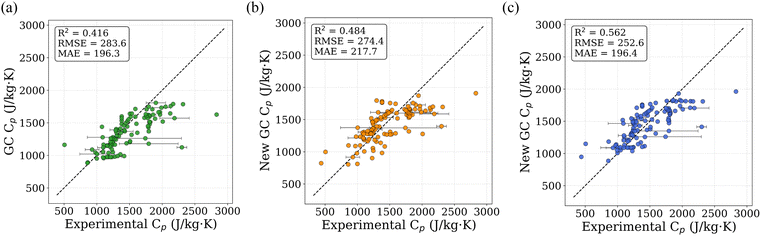
The regression analysis was performed using TL-predicted Cp values for 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 PolyInfo polymers and 1 million PI1M virtual polymers, and the resulting refitted GC values are reported in Table 3 alongside the original literature-based GC parameters (Satoh formulation) as compiled by van Krevelen and te Nijenhuis39 for direct comparison. To assess the performance of the newly proposed GC, we compared predicted Cp values against experimental values from the PolyInfo dataset. Fig. 8a shows the parity plot using the original literature-based GC values, which achieves an R2 value of 0.416. When recalculated using our newly fitted GC values derived from the 13
000 PolyInfo polymers and 1 million PI1M virtual polymers, and the resulting refitted GC values are reported in Table 3 alongside the original literature-based GC parameters (Satoh formulation) as compiled by van Krevelen and te Nijenhuis39 for direct comparison. To assess the performance of the newly proposed GC, we compared predicted Cp values against experimental values from the PolyInfo dataset. Fig. 8a shows the parity plot using the original literature-based GC values, which achieves an R2 value of 0.416. When recalculated using our newly fitted GC values derived from the 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 PolyInfo polymers, the R2 improves to 0.484 (Fig. 8b). The GC values fitted using the 1 million predicted PI1M data further enhance the correlation, yielding an R2 value of 0.562 (Fig. 8c), which corresponds to a 35% improvement over the original GC approach. The refitting procedure results in modest adjustments to the original literature-based GC values rather than introducing new functional groups or qualitative changes. Larger deviations are observed for certain halogen-containing groups (e.g., Br and I), which are interpreted as empirical corrections arising from correlations present in the large predicted dataset rather than as physically fundamental constants. Because the refitted GC parameters are derived from model-predicted Cp values, they necessarily inherit uncertainties and biases associated with the underlying TL model. Accordingly, these parameters are not interpreted as intrinsic physical constants, but as data-driven corrections that improve empirical consistency with experimental trends within the scope of the available data. Further experimental measurements across chemically diverse polymers will be required to fully validate and refine these group contributions.
000 PolyInfo polymers, the R2 improves to 0.484 (Fig. 8b). The GC values fitted using the 1 million predicted PI1M data further enhance the correlation, yielding an R2 value of 0.562 (Fig. 8c), which corresponds to a 35% improvement over the original GC approach. The refitting procedure results in modest adjustments to the original literature-based GC values rather than introducing new functional groups or qualitative changes. Larger deviations are observed for certain halogen-containing groups (e.g., Br and I), which are interpreted as empirical corrections arising from correlations present in the large predicted dataset rather than as physically fundamental constants. Because the refitted GC parameters are derived from model-predicted Cp values, they necessarily inherit uncertainties and biases associated with the underlying TL model. Accordingly, these parameters are not interpreted as intrinsic physical constants, but as data-driven corrections that improve empirical consistency with experimental trends within the scope of the available data. Further experimental measurements across chemically diverse polymers will be required to fully validate and refine these group contributions.
| Functional group | COrigp | CRefitp | Functional group | COrigp | CRefitp | Functional group | COrigp | CRefitp |
|---|---|---|---|---|---|---|---|---|
| GC parameters are defined in molar units (J mol−1 K−1) following the Satoh formulation as compiled by van Krevelen and te Nijenhuis.39 | ||||||||
| –CH3 | 30.90 | 35.54 | –O– | 16.80 | 25.98 | –F | 21.40 | 32.81 |
| –CH2 | 25.35 | 25.35 | –CO– | 23.05 | 30.71 | –Cl | 27.10 | 27.10 |
| >CH– | 15.60 | 15.50 | –COO– | 46.00 | 53.37 | –Br | 26.30 | 78.24 |
| >C< | 6.20 | 6.20 | –COOH | 50.00 | 50.00 | –I | 22.40 | 140.45 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
22.60 | 22.60 | –OH | 17.00 | 26.41 | –CN | 25.00 | 25.00 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
18.65 | 27.70 | –NO2 | 41.90 | 41.90 | –CONH– | 46.00 | 54.00 |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C< C< |
10.50 | 10.50 | –NH2 | 20.95 | 20.94 | –SO2– | 50.00 | 49.72 |
| –NH– | 14.25 | 14.24 | >N– | 17.10 | 17.10 | –SH | 46.80 | 46.80 |
| –S– | 24.05 | 24.00 | 1-Sub benzene | 85.60 | 92.00 | 2-Sub benzene | 78.80 | 85.00 |
| 3-Sub benzene | 65.00 | 80.00 | ||||||
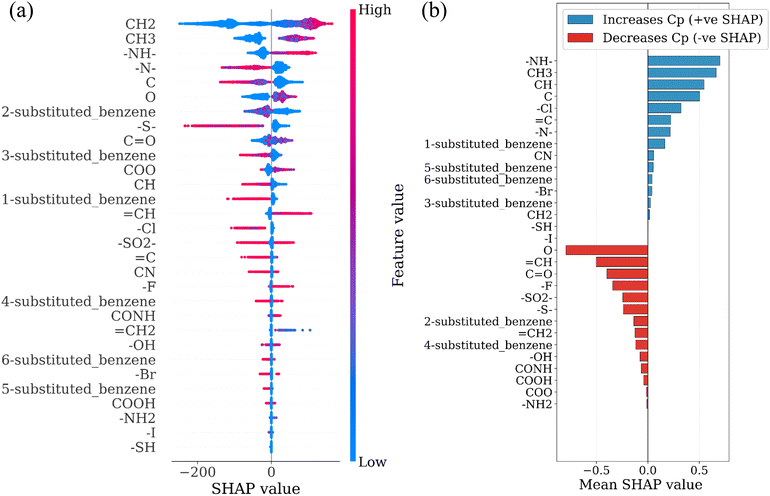
To extend the structural interpretation to the level of functional groups, we developed a separate tree-based regression model trained using functional-group occurrence counts as input features and the predicted polymer Cp values as targets. This approach captures how the presence of specific functional groups influences Cp across the dataset. The feature importance of this model was analyzed using the Shapley Additive Explanations (SHAP) method to quantify the direction and magnitude of each group's contribution (Fig. 9a and b).
Groups such as –NH–, CH3, and CH display positive SHAP values, indicating that their inclusion increases Cp. These structural motifs are associated with sp3 bonding and local torsional flexibility that enhances the density of low-frequency modes. In contrast, groups such as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O,
O, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH, aromatic rings, and –OH exhibit negative SHAP values, corresponding to their tendency to increase bond stiffness or restrict rotational motion. Halogen-containing groups show mixed behavior: heavier atoms such as Cl and Br yield small positive SHAP values, whereas strongly electronegative atoms such as F decrease Cp. The resulting SHAP hierarchy reproduces the same physical trend obtained from the descriptor analysis: chemical environments that promote soft, collective motions contribute positively to Cp, while those that introduce rigidity or strong electronic delocalization reduce it.
CH, aromatic rings, and –OH exhibit negative SHAP values, corresponding to their tendency to increase bond stiffness or restrict rotational motion. Halogen-containing groups show mixed behavior: heavier atoms such as Cl and Br yield small positive SHAP values, whereas strongly electronegative atoms such as F decrease Cp. The resulting SHAP hierarchy reproduces the same physical trend obtained from the descriptor analysis: chemical environments that promote soft, collective motions contribute positively to Cp, while those that introduce rigidity or strong electronic delocalization reduce it.
To qualitatively verify the SHAP-derived group ordering using an independent physical measure, we performed vibrational density of states (VDOS) analysis on a set of small molecules containing CH3, CH2, and other representative functional groups (Fig. 10). The VDOS was obtained from the Fourier transform of the mass-weighted velocity autocorrelation function (VACF). The velocity trajectories (vx, vy, vz) of all atoms were first extracted from the MD simulations. Prior to analysis, the overall translational and rotational (center-of-mass and rigid-body) motions were removed to isolate the intrinsic vibrational dynamics. Each atom i was assigned a mass-weighted velocity defined as
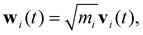 | (12) |
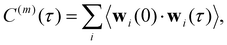 | (13) |
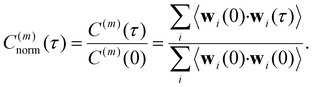 | (14) |
The normalized VACF was then Fourier-transformed to obtain the VDOS,
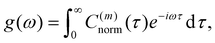 | (15) |
The VDOS from different chemical groups indicates their contributions to the overall Cp (Fig. 10) shows the low-frequency spectral area (0–250 cm−1). The vibrational frequency corresponding to room temperature is approximately 200 cm−1 based on the Bose–Einstein distribution. Therefore, we calculate the areas under the curve for different chemical groups in these studied cases. The integration window was extended to 0–250 cm−1 to capture all relevant torsional and skeletal motions before the onset of higher-frequency stretching vibrations.56
Across all test molecules, the CH3 group consistently exhibits the largest integrated low-frequency area (A0–250), confirming its strong association with soft torsional and skeletal vibrations. Functional groups such as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, aromatic, S, F, and Br display smaller A0–250 values compared to the CH3 group within the same molecule, indicating comparatively stiffer local bonding and reduced accessibility of low-frequency modes. The only group that shows a comparable or slightly larger spectral area than CH3 is –NH–. These observations generally align well with the SHAP ranking.
O, aromatic, S, F, and Br display smaller A0–250 values compared to the CH3 group within the same molecule, indicating comparatively stiffer local bonding and reduced accessibility of low-frequency modes. The only group that shows a comparable or slightly larger spectral area than CH3 is –NH–. These observations generally align well with the SHAP ranking.
In addition to descriptor-based analysis, SHAP interpretation, and VDOS decomposition, we further examine local, atom-level contributions using the GREA model. Based on nested cross-validation, GREA is not the best-performing predictive model and is therefore used here primarily as a tool for interpretability. The central feature of GREA is its environment-based augmentation, in which atomic representations are conditioned on their surrounding chemical context. This allows the model to distinguish similar functional groups embedded in different environments and yields chemically meaningful atom-level attributions. The details of the GREA framework and its underlying formulation are described in the original work by Liu et al.44 Fig. 11 presents representative rationale visualizations for two high-Cp polymers (Fig. 11a and b) and two low-Cp polymers (Fig. 11c and d). Highlighted regions indicate atoms that contribute most strongly to the predicted Cp. For high-Cp polymers, the model assigns greater importance to flexible aliphatic segments and heteroatom-containing linkages, which increase vibrational freedom and contribute to higher heat capacity. In contrast, low-Cp polymers are characterized by rigid, highly fluorinated backbones and heavy halogen substitution, consistent with reduced vibrational freedom. Overall, these atom-level rationales provide localized and chemically intuitive confirmation of trends identified through descriptor analysis, SHAP values, and VDOS calculations, and help connect the model predictions to underlying physical mechanisms. These atom-level rationales should be interpreted as associative rather than causal. The highlighted contributions reflect correlations learned from the available training data between local chemical environments and predicted Cp, and do not imply direct mechanistic causation.
With validated predictive models and a refined GC framework in place, we finally demonstrate how the predicted thermophysical properties can be used for application-oriented polymer screening and categorization. Using the ML-predicted Cp values, we identified promising polymer candidates for various thermal applications. Although the primary focus of this study is on Cp, selecting materials based solely on Cp is not sufficient for practical applications. As a demonstration of practical screening scenarios, we therefore incorporated two additional thermal properties, thermal conductivity (TC) and glass transition temperature (Tg), sourced from our previous studies.9,13,28 Table 4 provides a comprehensive overview of the categorization framework used. It includes: (i) the names of four application-specific polymer categories; (ii) threshold values for Cp, TC, and Tg, defined separately for the PolyInfo dataset and for the larger PI1M database; (iii) functional descriptions outlining the role of each category; and (iv) representative example applications. Because PI1M contains a substantially larger and more diverse set of polymers, the corresponding thresholds were set at slightly higher values to reflect its broader property distribution. The threshold values for each property were chosen based on the distribution and upper–lower bounds of the TL-predicted values in each dataset, highlighting polymers with clearly distinct thermal behaviors. The application-oriented categorization presented here is intended as a high-level screening and prioritization framework rather than a device-level design or certification scheme. The Cp, TC, and Tg thresholds are defined heuristically to translate large-scale property predictions into application-relevant guidance, rather than as strict performance requirements. The selected threshold ranges are consistent with typical thermophysical property values reported for polymers in the literature. Mass-specific Cp of common polymers are generally reported in the range of approximately 1200–3000 J kg−1 K−1 at ambient conditions, while bulk polymer TCs typically lie between about 0.1 and 0.5 W m−1 K−1.39 Reported Tg span a broad range, from below room temperature for flexible polymers to above 150–200 °C for thermally stable engineering polymers.39,57 These literature-consistent ranges provide physical context for the heuristic thresholds adopted in Table 4.
| Category | Thresholds (PolyInfo) | Thresholds (PI1M) | Functional description | Example applications | Representative examples |
|---|---|---|---|---|---|
| Thermal interface materials (high Cp, high TC, high Tg) | Cp ≥ 1600 | Cp ≥ 1800 | Efficient heat transfer across interfaces with high thermal stability under operating conditions | Interface pads in CPUs/GPUs, power electronics, EV battery modules | High-Tg engineering polymers (e.g., PEEK-like systems) used in thermally demanding structural applications |
| TC ≥ 0.4 | TC ≥ 0.5 | ||||
| Tg ≥ 100 °C | Tg ≥ 130 °C | ||||
| Thermal insulators (high Cp, low TC, high Tg) | Cp ≥ 1700 | Cp ≥ 2000 | Minimizes heat transfer while maintaining thermal and mechanical stability at elevated temperatures | Fire-resistant coatings, aerospace insulation, protective gear | Polyethylene-based materials exhibiting low TC and moderate-to-high Cp under ambient conditions |
| TC ≤ 0.2 | TC ≤ 0.2 | ||||
| Tg ≥ 120 °C | Tg ≥ 110 °C | ||||
| Thermal buffers (high Cp, low TC, low Tg) | Cp ≥ 1800 | Cp ≥ 2200 | Acts as a thermal reservoir for energy absorption and damping at sub-ambient conditions | Cold chain packaging, biomedical storage, low-temperature wraps | HDPE and related polyolefins with low Tg and strong thermal buffering behavior |
| TC ≤ 0.2 | TC ≤ 0.2 | ||||
| Tg ≤ 10 °C | Tg ≤ −50 °C | ||||
| Heat spreaders (low Cp, high TC, high Tg) | Cp ≤ 1000 | Cp ≤ 700 | Rapid dissipation of localized heat under high thermal loads and cycling | LED spreaders, aerospace electronics, laser cooling systems | Sulfur- and heteroatom-rich polymers reported to exhibit elevated TC and thermal robustness |
| TC ≥ 0.4 | TC ≥ 0.6 | ||||
| Tg ≥ 150 °C | Tg ≥ 150 °C |
We propose a categorization framework to link predicted thermal properties with application-specific needs. The thermal interface materials category targets applications requiring efficient heat dissipation and structural stability, favoring polymers with high Cp, high TC, and high Tg.58 Thermal insulators, commonly used in high-temperature environments, are characterized by high Cp, low TC, and high Tg, which minimize heat transfer.59 Thermal buffers, relevant for energy storage or damping applications, require high Cp, low TC, and low Tg to provide thermal management at sub-ambient conditions.60 Finally, we define heat spreaders as materials prioritizing rapid heat conduction and thermal resilience, requiring low Cp, high TC, and high Tg, which are ideal for high-performance electronics.61 As a qualitative validation of the application-oriented categorization, we examine whether well-known polymers are placed into categories consistent with their established thermophysical behavior reported in the literature. This comparison is intended to verify the physical plausibility of the screening framework rather than to serve as device-level validation. For example, polyethylene-based materials are widely used in applications where low TC and thermal buffering are desirable. High-density polyethylene (HDPE) exhibits mass-specific Cp in the range of approximately 1300–2400 J kg−1 K−1 and bulk TC on the order of 0.3–0.5 W m−1 K−1 at ambient conditions, together with a very low Tg.39 These literature-reported properties satisfy the defining criteria of the low-conductivity categories in Table 4 (thermal insulators/thermal buffers), consistent with the established use of polyethylene materials in insulating and thermal buffering roles. Similarly, high-performance engineering polymers such as poly(ether ether ketone) (PEEK), which exhibits a high Tg of approximately 143 °C and is commonly employed in thermally demanding environments requiring structural stability, are preferentially grouped into categories characterized by elevated Tg thresholds.39,57 While PEEK is not selected for high thermal conductivity, its classification reflects the intended role of high-Tg criteria in identifying thermally stable polymer classes. These examples demonstrate that the proposed threshold-based categorization recovers well-established qualitative distinctions among polymer classes, supporting its use as a first-pass screening and prioritization tool. The case studies show that ML models can quickly identify polymer candidates given property targets, and that this approach is generalizable to any custom-defined property targets.
Fig. 12a shows a scatter plot of the PolyInfo polymers, visualizing the relationship between Cp, TC, and Tg. The overlaid shaded regions indicate the approximate areas occupied by polymers with distinct combinations of thermal properties, corresponding to the four application categories discussed in Table 4. These regions highlight clusters of datapoints with relatively high or low values of Cp, TC, and Tg, representing typical candidates for applications such as thermal interface materials, insulators, buffers, and heat spreaders. Similarly, Fig. 12b presents the plot for the PI1M dataset. The same region boundaries are overlaid to visualize the distribution of newly screened polymers across the functional application space. With 1 million polymers, the PI1M dataset spans a larger chemical space, and since the threshold values are higher, it offers a selection of polymer candidates with more extreme properties.
Fig. 13 presents the selected polymer candidates from the PolyInfo database, with five representative polymers shown for each of the four application categories. Each polymer is depicted with its chemical structure, along with its polymer class, and corresponding thermal property values. For the selected polymers, the Cp values predicted using the ML model were cross-checked using the newly proposed GC method. For selection, only polymers where both ML-predicted and GC-derived Cp values satisfied the threshold criteria, defined in Table 4, were included. We adopted the GC method for Cp validation instead of MD simulations, as MD-predicted values tend to be systematically overestimated. This figure also illustrates the structural and thermal property diversity of representative polymers across four functional categories. In the Thermal Interface group, polyesters and polyphenylenes stand out with high values of Cp, TC, and Tg. The thermal insulator and buffer categories are mostly polyacrylics, polyolefins, and polyvinyls, which exhibit high Cp but low TC, which are favorable for thermal resistance and energy absorption. Conversely, the heat spreader category includes polymers such as polysulfides and polyimines, which display relatively low Cp and high TC and Tg, ideal for efficient heat spreading. These examples highlight real polymer candidates tailored for specific thermal roles, reinforcing the utility of data-driven screening in materials design.
 | ||
| Fig. 13 Selected polymer candidates from the PolyInfo dataset representing four functional categories based on predicted Cp, TC, and Tg, with corresponding polymer class labels. Selection was based on threshold criteria from Table 4. | ||
Similarly, Fig. 14 shows the selected polymer candidates from the P11M dataset, with five representative polymers displayed for each application category. The selections are based on the higher threshold values defined for P11M in Table 4. Each polymer is shown with its ML-predicted Cp value, along with the TC and Tg. Because the proposed application categories are derived from multiple predicted properties (Cp, TC, and Tg), uncertainties from the individual predictive models may accumulate in the final classification. Accordingly, the resulting application labels should be interpreted probabilistically and used for candidate prioritization rather than definitive assignment. In addition, we verified that modest variations (on the order of ±10%) in the threshold values for Cp, TC, and Tg do not qualitatively alter the overall distribution of polymers across application categories, indicating that the screening results are robust to small threshold perturbations. By leveraging both established and large-scale virtual datasets, we demonstrate the potential to discover high-performing candidates across a broad chemical space. These selected polymers provide a strong foundation for further computational or experimental evaluation and showcase the practical relevance of data-driven screening strategies in polymer thermal property design.
 | ||
| Fig. 14 Selected polymer candidates from the PI1M dataset representing four functional categories based on predicted Cp, TC, and Tg. Selection was based on threshold criteria from Table 4 with stricter cutoffs for this dataset. | ||
Conclusion
This work presents a comprehensive TL framework for predicting the Cp of polymers, a key property for efficient thermal energy management in various applications. ML models were first pretrained using large datasets generated from MD simulations and GC method calculations, and then fine-tuned on experimental data to improve accuracy. Multiple ML models were evaluated, including MLP, GNN, and GREA architectures, using a range of molecular fingerprints and structural descriptors. MLP model with TL showed superior performance, highlighting the effectiveness of combining structural priors with experimental trends.The trained models were applied to polymers from both known and virtual datasets to perform large-scale Cp screening. We further explored LLMs as few-shot, training-free baselines; however, their performance was substantially inferior to domain-specific ML models, limiting their applicability for quantitative property prediction. Structure–property analysis, supported by SHAP interpretation and VDOS analysis, revealed that polymers with a higher fraction of sp3-hybridized carbons and more rotatable bonds tend to exhibit increased Cp values because enhanced vibrational flexibility increases the number of accessible low-frequency modes. These trends align with the theoretical understanding that a greater number of low-energy, thermally accessible vibrational DOF significantly contributes to Cp in polymers.
In addition, we proposed new GC values through data-driven regression, providing an interpretable and lightweight alternative for Cp estimation. Based on predicted Cp, along with TC and Tg, polymers were classified into four application-relevant categories: thermal interface materials, insulators, buffers, and heat spreaders. Representative candidates were identified for each category, demonstrating the practical utility of the screening framework. Overall, this study demonstrates how integrating multi-fidelity data, ML, and interpretable modeling can accelerate polymer discovery. The framework is adaptable and can be extended to other thermophysical properties, offering a valuable tool for guiding the design of advanced materials for thermal energy applications.
Conflicts of interest
There are no conflicts to declare.Data availability
All data and code supporting this study are publicly available. The complete implementation of the machine-learning workflows is provided at https://github.com/sobinalosious/POLY-CP-TL. The repository includes: (i) the curated experimental Cp dataset used for training and evaluation, with corresponding SMILES representations; (ii) the proxy datasets used for pretraining, including MD and GC derived Cp values; (iii) the full MD workflow used to compute Cp, including LAMMPS input scripts and Python post-processing codes for both EMD and NEMD methods; (iv) the GC calculation code and parameter tables used to estimate Cp from SMILES; (v) all scripts required to reproduce the results reported in Table 1, including nested cross-validation, Optuna-based hyperparameter optimization, pretraining, fine-tuning, and evaluation pipelines; (vi) the exact cross-validation splits, random seeds, and fold-wise optimal hyperparameters; and (vii) trained model weights for the best-performing configurations.No human-subject or confidential data were used.
Acknowledgements
This work was supported by the Lucy Family Institute for Data & Society Postdoctoral Fellowship and National Science Foundation grants 2332270, 2102592 and 2146761. The authors also acknowledge the Center for Research Computing at the University of Notre Dame for providing the necessary computing resources.References
- X. C. Tong, Advanced Materials for Thermal Management of Electronic Packaging, Springer, 2010, pp. 527–593 Search PubMed.
- M. Sun, T. Liu, X. Wang, T. Liu, M. Li, G. Chen and D. Jiang, Roles of thermal energy storage technology for carbon neutrality, Carbon Neutrality, 2023, 2, 12 CrossRef.
- W. Wang, J. Ren, X. Yin, Y. Qiao and F. Cao, Energy-efficient operation of the thermal management system in electric vehicles via integrated model predictive control, J. Power Sources, 2024, 603, 234415 CrossRef CAS.
- S. V. Garimella, T. Persoons, J. A. Weibel and V. Gektin, Electronics thermal management in information and communications technologies: Challenges and future directions, IEEE Trans. Compon., Packag., Manuf. Technol., 2016, 7, 1191–1205 Search PubMed.
- B. Lamrani, S. El Marbet, T.-u. Rehman and T. Kousksou, Comprehensive analysis of waste heat recovery and thermal energy storage integration in air conditioning systems, Energy Convers. Manage.: X, 2024, 24, 100708 CAS.
- A. R. Dhumal, A. P. Kulkarni and N. H. Ambhore, A comprehensive review on thermal management of electronic devices, J. Eng. Appl. Sci., 2023, 70, 140 CrossRef.
- X. Zhang, Z. Li, L. Luo, Y. Fan and Z. Du, A review on thermal management of lithium-ion batteries for electric vehicles, Energy, 2022, 238, 121652 CrossRef CAS.
- I. Sarbu and A. Dorca, Review on heat transfer analysis in thermal energy storage using latent heat storage systems and phase change materials, Int. J. Energy Res., 2019, 43, 29–64 CrossRef CAS.
- J. Xu and T. Luo, Unlocking enhanced thermal conductivity in polymer blends through active learning, npj Comput. Mater., 2024, 10, 74 CrossRef CAS.
- T. Zhang, X. Wu and T. Luo, Polymer nanofibers with outstanding thermal conductivity and thermal stability: fundamental linkage between molecular characteristics and macroscopic thermal properties, J. Phys. Chem. C, 2014, 118, 21148–21159 CrossRef CAS.
- T. Luo, J. Garg, J. Shiomi, K. Esfarjani and G. Chen, Gallium arsenide thermal conductivity and optical phonon relaxation times from first-principles calculations, Europhys. Lett., 2013, 101, 16001 CrossRef.
- L. Chen, H. Tran, R. Batra, C. Kim and R. Ramprasad, Machine learning models for the lattice thermal conductivity prediction of inorganic materials, Comput. Mater. Sci., 2019, 170, 109155 CrossRef CAS.
- R. Zhang, J. Xu, H. Zhang, G. Xu and T. Luo, Active learning-guided exploration of thermally conductive polymers under strain, Digital Discovery, 2025, 4, 812–823 RSC.
- X. Wei, Z. Wang, Z. Tian and T. Luo, Thermal transport in polymers: a review, J. Heat Transfer, 2021, 143, 072101 CrossRef CAS.
- S. Kharbanda, T. Bhadury, G. Gupta, D. Fuloria, P. R. Pati, V. K. Mishra and A. Sharma, Polymer composites for thermal applications–A review, Mater. Today: Proc., 2021, 47, 2839–2845 CAS.
- A. Henry, Thermal transport in polymers, Annu. Rev. Heat Transfer, 2014, 17, 485–520 CrossRef.
- M. Q. Le, J.-F. Capsal, J. Galineau, F. Ganet, X. Yin, M. Yang, J.-F. Chateaux, L. Renaud, C. Malhaire and P.-J. Cottinet, et al., All-organic electrostrictive polymer composites with low driving electrical voltages for micro-fluidic pump applications, Sci. Rep., 2015, 5, 11814 CrossRef PubMed.
- H. Luo, F. Wang, R. Guo, D. Zhang, G. He, S. Chen and Q. Wang, Progress on polymer dielectrics for electrostatic capacitors application, Adv. Sci., 2022, 9, 2202438 CrossRef CAS.
- Y. Liu, S. Alosious, J. Zhou, M. Jiang and T. Luo, Machine Learning in Nanoscale Thermal Transport, Annu. Rev. Heat Transfer, 2025, 28, 173–214 CrossRef.
- M. O′neill, Measurement of Specific Heat Functions by Differential Scanning Calorimetry., Anal. Chem., 1966, 38, 1331–1336 CrossRef.
- R. Bhowmik, S. Sihn, V. Varshney, A. K. Roy and J. P. Vernon, Calculation of specific heat of polymers using molecular dynamics simulations, Polymer, 2019, 167, 176–181 CrossRef CAS.
- Q. Waheed and O. Edholm, Quantum corrections to classical molecular dynamics simulations of water and ice, J. Chem. Theory Comput., 2011, 7, 2903–2909 Search PubMed.
- D. Rihani and L. Doraiswamy, Estimation of heat capacity of organic compounds from group contributions, Ind. Eng. Chem. Fundam., 1965, 4, 17–21 CrossRef CAS.
- R. Bhowmik, S. Sihn, R. Pachter and J. P. Vernon, Prediction of the specific heat of polymers from experimental data and machine learning methods, Polymer, 2021, 220, 123558 Search PubMed.
- S. Alosious, M. Jiang and T. Luo, Computation and machine learning for materials: Past, present, and future perspectives, MRS Bull., 2025, 1–13 Search PubMed.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, RadonPy: automated physical property calculation using all-atom classical molecular dynamics simulations for polymer informatics, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- I. P. Malashin, V. S. Tynchenko, V. A. Nelyub, A. S. Borodulin and A. P. Gantimurov, Estimation and prediction of the polymers’ physical characteristics using the machine learning models, Polymers, 2023, 16, 115 CrossRef PubMed.
- R. Ma, H. Zhang, J. Xu, L. Sun, Y. Hayashi, R. Yoshida, J. Shiomi, J.-x. Wang and T. Luo, Machine learning-assisted exploration of thermally conductive polymers based on high-throughput molecular dynamics simulations, Mater. Today Phys., 2022, 28, 100850 CrossRef CAS.
- D. Weininger, SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- M. E. Fortunato and C. M. Colina, pysimm: A python package for simulation of molecular systems, SoftwareX, 2017, 6, 7–12 CrossRef.
- D. Vassetti, M. Pagliai and P. Procacci, Assessment of GAFF2 and OPLS-AA general force fields in combination with the water models TIP3P, SPCE, and OPC3 for the solvation free energy of druglike organic molecules, J. Chem. Theory Comput., 2019, 15, 1983–1995 Search PubMed.
- Y. Wu, B. Yao, X. Huang and Y. Chen, Integrating machine learning and molecular dynamics for accelerated discovery of polymers with high thermal conductivity, J. Appl. Phys., 2025, 138(17), 175101 CrossRef CAS.
- H. Yue, S. Wang, X. Sha and Q. Wang, Discovery of polymers with high bulk modulus and low thermal conductivity using a hybrid generative pipeline, Chem. Eng. J., 2025, 164763 CrossRef CAS.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 Search PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes, J. Comput. Phys., 1977, 23, 327–341 Search PubMed.
- R. W. Hockney and J. W. Eastwood, Computer simulation using particles, CRC Press, 2021 Search PubMed.
- M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford University Press, 2017 Search PubMed.
- B. Jasiok, A. A. Pribylov, E. B. Postnikov, P. Friant-Michel and C. Millot, Thermophysical properties of the SPC/E model of water between 250 and 400 K at pressures up to 1000 MPa, Fluid Phase Equilib., 2024, 584, 114118 CrossRef CAS.
- D. W. Van Krevelen and K. Te Nijenhuis, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier, 2009 Search PubMed.
- A. P. Bento, A. Hersey, E. Félix, G. Landrum, A. Gaulton, F. Atkinson, L. J. Bellis, M. De Veij and A. R. Leach, An open source chemical structure curation pipeline using RDKit, J. Cheminf., 2020, 12, 1–16 Search PubMed.
- R. Ma and T. Luo, PI1M: a benchmark database for polymer informatics, J. Chem. Inf. Model., 2020, 60, 4684–4690 CrossRef CAS PubMed.
- A. Gulli and S. Pal, Deep learning with Keras, Packt Publishing Ltd, 2017 Search PubMed.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 2019, pp. 2623–2631.
- G. Liu, T. Zhao, J. Xu, T. Luo and M. Jiang, Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 2022, pp. 1069–1078.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, How powerful are graph neural networks?, arXiv, 2018, preprint, arXiv:1810.00826, DOI:10.48550/1810.00826.
- T. N. Kipf and M. Welling, Semi-supervised classification with graph convolutional networks, arXiv, 2016, preprint, arXiv:1609.02907, DOI:10.48550/1609.02907.
- D. Bajusz, A. Rácz and K. Héberger, Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations?, J. Cheminf., 2015, 7, 1–13 CAS.
- S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki, 2011 International Conference on Emerging Intelligent Data and Web Technologies, 2011, pp. 22–29.
- D. A. McQuarrie, Quantum chemistry, University Science Books, 2008 Search PubMed.
- J. R. Lukes, D. Y. Li, X.-G. Liang and C.-L. Tien, Molecular Dynamics Study of Solid Thin-Film Thermal Conductivity, J. Heat Transfer, 2000, 122, 536–543 CrossRef CAS.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, 2003 Search PubMed.
- C. Kittel and P. McEuen, Introduction to solid state physics, John Wiley & Sons, 2018 Search PubMed.
- X. Xie, K. Yang, D. Li, T.-H. Tsai, J. Shin, P. V. Braun and D. G. Cahill, High and low thermal conductivity of amorphous macromolecules, Phys. Rev. B, 2017, 95, 035406 Search PubMed.
- B. Wunderlich and L. D. Jones, Heat capacities of solid polymers, J. Macromol. Sci., Part B: Phys., 1969, 3, 67–79 Search PubMed.
- A. Giri, C. J. Dionne and P. E. Hopkins, Atomic coordination dictates vibrational characteristics and thermal conductivity in amorphous carbon, npj Comput. Mater., 2022, 8, 55 CrossRef CAS.
- K. A. Bensley, R. V. Chimenti and S. E. Lofland, Low-Frequency Raman Spectroscopy of Polymers, Macromol. Chem. Phys., 2025, 70004 Search PubMed.
- J. Bicerano, Prediction of polymer properties, CRC Press, 2002 Search PubMed.
- C.-P. Feng, L.-Y. Yang, J. Yang, L. Bai, R.-Y. Bao, Z.-Y. Liu, M.-B. Yang, H.-B. Lan and W. Yang, Recent advances in polymer-based thermal interface materials for thermal management: A mini-review, Compos. Commun., 2020, 22, 100528 CrossRef.
- S. Cai, X. Deng, J. Beiyuan, X. Chen, D. Liu, D. Lv, C. Duan, L. Lin, R. Cha, W. Xie, H. Chen, J. Zhou, Z. Lu, L. Huang and W. Yuan, Review of synthetic polymer-based thermal insulation materials in construction and building, J. Build. Eng., 2024, 97, 110846 CrossRef.
- Y. Jing, Z. Zhao, X. Cao, Q. Sun, Y. Yuan and T. Li, Ultraflexible, cost-effective and scalable polymer-based phase change composites via chemical cross-linking for wearable thermal management, Nat. Commun., 2023, 14, 8060 CrossRef CAS PubMed.
- C. Oshman, Q. Li, L.-A. Liew, R. Yang, Y. Lee, V. M. Bright, D. J. Sharar, N. R. Jankowski and B. C. Morgan, Thermal performance of a flat polymer heat pipe heat spreader under high acceleration, J. Micromech. Microeng., 2012, 22, 045018 Search PubMed.
| This journal is © The Royal Society of Chemistry 2026 |