Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Magnetic structure and properties of the honeycomb antiferromagnet [Na(OH2)3]Mn(NCS)3†
Madeleine
Geers
 ab,
Thomas B.
Gill
ab,
Thomas B.
Gill
 c,
Andrew D.
Burnett
c,
Andrew D.
Burnett
 d,
Euan N.
Bassey‡
d,
Euan N.
Bassey‡
 e,
Oscar
Fabelo
e,
Oscar
Fabelo
 b,
Laura
Cañadillas-Delgado
b,
Laura
Cañadillas-Delgado
 b and
Matthew J.
Cliffe
b and
Matthew J.
Cliffe
 *a
*a
aSchool of Chemistry, University Park, Nottingham, NG7 2RD, UK. E-mail: matthew.cliffe@nottingham.ac.uk
bInstitut Laue Langevin, 71 avenue des Martyrs CS 20156, 38042 Grenoble Cedex 9, France
cSchool of Electronic and Electrical Engineering, University of Leeds, Leeds, LS2 9JT, UK
dSchool of Chemistry, University of Leeds, Leeds, LS2 9JT, UK
eYusuf Hamied Department of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
First published on 14th May 2024
Abstract
We report the magnetic structure and properties of a thiocyanate-based honeycomb magnet [Na(OH2)3]Mn(NCS)3 which crystallises in the unusual low-symmetry trigonal space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) . Magnetic measurements on powder samples show this material is an antiferromagnet (ordering temperature TN,mag = 18.1(6) K) and can be described by nearest neighbour antiferromagnetic interactions J = −11.07(4) K. A method for growing neutron-diffraction sized single crystals (>10 mm3) is demonstrated. Low temperature neutron single crystal diffraction shows that the compound adopts the collinear antiferromagnetic structure with TN,neut = 18.94(7) K, magnetic space group P
. Magnetic measurements on powder samples show this material is an antiferromagnet (ordering temperature TN,mag = 18.1(6) K) and can be described by nearest neighbour antiferromagnetic interactions J = −11.07(4) K. A method for growing neutron-diffraction sized single crystals (>10 mm3) is demonstrated. Low temperature neutron single crystal diffraction shows that the compound adopts the collinear antiferromagnetic structure with TN,neut = 18.94(7) K, magnetic space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′. Low temperature second-harmonic generation (SHG) measurements provide no evidence of breaking of the centre of symmetry.
′. Low temperature second-harmonic generation (SHG) measurements provide no evidence of breaking of the centre of symmetry.
Honeycomb magnets, due to their high symmetry and two-dimensionality, can host a wide range of magnetic phases, including monolayer ferromagnetism in CrI3,1 proximate Kitaev spin liquid states in RuCl3 and Na2Co2TeO6,2,3 complex spin textures in FeCl3,4 and magnetoelectricity in Co2Mo3O8.5
Molecular magnets are of particular interest for low-dimensional magnetism as it is often more straightforward to produce well-isolated low-dimensional connectivity, and the molecular ligands offer the potential for a high degree of tunability.6 Honeycomb molecular magnets are no exception to this, particularly those based on chelating ligands such as (ox2− = C2O42−),7–9 tetraoxolene (C6O4R2n−)10 amongst others.11,12 These structures often have multiple different paramagnetic species producing ferrimagnetic order, whether this is alternating metal sites A[MIIMIII](ox)3,7 A[MIIMIII](C6O4R2)313,14 or the presence of radical ligands in A2[M2(C6O4R2)3],10 where A is charge balancing cation (typically alkylammonium). Equally, distorted honeycomb structures, with multiple different exchange pathways are common.12,15,16 Examples of ideal honeycomb lattice magnets are thus comparatively rare.
One promising material family to search for honeycomb magnets are the metal thiocyanates, which show a range of low dimensional magnetic properties due to the layered structural connectivity and have interactions as strong as comparable halides.18,19 In this paper we investigate the magnetic properties of [Na(OH2)3]Mn(NCS)3 (NaMn(NCS)3·3H2O),20 formed of ideal two-dimensional honeycomb [Mn(NCS)3]− layers with the hexagonal void filled by 1D [Na(OH2)3]+ rods [Fig. 1]. It crystallises in the low-symmetry but still trigonal P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) space-group, comparatively rare in inorganic materials (fewer than 0.25% of ICSD structures21). As a result, the Mn(II) sites do not lie on inversion centres, which raises the possibility that magnetic ordering may break the centre of symmetry and hence induce simultaneous magnetic and electric order (type II multiferroicity).22 Although the structure of this compound has been reported, because it is very sensitive to humidity, very little is known about its physical properties.20 We report a method for the synthesis of large [Na(OH2)3]Mn(NCS)3 single crystals (12 mm3) of suitable quality for neutron diffraction measurements, which mitigates the strong humidity dependence of this compound. Using a combination of bulk magnetic property measurements, low-temperature single crystal neutron diffraction and SHG measurements, we have determined its magnetic properties. We find that [Na(OH2)3]Mn(NCS)3 orders with the classical honeycomb antiferromagnetic ground state, ordering into the centrosymmetric collinear antiferromagnetic P
space-group, comparatively rare in inorganic materials (fewer than 0.25% of ICSD structures21). As a result, the Mn(II) sites do not lie on inversion centres, which raises the possibility that magnetic ordering may break the centre of symmetry and hence induce simultaneous magnetic and electric order (type II multiferroicity).22 Although the structure of this compound has been reported, because it is very sensitive to humidity, very little is known about its physical properties.20 We report a method for the synthesis of large [Na(OH2)3]Mn(NCS)3 single crystals (12 mm3) of suitable quality for neutron diffraction measurements, which mitigates the strong humidity dependence of this compound. Using a combination of bulk magnetic property measurements, low-temperature single crystal neutron diffraction and SHG measurements, we have determined its magnetic properties. We find that [Na(OH2)3]Mn(NCS)3 orders with the classical honeycomb antiferromagnetic ground state, ordering into the centrosymmetric collinear antiferromagnetic P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ space group.
′ space group.
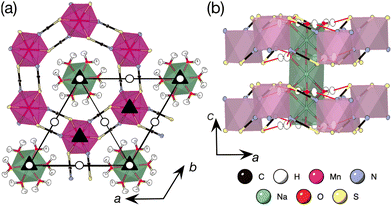 | ||
Fig. 1 Neutron single crystal structure of [Na(OH2)3]Mn(NCS)3 (D19 at the ILL, 25 K).17 (a) View along the c axis. Space group diagram for P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) overlaid, overlaid, ![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) : white circle, 3: black triangle. (b) View along the b axis. Hydrogen bonds shown as red lines. : white circle, 3: black triangle. (b) View along the b axis. Hydrogen bonds shown as red lines. | ||
We synthesised [Na(OH2)3]Mn(NCS)3 using a method adapted from that of Biedermann1998, using the salt metathesis of manganese(II) sulfate and barium thiocyanate with additional sodium thiocyanate in aqueous solution in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. After filtering the precipitated BaSO4 and removing the water, a pale green-yellow powder was obtained, deliquescent in ambient conditions, which can be recovered from its own solution by heating at no more than 60 °C. The powder sample is also sensitive to dry environments, and will decompose to Mn(NCS)2 and NaNCS on heating.
1 ratio. After filtering the precipitated BaSO4 and removing the water, a pale green-yellow powder was obtained, deliquescent in ambient conditions, which can be recovered from its own solution by heating at no more than 60 °C. The powder sample is also sensitive to dry environments, and will decompose to Mn(NCS)2 and NaNCS on heating.
On concentration in vacuo, aqueous solutions of [Na(OH2)3]Mn(NCS)3 change colour sequentially from colourless to pale pink, pale green and eventually to aqua blue [Fig. S1, ESI†]. We found that the optimal concentration for crystal growth is when the solution is an intense green colour, just before it begins turning blue. More concentrated, blue, solutions very rapidly crystallised, which led to many smaller crystals. Less concentrated solutions were not sufficiently supersaturated for crystal growth [Fig. S2, ESI†]. On leaving this green solution to stand for 24 h at 7 °C we obtained large regular-hexagonal crystals. As the supersaturated solution absorbs water from the air, the concentration falls below the level required for optimal crystal growth after 24 h. The harvested crystals from this initial crystallisation were then used as seeds for future crystallisation with the growth solution being reconcentrated to the optimal concentrations. After nine iterations of seeded crystallisation we obtained pale green, hexagonal crystals of [Na(OH2)3]Mn(NCS)3 suitable for neutron diffraction experiments: 4 × 3 × 1 mm3 [Fig. 3(a)]. Due to the humidity sensitivity of this compound, we explored a variety of conditions for storage using saturated aqueous salt solutions to control the atmosphere: 54% (Mg(NO3)2(aq.)), 39% (NaI(aq.)), 32% (CaCl2(aq.)) and 23% (KCH3COO(aq.)).23,24 We found that the crystals were indefinitely stable at 32% humidity (>23 months). We confirmed the phase purity of powder samples with powder X-ray diffraction and the quality of smaller single crystals was checked using ambient temperature X-ray single crystal diffraction.
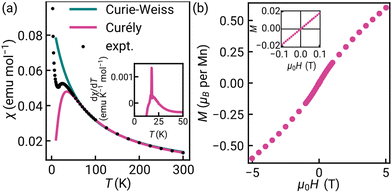
Previous work has established that manganese thiocyanate compounds show moderately strong magnetic interactions,18,19 and so to investigate the magnetic properties of [Na(OH2)3]Mn(NCS)3 and uncover any magnetic phase transitions, we carried out magnetic susceptibility (μ0H = 0.01 T) and isothermal magnetisation measurements on a powder sample (2 K, −5 to +5 T). We found that the magnetic susceptibility increases on cooling until a broad maximum is reached around 25 K. Below this temperature, the susceptibility decreases until a sharp drop at the ordering temperature, TN = 18.1(6) K [Fig. 2(a)]. The temperature dependence of the moment was fitted to the Curély model of a nearest neighbour classical honeycomb magnet,12 using the following Hamiltonian:
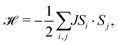 | (1) |
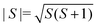 , and the sum is only over nearest neighbours. In this convention, antiferromagnetic superexchange will give negative J. We fitted the data over the full temperature range, with an additional 1/T term to account for paramagnetic impurities due to sample hydration, giving J = −10.0(2) K and g = 1.8 with 7.0(2)% paramagnetic impurities. We also fitted just the high temperature regime (T > 60 K), using both the Curély model, giving J = −11.07(4) K, g = 2.02, and using the Curie–Weiss model which gives a Curie–Weiss temperature, θCW = −51.4(1.4) K, equivalent to J = −17.4(5) K and g = 2.09, the overestimated Curie–Weiss temperature being typical of analysis of low-dimensional magnets. The presence of a small fraction of hydrated impurity means the extracted values of g are unreliable.
, and the sum is only over nearest neighbours. In this convention, antiferromagnetic superexchange will give negative J. We fitted the data over the full temperature range, with an additional 1/T term to account for paramagnetic impurities due to sample hydration, giving J = −10.0(2) K and g = 1.8 with 7.0(2)% paramagnetic impurities. We also fitted just the high temperature regime (T > 60 K), using both the Curély model, giving J = −11.07(4) K, g = 2.02, and using the Curie–Weiss model which gives a Curie–Weiss temperature, θCW = −51.4(1.4) K, equivalent to J = −17.4(5) K and g = 2.09, the overestimated Curie–Weiss temperature being typical of analysis of low-dimensional magnets. The presence of a small fraction of hydrated impurity means the extracted values of g are unreliable.
The isothermal magnetisation does not saturate up to 5.00(1) T, consistent with the moderately strong antiferromagnetism, and there is no observable hysteresis within the error limits of the measurements (<1 mT) [Fig. 2(b)]. A change in the gradient at 2.0(3) T is suggestive of a spin reorientation transition [Fig. S8, ESI†].
The combination of the negative θCW and lack of hysteresis in the isothermal magnetisation data, suggests that [Na(OH2)3]Mn(NCS)3 has ground-state antiferromagnetic order. If there is a ferromagnetic component due to spin canting, which could explain the up-turn in the low temperature susceptibility data, it must be small in magnitude.
To determine the low temperature nuclear and magnetic structure of [Na(OH2)3]Mn(NCS)3, single crystal neutron diffraction measurements were performed (D19, ILL).17 Full datasets were collected above (25 K) and below (2 K) the ordering temperature of TN = 18.1(6) K. The data at 25 K (λ = 1.45 Å, 631 independent reflections) could be integrated with the same space group as the reported structure at ambient temperature, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , indicating the absence of any structural transitions. The atom positions and anisotropic displacement parameters were refined freely, with a final χ2 = 23.20, obtained by refinement using the FullProf programme.25 From each H2O molecule one hydrogen is directed towards a nitrogen, whilst the other hydrogen is positioned towards a sulfur atom with ∠O–H⋯N = 153.291(2)° and ∠O–H⋯S = 164.258(2)°. The distances of the hydrogens to the acceptor atoms are dH1⋯N = 2.355(5) Å and dH2⋯S = 2.326(7) Å, consistent with previous reports.26
, indicating the absence of any structural transitions. The atom positions and anisotropic displacement parameters were refined freely, with a final χ2 = 23.20, obtained by refinement using the FullProf programme.25 From each H2O molecule one hydrogen is directed towards a nitrogen, whilst the other hydrogen is positioned towards a sulfur atom with ∠O–H⋯N = 153.291(2)° and ∠O–H⋯S = 164.258(2)°. The distances of the hydrogens to the acceptor atoms are dH1⋯N = 2.355(5) Å and dH2⋯S = 2.326(7) Å, consistent with previous reports.26
In the low temperature dataset (2 K) all the Bragg reflections (651 unique reflections) could be indexed by the nuclear space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , implying the propagation vector is k = (0,0,0). The potential magnetic space groups with this propagation vector were identified using the Bilbao Crystallographic Server,27–29P
, implying the propagation vector is k = (0,0,0). The potential magnetic space groups with this propagation vector were identified using the Bilbao Crystallographic Server,27–29P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′, P
′, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , P3, P
, P3, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ′, P
′, P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and P1 in BNS notation.28 We initially focussed on the three maximal symmetry magnetic space groups: P
and P1 in BNS notation.28 We initially focussed on the three maximal symmetry magnetic space groups: P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′, P
′, P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) and P3. Of these, the P
and P3. Of these, the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) magnetic space group only allows for a collinear ferromagnetic order and so was neglected as it is inconsistent with our magnetic property measurements; P
magnetic space group only allows for a collinear ferromagnetic order and so was neglected as it is inconsistent with our magnetic property measurements; P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ permits only collinear antiferromagnetic order and P3 allows antiferromagnetic, ferromagnetic or ferrimagnetic arrangement of the moments as it contains two distinct Mn(II) sites.
′ permits only collinear antiferromagnetic order and P3 allows antiferromagnetic, ferromagnetic or ferrimagnetic arrangement of the moments as it contains two distinct Mn(II) sites.
Refinements were carried out with both the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ and P3 space groups. The results of the refinements provided comparable models with similar refinement statistics, χ2 = 9.49 (P
′ and P3 space groups. The results of the refinements provided comparable models with similar refinement statistics, χ2 = 9.49 (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′) and χ2 = 9.8 (P3) [Fig. S6 and S7, ESI†]. The significant difference between these models is the loss of the inversion centres in the P3 space group, which produces the two unique Mn sites. In both structures the Mn atoms are positioned on a 3-fold rotation axis and thus the moments are constrained to lie along c. The antiferromagnetic P
′) and χ2 = 9.8 (P3) [Fig. S6 and S7, ESI†]. The significant difference between these models is the loss of the inversion centres in the P3 space group, which produces the two unique Mn sites. In both structures the Mn atoms are positioned on a 3-fold rotation axis and thus the moments are constrained to lie along c. The antiferromagnetic P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ model has a moment size, gS, of 4.9(2)μB per Mn, whereas in the P3 model, the magnitude of the two moments are −3.4(3) and 5.4(2)μB. These moments were closely correlated, and were only stable during the refinements when the moments were constrained to refine between −5.0 and 5.0μB. This resulted in moments of −4.0(2) and 3.9(2)μB. Within error these moments have the same magnitude, although any uncompensated moment would result in a net magnetisation along the c axis. We also investigated the potential for lower symmetry k = 0 orderings, with canted moments or significant magnetostructural distortions, which would require triclinic symmetry. We integrated the data with triclinic symmetry, which produced a cell which was trigonal within error, and then refined the magnetic and nuclear structures in P
′ model has a moment size, gS, of 4.9(2)μB per Mn, whereas in the P3 model, the magnitude of the two moments are −3.4(3) and 5.4(2)μB. These moments were closely correlated, and were only stable during the refinements when the moments were constrained to refine between −5.0 and 5.0μB. This resulted in moments of −4.0(2) and 3.9(2)μB. Within error these moments have the same magnitude, although any uncompensated moment would result in a net magnetisation along the c axis. We also investigated the potential for lower symmetry k = 0 orderings, with canted moments or significant magnetostructural distortions, which would require triclinic symmetry. We integrated the data with triclinic symmetry, which produced a cell which was trigonal within error, and then refined the magnetic and nuclear structures in P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ′ [Fig. S4 and Table S1, ESI†]. This model has a single Mn site, M = 4.1(2)μB, with the moment pointing primarily along the c axis with a significant canting, though the errors in this model prevent reliable determination of moment direction. The atomic coordinates and displacement parameters were refined freely, however there was no evidence beyond error of any symmetry lowering beyond trigonal symmetry and the refinement fit was significantly worse than that for the higher symmetry models, with χ2 = 51.3. We therefore concluded that the triclinic models were not required to describe this system.
′ [Fig. S4 and Table S1, ESI†]. This model has a single Mn site, M = 4.1(2)μB, with the moment pointing primarily along the c axis with a significant canting, though the errors in this model prevent reliable determination of moment direction. The atomic coordinates and displacement parameters were refined freely, however there was no evidence beyond error of any symmetry lowering beyond trigonal symmetry and the refinement fit was significantly worse than that for the higher symmetry models, with χ2 = 51.3. We therefore concluded that the triclinic models were not required to describe this system.
To gain more detailed understanding of the transition we collected data between 2 and 25 K with 0.25 K steps to follow specific reflections. We focussed in particular on the 100 Bragg reflection, which has significant magnetic contribution in the magnetically ordered state. We fitted the intensity of this reflection to a power law:
| I = M2 = A(TN − T)2β + C, | (2) |
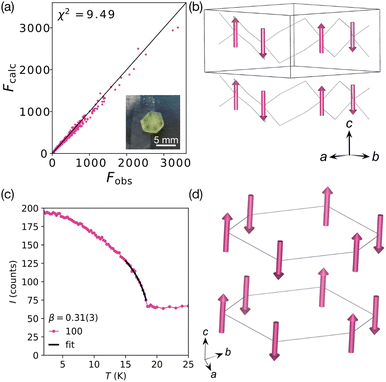 | ||
Fig. 3 Summary of the refined magnetic structure in P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ at 2 K (D19, ILL).17 (a) Fobs against Fcalc plot. Inset: The measured single crystal. (b) Magnetic structure viewed along the [110] direction showing the antiferromagnetic arrangement of moments (pink arrows). [Mn(NCS)3]− framework is shown as a wireframe. (c) Temperature dependence of the 100 Bragg reflection, which has a significant magnetic contribution, fitted to a power law (black line), β = 0.31(3). (d) Alternate view of the magnetic structure, with the magnetic lattice (connecting Mn atoms) shown. ′ at 2 K (D19, ILL).17 (a) Fobs against Fcalc plot. Inset: The measured single crystal. (b) Magnetic structure viewed along the [110] direction showing the antiferromagnetic arrangement of moments (pink arrows). [Mn(NCS)3]− framework is shown as a wireframe. (c) Temperature dependence of the 100 Bragg reflection, which has a significant magnetic contribution, fitted to a power law (black line), β = 0.31(3). (d) Alternate view of the magnetic structure, with the magnetic lattice (connecting Mn atoms) shown. | ||
Our refinements suggested that the magnetic structure is most likely the centrosymmetric antiferromagnetic P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′, rather than the noncentrosymmetric weak ferromagnetic P3. To confirm this model and to determine if [Na(OH2)3]Mn(NCS)3 is centrosymmetric in its ground state, we therefore carried out second harmonic generation measurements at 4 K and room temperature, along with variable temperature measurements between 4 and 30 K. Optical excitation was performed using Spectra Physics Spitfire Ace PA amplified laser system (40 fs pulses at a 1 kHz repetition rate) at 800 nm (<1 W average power) and 400 nm (<500 mW). We found no evidence of SHG signal generation, suggesting the compound is centrosymmetric. The results suggest that [Na(OH2)3]Mn(NCS)3 retains its inversion centres, therefore ordering in the P
′, rather than the noncentrosymmetric weak ferromagnetic P3. To confirm this model and to determine if [Na(OH2)3]Mn(NCS)3 is centrosymmetric in its ground state, we therefore carried out second harmonic generation measurements at 4 K and room temperature, along with variable temperature measurements between 4 and 30 K. Optical excitation was performed using Spectra Physics Spitfire Ace PA amplified laser system (40 fs pulses at a 1 kHz repetition rate) at 800 nm (<1 W average power) and 400 nm (<500 mW). We found no evidence of SHG signal generation, suggesting the compound is centrosymmetric. The results suggest that [Na(OH2)3]Mn(NCS)3 retains its inversion centres, therefore ordering in the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ magnetic space group, and providing further evidence that this compound is a good example of a classical Heisenberg honeycomb antiferromagnet.
′ magnetic space group, and providing further evidence that this compound is a good example of a classical Heisenberg honeycomb antiferromagnet.
The [Mn(NCS)3]− layers of [Na(OH2)3]Mn(NCS)3 stack uniformly along the c axis, in contrast to the ABC stacking found in NaMnCl3.34 We found no evidence of stacking faults, slip-stacking transitions or symmetry-lowering due to stacking, in contrast to van der Waals materials such as MnPS3 and RuCl3 which have monoclinic symmetry because of the layer sequence.35,36 This is likely due to the infinite rod [Na(OH2)3]n+ countercation, which forces hydrogen bonds to the framework and force the layers to stack in alignment.
The importance of the trigonal symmetry of the cation, together with its templating hydrogen bonds, can be seen by comparison with [1,3-Im]Mn(NCS)3 (1,3-Im = 1-ethyl-3-methyl imidazolium) which has the bulky 1,3-Im cation as the charge balance to the [Mn(NCS)3]− honeycomb.37 The 1,3-Im cation has no strong hydrogen bond donors and its size and bulk means the framework forms irregular hexagons. This distortion away from perfect symmetry is often found in molecular framework honeycomb magnets, for example Co(N3)2(bpg)·DMSO (bpg = 1,2-dipyridine-4-ethane-1,2-diol, DMSO = SO(CH3)2).15,16 The [Na(OH2)3]+ countercation rod is not unique to [Na(OH2)3]Mn(NCS)3, occurring in a handful of other compounds, e.g. [Na(OH2)3]2[TeBr6].38 Neutron diffraction allows a close look at the H-bond interactions between this cation and the framework.
The magnetic properties of [Na(OH2)3]Mn(NCS)3 are quite distinct from the halide analogue NaMnCl3, which orders at TN = 6.5 K with ferromagnetic layers, coupled antiferromagnetically.39 [Na(OH2)3]Mn(NCS)3 has an ordering temperature almost three times as high as NaMnCl3 (TN = 18.1(6) K) and the net magnetic interactions are also stronger, θCW = −51(1) K, compared to NaMnCl3, θCW = −4.2 K. The increase strength of interactions in the thiocyanate compared to the halide despite the significantly longer superexchange pathway (Mn–Cl–Mn compared to Mn–NCS–Mn) is consistent with investigations of the binary compounds.18 This difference may be due to the harder NCS− ligand having better orbital overlap with Mn2+ and the single-orbital nature of the superexchange pathway, rather than the two-orbital pathway in manganous chlorides.
Our results establish that [Na(OH2)3]Mn(NCS)3 adopts the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ space group, but it is worth exploring implications of the P3 magnetic symmetry with two uncompensated moments [Fig. S10, ESI†], particularly as analogous structures with different metals may adopt different ground states. P3 has no inversion centre and is polar, and so this structure (if it can be engineered in analogues or through application of stimulus e.g. strain) would have electrical polarisation produced directly by magnetic order (type II multiferroicity).22 Generally, type II multiferroics adopt complex magnetic orderings, for example helical incommensurate states,40 or with structural triangular lattice arrangements which introduce frustration, e.g. triangular Sr3NiTa2O941 and Ba3MnNb2O9.42 It would be unusual for a collinear magnetic ordering to induce this behaviour, and even more so for a molecular framework. These results illustrate the importance of magnetic structure determination for understanding the function of magnetic molecular framework compounds, as also shown by other recent works on frameworks containing both Mn(II)43–46 and other metals.47–49
′ space group, but it is worth exploring implications of the P3 magnetic symmetry with two uncompensated moments [Fig. S10, ESI†], particularly as analogous structures with different metals may adopt different ground states. P3 has no inversion centre and is polar, and so this structure (if it can be engineered in analogues or through application of stimulus e.g. strain) would have electrical polarisation produced directly by magnetic order (type II multiferroicity).22 Generally, type II multiferroics adopt complex magnetic orderings, for example helical incommensurate states,40 or with structural triangular lattice arrangements which introduce frustration, e.g. triangular Sr3NiTa2O941 and Ba3MnNb2O9.42 It would be unusual for a collinear magnetic ordering to induce this behaviour, and even more so for a molecular framework. These results illustrate the importance of magnetic structure determination for understanding the function of magnetic molecular framework compounds, as also shown by other recent works on frameworks containing both Mn(II)43–46 and other metals.47–49
In conclusion, we have determined the low temperature structure and magnetic properties of [Na(OH2)3]Mn(NCS)3 by developing crystal growth methodology for this humidity sensitive compound. Neutron diffraction data permitted the hydrogen atoms to be located and hence the key role of the hydrogen bonding network in framework structuration. Refinement of single crystal neutron diffraction data shows that the compound magnetically orders in P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ′ magnetic space group, supported by SHG measurements for which we saw no signal at the wavelengths we excited, consistent with this centrosymmetric magnetic structure. The unusual low-symmetry trigonal space group exhibited in this compound suggests that investigations into the analogues incorporating metal ions which exhibit magnetic anisotropy (e.g. Co(II), Ni(II), Fe(II)) may lead to the complex spin structure and hence multiferroic behaviour. Substitutions for metals which form metal thiocyanate frameworks less sensitive to ambient humidity, e.g. Ni(II), may also lead to more straightforward methods to grow and store these compounds.
′ magnetic space group, supported by SHG measurements for which we saw no signal at the wavelengths we excited, consistent with this centrosymmetric magnetic structure. The unusual low-symmetry trigonal space group exhibited in this compound suggests that investigations into the analogues incorporating metal ions which exhibit magnetic anisotropy (e.g. Co(II), Ni(II), Fe(II)) may lead to the complex spin structure and hence multiferroic behaviour. Substitutions for metals which form metal thiocyanate frameworks less sensitive to ambient humidity, e.g. Ni(II), may also lead to more straightforward methods to grow and store these compounds.
Author contributions
M. G. and E. B. synthesised the samples; M. G. grew the crystals; M. G. and M. J. C. carried out the magnetic measurements and the single crystal X-ray experiments; M. G., O. F., L. C. D. and M. J. C. carried out the neutron diffraction experiments and magnetic property analysis; T. B. G. and A. D. B. carried out the second harmonic generation measurements; M. G., L. C. D. and M. J. C. wrote the paper with contributions from all the authors.Conflicts of interest
No conflicts of interest to declare.Acknowledgements
M. G. acknowledges the ILL Graduate School for provision of a studentship. M. J. C. acknowledges funding from UKRI (EP/X042782/1) and the Hobday Bequest, School of Chemistry, University of Nottingham. We acknowledge the ILL for beamtime under proposal numbers 5-41-1167. Raw data sets from ILL experiments can be accessed via links provided in references. SHG measurements were performed using equipment funded by EPSRC strategic equipment grant EP/P001394/1.References
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- J. A. Sears, M. Songvilay, K. W. Plumb, J. P. Clancy, Y. Qiu, Y. Zhao, D. Parshall and Y.-J. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144420 CrossRef.
- W. Yao, K. Iida, K. Kamazawa and Y. Li, Phys. Rev. Lett., 2022, 129, 147202 CrossRef CAS PubMed.
- S. Gao, M. A. McGuire, Y. Liu, D. L. Abernathy, C. D. Cruz, M. Frontzek, M. B. Stone and A. D. Christianson, Phys. Rev. Lett., 2022, 128, 227201 CrossRef CAS PubMed.
- S. Reschke, D. G. Farkas, A. Strinić, S. Ghara, K. Guratinder, O. Zaharko, L. Prodan, V. Tsurkan, D. Szaller, S. Bordács, J. Deisenhofer and I. Kézsmárki, npj Quantum Mater., 2022, 7, 1–7 CrossRef.
- A. E. Thorarinsdottir and T. D. Harris, Chem. Rev., 2020, 120, 8716–8789 CrossRef CAS PubMed.
- Z. J. Zhong, N. Matsumoto, H. Okawa and S. Kida, Chem. Lett., 1990, 87–90 CrossRef CAS.
- R. Pellaux, H. W. Schmalle, R. Huber, P. Fischer, T. Hauss, B. Ouladdiaf and S. Decurtins, Inorg. Chem., 1997, 36, 2301–2308 CrossRef CAS PubMed.
- C. Mathonière, S. G. Carling, D. Yusheng and P. Day, J. Chem. Soc., Chem. Commun., 1994, 1551–1552 RSC.
- I.-R. Jeon, B. Negru, R. P. Van Duyne and T. D. Harris, J. Am. Chem. Soc., 2015, 137, 15699–15702 CrossRef CAS PubMed.
- A. Rodríguez-Diéguez, J. Cano, R. Kivekäs, A. Debdoubi and E. Colacio, Inorg. Chem., 2007, 46, 2503–2510 CrossRef PubMed.
- J. Curély, F. Lloret and M. Julve, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 11465–11483 CrossRef.
- A. Abhervé, M. Clemente-León, E. Coronado, C. J. Gómez-García and M. Verneret, Inorg. Chem., 2014, 53, 12014–12026 CrossRef PubMed.
- M. Atzori, S. Benmansour, G. Mínguez Espallargas, M. Clemente-León, A. Abhervé, P. Gómez-Claramunt, E. Coronado, F. Artizzu, E. Sessini, P. Deplano, A. Serpe, M. L. Mercuri and C. J. Gómez García, Inorg. Chem., 2013, 52, 10031–10040 CrossRef CAS PubMed.
- X.-Y. Wang, L. Wang, Z.-M. Wang and S. Gao, J. Am. Chem. Soc., 2006, 128, 674–675 CrossRef CAS PubMed.
- M. A. S. Goher, J. Cano, Y. Journaux, M. A. M. Abu-Youssef, F. A. Mautner, A. Escuer and R. Vicente, Chem. – Eur. J., 2000, 6, 778–784 CrossRef CAS PubMed.
- M. Geers, L. Cañadillas-Delgado, M. J. Cliffe and Ó. Fabelo, ILL Experiment 5-41-1167 DOI:10.5291/ILL-DATA.5-41-1167.
- E. N. Bassey, J. A. M. Paddison, E. N. Keyzer, J. Lee, P. Manuel, I. da Silva, S. E. Dutton, C. P. Grey and M. J. Cliffe, Inorg. Chem., 2020, 59, 11627–11639 CrossRef CAS PubMed.
- M. Geers, J. Y. Lee, S. Ling, O. Fabelo, L. Cañadillas-Delgado and M. J. Cliffe, Chem. Sci., 2023, 14, 3531–3540 RSC.
- M. Biedermann, H. Hartung, H. Böhlandb and R. Matthäus, Z. Naturforsch. B, 1998, 53, 416–422 CrossRef CAS.
- D. Zagorac, H. Müller, S. Ruehl, J. Zagorac and S. Rehme, J. Appl. Crystallogr., 2019, 52, 918–925 CrossRef CAS PubMed.
- D. Khomskii, Physics, 2009, 2, 20 CrossRef.
- L. Greenspan, J. Res. Natl. Bur. Stand., Sect. A, 1977, 81, 89 CrossRef.
- F. E. M. O'Brien, J. Sci. Instrum., 1948, 25, 73–76 CrossRef.
- J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef.
- J. P. M. Lommerse and J. C. Cole, Acta Crystallogr., 1998, B54, 316–319 CAS.
- M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. M. R. E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197 CAS.
- S. V. Gallego, E. S. Tasci, G. de la Flor, J. M. Perez-Mato and M. I. Aroyo, J. Appl. Crystallogr., 2012, 45, 1236–1247 CrossRef CAS.
- J. Perez-Mato, S. Gallego, E. Tasci, L. Elcoro, G. De La Flor and M. Aroyo, Annu. Rev. Mater. Res., 2015, 45, 217–248 CrossRef CAS.
- S. Blundell, Magnetism in Condensed Matter, Oxford University Press, Oxford, 2001 Search PubMed.
- A. Cole, A. Streeter, A. O. Fumega, X. Yao, Z.-C. Wang, E. Feng, H. Cao, J. L. Lado, S. E. Nagler and F. Tafti, Phys. Rev. Mater., 2023, 7, 064401 CrossRef CAS.
- P. A. Lindgard, R. J. Birgeneau, H. J. Guggenheim and J. Als-Nielsen, J. Phys. C: Solid State Phys., 1975, 8, 1059–1069 CrossRef CAS.
- W. B. Yelon and R. J. Birgeneau, Phys. Rev. B: Solid State, 1972, 5, 2615–2621 CrossRef.
- C. J. J. van Loon and G. C. Verschoor, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 1224–1228 CrossRef CAS.
- E. Ressouche, M. Loire, V. Simonet, R. Ballou, A. Stunault and A. Wildes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 100408 CrossRef.
- R. D. Johnson, S. C. Williams, A. A. Haghighirad, J. Singleton, V. Zapf, P. Manuel, I. I. Mazin, Y. Li, H. O. Jeschke, R. Valentí and R. Coldea, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235119 CrossRef.
- T. Peppel and M. Köckerling, IUCrData, 2019, 4, x191659 CrossRef CAS.
- W. Abriel, Z. Naturforsch. B, 1983, 38, 1543–1547 CrossRef.
- N. Fedoseeva, I. Spevakova, G. Petrakovskii, V. Chuev and S. Petrov, J. Magn. Magn. Mater., 1980, 15, 539–541 CrossRef.
- T. Kimura, J. C. Lashley and A. P. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 220401 CrossRef.
- M. Liu, H. Zhang, X. Huang, C. Ma, S. Dong and J.-M. Liu, Inorg. Chem., 2016, 55, 2709–2716 CrossRef PubMed.
- M. Lee, E. S. Choi, X. Huang, J. Ma, C. R. Dela Cruz, M. Matsuda, W. Tian, Z. L. Dun, S. Dong and H. D. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224402 CrossRef.
- J. M. Bulled, J. A. M. Paddison, A. Wildes, E. Lhotel, S. J. Cassidy, B. Pato-Doldán, L. C. Gómez-Aguirre, P. J. Saines and A. L. Goodwin, Phys. Rev. Lett., 2022, 128, 177201 CrossRef CAS PubMed.
- S. Calder, R. Baral, N. Narayanan and L. D. Sanjeewa, Phys. Rev. Mater., 2023, 7, 124408 CrossRef CAS.
- H. C. Walker, H. D. Duncan, M. D. Le, D. A. Keen, D. J. Voneshen and A. E. Phillips, Phys. Rev. B, 2017, 96, 2–7 CrossRef.
- J. L. Manson, Q.-z Huang, J. W. Lynn, H.-J. Koo, M.-H. Whangbo, R. Bateman, T. Otsuka, N. Wada, D. N. Argyriou and J. S. Miller, J. Am. Chem. Soc., 2001, 123, 162–172 CrossRef CAS PubMed.
- J. Pitcairn, A. Iliceto, L. Cañadillas-Delgado, O. Fabelo, C. Liu, C. Balz, A. Weilhard, S. P. Argent, A. J. Morris and M. J. Cliffe, J. Am. Chem. Soc., 2023, 145, 1783–1792 CrossRef CAS PubMed.
- J. López-Cabrelles, S. Mañas-Valero, I. J. Vitórica-Yrezábal, P. J. Bereciartua, J. A. Rodríguez-Velamazán, J. C. Waerenborgh, B. J. C. Vieira, D. Davidovikj, P. G. Steeneken, H. S. J. van der Zant, G. Mínguez Espallargas and E. Coronado, Nat. Chem., 2018, 10, 1001–1007 CrossRef PubMed.
- L. Cañadillas-Delgado, L. Mazzuca, O. Fabelo, J. Rodríguez-Carvajal and V. Petricek, Inorg. Chem., 2020, 59, 17896–17905 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional experimental details for synthesis, single crystal neutron diffraction measurements and analysis, second harmonic generation, mCIF. Research data and analysis notebooks are available at the Nottingham Research Data Management Repository DOI: https://doi.org/10.17639/nott.7396. See DOI: https://doi.org/10.1039/d4cp01265h |
| ‡ Present address: Materials Department and Materials Research Laboratory, University of California, Santa Barbara, California 93106, USA. |
| This journal is © the Owner Societies 2024 |