Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Anti-Arrhenius passage of gaseous molecules through nanoporous two-dimensional membranes
Petr
Dementyev
 * and
Armin
Gölzhäuser
* and
Armin
Gölzhäuser

Physics of Supramolecular Systems and Surfaces, Bielefeld University, 33615 Bielefeld, Germany. E-mail: dementyev@physik.uni-bielefeld.de
First published on 1st February 2024
Abstract
The passage of molecules through membranes is known to follow an Arrhenius-like kinetics, i.e. the flux is accelerated upon heating and vice versa. There exist though stepwise processes whose rates can decrease with temperature if, for example, adsorbed intermediates are involved. In this study, we perform temperature-variable permeation experiments in the range from −50 to +50 °C and observe anti-Arrhenius behaviour of water and ammonia permeating in two-dimensional freestanding carbon nanomembranes (CNMs). The permeation rate of water vapour is found to decrease many-fold with warming, while the passage of ammonia molecules strongly increases when the membrane is cooled down to the dew point. Liquefaction of isobutylene shows no enhancement for its transmembrane flux which is consistent with the material's pore architecture. The effects are described by the Clausius–Clapeyron relationship and highlight the key role of gas–surface interactions in two-dimensional membranes.
Introduction
Material transport through two-dimensional (2D) membranes is of fundamental physical interest as well as of critical importance for separation applications. Recently, an investigation of molecular movements in spatially confined nanoconduits contributed to the exploration of quantum friction, i.e. molecule–wall interactions at the boundary between classical and quantum mechanical behaviours.1 In technical applications, the type of flow when molecules and atoms translocate through nanopores defines a 2D membrane's separation behaviour. Porous 2D materials have been suggested to be developed into perfect membranes and in the last decade, perforated graphene has been serving as a prototypical and frequently used 2D membrane.2–13 Its ultimate thickness was believed to enable high-flux and high-selectivity separation and allow for distinct mass transfer behaviour.14Gas permeation in 2D membranes was predicted to include a surface pathway where gaseous molecules would cross the pores in the adsorbed state.15 This could offer additional routes to control the permselectivity; however, such a surface diffusion of adsorbates was barely observed in experiments with perforated graphene as the size distribution of its artificial pores is broad, and the permeation rate can thus be easily dominated by the gas-phase pathway across larger openings. In addition, physisorption of noble and atmospheric gases on the inert graphitic surface is unfavourable under normal conditions, and the material integrity limits the areal pore density in graphene membranes; therefore, the likelihood of adsorbed species to overcome long distances towards the defects seems to be rather small.
Unlike regular gases with low boiling points, vaporous water and organic solvents exhibit strong intermolecular interactions and readily adsorb at room temperature.16 As prescribed by the classical adsorption isotherms, exposing flat substrates to saturated vapours results in multimolecular surface coverages.17 Given little spacing between the openings, various 2D membranes with intrinsic microporosity were found to pass vaporous substances at high rates.18–20 While the surface flow is accompanied by molecular effusion in pores larger than one nm, it appears to prevail at sub-nanometer dimensions. The selectivity over ordinary gases agrees with early predictions suggesting greater probability of adsorbates to permeate through nanoscale membranes.21 In order to increase the residence time of gas particles in the vicinity of the pores, the membrane surface can be modified with ionic liquids or other chemical absorbents.22–24 However, there is another unexplored way to impact the number of surface species according to adsorption–desorption equilibria, and that is the membrane temperature.
To identify and understand surface pathways in molecular transport through 2D membranes, we have performed temperature dependent gas permeation measurements through freestanding carbon nanomembranes (CNMs). CNMs possess a high density of sub-nanometer channels that are known to rapidly transmit water molecules.25 We investigated the permeation of three different substances: water, ammonia, and isobutylene while the CNMs were held at temperatures between −50 °C and +50 °C. To vary the temperature, we designed a simple heat conductor that is capable of both cooling and heating the membrane in a vacuum apparatus developed before.18 The transient-temperature experiments are carried out upon immersing the heat conductor into either liquid nitrogen or hot water, whereas the feed pressure is fixed. For water, we found that elevating the membrane temperature to +50 °C considerably decreases the flux which indicates that less water molecules adsorb. In turn, ammonia molecules do not permeate CNMs at room temperature. This changes drastically when the membrane temperature is lowered to −50 °C, and the relative pressure approaches saturation. We found that the onset of permeation depends on both the gas pressure and the membrane temperature reflecting a gas-to-liquid phase transition aka condensation. In the case of isobutylene, we observed no permeation in the investigated temperature range.
Experimental
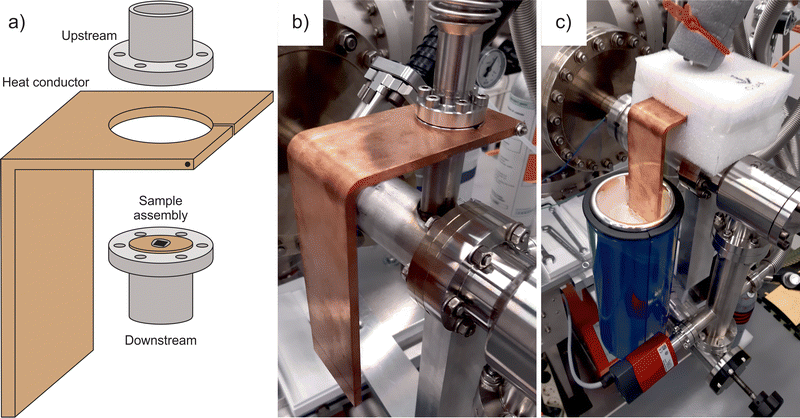
The experimental system for the vapour and gas permeation measurements is based on a high-vacuum detection chamber with a quadrupole mass spectrometer (QMS) from Hiden Analytical and a feed chamber with a Baratron capacitance manometer from MKS Instruments.18 The membrane cell separating the down- and upstream compartments includes two DN 16 CF flanges that enclose the sample assembly as illustrated in Fig. 1a. In this configuration, the copper disc carrying a freestanding membrane plays a role of a gasket that seals the flanges and has no direct contact with anything else. The heat conductor represents an L-shaped copper block of around 0.5 kg in weight and is equipped with a circular opening for mounting onto the membrane cell. Fig. 1b shows the heat conductor tightly clamped on the downstream flange to ensure greater temperature changes in the sample compared to the walls of the feed compartment. This is because the heat transfer between the flanges occurs through the copper disc.Two chromel–alumel thermocouples were used to monitor the membrane temperature with the help of a digital thermometer Voltcraft. One sensor was placed on the heat conductor near the cell, while the second one was placed into the side groove between the flanges. The latter reading was assumed to be the most appropriate estimate for the sample temperature although the two measurements differed little. During the operation, the membrane cell and the head of the heat conductor were wrapped with a polyethylene foam Mantel in order to provide thermal isolation and prevent frosting (Fig. 1c). A Dewar with liquid nitrogen and a hot water bath were employed to affect the tail of the heat conductor and thereby the temperature of the membrane cell. The newly designed experiment allows for the simultaneous recording of the feed pressure, the sample temperature, and the QMS output as a function of time. As the current in the QMS is proportional to the partial pressure of permeating molecules, the resulting p–T–I data are a convenient way to show how the transmembrane flow rate changes with temperature at a given concentration gradient.
The preparation of CNMs from self-assembled biphenyl-4-carboxylic acid (TCI) by electron irradiation is detailed elsewhere.23 The material is known to preserve a highly uniform thickness of around 1 nm with a sponge-like morphology. The areal pore density is estimated to be over 1013 cm−2, and the pore diameter varies between 0.4 and 1.0 nm.25 The membrane was transferred onto a silicon nitride window with a 5 μm aperture (Silson Ltd) and fixed on the copper disc with epoxy glue (UHU Plus Endfest 300). After system evacuation, a leak test with helium was performed to prove intactness of the membrane. The permeation measurements were conducted at 2.0 × 10−9 mbar base pressure in the detection chamber. Heavy water (Sigma-Aldrich) was repeatedly degassed before experiments; ammonia (Linde) and isobutylene (Messer) were used as obtained.
Results and discussion
Fig. 2 illustrates the results of temperature-varied permeation measurements with vaporous heavy water. The mass spectrometer was set to detect D2O+ ions (m/z = 20), and the room temperature was 22 °C. In the beginning, the upstream compartment was connected to a turbomolecular pump; therefore, the QMS signal was at the constant background level. Then, we allow water vapour to a reference nanoaperture in order to calibrate the detector as described previously.18 This can be tracked by the synchronous signals in the pressure and the QMS output between 5 and 10 min that disappeared as soon as the gas molecules were pumped out. Starting from 18 min, the membrane was gradually fed with D2O, and permeation caused the rise in the QMS signal. The container with the liquid was closed at 29 min when the pressure reached 14 mbar; at this point, the transmembrane flow entered a steady-state regime. The feed pressure slightly decreased due to adsorption on the walls of the feed chamber but stabilized above 13 mbar. The effective permeation rate was equal to 1.2 × 10−4 mol s−1 m−2 Pa−1 in the time interval from 30 to 34 min.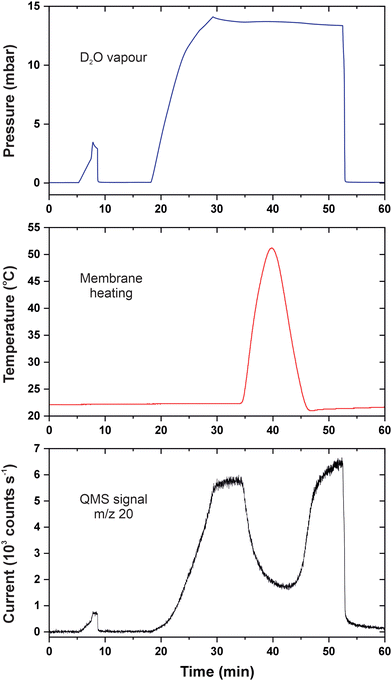 | ||
| Fig. 2 p–T–I data for permeation of heavy water in CNMs. The blue curve is the feed pressure; the red curve is the membrane temperature; the black curve is the baseline-corrected QMS current. | ||
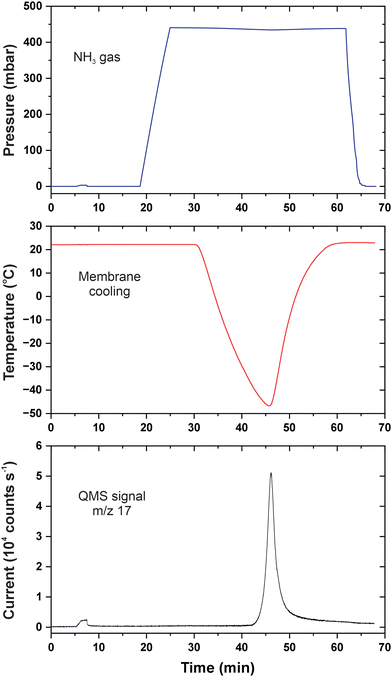
We began warming the heat conductor at 34 min which resulted in the rapid temperature increase in the membrane cell. For thermally activated processes, the temperature dependence of the rate constant k is described by the Arrhenius equation:
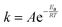 | (1) |
Our experimental arrangement does not allow for establishing equilibria at different temperatures because employing the heat conductor longer would induce slow warming of the entire vacuum system. As soon as the sample temperature reached +50 °C, we reversed the process with the help of liquid nitrogen. From 40 to 45 min, the temperature quickly went down and was later brought to almost the ambient value by a bath of tap water. One can see that permeation of water molecules reacted swiftly to the cooling and the transmembrane flux also came back. The change in the membrane temperature seems to restore the surface coverage of adsorbed molecules even though the gas pressure was unaltered. The QMS signal at 50 min was somewhat higher than that at 30 min which is explained by the lower temperature and accumulation of D2O in the detection chamber. At 53 min, the feed compartment was evacuated which led to the abrupt and simultaneous fall in the pressure and the number of permeating species. It follows that the surface-mediated flow across 2D membranes depends on pressure and temperature in line with gas adsorption isobars and isotherms.
In contrast to water that has a normal boiling point of +100 °C (nearly the same for heavy water), physisorption of inert gases is unfavourable at room temperature. The fact that nitrogen, argon, and oxygen cannot permeate through CNMs is consistent with their normal boiling points of −196, −186, and −183 °C, respectively.26 To demonstrate the role of temperature on permeation of ordinary gases, we selected ammonia with a normal boiling point of −33 °C and molecular dimensions resembling water.27Fig. 3 shows the p–T–I data obtained with ammonia upon cooling the membrane cell with liquid nitrogen. The initial QMS signal corresponded to the residual concentration of particles with m/z = 17, and the upstream side was under vacuum. Again, detector calibration was first performed upon supplying 3 mbar ammonia to the reference nanoaperture which can be tracked by the small signal at around 7 min. Unlike Fig. 2, the corresponding signal at the pressure curve is barely seen because the scale spans a much greater range. From 18 to 25 min, the feed compartment was filled with ammonia up to 440 mbar which had virtually no impact on the QMS signal, i.e. the permeation of NH3 molecules through CNMs was hindered.
 | ||
| Fig. 3 p–T–I data for permeation of ammonia in CNMs. The blue curve is the feed pressure; the red curve is the membrane temperature; the black curve is the baseline-corrected QMS current. | ||
For the steady-state mode (25–30 min), the ammonia permeance was calculated to be 3.8 × 10−8 mol s−1 m−2 Pa−1 which was practically at the limit of detection. The result is analogous to those obtained with other regular gases under similar pressure differentials. This is not surprising given the saturation vapour pressure of ammonia at room temperature was about 8.5 bar which translates the experimental parameters into the relative pressure of just 0.05. After 30 min, the membrane was rapidly cooled down below −30 °C, and the relative pressure in proximity of its surface increased accordingly. Contradictory to eqn (1), the data in Fig. 3 clearly show a sudden start of ammonia permeation around 43 min with the QMS signal going upward almost vertically. When the temperature turned to the opposite direction at 46 min, the flow rate of NH3 molecules crossing the membrane fell instantly as well. The cooling was accompanied by a small decline in the upstream pressure indicating gas condensation on the walls of the membrane cell. The feed compartment was emptied at 62 min once the ambient temperature was regained.
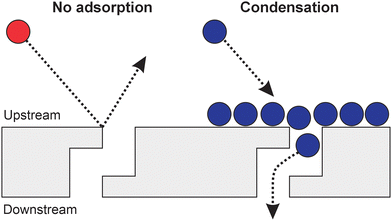
Fig. 4 illustrates the permeation mechanism and highlights the difference between non-adsorbing and condensing species. For non-adsorbing particles, the probability of entering nanoscopic pores of comparable sizes is predicted to be low because of the repulsion by the atoms comprising the membrane.28 At lower temperatures though, van der Waals attractions are favoured between the molecules and the membrane surface thus making the adsorbates pass into the pores much easier. In terms of eqn (1), this can be considered as an effective increase of the pre-exponential factor for the net permeation rate. One can alternatively break down the process into two steps and express the permeation rate as a function of the adsorbate surface coverage.18 Then, it becomes straightforward that cooling turns on the permeation by promoting physical adsorption and condensation.
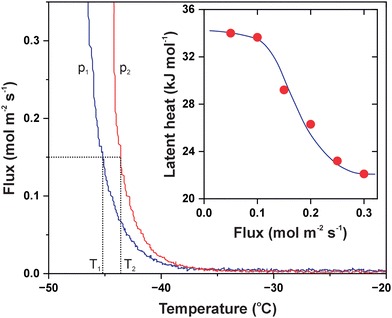
The influx of ammonia into the detection chamber was so intense that the pressure was increased to 2.7 × 10−9 mbar. Like during the heating experiments, it was only reasonable to cool the cell transiently in order not to affect other parts of the setup; besides, the stability of the sample fixture was not tested below −50 °C. When the process was reversed, the peak permeation rate amounted to 1.2 × 10−5 mol s−1 m−2 Pa−1, and compared to the permeance of water vapour, there was probably much room for further increase. The sharp kinetics is reminiscent of zero-order curves in temperature programmed desorption (TPD) which is the characteristic to phase transitions and implies the applicability of the Clausius–Clapeyron relationship.29 We also conducted the experiment with NH3 at an increased feed pressure of 490 mbar and plotted the resulting isobars as the transmembrane flux versus temperature (Fig. 5). As evident, there is a noticeable shift of the onset of permeation to higher temperatures which directly relates it to adsorption–desorption equilibria. This representation allows for extracting the temperature values T1 and T2 that yield the same flux at different gas pressures. The p1, T1 and p2, T2 pairs obtained can now be plugged to the approximate solution as follows:
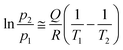 | (2) |
This evaluation evidences that gas permeation in 2D membranes is sensitive to the presence of condensed molecules as long as their size fits the pores dimensions. Fig. 6 shows our next experiment with isobutylene that boils at −7 °C and liquefies easier than ammonia.31 Its saturation pressure does not exceed 3 bar at room temperature, but the molecules are bulky and hydrophobic. The detector was counting C3H5+ ions (m/z = 41) when the calibration was done with 2.5 mbar isobutylene dosed to the reference nanoaperture between 6 and 7 min. The respective pressure rise appears very small with regard to the scale because 450 mbar of the gas was subsequently applied to the CNM. The steady-state mode between 17 and 21 min revealed no permeation of isobutylene which was followed by cooling the heat conductor with liquid nitrogen. The membrane temperature was decreased to −40 °C making the pressure decrease to 335 mbar; the feed pressure recovered with warming and vanished upon pumping at 45 min. The reversible pressure change clearly revealed massive condensation of C4H8 molecules in the membrane cell forming droplets or a thin layer. Nevertheless, the transmembrane flux remained negligible regardless of the temperature which was likely associated with the sieving properties of CNMs. It is known from prior studies that the interior of tortuous pores in the membrane is narrower in dimensions than their surface appearance.32 It is also possible though that the liquefied hydrocarbon molecules were residing away from the hydrophilic CNM surface.
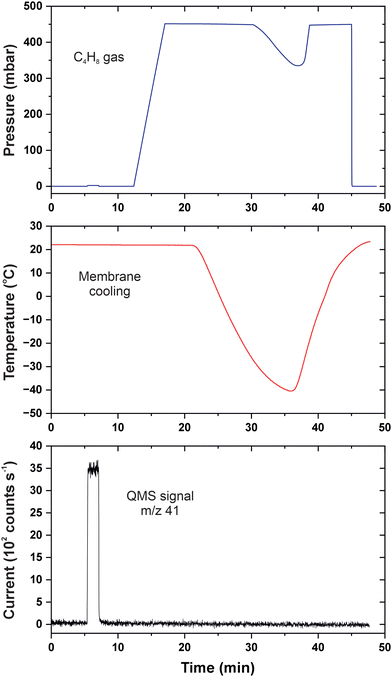 | ||
| Fig. 6 p–T–I data for permeation of isobutylene in CNMs. The blue curve is the feed pressure; the red curve is the membrane temperature; the black curve is the baseline-corrected QMS current. | ||
Recently, Stroganov et al. reported on gas transport experiments with morphologically similar CNMs and also observed the anti-Arrhenius behaviour of water vapour.33 They measured the permeation rate of D2O molecules as a function of pressure at 23, 41, 60 and 81 °C, and the heating appeared to slow down the transmembrane flow, especially when the membrane was exposed to the saturated vapour. The data plotted as a logarithm of the permeance versus reciprocal of the temperature revealed non-linear curves with negative values of the apparent activation energy. Thermodynamic estimates agreed well with the enthalpy of water adsorption and confirmed the two-step permeation mechanism, i.e. adsorption on the membrane surface followed by diffusion through the pores.
Conclusions
We introduced a viable experimental approach for probing molecular permeation in 2D membranes at elevated and cryogenic temperatures. The devised heat conductor enables prompt cooling down to −50 °C and heating up to +50 °C, and the achieved working range is extendable in both directions. As a case study, inherently microporous CNMs were subjected to transport measurements with vaporous heavy water, ammonia and isobutylene under isobaric conditions. Membrane heating was found to diminish the permeation rate of heavy water which was consistent with the surface-mediated mechanism. The pronounced anti-Arrhenius behaviour underscored the fact that transmembrane passage was interfered by desorption. Furthermore, the flow rate of ammonia was enhanced by orders of magnitude upon cooling while thermodynamic analysis confirmed gas condensation on the membrane surface. It was also shown that narrow pores in CNMs did not transmit isobutylene molecules in spite of their facile liquefaction at low temperatures. Our work proves the importance of interfacial processes in permeation across 2D membranes and justifies selectivity towards vapours over regular gases. The implication is that gas separation can be facilitated by tuning the number of adsorbates via temperature, pressure, and surface affinity.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, Projektnummer 459401588) and the ‘Fonds der Chemischen Industrie (FCI)’ (Liebig Fellowship). The authors also thank Dr Daniil Naberezhnyi for synthesizing CNMs.References
- N. Kavokine, M.-L. Bocquet and L. Bocquet, Nature, 2022, 602, 84 CrossRef CAS PubMed; X. Yu, A. Principi, K.-J. Tielrooij, M. Bonn and N. Kavokine, Nat. Nanotechnol., 2023, 18, 898 CrossRef PubMed.
- S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728 CrossRef CAS PubMed.
- K. Celebi, J. Buchheim, R. M. Wyss, A. Droudian, P. Gasser, I. Shorubalko, J.-I. Kye, C. Lee and H. G. Park, Science, 2014, 344, 289 CrossRef CAS PubMed.
- S. C. O’Hern, M. S. H. Boutilier, J.-C. Idrobo, Y. Song, J. Kong, T. Laoui, M. Atieh and R. Karnik, Nano Lett., 2014, 14, 1234 CrossRef PubMed.
- S. P. Surwade, S. N. Smirnov, I. V. Vlassiouk, R. R. Unocic, G. M. Veith, S. Dai and S. M. Mahurin, Nat. Nanotechnol., 2015, 10, 459 CrossRef CAS PubMed.
- M. S. H. Boutilier, D. Jang, J.-C. Idrobo, P. R. Kidambi, N. G. Hadjiconstantinou and R. Karnik, ACS Nano, 2017, 11, 5726 CrossRef CAS PubMed.
- Z. Yuan, J. D. Benck, Y. Eatmon, D. Blankschtein and M. S. Strano, Nano Lett., 2018, 18, 5057 CrossRef CAS PubMed.
- C. T. Nguyen and A. Beskok, Phys. Chem. Chem. Phys., 2019, 21, 9483 RSC.
- K.-P. Schlichting and D. Poulikakos, ACS Appl. Mater. Interfaces, 2020, 12, 36468 CrossRef CAS PubMed.
- M. Ghosh, L. Madauß, M. Schleberger, H. Lebius, A. Benyagoub, J. A. Wood and R. G. H. Lammertink, Langmuir, 2020, 36, 7400 CrossRef CAS PubMed.
- P. Z. Sun, M. Yagmurcukardes, R. Zhang, W. J. Kuang, M. Lozada-Hidalgo, B. L. Liu, H.-M. Cheng, F. C. Wang, F. M. Peeters, I. V. Grigorieva and A. K. Geim, Nat. Commun., 2021, 12, 7170 CrossRef CAS PubMed.
- J. Liu, L. Jin, F. I. Allen, Y. Gao, P. Ci, F. Kang and J. Wu, Nano Lett., 2021, 21, 2183 CrossRef CAS PubMed.
- D. Hou, S. Zhang, X. Chen, R. Song, D. Zhang, A. Yao, J. Sun, W. Wang, L. Sun, B. Chen, Z. Liu and L. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 10328 CrossRef CAS PubMed.
- L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Nat. Nanotechnol., 2017, 12, 509 CrossRef CAS PubMed.
- L. W. Drahushuk and M. S. Strano, Langmuir, 2012, 28, 16671 CrossRef CAS PubMed; C. Sun, M. S. H. Boutilier, H. Au, P. Poesio, B. Bai, R. Karnik and N. G. Hadjiconstantinou, Langmuir, 2014, 30, 675 CrossRef PubMed; A. Jana, D. S. Bergsman and J. C. Grossman, Nanoscale Adv., 2021, 3, 4502 RSC.
- P. Dementyev, N. Khayya, J. Kreie and A. Gölzhäuser, ChemPhysChem, 2022, 23, 72 CrossRef PubMed.
- N. Khayya, A. Gölzhäuser and P. Dementyev, Phys. Chem. Chem. Phys., 2022, 24, 12563 RSC.
- P. Dementyev, T. Wilke, D. Naberezhnyi, D. Emmrich and A. Gölzhäuser, Phys. Chem. Chem. Phys., 2019, 21, 15471 RSC.
- D. Naberezhnyi, S.-W. Park, W. Li, M. Westphal, X. Feng, R. Dong and P. Dementyev, Small, 2021, 17, 2104392 CrossRef CAS PubMed.
- D. Naberezhnyi, L. Mai, N. Doudin, I. Ennen, A. Hütten, E. I. Altman, A. Devi and P. Dementyev, Nano Lett., 2022, 22, 1287 CrossRef CAS PubMed.
- J. Schrier, ACS Appl. Mater. Interfaces, 2012, 4, 3745 CrossRef CAS PubMed.
- G. He, S. Huang, L. F. Villalobos, J. Zhao, M. Mensi, E. Oveisi, M. Rezaei and K. V. Agrawal, Energy Environ. Sci., 2019, 12, 3305 RSC.
- D. Naberezhnyi and P. Dementyev, Phys. Chem. Chem. Phys., 2020, 22, 9808 RSC; P. Dementyev, D. Naberezhnyi, M. Westphal, M. Buck and A. Gölzhäuser, ChemPhysChem, 2020, 21, 1006 CrossRef CAS PubMed.
- W. Guo, S. M. Mahurin, R. R. Unocic, H. Luo and S. Dai, Nano Lett., 2020, 20, 7995 CrossRef CAS PubMed.
- Y. Yang, P. Dementyev, N. Biere, D. Emmrich, P. Stohmann, R. Korzetz, X. Zhang, A. Beyer, S. Koch, D. Anselmetti and A. Gölzhäuser, ACS Nano, 2018, 12, 4695 CrossRef CAS PubMed; Y. Yang, R. Hillmann, Y. Qi, R. Korzetz, N. Biere, D. Emmrich, M. Westphal, B. Büker, A. Hütten, A. Beyer, D. Anselmetti and A. Gölzhäuser, Adv. Mater., 2020, 32, 1907850 CrossRef PubMed.
- R. F. Barron, Cryogenic Systems, Oxford University Press, New York, 2nd edn, 1985 Search PubMed.
- C. S. Cragoe, C. H. Meyers and C. S. Taylor, J. Am. Chem. Soc., 1920, 42, 206 CrossRef CAS.
- Z. Yuan, R. P. Misra, A. G. Rajan, M. S. Strano and D. Blankschtein, ACS Nano, 2019, 13, 11809 CrossRef CAS PubMed; A. Rodriguez, K.-P. Schlichting, D. Poulikakos and M. Hu, ACS Appl. Mater. Interfaces, 2021, 13, 39701 CrossRef PubMed.
- W. Weiss and W. Ranke, Prog. Surf. Sci., 2002, 70, 1 CrossRef CAS.
- J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2003, 32, 519 CrossRef CAS.
- A. B. Lamb and E. E. Roper, J. Am. Chem. Soc., 1940, 62, 806 CrossRef CAS.
- P. Dementyev, Y. Yang, M. Rezvova and A. Gölzhäuser, J. Phys. Chem. Lett., 2020, 11, 238 CrossRef CAS PubMed.
- V. Stroganov, D. Hüger, C. Neumann, T. Noethel, M. Steinert, U. Hübner and A. Turchanin, Small, 2023, 19, 2300282 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |