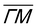Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Evolution of ordered nanoporous phases during h-BN growth: controlling the route from gas-phase precursor to 2D material by in situ monitoring†
Adrian
Ruckhofer
 a,
Marco
Sacchi
a,
Marco
Sacchi
 b,
Anthony
Payne
b,
Anthony
Payne
 b,
Andrew P.
Jardine
c,
Wolfgang E.
Ernst
b,
Andrew P.
Jardine
c,
Wolfgang E.
Ernst
 a,
Nadav
Avidor
a,
Nadav
Avidor
 c and
Anton
Tamtögl
c and
Anton
Tamtögl
 *a
*a
aInstitute of Experimental Physics, Graz University of Technology, Graz, Austria. E-mail: tamtoegl@tugraz.at
bDepartment of Chemistry, University of Surrey, Guildford GU2 7XH, UK
cCavendish Laboratory, J. J. Thompson Avenue, Cambridge CB3 0HE, UK. E-mail: na364@cantab.ac.uk
First published on 21st September 2022
Abstract
Large-area single-crystal monolayers of two-dimensional (2D) materials such as graphene and hexagonal boron nitride (h-BN) can be grown by chemical vapour deposition (CVD). However, the high temperatures and fast timescales at which the conversion from a gas-phase precursor to the 2D material appears, make it extremely challenging to simultaneously follow the atomic arrangements. We utilise helium atom scattering to discover and control the growth of novel 2D h-BN nanoporous phases during the CVD process. We find that prior to the formation of h-BN from the gas-phase precursor, a metastable (3 × 3) structure is formed, and that excess deposition on the resulting 2D h-BN leads to the emergence of a (3 × 4) structure. We illustrate that these nanoporous structures are produced by partial dehydrogenation and polymerisation of the borazine precursor upon adsorption. These steps are largely unexplored during the synthesis of 2D materials and we unveil the rich phases during CVD growth. Our results provide significant foundations for 2D materials engineering in CVD, by adjusting or carefully controlling the growth conditions and thus exploiting these intermediate structures for the synthesis of covalent self-assembled 2D networks.
New conceptsAs a key to understand both the formation and stability of 2D materials grown via on-surface synthesis, the individual steps, transformations and multiple pathways from the gas-phase precursor to the 2D layer need to be controlled and understood. However, the temporal evolution of these steps has so far only briefly been discussed in the context of graphene formation and no experimental reports on the individual steps have been reported up to now. We demonstrate that precise control of the growth of 2D materials is achievable by employing in situ time-resolved He atom scattering, which reveals products formed by the decomposition of the gas-phase precursor on the metal substrate. We exploit the technique to observe two previously unreported 2D phases of hexagonal boron nitride constituted by open-porous networks. Our work shows that it is possible to directly monitor the growth kinetics of 2D materials and isolate intermediate and metastable phases, paving the way to a greater control of 2D materials by chemical vapour deposition. |
Introduction
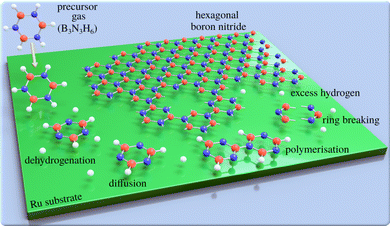
Two-dimensional (2D) materials such as graphene and hexagonal boron nitride (h-BN) offer technological promise,1,2e.g. with h-BN being considered to be the “ideal” dielectric for 2D based field-effect transistors.3 However, their properties are highly dependent on the perfection of the 2D layers. For this reason, intense efforts have been devoted to study and improve the growth of defect-free 2D materials.4,5 A promising method of synthesising large-area 2D layers is chemical vapour deposition (CVD) and the CVD synthesis of atomically thin h-BN on metal substrates is described in several review articles.6,7 The process, which is illustrated in Fig. 1, involves a gas-phase precursor deposited on a solid substrate at elevated temperatures. By diffusion8 and dehydrogenation or fragmentation of the precursor, the adsorbates are attached to growing clusters and eventually form the 2D layer. A complete dehydrogenation of the precursor requires overcoming multiple energy barriers. As a result, it might be expected that at intermediate temperatures, dehydrogenation would not be complete, which in-turn can result in metastable or intermediate structures. For the synthesis of bulk h-BN it is known that the process involves several steps of borazine-polymerisation.9–12 There are several routes, but even in the bulk, the process has not been studied in great detail. Here, we follow a series of structural changes to identify intermediate structures in 2D growth.While it is crucial to understand the growth process, mechanistic and kinetic studies are rare and mostly focus on the growth of nanocarbons.13–16 Dehydrogenation and intermediate structures during CVD of 2D materials have been proposed,17–23 but to the best of our knowledge have not been studied experimentally. In general, kinetics and the thermochemistry of intermediate products, may lead to metastable structures. However, phase-diagrams due to partially dehydrogenated precursors have not been reported. Most studies report completed overlayer structures while the complexity and individual steps, as illustrated in Fig. 1, are often ignored. In particular, previous h-BN studies using real space methods24–27 concentrate on local order in completed h-BN structures, while reciprocal space studies28–30 have provided information about long-range order.31
In this paper we present a systematic analysis, at various temperatures beyond the ones reported for best growth conditions (1050 to 1100 K24,26,29) and at various dosing rates. By following h-BN growth in situ using helium atom scattering (HAS) we demonstrate the existence of metastable structures during the formation of h-BN from borazine (B3N3H6). HAS is a well-established technique for monitoring thin-film growth modes32–34 and has been used to study the quality of CVD-grown 2D materials35–38 and inter-layer interaction,39 yet investigations of intermediate structures have not been performed. In particular, we find that there is one precursor structure with a well-defined (3 × 3) periodicity, meaning a well-defined route for the polymerisation reaction which leads to h-BN. We further find that by dosing excess borazine, a (3 × 4) structure forms, which could be attributed to a partially polymerised second-layer on top of the formed h-BN.
Our experimental results are complemented by van der Waals (vdW) corrected density functional theory (DFT) calculations which confirm the nature of the system, helping us to determine which self-assembled structures are compatible with the experimental results.
Results and discussion
The adsorption of the precursor gas (borazine, B3N3H6) on the Ru substrate has been investigated in several other studies using Auger electron spectroscopy, X-ray photoelectron spectroscopy, electron energy loss spectroscopy and low energy electron diffraction.40–42 There is general consensus in the literature, that borazine only adsorbs molecularly at low (<140 K) temperatures41–43 with dehydrogenation setting in at temperatures of 150–250 K, depending on the substrate.41,42,44 Starting from about 600 K, depending on the metallic substrate, the B–N ring is reported to break down into its atomic constituents.43,44 According to Paffet et al. 1000 K are necessary for h-BN formation on Ru(0001)40,41 while hydrogen desorption occurs over a wide temperature range42 and may even intercalate below the h-BN layer.45,46Helium diffraction allows in situ measurements even at growth temperature, and is known for its unique sensitivity to adsorbates, including hydrogen atoms.47–55 Furthermore, unlike other established techniques,56 HAS is completely inert and does not modify the process under investigation.57 While the specular reflection gives an estimate of adsorbate coverage on the clean surface, the angular distribution provides insight in the time evolution of periodic structures being formed on the surface.31,36 In the present work, CVD growth was performed at a set crystal temperature while monitoring the surface using repeated one-dimensional angular diffraction scans, where we observe the emergence and disappearance of additional superstructures followed by the formation of h-BN.
All experimental data was obtained with the Cambridge spin-echo apparatus which uses a nearly monochromatic atomic beam of 3He, scattered off the sample in a total scattering angle of 44.4° and with an incident energy of 8 meV (see Experimental section in the ESI†). The parallel momentum transfer ΔK is given by ΔK = |ΔK| = |Kf − Ki| = |ki|(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑf − sin
ϑf − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϑi), with ki being the incident wavevector and ϑi and ϑf the incident and final angles with respect to the surface normal, respectively.58–60 Compared to techniques such as scanning tunnelling microscopy (STM), HAS averages over larger surface areas, typically ≈3 mm2. Therefore, the advantage of HAS is to give precise information about any long-range periodicity of surface structures. For ease of comparison, the diffraction scans for the different structures are plotted as a function of the parallel momentum transfer, ΔK, relative to the G01 peak of the Ru(0001) substrate, |ΔK/G01|. By converting the abscissa in this way, the position of the observed diffraction peaks directly relates their periodicity with respect to the substrate lattice spacing.
ϑi), with ki being the incident wavevector and ϑi and ϑf the incident and final angles with respect to the surface normal, respectively.58–60 Compared to techniques such as scanning tunnelling microscopy (STM), HAS averages over larger surface areas, typically ≈3 mm2. Therefore, the advantage of HAS is to give precise information about any long-range periodicity of surface structures. For ease of comparison, the diffraction scans for the different structures are plotted as a function of the parallel momentum transfer, ΔK, relative to the G01 peak of the Ru(0001) substrate, |ΔK/G01|. By converting the abscissa in this way, the position of the observed diffraction peaks directly relates their periodicity with respect to the substrate lattice spacing.
After formation of the complete 2D layer, HAS can also be used to determine the lattice constant, crystal quality and bonding to the substrate of the 2D material as e.g. shown for CVD-grown graphene.37,39,61,62 As the main focus of this work is the route from the gas-phase precursor to h-BN, the periodicity, reconstruction and quality of the complete h-BN layer is instead discussed in Section 5 of the ESI.†
A precursor structure to h-BN growth
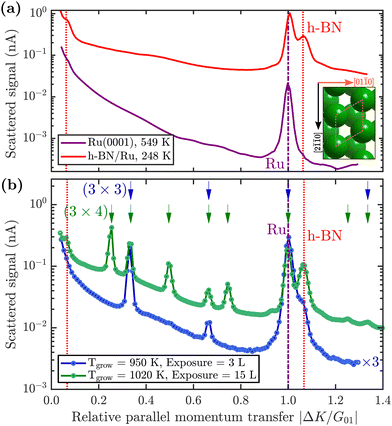
First, we describe how borazine exposure at low temperature (T < 880 K) reveals a precursor structure on Ru(0001), which by further annealing at T = 880 K can be converted to h-BN.The purple line in Fig. 2(a) shows a diffraction scan of the clean Ru(0001) substrate. Exposing Ru to 7 Langmuir (L) of borazine at a surface temperature of 600 K, results in decreased diffraction intensities and helium reflectivity. Moreover, the lack of any additional diffraction peaks is typical of a disordered structure.55 The behaviour is consistent with earlier studies showing that the B–N ring starts to break down into its constituents only above about 600 K.40,43,44
Upon increasing the temperature to 750 K while maintaining borazine overpressure, additional peaks start to appear between the specular and first order Ru diffraction peaks. Fig. 2(b) (blue curve) shows the characteristic diffraction pattern that emerges. Equidistant peaks at |ΔK/G01| = 0.33 and 0.66 indicate a (3 × 3) periodic structure on the surface, which we label BNI. If dosing is performed at even higher temperatures (T ≥ 880 K), in addition to the observed BNI structure, a shoulder appears to the right-hand side of the first order Ru diffraction peak, indicating the formation of a h-BN structure on the surface (vertical red dotted line in Fig. 2). The peak, which occurs at |ΔK/G01| = 1.08, is a result of the commensurate Moiré pattern on Ru29 (see also h-BN periodicity in the ESI†).
Since a (3 × 3) superstructure composed of intact borazine molecules shows only weak binding to the substrate, the observed BNI structure, as shown later in our DFT calculations, must be composed of partly dehydrogenated borazine molecules, in line with the reported low experimental dehydrogenation temperature on other substrates.44Fig. 3 illustrates in situ monitoring of the integrated peak intensities, which demonstrates that the BNI structure precedes the growth of h-BN. The exposure dependent intensities are obtained from repeated angular diffraction scans. Immediately after dosing begins, the (3 × 3) peaks start to rise rapidly (blue line), while only after a short delay the h-BN diffraction peak increases (red line), although less quickly than the BNI structure. The h-BN peak intensity reaches its maximum at the same point where the BNI structure disappears. We conclude that the BNI structure is converted into h-BN and acts as a precursor structure to the complete h-BN overlayer. Since the intensity of the BNI structure drops to almost zero at ≈9 L, it indicates that virtually all (3 × 3) domains are converted to h-BN.
The temperature region where the BNI structure evolves is in excellent agreement with the borazine decomposition reported by Paffett et al.,40 which helps to confirm the dehydrogenation process. Further, as mentioned earlier, bulk h-BN is known to form by a sequence of dehydrogenation processes, in which borazine polymerises to polyborazylene, which is then cross-linked in one or more steps.10,11 Our results suggest that a similar process happens at the ruthenium surface, but that in the 2D case, there is one clear intermediate step, i.e. the BNI structure, before the formation of h-BN. There are several possible real space structures, which are in line with the observed periodicity and composition.23 We concentrate on providing experimental proof that such intermediate/precursor structures with long-range order exist, while the exact chemical composition of these structures is better probed with X-ray photoemission spectroscopy (XPS) studies,41 beyond the mentioned structural analysis. Moreover, the precursor gas imposes a B/N ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 which we do not expect to change and we have therefore focussed on supporting our structural characterisation through detailed DFT modelling of appropriate candidate structures.
1 which we do not expect to change and we have therefore focussed on supporting our structural characterisation through detailed DFT modelling of appropriate candidate structures.
DFT structural modelling
We understand the BNI structure to consist of partially dehydrogenated, polymerised borazine analogous to the synthesis of bulk h-BN. Thus it is apparent that the 2D growth occurs in a step-by-step process and that not all hydrogen atoms are expected to be removed at the same time, due to the different bonding strengths to N and B atoms, as well as the bond formation between the N and the Ru atoms.41,42,44 Based on this attribution, we have made a vdW-corrected DFT investigation into the energetics of the BNI structure, from adsorption of the precursor gas to the complete h-BN overlayer.We start by considering a single borazine molecule in a (3 × 3) supercell (see Computational methods in the ESI†), and move on to partially dehydrogenated borazine polymers. From the adsorption energies of isolated borazine molecules we observe that the bonding becomes much stronger with dehydrogenation, but the calculations cannot provide a definitive answer in terms of the dehydrogenation sequence (dehydrogenation of the B atoms is slightly more favourable than of the N atoms by ≈ 15 meV). However, as shown later for two borazine molecules per supercell, the N atoms can dehydrogenate more easily than the B atoms and the candidate structures for our observations can be clearly distinguished in terms of the adsorption energies.
In Table 1 we compare the binding energies from vdW-corrected DFT for an intact (B3N3H6) and a partially dehydrogenated (B3N3H3) borazine molecule with one molecule per (3 × 3) supercell, confirming a much stronger bonding of B3N3H3. We consider various initial adsorption sites (Fig. 4(a)) with respect to the C3 rotational axis through the centre of the molecule and a rotation of 60°. Adsorption occurs in a flat face-to-face configuration, while bonding of the same adsorbates with a rotation of 0° is slightly weaker – the results are shown in the ESI† (see Supplementary DFT calculations).
| B3N3H6 | B3N3H3 | ||||
|---|---|---|---|---|---|
| Site | E ads (eV) | ΔE (eV) | Site | E ads (eV) | ΔE (eV) |
| fcc | −4.08 | 0.00 | fcc | −8.95 | 0.00 |
| top | −1.21 | 2.86 | top | −6.60 | 2.35 |
| b → fcc | −4.08 | 0.00 | b → fcc | −8.95 | 0.00 |
| hcp | −1.31 | 2.77 | hcp | −5.88 | 3.07 |
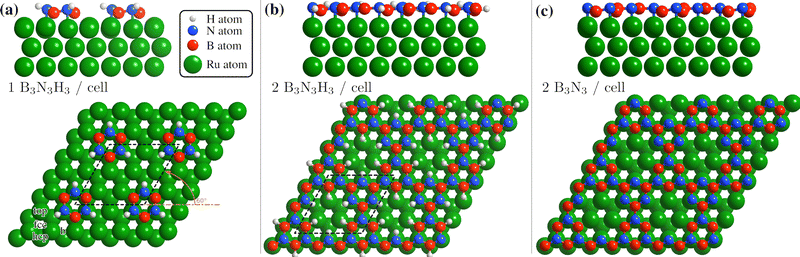 | ||
| Fig. 4 Side and top view of the energetically most favourable configurations on the Ru(0001) surface, from one to two borazine molecules per supercell. Dehydrogenation occurs in stages40–42 with bonding to the substrate facilitated via the N atoms6,24 and we thus expect that dehydrogenation starts at the site of the B atoms for two or more molecules per supercell, as also confirmed by the DFT calculations (see text). (a) For one partially dehydrogenated borazine molecule (B3N3H3) adsorption occurs on the fcc site, forming a (3 × 3) structure. (b) Shows the structure for two partially dehydrogenated B3N3H3 molecules per supercell, where bound B–N rings form a nanostructured network and hydrogen atoms remain adsorbed on the Ru lattice inside the nanopores. In (c) the optimised structure for two fully dehydrogenated borazine molecules is shown, leading to the same nanopore structure with a (3 × 3) periodicity. | ||
In Table 1 the energy differences ΔE are given with respect to the minimum energy of the same dehydrogenation state in addition to the respective adsorption energies Eads. For both stoichiometric configurations the most favourable position is the fcc site and if the borazine molecule is initially placed on a bridge site it undergoes a transition to this position. The fcc configuration for partially dehydrogenated borazine yields an adsorption energy of Eads = −8.95 eV and is shown in Fig. 4(a) with the (3 × 3) supercell highlighted by the black dashed rhombus. The results for the intact borazine molecule (B3N3H6) are very similar with respect to the adsorption site, however, we obtain significantly weaker bonding strengths compared to the dehydrogenated molecule.
Based on bulk h-BN studies we conclude that it is more likely that polymerised networks are formed.10,11 Starting from the minimum energy configuration of a single borazine molecule on the fcc site we continue by adding a second borazine molecule in the supercell. By considering various initial rotations of the additional molecule the energetically most favourable configurations were then identified. In contrast to the case of an isolated borazine molecule, the dehydrogenation sequence becomes clearly discernible in terms of the adsorption energies, with two borazine molecules. The N atoms in the ring adsorb on top of the Ru atoms and the borazine molecules lose all hydrogen atoms associated with the N atoms upon bond formation, in line with experimental results of the completed h-BN overlayer where inter-layer bonding is facilitated via the N atoms.6,24 Such a scenario is, however, different to bulk h-BN growth where ruthenium is not present and thus interaction with the substrate may give rise to an even faster loss of hydrogen compared to bulk studies.
The calculations for two intact borazine molecules per supercell (2B3N3H6, not shown) yield weak binding, since the H atoms start to overlap resulting in a tilt of the complete molecules with respect to the surface. Moreover, due to desorption of hydrogen atoms from the borazine at low temperatures it is unlikely that intact borazine will remain and so intact molecules will not be considered further.40
Therefore, we concentrate on partially and fully dehydrogenated borazine molecules. Fig. 4(b) and (c) shows the final optimised structure for 2B3N3H3 per supercell, illustrating that individual borazine molecules form bonds to each other. The bound B–N rings build up a nanostructured network with nanopores, i.e. where in between the B–N rings vacancies/pores of the Ru substrate are left behind. The high binding energy of the structure in Fig. 4(b) with −6.28 eV compared to −6.74 eV for the complete h-BN/Ru, may therefore explain the stability of the BNI structure at temperatures ≈ 750 K as observed in the experiments.
The structure in Fig. 4(b) acts as an intermediate prior to complete dehydrogenation which is expected at elevated temperatures. The calculations show that first the hydrogen atoms detach from the nitrogen and bind to the Ru substrate on the hcp sites, inside the nanopores. The excess hydrogen adatoms inside the nanopores are likely to desorb relatively quickly at the temperature of the experiment.63 Therefore, Fig. 4(c) shows the optimised structure, starting with two fully dehydrogenated borazine molecules per supercell, leading again to the formation of nanopores. Such an open structure could easily act as a precursor to the complete h-BN overlayer, since each pore only has to be “filled” with an additional dehydrogenated borazine molecule. Finally, the addition of further borazine molecules in the calculations, i.e. three per supercell, essentially leads to the formation of h-BN which gives rise to the strongest binding energy in the calculations. The route from the precursor BNI structure to the final h-BN overlayer, with several intermediate steps, is illustrated in Fig. S3 of the ESI.†
In addition to providing us with real-space structures of the observed BNI precursor, there are several points which we note from the vdW DFT calculations: dehydrogenation of borazine always gives rise to a stronger bonding to the substrate and the results show that the thermodynamically most stable configuration for three adsorbed borazine molecules is h-BN (Fig. S2(b), ESI†). We also see from the side views in Fig. 4 that there occurs always some buckling (0.21–0.35 Å) and the adlayer is never perfectly flat. The results show that by carefully controlling the substrate temperature and thus the amount of excess hydrogen in future experiments, several BN nano-structures could be synthesized as shown for two cases in Fig. 4(b) and (c). Moreover, careful changes of the starting conditions in the DFT calculations may even yield a “local” minimum energy configuration as in Fig. S2(c) (ESI†). Thus the system may be an ideal playground for the growth of different nano-structures and further metastable networks beside the ones reported in this work.
Additional structures accompanying the h-BN growth
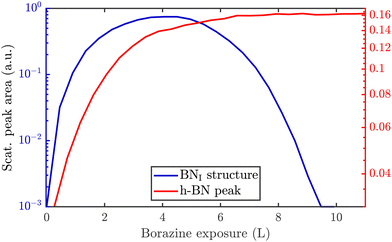
So far, we have described the formation of a BNI structure at T ≥ 750 K, which is converted to h-BN at T ≥ 880 K. However, upon complete conversion of the BNI structure to h-BN, exposing the surface to excess borazine results in the emergence of an additional structure with a (3 × 4) periodicity, which we label BNII. The green line in Fig. 2(b) illustrates the corresponding diffraction pattern with the h-BN Moiré diffraction peak being still present next to the first order Ru peak. As shown in a two-dimensional diffraction scan in Fig. S5 (ESI†), the (3 × 4) peaks are not a subset of the h-BN Moiré pattern. In addition, a smaller peak to the left of the first order Ru peak becomes visible which can be attributed to a substrate reconstruction peak29 due to the h-BN growth.To monitor the growth of the BNII structure we use a smaller borazine overpressure while holding the sample temperature at 915 K. Fig. 5(a) shows the evolution of the BNII and the BNI structure as blue and green curves, respectively. Here, the red line is again the integrated peak intensity of the h-BN diffraction peak. Immediately after exposing the surface to borazine, the BNI structure increases together with the h-BN peak. Further exposure leads to a decay of the BNI structure, while the h-BN feature still rises, indicating the growth of h-BN islands. At 7 L the h-BN diffraction peak saturates, while at the same time the BNI structure disappears. At this stage the h-BN overlayer is complete and after further dosing of borazine, the BNII structure starts to emerge. As discussed later this may be interpreted as a second layer being formed on top of h-BN.
The measurement was repeated at an even lower dosing pressure, while holding the sample at the lower temperature of 880 K. In Fig. 5(b) the same behaviour is reproduced, yielding a h-BN layer with two additional structures, except that the emergence is delayed to longer/higher exposures, thus indicating a kinetically driven conversion.
With continuing borazine exposure to 20 L in Fig. 5(b), the BNII structure reaches its maximum with no further changes in the scattered intensity. Together with the rise of the BNII structure the h-BN peak intensity slowly starts to decay, likely due to diffuse scattering from additional adsorbates at the surface or from domain walls of the BNII structure. Increasing the surface temperature to 1000 K gives rise to a decay of the BNII structure while the h-BN peak intensity starts to recover to its original value. Further temperature increase accelerates this process giving rise to a faster transition/conversion until the intermediate peaks disappear, leaving behind only the h-BN layer. Such a behaviour illustrates that ultimately h-BN is the most stable structure. Even though the borazine overpressure was still present, no additional peaks formed and the h-BN overlayer is the only remaining structure at the surface.
From Fig. 5(b) it becomes evident, that in contrast to the BNI structure, the BNII structure is much more stable at higher temperatures since the (3 × 4) diffraction peaks are observed up to 1000 K. Further increase of the temperature to ≈1200 K gives rise to the surface migration of bulk-dissolved carbon, leading to the formation of graphene (see Supplementary diffraction scans in the ESI†) and thus eventually destroys the h-BN overlayer. The latter may open up the possibility to study the growth of h-BN/graphene heterostructures.64–67
From our experiments it is likely that the BNII structure is a second chemisorbed layer on top of already grown h-BN. Earlier works on an Ir(111) substrate showed the evolution of additional compact reconstructed regions with a (6 × 2) superstructure, which were attributed to reconstructed boron areas.68 On the other hand, CVD growth on polycrystalline Cu provided evidence for boron dissolution into the bulk together with multilayer h-BN formation via intercalation.69 However, both systems and studies are significantly different from our approach. E.g., the different behaviour in the first study could be due to changes of both the lattice constant and the h-BN-substrate bonding between Ru and Ir. Moreover, in light of the recent observation of h-BN multilayer growth,3 a second chemisorbed layer is much more plausible.
The BNII structure, as a second chemisorbed layer, consists of partly or completely dehydrogenated borazine molecules with a desorption temperature slightly above our performed measurements, since we see an adsorption/desorption equilibrium at temperatures ⪅1000 K with an ultimate desorption at temperatures above this value. We can rule out the existence of multilayer growth due to the absence of intensity oscillations in our experiments32 or observations of any other periodicity, that would be indicative of multilayer h-BN growth. On the other hand, considering different growth conditions at higher pressures or via boron dissolution in the substrate,3 the BNII structure may well act as a precursor to multilayer synthesis, in particular if the original h-BN layer is of poor quality thus providing a high density of growth nuclei and further facilitating multilayer growth.3,69–72
In a set of additional DFT calculations summarised in Table S2 of the ESI,† we considered also the possibility of borazine adsorption on top of h-BN/Ru as well as the formation of bi-layer h-BN.69–72 As mentioned above, we can rule out the latter at our experimental conditions. Thus it is more likely that the BNII structure consists of adsorbed molecules or polymerised borazine structures, with a weaker bonding compared to the first h-BN layer3 and therefore more likely to desorb, in line with the multi-stage process of h-BN bulk formation. Further unlikely scenarios are discussed in Supplementary discussion in the ESI.†
h-BN growth diagram on Ru(0001)
The combination of measurements and DFT calculations allows us to conclude that the whole system passes through various structural phases:| Ru + BZ → BNI + h-BN → h-BN → BNII + h-BN → h-BN, |
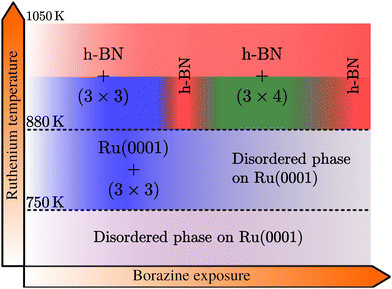
Below 750 K no periodic overlayer structure on the Ru(0001) surface is found. Between 750 and 880 K the BNI structure forms on the surface which upon further borazine exposure vanishes and leaves a disordered phase behind. The minimum temperature to form a h-BN overlayer on the surface was determined to be 880 K. Above this temperature we observe additional structures, starting with a (3 × 3) structure (BNI) followed by a (3 × 4) periodic diffraction pattern (BNII). These structures always appear in addition to the h-BN layer and ultimately vanish, leaving a complete h-BN overlayer behind (see Fig. 2(a) for a diffraction scan of a complete h-BN overlayer without any additional structures). We have thus identified two kinetic barriers which need to be overcome in order to form ordered structures on the Ru substrate: a temperature of 750 K is necessary for the precursor structure to result, while at 880 K the h-BN formation sets in. As mentioned above, the BNI precursor structure is always present, however, with increasing temperature its transformation into h-BN becomes faster.
As further illustrated in h-BN periodicity in the ESI,† the h-BN periodicity and superstructure are strongly dependent on the experimental parameters, in particular the growth temperature. The exact h-BN periodicity and the Moiré pattern upon h-BN formation on Ru(0001),24,26 due to the small lattice mismatch between ah-BN and aRu(0001), is determined by the growth temperature due to a so-called “lock-in” effect at that respective growth temperature.73 Together with the above reported additional structures, it confirms the complexity of the whole system and its dependence on minute changes of the growth parameters.
Discussion and summary
In summary, we investigated the growth of h-BN on a Ru(0001) substrate using helium atom scattering. Employing various growth conditions, characteristic periodic structures are measured during borazine exposure in addition to the h-BN diffraction peak as outlined in the diagram of Fig. 6. Between 750 and 880 K a structure with (3 × 3) periodicity, that precedes the growth of h-BN, is observed with the minimum temperature necessary to form a h-BN overlayer being 880 K. Above this temperature, in addition to the emerging h-BN layer, we observe additional structures with a (3 × 3) superstructure followed by a (3 × 4) diffraction pattern, eventually disappearing and leaving a complete h-BN overlayer behind.It is clearly evident from our observations that a precursor structure precedes the growth of h-BN at lower temperatures and an additional structure co-exists with h-BN at higher temperatures. Both are strongly dependent on the growth conditions, but always transform into a fully h-BN covered substrate at sufficiently high temperatures, thus confirming that the latter is the thermodynamically most stable structure. Our study of the structural evolution during the arrangement of h-BN from the precursor gas illustrates steps in the formation process itself and we hope to encourage future studies linking our structural information with chemical characterisation.
We believe that these intermediate metastable structures may be present in many more systems where 2D materials are grown based on CVD, at least at lower temperatures and for higher amounts of excess hydrogen compared to the “ideal” growth conditions (see Outlook for other 2D materials in the ESI†). In the case studied here, they ultimately always transform into the complete 2D layer – and thus usually higher temperatures are reported as the “ideal” growth conditions for h-BN in the literature.
These intermediate structures seem to have been largely overlooked so far. Possibly, because they are difficult to detect owing to experimental complications since the structural advent of 2D materials is often not investigated during the growth itself, or is only accessible ex situ. More importantly, with increasing growth temperature the transformation to h-BN may occur so fast that they are easily missed.27
The strong dependence regarding the emergence of these structures on temperature and exposure suggests that further uncovered “routes” and polymerisation steps are viable and the system may present an ideal playground to end up with different nano-structures. It further suggests that a careful tuning of the growth conditions via temperature and excess hydrogen from the precursor may provide new broadly applicable strategies for controlling the growth of specific nanostructures. Additional possibilities involve changing the substrate or the precursor gas, and hence tuning the thermochemistry of the surface–adsorbate complex which may further alter the subsequent reaction pathway. E.g. by changing the substrate, the metal–N bond strength may be tuned since one expects the bonding strength to increase as one moves from right to left in the transition metal series. We hope that the wide ranging implications for a controlled growth of 2D materials and nanostructures will stimulate a broad range of new research, understanding and application.
Author contributions
A. R. and N. A. carried the diffraction measurements out, with M. S. and A. P. performing the ab initio (DFT) calculations. A. T. and A. R. worked on the structural analysis, while A. T., A. R., M. S. and N. A. developed the physical interpretation of the data. A. P. J. and W. E. contributed to the conception of the project and all authors discussed the results and contributed to writing the manuscript.Data availability
The datasets generated and analysed during the current study are available from the TU Graz repository, with the identifier DOI: https://10.3217/1hwgj-rgg36.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was funded in whole, or in part, by the Austrian Science Fund (FWF) [P29641-N36 & P34704]. For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. We would also like to thank W. Allison for helpful discussion regarding the interpretation of the data, Chris Pickard for additional structure calculations based on a neural network approach and Moritz Will for his advice in terms of the precursor (borazine) purchase and treatment. A. R. acknowledges funding by the Doctoral School and a scholarship of TU Graz. The authors acknowledge use of facilities at and support by the Cambridge Atom Scattering Centre (https://atomscattering.phy.cam.ac.uk) and the EPSRC award EP/T00634X/1 with the help of J. Ellis. M. S. is grateful for support from the Royal Society (URF/R/191029) and funding through the EPSRC (EP/S029834/1). This work used the ARCHER2 UK National Supercomputing Service (http://www.archer2.ac.uk) via membership of the UK's HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/R029431).References
- C. Anichini, W. Czepa, D. Pakulski, A. Aliprandi, A. Ciesielski and P. Samorì, Chem. Soc. Rev., 2018, 47, 4860–4908 RSC.
- H. X. Jiang and J. Y. Lin, Semicond. Sci. Technol., 2014, 29, 084003 CrossRef CAS.
- K. Y. Ma, L. Zhang, S. Jin, Y. Wang, S. I. Yoon, H. Hwang, J. Oh, D. S. Jeong, M. Wang, S. Chatterjee, G. Kim, A.-R. Jang, J. Yang, S. Ryu, H. Y. Jeong, R. S. Ruoff, M. Chhowalla, F. Ding and H. S. Shin, Nature, 2022, 606, 88–93 CrossRef CAS PubMed.
- A. Zavabeti, A. Jannat, L. Zhong, A. A. Haidry, Z. Yao and J. Z. Ou, Nano-Micro Lett., 2020, 12, 66 CrossRef CAS PubMed.
- K. Zhang, Y. Feng, F. Wang, Z. Yang and J. Wang, J. Mater. Chem. C, 2017, 5, 11992–12022 RSC.
- W. Auwärter, Surf. Sci. Rep., 2019, 74, 1–95 CrossRef.
- M. Jana and R. N. Singh, Int. Mater. Rev., 2018, 63, 162–203 CrossRef CAS.
- I. Calvo-Almazán, M. Sacchi, A. Tamtögl, E. Bahn, M. M. Koza, S. Miret-Artés and P. Fouquet, J. Phys. Chem. Lett., 2016, 7, 5285–5290 CrossRef PubMed.
- P. J. Fazen, E. E. Remsen, J. S. Beck, P. J. Carroll, A. R. McGhie and L. G. Sneddon, Chem. Mater., 1995, 7, 1942–1956 CrossRef CAS.
- Y. Shi, C. Hamsen, X. Jia, K. K. Kim, A. Reina, M. Hofmann, A. L. Hsu, K. Zhang, H. Li, Z.-Y. Juang, M. S. Dresselhaus, L.-J. Li and J. Kong, Nano Lett., 2010, 10, 4134–4139 CrossRef CAS PubMed.
- S. Bernard and P. Miele, Mater. Today, 2014, 17, 443–450 CrossRef CAS.
- S. Bernard, C. Salameh and P. Miele, Dalton Trans., 2016, 45, 861–873 RSC.
- A. Talyzin, S. Luzan, K. Leifer, S. Akhtar, J. Fetzer, F. Cataldo, Y. Tsybin, C.-W. Tai, A. Dzwilewski and E. Moons, J. Phys. Chem. C, 2011, 115, 13207–13214 CrossRef CAS.
- J. Li, E. Croiset and L. Ricardez-Sandoval, Phys. Chem. Chem. Phys., 2014, 16, 2954–2961 RSC.
- H. Chen, W. Zhu and Z. Zhang, Phys. Rev. Lett., 2010, 104, 186101 CrossRef PubMed.
- L. Wang, R. Lai, L. Zhang, M. Zeng and L. Fu, ACS Mater. Lett., 2022, 4, 528–540 CrossRef CAS.
- M. Losurdo, M. M. Giangregorio, P. Capezzuto and G. Bruno, Phys. Chem. Chem. Phys., 2011, 13, 20836–20843 RSC.
- X. Zhang, L. Wang, J. Xin, B. I. Yakobson and F. Ding, J. Am. Chem. Soc., 2014, 136, 3040–3047 CrossRef CAS PubMed.
- G. Lu, T. Wu, Q. Yuan, H. Wang, H. Wang, F. Ding, X. Xie and M. Jiang, Nat. Commun., 2015, 6, 6160 CrossRef CAS PubMed.
- J.-H. Choi, P. Cui, W. Chen, J.-H. Cho and Z. Zhang, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1300 Search PubMed.
- Z. Qiu, P. Li, Z. Li and J. Yang, Acc. Chem. Res., 2018, 51, 728–735 CrossRef CAS PubMed.
- M. R. Habib, T. Liang, X. Yu, X. Pi, Y. Liu and M. Xu, Rep. Prog. Phys., 2018, 81, 036501 CrossRef PubMed.
- H. Li, H. Zhu and R. Zhao, New J. Chem., 2022, 46, 17496–17504 RSC.
- A. Goriachko, He, M. Knapp, H. Over, M. Corso, T. Brugger, S. Berner, J. Osterwalder and T. Greber, Langmuir, 2007, 23, 2928–2931 CrossRef CAS PubMed.
- S. Joshi, D. Ecija, R. Koitz, M. Iannuzzi, A. P. Seitsonen, J. Hutter, H. Sachdev, S. Vijayaraghavan, F. Bischoff, K. Seufert, J. V. Barth and W. Auwärter, Nano Lett., 2012, 12, 5821–5828 CrossRef CAS PubMed.
- J. Lu, P. S. E. Yeo, Y. Zheng, H. Xu, C. K. Gan, M. B. Sullivan, A. Castro Neto and K. P. Loh, J. Am. Chem. Soc., 2013, 135, 2368–2373 CrossRef CAS PubMed.
- D. Steiner, F. Mittendorfer and E. Bertel, ACS Nano, 2019, 13, 7083–7090 CrossRef CAS PubMed.
- F. Müller, S. Hüfner and H. Sachdev, Surf. Sci., 2009, 603, 425–432 CrossRef.
- D. Martoccia, T. Brugger, M. Björck, C. Schlepütz, S. Pauli, T. Greber, B. Patterson and P. Willmott, Surf. Sci., 2010, 604, L16–L19 CrossRef CAS.
- F. Orlando, P. Lacovig, L. Omiciuolo, N. G. Apostol, R. Larciprete, A. Baraldi and S. Lizzit, ACS Nano, 2014, 8, 12063–12070 CrossRef CAS PubMed.
- J. Kelsall, P. S. M. Townsend, J. Ellis, A. P. Jardine and N. Avidor, Phys. Rev. Lett., 2021, 126, 155901 CrossRef CAS PubMed.
- D. Farias and K.-H. Rieder, Rep. Prog. Phys., 1998, 61, 1575 CrossRef CAS.
- J. Braun, J. P. Toennies and C. Wöll, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 117075 CrossRef.
- E. M. McIntosh, J. Ellis, A. P. Jardine, P. Licence, R. G. Jones and W. Allison, Chem. Sci., 2014, 5, 667 RSC.
- B. Borca, S. Barja, M. Garnica, M. Minniti, A. Politano, J. M. Rodriguez-García, J. J. Hinarejos, D. Farías, A. L. V. d Parga and R. Miranda, New J. Phys., 2010, 12, 093018 CrossRef.
- A. Tamtögl, E. Bahn, J. Zhu, P. Fouquet, J. Ellis and W. Allison, J. Phys. Chem. C, 2015, 119, 25983–25990 CrossRef PubMed.
- G. Anemone, E. Climent-Pascual, H. K. Yu, A. Al Taleb, F. Jiménez-Villacorta, C. Prieto, A. M. Wodtke, A. De Andrés and D. Farías, RSC Adv., 2016, 25, 21235 RSC.
- K. D. Gibson and S. J. Sibener, J. Phys. Chem. C, 2016, 120, 24158–24164 CrossRef CAS.
- A. A. Taleb, G. Anemone, R. Miranda and D. Farías, 2D Mater., 2018, 5, 045002 CrossRef.
- M. T. Paffett, R. J. Simonson, P. Papin and R. T. Paine, Surf. Sci., 1990, 232, 286–296 CrossRef CAS.
- F. Orlando, R. Larciprete, P. Lacovig, I. Boscarato, A. Baraldi and S. Lizzit, J. Phys. Chem. C, 2012, 116, 157–164 CrossRef CAS.
- A. Farkas, P. Török, F. Solymosi, J. Kiss and Z. Kónya, Appl. Surf. Sci., 2015, 354, 367–372 CrossRef CAS.
- J.-W. He and D. W. Goodman, Surf. Sci., 1990, 232, 138–148 CrossRef CAS.
- L. Haug, J. P. Roth, M. Thaler, D. Steiner, A. Menzel, S. Tosoni, G. Pacchioni and E. Bertel, Phys. Chem. Chem. Phys., 2020, 22, 11704–11712 RSC.
- F. Späth, J. Gebhardt, F. Düll, U. Bauer, P. Bachmann, C. Gleichweit, A. Görling, H.-P. Steinrück and C. Papp, 2D Mater., 2017, 4, 035026 CrossRef.
- M. Kim, S. W. Moon, G. Kim, S. I. Yoon, K. Kim, S. K. Min and H. S. Shin, Chem. Mater., 2020, 32, 4584–4590 CrossRef CAS.
- J. Lau, I. Calvo-Almazán, P. Townsend, D. Ward, A. Jardine, W. Allison, J. Ellis, B. Hinch and N. Avidor, J. Phys. Chem. C, 2018, 122, 8941–8945 CrossRef CAS.
- N. Avidor, H. Hedgeland, G. Held, A. Jardine, W. Allison, J. Ellis, T. Kravchuk and G. Alexandrowicz, J. Phys. Chem. A, 2011, 115, 7205–7209 CrossRef CAS PubMed.
- P. Kraus, C. Gösweiner, A. Tamtögl, F. Apolloner and W. E. Ernst, EPL, 2016, 114, 56001 CrossRef.
- E. Bahn, A. Tamtögl, J. Ellis, W. Allison and P. Fouquet, Carbon, 2017, 114, 504–510 CrossRef CAS.
- N. Avidor and W. Allison, J. Phys. Chem. Lett., 2016, 7, 4520–4523 CrossRef CAS PubMed.
- C. Lin, G. Corem, O. Godsi, G. Alexandrowicz, G. R. Darling and A. Hodgson, J. Am. Chem. Soc., 2018, 140, 15804–15811 CrossRef CAS PubMed.
- A. Tamtögl, M. Sacchi, N. Avidor, I. Calvo-Almazán, P. S. M. Townsend, M. Bremholm, P. Hofmann, J. Ellis and W. Allison, Nat. Commun., 2020, 11, 278 CrossRef PubMed.
- A. Tamtögl, A. Ruckhofer, D. Campi, M. Bremholm, W. E. Ernst, P. Hofmann and W. Allison, Phys. Chem. Chem. Phys., 2021, 23, 7637–7652 RSC.
- A. Tamtögl, E. Bahn, M. Sacchi, J. Zhu, D. J. Ward, A. P. Jardine, S. J. Jenkins, P. Fouquet, J. Ellis and W. Allison, Nat. Commun., 2021, 12, 3120 CrossRef PubMed.
- C.-Y. Lin, C.-E. Cheng, S. Wang, H. W. Shiu, L. Y. Chang, C.-H. Chen, T.-W. Lin, C.-S. Chang and F. S.-S. Chien, J. Phys. Chem. C, 2015, 119, 12910–12915 CrossRef CAS.
- G. Benedek and J. P. Toennies, Atomic Scale Dynamics at Surfaces, Springer Berlin Heidelberg, 2018 Search PubMed.
- A. Jardine, H. Hedgeland, G. Alexandrowicz, W. Allison and J. Ellis, Prog. Surf. Sci., 2009, 84, 323–379 CrossRef CAS.
- G. Alexandrowicz and A. P. Jardine, J. Phys.: Condens. Matter, 2007, 19, 305001 CrossRef.
- B. Holst, G. Alexandrowicz, N. Avidor, G. Benedek, G. Bracco, W. E. Ernst, D. Farías, A. P. Jardine, K. Lefmann, J. R. Manson, R. Marquardt, S. M. Artés, S. J. Sibener, J. W. Wells, A. Tamtögl and W. Allison, Phys. Chem. Chem. Phys., 2021, 23, 7653–7672 RSC.
- H. Shichibe, Y. Satake, K. Watanabe, A. Kinjyo, A. Kunihara, Y. Yamada, M. Sasaki, W. W. Hayes and J. R. Manson, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155403 CrossRef.
- A. Al Taleb, H. K. Yu, G. Anemone, D. Farías and A. M. Wodtke, Carbon, 2015, 95, 731–737 CrossRef CAS.
- P. Feulner and D. Menzel, Surf. Sci., 1985, 154, 465–488 CrossRef CAS.
- P. Sutter, R. Cortes, J. Lahiri and E. Sutter, Nano Lett., 2012, 12, 4869–4874 CrossRef CAS PubMed.
- J. Yin, J. Li, Y. Hang, J. Yu, G. Tai, X. Li, Z. Zhang and W. Guo, Small, 2016, 12, 2942–2968 CrossRef CAS PubMed.
- C. Zhang, S. Zhao, C. Jin, A. L. Koh, Y. Zhou, W. Xu, Q. Li, Q. Xiong, H. Peng and Z. Liu, Nat. Commun., 2015, 6, 6519 CrossRef CAS PubMed.
- A. Kutana, A. Goriachko, Z. Hu, H. Sachdev, H. Over and B. I. Yakobson, Adv. Mater. Interfaces, 2015, 2, 1500322 CrossRef.
- M. Petrović, U. Hagemann, M. Horn-von Hoegen and F.-J. Meyer zu Heringdorf, Appl. Surf. Sci., 2017, 420, 504–510 CrossRef.
- P. R. Kidambi, R. Blume, J. Kling, J. B. Wagner, C. Baehtz, R. S. Weatherup, R. Schloegl, B. C. Bayer and S. Hofmann, Chem. Mater., 2014, 26, 6380–6392 CrossRef CAS PubMed.
- L. Song, L. Ci, H. Lu, P. B. Sorokin, C. Jin, J. Ni, A. G. Kvashnin, D. G. Kvashnin, J. Lou, B. I. Yakobson and P. M. Ajayan, Nano Lett., 2010, 10, 3209–3215 CrossRef CAS PubMed.
- N. Guo, J. Wei, L. Fan, Y. Jia, D. Liang, H. Zhu, K. Wang and D. Wu, Nanotechnology, 2012, 23, 415605 CrossRef PubMed.
- S. M. Gilbert, T. Pham, M. Dogan, S. Oh, B. Shevitski, G. Schumm, S. Liu, P. Ercius, S. Aloni, M. L. Cohen and A. Zettl, 2D Mater., 2019, 6, 021006 CrossRef CAS.
- D. Martoccia, S. Pauli, T. Brugger, T. Greber, B. Patterson and P. Willmott, Surf. Sci., 2010, 604, L9–L11 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nh00353h |
| This journal is © The Royal Society of Chemistry 2022 |

![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] scanning direction (
0] scanning direction (