Can the local electric field be a descriptor of catalytic activity? A case study on chorismate mutase

Abstract

The current theoretical perception of enzymatic activity is highly reliant on the determination of the activation energy of the reactions, which is often calculated using computationally demanding quantum mechanical calculations. With the ever-increasing use of bioengineering techniques that produce too many variants of the same enzyme, a fast and accurate way to study the relative efficiency of enzymes is currently in high demand. Here, we propose the local electric field (LEF) of the enzyme along the reaction axis as a descriptor for the enzymatic activity using the example of chorismate mutase in its native form and several variants (R90A, R90G, and R90K/C88S). The study shows a direct correlation between the calculated enzymatic EF and the enzymatic activity for all the complexes. MD simulations of the Michaelis complex and the transition state analog (TSA) show a stabilizing force on the TSA due to the enzymatic EF. QM/MM and QM-only DFT calculations in the presence of an external electric field (EEF) oriented along the reaction axis show that the electric field can interact with the dipole moment of the TS, thereby stabilizing it and thus lowering the activation energy.

---

1. Introduction

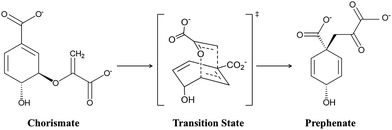
Designing target-based enzymes is an ultimate goal for bioengineers as it gives a greener and sustainable approach for the synthesis of desired products.^1–5 This goal is now possible by mutating some key strategic residues of the active sites using directed evolution methods.^6–10 This approach is efficient, however, but at the same time random. Therefore, a comprehensive understanding of the molecular mechanism that confers better activity could improve such design protocols and could also guide the development of smarter mutagenesis and screening strategies. However, unlike protein–drug interactions where the binding information of the drug using the lock–key concept could be enough,^11–14 understanding the molecular mechanism of enzyme catalysis is somewhat tricky. According to Warshel, an enzymatic reaction can involve two components:^15–17 the first component is the entropic contribution to the binding free energy for bringing the reactive fragment into the catalytic site, which is equivalent to the dissociation constant; and the second component is the free energy needed to reach the TS from the reactant geometry, which is equivalent to the activation energy. Fortunately, modern methods like MD simulations^13,18–20 can deal with the information related to the first component (the binding stability), while hybrid QM/MM calculations can reveal the second component, i.e., the activation energy.^21–24 A combination of these two methods, therefore, provides a crucial lead to design more effective and powerful enzymes for modern use. More recently, with an ever-increasing rate, the external electric field (EEF) is being used to harness the catalytic activity of many chemical reactions.^25–35 In fact, nature routinely harnesses pre-oriented local-electric fields (LEFs) for the electrostatic catalysis that is observed in enzymes. Therefore, quantification of the electric field in an enzyme system using computational tools could be an add-on to the logic-based design of enzymes. In the present study, we show how quantification of the local electric field (LEF) along the axis of reaction could be used as a descriptor of the enzyme activity.

Here, we quantify the local electric field produced by chorismate mutase (CM) and calculate the reactivity of the enzyme in the presence of the oriented electric field using hybrid QM/MM calculations. CM is an enzyme formally known to catalyse the Claisen rearrangement where (−) chorismate is converted into prephenate as shown in Scheme 1, and hence presents a rare example of an enzyme-catalysed pericyclic process.^36–42

Scheme 1 Schematic representation of the conversion of chorismate to prephenate.

Our choice of CM as a model system to study the electric field effect is based mainly on its peculiar characteristic to being able to catalyse reactions using the electrostatic environment created by the protein without the involvement of any covalent bonding, and therefore, the effect of the electric field could be more prominent in CM. Furthermore, sufficient experimental studies for the wild-type (WT) enzyme and its several variants are also available, which can be used to benchmark the computational findings.^38,39,43,44 In the same context, Hilvert's group, using experimental gene engineering of the active-site residues, emphasized the role of positively charged residues, e.g., R90, to stabilize the transition state (TS) of the charismatic rearrangement. This finding was further justified by site-directed mutagenesis studies performed by the same group in a separate study where they mutated R90 with alanine and glycine, and found that the catalytic activity was decreased fivefold relative to the WT complex. The activity was again restored when a lysine residue was reinstated at the same position. These findings clearly confirm the crucial role of the electrostatic environment in the catalysis. In a similar reference, Marti et al. studied the effect of the solvent environment on the activation energy using QM/MM calculations, and they comprehensively studied the role of electrostatic effects on the reaction mechanism of this enzyme.^40–42 In the present study, therefore, we have used WT chorismate mutase along with its variants to establish a direct correlation between the enzymatic electric field and its catalytic efficiency using MD simulations and hybrid QM/MM calculations. Using the example of chorismate mutase, we show that the local electric field can be used as an efficient descriptor of the enzymatic activity.

2. Computational details

In the present study, we used MD simulations for the conformational and binding stabilities of CM and its variants, QM/MM calculations for the mechanism of chorismate to prephenate conversion, quantification of the local electric field for WT and its mutant complexes and QM-only DFT calculations to study the effect of solvation and varying the oriented external electric field (OEEF) onto the reaction axis. The details of each method are described below.

2.1. System setup

The initial coordinates for the WT CM complex were taken from the crystal structure of Bacillus subtilis chorismate mutase enzyme bound with Bartlett's inhibitor (a transition state analog inhibitor) from the protein data bank (PDB code: 2CHT).⁴⁵ The imported structure contains several missing hydrogen atoms that were added using the Leap module of the Amber20 suite. Three different variants of the Bacillus subtilis chorismate mutase enzyme, i.e., R90A, R90G and R90K/C88S, were produced by mutating R90 and C88 residues using the pdb4amber module of Amber20. The parameters for the TSA inhibitor and chorismate substrate were generated using the antechamber module of Amber20 for GAFF2 parameters for a QM-optimized geometry at the HF/6-31G(d,p) level of theory. Thereafter, all complexes were solvated in a truncated octahedron box of TIP3P water molecules with a 12 Å cutoff from the protein boundary.⁴⁶ An appropriate number of Na⁺ ions were added to neutralize the total charge of the system. Since the crystal structure of CM was with a TSA, we used the same active-site conformation to dock the chorismate substrate using AutoDock Vina implemented in UCSF Chimera.⁴⁷

2.2. MD simulations

After the initial setup of the complexes in the WT enzyme and its mutants, systems were minimized in two steps for removing the bad contacts. In step 1, only solvent molecules were minimized using 5000 steps of the steepest descent followed by 5000 steps of the conjugate gradient minimizer. In step 2, all the complexes were minimized without any constraints using the same minimizer as in step 1. All the systems were then gently annealed from 10 to 300 K under the NVT ensemble for 50 ps with a weak restraint of 5 kcal mol⁻¹ Å⁻². Subsequently, a density equilibrium was performed using the NPT ensemble at a targeted temperature of 300 K and pressure of 1 atm for 1 ns using the Langevin thermostat and the Berendsen barostat, with a weak restraint of 1 kcal mol⁻¹ Å⁻².^48,49 Thereafter, we removed all the restraints and the systems were further equilibrated for 3 ns followed by 50 ns of production simulations for each system with the TSA and 100 ns for the Michaelis complex. The covalent bonds that contain hydrogens were constrained using the SHAKE algorithm, and a particle mesh Ewald (PME) method was utilized to treat long-range electrostatic interactions during all the MD simulations.^50,51 An integration step of 2 fs was used during the entire simulation. All the MD simulations were performed using the GPU version of the Amber20 package.⁵²

2.3. QM/MM calculations

The reaction mechanism was investigated using QM/MM calculations for the representative snapshots from the MD trajectories for each system.

The QM regions included R90, E78 and the entire substrate molecule, where the coordinates for the QM region can be found in the ESI.† All protein residues and water molecules within 8 Å of the substrate were included in the ‘active region’ of the QM/MM calculations. The atoms in the ‘active region’ interact with the QM atoms through electrostatic and van der Waals interactions and the corresponding polarization effects were considered in the subsequent QM/MM calculations. All the QM/MM calculations were performed using ChemShell, by combining Turbomole for the QM part and DL_POLY for the MM part.^53–56 The MM region was described using the Amber ff14SB force field, and the electronic embedding scheme was used to account for the polarizing effect of the enzyme environment on the QM region.⁵⁷ The QM/MM boundary was treated using the hydrogen link atoms of the charge-shift model.⁵⁴

During the QM/MM geometry optimizations, the QM region was treated using the hybrid B3LYP functional with the def2-SVP basis set.⁵⁸ Results were further validated with single-point calculations at a higher basis set (def2-TZVPP) using the B3LYP-D3 functional.⁵⁹ The TS optimization was performed using the dimer method included in the ChemShell package.⁵³

2.4. QM only DFT calculations

Potential energy surface (PES) scanning for the interconversion reactions of chorismate to prephenate in the gas-phase and with a water solvent was determined using Gaussian09.⁶⁰ The solvation effect on the interconversion reactions was studied using the polarizable continuum model (PCM), using water as the solvent. For geometry optimization and frequency calculations, we used the hybrid B3LYP/def2-SVP level of theory.⁵⁸ The results were further validated using single-point calculations at a higher basis set (def2-TZVPP) using the B3LYP-D3 functional.⁵⁹ The effects of the EEFs were also studied using Gaussian09. A range of the electric field strength (F_y) was explored, while allowing it to be oriented along the y-axis, i.e., the reaction axis, along which the bonds were being broken and formed. For the geometry optimization in the presence of the EEF, we used internal coordinates to avoid the misalignment of the EEF during the variation of the geometry.

2.5. Free-energy calculations

To observe the differences in the binding of the chorismate substrate and the transition state analog (TSA) inhibitor with the active-site residues of the enzyme, we used MMPBSA calculations for the computation of the free energy of binding.^61,62 This method contains well-established principles^63,64 that have been used successfully in various previous studies.^65–68 For all the MMPBSA calculations, the most populated MD trajectories were used. Initially, we stripped all the water molecules and counter ions from the trajectory and used dielectric constants of 1 and 80 for the solute and the solvent, respectively. Then, we performed the MMPBSA calculations for the most populated trajectories.

3. Results and discussion

3.1. MD simulations of the Michaelis complex and transition state analog (TSA) in WT chorismate mutase

We performed MD simulations of the WT complex of chorismate mutase with the substrate for the Michaelis complex (MC) and transition state analog (TSA) to study the effect of the local electric field produced by the native enzyme on the stability of the reactant and the transition state. Although the active site of the enzyme is surrounded by many charged residues, such as R7, E78, R90, Y108, K60 and R63, the reactant shows a significant degree of flexibility during the simulations. Fig. 1 shows three representative snapshots from the MD simulations of the MC at different timescales. It is evident from the figure that during the simulation, the substrate loses several interactions with key residues such as R7 and Y108, which can be anticipated by the increasing distances of these residues from the substrate continuously with the simulation time. To further quantify the effect of the charged residues on the reactant, we calculated the total change in binding free energy using the MMPBSA method. The calculation shows ΔG_binding as −31.0 kcal mol⁻¹, which is mainly dominated by strong and favorable interactions with R7, R90, K60 and R63.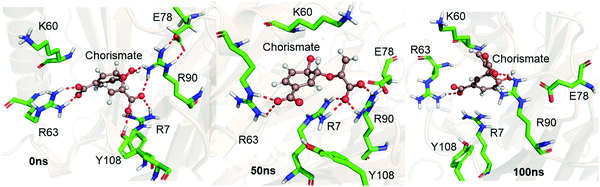

Fig. 1 Representative snapshots of the MD trajectory of the Michaelis complex in WT chorismate mutase showing the interaction of the substrate with the key residues at different timescales.

Unlike the MC, the simulation of the TSA with the WT shows a stable complex during the entire simulation. A consistent interaction is shown with R7 and Y108 during the entire simulation, as shown in Fig. 2a. The root mean square fluctuations of both complexes (MC and TSA) are shown in Fig. 2b, and clearly indicate TSA as being less flexible and hence more stable during the simulations. It is further substantiated via a comparison of the residue interaction networks for the MC and TSA, as shown in Fig. 2c, which also shows more favorable interactions relative to the MC. The variation of the H-bonds for both the MC and TSA are shown in the ESI.† Therefore, in a nutshell, chorismate mutase evolves in such a manner that the local electric field produced by the enzyme increases the entropic penalties of the TS and thus lowers the overall barrier of reactions.

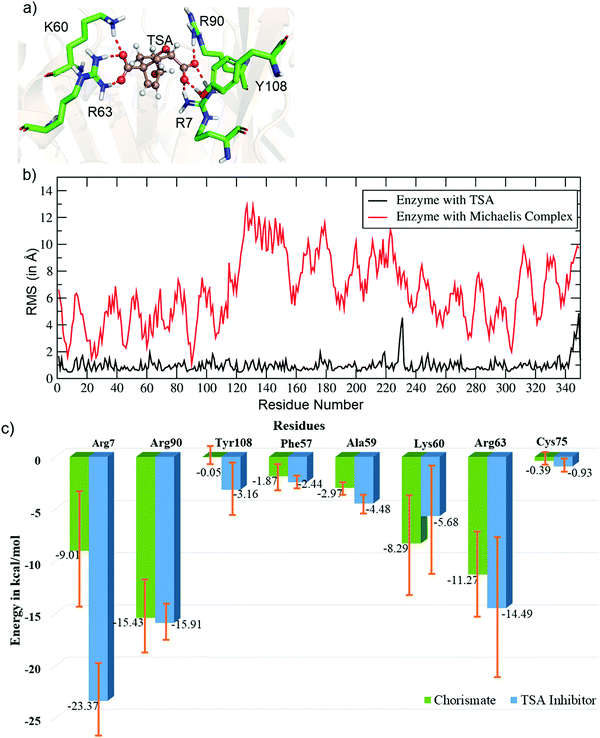Fig. 2 (a) Key residues of WT CM interacting with the TSA. (b) Plot showing the RMSF values (in Å) for the TSA and Michaelis complex in WT chorismate mutase. (c) Comparative residue interaction map between chorismate and the TSA inhibitor for the most populated trajectories. More detailed values with composed energy values and standard deviations are shown in the ESI.†

3.2. The mechanism of reaction of chorismate mutase via QM/MM calculations

So far, using MD simulation of the Michaelis complex and TSA, we have seen that the local electric field produced by the enzyme provides an entropic favor in the transition state. However, we complemented our study with QM/MM calculations and gas-phase density functional calculations to explain the role of electrostatics on the activation energy for chorismate to prephenate. Gas-phase density functional calculations show that the conversion of chorismate to prephenate is an energetically demanding process and that the energy barrier for this process (in the absence of the enzymatic system) is 32.90 kcal mol⁻¹ (Fig. 3).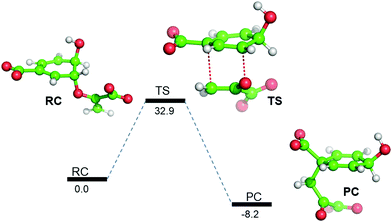

Fig. 3 B3LYP/Def2-SVP gas-phase energy profile diagram for the interconversion of chorismate to prephenate. The energies are reported in kcal mol⁻¹ relative to the reactant complex (RC).

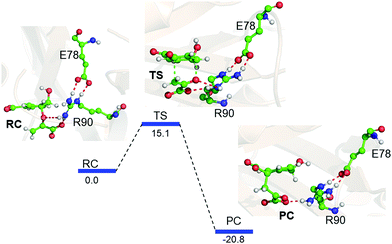
Interestingly, when we included the enzyme environment using the QM/MM calculations the barrier of the same reaction decreased by a significant amount (see Fig. 4 for the QM/MM reaction profile). The QM/MM calculations were started by considering a representative snapshot from the MD simulations and subsequent optimization of the Michaelis complex. Relaxed potential energy surface (PES) scanning was performed for the conversion of chorismate to prephenate. The energy profile shows a feasible reaction with a TS barrier of 15.1 kcal mol⁻¹ for this transformation when it occurs in the enzymatic environment. In addition, the product prephenate is more exothermic relative to the gas-phase reaction.

Fig. 4 QM/MM/B3LYP/Def2-SVP energy profile for the rearrangement of chorismate to prephenate, with its characteristic species indicated as follows: reactant complex (RC), transition state (TS) and product complex (PC). The energies (relative to the RC) are shown in kcal mol⁻¹.

It is noteworthy that none of the protein residues of CM participate in the reaction; therefore, how does the enzyme catalyze the reaction so efficiently? In order to explore the possible cause, we further quantified the LEF produced by the enzyme using the TITAN program.

3.3. Quantification of the electric field of the enzyme and its catalytic effect

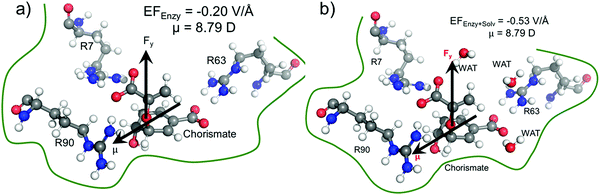
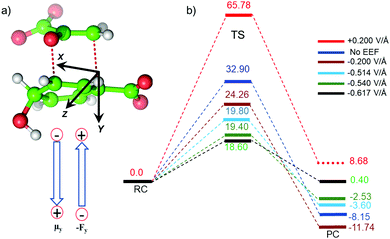
We quantified the electric field exerted by the enzyme along the C–O bond of the substrate (see Fig. 5a and b) to probe the electric-field effect. For doing so, we used the optimized structures from the QM/MM calculations as mentioned above. Our calculations show a net electric field of −0.2 V Å⁻¹ directed along of reaction centre in the C–O axis at the site in the absence of solvent molecules (the LEF of the enzyme alone) while it is −0.53 V Å⁻¹ in the presence of solvent molecules (see Fig. 5a and b).

Fig. 5 Local electric field quantification for wild-type chorismate mutase, (a) without solvent, and (b) with solvent. We used the Gaussian sign convention for the electric field and the dipole moments.

To further justify the effect of the electric field of the enzyme on the catalysis, we performed gas-phase DFT calculations in the presence of an external electric field of the same order of intensity exerted by the enzyme as calculated above. Fig. 6 shows different TS barriers for the chorismate-to-prephenate conversion for different electric fields oriented along the y-axis (the reaction axis) in the positive and negative directions. The energy profiles at different EF values clearly indicate that the electric field has a significant effect on the TS barrier.

Fig. 6 (a) Sign convention (Gaussian) used in current study, and (b) energy profiles at different external electric fields, where the values of the EEF are indicated by different colored bars. The unit of the EEF is V Å⁻¹, while energies relative to RC are in kcal mol⁻¹.

We have seen that the prephenate conversion from chorismate in the absence of any enzymatic environment (i.e., in the gas phase, cf.Fig. 3) is highly unfavorable; however, at an electric field of −0.54 V Å⁻¹, which is the EF of the enzyme, the TS barrier surprisingly reduces to ∼19.0 kcal mol⁻¹ (∼17.0 kcal mol⁻¹ on single-point calculations with a larger basis set), which is closer to the TS barrier in the enzymatic environment calculated using the QM/MM method. To be more precise, we also calculated the effect of the EEF on the dipole moments (see ESI†). It is quite apparent that the dipole moments of the TS along the y-axis are positively signed, and further increase towards the positive scale on increasing the magnitude of the EEF along the negative direction of the y-axis. Hence, we can speculate that the application of the EEF polarizes the TS in a favourable manner and in turn decreases the TS barrier. The effect of the EEF on the dipole and hence on the activation energy can also be validated by applying the EEF in the opposite direction. As can be seen in Fig. 6b, the reversal of the direction of the external electric field with a magnitude 0.2 V Å⁻¹ increased the TS barrier to 65.78 kcal mol⁻¹, which is almost double that observed in the absence of the EEF. The TS dipole moment due to reversal of the EEF is also decreased to 13.03 Debye, thereby, validating the effect of TS polarization of the reaction barrier. These results from the application of an external electric field that mimics the LEF of the enzymatic environment indicate that the catalysis observed by the Bacillus subtilis chorismate mutase enzyme is electric-field-induced catalysis, i.e., it uses its local electric field (LEF) to enhance the reaction a millionfold. Furthermore, these results provide qualitative agreement with the fact that the protein environment of the enzyme produces a favorable electric field for the Claisen rearrangement reaction despite there being no covalent participation of protein residues.

3.4. Local electric field: a descriptor for catalysis

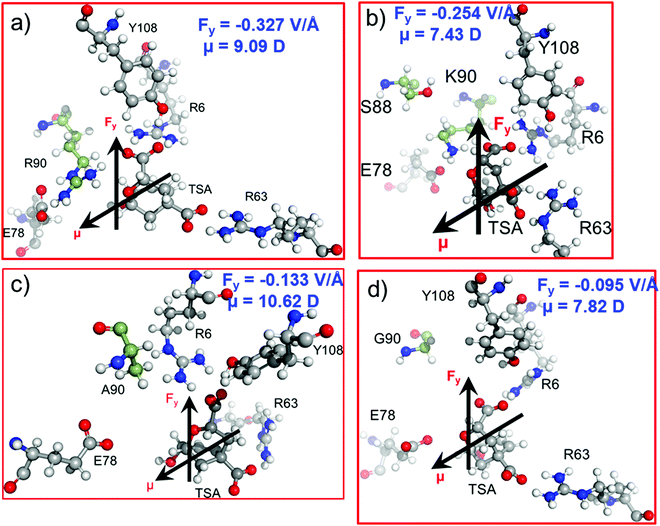
In the previous sections, we have seen that the enzymatic activity of wild-type CM is dependent on the local electric field produced by the enzyme. So, could we use the local electric field as a descriptor for the enzymatic activity? We, therefore, focused to construe a correlation between the local electric field of the chorismate mutase mutants with their enzymatic activities. For this, initially we performed MD simulations of the R90G, R90A and R90K/C88S mutant complexes with the TSA. The local electric field of the enzyme was calculated at regular intervals of 5 ns projected along the ether-like C–O bond vector of the TSA, and we reported the averaged value. The choice of these systems was based solely on the fact that the reactivity of these mutants is already known using experimental site-directed mutagenesis.⁴³ The local electric field for the WT enzyme is found to be −0.327 V Å⁻¹ (Fig. 7a), and it is opposite to the C–O bond dipole vector, illustrating that this EF could help the C–O bond to become polarized and favor the reaction, which is in accord with the QM/MM calculations.

Fig. 7 Dipole moment μ (in Debye) and LEF (F_y in V Å⁻¹) values along the C–O bond axis of the TSA for (a) WT CM and the (b) R90K/C88S, (c) R90A and (d) R90G mutants. The Gaussian convention is used to describe the direction of the EF and dipole moments.

As shown in Fig. 1 and 2a, Arg90 forms a close and stable contact with the substrate and, therefore, we anticipated the loss of the LEF due to the mutation of R90 with either glycine or alanine.

In addition, the LEF values for the R90A and R90G mutants were found to be −0.133 V Å⁻¹ and −0.095 V Å⁻¹, respectively, which are approximately three times lower in magnitude than that of the wild-type enzyme (Fig. 7c and d). Interestingly, the experimental site-directed mutagenesis for these mutations shows that the catalytic rates of mutants decrease by more than 5 orders of magnitude, which is qualitatively in good agreement with the calculated LEFs of the mutant complexes. To further confirm the role of the electric field on the catalysis, R90 was strategically mutated to the charged residue K90. We also quantified the LEF for this R90K/C88S mutant and found that the electric field increases significantly to −0.254 V Å⁻¹, which is close to that of the WT complex (Fig. 7b). Interestingly, the experimental determination of the catalytic rate shows that the lost activities due to R90G and R90A mutations were restored. This clearly indicates that quantification of the relative local electric field along the reaction axis can be used as a descriptor to qualify the relative reactivities of similar enzymes. However, a thorough benchmarking with different families of enzymes and their mutants may be needed for a generalized scope.

4. Conclusion

In the present study, we have comprehensively studied the effect of local and external electric fields on the catalytic activity of chorismate mutase using MD simulations, hybrid QM/MM calculations, EF quantification and the application of an EEF. The MD simulations of the Michaelis complex (MC) and the transition state analog (TSA) show that the LEF of the CM enzyme stabilizes the TSA, and it evolves in such a way that the EF produced by the enzyme stabilizes the TS to reduce the activation energy. DFT calculations in gas phase and enzyme environment confirm that the electric field produced by the enzyme polarizes the transition state, while interacting with its dipole moment, which further reduces the TS barrier of the reaction. The change in the dipole moment of the TS demonstrates the electric-field-induced catalysis in chorismate mutase. Quantification of the EFs for WT CM and its mutants along the reactive axis shows a direct correlation between the enzymatic electric field and the reactivity of the enzymes (Fig. S1, ESI†); therefore, the EF along the reactive axis could be used as a descriptor for the enzymatic activity. The LEF as a descriptor for the enzymatic activity has computational advantages over other activation energies as the quantification of the EF is very simple and easy. However, this perception is limited to CM and its different variants; therefore, we believe that a rigorous benchmarking of a correlation between the EF along the reaction axis and the enzymatic activity using different enzyme–substrates is needed in future studies.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

K. D. D. acknowledges the Department of Biotechnology, Govt. of India for Ramalingaswami Re-entry research grant (BT/RLF/Re-entry/10/2017).

References

1. S. Cocco, C. Feinauer, M. Figliuzzi, R. Monasson and M. Weigt, Rep. Prog. Phys., 2018, 81, 032601.
2. K. Davidsen, B. J. Olson, W. S. DeWitt III, J. Feng, E. Harkins, P. Bradley and F. A. Matsen IV, eLife, 2019, 8, e46935.
3. D. Repecka, V. Jauniskis, L. Karplus, E. Rembeza, J. Zrimec, S. Poviloniene, I. Rokaitis, A. Laurynenas, W. Abuajwa, O. Savolainen, R. Meskeys, M. K. M. Engqvist and A. Zelezniak, Nat. Mach. Intell., 2021, 3, 324–333.
4. K. A. Reynolds, W. P. Russ, M. Socolich and R. Ranganathan, Methods Enzymol., 2013, 523, 213–235.
5. A. C. Anderson, Chem. Biol., 2003, 10, 787–797.
6. R. Otten, R. A. P. Pádua, H. A. Bunzel, V. Nguyen, W. Pitsawong, M. Patterson, S. Sui, S. L. Perry, A. E. Cohen, D. Hilvert and D. Kern, Science, 2020, 370, 1442–1446.
7. M. T. Reetz, Acc. Chem. Res., 2019, 52, 336–344.
8. F. H. Arnold, Acc. Chem. Res., 1998, 31, 125–131.
9. F. H. Arnold, Angew. Chem., Int. Ed., 2019, 58, 14420–14426.
10. M. T. Reetz, J. Am. Chem. Soc., 2013, 135, 12480–12496.
11. O. Keskin, A. Gursoy, B. Ma and R. Nussinov, Chem. Rev., 2008, 108, 1225–1244.
12. P. Tuffery and P. Derreumax, J. R. Soc., Interface, 2012, 9, 20–33.
13. K. D. Dubey, R. K. Tiwari and R. P. Ojha, Curr. Comput.-Aided Drug Des., 2013, 9, 518–531.
14. R. E. Babine and S. L. Bender, Chem. Rev., 1997, 97, 1359–1472.
15. S. Strajbl, J. Florian and A. Warshel, J. Am. Chem. Soc., 2000, 122, 5354–5366.
16. J. Villa and A. Warshel, J. Phys. Chem. B, 2001, 105, 7887–7907.
17. A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. M. Olsson, Chem. Rev., 2006, 106, 3210–3235.
18. J. A. McCammon, B. R. Gelin and M. Karplus, Nature, 1977, 267, 585–590.
19. M. Karplus and J. A. McCammon, Nat. Struct. Biol., 2002, 9, 646–652.
20. K. D. Dubey and R. P. Ojha, in Nanoscience and Computational Chemistry, ed. A. G. Mercader, E. A. Castro and A. K. Haghi, CRC Press, Taylor and Francis Group, New Jersey, 1st edn, 2013, ch. 11, pp. 371–399.
21. H. M. Senn and W. Thiel, Angew. Chem., Int. Ed., 2009, 48, 1198–1229.
22. H. Hu, M. Elstner and J. Hermans, Proteins: Struct., Funct., Genet., 2003, 50, 451–463.
23. H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185–199.
24. U. Ryde, Curr. Opin. Chem. Biol., 2003, 7, 136–142.
25. T. Stuyver, J. Huang, D. Mallick, D. Danovich and S. Shaik, J. Comput. Chem., 2020, 41, 74–82.
26. T. Stuyver, J. Joy, D. Danovich and S. Shaik, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 6, pp. 195–224.
27. S. Shaik and T. Stuyver, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 1, pp.1–11.
28. S. Shaik, D. Danovich, K. D. Dubey and T. Stuyver, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 2, pp. 12–70.
29. M. T. Blyth and M. L. Coote, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 4, pp. 119–146.
30. S. Sowlati-Hashjin, N. Karttunen and C. F. Matta, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 7, pp. 225–262.
31. N. J. English, J. Mol. Liq., 2021, 342, 116949.
32. N. J. English, in Effects of Electric Fields on Structure and Reactivity: New Horizons in Chemistry, ed. S. Shaik and T. Stuyver, Royal Society of Chemistry, London, 1st edn, 2021, ch. 8, pp. 225–262.
33. S. Shaik, D. Mandal and R. Ramanan, Nat. Chem., 2016, 8, 1091–1098.
34. S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Chem. Soc. Rev., 2018, 47, 5125–5145.
35. S. Ciampi, N. Darwish, H. M. Aitken, I. Diez-Pérez and M. L. Coote, Chem. Soc. Rev., 2018, 47, 5146–5164.
36. P. R. Andrews, G. D. Smith and I. G. Young, Biochemistry, 1973, 12, 3492–3498.
37. S. D. Copley and J. R. Knowles, J. Am. Chem. Soc., 1987, 109, 5008–5013.
38. P. Kast, M. Asif-Ullah and D. Hilvert, Tetrahedron Lett., 1996, 37, 2691–2694.
39. P. Kast, M. Asif-Ullah, M. N. Jiang and D. Hilvert, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 5043–5048.
40. S. Martí, J. Andrés, V. Moliner, E. Silla, I. Tuñón, J. Bertrán and M. J. Field, J. Am. Chem. Soc., 2001, 123, 1709–1712.
41. S. Martí, J. Andrés, V. Moliner, E. Silla, I. Tuñón and J. Bertrán, Chem. – Eur. J., 2003, 9, 984–991.
42. S. Martí, J. Andrés, V. Moliner, E. Silla, I. Tuñón and J. Bertrán, J. Am. Chem. Soc., 2004, 126, 311–319.
43. A. Mandal and D. Hilvert, J. Am. Chem. Soc., 2003, 125, 5598–5599.
44. A. Aemissegger, B. Jaun and D. Hilvert, J. Org. Chem., 2002, 67, 6725–6730.
45. Y. M. Chook, H. Ke and W. N. Lipscomb, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 8600–8603.
46. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
47. O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461.
48. J. A. Izaguirre, D. P. Catarello, J. M. Wozniak and R. D. Skeel, J. Chem. Phys., 2001, 114, 2090–2098.
49. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
50. J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
51. T. Darden, D. York and L. Pederson, J. Chem. Phys., 1993, 98, 10089–10092.
52. R. S. Ferrer, A. W. Götz, D. Poole, S. L. Grand and R. C. Walker, J. Chem. Theory Comput., 2013, 9, 3878–3888.
53. P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28.
54. S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110.
55. R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169.
56. W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141.
57. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
58. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
59. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
60. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
61. H. Gohlke and D. A. Case, J. Comput. Chem., 2003, 25, 238–250.
62. F. Fogolari, A. Brigo and H. Molinari, Biophys. J., 2003, 85, 159–166.
63. P. Grochowaski and J. Trylska, Biopolymers, 2007, 89, 93–113.
64. V. Tsui and D. A. Case, Biopolymers, 2001, 56, 271–291.
65. K. D. Dubey, A. K. Chaubey and R. P. Ojha, Biochim. Biophys. Acta, Proteins Proteomics, 2013, 1834, 53–64.
66. A. K. Chaubey, K. D. Dubey and R. P. Ojha, J. Comput.-Aided Mol. Des., 2012, 26, 289–299.
67. K. D. Dubey, G. Tiwari and R. P. Ojha, J. Mol. Model., 2017, 23, 102.
68. S. Yadav, V. Pandey, R. K. Tiwari, R. P. Ojha and K. D. Dubey, Molecules, 2021, 26, 239.

---

Footnote

† Electronic supplementary information (ESI) available: Energy contributions calculated using MMPBSA calculations, dipole moments, barrier vs. EEF graph, hydrogen-bond analysis and energy values for different variants and coordinates for the QM and QM/MM-optimized geometry of RC, TS and PC. See DOI: 10.1039/d1cp03978d

---