DOI:
10.1039/D2YA00114D
(Paper)
Energy Adv., 2022,
1, 900-907
Predictive energetic tuning of quinoid O-nucleophiles for the electrochemical capture of carbon dioxide†
Received
19th May 2022
, Accepted 26th September 2022
First published on 18th October 2022
Abstract
The need for robust, scalable methods for the capture and storage of carbon dioxide is increasingly pressing. Electric power-based carbon capture methods have drawn attention as a promising strategy due to their potential to couple to renewable energy sources. Materials for the capture of CO2 from air need to overcome the challenges of parasitic reactivity with oxygen, selective removal of CO2 at 415 ppm, and long-term durability in air. Quinones and their reduced forms are a promising family of such sorbents. However, the design of robust quinone sorbents has been limited, and no systematic study exists that unifies the relationship between reduction potential, binding free energy and the effect of CO2 concentration on the average number of CO2 molecules captured. Our work addresses this knowledge gap through a synergistic computational and experimental study of a family of electrochemically generated quinoid molecular sorbents for CO2 capture with tunable redox chemistries. Our findings indicate that while quinones with reduction potentials positive of oxygen reduction exist, the O-nucleophiles generated at these potentials are weak CO2 binders. Using microkinetic analysis to examine binding speciation, we identify sorbent candidates that bind one CO2 molecule within a narrow potential window positive of oxygen reduction. This behavior is calculated to occur at CO2 concentrations relevant to direct air capture. Additionally, while electron-rich quinones are found to generally bind two CO2 units per quinone dianion with little variation across CO2 concentrations relevant to carbon capture, weaker quinones generally exhibit lower stoichiometries and are more sensitive to CO2 concentration. Furthermore, we establish a linear correlation between the second reduction potential of a quinone and the free energy of binding CO2 to the quinone dianion. This correlation has important predictive power, as it allows new molecular materials of the quinoid family to be assessed with simple electrochemical measurements. However, based on our findings, such analyses must be punctuated by careful considerations of reaction stoichiometry and operating concentration ranges.
Introduction
Accumulation of CO2 in the atmosphere has sparked an urgency in the development of methods for the capture and storage of CO2.1,2 While amine or aqueous sorbents of CO2 are common, they require release steps with thermal swings and are more often used near concentrated emission sources.3,4 These capture mechanisms are commonly not compatible with capture from a dilute source such as air and cannot be deployed in a dispersed, decentralized fashion.5
An analysis of CO2 binding energetics for direct air capture reveals that sorbents for the capture of CO2 do not need to be particularly strong CO2 binders for applications that involve “skimming” small amounts of CO2 from a stream rather than seeking complete CO2 removal.6
Carbon capture using electrochemically generated species has attracted considerable attention in recent years due to its ability to couple with renewable power sources and the modularity of electrochemical devices.3 Early work by Noble and coworkers7 demonstrated that quinoid molecular sorbents can be used to harvest CO2 from dilute streams in nitrogen. More recently, Hatton and coworkers have demonstrated faradaic electro-swing in an organic battery-like device in which quinones tethered to the electrodes are able to capture CO2 when reduced and release it when oxidized.8 In a related recent report, several quinones were categorized as strong vs. medium vs. weak binders of CO2.9
In recent work from our group,10 we identified an empirical linear correlation between the reduction potential necessary for the generation of a nucleophile and the nucleophile's ability to bind CO2. Herein, we seek to extend this analysis to quinones due to their high importance in the field of reactive carbon capture. The equation of best fit from such a correlation can, in principle, be used to screen new quinoid molecules and to quickly estimate the free energy of binding of the electrogenerated nucleophile to CO2. This can be achieved without CO2 experiments and has a strong predictive value. We chose a subset of commercially available quinones that include electron poor quinones such as dichlorodicyanoquinone (DDQ), chloranil (4ClQ), 1,4-Dichloroquinone (2ClQ), and 1,2-dichloronaphthoquinone (2ClNQ). We hypothesized that a shift in the quinones’ reduction potentials to potentials more positive than the reduction of oxygen would render sorbent systems impervious to O2 degradation. Known strong binders such as reduced forms of benzoquinone (BQ), 1,5-dimethylbenzoquinone (2MeQ), and naphthoquinone (NQ) were also included as a comparison across a broader range of potentials. Cyclic voltammograms of 1 mM solutions of these quinones in acetonitrile at glassy carbon working electrodes are shown in Fig. 1. The quinones all exhibit the same reactivity pattern with two successive 1e− reduction waves. Among the quinones screened, DDQ is most easily reduced (has the most positive reduction potential) and NQ is the most difficult to reduce (has the most negative reduction potential). Because species generated at more negative reduction potentials are more nucleophilic and therefore stronger CO2 binders,11,12 we expect the quinoid dianion nucleophiles generated from NQ to be the strongest binder of CO2 in the series. The reduction potentials for the quinones listed above are provided in Table 1.
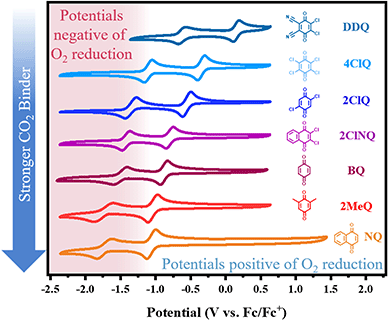 |
| | Fig. 1 Cyclic voltammetry of 1 mM solutions of quinone in MeCN with NBu4PF6 under Ar at 100 mV s−1. Working electrode: glassy carbon; counter electrode: Pt wire; reference electrode: single-junction Ag electrode referenced externally vs. Fc/Fc+. | |
Table 1 Experimental and DFT data for the family of quinones considered in this study
| Entry |
Stoichiometry Q2−/CO2a |
DFT ΔGbindb |
Experimental ΔGbindbc |
Experimental uncertainty in ΔGbindbd |
DFT Ered1e (V) |
DFT Ered2e (V) |
Experimental Ered1e (V) |
Experimental Ered2e (V) |
|
Stoichiometry identified using DFT calculations.
ΔG values in kcal mol−1.
The experimental ΔGbind was obtained using the stoichiometry identified by DFT and corroborated through function fitting.
Experimental uncertainty in ΔGbind was propagated from the uncertainty in K from the function fits.
vs. Fc/Fc+.
Experiments suggest that the there is no measurable binding between the DDQ2− dianion and CO2.
The calculated binding energy for the DDQ2− is reported for the first binding.
|
| DDQ |
0f |
3.1g |
N/A |
N/A |
0.31 |
−0.95 |
0.12 |
−0.69 |
| 4ClQ |
1 |
−4.90 |
−3.88 |
0.10 |
−0.27 |
−1.48 |
−0.40 |
−1.18 |
| 2ClQ |
2 |
−8.90 |
−9.42 |
0.15 |
−0.48 |
−1.76 |
−0.62 |
−1.43 |
| 2ClNQ |
1 |
−8.80 |
−5.00 |
0.25 |
−0.8 |
−1.91 |
−0.84 |
−1.49 |
| BQ |
2 |
−20.90 |
−12.53 |
0.22 |
−0.83 |
−2.16 |
−0.93 |
−1.74 |
| 2MeQ |
2 |
−22.80 |
−13.75 |
0.23 |
−1 |
−2.34 |
−1.10 |
−1.94 |
| NQ |
2 |
−16.70 |
−12.28 |
0.38 |
−1.09 |
−2.28 |
−1.15 |
−1.82 |
With this potential ranking in hand, we proceeded to measure and quantify the free energy of CO2 binding to establish the desired correlation. At the same time, we aimed to identify differences in reaction stoichiometry across the series, as this is an underexplored, yet critical topic. The goal of this work is to deliver a predictive tool for the estimation of CO2 binding energies to electrochemically generated quinoid O-nucleophiles while carefully considering reaction stoichiometry.
Experimental determination of binding free energies
The strength of binding of an electroactive analyte to another species in solution can be determined electrochemically by monitoring the shift in potential of the corresponding electrochemical feature by CV. Similar analyses have been performed previously for association of reduced quinone species with ions in solution.11,12 Creutz and coworkers used this analysis in their assessment of binding energies in reactions of CO2 and metal centers.13 In a related study, DuBois estimated binding constants to CO2 for a small subset of reduced quinones using electroanalytical methods coupled to UV-Vis analysis and the Benesi–Hildebrand method.14 Previous work by Nagaoka has also used similar methods to investigate the binding stoichiometry of weak binders.15
Electrochemical experiments for this study were conducted in acetonitrile (MeCN). MeCN was selected as a model polar aprotic solvent due to its minimal evaporation over the course of the experiment, high electrolyte solubility and thus high solution conductivity, and high CO2 solubility. Protic solvents or additives are known to significantly affect the electrochemical responses of quinones due to hydrogen bonding or coupled protonation steps;16 avoiding the use of protic solvents thus enables the evaluation of isolated reduction and CO2 binding steps relevant to our analysis without concern of accompanying protonation steps. Although aqueous systems offer the advantages of lower volatility, low cost, and non-flammability, CO2 solubility in neutral or acidic water is limited and suffers from the additional complication of carbonic acid equilibria. MeCN was hence selected as the optimal solvent for the present study, although recent work by Barlow and Yang has demonstrated the promising benefit of hydrogen-bonding stabilization by protic solvents of relevant quinone dianion and CO2 adduct species.17
First, we define the reactions leading to the binding of CO2 by the reduced quinone, given as follows:
| | 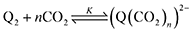 | (3) |
A generic quinone, Q, first undergoes a single-electron reduction to generate the semiquinone radical anion, Q˙− (eqn (1)). The radical anion then undergoes reduction to the dianion, Q2− (eqn (2)), which then binds n CO2 molecules, as represented in eqn (3). The two reversible single-electron reduction features associated with eqn (1) and (2) are well known for quinones in aprotic solvents in the absence of electrophiles such as CO2.12,18,19 Furthermore, we posit that CO2 binding (eqn (3)) occurs primarily after the second reduction due to the observed lack of a shift in the potential of the first reduction for all quinones studied herein. Although previous studies have found evidence for binding of CO2 to the semiquinone radical anion,20 the contribution of these species to CO2 binding is negligible relative to that of the dianion, and thus is not expected to significantly affect the calculated values for the free energy of CO2 binding. Due to spectrochemical evidence for stepwise CO2 binding to reduced quinones species, we propose that stepwise addition is most likely.14 As such, experimental K values describe a single CO2 addition reaction (in the case of n = 1) or the sum of two stepwise CO2 additions that sum to eqn (3) (in the case of n = 2).
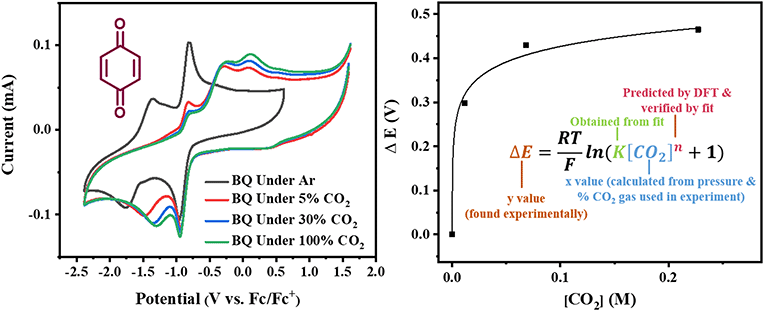
Next, we consider the equilibria and Nernstian relationships governing the reactions and the electrochemical potentials at which they are observed. The half-wave potential for a given redox couple is given by the Nernst equation, eqn (4):
| | 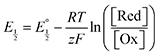 | (4) |
Here  is the observed half-wave potential,
is the observed half-wave potential, 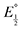 is the standard half-wave potential, R is the gas constant, T is the temperature in Kelvin, z is the number of electrons transferred in the redox process, F is the Faraday constant, [Red] is the concentration of the reduced species, and [Ox] is the concentration of the oxidized species.
is the standard half-wave potential, R is the gas constant, T is the temperature in Kelvin, z is the number of electrons transferred in the redox process, F is the Faraday constant, [Red] is the concentration of the reduced species, and [Ox] is the concentration of the oxidized species.
Because CO2 binding is both observed electrochemically and predicted by DFT to occur after the second reduction (described by eqn (2), the number of electrons transferred is one (i.e. z = 1). Additionally, the reduced species is Q2−(i.e. [Red] = [Q2−]) and the oxidized species is Q˙− (i.e. [Ox] = [Q˙−]). As Q2− binds CO2, the ratio [Red]/[Ox] inside the logarithmic term of eqn (4) decreases. Thus, if the reaction in eqn (3) described by equilibrium constant K occurs sufficiently rapidly for the timescale of the CV, we expect to see a shift in half-wave potential 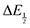 upon introduction of CO2 that increases in magnitude with stronger binding to CO2. This shift in potential is described by eqn (5):
upon introduction of CO2 that increases in magnitude with stronger binding to CO2. This shift in potential is described by eqn (5):
| | 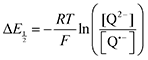 | (5) |
The relationships between the concentrations of the oxidized and reduced species are described by eqn (6)–(8). At equilibrium,
| | 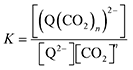 | (6) |
and therefore,
| | | [(Q(CO2)n)2−] = K[Q2−][CO2]n. | (7) |
Additionally, at the half-wave potential, the starting oxidized species is half-converted, and so
| | | [Q˙−] = [Q2−] + [(Q(CO2)n)2−]. | (8) |
If the coupled chemical step reaches equilibrium on the timescale of the CV, by combining eqn (7) and (8), we find that
| | | [Q˙−] = (K[CO2]n + 1)[Q2−]. | (9) |
Substituting
eqn (9) into
eqn (5) and rearranging, we obtain
| | 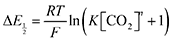 | (10) |
With
eqn (10) in hand, values for
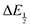
and [CO
2] were calculated for each quinone for CVs taken under 5%, 30%, and 100% CO
2 (
Fig. 2). Dissolved CO
2 concentrations were calculated using a Henry's Law method and the local barometric pressure at the time of data collection (see ESI
† for details).
21–23
 |
| | Fig. 2 Left: Cyclic voltammograms of benzoquinone (BQ) under Ar, 5% CO2, 30% CO2 and 100% CO2 taken with a scan rate of 1000 mV s−1. Right: Estimation of CO2 binding thermodynamics from plots of potential shifts ΔE vs. CO2 concentration [CO2] through the electrochemical titration of CO2 and function fitting of eqn (10). | |
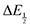 for each data point was obtained by taking the difference between the half-wave potential for the second quinone reduction under Ar and the corresponding value under CO2. Because the quinone reductions in the presence of CO2 are not electrochemically reversible, the typical method of determining
for each data point was obtained by taking the difference between the half-wave potential for the second quinone reduction under Ar and the corresponding value under CO2. Because the quinone reductions in the presence of CO2 are not electrochemically reversible, the typical method of determining 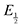 (namely, averaging the potentials at which the peak cathodic and anodic currents occur for the feature) is not applicable. Instead, the inflection point of the feature was taken as an approximate
(namely, averaging the potentials at which the peak cathodic and anodic currents occur for the feature) is not applicable. Instead, the inflection point of the feature was taken as an approximate 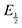 by finding the zero-point of the smoothed second derivative of the curve, as the inflection point has been previously demonstrated to be a good approximation of
by finding the zero-point of the smoothed second derivative of the curve, as the inflection point has been previously demonstrated to be a good approximation of 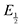 .24
.24
For quinones with extremely large K values for CO2 binding (NQ, BQ, and 2MeQ), the peak separation between the first and second reduction features in the CVs becomes minimal. The merging of the two redox waves in the presence of CO2 renders the inflection point of the second wave difficult to obtain. In these cases, the potential shift for the peak of the feature ΔEp is taken as an approximation of 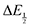 . Therefore, the potential values at which the peak current was observed under Ar and under CO2 were compared to obtain the potential difference. This approximation
. Therefore, the potential values at which the peak current was observed under Ar and under CO2 were compared to obtain the potential difference. This approximation 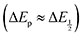 was tested and found to be reliable for quinones for which both ΔEp and
was tested and found to be reliable for quinones for which both ΔEp and 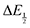 values were readily obtainable. Because separation of the reduction features requires a faster scan rate, these three quinones were given less time to equilibrate with their respective CO2 adducts over the time course of the CV. Therefore, the K values obtained for these three quinones should be taken as an inherent underestimate (whereas the obtained ΔG is an overestimate, i.e. less negative than the true value).
values were readily obtainable. Because separation of the reduction features requires a faster scan rate, these three quinones were given less time to equilibrate with their respective CO2 adducts over the time course of the CV. Therefore, the K values obtained for these three quinones should be taken as an inherent underestimate (whereas the obtained ΔG is an overestimate, i.e. less negative than the true value).
Once values for [CO2] and 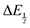 (or ΔEp) were obtained for each data point, a plot of [CO2] vs.
(or ΔEp) were obtained for each data point, a plot of [CO2] vs.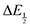 was constructed for each quinone. A user-defined fit function in Origin 2019b was used to determine a best-fit curve with free parameter K based upon eqn (10). The value of n in this equation was defined for each quinone on the basis of DFT results for the favorability of the first and second CO2 binding events. In the case of quinones with ambiguous DFT binding free energies, n values were determined by comparison of experimental fits with n = 1 and n = 2. Finally, with K values determined for each quinone, the free energy of CO2 binding, ΔGbind, was calculated using the well-known relationship given by eqn (11).
was constructed for each quinone. A user-defined fit function in Origin 2019b was used to determine a best-fit curve with free parameter K based upon eqn (10). The value of n in this equation was defined for each quinone on the basis of DFT results for the favorability of the first and second CO2 binding events. In the case of quinones with ambiguous DFT binding free energies, n values were determined by comparison of experimental fits with n = 1 and n = 2. Finally, with K values determined for each quinone, the free energy of CO2 binding, ΔGbind, was calculated using the well-known relationship given by eqn (11).
| | ΔGbind = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K) ln(K) | (11) |
Data obtained from experiment was compared with DFT-computed results and is summarized in
Table 1.
Results and discussion
The doubly reduced forms of 2MeQ, NQ and BQ, the three electron-rich quinones in the list, bind CO2 strongly. They were all found to bind two CO2 units, consistent with literature precedent.25 Not only are they strong binders of CO2, but the kinetics of the process are predicted by DFT to be fast with barriers of only 2.4, 4.4, and 5.6 kcal mol−1, respectively, for the first CO2 binding (Table 2). The second CO2 binding event is similarly rapid for all three quinones, with barriers of 3.2, 6.1, and 5.1 kcal mol−1, respectively. In fact, the binding of these quinones is so strong and rapid that in order to observe two separate reduction features by CV, scan rates of 300 to 1000 mV s−1 were required. The systematic underestimate of binding strength is corroborated by the DFT-computed values of ΔGbind, which are more negative than the experimental values by a larger margin than that of the electron-poor quinones.
Table 2 DFT-computed thermodynamic and kinetic data obtained using the MN15/6-311+G(d,p) level of theory coupled with the SMD solvation model to account for acetonitrile solvent effects. ΔGtotal is the free energy of binding the first and second CO2 molecules. Binding and Release ΔG‡ are the activation free energies for the forward and reverse reactions, respectively, as depicted in Scheme 1. All energies are reported in kcal mol−1
| Molecule |
ΔGbind |
Binding ΔG‡ |
Release ΔG‡ |
| 1st CO2 |
2nd CO2 |
ΔGtotal |
1st CO2 |
2nd CO2 |
1st CO2 |
2nd CO2 |
| DDQ |
3.1 |
11.3 |
14.4 |
7.8 |
12.8 |
4.7 |
1.5 |
| 4ClQ |
−4.9 |
4.5 |
−0.5 |
5.1 |
8.3 |
10.0 |
3.8 |
| 2ClQ |
−9.8 |
0.9 |
−8.9 |
4.1 |
6.8 |
13.9 |
5.9 |
| 2ClNQ |
−8.8 |
1.8 |
−7.0 |
4.9 |
8.2 |
13.7 |
6.3 |
| BQ |
−15.1 |
−5.8 |
−20.9 |
5.6 |
5.1 |
20.7 |
10.9 |
| 2MeQ |
−16.8 |
−5.9 |
−22.8 |
2.4 |
3.2 |
19.3 |
9.1 |
| NQ |
−13.7 |
−2.9 |
−16.7 |
4.4 |
6.1 |
18.2 |
9.0 |
For the electron-poor quinones in the series, 2ClNQ, 2ClQ, and 4ClQ, the calculated free energies of binding are in close agreement with the experimental values. A peculiar observation about 2ClQ is that although it falls in the electron-poor category, it binds two equivalents of CO2. This observation is corroborated experimentally, with fit functions utilizing two equivalents of CO2 (n = 2) yielding better fit results (Fig. S2.4 and S2.5, ESI†). The final electron-poor quinone, DDQ, was found experimentally to exhibit minimal binding to CO2, without observable shift in Ered2 (Fig. S2.8, ESI†), which is consistent with the unfavorable endergonic free energy predicted by DFT. Although in principle a fraction of DDQ may bind CO2 at high concentrations due to the relatively small positive value of the free energy of binding, our results indicate that binding was too weak under experimental conditions to quantify even with n = 1.
Finally, the CO2 binding behavior of 4ClQ is of particular interest. With a second reduction potential of −1.18 V vs. Fc/Fc+ in dry acetonitrile (positive of the observed reduction potential of O2 in dry acetonitrile, −1.23 V vs. Fc/Fc+),26 4ClQ is the only quinone studied which avoids O2 reduction while still exhibiting CO2 binding as predicted by DFT and observed experimentally (Table 1 and Fig. S2.6, ESI†). Although the binding free energy of 4ClQ is not as strong as that of the electron-rich quinones, this suggests that quinones with reduction potentials similar to 4ClQ may be in an optimal range for applications in which complete scrubbing of CO2 is not required. CV can be used to identify quinones of desired ΔGbind through the correlation between their second reduction potential and CO2 binding strength, as presented in Fig. 3.
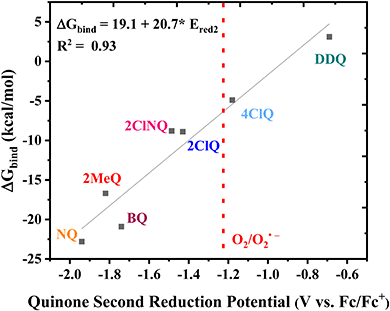 |
| | Fig. 3 Linear correlation between the DFT-calculated free energy of CO2 binding and the experimental second reduction potential of the family of quinones in Fig. 1. The dashed line indicates the approximate potential of O2 reduction in dry acetonitrile for comparison. | |
DFT and MK model
Our calculations, summarized in Table 2, indicate that 2ClQ and 2ClNQ are moderate CO2 binders, with favorable binding of 1 CO2 and thermoneutral binding of the subsequent CO2. DDQ and 4ClQ are weak binders as they have less favorable binding of the first CO2 and endergonic binding of the second CO2, accompanied by slightly larger activation free energies. Lastly, BQ, NQ and 2MeQ are predicted to be very strong binders, with sequential exergonic CO2 binding steps and small forward reaction barriers. As such, we expect them to consistently bind 2 CO2 molecules, in agreement with experiment.
Next, we built a microkinetic model based on DFT-computed thermodynamics (ΔG0bind) and kinetics (ΔG‡bind) to calculate the weighted stoichiometry of CO2 molecules per sorbent molecule. This analysis is performed by solving for equilibrium concentrations of A [Q2−], B [Q(CO2)2−], and C [(Q(CO2)2)2−], for the reactions displayed in Scheme 1 and described in eqn (12)–(20).
 |
| | Scheme 1 Overall reaction equilibrium between A, B, and C. | |
Equilibrium concentrations are obtained by solving a system of differential equations describing the rates of formation and degradation of each complex, as described by eqn (12)–(14).
| | 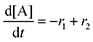 | (12) |
| | 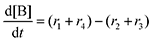 | (13) |
| | 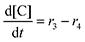 | (14) |
The forward reactions describing the binding of the 1st and 2nd CO
2 molecules are treated as bimolecular reactions. The rates
r1 and
r3, respectively, depend on the concentrations of the quinone complex as well as that of solvated CO
2:
| | 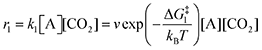 | (15) |
| | 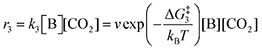 | (16) |
On the other hand, the reverse reactions describing CO
2 release are unimolecular as the reactant in this case decomposes into a dianion quinone and a solvated CO
2. Rates of CO
2 release are thus not dependent on solvated CO
2 concentrations:
| | 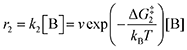 | (17) |
| | 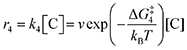 | (18) |
Finally, to maintain a mass balance, we assume the sum of concentrations of A, B and C, is always equivalent to the concentration of starting material Q
2−, which for this study is set to 0.001 M to match experimental conditions.
| | 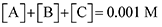 | (19) |
Section S3 of the ESI
† provides further details on this system of differential equations. Equilibrium concentrations are then analyzed using
eqn (20) to determine the weighted stoichiometry of CO
2 molecules captured at equilibrium, where the ratio
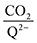
yields a value between 0 and 2.
| | 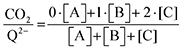 | (20) |
Fig. 4 demonstrates the ratio
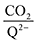
for all 7 quinones investigated at 4 varying concentrations of solvated CO
2, ranging from 10
−5 M to 0.3 M. In agreement with experiment (
Table 1), our model predicts that BQ, NQ, and 2MeQ are very strong CO
2 binders, averaging a 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 stoichiometry of CO
2 per Q
2− dianion across experimentally relevant concentrations of CO
2 (0.01 M < [CO
2] < 0.3 M). This results from sequentially exergonic CO
2 binding thermodynamics and small reaction barriers, as shown in
Table 2. The moderate binders – 2ClQ and 2ClNQ – also have a weighted
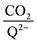
stoichiometry closer to 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
1 at high CO
2 concentrations, although the stoichiometry drops at smaller [CO
2] values. This indicates that moderate binders favor the binding of only one CO
2 molecule at lower concentrations, as expected from computed Δ
Gbind values that are exergonic for the 1st CO
2 binding step and only slightly more positive than thermoneutral for the second CO
2 binding step. 4ClQ maintains a
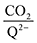
ratio of ∼1 that increases gradually as the CO
2 saturation limit is approached, as depicted in
Fig. 4d. DDQ is mostly unreactive, however higher concentrations of CO
2 push the 1st CO
2 binding step forward to some extent, resulting in a value of
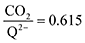
at the saturation limit.
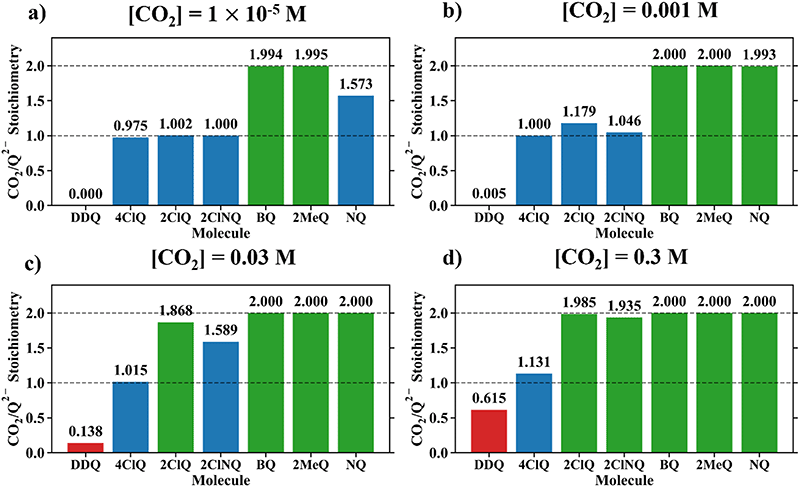 |
| | Fig. 4 CO2 stoichiometry relative to Q2− evaluated using eqn (20) at (a) [CO2] = 10−5 M, (b) [CO2] = 0.001 M, (c) [CO2] = 0.03 M, and (d) [CO2] = 0.3 M, assuming the starting concentration for [Q2−] = 0.001 M. The model is representative of the dataset obtained using the MN15/6-311+G(d,p) level of theory with acetonitrile solvation as described by the SMD implicit solvent model.27–30 0.3 M of CO2 is the saturation limit in acetonitrile.21 3 classes of binders can be specified based on this data – strong binders (Q, NQ, and 2MeQ), moderate binders (2ClNQ and 2ClQ), and weak binders (4ClQ and DDQ). Strong binders are generally insensitive to [CO2] across 5 orders of magnitude, as they consistently bind 2 CO2 molecules. Moderate and weak binders are sensitive to CO2 concentrations, as moderate binders produce a stoichiometry range of 1 to 2 and weaker binders a stoichiometry range of 0 to 1 across the examined range of CO2 concentrations. | |
To further illustrate the dependence of the calculated weighted stoichiometry 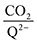 on CO2 concentrations, we plot
on CO2 concentrations, we plot 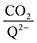 as a function of log[CO2], as shown in Fig. 5. This enables the analysis of the dependence [CO2] over the span of 8 orders of magnitude for all 7 quinones in our study. We find that the weighted stoichiometry of strong binders falls for [CO2] < 10−5 M. This suggests that their efficiency as sorbents is independent of CO2 concentration at atmospheric concentrations (415 ppm) or higher. The moderate binders – 2ClQ and 2ClNQ – are strongly dependent on CO2 concentration at high values ([CO2] > 10−4 M), whereas at lower CO2 concentrations they exhibit a
as a function of log[CO2], as shown in Fig. 5. This enables the analysis of the dependence [CO2] over the span of 8 orders of magnitude for all 7 quinones in our study. We find that the weighted stoichiometry of strong binders falls for [CO2] < 10−5 M. This suggests that their efficiency as sorbents is independent of CO2 concentration at atmospheric concentrations (415 ppm) or higher. The moderate binders – 2ClQ and 2ClNQ – are strongly dependent on CO2 concentration at high values ([CO2] > 10−4 M), whereas at lower CO2 concentrations they exhibit a 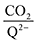 stoichiometry value of 1. As such, unlike the strong binders, the carbon capture efficiency of the moderate binder quinones benefit from higher CO2 concentrations. 4ClQ appears to be only dependent on [CO2] at extremely low or extremely high concentrations. DDQ is generally unreactive unless the solvent is saturated with CO2.
stoichiometry value of 1. As such, unlike the strong binders, the carbon capture efficiency of the moderate binder quinones benefit from higher CO2 concentrations. 4ClQ appears to be only dependent on [CO2] at extremely low or extremely high concentrations. DDQ is generally unreactive unless the solvent is saturated with CO2.
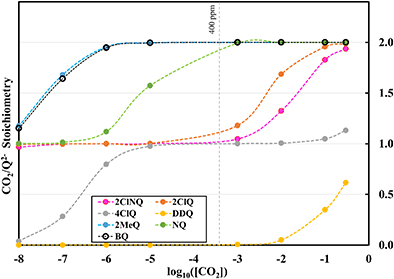 |
| | Fig. 5 CO2 stoichiometry relative to Q2− as a function of CO2 concentration in logarithmic scale. Stoichiometry values are obtained by solving the system of differential equations (eqn (12)–(20)) at varying CO2 concentrations. CO2 concentrations in our analyses span 8 orders of magnitude, ranging from 10−8 M to 0.3 M. The vertical dashed grey line represents atmospheric concentration of ∼400 ppm. | |
Conclusions
As previously observed for a family of C-nucleophiles,10 we now report a linear correlation between the potential required to generate quinone dianions and their free energy of CO2 binding. Unlike the relatively simple electrogenerated C-nucleophiles of our previous report, the doubly reduced quinones exhibit variable stoichiometric coefficients when binding to CO2. This observation has direct implications for the development of O2-impervious quinone molecular sorbents, where maximal CO2 loading is sought. Our findings suggest that CO2-reactive quinone dianions can in fact be generated at potentials more positive than oxygen reduction. However, in some cases, such dianions have a binding stoichiometry of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rather than the previously observed stoichiometry CO2/Q2− of 2
1 rather than the previously observed stoichiometry CO2/Q2− of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for well-studied, electron-rich quinones such as NQ. This experimental observation is corroborated by DFT-computed thermodynamics and kinetics. The calculations inform a microkinetic model and validate the variability in quinone behavior at different concentrations of CO2. Moderate and weak CO2 binders exhibit CO2/Q2− stoichiometries that vary between 0 and 2, depending on CO2 concentration, whereas strong binders are not as sensitive to CO2 concentrations and maintain a CO2/Q2− stoichiometry of 2
1 for well-studied, electron-rich quinones such as NQ. This experimental observation is corroborated by DFT-computed thermodynamics and kinetics. The calculations inform a microkinetic model and validate the variability in quinone behavior at different concentrations of CO2. Moderate and weak CO2 binders exhibit CO2/Q2− stoichiometries that vary between 0 and 2, depending on CO2 concentration, whereas strong binders are not as sensitive to CO2 concentrations and maintain a CO2/Q2− stoichiometry of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 across CO2 concentrations for [CO2] > 10 ppm. The sensitivity of chemical equilibrium to CO2 concentration indicates that strong quinones do not require higher CO2 concentrations to bind 2 CO2 molecules, whereas moderate binders (e.g. 2ClNQ and 2ClQ, whose values for ΔGbind fall between −5 and −10 kcal mol−1) benefit from higher CO2 concentrations as their weighted stoichiometries increase substantially from ∼1
1 across CO2 concentrations for [CO2] > 10 ppm. The sensitivity of chemical equilibrium to CO2 concentration indicates that strong quinones do not require higher CO2 concentrations to bind 2 CO2 molecules, whereas moderate binders (e.g. 2ClNQ and 2ClQ, whose values for ΔGbind fall between −5 and −10 kcal mol−1) benefit from higher CO2 concentrations as their weighted stoichiometries increase substantially from ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at atmospheric concentrations to ∼2
1 at atmospheric concentrations to ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 near the saturation limit. Synergistic theoretical and experimental results indicate that one quinone studied, 4ClQ, exhibits reduction potentials positive of O2/O2− while still binding CO2 sufficiently strongly for an average of one CO2 bound per quinone even at low CO2 concentrations. Combined with careful consideration of the lower CO2 capacity of 1
1 near the saturation limit. Synergistic theoretical and experimental results indicate that one quinone studied, 4ClQ, exhibits reduction potentials positive of O2/O2− while still binding CO2 sufficiently strongly for an average of one CO2 bound per quinone even at low CO2 concentrations. Combined with careful consideration of the lower CO2 capacity of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and the predictive ability of the correlation, this observation could allow for facile identification of other O2-impervious quinones capable of binding CO2. Using simple electrochemical measurements, the correlation between reduction potential and CO2 binding strength can be used to predict carbon capture performance of new molecular materials in the quinoid family. Based on our findings, binding stoichiometry varies depending on assay conditions.
1 stoichiometry and the predictive ability of the correlation, this observation could allow for facile identification of other O2-impervious quinones capable of binding CO2. Using simple electrochemical measurements, the correlation between reduction potential and CO2 binding strength can be used to predict carbon capture performance of new molecular materials in the quinoid family. Based on our findings, binding stoichiometry varies depending on assay conditions.
Conflicts of interest
The authors declare no competing interests.
Acknowledgements
We thank Prof. Carl Koval, and Prof. Rich Noble for useful discussions. ORL thanks the University of Colorado for startup funds. HP thanks the University of Colorado Department of Chemistry for a summer 2021 research fellowship and the National Science Foundation Graduate Research Fellowship Program. AWH acknowledges support from a fellowship provided by Kuwait University. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE 2040434. SNS would like to acknowledge the University of Colorado Boulder UROP program.
References
- S. Fuss, J. G. Canadell, P. Ciais, R. B. Jackson, C. D. Jones, A. Lyngfelt, G. P. Peters and D. P. Van Vuuren, One Earth, 2020, 3, 145–149 CrossRef.
- C. Koven, V. K. Arora, P. Cadule, R. A. Fisher, C. D. Jones, D. M. Lawrence, J. Lewis, K. Lindsey, S. Mathesius and M. Meinshausen, Earth Syst. Dyn. Discuss., 2021, 1–32 Search PubMed.
- J. Wilcox, Nat. Energy, 2020, 5, 121–122 CrossRef.
-
J. Wilcox, Carbon capture, Springer Science & Business Media, 2012 Search PubMed.
- C. Hou, D. R. Kumar, Y. Jin, Y. Wu, J. J. Lee, C. W. Jones and T. Wang, Chem. Eng. J., 2021, 413, 127532 CrossRef CAS.
- H. A. Petersen and O. R. Luca, Phys. Chem. Chem. Phys., 2021, 23, 12533–12536 RSC.
- P. Scovazzo, J. Poshusta, D. DuBois, C. Koval and R. Noble, J. Electrochem. Soc., 2003, 150, D91 CrossRef CAS.
- S. Voskian and T. A. Hatton, Energy Environ. Sci., 2019, 12, 3530–3547 RSC.
- F. Simeon, M. C. Stern, K. M. Diederichsen, Y. Liu, H. J. Herzog and T. A. Hatton, J. Phys. Chem. C, 2022, 126, 1389–1399 CrossRef CAS.
- H. A. Petersen, A. W. Alherz, T. A. Stinson, C. G. Huntzinger, C. B. Musgrave and O. R. Luca, iScience, 2022, 25, 103997 CrossRef CAS PubMed.
- B. Gurkan, F. Simeon and T. A. Hatton, ACS Sustainable Chem. Eng., 2015, 3, 1394–1405 CrossRef CAS.
- M. E. Peover and J. D. Davies, J. Electroanal. Chem., 1963, 6, 46–53 CAS.
-
C. Creutz, Electrochemical and Electrocatalytic Reactions of Carbon Dioxide, Elsevier, 1993, pp. 19–67 Search PubMed.
-
A. M. D. L. DuBois, W. Bell and J. C. Smart, in Electrochemical and Electrocatalytic Reactions of Carbon Dioxide, ed. K. K. B. P. Sullivan, and H. E. Guard, Elsevier, Amsterdam, 1993 Search PubMed.
- T. Nagaoka, N. Nishii, K. Fujii and K. Ogura, J. Electroanal. Chem., 1992, 322, 383–389 CrossRef CAS.
- N. Gupta and H. Linschitz, J. Am. Chem. Soc., 1997, 119, 6384–6391 CrossRef CAS.
- J. M. Barlow and J. Y. Yang, J. Am. Chem. Soc., 2022, 144, 14161–14169 CrossRef CAS PubMed.
- M. E. Peover, J. Chem. Soc. (Resumed), 1962, 4540, 10.1039/jr9620004540.
- M. T. Huynh, C. W. Anson, A. C. Cavell, S. S. Stahl and S. Hammes-Schiffer, J. Am. Chem. Soc., 2016, 138, 15903–15910 CrossRef CAS PubMed.
- M. B. Mizen and M. S. Wrighton, J. Electrochem. Soc., 1989, 136, 941–946 CrossRef CAS.
- A. Gennaro, A. A. Isse and E. Vianello, J. Electroanal. Chem. Interfacial Electrochem., 1990, 289, 203–215 CrossRef CAS.
- M. B. Ewing and J. C. S. Ochoa, J. Chem. Eng. Data, 2004, 49, 486–491 CrossRef CAS.
- National Center for Atmospheric Research Lab, NCAR Foothills Lab Weather, NCAR, Boulder, CO.
- E. M. Espinoza, J. A. Clark, J. Soliman, J. B. Derr, M. Morales and V. I. Vullev, J. Electrochem. Soc., 2019, 166, H3175–H3187 CrossRef CAS.
- S. Voskian and T. A. Hatton, Energy Environ. Sci., 2019, 12, 3530–3547 RSC.
-
M. Zimmermann, Oxygen reduction reaction mechanism on glassy carbon in aprotic organic solvents, Doctoral dissertation, Université Grenoble Alpes (ComUE), 2015 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051 RSC.
- D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123–141 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- A. Marenich, C. Cramer and D. Truhlar, J. Phys. Chem. B, 2009, 113, 6378 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article bc,
Haley A.
Petersen‡
bc,
Haley A.
Petersen‡
 a,
Nicholas R.
Singstock
a,
Nicholas R.
Singstock
 b,
Sohan N.
Sur
a,
Charles B.
Musgrave
*bd and
Oana R.
Luca
b,
Sohan N.
Sur
a,
Charles B.
Musgrave
*bd and
Oana R.
Luca
 *a
*a
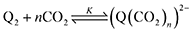
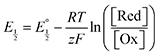
 is the observed half-wave potential,
is the observed half-wave potential, 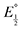 is the standard half-wave potential, R is the gas constant, T is the temperature in Kelvin, z is the number of electrons transferred in the redox process, F is the Faraday constant, [Red] is the concentration of the reduced species, and [Ox] is the concentration of the oxidized species.
is the standard half-wave potential, R is the gas constant, T is the temperature in Kelvin, z is the number of electrons transferred in the redox process, F is the Faraday constant, [Red] is the concentration of the reduced species, and [Ox] is the concentration of the oxidized species.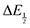 upon introduction of CO2 that increases in magnitude with stronger binding to CO2. This shift in potential is described by eqn (5):
upon introduction of CO2 that increases in magnitude with stronger binding to CO2. This shift in potential is described by eqn (5):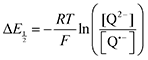
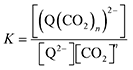
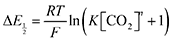
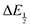 and [CO2] were calculated for each quinone for CVs taken under 5%, 30%, and 100% CO2 (Fig. 2). Dissolved CO2 concentrations were calculated using a Henry's Law method and the local barometric pressure at the time of data collection (see ESI† for details).21–23
and [CO2] were calculated for each quinone for CVs taken under 5%, 30%, and 100% CO2 (Fig. 2). Dissolved CO2 concentrations were calculated using a Henry's Law method and the local barometric pressure at the time of data collection (see ESI† for details).21–23

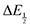 for each data point was obtained by taking the difference between the half-wave potential for the second quinone reduction under Ar and the corresponding value under CO2. Because the quinone reductions in the presence of CO2 are not electrochemically reversible, the typical method of determining
for each data point was obtained by taking the difference between the half-wave potential for the second quinone reduction under Ar and the corresponding value under CO2. Because the quinone reductions in the presence of CO2 are not electrochemically reversible, the typical method of determining 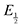 (namely, averaging the potentials at which the peak cathodic and anodic currents occur for the feature) is not applicable. Instead, the inflection point of the feature was taken as an approximate
(namely, averaging the potentials at which the peak cathodic and anodic currents occur for the feature) is not applicable. Instead, the inflection point of the feature was taken as an approximate 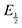 by finding the zero-point of the smoothed second derivative of the curve, as the inflection point has been previously demonstrated to be a good approximation of
by finding the zero-point of the smoothed second derivative of the curve, as the inflection point has been previously demonstrated to be a good approximation of 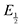 .24
.24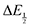 . Therefore, the potential values at which the peak current was observed under Ar and under CO2 were compared to obtain the potential difference. This approximation
. Therefore, the potential values at which the peak current was observed under Ar and under CO2 were compared to obtain the potential difference. This approximation 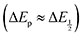 was tested and found to be reliable for quinones for which both ΔEp and
was tested and found to be reliable for quinones for which both ΔEp and 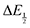 values were readily obtainable. Because separation of the reduction features requires a faster scan rate, these three quinones were given less time to equilibrate with their respective CO2 adducts over the time course of the CV. Therefore, the K values obtained for these three quinones should be taken as an inherent underestimate (whereas the obtained ΔG is an overestimate, i.e. less negative than the true value).
values were readily obtainable. Because separation of the reduction features requires a faster scan rate, these three quinones were given less time to equilibrate with their respective CO2 adducts over the time course of the CV. Therefore, the K values obtained for these three quinones should be taken as an inherent underestimate (whereas the obtained ΔG is an overestimate, i.e. less negative than the true value).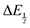 (or ΔEp) were obtained for each data point, a plot of [CO2] vs.
(or ΔEp) were obtained for each data point, a plot of [CO2] vs.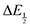 was constructed for each quinone. A user-defined fit function in Origin 2019b was used to determine a best-fit curve with free parameter K based upon eqn (10). The value of n in this equation was defined for each quinone on the basis of DFT results for the favorability of the first and second CO2 binding events. In the case of quinones with ambiguous DFT binding free energies, n values were determined by comparison of experimental fits with n = 1 and n = 2. Finally, with K values determined for each quinone, the free energy of CO2 binding, ΔGbind, was calculated using the well-known relationship given by eqn (11).
was constructed for each quinone. A user-defined fit function in Origin 2019b was used to determine a best-fit curve with free parameter K based upon eqn (10). The value of n in this equation was defined for each quinone on the basis of DFT results for the favorability of the first and second CO2 binding events. In the case of quinones with ambiguous DFT binding free energies, n values were determined by comparison of experimental fits with n = 1 and n = 2. Finally, with K values determined for each quinone, the free energy of CO2 binding, ΔGbind, was calculated using the well-known relationship given by eqn (11).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(K)
ln(K)
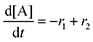
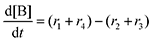
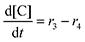
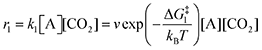
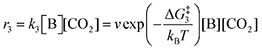
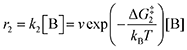
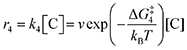
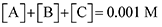
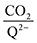 yields a value between 0 and 2.
yields a value between 0 and 2.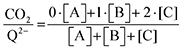
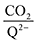 for all 7 quinones investigated at 4 varying concentrations of solvated CO2, ranging from 10−5 M to 0.3 M. In agreement with experiment (Table 1), our model predicts that BQ, NQ, and 2MeQ are very strong CO2 binders, averaging a 2
for all 7 quinones investigated at 4 varying concentrations of solvated CO2, ranging from 10−5 M to 0.3 M. In agreement with experiment (Table 1), our model predicts that BQ, NQ, and 2MeQ are very strong CO2 binders, averaging a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry of CO2 per Q2− dianion across experimentally relevant concentrations of CO2 (0.01 M < [CO2] < 0.3 M). This results from sequentially exergonic CO2 binding thermodynamics and small reaction barriers, as shown in Table 2. The moderate binders – 2ClQ and 2ClNQ – also have a weighted
1 stoichiometry of CO2 per Q2− dianion across experimentally relevant concentrations of CO2 (0.01 M < [CO2] < 0.3 M). This results from sequentially exergonic CO2 binding thermodynamics and small reaction barriers, as shown in Table 2. The moderate binders – 2ClQ and 2ClNQ – also have a weighted 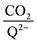 stoichiometry closer to 2
stoichiometry closer to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at high CO2 concentrations, although the stoichiometry drops at smaller [CO2] values. This indicates that moderate binders favor the binding of only one CO2 molecule at lower concentrations, as expected from computed ΔGbind values that are exergonic for the 1st CO2 binding step and only slightly more positive than thermoneutral for the second CO2 binding step. 4ClQ maintains a
1 at high CO2 concentrations, although the stoichiometry drops at smaller [CO2] values. This indicates that moderate binders favor the binding of only one CO2 molecule at lower concentrations, as expected from computed ΔGbind values that are exergonic for the 1st CO2 binding step and only slightly more positive than thermoneutral for the second CO2 binding step. 4ClQ maintains a 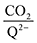 ratio of ∼1 that increases gradually as the CO2 saturation limit is approached, as depicted in Fig. 4d. DDQ is mostly unreactive, however higher concentrations of CO2 push the 1st CO2 binding step forward to some extent, resulting in a value of
ratio of ∼1 that increases gradually as the CO2 saturation limit is approached, as depicted in Fig. 4d. DDQ is mostly unreactive, however higher concentrations of CO2 push the 1st CO2 binding step forward to some extent, resulting in a value of 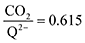 at the saturation limit.
at the saturation limit.

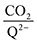 on CO2 concentrations, we plot
on CO2 concentrations, we plot 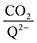 as a function of log[CO2], as shown in Fig. 5. This enables the analysis of the dependence [CO2] over the span of 8 orders of magnitude for all 7 quinones in our study. We find that the weighted stoichiometry of strong binders falls for [CO2] < 10−5 M. This suggests that their efficiency as sorbents is independent of CO2 concentration at atmospheric concentrations (415 ppm) or higher. The moderate binders – 2ClQ and 2ClNQ – are strongly dependent on CO2 concentration at high values ([CO2] > 10−4 M), whereas at lower CO2 concentrations they exhibit a
as a function of log[CO2], as shown in Fig. 5. This enables the analysis of the dependence [CO2] over the span of 8 orders of magnitude for all 7 quinones in our study. We find that the weighted stoichiometry of strong binders falls for [CO2] < 10−5 M. This suggests that their efficiency as sorbents is independent of CO2 concentration at atmospheric concentrations (415 ppm) or higher. The moderate binders – 2ClQ and 2ClNQ – are strongly dependent on CO2 concentration at high values ([CO2] > 10−4 M), whereas at lower CO2 concentrations they exhibit a 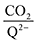 stoichiometry value of 1. As such, unlike the strong binders, the carbon capture efficiency of the moderate binder quinones benefit from higher CO2 concentrations. 4ClQ appears to be only dependent on [CO2] at extremely low or extremely high concentrations. DDQ is generally unreactive unless the solvent is saturated with CO2.
stoichiometry value of 1. As such, unlike the strong binders, the carbon capture efficiency of the moderate binder quinones benefit from higher CO2 concentrations. 4ClQ appears to be only dependent on [CO2] at extremely low or extremely high concentrations. DDQ is generally unreactive unless the solvent is saturated with CO2.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 rather than the previously observed stoichiometry CO2/Q2− of 2
1 rather than the previously observed stoichiometry CO2/Q2− of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for well-studied, electron-rich quinones such as NQ. This experimental observation is corroborated by DFT-computed thermodynamics and kinetics. The calculations inform a microkinetic model and validate the variability in quinone behavior at different concentrations of CO2. Moderate and weak CO2 binders exhibit CO2/Q2− stoichiometries that vary between 0 and 2, depending on CO2 concentration, whereas strong binders are not as sensitive to CO2 concentrations and maintain a CO2/Q2− stoichiometry of 2
1 for well-studied, electron-rich quinones such as NQ. This experimental observation is corroborated by DFT-computed thermodynamics and kinetics. The calculations inform a microkinetic model and validate the variability in quinone behavior at different concentrations of CO2. Moderate and weak CO2 binders exhibit CO2/Q2− stoichiometries that vary between 0 and 2, depending on CO2 concentration, whereas strong binders are not as sensitive to CO2 concentrations and maintain a CO2/Q2− stoichiometry of 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 across CO2 concentrations for [CO2] > 10 ppm. The sensitivity of chemical equilibrium to CO2 concentration indicates that strong quinones do not require higher CO2 concentrations to bind 2 CO2 molecules, whereas moderate binders (e.g. 2ClNQ and 2ClQ, whose values for ΔGbind fall between −5 and −10 kcal mol−1) benefit from higher CO2 concentrations as their weighted stoichiometries increase substantially from ∼1
1 across CO2 concentrations for [CO2] > 10 ppm. The sensitivity of chemical equilibrium to CO2 concentration indicates that strong quinones do not require higher CO2 concentrations to bind 2 CO2 molecules, whereas moderate binders (e.g. 2ClNQ and 2ClQ, whose values for ΔGbind fall between −5 and −10 kcal mol−1) benefit from higher CO2 concentrations as their weighted stoichiometries increase substantially from ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at atmospheric concentrations to ∼2
1 at atmospheric concentrations to ∼2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 near the saturation limit. Synergistic theoretical and experimental results indicate that one quinone studied, 4ClQ, exhibits reduction potentials positive of O2/O2− while still binding CO2 sufficiently strongly for an average of one CO2 bound per quinone even at low CO2 concentrations. Combined with careful consideration of the lower CO2 capacity of 1
1 near the saturation limit. Synergistic theoretical and experimental results indicate that one quinone studied, 4ClQ, exhibits reduction potentials positive of O2/O2− while still binding CO2 sufficiently strongly for an average of one CO2 bound per quinone even at low CO2 concentrations. Combined with careful consideration of the lower CO2 capacity of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry and the predictive ability of the correlation, this observation could allow for facile identification of other O2-impervious quinones capable of binding CO2. Using simple electrochemical measurements, the correlation between reduction potential and CO2 binding strength can be used to predict carbon capture performance of new molecular materials in the quinoid family. Based on our findings, binding stoichiometry varies depending on assay conditions.
1 stoichiometry and the predictive ability of the correlation, this observation could allow for facile identification of other O2-impervious quinones capable of binding CO2. Using simple electrochemical measurements, the correlation between reduction potential and CO2 binding strength can be used to predict carbon capture performance of new molecular materials in the quinoid family. Based on our findings, binding stoichiometry varies depending on assay conditions.


