 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Trimethylamine-N-oxide: its hydration structure, surface activity, and biological function, viewed by vibrational spectroscopy and molecular dynamics simulations
Tatsuhiko
Ohto
a,
Johannes
Hunger
b,
Ellen H. G.
Backus
b,
Wataru
Mizukami
c,
Mischa
Bonn
 b and
Yuki
Nagata
b and
Yuki
Nagata
 *bd
*bd
aGraduate School of Engineering Science, Osaka University, 1-3 Machikaneyama, Toyonaka, Osaka 560-8531, Japan
bMax Planck Institute for Polymer Research, Ackermannweg 10, 55128 Mainz, Germany. E-mail: nagata@mpip-mainz.mpg.de
cDepartment of Energy and Material Sciences, Faculty of Engineering Sciences, Kyushu University, 6-1 Kasuga-Park, Fukuoka, 816-8580, Japan
dDepartment of Theoretical and Computational Molecular Science, Institute for Molecular Science, Myodaiji, Okazaki, Aichi 444-8585, Japan
First published on 11th January 2017
Abstract
The osmolyte molecule trimethylamine-N-oxide (TMAO) stabilizes the structure of proteins. As functional proteins are generally found in aqueous solutions, an important aspect of this stabilization is the interaction of TMAO with water. Here, we review, using vibrational spectroscopy and molecular dynamics simulations, recent studies on the structure and dynamics of TMAO with its surrounding water molecules. This article ends with an outlook on the open questions on TMAO–protein and TMAO–urea interactions in aqueous environments.
I. Introduction
Trimethylamine-N-oxide (TMAO) is a small zwitterionic molecule in which the oxygen (OTMAO) and nitrogen (NTMAO) atoms are negatively and positively charged, respectively. This O–N group can be considered as the hydrophilic part of the molecule. The rest of the TMAO molecule is composed of three methyl groups and can thus be considered as the hydrophobic part. This is the reason for TMAO being called an amphiphilic molecule.TMAO also serves as an osmolyte, enabling, for instance, marine organisms to adjust their osmotic pressure. In fact, sharks contain both urea and TMAO.1,2 Although both urea and TMAO function as osmolytes, the effects of these molecules on protein stability are opposite. TMAO stabilizes the structure of proteins, while urea destabilizes them. It has been believed that by balancing the destabilization effects of urea with the stabilization effects of TMAO, living organisms which contain both TMAO and urea can maintain their protein structure and at the same time adjust the osmotic pressure.1
To understand the biological function of TMAO, one should understand the solvation structure of TMAO, the nature and strength of the interaction of TMAO with proteins, and the conformations of TMAO and urea in an aqueous environment not only under ambient conditions but also under extreme conditions such as at high pressure.3,4 Typical questions regarding TMAO are: although TMAO is known to be an amphiphilic molecule, to what extent is the methyl group of TMAO hydrophobic? How do the surrounding water molecules interact with a TMAO molecule? How does TMAO interact with urea? How does TMAO stabilize the structure of a protein? Infrared (IR) spectroscopy,5–8 Raman spectroscopy,9,10 nuclear magnetic resonance spectroscopy,11,12 X-ray spectroscopy,13,14 dielectric relaxation spectroscopy,5,15 and molecular dynamics (MD) simulations16–18 have been used to address these questions.
These reports contain different views of TMAO. For example, the slowing down of the water motion near TMAO has been attributed to the hydrophobic hydration of the methyl groups of TMAO6 or strong hydrogen bonds between water and the hydrophilic oxygen atom.19 In contrast to the dynamics of water near the methyl groups of TMAO, the structure of water in an aqueous TMAO solution has been found to be very similar to that of neat water.20–24 Moreover, the nature of the TMAO methyl group – hydrophilic or hydrophobic – has been debated.25–27 To resolve these apparent contradictions, new technologies have been used to study aqueous TMAO solutions: beyond the classical force field MD simulations, ab initio MD (AIMD) simulations28 have been employed. Experimentally, beyond the linear vibrational spectroscopy, surface-specific, time-resolved, two-dimensional vibrational spectroscopy29 has been used. More importantly, the combination of simulations and advanced spectroscopy has potential for providing a unified picture of TMAO.
In this review, we provide an overview of the recent studies on TMAO using vibrational spectroscopy and/or MD simulations. In Section II, the vibrational frequency assignment of TMAO C–H stretching modes and the frequency modulation of the water O–H stretching modes due to the presence of TMAO are discussed. In Section III, the spectroscopic investigation on the TMAO hydration structure and dynamics is introduced. Furthermore, recent efforts towards understanding these spectroscopic data based on MD simulations are also reviewed. Section IV explains the study to examine the hydrophilicity of TMAO using surface-specific sum-frequency generation (SFG) spectroscopy. We end with an outlook and challenges in understanding the complex interplay of TMAO, urea, and proteins.
II. Fundamental properties of TMAO molecules
II-A. Electronic structure of TMAO
In this section, we summarize the molecular properties of TMAO by comparing it with tert-butyl alcohol (TBA). Fig. 1 displays the molecular structures of TMAO and TBA. Both molecules have three methyl groups, while TMAO has a zwitterionic N+–O− group and TBA has a C–O–H hydroxyl group. Although the chemical compositions of TMAO and TBA are similar, the molecular properties are very different. The calculated dipole moment of TBA is 1.49 Debye at the M06/cc-pVTZ level of theory calculated using the GAMESS code,30 while the dipole moment of TMAO is 4.55 Debye, much larger than that of TBA. Due to this large difference in the dipole moment, TBA aggregates in aqueous solution but TMAO does not.8,31 Note that the experimentally measured dipole moments of TMAO and TBA in apolar solutions are 5.04 Debye53 and 1.76 Debye,93 respectively, which are close to the calculated values. As discussed in ref. 5, the effective dipole moment of the hydrated TMAO–water complex is substantially higher (10.7 Debye).For TMAO, the dipole moment calculated from the electrostatic potential fitted charge32 at the OTMAO atom of −0.629 e and the N+–O− distance of 1.34 Å is 4.05 Debye, meaning that 90% of the dipole moment of TMAO is generated by the N+–O− part. Note that similar values have been reported in various studies.33,34 This large dipole moment of the N+–O− part characterizes the hydrophilicity of the TMAO. In contrast, the molecular polarizabilities of TMAO and TBA are similar.
II-B. C–H stretching mode of the methyl group of TMAO
Understanding the vibrational nature of TMAO is essential to interpret the vibrational spectra and extract molecular level insight into the structure of TMAO from the vibrational data. In general, symmetric and anti-symmetric C–H stretching modes contribute to the optical spectra in the very narrow frequency range around 2900 cm−1. In addition, the C–H stretching mode is often modulated by the overlap of the C–H stretching and the overtone of the H–C–H bending modes, which is called Fermi resonance.35,36 The Fermi resonance peak often overlaps the peak of the anti-symmetric C–H stretching modes, which alters their peak intensities.37 Vibrational mode assignments have been frequently made by performing ab initio harmonic calculations.9 Since the anharmonic effect is not included in the harmonic calculation, the calculated frequencies are usually scaled to compensate the effects of anharmonicity of potential to the vibrational frequency.38 In this scheme, we have used a common scaling factor for different vibrational modes.39 Moreover, the harmonic calculations cannot address the contribution of the Fermi resonance, because they do not take into account any vibrational mode couplings. To address the anharmonic correction and the Fermi resonance, the vibrational Hamiltonian approach,40,41 vibrational self-consistent field (VSCF) approach,42–44 or perturbative approach45 should be employed. The vibrational Hamiltonian approach is more computationally inexpensive, but it is more empirical than the VSCF-based approach.We summarize the C–H stretching vibrational signature of TMAO calculated from the post-VSCF-based approach in Table 1. For a methyl group, three C–H stretching modes (symmetric, in-plane anti-symmetric, and out-of-plane anti-symmetric) contribute to the optical spectra at frequencies ranging from 2800 cm−1 to 3100 cm−1. However, the frequencies of the C–H stretching modes vary substantially for each molecule; for methanol, the frequency difference between the symmetric mode and the in-plane anti-symmetric mode is ∼150 cm−1, while it is ∼70 cm−1 for TMAO. The symmetric mode of methanol is 100 cm−1 lower than that of TMAO. Furthermore, the anti-symmetric in-plane mode can have a higher or lower frequency than the out-of-plane mode; for methanol, the in-plane mode provides a lower frequency than the out-of-plane mode, whereas it is reversed for TMAO. Table 1 also shows that the Fermi resonance frequency is very close to the out-of-plane antisymmetric mode frequency for methanol and TBA, while it is very close to the symmetric mode frequency for TMAO. As such, peak assignments of the C–H stretching mode are highly dependent on the molecules. Accurate quantum chemistry calculations beyond the harmonic calculations therefore seem to be necessary for correct peak assignment.
| Methanol | TBA | TMAO | |
|---|---|---|---|
| Symmetric | 2818 | 2854–2922 | 2922–2928 |
| (2845) | (2880–2913) | (2952) | |
| Fermi resonance | 2919 | 2930, 2945 | 2938 |
| (2925) | |||
| Out-of-plane anti-symmetric | 2924 | 2936–2955 | 3009–3015 |
| (2961) | (3036) | ||
| In-plane anti-symmetric | 2972 | 2940–2959 | 2989–2997 |
| (2980) | (3006–3018) | ||
II-C. Modulation of the O–H stretching mode of water due to TMAO
The O–H stretching frequency of H2O molecules (or O–D for D2O molecules) is strongly dependent on the intermolecular interactions of water, in particular, hydrogen bond interactions; the strong hydrogen bond interaction lowers the O–H/O–D stretching frequency.50 Through this sensitivity of the O–H/O–D stretching frequency to the molecular interactions, we can understand how the solute molecules affect the hydrogen bond structure of water.50 As is displayed in Fig. 2(a), HOD dissolved in H2O shows two bands in the 2100–2600 cm−1 range: a combination band at ∼2100 cm−1 and the O–D stretching mode at 2500 cm−1. Addition of TMAO results in a strong increase of the absorption of the solutions at ∼2200–2400 cm−1,5,51 indicative of red-shifted O–D oscillators. A similar red-shifted contribution to the O–H stretching band has been reported for a solution of TMAO in H2O.8 Thus, IR spectra indicate the presence of a strong hydrogen bond between TMAO and water. However, it is not clear how water molecules interact with TMAO and which interaction of water and TMAO gives rise to the low frequency O–H stretching band. High-level vibrational spectral simulations are clearly required to identify the molecular origin of the red-shift of the O–D stretching mode.52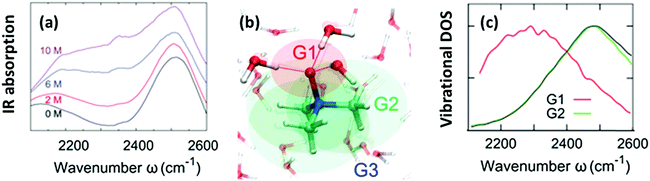 | ||
| Fig. 2 (a) Vibrational IR spectra of the O–D stretching mode of isotopically diluted water (8% HDO in H2O) at various concentrations of TMAO. Note that the small, narrow feature at 2350 cm−1 stems from the absorption of atmospheric CO2. (b) Schematics of the categorization of water (G1, G2, and G3). (c) Simulated vibrational density of states for sub-ensembles G1 and G2 together with the vibrational density of states for pure D2O (black line). Figures are adapted from ref. 5 and 19 with permission of the American Chemical Society. | ||
Here, we identify which of the O–D groups that interact with TMAO cause the appearance of the band at ∼2200–2400 cm−1. To do so, we categorized all the O–D groups of D2O molecules in a simulation cell into the O–D groups near the hydrophilic OTMAO atom (sub-ensemble G1), the O–D groups near the hydrophobic methyl group (G2), and the O–D groups that are away from TMAO (G3). These sub-ensembles are schematically depicted in Fig. 2(b).19 By calculating the vibrational density of states for these sub-ensembles, we could assign the vibrational spectra to the specific ensemble. The simulated vibrational densities of states for the sub-ensembles G1 and G2 using AIMD trajectories are plotted in Fig. 2(c).19 This indicates that the ∼200 cm−1 red-shifted band observed in IR spectra5 arises from the strong hydrogen-bond of water's O–D group and the OTMAO atom (sub-ensemble G1). On the other hand, the contribution of the O–D stretching chromophores near the hydrophobic group of TMAO almost completely overlaps with the bulk O–D stretching band (black line in Fig. 2(c)), making their contributions invisible in the O–D stretching vibrational spectra.
III. Hydration structure of and dynamics near TMAO
III-A. Time-resolved vibrational spectroscopy
Time-resolved pump–probe vibrational spectroscopy52 has been used for understanding the hydration structure and dynamics near TMAO.5,6,10,54–56 For example, by exciting and subsequently probing the vibrational modes with different light polarization combinations, one can monitor the rotational dynamics of molecules.52 By applying this time-resolved vibrational approach to the O–D stretching mode of HDO in isotopically diluted aqueous TMAO solution, it was revealed that the rotational motions of the water molecules near TMAO are largely frozen.5,6Fig. 3 plots the decay of the orientation (anisotropy decay, defined later in eqn (1)) of the O–D group by pumping the low frequency side of the O–D stretching mode (left) and the high frequency side (right). These panels show very different anisotropy decays; for pumping at 2440 cm−1, the anisotropy decay is very strongly slowed down with increasing TMAO concentration, while for pumping at 2560 cm−1, the slowdown is less dramatic and changes more gradually. Since the low frequency O–D stretching mode originates from the O–D group hydrogen bonded to the OTMAO atom as discussed in Section II, the frozen motion of water arises from the strong O–D⋯OTMAO hydrogen bond. Further simulation evidence is given in the next subsection.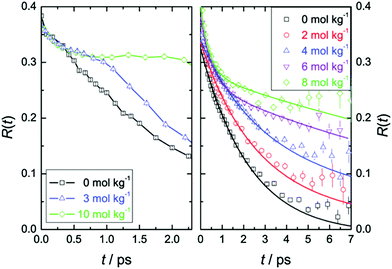 | ||
| Fig. 3 (left) Anisotropy decay, R(t), for the O–D vibration of HDO molecules in aqueous TMAO solutions with the pump pulse centered at around 2440 cm−1 for various TMAO concentrations. (right) R(t) with the pump pulse centered at around 2560 cm−1. Figures are adapted from ref. 5 with permission of the American Chemical Society. | ||
This dramatic slowing down of the water motion can be found not only for TMAO solution but also for tetramethylurea (TMU), proline, N-methylacetamide (NMA),6 and TBA solutions.54 This is evidenced not only by the anisotropy decay data but also from vibrational dynamics data obtained by two-dimensional IR (2DIR) spectroscopy. In 2DIR, the signals are plotted in contour maps by using two frequency axes – the excitation frequency (ω1) and the probing frequency (ω3).29,50,52 In the two-dimensional contour map, the center line slope (CLS) of the diagonal peak is almost parallel to the diagonal line (ω1 = ω3) at T = 0 ps and becomes parallel to the ω1 axis for long time T between excitation and probe pulses. By monitoring this CLS over time,57 we can obtain information on the time-scale of the spectral diffusion, i.e. how fast the vibrational modes experience different frequencies. Fig. 4 shows the 2DIR spectra in the O–H stretch region for pure water, a TMAO solution, and a TBA solution for various waiting times T.54 Clearly, the CLS of the diagonal peak changes rapidly for pure H2O, while for the TMAO and TBA solutions, the CLS dynamics are slower. This again indicates that the vibrational dynamics of the O–H stretching mode slow down due to the presence of TMAO/TBA molecules, consistent with the conclusions from the anisotropy decay measurements.6
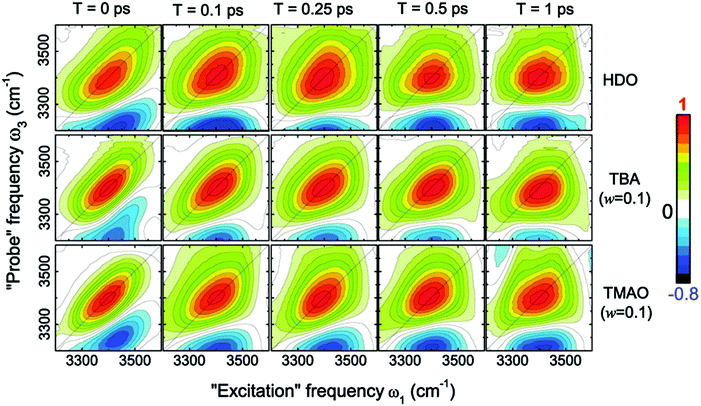 | ||
| Fig. 4 Two-dimensional correlation spectra of pure HDO:D2O and solutions of TBA and TMAO in HDO:D2O at the concentration of 0.1 wt%, measured at different waiting times T. Figures are adapted from ref. 54 with permission of the American Chemical Society. | ||
III-B. Molecular dynamics simulations
The anisotropy decay can be computed from a MD simulation trajectory.52 The anisotropy decay R(t) of the O–D group of D2O can be given by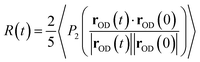 | (1) |
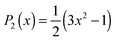 . R(t) calculated from the force field MD trajectories using the Kast model of TMAO58 shows that the slowing down of the water orientation when TMAO is added to water is rather moderate.16 This moderate slowing down can be attributed to the excluded volume effects of TMAO hydrophobic methyl groups which suppress the jump-like water reorientation.59 However, this cannot account for the experimentally observed strong pump frequency dependence of the anisotropy decay of water.5 Moreover, the MD simulations predicted that the addition of TMAO does not affect the IR spectra of the water O–H stretching mode,17 which deviates strongly from the experimental data.5 This questions the accuracy of the force field model of TMAO.58 In fact, discrepancies between experimental data and simulated data with the Kast force field model58 were reported and therefore many revised force field models of TMAO have been proposed.60–63 In contrast to the force field MD, in AIMD simulations, the forces acting on the atoms are calculated based on electronic structure theory and therefore AIMD can be considered as a parameter-free technique. AIMD simulations would thus be a unique tool to re-examine the hydration structure and dynamics of TMAO.
. R(t) calculated from the force field MD trajectories using the Kast model of TMAO58 shows that the slowing down of the water orientation when TMAO is added to water is rather moderate.16 This moderate slowing down can be attributed to the excluded volume effects of TMAO hydrophobic methyl groups which suppress the jump-like water reorientation.59 However, this cannot account for the experimentally observed strong pump frequency dependence of the anisotropy decay of water.5 Moreover, the MD simulations predicted that the addition of TMAO does not affect the IR spectra of the water O–H stretching mode,17 which deviates strongly from the experimental data.5 This questions the accuracy of the force field model of TMAO.58 In fact, discrepancies between experimental data and simulated data with the Kast force field model58 were reported and therefore many revised force field models of TMAO have been proposed.60–63 In contrast to the force field MD, in AIMD simulations, the forces acting on the atoms are calculated based on electronic structure theory and therefore AIMD can be considered as a parameter-free technique. AIMD simulations would thus be a unique tool to re-examine the hydration structure and dynamics of TMAO.
To compare the anisotropy decay of the AIMD and force field MD, the left panel of Fig. 5 plots R(t) calculated from the AIMD trajectories at the BLYP/TZV2P level of theory using the Grimme's D3 van der Waals correction64 and the force field MD trajectories using the Kast force field model.58 The anisotropy decay is decomposed to the O–D groups near the hydrophilic OTMAO atom (sub-ensemble G1), the O–D groups near the hydrophobic methyl group (G2), and the O–D groups that are away from TMAO (G3), as discussed in Fig. 2(b). The simulated anisotropy data plotted in Fig. 5 show that the force field MD simulations predict a very quick decay for the G1 sub-ensemble, whereas the AIMD simulations predict a much slower G1 anisotropy decay. This indicates that the solvation dynamics in the AIMD simulations differ qualitatively from those in the force field MD simulations.19 This difference in the force field MD and AIMD simulations arises from the sp3 hybrid orbital of the OTMAO atom; the hybrid orbital fixes the O–D⋯OTMAO hydrogen bond direction, extending the hydrogen bond lifetime in the AIMD simulations, while this effect cannot be captured by the force field MD simulations.19
 | ||
| Fig. 5 (left) Simulated anisotropy decays of the G1, G2, and G3 O–D groups in aqueous TMAO solutions, obtained from AIMD and force field MD simulations. (right) Two mechanisms for the G1 O–D groups to lose their initial orientation. The upper route (a to b) shows the mechanism for the case that the O–D⋯OTMAO hydrogen-bond remains intact, and reorientation occurs as the entire TMAO+D2O complex rotates (denoted as sub-ensemble G1′), while the lower pathway (a, c, to d) shows the mechanism by which reorientation occurs by breaking of the hydrogen-bond and subsequent rotation of the O–D group. Figures are adapted from ref. 19 with permission of the American Chemical Society. | ||
Subsequently, we turn our focus to the detailed dynamics of the G1 decay. The G1 decay may arise from the following two mechanisms: (i) the O–D groups are strongly hydrogen bonded to the OTMAO atom and rotate together with the TMAO molecule (see (a) and (b) in the right panel of Fig. 5). The other scenario (ii) is that the O–D⋯OTMAO hydrogen-bond is broken, and the O–D group can subsequently rotate more freely in the bulk water (see pathways (a), (c) and (d) in the left panel of Fig. 5). To extract the effect of the mechanisms (i) on the rotational dynamics of G1 anisotropy decay, we simulated the anisotropy decay of those O–D groups within the G1 ensemble which keep the O–D⋯OTMAO hydrogen-bond intact (sub-ensemble G1′); the difference in the G1 and G1′ anisotropy decay arises from mechanism (ii), while the G1′ decay arises solely from mechanism (i). The simulated G1′ anisotropy decay is represented by the broken red line in the right panel of Fig. 5. The G1′ decay is roughly half of the G1 decay, indicating that both the mechanisms (i) and (ii) ((a) to (b), and (a) to (c) and (d) in the left panel of Fig. 5) contribute to the anisotropy decay of water interacting with the OTMAO atom.
Above, we show that AIMD simulations are very powerful to uniquely identify the structure and dynamics of water near the amphiphilic TMAO molecules. AIMD simulations have been applied not only for aqueous TMAO solutions but also for the aqueous solutions of other amphiphilic molecules.65–68 In fact, the slowing down mechanism of water near the amphiphilic TMU molecule has been investigated, but the mechanism for TMU seems to differ from that of TMAO.66 Ensing and co-workers found that the hydration dynamics near TMU are mainly attributed to the water molecules located near the hydrophobic group.66 As is commented in ref. 66, different hydration structures of TMAO and TMU may arise from the zwitterionic nature of TMAO and the polar nature of TMU. This requires further understanding of how hydrophilic the N–O group of TMAO and the C–O group of TMU are, and how hydrophobic the methyl groups of TMAO and TMU are.
IV. TMAO at the water–air interface: hydrophilicity vs. hydrophobicity
IV-A. C–H stretching SFG spectra
Above we discussed the water solvation dynamics near TMAO, when TMAO is fully solvated in the bulk. However, to examine the hydrophobicity/hydrophilicity of the specific part of TMAO, full solvation of TMAO is not ideal. Rather, placing TMAO at the interface consisting of hydrophobic/hydrophilic media and observing the orientation of TMAO with respect to the interface is very useful for examining the hydrophobicity/hydrophilicity of TMAO. The water–air interface is an ideal platform for this investigation. Here, to probe TMAO near the interface spectroscopically, we consider surface specific vibrational SFG spectroscopy69,70 at the TMAO aqueous solution–air interface. The SFG signals are generated by overlapping an IR pulse and a visible pulse at the surface. Since the SFG optical process is a second-order nonlinear process, the signal from the centrosymmetric bulk vanishes, providing selectively the response from molecules located at the interfaces.69,70 As such, we can selectively probe the molecular response near the interface.To understand the orientation of TMAO at the water–air interface, we can probe either the C–H stretching mode or the N–O stretching mode with SFG. Interpreting the C–H stretching mode is more complicated, because of the energy splitting and Fermi resonance, as is discussed in Section II. Nevertheless, the C–H mode is frequently probed, as it is easily addressed with experiments. Here, we examine the orientation of the TMAO by focusing on the C–H stretching mode (Fig. 6).
 | ||
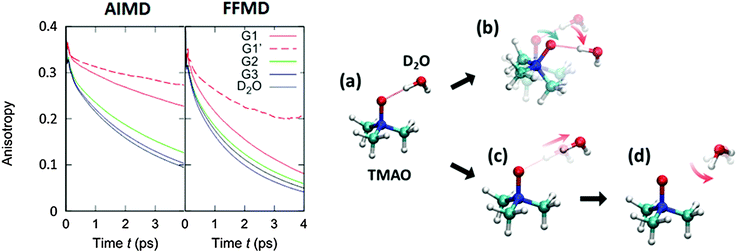
| Fig. 6 Imaginary parts of SFG spectra for the C–H stretching mode at the aqueous TMAO solution–air interface reported in various papers (Ohto;27 Sagle;71 and Mondal74). | ||
The first attempt to identify the TMAO orientation at the water–air interface was conducted by Cremer and co-workers;71 they performed the homodyne-detected SFG measurement for the aqueous TMAO solution–air interface and obtained the imaginary part of the second-order susceptibility (Im(χ(2)(ω))) from the SFG intensity data (|χ(2)(ω)|2)71 using the maximum entropy method.72,73 Im(χ(2)(ω)) provides the information on the absolute orientation (up-oriented toward air or down-oriented toward the bulk) with respect to the surface. Later, heterodyne detected SFG measurements have been conducted, which allow us to access Im(χ(2)(ω)) directly.26,74 Furthermore, to remove the effects of the intra-/inter-molecular coupling of water on the SFG spectra, isotopically diluted water was used instead of neat water in the heterodyne-detected SFG measurement.27
For the vibrational response of the methyl group of lipids and surfactants, the negative peak at the C–H symmetric stretching mode indicates that the C–H group points up to the air.75 However, the vibrational mode assignment of TMAO is much more complicated, as is discussed in Section II and shown in Table 1; since the C–H symmetric stretching mode overlaps substantially with the C–H Fermi resonance, we have to be careful to conclude that the negative 2960–2980 cm−1 evidences that the methyl group points up to the air. In contrast to the complex interplay between the symmetric stretching mode and the Fermi resonance, the anti-symmetric mode is not affected by the Fermi resonance, meaning that this mode is suitable for determining the orientation of the methyl group of TMAO. The positive anti-symmetric in-plane mode manifests that the methyl group points up from the bulk water to the air.27
IV-B. O–H stretching SFG spectra
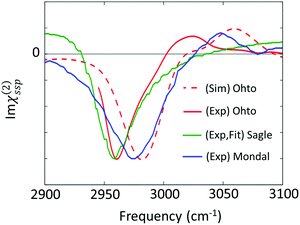
The effects of TMAO molecules on the O–H stretching mode of water in the SFG spectra have been interrogated through the comparison between the water–air interface and the aqueous TMAO solution–air interface.26,27,71,74 Here, we overview the SFG signatures of the O–H stretching mode of water at the water–air interface in the presence of TMAO. The SFG spectra of water at the neat H2O/air interface are displayed in Fig. 7(a) and (b), showing a 3400 cm−1 negative peak and the free O–H stretching peak at 3700 cm−1. Note that after a long debate, the absence of the 3100 cm−1 positive SFG feature at the water–air interface has been agreed upon.76,77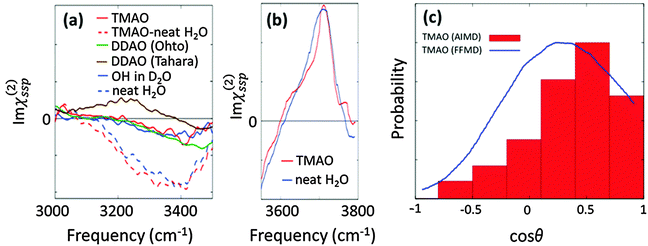 | ||
| Fig. 7 (a) Experimental SFG spectra (Imχ(2)ssp(ω)) in the hydrogen bonded O–H stretching mode region. The TMAO solution–air interface for neat H2O (red broken line) and isotopic diluted water (red solid line), the water/air interface for both pure water (blue broken line) and isotopic diluted water (blue solid line), and the DDAO/isotopic diluted water interface (green and line). The DDAO spectral amplitude was normalized to the same C–H negative amplitude as TMAO. Note that the frequency range covered in the experiment is given by the finite bandwidth of the IR pulse. The data are obtained from ref. 27, 74, 78, and 79. (b) Experimentally measured Imχ(2)ssp(ω) for the free O–H stretching mode.74 (c) Probability distribution of the angle formed by the N–O group of TMAO at the interface and the surface normal, which is denoted by red bars.27 The angle distribution with the force field MD (3 M TMAO concentration) was taken from ref. 80 for comparison, and is shown as the blue line. | ||
We now turn our focus on the variation of the O–H stretching SFG spectra in the presence of the amine-N-oxide group. The SFG spectra of interfacial water in the presence of TMAO and dodecyl-dimethyl-amine-N-oxide surfactant (DDAO) molecules are shown in Fig. 7(a). For TMAO, the water response is indistinguishable from that of pure water; for DDAO, the SFG spectra in isotopically diluted water show a negative response very similar to that in pure water around 3400 cm−1, and, in addition, an enhanced amplitude of the negative peak around 3500–3600 cm−1. This distinct feature of the DDAO–surfactant case can be attributed to the absence of the free O–H positive peak, because the water–air interface is fully covered by the DDAO–surfactant, unlike the TMAO solution–air interface and the water–air interface. The similar 3200–3400 cm−1 SFG features of the TMAO solution and DDAO–surfactant–water interface indicate that the influence of the AO group on the water is independent of the length of the alkyl chains. This again manifests that the methyl groups of TMAO are hydrophobic, like the alkyl chains of the AO–surfactant. Note that the SFG spectra at the DDAO–surfactant–water interface show a distinct feature between ref. 27 and 78; ref. 78 reports the presence of a ∼3200 cm−1 positive peak which is missing in ref. 27. This should be addressed in future work.
Above, we have learned that TMAO is present near the interface and therefore the SFG signal of TMAO is non-zero. The remaining question is whether TMAO is excluded from the topmost water layer at the water–air interface and located in the near bulk region or really in the outermost surface region. In both AIMD and force field MD simulations, TMAO molecules can be found in the topmost layer of the water interface. This, however, contradicts the conclusion drawn from SFG spectra showing that the free O–H stretching SFG band of water is insensitive to the presence/absence of TMAO (see Fig. 7(b)). Mondal and co-workers attributed this insensitivity to an equal number of free O–H stretching chromophores present at the TMAO–solution/air and water/air interfaces,74 and concluded that TMAO is therefore not present at the topmost water layer.
However, the SFG signal is proportional to both the number of vibrational chromophores in the laser spot and the orientation of the transition dipole moment. Thus, for attributing an invariance of O–H stretching SFG signal to an equal number of O–H stretching chromophores at the topmost water layer, one needs to assume that the orientation of the transition dipole moment is unchanged upon adding TMAO. With experimental tools, it is quite difficult to disentangle the variation of the number of chromophores and the variation of the molecular orientation as a result of the possible presence of TMAO. Therefore, again, a combination of SFG and MD simulations would be very powerful to uniquely address the molecular conformation near the interfaces. Such a combined experimental and simulation study indeed reveals that, despite the free O–H signal not changing upon addition of TMAO, TMAO is present in the outermost surface region, and, for the SFG response, the reduction in the number of free O–H groups is compensated by their increased orientation.
This conclusion was drawn from calculating the axial profiles of the average angle formed by the free O–H group and the surface normal for the water–air interface and the TMAO–solution–air interface. These are plotted in Fig. 7(c). Here, we define the free O–H group whose hydrogen atom cannot find any intermolecular oxygen atom within a 3.3 Å cutoff sphere. The data indicate that the angular distribution of the free O–H groups is indeed affected by the presence of TMAO; due to TMAO, the O–H groups point more up to the air. As such, although some free O–H groups are displaced by TMAO, and the number of free O–H groups is accordingly reduced, the free O–H stretching SFG signal seems invariant, due to the enhanced up-orientation of the remaining free O–H groups. This clearly demonstrates that the TMAO methyl groups are hydrophobic and are present near the hydrophobic surface, despite the free O–H signal remaining constant.
V. Outlook of TMAO research
V-A. TMAO–urea interaction in an aqueous environment
TMAO or other amine-oxides are found to counter the osmotic stress due to urea.81–83 Intriguingly, in many marine environments both osmolytes are found in a rather well-defined stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (TMAO
2 (TMAO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) urea).83 Indeed, the activity of many enzymes seems to be unaffected when TMAO and urea are present at a 1
urea).83 Indeed, the activity of many enzymes seems to be unaffected when TMAO and urea are present at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio,83 while for some biomolecules higher amounts of TMAO are required to compensate the osmotic stress of urea.84–86 It is well established that urea is an efficient protein denaturant and that TMAO can efficiently stabilize proteins. Nevertheless, the observed compensation of both effects at this 1
2 ratio,83 while for some biomolecules higher amounts of TMAO are required to compensate the osmotic stress of urea.84–86 It is well established that urea is an efficient protein denaturant and that TMAO can efficiently stabilize proteins. Nevertheless, the observed compensation of both effects at this 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio has stimulated many studies aiming at exploring the underlying molecular-level interactions, which balance the physiological effects of both osmolytes at this stoichiometry.
2 ratio has stimulated many studies aiming at exploring the underlying molecular-level interactions, which balance the physiological effects of both osmolytes at this stoichiometry.
While some evidence exists for direct complexation between TMAO and urea in bulk solution,18,87 other studies82,85,88 indicate that TMAO–urea contacts in solution are not more frequent than what would be expected based on random collisions. In line with this notion, experimental and theoretical studies arrived at the conclusion that TMAO and urea can be considered independent of each other in bulk and that there is no evidence for specific interactions between those two molecules being the origin of the counteraction.13,89–92 Although there seems to be no specific direct interaction between TMAO and urea in bulk, indirect effects mediated via water have been reported.55,82 In this context a detailed study of the behavior of mixed TMAO:urea solutions at interfaces is of particular interest, as the water hydrogen-bonded network, which mediates such indirect effects in bulk, is very different at interfaces. Indeed, classical MD simulations suggest that the situation of TMAO and urea may be drastically different if an interface is present,94,95 while it needs to be stressed that for such studies the choice of the force-field models is extremely critical.94,96 Therefore, only advances in both experimental methods and computational studies will be able to shed light on the underlying mechanisms for such complex multi-component systems.
V-B. Role of TMAO at water–protein interfaces
The variation of the biological function due to the presence of TMAO is directly linked with the molecular interaction of TMAO with proteins. The stabilization mechanism of protein structures has been intensively discussed with MD simulation techniques.80,97–100 Using the Kast force field model,58 Thirumalai and co-workers have demonstrated that TMAO limits the degrees of freedom for the unfolded conformation of proteins, making the folded state more preferable.98 However, as is discussed in Section III-B, the Kast model has serious drawbacks for describing the hydrogen-bonding dynamics and hydration structure. These may affect the stabilization mechanism of protein folding. In fact, Garcia and co-workers have shown that the Kast model of TMAO does not show preferable exclusion from the protein surface.62 For the careful assessment of the TMAO–urea and TMAO–protein interactions, the development of an accurate force field model is crucial.60–63 The AIMD data discussed above can offer a unique check for the developed force field model of TMAO.Experimentally, the protein folding/unfolding dynamics have been investigated by time-resolved vibrational spectroscopy including 2DIR spectroscopy. Gai and co-workers conducted 2DIR measurement for the TMAO–protein system by probing the C–N stretch mode of an unnatural amino acid.101,102 The results indicate two possible mechanisms: TMAO decreases the hydrogen bonding ability of water, stabilizing the unfolded state or TMAO acts as a molecular crowder, increasing the stability of the folded state via the excluded volume effect.98,101 Such a solvent-excluded volume effect in the stabilizing action of TMAO has also been revealed via an approach based on classical scaled particle modelling.103,104 MD simulations investigating these possible mechanisms would be again critically dependent on the accuracy of the force field model of TMAO and the interactions between TMAO and proteins in the force field MD simulations. Therefore, we need to combine spectroscopy with simulations to gain accurate molecular level insight into the TMAO–protein interactions. Typical questions concerning the effect of TMAO on proteins include: how does TMAO stabilize the protein structure? Does TMAO affect the hydrogen bond network around proteins, e.g. via binding of available water molecules? Does the roughness of the protein surface enhance or suppress the activity of TMAO with regard to protein (de-)stabilization?
To answer the question of how TMAO affects proteins, we need to understand the orientation of TMAO with respect to the protein–water interface. To do so, the SFG technique would be again useful; when TMAO can interact with a specific site of a protein, TMAO can have a specific orientation resulting in a non-zero SFG signal. As such, we will be able to probe the TMAO near the protein surface selectively by SFG spectroscopy and be able to learn the orientation of TMAO.
For monitoring the association dynamics of TMAO, the chemical exchange type of two-dimensional SFG (2DSFG) would be useful. In fact, this chemical exchange 2DIR technique has been used for over 10 years,105,106 though it has not been applied for 2DSFG. In the chemical exchange 2DIR technique, different vibrational frequencies for associated and dissociated conformations of the TMAO–protein system generate an off-diagonal peak in the two-dimensional spectra. Monitoring the creation and annihilation of this off-diagonal peak provides information on the speed of the chemical exchanges. Chemical exchange 2DSFG would be not only powerful to address the TMAO–protein association dynamics but also to monitor the association–dissociation liquid dynamics at the interfaces.
Finally, we comment on the previous combined studies of MD simulations and SFG spectroscopy at the water–protein interfaces. Since both SFG and MD can address the bond orientations and conformation of the protein, these techniques have been successfully combined.107–111 Moreover, the recent advances in MD simulations allow us to calculate the SFG spectra and compare the simulated SFG spectra with the experimentally measured spectra.112,113 Information on the orientational motion obtained from time-resolved data is also compared with the simulation data.114 These would be powerful tools to achieve a tight collaboration between MD simulation and SFG spectroscopy, contributing to the sophistication of the force field models and an accurate description of the protein–TMAO interactions.
VI. Concluding remarks
We have provided an overview of recent progress on the solvation structure and dynamics of water near TMAO and other amphiphilic molecules. In particular, we focus on vibrational spectroscopy and simulation studies. Several mysteries have been unveiled by combining MD simulations with vibrational spectroscopy. The hydrophilic part of TMAO forms exceptionally strong hydrogen-bonds with water, which results in a strongly red-shifted contribution to the O–H stretching band in the vibrational spectrum. These strong hydrogen bonds are important to understand TMAO's function as a molecular crowder as the strong interaction can reduce the number of water molecules that are available to hydrate a biomolecule. These strong hydrogen-bonds are also at the heart of the slowing down of the water molecules' motion near TMAO. The vibrational/computational (mainly AIMD simulation) study unambiguously revealed that the slowing down of the rotation of the O–H groups arises from the O–H group interacting with the OTMAO atom rather than from hydrophobic hydration of methyl groups of TMAO nor from the excluded volume effects due to the hydrophobic methyl group.The other highlight is uncovering the nature of the methyl group of TMAO. This can be characterized by placing TMAO at the water–air interface; the orientation and location of TMAO can be linked to the hydrophobicity/hydrophilicity of TMAO. The orientation of TMAO can be determined from the sign of the imaginary part of the SFG spectra. The combined SFG measurement and AIMD simulations revealed that the N–OTMAO group of TMAO points down to the water phase. Moreover, TMAO can be found at the water–air interface, manifesting that the methyl group of TMAO is hydrophobic rather than hydrophilic. Finally, we believe that the combination of vibrational spectroscopy and simulation techniques can play an important role in unveiling molecular insights into TMAO–protein and TMAO–urea interactions.
Competing financial interest
The authors declare no competing financial interest.Acknowledgements
We are grateful to Helmut Lutz and Wenjun Xie for fruitful discussion. Open Access funding provided by the Max Planck Society.References
- P. H. Yancey, J. Exp. Biol., 2005, 208, 2819–2830 CrossRef CAS PubMed.
- A. D. M. Dove, J. Leisen, M. Zhou, J. J. Byrne, K. Lim-hing, H. D. Webb, L. Gelbaum, M. R. Viant, J. Kubanek and F. M. Ferna, PLoS One, 2012, 7, e49379 CAS.
- C. Krywka, C. Sternemann, M. Paulus, M. Tolan, C. Royer and R. Winter, ChemPhysChem, 2008, 9, 2809–2815 CrossRef CAS PubMed.
- J. L. Silva, A. C. Oliveira, T. C. Vieira, G. A. de Oliveira, M. C. Suarez and D. Foguel, Chem. Rev., 2014, 114, 7239–7267 CrossRef CAS PubMed.
- J. Hunger, K. J. Tielrooij, R. Buchner, M. Bonn and H. J. Bakker, J. Phys. Chem. B, 2012, 116, 4783–4795 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, Phys. Rev. Lett., 2007, 99, 148301 CrossRef CAS PubMed.
- K. A. Sharp, B. Madan, E. Manas and J. M. Vanderkooi, J. Chem. Phys., 2001, 114, 1791–1796 CrossRef CAS.
- M. Freda, G. Onori and A. Santucci, J. Phys. Chem. B, 2001, 105, 12714–12718 CrossRef CAS.
- K. L. Munroe, D. H. Magers and N. I. Hammer, J. Phys. Chem. B, 2011, 115, 7699–7707 CrossRef CAS PubMed.
- K. Mazur, I. a. Heisler and S. R. Meech, Phys. Chem. Chem. Phys., 2012, 14, 6343–6351 RSC.
- R. Sinibaldi, C. Casieri, S. Melchionna, G. Onori, A. L. Segre, S. Viel, L. Mannina and F. De Luca, J. Phys. Chem. B, 2006, 110, 8885–8892 CrossRef CAS PubMed.
- J. Qvist and B. Halle, J. Am. Chem. Soc., 2008, 130, 10345–10353 CrossRef CAS PubMed.
- C. J. Sahle, M. A. Schroer, I. Juurinen and J. Niskanen, Phys. Chem. Chem. Phys., 2016, 18, 16518–16526 RSC.
- Y. Sasaki, Y. Horikawa, T. Tokushima, K. Okada, M. Ourab and M. Aida, Phys. Chem. Chem. Phys., 2016, 18, 27648–27653 RSC.
- T. Shikata and S. Itatani, J. Solution Chem., 2002, 31, 823–844 CrossRef CAS.
- D. Laage, G. Stirnemann and J. T. Hynes, J. Phys. Chem. B, 2009, 113, 2428–2435 CrossRef CAS PubMed.
- G. Stirnemann, J. T. Hynes and D. Laage, J. Phys. Chem. B, 2010, 114, 3052–3059 CrossRef CAS PubMed.
- S. Paul and G. N. Patey, J. Am. Chem. Soc., 2007, 129, 4476–4482 CrossRef CAS PubMed.
- K. Usui, J. Hunger, M. Sulpizi, T. Ohto, M. Bonn and Y. Nagata, J. Phys. Chem. B, 2015, 119, 10597–10606 CrossRef CAS PubMed.
- J. L. Finney, D. T. Bowron, R. M. Daniel, P. A. Timmins and M. A. Roberts, Biophys. Chem., 2003, 105, 391–409 CrossRef CAS PubMed.
- P. Buchanan, N. Aldiwan, A. K. Soper, J. L. Creek and C. A. Koh, Chem. Phys. Lett., 2005, 415, 89–93 CrossRef CAS.
- N. Galamba, J. Phys. Chem. B, 2014, 117, 2153–2159 CrossRef PubMed.
- G. Graziano, J. Phys. Chem. B, 2014, 118, 2598–2599 CrossRef CAS PubMed.
- N. Galamba, J. Phys. Chem. B, 2014, 118, 2600–2603 CrossRef CAS PubMed.
- Y. Koga, P. Westh, K. Nishikawa and S. Subramanian, J. Phys. Chem. B, 2011, 115, 2995–3002 CrossRef CAS PubMed.
- J. A. Mondal, J. Phys. Chem. Lett., 2016, 7, 1704–1708 CrossRef CAS PubMed.
- T. Ohto, E. H. G. Backus, W. Mizukami, J. Hunger, M. Bonn and Y. Nagata, J. Phys. Chem. C, 2016, 120, 17435–17443 CAS.
- D. Marx and J. Hutter, Ab initio molecular dynamics: basic theory and advanced methods, Cambridge University Press, 2009 Search PubMed.
- S. Mukamel, Annu. Rev. Phys. Chem., 2000, 51, 691–729 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- S. Paul and G. N. Patey, J. Phys. Chem. B, 2006, 110, 10514–10518 CrossRef CAS PubMed.
- S. R. Cox and D. E. Williams, J. Comput. Chem., 1981, 2, 304–323 CrossRef CAS.
- V. Kocherbitov, V. Veryazov and O. Söderman, J. Mol. Struct. THEOCHEM, 2007, 808, 111–118 CrossRef CAS.
- I. M. Pazos and F. Gai, J. Phys. Chem. B, 2012, 116, 12473–12478 CrossRef CAS PubMed.
- R. G. Snyder, H. L. Strauss and C. A. Elliger, J. Phys. Chem., 1982, 86, 5145–5150 CrossRef CAS.
- S. Abbate, S. L. Wunder and G. Zerbi, J. Phys. Chem., 1984, 88, 593–600 CrossRef CAS.
- S. Abbate, G. Zerbi and S. L. Wunder, J. Phys. Chem., 1982, 86, 3140–3149 CrossRef CAS.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- I. M. Alecu, J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2010, 6, 2872–2887 CrossRef CAS PubMed.
- H. M. Chase, B. Rudshteyn, B. T. Psciuk, M. A. Upshur, B. F. Strick, R. J. Thomson, V. S. Batista and F. M. Geiger, J. Phys. Chem. B, 2016, 120, 1919–1927 CrossRef CAS PubMed.
- J. Ho, B. T. Psciuk, H. M. Chase, B. Rudshteyn, M. A. Upshur, L. Fu, R. J. Thomson, H. Wang, F. M. Geiger and V. S. Batista, J. Phys. Chem. C, 2016, 120, 12578–12589 CAS.
- T. K. Roy and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 9468–9492 RSC.
- J. M. Bowman, Acc. Chem. Res., 1986, 19, 202–208 CrossRef CAS.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672–6687 RSC.
- J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108 CrossRef PubMed.
- K. Yagi, S. Hirata and K. Hirao, Phys. Chem. Chem. Phys., 2008, 10, 1781–1788 RSC.
- K. Yagi and H. Otaki, SINDO 3.6, RIKEN, 2014 Search PubMed.
- Y. Yu, Y. Wang, K. Lin, N. Hu, X. Zhou and S. Liu, J. Phys. Chem. A, 2013, 117, 4377–4384 CrossRef CAS PubMed.
- J. Korppi-tommola, Spectrochim. Acta, 1978, 34, 1077–1085 CrossRef.
- F. Perakis, L. De Marco, A. Shalit, F. Tang, Z. R. Kann, T. D. Ku, R. Torre, M. Bonn and Y. Nagata, Chem. Rev., 2016, 116, 7590–7607 CrossRef CAS PubMed.
- A. Panuszko, P. Bruździak, J. Zielkiewicz, D. Wyrzykowski and J. Stangret, J. Phys. Chem. B, 2009, 113, 14797–14809 CrossRef CAS PubMed.
- H. J. Bakker and J. L. Skinner, Chem. Rev., 2010, 110, 1498–1517 CrossRef CAS PubMed.
- E. P. Linton, J. Am. Chem. Soc., 1940, 62, 1945–1948 CrossRef CAS.
- A. A. Bakulin, M. S. Pshenichnikov, H. J. Bakker and C. Petersen, J. Phys. Chem. A, 2011, 115, 1821–1829 CrossRef CAS PubMed.
- Y. L. A. Rezus and H. J. Bakker, J. Phys. Chem. B, 2009, 113, 4038–4044 CrossRef CAS PubMed.
- K. Mazur, I. A. Heisler and S. R. Meech, J. Phys. Chem. B, 2011, 115, 2563–2573 CrossRef CAS PubMed.
- K. Kwak, S. Park, I. J. Finkelstein and M. D. Fayer, J. Chem. Phys., 2007, 127, 124503 CrossRef PubMed.
- K. M. Kast, J. Brickmann, S. M. Kast and R. S. Berry, J. Phys. Chem. A, 2003, 107, 5342–5351 CrossRef CAS.
- D. Laage and J. T. Hynes, Science, 2006, 311, 832–835 CrossRef CAS PubMed.
- E. Schneck, D. Horinek and R. R. Netz, J. Phys. Chem. B, 2013, 117, 8310–8321 CrossRef CAS PubMed.
- L. Larini and J.-E. Shea, J. Phys. Chem. B, 2013, 117, 13268–13277 CrossRef CAS PubMed.
- D. R. Canchi, P. Jayasimha, D. C. Rau, G. I. Makhatadze and A. E. Garcia, J. Phys. Chem. B, 2012, 116, 12095–12104 CrossRef CAS PubMed.
- C. Hölzl, P. Kibies, S. Imoto, R. Frach, S. Suladze, R. Winter, D. Marx, D. Horinek and S. M. Kast, J. Chem. Phys., 2016, 144, 144104 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. T. Titantah and M. Karttunen, J. Am. Chem. Soc., 2012, 134, 9362–9368 CrossRef CAS PubMed.
- W. H. Brandeburgo, S. T. van der Post, E. J. Meijer and B. Ensing, Phys. Chem. Chem. Phys., 2015, 17, 24968–24977 RSC.
- S. Imoto, H. Forbert and D. Marx, Phys. Chem. Chem. Phys., 2015, 17, 24224–24237 RSC.
- J. T. Titantah and M. Karttunen, Sci. Rep., 2013, 3, 2991 Search PubMed.
- Y. R. Shen, Nature, 1989, 337, 519–525 CrossRef CAS.
- M. Bonn, Y. Nagata and E. H. G. Backus, Angew. Chemie Int. Ed., 2015, 54, 5560–5576 CrossRef CAS PubMed.
- L. B. Sagle, K. Cimatu, V. a. Litosh, Y. Liu, S. C. Flores, X. Chen, B. Yu and P. S. Cremer, J. Am. Chem. Soc., 2011, 133, 18707–18712 CrossRef CAS PubMed.
- M. Sovago, E. Vartiainen and M. Bonn, J. Phys. Chem. C, 2009, 113, 6100–6106 CAS.
- A. G. F. de Beer, J.-S. Samson, W. Hua, Z. Huang, X. Chen, H. C. Allen and S. Roke, J. Chem. Phys., 2011, 135, 224701 CrossRef PubMed.
- M. Ahmed, V. Namboodiri, P. Mathi, A. K. Singh and J. A. Mondal, J. Phys. Chem. C, 2016, 10252–10260 CAS.
- S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Chem. Phys., 2009, 130, 204704 CrossRef PubMed.
- T. Ohto, K. Usui, T. Hasegawa, M. Bonn and Y. Nagata, J. Chem. Phys., 2015, 143, 124702 CrossRef PubMed.
- S. Yamaguchi, J. Chem. Phys., 2015, 143, 34202 CrossRef PubMed.
- J. A. Mondal, S. Nihonyanagi, S. Yamaguchi and T. Tahara, J. Am. Chem. Soc., 2012, 134, 7842–7850 CrossRef CAS PubMed.
- T. Ohto, E. H. G. Backus, C.-S. Hsieh, M. Sulpizi, M. Bonn and Y. Nagata, J. Phys. Chem. Lett., 2015, 6, 4499–4503 CrossRef CAS PubMed.
- A. Fiore, V. Venkateshwaran and S. Garde, Langmuir, 2013, 29, 8017–8024 CrossRef CAS PubMed.
- B. J. Bennion and V. Daggett, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 6433–6438 CrossRef CAS PubMed.
- J. Hunger, N. Ottosson, K. Mazur, M. Bonn and H. J. Bakker, Phys. Chem. Chem. Phys., 2015, 17, 298–306 RSC.
- P. H. Yancey and G. N. Somero, J. Exp. Zool., 1980, 212, 205–213 CrossRef CAS.
- H. R. Palmer, J. J. Bedford, J. P. Leader and R. A. Smith, J. Biol. Chem., 2000, 275, 27708–27711 CAS.
- L. M. Samuelsson, J. J. Bedford, R. A. J. Smith and J. P. Leader, Comp. Biochem. Physiol. A. Mol. Integr. Physiol., 2005, 141, 22–28 CrossRef CAS PubMed.
- T. C. Gluick and S. Yadav, J. Am. Chem. Soc., 2003, 125, 4418–4419 CrossRef CAS PubMed.
- F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Biophys. J., 2009, 97, 2559–2566 CrossRef CAS PubMed.
- F. Meersman, D. Bowron, A. K. Soper and M. H. J. Koch, Phys. Chem. Chem. Phys., 2011, 13, 13765 RSC.
- H. Kokubo, C. Y. Hu and B. M. Pettitt, J. Am. Chem. Soc., 2011, 133, 1849–1858 CrossRef CAS PubMed.
- J. Mondal, D. Halverson, I. T. S. Li, G. Stirnemann, G. C. Walker and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9270–9275 CrossRef CAS PubMed.
- J. Rösgen and R. Jackson-Atogi, J. Am. Chem. Soc., 2012, 134, 3590–3597 CrossRef PubMed.
- M. Lever, K. Randall and E. A. Galinski, Biochim. Biophys. Acta, 2001, 1528, 135 CrossRef CAS.
- U. S. Mohapatra, G. S. Roy and S. K. Dash, Phys. Chem. Liquids, 2001, 39, 443–451 CrossRef CAS.
- P. Ganguly, N. F. A. van der Vegt and J.-E. Shea, J. Phys. Chem. Lett., 2016, 7, 3052–3059 CrossRef PubMed.
- P. Ganguly, T. Hajari, J.-E. Shea and N. F. A. van der Vegt, J. Phys. Chem. Lett., 2015, 6, 581–585 CrossRef CAS PubMed.
- G. Borgohain and S. Paul, J. Phys. Chem. B, 2016, 120, 2352–2361 CrossRef CAS PubMed.
- Q. Zou, B. J. Bennion, V. Daggett and K. P. Murphy, J. Am. Chem. Soc., 2002, 124, 1192–1202 CrossRef CAS PubMed.
- S. S. Cho, G. Reddy, J. E. Straub and D. Thirumalai, J. Phys. Chem. B, 2011, 115, 13401–13407 CrossRef CAS PubMed.
- Z. A. Levine, L. Larini, N. E. LaPointe, S. C. Feinstein and J.-E. Shea, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2758–2763 CrossRef CAS PubMed.
- Y. Yang, Y. Mu and W. Li, Phys. Chem. Chem. Phys., 2016, 18, 22081–22088 RSC.
- J. Ma, I. M. Pazos and F. Gai, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8476–8481 CrossRef CAS PubMed.
- B. Ding, M. R. Hilaire and F. Gai, J. Phys. Chem. B, 2016, 120, 5103–5113 CrossRef CAS PubMed.
- G. Graziano, Phys. Chem. Chem. Phys., 2011, 13, 17689–17695 RSC.
- G. Graziano, Phys. Chem. Chem. Phys., 2012, 14, 13088 RSC.
- Y. S. Kim and R. M. Hochstrasser, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 11185–11190 CrossRef CAS PubMed.
- J. Zheng, K. Kwak, J. B. Asbury, C. Xin and M. D. Fayer, Science, 2005, 305, 61–66 Search PubMed.
- D. Schach, C. Globisch, S. J. Roeters, S. Woutersen, A. Fuchs, C. K. Weiss, E. H. G. Backus, K. Landfester, M. Bonn, C. Peter and T. Weidner, J. Chem. Phys., 2014, 141, 22D517 CrossRef PubMed.
- A. P. Boughton, I. Andricioaei and Z. Chen, Langmuir, 2010, 26, 16031–16036 CrossRef CAS PubMed.
- A. P. Boughton, K. Nguyen, I. Andricioaei and Z. Chen, Langmuir, 2011, 27, 14343 CrossRef CAS PubMed.
- H. Lutz, V. Jaeger, R. Berger, M. Bonn, J. Pfaendtner and T. Weidner, Adv. Mater. Interfaces, 2015, 2, 1500282 CrossRef.
- B. Ding, A. Panahi, J. J. Ho, J. E. Laaser, C. L. Brooks, M. T. Zanni and Z. Chen, J. Am. Chem. Soc., 2015, 137, 10190–10198 CrossRef CAS PubMed.
- J. K. Carr, L. Wang, S. Roy and J. L. Skinner, J. Phys. Chem. B, 2014, 119, 8969–8983 CrossRef PubMed.
- R. Pandey, K. Usui, R. A. Livingstone, S. A. Fischer, J. Pfaendtner, E. H. G. Backus, Y. Nagata, J. Fröhlich-nowoisky, L. Schmüser, S. Mauri, J. F. Scheel, D. A. Knopf, U. Pöschl, M. Bonn and T. Weidner, Sci. Adv., 2016, 2, e1501630 Search PubMed.
- M. A. Donovan, Y. Y. Yimer, J. Pfaendtner, E. H. G. Backus, M. Bonn and T. Weidner, J. Am. Chem. Soc., 2016, 138, 5226–5229 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2017 |







