 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic self-organization in fire ant rafts underpins collective longevity and threat responsiveness†
Zachary T. White and
Franck J. Vernerey *
*
Department of Mechanical Engineering, Materials Science and Engineering Program, University of Colorado Boulder, Boulder 80303, USA. E-mail: franck.vernerey@colorado.edu
First published on 10th July 2025
Abstract
Many living collectives must balance strategies between long-term energy conservation and short-term threat response; the ability for groups to dynamically self-organize into a variety of structures to address these needs is therefore essential. We show that fire ant Solenopsis invicta rafts which form buoyant bilayers in hostile flooded environments, adapt to conserve energy by separating into active and stationary phases. A simple kinetic model incorporating motility induced phase separation provides a useful framework to understand this transition, where ants form clusters by slowing down to participate in social interactions. We find that external stimuli either weakens or strengthens these interactions. The former leads to dissolution of clusters and fast-mobilization of surface ants, revealing how clusters could serve a secondary purpose with rapid mobilization aiding exploration through formation of bridges. These results highlight how swarms and other living groups can adapt survival strategies even in the absence of central control or global knowledge.
1 Introduction
In hostile environments, many organisms face the dual challenge of conserving energy for self-preservation while also being capable of rapid, energy-intensive responses to escape imminent threats.1–3 For instance, desert animals minimize activity during the hottest parts of the day to conserve water and energy, but can rapidly mobilize when a predator approaches.4 An added challenge arises when such survival decisions must be made by groups, as seen in swarming insects,5,6 and terrestrial,7 aquatic,8,9 and aerial flocks10–13 which generally function without central coordination or global knowledge of the system. In these systems, the ability for groups to coordinate the transition between survival strategies is therefore crucial.Social insects like the red imported fire ant Solenopsis invicta navigate hostile flooded environments, by constructing a buoyant bilayer, termed a raft.14 Ants directly on the water cohere into tough dynamic networks15,16 by connecting their limbs and tarsal claws,17 while atop free ants roam unencumbered. Our previous work found that ants mediate between these layers, in a process known as treadmilling.18 This drives continual change in the rafts shape, notably the stochastic emergence of protrusions. These tether-like structures likely aid in anchoring the raft and can grow into bridges to facilitate escape. The highly dynamic nature of fire ant rafts means that in comparison to nesting and towering colonies, active rafts remain the most energetically costly.19 However, fire ants alongside many other living collectives often dynamically employ strategies to conserve energy.20,21 It is well known that three-dimensional fire ant aggregates undergo spontaneous activity cycling with long periods of collective dormancy.22 In fact, recent experimental work by Anderson and Fernandez-Nieves have shown that non-flooded fire ant swarms form stationary clusters as agents slow down upon approaching one another.23 It is hypothesized that ants form these clusters both to participate in social behaviors such as allogrooming,24 but also to conserve energy. Interestingly, formation of these clusters can be understood through the framework of motility-induced phase separation (MIPS) a common feature of many active matter systems.25–28
In this work we show that during long periods of inactivity, ants on the raft surface gradually phase separate into an active population of free ants and a novel phase of inactive ants which remain in stationary clusters. In particular, we explore how clustering informs the global raft morphodynamics. Incorporating MIPS with previous work, which centered exclusively around the dynamics of active rafts, we develop a simple kinetic model that aims to capture the global raft morphodynamics. We then leverage the model to investigate how rafts respond under varying external stimuli. Here we find that stimuli either strengthens or weakens surface ant interactions with the latter leading to cluster collapse and a sudden shift in rafts morphodynamics. This work helps uncover how rafts manage the delicate balance between energy conservation and rapid mobilization, revealing insights into the collective decision-making processes that underpin their survival strategies.
2 Experimental methods
2.1 Ant collection & maintenance
The care and operation of animals followed the University of Colorado Boulder ethical standards for the study or invertebrate species. Fire ants were obtained from six distinct colonies in Fort Worth, TX in early July (see Fig. S1, ESI† for colony locations). Female workers were transferred to 5-gallon buckets where they acclimatized for 3 days before testing. Winged alates and brood were removed if found. They were fed a diet of mealworms and a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of honey and water provided in a 9 cm Petri dish ad libitum. Water was provided by plugging a half-filled test tube with a soaked cotton ball.
1 mixture of honey and water provided in a 9 cm Petri dish ad libitum. Water was provided by plugging a half-filled test tube with a soaked cotton ball.
To prepare a trial, the bucket side walls were generously coated in baby powder (cornstarch) to prevent ants from escaping. We gradually added water at a rate of about 2.5 mL s−1 until their mound was completely submerged under water, and ants formed a floating raft. The colony was then transferred to a dry bucket, where they were allowed to rest for 30 minutes. To prepare an experiment the desired number of ants was then siphoned from the dry bucket and weighed. Following experiments all ants were returned to a new sterile bucket filled with equal parts sand and mulch, in which they constructed a new subterranean mound.
2.2 Experimental setup
The set-up consisted of a water filled container 35 cm width by 55 cm length by 33 cm depth. An acrylic rod 8 mm in diameter was positioned vertically and held in place on the bottom of the container using a compression fitting. Water was added until the rod was submerged no more than 2 mm below the water line. The raft was affixed to the rod using either a needle or 1 cm square patch of velcro, with no significant difference observed between attachment styles. The needle, which was used for small rafts (N ∼ 500 ants), was fixed vertically from the rod and allowed to protrude above the water. When using Velcro, the patch was fixed to the top of the rod but below the water surface. A camera (iPhone 12) was mounted directly above the rod, perpendicular to the water surface and captured time lapse images with 1 s intervals between frames (see schematic Fig. 1A). We initially placed ants as a dense cluster and tracked rafts areal spread over several hours. We tested rafts of various sizes, from as few as N = 400, to upwards of N = 7000 ants. Raft areas were estimated from timelapse images, using Matlab 2023b. Frames were first segmented into a binary image through a manually adjusted color threshold. To remove small features, while still preserving the raft's area, a morphological closing was performed. This was followed by a filtering step that filled any remaining holes. Pixels corresponding to the raft were summed and converted to area (mm2) via a calibration object. Table S1, ESI† gives a detailed description of the experimental trials conducted. | ||
| Fig. 1 Quantifying global raft morphogenesis. (A) Apparatus used to track areal change of rafts. (B) Ants spread into a thin raft following initial placement. (C) Rafts over time adapt to a new morphology by forming dense clusters of stationary ants. (D) and (E) Normalized area A*(t) for rafts undergoing a wetting or dewetting transition; note that we offset the data from the long term normalized area A*(∞) such that it decays to zero, but does not alter the time constant. The dashed and dotted lines represent bounds for minimum and maximum values of the time constant. See Fig. S4 and S5, ESI† for raw data and fits. | ||
3 Results
3.1 Global raft dynamics
Rafts formed two distinct morphologies. Initially, clusters of ants rapidly spread wetting the water surface until a pancake shaped lens (Fig. 1B) was formed, consistent with early findings by Mlot et al.17 However, over longer periods of time, and in the absence of external stimuli, ants adapted their morphology by dewetting from the water. In the most extreme cases, the final shape consisted of a dense ‘droplet’ like cluster (Fig. 1C and Movie S1, ESI†), positioned atop the raft, where further analysis revealed ants within the cluster to remain stationary (Fig. S3 and Movie S2, ESI†). We employ analogies to fluids (wetting and dewetting) to describe the transition between spread and clustered morphologies. For both transitions, we plot the normalized area over time, where the raft area A(t) was extracted from timelapse images (see Experimental methods section for details). We assume a planar raft density (ρs = 0.304 ants mm−2)18 to remain roughly constant while the total number of ants N was estimated through their average mass 1.3 ± 0.8 mg17 (all measurements reported as mean ± SE). We find for both wetting (Fig. 1D) and dewetting (Fig. 1E) the data agrees to an exponential of the form,
over time, where the raft area A(t) was extracted from timelapse images (see Experimental methods section for details). We assume a planar raft density (ρs = 0.304 ants mm−2)18 to remain roughly constant while the total number of ants N was estimated through their average mass 1.3 ± 0.8 mg17 (all measurements reported as mean ± SE). We find for both wetting (Fig. 1D) and dewetting (Fig. 1E) the data agrees to an exponential of the form,| A*(t) = [A*(0) − A*(∞)]exp(−t/τi) + A*(∞) | (1) |
3.2 Kinetic raft model
In our previous work, we developed a discrete ant-inspired agent-based model which captured both treadmilling and the stochastic emergence of protrusions.29 While discrete agent-based models can provide great accuracy and insight into the local rules driving globally observed phenomena, when systems are complex, such as rafts which are multiphasic, they often must make many phenomenological assumptions, leading to a loss of generality. Thus in this work, we develop a global model that seeks to capture only the essential features that lead to changes in raft morphology over time (i.e. raft area). To do this, we model the raft as three distinct phases across two layers, (see schematic presented in Fig. 4). The choice to model the ant raft as a bilayer is supported by biological observations14,17,18 where, at the base is the structural phase, formed by tightly linked ants that create the floating scaffold of the raft. On top of this layer lies a population of ants that organize into two observable phases: a motile phase, where ants actively move across the surface, and an immobile dense phase, where ants remain largely stationary but densely packed. While our earlier models did not account for this upper immobile phase, we will show that including it is essential to explain key experimental observations. In our model, each i-th phase is assumed to occupy an area Ai related to the number of ants Ni through the planar density ρi. The total area A of the raft is the same area occupied by the structural ants Ns which pack into the bottom layer with the experimentally measured fixed planar density ρs = 0.304 ants mm−2. Meanwhile on the top layer free (Nf ants) and cluster (Nc ants) coexist. The combined area occupied by the top two phases is thus confined by the structural layer area, i.e. A = As = Af + Ac. Cluster ants much like structural ants are packed within close proximity of one another. Thus we assume a fixed density ρc = nρs where n helps account for the fact that clusters are often three-dimensional. We find a value of n = 7 works best when large clusters, like shown in Fig. 1B, form. The free ant density ρf varies freely according to raft size and number of free ants. Assuming that the total number of ants N = Ns + Nc + Nf remains conserved, we write:
 | (2) |
Furthermore, since by definition free and cluster ants sit atop the structural layer we can impose an additional constraint on the areal time-rate of change,
 | (3) |
To capture the dynamics, four rates (ant min−1) describe the conversion of ants between the three phases, (shown schematically in Fig. 2A). Between structural and free phases, the “treadmilling rates” are defined by the deposition rate J+ and ejection rate J−, while the so-called “MIPS rates” capture the conversion of ants between the free and cluster phases with inward and outward rates Jin and Jout, respectively. With these definitions, we assume that ants do not convert between structural and cluster phases. Since experimentally, cluster ants remain stationary (Fig. S3 and Movie S2, ESI†), and therefore do not directly deposit, we find this to be a reasonable assumption. Additionally, although structural ants could eject into the cluster, we believe it progresses at a much smaller rate than J− and thus ignore it out of simplicity. As ants in the structural layer remain tightly bound through their tarsal claws and mandibles17 and are also individually quite weak supporting about 200 dynes of force16 we feel that this assumption is reasonable. More advanced imaging techniques that could track ant trajectories within the cluster, such as X-ray spectroscopy of fire ants that have ingested radiographic contrast,30 could help confirm this assumption. Altogether, the time-rate of change for the three phases is
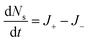 | (4) |
 | (5) |
 | (6) |
For clarity of the presentation, let us first ignore the formation of clusters by setting the number of cluster ants Nc equal to zero and disabling the rates pertaining to clustering (Jin = Jout = 0). This eliminates eqn (5) and leads to a simplified kinetic model – based exclusively on the underlying mechanisms of treadmilling. Fig. 2B. Schematically depicts the simplified treadmilling process in 1D in which structural ants Ns are mediated to the surface by ejection events, meanwhile free ants Nf deposit at the raft boundary. Assuming roughly conserved ρs, the rate of structural ants exiting to become free ants is
δ = 2ρs![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif)
| (7) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 1.75% min−1 is the linear contraction rate measured from experiments,18 with the factor two emerging because
= 1.75% min−1 is the linear contraction rate measured from experiments,18 with the factor two emerging because ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is a linear rate, while structural exit is an areal phenomenon. For simplicity we assume that contraction remains isotropic and constant giving an areal flux
is a linear rate, while structural exit is an areal phenomenon. For simplicity we assume that contraction remains isotropic and constant giving an areal flux| j− = δ | (8) |
| j+ = αg | (9) |
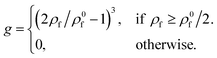 | (10) |
This expression ensures that ants cease to deposit below the target value ρ0f/2, while the deposition flux increases strongly with ρf above this threshold, due to the cubic exponent. This helps reflect the rapid growth in raft area often observed during the initial wetting process when the surface is dense. Experimentally for highly active rafts, ρ0f ∼ 0.072 ants mm−2,18 however to remain general we let ρ0f = Ωρs, where Ω is defined as the target density parameter. Effectively, Ω serves as a useful model parameter to control the ratio of free to structural ants at pseudo steady state, or packing fraction as shown in (Fig. S2, ESI†).
The above system of equations is solved numerically using MATLAB R2023b, given the initial number of ants, with a forward Euler integration scheme,
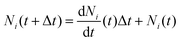 | (11) |
| Parameter | Description | Value | Units | Source |
|---|---|---|---|---|
| σ | Characteristic ant length | 2.93 | mm | 18 |
| ν0 | Mean ant self-propulsion velocity | 2.8128 | mm min−1 | 18 |
| ρs | Planar density of structural phase | 0.3037 | ants mm−2 | 18 |
| ρc | Planar density of cluster phase | 7ρs | ants mm−2 | |
| α | Deposition flux | 0.02 | Depositions min−1 ant−1 | 18 |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) |
Linear contraction rate | 0.0175 | % min−1 | 18 |
| δ | Ejection flux | 0.01 | Ejections min−1 mm−2 | Eqn (7) |
To model the raft wetting and dewetting we select initial phase fractions ϕi that match experiments and vary the only free model parameter Ω ∈ [0,5]. We fit the model through parameter regression analysis (see Fig. S6A and S7A, ESI† for details). From this, we obtain for wetting, a target density of Ω = 1.06 or about a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 free to structural ant ratio, which aligns closely with earlier wetting experiments by Mlot et al. where the ratio was found to vary between 0.6–1.5.17 Additionally, we predict a wetting time constant on the order of τw = 47.6 s (Fig. S6B, ESI†), in good agreement with experimental results. However, over the range of Ω explored, the simplified treadmilling model poorly captures dewetting (Fig. S7B, ESI†) with the best fit target density of Ω = 1.5 which yielded τdw = 4.33 min, about an order of magnitude faster than experiments on average. We hypothesize that this discrepancy arises from our initial assumption of a homogeneous free ant surface density (i.e. ignoring cluster ants), as small changes to the target density parameter Ω greatly reduce the total deposition since all free ants are available to deposit. Instead, separation of surface ants into active free ants and passive clustering ants, the latter which forgo participation in treadmilling altogether, is therefore key to capture the dewetting process.
1 free to structural ant ratio, which aligns closely with earlier wetting experiments by Mlot et al. where the ratio was found to vary between 0.6–1.5.17 Additionally, we predict a wetting time constant on the order of τw = 47.6 s (Fig. S6B, ESI†), in good agreement with experimental results. However, over the range of Ω explored, the simplified treadmilling model poorly captures dewetting (Fig. S7B, ESI†) with the best fit target density of Ω = 1.5 which yielded τdw = 4.33 min, about an order of magnitude faster than experiments on average. We hypothesize that this discrepancy arises from our initial assumption of a homogeneous free ant surface density (i.e. ignoring cluster ants), as small changes to the target density parameter Ω greatly reduce the total deposition since all free ants are available to deposit. Instead, separation of surface ants into active free ants and passive clustering ants, the latter which forgo participation in treadmilling altogether, is therefore key to capture the dewetting process.
3.3 Clustering drives raft morphodynamics
To explore how clusters influence evolution of the raft, we first characterized their extent and formation. We obtained the surface “density” by measuring the intensity of light transmitted through the raft, which yields a distribution of transmissivity values between zero and unity (see Section S1 and Fig. S8, ESI†). As the system phase separates this distribution should become bimodal reflecting the inhomogeneous surface density. We provide snapshots of the distribution, for a raft dewetting (Fig. 3A), and wetting (Fig. 3B). Additionally, we used particle image velocimetry (PIV) to detect the concomitant evolution in the surface ant velocity field (see Section S2 and Fig. S9, ESI† for details).31 This serves as a useful indicator towards which morphology the raft evolves. Particularly, surface ant speeds are expected to decrease as they join and remain stationary in the cluster. Dissolution of a cluster, on the other hand, should correlate with sustained ant speeds. Indeed Fig. 3A shows that as a raft dewets, the dense phase grows (Fig. 3A, circled 1) accompanied by a decrease in surface ant velocity. For a raft wetting, the dense peak (Fig. 3B, circled 1) gradually subsides as the cluster decreases until a single, albeit broad, dilute phase is present. As expected PIV analysis revealed surface ant velocity, particularly at protrusion tips, to remain sustained. Thus separation into dilute and dense phases atop the raft, arises when surface ants slow down to participate in social interactions, as seen in nesting fire ant colonies.23 While it is unclear as to the exact physiological mechanisms which drive ants to form these social interactions (although likely due to social allogrooming) ants individual behaviors control the rafts macroscopic features (i.e. clusters) consistent with the concepts of decentralized control. That clusters remain stable for long periods of time suggests that clusters help minimize energy expenditure. While here we do not present direct measurements such as metabolic data, recent work revealed that ants’ metabolic activity in tower-like structures, where ants are similarly confined and relatively stationary, was lower than their active rafting counterparts.19To quantify how clustering informs global raft morphology, we now reconsider our kinetic model by enabling free ants (Nf ants) to join into clusters (Nc ants) and vice versa. To capture the cluster dynamics (i.e. Jin and Jout), we employ the concept of motility induced phase separation (MIPS) proposed by Redner et al.32 which provides the inward and outward fluxes into the cluster. We should point out that Redner's model is a minimal model which assumes particles self-propel with a constant force and interactions between particles are restricted exclusively to isotropic excluded-volume repulsion. This is contrary to findings presented above and by Anderson and Fernandez-Nieves23 where ants slow down upon approaching their neighbors. A more accurate approach would be to subsume interactions into a density dependent velocity term that decreases agents self-propulsion with increasing local density.25,33 Redner's model is thus an extreme case where the density dependent velocity function is a step function, such that free particles are non-interacting, and cluster particles are completely trapped. While geometric confinement, especially in protrusions, leads to directional alignment of surface ants, our previous work found that surface ants directional correlation in the raft bulk is very weak,18 the assumption then that free ants are non-interacting is reasonable. Furthermore, there are several interaction rules that could give rise to the presented model, however, as we do not precisely know what they are, we constructed the model based on experimental observations. Since ultimately we seek to capture broad global trends in the raft morphodynamics we adopt Redner's model for its simplicity. Nevertheless, we expect differences between these two picture of MIPS to influence the onset of phase separation, but not to change the overall behavior of the model.
In any case, assuming the presence of a circular cluster, a priori, with a boundary length of  , free ants join the cluster through collisions with an incoming flux per unit length
, free ants join the cluster through collisions with an incoming flux per unit length
 | (12) |
 | (13) |
We first verified that this model, in the absence of treadmilling rates (i.e., J+ = J− = 0), exhibits the classical clustering behavior observed in other active particle systems.34–36 We also found that the presence of treadmilling rates in eqn (6) do not affect this result. A contour map of the relative cluster phase fraction ϕC = ϕc/(ϕf + ϕc) (ϕc and ϕf are the cluster and free phase fractions respectively) shows the binodal envelop beyond which clusters form (Fig. 5A). Thus although interactions may always be present, ants do not immediately form clusters, which only become stable past the binodal line. The onset of this envelop is also a function of the target density parameter Ω, with higher target densities resulting in larger clusters. This aligns with experimental observations on collections of dry ants, which found that clustering longevity varied with the level of confinement.23
We again perform a parameter regression analysis (see Fig. S10 and S11, ESI†) with the same initial phase fractions ϕi from before now varying Ω ∈ [0.01,2] and τR ∈ [0.01,25] s. For wetting we obtained a target density of Ω = 1.05 similar to before, with a social interaction time of τR = 0.2 s. As expected, when interaction times are short and clusters are unstable, the model predicts rapid wetting in good agreement with experiments (Fig. 5B) and the previous simplified treadmilling model. For dewetting we obtained a target density of Ω = 0.160 and τR = 7.6 s and as shown in (Fig. 5C) the model predicts gradual dewetting in good agreement with experimental data. While wait times individually may vary, τR reasonably agrees with previous observations which found ants within dense clusters to remain stationary for more than 30 s.23 We also note that the target density Ω = 0.160 corresponds to a target surface density of ρ0f = 0.0485 ants mm−2 which is close to the experimental surface density ρ0f = 0.072 ants mm−2 of active rafts observed in our previous work.18 Considering that dewetting rafts typically begin as active, a highly dilute population of free ants (or low Ω) seems reasonable. Instead of a singularly dense phase (high Ω) as modeled by the earlier simplified-treadmilling model, dewetting is characterized by the gradual growth of a cluster(s) with a coexisting dilute population of free ants. Clustering, especially over long time periods is therefore key to explain raft morphodynamics.
Of the rafts observed to dewet, a significant fraction of the colony participated in clustering, as revealed by both the model and through the cluster ant phase fraction (Fig. 5D). Recently, it was shown that spread rafts display higher group metabolic rates than both ants on dry land and when forming towers.19 Assuming that rafting ants consume more energy than their clustering counterparts, variation in energy expenditure between tasks points to an unequal division of labor. We quantify this energy inequality by computing an effective “Gini” coefficient37 G = (Nc)/(N − 1), where Nc is the number of inactive cluster ants. This coefficient measures the workload deviation from fully cooperative (G = 0, all ants participate in treadmilling) to unshared (G = 1, a single worker performs all work). Although it is difficult to compute G experimentally, our model predicts upwards ∼80% (G = 0.83) of the colony to remain in the cluster, in good agreement with observations of extreme clusters (Fig. 1C). Recall that some fraction of ants must form the structural layer and so G does not approach unity in the limit as τR → ∞ shown by the dashed line in Fig. 5E. In any case, we believe that labor inequality reinforces our theory that rafts follow a long-term self-preservation strategy to reduce collective energy expenditure. In the absence of external stimuli, clustering becomes an attractive way to improve energy conservation. Meanwhile a constant flux of ants due to treadmilling and MIPS, ensures continual recycling of ants, such that no one ant does all the work. While clustering may improve aggregate survivability, rafts must also contend with other objectives, including colony defense and colonization of new land. To gain insight into how rafts might adapt their morphology to meet these needs, we turn to the role external stimuli plays on raft response.
3.4 Surface ants modify social interactions in response to stimulus
Ants, whose vision is relatively limited, rely on chemical signaling and mechanosensitive antenna to communicate and initiate retaliatory behaviors (e.g. stinging).38 If inter-ant communication tends to condense the raft, we expect external stimuli to disrupt these social interactions altogether, leading to cluster dissolution, as ants react to improve defensiveness. To test this hypothesis, we conducted a stimulus-response study on n = 4 rafts, schematically illustrated in Fig. 6A, where rafts were first allowed to dewet the surface until a substantial cluster was formed, followed by a rapid and forceful burst of air for 10 seconds. Remarkably, our observations in Fig. 6B and C (and Movie S3, ESI†) show a marked transition in raft behavior, where exposed surface ants suddenly activated leading to a rapid growth in the normalized area A*. This sudden activation and subsequent growth, on the order of minutes, is reminiscent of the initial spreading seen earlier. We simulated the breakdown in ants social interactions, by reducing τsR during the stimulus period. Fig. 6C shows that our results agree quite well with experiments. We find lower values of τsR result in larger peak raft areas, but despite a significant reduction in the interaction time only in the limit as τsR → 0 does our model predict complete cooperation (G = 0) in the raft, (Fig. 6C inset). That ants should to some extent maintain interactions despite external influence is unsurprising. Indeed throughout all observed trials, complete dissolution of the cluster was not observed. Lack of penetration by the stimulus into the core of the cluster, likely explains this observation, as unaffected ants retained strong social interactions. In experiments, raft spreading persisted after stimulus removal (Fig. 6D), suggesting a refractory period as ants slowly reactivated social interactions. PIV analysis of the raft surface supports this, with the mean surface ant velocity 〈v〉 rapidly increasing at stimulus, before decaying to its pre-stimulus value over the course of several minutes, (Fig. 6D).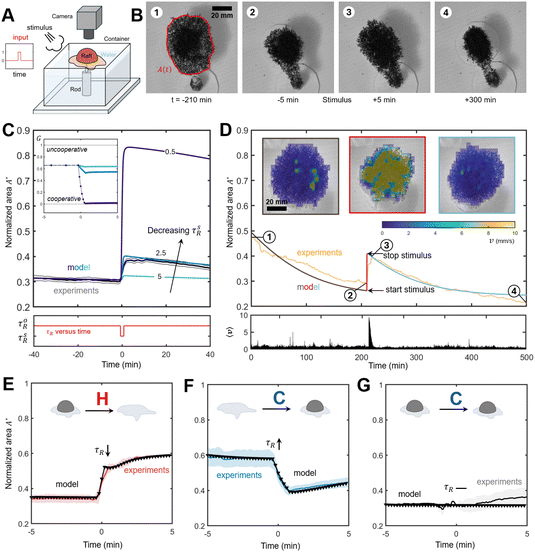 | ||
| Fig. 6 Raft response to external stimuli. (A) Schematic illustration of apparatus to track rafts response to stimulus. (B) Snapshots of the raft adapting during stimulus experiment where negative time denotes pre-stimulus, and positive post-stimulus. The raft area is highlighted in red. (C) Top panel: Shown in black is the normalized area A*(t) of n = 4 rafts. In color are simulated results for Ω = 0.165 and τsR ∈ [0.5,2.5,5] s. Lower values of τsR correspond to shorter interaction times between agents. A value of τoR = 7.4 s was used otherwise. Inset: Effective Gini coefficient, G, between t = −5 and +5 min shows how cooperation in the raft increases during stimulus. Bottom panel: The interaction time versus time for simulations where τsR is during stimulus. (D) Top panel: Normalized area A*(t) of a raft adapting to stimulus. Numeric labels correspond to snapshots presented in (B). Simulated response to stimulus is shown in red, the absence of stimulus with grey and blue. Velocity contours of the raft surface, extracted using PIV analysis, are shown before stimulus (grey), immediately after stimulus (red) and after stimulus (blue) taken in approximately 2 hour intervals. Bottom panel: Mean surface velocity over time revealing sudden activation in surface ants from the stimulus. (E) Area for (n = 2) clustered rafts (red) spreads rapidly on introduction of hot water (40 °C). (F) Normalized area of (n = 4) rafts (blue) following application of cold water (13 °C) to an initially spread raft causes sudden contraction and clustering. (G) The normalized area (grey) remains effectively unchanged when (n = 2) already clustered rafts are subjected to cold water (13 °C). For all (E)–(G) simulations are shown in black where to simulate application of water the interaction time τR is either increased or decreased (denoted by arrows) only during the stimulus period. See Tables S2 and S3, ESI† for simulation parameters. All shaded regions denote SE. | ||
So far we have restricted our study to the interaction time τr. Yet, ant metabolic activity is known to scale with temperature.19 This implies a temperature dependent self-propulsion speed νo(T) with higher temperatures increasing consumption of andensoine triphosphate (ATP) driving faster agent motility. To test its effect on raft morphodynamics we subjected rafts to cold (13 °C) and hot water (40 °C) by evenly spraying the raft surface with a jet of water for 5 seconds. Our results in Fig. 6E–G clearly show a temperature dependent response on raft behavior measured by the change in normalized area. To simulate these observations, we vary Ω, τR, and νo, see Table S3, ESI† for parameters obtained pre-stimulus, during stimulus, and post-stimulus.
Hot water, just as air, causes cluster dissolution and subsequent wetting (Fig. 6E and Movie S4, ESI†), which suggests that hot water weakens ants interactions (reduced τR), possibly due to the abnormally high temperature. This is also supported by our simulations which found that increasing ν0 was unable to capture experimental trends, contrary to our initial hypothesis which predicted that larger ν0 should increase the inward flux jin due to increased collision probability. Yet, if one considers inertial effects in systems of active particles then increasing propulsion has been shown to lead to dissolution of the dense phase as particles inertia begins to play an important role in clustering stability.39 While generally, inertial effects are ignored in systems of ants, phase separation in ants may be re-entrant at higher temperatures, due to weakening interactions within the cluster. Instead we find during stimulus, the social interaction time reduces to τR = 0.8 s, consistent with wetting. Additionally, we obtain an increase in the target density from Ω = 0.165 pre-stimulus, to Ω = 0.60 post-stimulus, which are also close to values obtained for the earlier dewetting and wetting experiments, respectively. Interestingly, application of cold water to an active raft, leads to clearly contrasting results from previous observations, with an abrupt reduction in the rafts area, (Fig. 6F and Movie S5, ESI†). Contrary to both air and hot water, cold water thus appears to reinforce interactions (increased τR), perhaps as colder water is perceived more naturally to ants. We find that modifying τR or ν0 was not enough to capture the rafts abrupt response, with our model suggesting an increase to the ejection flux δ = 0.15 ejections min−1 mm−2 about 15 times that of unperturbed rafts (δ = 0.01 ejections min−1 mm−2). This, however, aligns with experiments where closer inspection reveals rapid contraction of structural ants, while free ants appear to freeze into a stationary cluster (Movies S5 and S6, ESI†). Unsurprisingly, for already clustered rafts application of cold water lead to no significant change in the morphology (Fig. 6G and Movie S6, ESI†), although following removal of stimulus, rafts grew slightly. This is likely since even cold water leads to some free ant activity, which also might explain the slight increase in raft area observed after stimulus for cold water applied to an active raft, Fig. 6F. In any case, external stimuli seems to either weaken or reinforce interactions thereby informing the overall morphodynamics.
This rapid response to external stimuli is crucial for the rafts survival and ability to evade threats. We finally aim to demonstrate this adaptive behaviour by evaluating the raft's capacity to extend bridge-like protrusions in response to mechanical sensing. When perturbed by the placement of secondary protuberance (rod) placed 178.4 mm or about 60σ from the first rod and adjacent to a protrusion, we observed the rapid emergence of a bridge like structure (Fig. 7A and B) that grew with an average rate of ![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) = 10.9 mm min−1 approximately 350% faster than protrusions (for which we measured
= 10.9 mm min−1 approximately 350% faster than protrusions (for which we measured ![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) = 3.6 mm min−1) in good agreement with previous work
= 3.6 mm min−1) in good agreement with previous work ![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) = 2.59 mm min−1 (ref. 18) (Fig. 7D). See Section S3 and Fig. S12 and S13, ESI† for details and raw data for bridge and protrusion growth. Notice that we classify protrusions, which form stochastically, as less then 40 ants in length. Onset of bridge formation was followed by a decrease in global cluster fraction, Fig. 7C (see Fig. S14 and Movies S7, S8 for details, ESI†). Thus the sensing of new anchor points, acts similarly to a sudden stimulus, although how this localized detection quickly propagates (i.e. through chemical or mechanical signals24,40,41) to the full raft remains to be investigated. Nonetheless, clusters could serve as an “ant reserve” ready to be rapidly deployed when a protrusion makes contact with a mechanical anchor. Interestingly, growth rate of both protrusions and bridges decreased with colony age (Fig. 7E) which supports our hypothesis that ants form large stationary clusters and suppress raft growth in order to conserve energy.
= 2.59 mm min−1 (ref. 18) (Fig. 7D). See Section S3 and Fig. S12 and S13, ESI† for details and raw data for bridge and protrusion growth. Notice that we classify protrusions, which form stochastically, as less then 40 ants in length. Onset of bridge formation was followed by a decrease in global cluster fraction, Fig. 7C (see Fig. S14 and Movies S7, S8 for details, ESI†). Thus the sensing of new anchor points, acts similarly to a sudden stimulus, although how this localized detection quickly propagates (i.e. through chemical or mechanical signals24,40,41) to the full raft remains to be investigated. Nonetheless, clusters could serve as an “ant reserve” ready to be rapidly deployed when a protrusion makes contact with a mechanical anchor. Interestingly, growth rate of both protrusions and bridges decreased with colony age (Fig. 7E) which supports our hypothesis that ants form large stationary clusters and suppress raft growth in order to conserve energy.
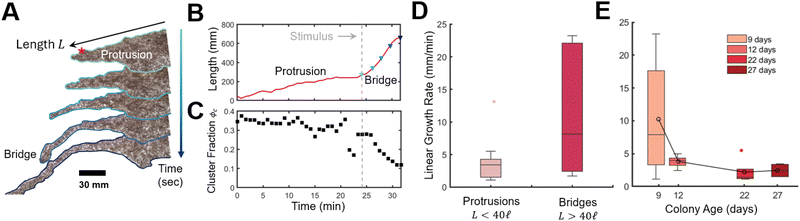 | ||
Fig. 7 Dynamics of bridge and protrusion growth in rafts. (A) Experimental timelapse of a bridge emerging after placement of a secondary protuberance (red asterisk) (see Movies S7 and S8, ESI†). Snapshots are provided at about 75 s intervals. (B) Length of single protrusion/bridge over time. Here length is measured as distance of a line that conforms to the protrusion from base to tip. The base of the protrusion is identified at the inflection point (change in concavity) between the bulk raft and protrusion (see Fig. S12, ESI†). The dashed line indicates when a secondary rod was added. Colored triangles correspond to preceding snapshots in (A). (C) Cluster fraction of the raft over time, determined by thresholding the transmission distribution where measured transitivity values below Tthreshold = 0.3 defines regions of the raft belonging to a cluster (see Fig. S14, ESI†). (D) Linear growth rate ![[L with combining dot above]](https://www.rsc.org/images/entities/i_char_004c_0307.gif) for protrusions n = 19 and bridges n = 6. (E) Effect of age on linear growth rate for both bridges and protrusions. Age refers to the number of elapsed days from date of collection to experiment. for protrusions n = 19 and bridges n = 6. (E) Effect of age on linear growth rate for both bridges and protrusions. Age refers to the number of elapsed days from date of collection to experiment. | ||
4 Conclusions
We have shown how fire ant rafts adapt their morphology over long periods of time by separating into active and passive phases. The latter consists of a stationary cluster which arises due to inter-ant interactions on the raft surface. We demonstrated that application of external stimulus can either weaken or strengthen these interactions leading to an abrupt collective response, thereby informing the rafts morphology. Taken together, our results show how groups of fire ants collectively manage dual environmental pressures. Despite ants' inability to coordinate globally, inter-agent interactions enables rapid and dynamic self-organization of the collective, whether for energy conservation or threat response. Here perception of stimulus plays a key role in how ants modify these interactions. Beyond ant rafts this phenomena, of socially-induced phase separation, could play a broader role across other living collectives including fish, birds, bacteria, and other swarming insects, such as the European honeybee which for example cluster to thermoregulate and dissolve when under threat.42,43 Such simple rules, could endow collectives with a vast arsenal of tools to coordinate their morphodynamic response to an evolving world. Beyond living systems, this work could provide insight into designing robotic swarms44 that could autonomously transition between task active and energy conserving states.It should be noted that our model assumes external stimuli uniformly and spontaneously influences surface ant interactions (i.e. τR), however, since we focus on smaller rafts, with no more than 7000 ants, this simplifying assumption seems to be reasonable. Even in the largest raft, which spanned ∼100 mm, it would take an active surface ant roughly 50 s to superdiffusively18 travel from the rafts edge to the center, where clusters predominately form. For larger rafts, with upwards of a hundred thousand ants, it is unclear how and at what timescales external stimuli might propagate across the collective, or even that a morphodynamic response could remain localized, or even agent specific.
Furthermore we limit the complexity of how we model surface ants by treating them as active particles which interact exclusively through isotropic excluded-volume propulsion. This subsequently assumes that free ants are non-interacting and that cluster ants are completely trapped. Here we define “social interactions” as the timescale for ants to escape the cluster. In reality fire ants interact in other non-trivial ways, including alignment interactions that dominate around geometrically confined regions of the raft such as around protrusions.18 More generally, like many social insects, fire ants rely on a variety of different social interactions to communicate. For instance fire ants participate in allogrooming, produce chirping sounds via stridulation of their body parts,24 and aerosolize antibiotic venom by vibrating their gaster (gaster-flagging). Many of these interactions are context specific, with ants likely performing one or multiple of the above behaviours when rafting. While allogroming has been documented in clusters of nesting and rafting ants, it is unclear if ants use chemical (gaster-flagging) or auditory (stridulation) signals when rafting, and if so how these signals might led to more complex inter-agent interactions that impact the morphodynamics. Moreover, fire ant queens are known to regulate division of labor across the collective,45 however we strictly study rafts of female workers. Future work should explore the influence other fire ant castes might have on raft dynamics.
Lastly, all ant colonies were collected within the same date and geographical region, which coincided with a period of drought. Previous work found that colony health was the most important pre-factor in order to repeatedly observe spontaneous activity waves.46 Whether or not rafts easily phase separate, likely depends on the colonies health or access to nutrients at time of collection. Although colonies were collected during the same time period, raft activity (measured through the linear growth rate of protrusions Fig. 7E) did decrease with longer captive times. Extreme clustering (Fig. 1C) only formed after about 20 days in captivity. Thus the colony state, (time in captivity, health at collection, etc.) undoubtedly influences the strength of phase separation in the raft.
Conflicts of interest
Authors declare that there are no conflicts of interest.Data availability
Data for this article, including raw video footage, are available in the ESI† and at https://doi.org/10.5061/dryad.d51c5b0cv. The code for the ant kinetic model can be found at https://doi.org/10.5281/zenodo.15833099.Acknowledgements
F. J. V. greatly acknowledges the support of the National Science Foundation (NSF) under award no. 2135032. This content is solely the responsibility of the authors and does not necessarily represent the official view of NSF. Z. T. W. and F. J. V. acknowledge the support by the Department of Energy, National Nuclear Security Administration, Predictive Science Academic Alliance Program under Award Number DE-NA0003962. This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. We thank A. Abdulla and A. Roux for assisting with experiments.Notes and references
- J. C. Boren and B. D. Wright, N. M. J. Sci., 1999, 39 Search PubMed.
- L. Miller, Comp. Biochem. Physiol., 1978, 59, 327–334 CrossRef.
- C. Morosinotto, A. Villers, R. Varjonen and E. Korpimäki, Oikos, 2016, 126, 863–873 CrossRef.
- J. R. Merkt and C. R. Taylor, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12313–12316 CrossRef CAS PubMed.
- D. M. T. Nguyen, M. L. Iuzzolino, A. Mankel, K. Bozek, G. J. Stephens and O. Peleg, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2011916118 CrossRef PubMed.
- M. Beekman, D. J. T. Sumpter and F. L. W. Ratnieks, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 9703–9706 CrossRef CAS PubMed.
- I. R. Fischhoff, S. R. Sundaresan, J. Cordingley, H. M. Larkin, M.-J. Sellier and D. I. Rubenstein, Anim. Behav., 2007, 73, 825–831 CrossRef.
- C. Becco, N. Vandewalle, J. Delcourt and P. Poncin, Phys. A, 2006, 367, 487–493 CrossRef.
- J. K. Parrish, S. V. Viscido and D. Grünbaum, Biol. Bull., 2002, 202, 296–305 CrossRef PubMed.
- M. Nagy, Z. Ákos, D. Biro and T. Vicsek, Nature, 2010, 464, 890–893 CrossRef CAS PubMed.
- T. Mora, A. M. Walczak, L. Del Castello, F. Ginelli, S. Melillo, L. Parisi, M. Viale, A. Cavagna and I. Giardina, Nat. Phys., 2016, 12, 1153–1157 Search PubMed.
- W. Cresswell, J. Ornithol., 2011, 152, 251–263 CrossRef.
- M. Mangel, Anim. Behav., 1990, 39, 1163–1172 CrossRef.
- B. J. Adams, L. M. Hooper-Bùi, R. M. Strecker and D. M. O’Brien, J. Insect Sci., 2011, 11, 1–14 CrossRef PubMed.
- F. J. Vernerey, T. Shen, S. L. Sridhar and R. J. Wagner, J. R. Soc. Interface, 2018, 15, 20180642 CrossRef PubMed.
- R. J. Wagner, S. C. Lamont, Z. T. White and F. J. Vernerey, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2314772121 CrossRef CAS PubMed.
- N. J. Mlot, C. A. Tovey and D. L. Hu, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 7669–7673 CrossRef CAS PubMed.
- R. J. Wagner, K. Such, E. Hobbs and F. J. Vernerey, J. R. Soc. Interface, 2021, 18, 20210213 CrossRef PubMed.
- H. Ko, K. Komilian, J. S. Waters and D. L. Hu, Biol. Open, 2022, 11, bio059076 CrossRef CAS PubMed.
- Y. Zhang and G. V. Lauder, J. Exp. Biol., 2023, 226, jeb245617 CrossRef PubMed.
- Y. Zhang and G. V. Lauder, eLife, 2024, 12, RP90352 CrossRef PubMed.
- M. Tennenbaum and A. Fernandez-Nieves, Phys. Rev. E., 2017, 96, 052601 CrossRef PubMed.
- C. Anderson and A. Fernandez-Nieves, Nat. Commun., 2022, 13, 6710 CrossRef CAS PubMed.
- S. J. Rauth and S. B. Vinson, J. Insect Behav., 2006, 19, 293–304 CrossRef.
- J. Barré, R. Chétrite, M. Muratori and F. Peruani, J. Stat. Phys., 2015, 158, 589–600 CrossRef.
- M. N. Van Der Linden, L. C. Alexander, D. G. Aarts and O. Dauchot, Phys. Rev. Lett., 2019, 123, 098001 CrossRef CAS PubMed.
- W. J. Ridgway, M. P. Dalwadi, P. Pearce and S. J. Chapman, Phys. Rev. Lett., 2023, 131, 228302 CrossRef CAS PubMed.
- H. Zhao, A. Košmrlj and S. S. Datta, Phys. Rev. Lett., 2023, 131, 118301 CrossRef CAS PubMed.
- R. J. Wagner and F. J. Vernerey, PLoS Comput. Biol., 2022, 18, e1009869 CrossRef CAS PubMed.
- S. Phonekeo, N. Mlot, D. Monaenkova, D. L. Hu and C. Tovey, R. Soc. Open Sci., 2017, 4, 170475 CrossRef PubMed.
- W. Thielicke and E. J. Stamhuis, J. Open Res. Softw., 2014, 2, e30 Search PubMed.
- G. S. Redner, M. F. Hagan and A. Baskaran, Phys. Rev. Lett., 2013, 110, 055701 CrossRef PubMed.
- G. Gonnella, D. Marenduzzo, A. Suma and A. Tiribocchi, C. R. Phys., 2015, 16, 316–331 CrossRef CAS.
- S. R. McCandlish, A. Baskaran and M. F. Hagan, Soft Matter, 2012, 8, 2527 RSC.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E, 2006, 74, 030904 CrossRef PubMed.
- Y. Yang, V. Marceau and G. Gompper, Phys. Rev. E, 2010, 82, 031904 CrossRef PubMed.
- J. Aguilar, D. Monaenkova, V. Linevich, W. Savoie, B. Dutta, H.-S. Kuan, M. D. Betterton, M. A. D. Goodisman and D. I. Goldman, Science, 2018, 361, 672–677 CrossRef CAS PubMed.
- K. L. Haight, Insectes Soc., 2006, 53, 32–36 CrossRef.
- J. Su, M. Feng, Y. Du, H. Jiang and Z. Hou, Commun. Phys., 2023, 6, 58 CrossRef.
- D. Cassill, K. Ford, L. Huynh, D. Shiffman and S. B. Vinson, J. Bioecon., 2016, 18, 159–167 CrossRef.
- R. K. V. Meer, C. S. Lofgren and F. M. Alvarez, Physiol. Entomol., 1990, 15, 483–488 CrossRef.
- J. M. Peters, O. Peleg and L. Mahadevan, J. Exp. Biol., 2022, 225, jeb242234 CrossRef PubMed.
- S. M. Cully and T. D. Seeley, Insectes Soc., 2004, 51, 317–324 CrossRef.
- M. Rubenstein, C. Ahler and R. Nagpal, International Conference on Robotics and Automation, 2012, 3293–3298 Search PubMed.
- F. Manfredini, C. Lucas, M. Nicolas, L. Keller, D. Shoemaker and C. M. Grozinger, Mol. Ecol., 2014, 23, 660–672 CrossRef PubMed.
- C. Anderson, G. Goldsztein and A. Fernandez-Nieves, Sci. Adv., 2023, 9, eadd0635 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00390c |
| This journal is © The Royal Society of Chemistry 2025 |




