Open Access Article
Open Access ArticleAn artificial protein cage made from a 12-membered ring†
Izabela
Stupka‡
 ab,
Artur P.
Biela
ab,
Artur P.
Biela
 *ac,
Bernard
Piette
*ac,
Bernard
Piette
 d,
Agnieszka
Kowalczyk
ae,
Karolina
Majsterkiewicz
d,
Agnieszka
Kowalczyk
ae,
Karolina
Majsterkiewicz
 ab,
Kinga
Borzęcka-Solarz
a,
Antonina
Naskalska
a and
Jonathan G.
Heddle§
ab,
Kinga
Borzęcka-Solarz
a,
Antonina
Naskalska
a and
Jonathan G.
Heddle§
 *a
*a
aMalopolska Centre of Biotechnology, Jagiellonian University, Krakow, Poland. E-mail: artur.biela@uj.edu.pl; jonathan.heddle@uj.edu.pl
bPostgraduate School of Molecular Medicine, Warsaw, Poland
cInstitute of Zoology and Biomedical Research, Jagiellonian University, Krakow, Poland
dDepartment of Mathematical Sciences, Durham University, Durham, UK
eFaculty of Mathematics and Computer Science, Jagiellonian University, Krakow, Poland
First published on 13th December 2023
Abstract
Artificial protein cages have great potential in diverse fields including as vaccines and drug delivery vehicles. TRAP-cage is an artificial protein cage notable for the way in which the interface between its ring-shaped building blocks can be modified such that the conditions under which cages disassemble can be controlled. To date, TRAP-cages have been constructed from homo-11mer rings, i.e., hendecamers. This is interesting as convex polyhedra with identical regular faces cannot be formed from hendecamers. TRAP-cage overcomes this limitation due to intrinsic flexibility, allowing slight deformation to absorb any error. The resulting TRAP-cage made from 24 TRAP 11mer rings is very close to regular with only very small errors necessary to allow the cage to form. The question arises as to the limits of the error that can be absorbed by a protein structure in this way before the formation of an apparently regular convex polyhedral becomes impossible. Here we use a naturally occurring TRAP variant consisting of twelve identical monomers (i.e., a dodecamer) to probe these limits. We show that it is able to form an apparently regular protein cage consisting of twelve TRAP rings. Comparison of the cryo-EM structure of the new cage with theoretical models and related cages gives insight into the rules of cage formation and allows us to predict other cages that may be formed given TRAP-rings consisting of different numbers of monomers.
Introduction
The ability to produce novel protein assemblies through protein engineering and protein design is of great interest as it allows the synthesis of proteins structures with novel geometries and functionality.1,2 It also has the potential to offer new insights into protein structure and function in general, leading to the design of new materials and new therapeutics. This is particularly apparent in the case of artificial protein cages which have recently been shown to be able to act as scaffolds for attachment of viral antigens and subsequently proved to be effective vaccines,3–5 at least one of which is already in clinical use.6Protein cages in nature are perhaps best understood in terms of viral capsids. Crick and Watson suggested that these are likely made from a small number of proteins present in multiple copies.7 This solves the folding problem which would occur if a capsid was to be made from a single polypeptide chain as well as the fact that the nucleic acid encoding such a chain would be likely too large to fit within the produced capsid. The geometry of such capsids was suggested to be icosahedral given that this results in the most efficient ratio of surface area to internal volume.8 Through quasi-equivalence theory, Caspar and Klug showed how identical proteins could form the necessary mix of pentagons and hexagons required to construct such capsids where the T number was greater than 1.8 Almost all known sphere-like capsids follow these rules, having icosahedral symmetry. Likewise, almost all artificial protein cages demonstrated to date follow similar patterns being one of a limited number of Platonic solids, typically icosahedra.
Recently however several theoretical and experimental works have shown that (apparently) regular protein cages are able to form with geometries that go beyond those associated with Platonic solids. Twarock and colleagues have shown that icosahedral architecture can be expanded to explain the structures of viral capsids that do not conform to classical quasi-equivalence predictions, including the formation of Archimedean solids.9 Meanwhile, in experimental work, our own lab showed that an apparently regular-faced convex polyhedron could be formed from a hendecagonal (11-sided) protein. This was achieved using trp-RNA binding attenuation protein (TRAP) from G. stearothermophilus. TRAP is typically a homo-11mer forming a ring-like truncated cone. By substituting a cysteine for a lysine at position 35 we produced a modified TRAP ring bearing 11 cysteines equally spaced around the outer rim of the ring (Fig. 1(a)). These are the only cysteines in the protein. When mixed with a source of gold(I) ions supplied either by gold nanoparticles or in the form of a monosulfonated chloro(triphenylphosphine)gold(I) (Au-TPPMS) these proteins assemble into capsid-like structures being apparently regular protein cages consisting of either 24 or 12 TRAP rings (Fig. 1(c)–(f)) depending on the relative concentration of gold used. The gold ions form bonds between the thiols of opposing cysteines thus linking rings in the cage with neighbours. On first inspection the formed cages appear to be regular-faced convex polyhedra but, given the hendecagonal nature of the TRAP rings (and putting aside prisms and anti-prisms) such cages cannot form.11–13 Our initial work explained this by noting that each of the twenty-four rings can be placed on each of the faces of a pentagonal icositetrahedron (the dual polyhedron of the snub cube) such that each ring is almost perfectly inscribed by the pentagonal face. However, some slight irregularity needs to occur in the protein structure to allow this to happen. Thus, the deviation from regularity is accounted for by flexibility in the protein structure.
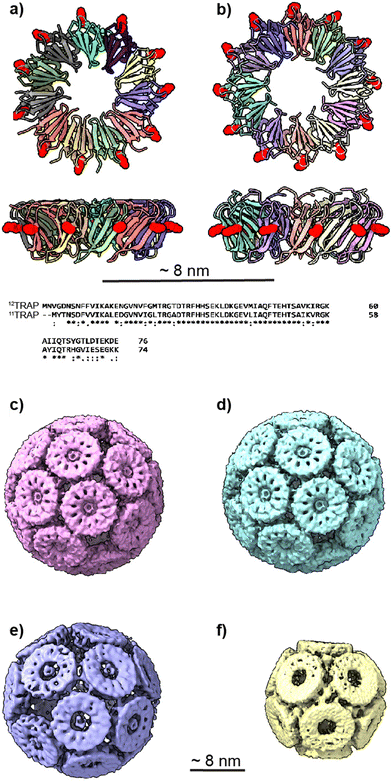 | ||
| Fig. 1 11mer and 12mer TRAP-ring structures and known TRAP-cage structures made from 11mer and 12mer rings (a), Crystal structure of 11-membered TRAP from G. stearothermophilus (pdb 1qaw). Residue K35 highlighted in red space-filling and position S33 shown in yellow space-filling. Shown in two orthogonal views. (b) Crystal structure of TRAP from A. halodurans (pdb 3zzl) with the equivalent residue (K37) highlighted in red space-filling, shown in two orthogonal views. In both a and b, structures are represented in cartoon views and each monomer is individually coloured. Text shows a Clustal Omega10 alignment of the amino acid sequences of both TRAPs. Asterisks denote identity, colons denote homology. (c) and (d) Cryo electron density maps of TRAP 24-ring cage (emdb 11413 and 11412 respectively) representing left-handed and right-handed forms respectively. Maps shown at contour level 1.5 Sigma. (e) Cryo electron density maps of TRAP-cage consisting of 20 TRAP rings (emdb 13924) shown at step level 2, contour level 0.09 Sigma (f), cryo electron density maps of TRAP-cage consisting of 12 TRAP rings (emdb 13924) constructed via mixing with GNPs. Maps shown at step level 2, contour level 0.4 Sigma. All TRAP-cages shown are made from 11mer TRAP rings. | ||
This result was of interest as the pentagonal icositetrahedron is a Catalan solid and the work was, therefore, a practical demonstration of how the geometrical space for artificial protein cages can expand beyond the Platonic solids. It also showed how proteins that formally lack the required symmetry to form particular convex polyhedra may approximate them very closely with a small amount of structural deviation. Whether this actually occurs experimentally is likely a complex outcome resulting from an interplay of factors such as the energetically favourable formation of bonds in the assembled structure. We tried to catalogue the possible convex polyhedral cages that could be produced from protein faces with a given number of edges assuming errors within what had been shown to be experimental reasonable ranges. The results showed multiple possibilities exist within ranges of numbers of sides that are tractable for real-world proteins.12–14
Subsequent to our understanding of the structure of the 24-ring TRAP-cage, we determined the structure of the 12-ring TRAP-cage (Fig. 1(f))15 which is formed at higher concentrations of gold ions. We showed that in this case, the rings of the cage were arranged in a structure approximating a dodecahedron wherein each ring appeared to be connected to neighbours via bridging golds between opposing thiols but where the distances involved suggested the presence of more than one gold atom in these “staples” and possible staple heterogeneity. The overall structural error required was larger than that seen for the 24-ring TRAP-cage.14,15
We also changed the location of the cysteine that is bridged by the gold ions from position 35 to position 33 (Fig. 1(e)).16 If we consider the TRAP ring as a highly truncated cone, this moved the position of the cysteines on the outer circumference of TRAP further toward the narrow end of the cone. These modified TRAP rings were still able to form TRAP-cages upon mixing with gold(I). However, the cages formed were different, consisting of 20 rather than 24 rings and having a distorted egg-like appearance (Fig. 1(e)).
It is known that TRAP from Alkalihalobacillus halodurans, while highly homologous at both the sequence and structural level to TRAPs from G. stearothermophilus and B. subtilis (Fig. 1(a) and (b)) form rings that consist of 12 TRAP monomers rather than 11 and so can be thought of as dodecagons. Dodecagons, like hendecagons, are also formally forbidden from forming the faces of regular-faced convex polyhedra. Therefore, we wondered if the 12-membered rings carrying the equivalent of the K35C mutation could also form cages and if so what the geometry of such cages may be. Given that such cages would have to be geometrically distinct from the cages formed from 11-membered rings, these data could give us further insights into how cages with unusual geometries can form. They would also allow us to test the predictive power of our mathematical models and give greater confidence in the accuracy of predicted structures of cages constructed from rings having greater or fewer numbers of monomers.
Results
Here we adopt a nomenclature to describe TRAP-cages where the initial superscript refers to the number of monomers per TRAP ring and the terminal subscript refers to the number of these rings in the assembled TRAP-cage. For example, 11TRAP12 and 11TRAP24 refer to TRAP-cages constructed from 12 homo-11mer rings and 24 homo-11mer rings respectively.Production of 11TRAP-cages and 12TRAP-cages
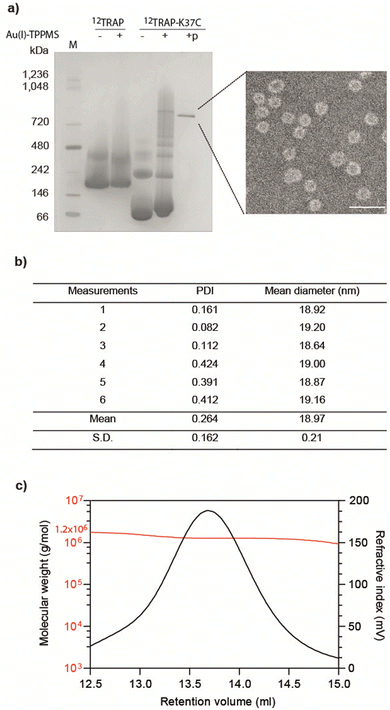
We formed cages from 12TRAP rings and 11TRAP rings. For 12TRAP-cages, cage formation experiments were conducted for both 12TRAP wild-type protein and variant 12TRAP(K37C). This was carried out as previously described, consisting of incubating the protein with Au-TPPMS as a source of gold(I) ions. Prior to incubation with Au-TPPMS, both forms of protein occur as toroidal rings in their native state as shown using native PAGE gel electrophoresis (Fig. 2(a)) After incubation of 12-mer wild type 12TRAP with Au-TPPMS, no change in appearance was observed, i.e., the proteins remained in their ring form (Fig. 2(a)). In contrast, the corresponding experiment conducted with 12TRAP(K37C) revealed dramatic changes in the structure of the protein and formation of cages as evidenced by native PAGE (Fig. 2(a)). TEM confirmed this result and showed the cages to be approximately 17 nm in diameter, uniform in size and having an interior cavity being less electron-dense compared to the perimeter (Fig. 2(a), inset, Fig. S1a, ESI†). DLS showed similar results, giving a diameter of approximately 19 nm (Fig. 2(b)). RALS analysis suggested a particle mass of approximately 1.2–1.3 MDa consistent with approximately 12 TRAP rings (Fig. 2(c)) while 12TRAP lacking the K37C change did not form cages (Fig. S1b, ESI†). The RALS data for 12TRAP rings prior to the addition of Au(I)-TPPMS showed a lower molecular weight shoulder, likely representing aggregated TRAP-rings. Therefore, TRAP cages made from 12TRAP are referred to here onwards as 12TRAP-cages. For 11TRAP12 modified TRAP-cages were produced in a similar way and cage formation was confirmed using native PAGE (Fig. S2, ESI†).Stability of 12TRAP-cage
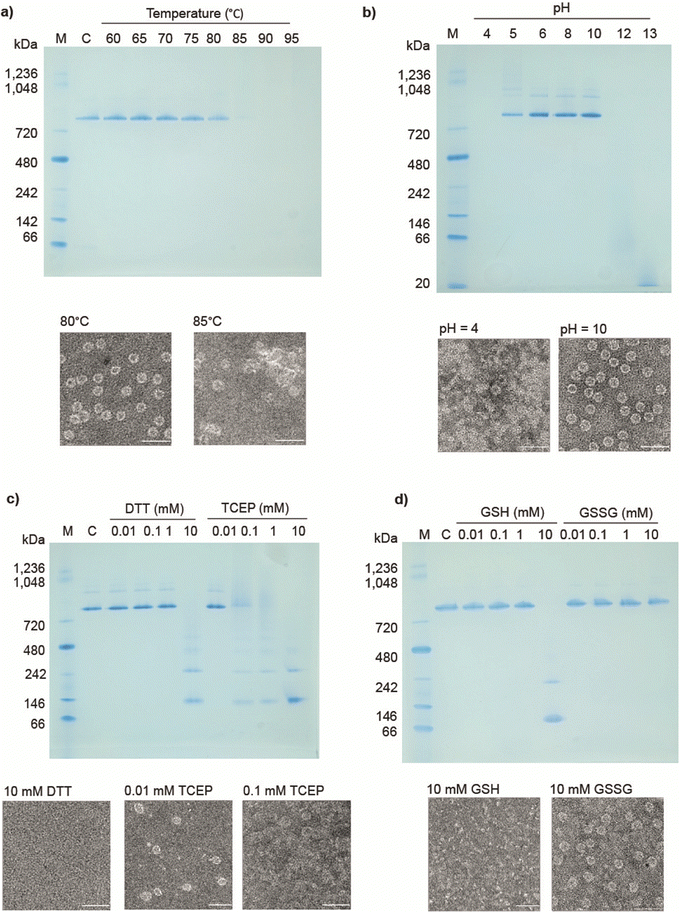
Previously reported 12- and 24-ring cages were highly stable and were variously able to withstand extremes of temperature, pH and various surfactants/denaturants. However, they were easily disassembled in the presence of a number of reducing agents,14,17 most likely due to an “etching” exchange reaction that removes the bridging gold. Given this, we decided to test the stability of cages built from 12mer rings. Table S1 (ESI†) summarises the results.In thermal stability tests, we incubated cages for 10 min. in different temperatures. The results showed that the structures were maintained up to approx. 80 °C as confirmed by native PAGE and TEM analysis (Fig. 3(a)). As a comparison 11TRAP12 was previously found to have some level of stability up to >70 °C while 11TRAP24 remained stable even after 3 hours at 95 °C. pH stability tests showed the 12TRAP-cage to be stable over a wide pH range spanning approximately pH 5 to pH 10 (Fig. 3(b)) compared to pH 4–11 for 11TRAP12 and pH 3–12 for 11TRAP24.
We also tested the response of 12TRAP-cages to reducing agents by incubation with DTT and TCEP in different concentrations. The results showed the disassembly of the cage into rings above 1 mM DTT and 0.01 mM TCEP (Fig. 3(c)) suggesting similar interactions between rings as seen for 11TRAP24. To further investigate the potential behaviour in cell cytoplasm we also measured the response of 12TRAP-cage to the cellular reducing agent glutathione in both reduced (GSH) and oxidized (GSSG) forms. Results showed the cages be stable to between 1 and 10 mM GSH and >10 mM GSSG, the highest concentration tested (Fig. 3(d)).
12TRAP-cages were tested against urea and guanidine hydrochloride (Fig. S3a, ESI†) and were stable up to approx. 3 M urea and 1 M guanidine compared to 3 M and 2 M respectively for 11TRAP1215 and 7 M and approx. 2 M respectively for 11TRAP24.14
Stability against detergents diverged most from previously TRAP-cage variants: 12TRAP-cage appeared to disassemble in the presence of relatively low concentrations (0.05%) of anionic detergents represented here by SDS. (Fig. S3b, ESI†). In contrast, they were less affected by non-ionic detergents like Triton X-100 in which they remained intact up to 0.5% suggesting the influence of ionic interactions (Fig. S3c).
Prediction of possible TRAP-cage structures
Working on the assumption that cages constructed from modified 12TRAP rings consisted of 12 such rings, we tried to understand how a near-regular convex polyhedron could be made from dodecamer building blocks and gain some insight into why a 12-ring cage is apparently preferred. To do this, we carried out mathematical investigations whereby possible arrangements for cages constructed of 12 rings each having 12 identical monomers alongside possible cages made from near neighbour rings (made from 10, 11, or 13 identical monomers), were identified using a set of rules as described in the methods. In brief, we followed the previously reported “gluing” pattern connecting faces together as was demonstrated for the 11TRAP24 and quantified the deviations from ideality (i.e., errors). As proved in12,13 there are no regular polyhedral cages made out of 10, 11, or 13-sided rings/faces and this is confirmed in the results (Tables S2–S4, ESI†). In contrast, regular cages made from 12 rings can have the symmetry derived from the icosahedron, cuboctahedron or truncated tetrahedron.A selection of results for 10, 11 and 13 member rings is shown in Table S2 (ESI†). For potential cages made from 12-membered rings we considered all the symmetric cages made out of 12 rings and with deformations in the range allowed by previously realised cages using 11TRAP rings and 12TRAP rings. The results Table S3 (ESI†) showed that cages derived from the truncated tetrahedron have very large holes and as a result, a relatively large diameter. The cage derived from the icosahedron has a larger deformation and a number of dihedral angles. We are then left with 2 cages derived from the cuboctahedron with a very similar amount of deformation and diameters and both exhibits the same dihedral angles between every pair of faces.
The results with the smallest polygon/ring deformation for 12-ring cages made from 10, 11, 12 and 13 member rings are shown in Fig. 4. The model 12-ring cage made from 11TRAP rings is included for comparison as this was previously shown to be constructed in some cases (using gold nanoparticles (GNPs) as the source of gold atoms).15 The full set of results (defined as all cages identified by the algorithm) consisted of many more candidate cages, the majority of which were discarded (see Table S4, ESI† for the list of discarded cages). Discarded cages had features which were judged unfavourable such as larger deformation than the nearest equivalent structures.
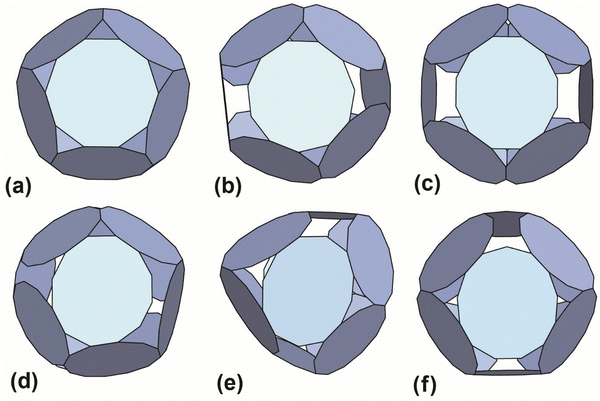 | ||
| Fig. 4 Best-predicted theoretical models (see ref. 12 and 13) for polyhedral cages made out of 12 rings: (a) 10TRAP12 (Pdo_P10_1_1_1_1_1): p-cages made from 12 10-membered rings. The decagons are regular and the structure has the symmetry of the icosahedron. Dihedral angle 138.19°. (b) 11TRAP12 (Aco_P11_1_2_1_3): p-cages made from 11-membered rings, where the number of rings is restricted to 12 (as previously presented in ref. 15), the edge length and angle vary respectively by 1.76% and 1.8%. Dihedral angle 119.4°. Symmetry: cuboctahedron. (c) 12TRAP12 (Aco_P12_1_3_1_3) p-cages made from 12-membered rings. The edges are identical and the angle vary by 1.75%. Dihedral angle 120°. Symmetry: cuboctahedron. (d) 12TRAP12 (Aco_P12_1_2_1_4) p-cages made from 12-membered rings. The edge length and angle both vary by 3.8%. Dihedral angle 118°. Symmetry: cuboctahedron. (e) 11TRAP12 (Aco_P12_2_2_2_2): p-cages made from 12 12-membered rings, The edge length and angle vary respectively by 0% and 4.3%. Dihedral angle 139.5° and 101.5°. Symmetry: cuboctahedron. (f) 13TRAP12 (Aco_P13_2_2_2_3) pcages made from 13-membered rings. The edge length and angle vary respectively by 0.00823% and 0.943%. Dihedral angle 119.5°. Symmetry: cuboctahedron. | ||
To confirm the validity of our predictions we proceeded to determine the structure of the hypothesised 12TRAP12 and 11TRAP12. Although the latter structure was previously determined, it was for a cage formed by addition of GNPs as the source of Au(I) rather than Au-TPPMS and the structure included embedded GNPs and it was not known if these were necessary for cage formation. The structure of 11TRAP12 constructed using Au-TPPMS was therefore determined for purposes of structural comparison but was not otherwise characterised.
Cryo-EM determination of the 12TRAP-cage and 11TRAP12 structures
We used cryo-EM to determine the structure of the 12TRAP-cage (Fig. S4, ESI†) allowing us to compare it to the predicted structure. The determined structure showed the cage to be composed of 12 identical rings bearing the same K37C mutation (Fig. 1(b)) and as such can be referred to as 12TRAP12. The final symmetry was found to be tetrahedral (T). The imposed tetrahedral symmetry and dodecagonal shape of the individual rings make each single ring symmetrically equivalent. Consistent with previously determined TRAP-cage structures, each ring contacts 5 neighbours (as expected based on both the 11TRAP-cages previously published and mathematical predictions). Despite similarities to the 11TRAP12 and the larger (24-ring)14 and small (12-ring)1511TRAP-cages, differences in the symmetry of the basic building block (the ring itself) results in a different number of cysteine residues involved in direct connections between the rings. In the case of 11TRAP24, almost all cysteines were saturated with gold ion bridges (10 out of 11 residues14). This leads to higher flexibility of the complete 12TRAP12 cage assembly which was calculated using 3D variability (3DVA) of the reconstructed cryoEM volume (SupplMovie1, ESI†).We also determined the structure of the 11TRAP-cage formed by addition of Au-TPPMS (Fig. S5, ESI†) and, as expected, found it to be highly similar to the 11TRAP12-cage formed in the presence of GNPs, both cages consisting of 12 rings and approximating a dodecahedron.
We compared the two cages having different numbers of subunits in the constituent rings (12TRAP12vs.11TRAP12) and formed using Au-TPPMS as a source of Au(I) ions. Overall, the cages are very similar in terms of dimensions: 19.0 nm vs. 19.3 nm (11TRAP12vs.12TRAP12 respectively), having identical overall symmetry (tetrahedral) and both being composed of 12 rings. But because of different rotational symmetry of the individual rings (C11 vs. C12) the connection network is necessarily divergent. Moreover, both cages display geometrical features that were predicted by mathematical modelling (Fig. 5).
 | ||
| Fig. 5 Structures of 11TRAP12 and 12TRAP-cages obtained by cryo-EM reconstruction. 11TRAP12 is shown in three different views centred at (a), local 3-fold symmetry, (b), face and (c), local 2-fold symmetry. 12TRAP12 is shown in three different views centred at (d), local 3-fold symmetry, (e) face and (f), local 2-fold symmetry showing very good agreement with the best mathematical models (insets, see also Fig. 2) and experimental results. | ||
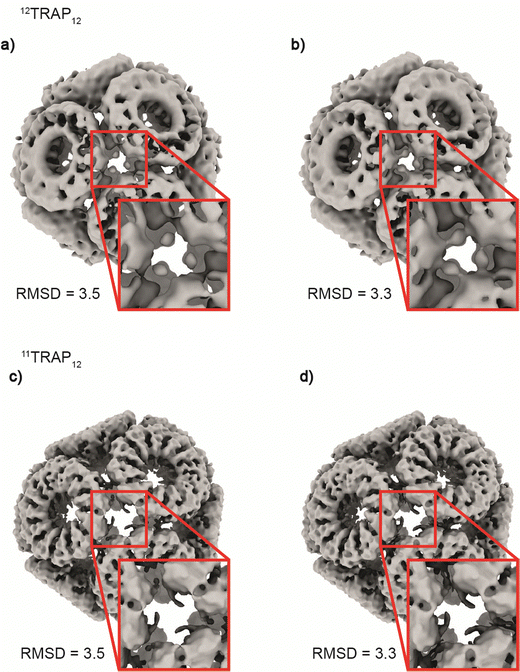
Considering the 12TRAP11 and 12TRAP12, we see that overall, they have proportionally similar numbers of bonds despite different numbers of individual TRAP monomer subunits (12 × 11 vs. 12 × 12 respectively). This suggests that 12TRAP12 has fewer bonded cysteines. Using the cryo-EM map contoured at RMSD level 3.5 as a guide, we were able to map the number and type of ring–ring connections using the same nomenclature for different types of connections as developed previously15 (Fig. S6, ESI†). For 11TRAP12, considering the connections of one ring to its neighbours, there are two so-called Type I connections (4 cysteines involved), two Type II connections (2 cysteines involved) and one Type III connection (2 cysteines involved) which give 8/11 (73%) cysteine residues per ring involved in the inter-ring connection network.1512TRAP12 (cryo-EM map contoured at the same RMSD threshold) uses a somewhat different connection network. It consists of the same Type I connection (but only one; 2 cysteines involved), one Type II connection (1 cysteine involved), and one Type III connection (so-called “zip type”, 2 cysteines involved). In addition, there are two Type IV connections present (V-shaped, 3 cysteines involved) which exist in two opposite orientations. That gives 8/12 (66%) of the cysteine residues involved in the connection network. In both cases, only 4 cysteine residues remained uninvolved. Considering 12TRAP12, the additional one cysteine per ring could potentially provide for additional gold-mediated ring–ring bonds which would require increased distortion of the cage in order to be accommodated compared to 11TRAP12. Indeed, we do see evidence for this in the Cryo-EM densities: additional, discrete densities around unconnected cysteines can be seen at RMSD = 3.5 but when lowering the threshold to RMSD = 3.3 they are observed to connect to each other giving the evidence that these additional connections can occasionally occur and most probably are present in the structure but at relatively low occupancy (Fig. 6(a) and (b)). This situation is not observable in the case of the analogous cage made from 11TRAP rings (Fig. 6(c) and (d)). This can be also visible when we compare local resolution limits on both structures. The 11TRAP12 displays less distortions and more rigid structure overall, which manifests itself in more uniform local resolution limits throughout the reconstructed volume (Fig. S7a, ESI†). In contrast to that, 12TRAP12 appeared to be less resolved (lower overall resolution) and much more flexible in the inter-ring regions, suggesting that the distortion present in this case are much bigger, than in case of 11TRAP12 (Fig. S7b, ESI†).
Both cages (11TRAP12 and 12TRAP12) due to their overall geometry (T symmetry) appear to be spherical in shape, which can be easily seen when their density is coloured in respect to the distance from the particle's centre (Fig. S8a and b, ESI,† respectively).
Methods
Mathematical modelling
A second C++ program (of around 8400 lines of code) was then used to obtain the geometric attributes of the prospective cages. First, the dodecagonal faces were modelled as rigid bodies, with adjacent faces linked by two Hookean springs with a rest position set to 5% of the edge length. The energy of the system was then minimized via simulated annealing. The coordinates of the resulting assembly were then used by the program to model the cage as a set of rigid rods using an energy function divided into three terms: edge length deviations, face edge angular deviations, and degree of non-planarity. The first one measured by how much the edge lengths deviated from a chosen reference length. The second one is quantified by how much the angle between the hendecagon edges deviated from the internal angle of the regular dodecagon. The third term computed the level of nonplanarity of the dodecagons. Each term was assigned a weight factor, with the planarity weight set to three orders of magnitude larger than for the lengths and the angles. This gave us structures with preserved planarity (with zero planarity distortions modulo numerical error). The energy function was minimized using a simulated annealing method and the program output a file containing the vertex coordinates, the topology of the cage, as well as the order of deformations obtained for the angles and edge lengths. The exact explanation of the algorithm was provided in previous work.13,14,18 From the polyhedral cages generated by the method described above, we selected two candidate models for which the diameter, shape and rough arrangement of rings were in line with the cryo-EM measurements, and the deformation level was less than 10%.
Protein expression and purification
12TRAP(K37C) and 12TRAP(wt) along with 11TRAP(K35C/R64S) were produced using a similar protocol as described previously for 11TRAP(K35C/R64S).14 During the initial purification steps of 12TRAP(K37C), 2 mM DTT was added in buffers to avoid undesired cysteine oxidation. 11TRAP12 formed more easily when 11TRAP(K35C/R64S) was purified in the absence of DTT. Briefly, E. coli strain BL21(DE3) cells were transformed with either pET21b_TRAP- or pET21b_12-mer-TRAP-wt K37C (for details of plasmids and protein sequences see Table S5 (ESI†)). Cells were grown in 1 L LB medium supplemented with ampicillin at 37 °C and shaken until OD600 = 0.5–0.7. At this point, protein expression was induced by the addition of 0.5 mM IPTG. Cells were further shaken for 4 hours at 37 °C and then harvested by centrifugation for 20 min at 6000 × g at 4 °C. Cell pellets were stored at −80 °C until use. Pellets were resuspended in 50 mL lysis buffer (50 mM Tris–HCl, 50 mM NaCl, pH 7.9) with the addition of DNase I, tablet of protease inhibitor cocktail and 2 mM DTT (for12TRAP(K37C) only) and stirred for 30 min at RT. Then, the samples were sonicated and clarified by centrifugation at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g at 4 °C for 25 min. The supernatant fractions were heated to 70 °C for 10 min, and centrifuged again at 20
000 × g at 4 °C for 25 min. The supernatant fractions were heated to 70 °C for 10 min, and centrifuged again at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g for 25 min at 4 °C. The supernatants were subjected to ion-exchange chromatography on an ÄKTA purifier (GE Healthcare Life Sciences) using 4 × 5 mL HiTrap QFF columns with binding in 50 mM Tris–HCl, pH 7.9, 50 mM NaCl buffer and eluting with a 50 mM–1000 mM NaCl gradient. Fractions containing 12-mer 12TRAP(K37C) or 12TRAP(wt) were pooled and concentrated using Amicon Ultra 50 kDa MWCO centrifugal filter units (Millipore). The samples were further subjected to size-exclusion chromatography (SEC) on a HiLoad 26/600 Superdex 200 pg column in 50 mM Tris–HCl, pH 7.9, and 150 mM NaCl at RT. Protein concentrations were determined by absorbance measured at 280 nm using a Nanodrop ND-1000 spectrophotometer (NanoDrop Technologies).
000 × g for 25 min at 4 °C. The supernatants were subjected to ion-exchange chromatography on an ÄKTA purifier (GE Healthcare Life Sciences) using 4 × 5 mL HiTrap QFF columns with binding in 50 mM Tris–HCl, pH 7.9, 50 mM NaCl buffer and eluting with a 50 mM–1000 mM NaCl gradient. Fractions containing 12-mer 12TRAP(K37C) or 12TRAP(wt) were pooled and concentrated using Amicon Ultra 50 kDa MWCO centrifugal filter units (Millipore). The samples were further subjected to size-exclusion chromatography (SEC) on a HiLoad 26/600 Superdex 200 pg column in 50 mM Tris–HCl, pH 7.9, and 150 mM NaCl at RT. Protein concentrations were determined by absorbance measured at 280 nm using a Nanodrop ND-1000 spectrophotometer (NanoDrop Technologies).
12TRAP12 assembly and purification
Formation and purification of gold(I)-induced 12TRAP12 were performed using a method similar to that described previously.14 First, 12TRAP(K37C) (100 μM) in 50 mM Tris, 150 mM NaCl, pH = 7.9 was mixed with various molar ratios of TRAP monomer to Au(I) (provided in the form of Au-TPPMS) and kept at RT for 1–3 days to assess the best ratio for cage formation. Samples were then briefly centrifuged, and cage formation was assessed using native PAGE. For larger scale cage formation, 12TRAP(K37C) (200–1000 μM) in 50 mM Tris, 150 mM NaCl, pH = 7.9 was mixed with the excess of Au-TPPMS in a ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (TRAP monomer: Au(I)) and kept at room temperature for 1–3 days. Any precipitated material was removed by centrifugation for 5 min at 12
2 (TRAP monomer: Au(I)) and kept at room temperature for 1–3 days. Any precipitated material was removed by centrifugation for 5 min at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g and supernatants were purified by size-exclusion chromatography using a Superose 6 Increase 10/300 GL column (GE Healthcare) at 0.5 mL min−1 flow rate on an ÄKTA purifier FPLC (GE Healthcare). Fractions containing 12TRAP12 were pooled and concentrated using Amicon Ultra-4 (100k MWCO) centrifugal filter units. Protein concentration was determined by absorbance measured using a Nanodrop ND-1000 spectrophotometer (NanoDrop Technologies). 11TRAP12 were formed using a similar protocol. After finding the best ratio for cage formation reaction in larger volume and the same protein concentration was performed. 11TRAP(K35C/R64S) (100 μM) was incubated with excess of Au-TPPMS in ratio 1
000 × g and supernatants were purified by size-exclusion chromatography using a Superose 6 Increase 10/300 GL column (GE Healthcare) at 0.5 mL min−1 flow rate on an ÄKTA purifier FPLC (GE Healthcare). Fractions containing 12TRAP12 were pooled and concentrated using Amicon Ultra-4 (100k MWCO) centrifugal filter units. Protein concentration was determined by absorbance measured using a Nanodrop ND-1000 spectrophotometer (NanoDrop Technologies). 11TRAP12 were formed using a similar protocol. After finding the best ratio for cage formation reaction in larger volume and the same protein concentration was performed. 11TRAP(K35C/R64S) (100 μM) was incubated with excess of Au-TPPMS in ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. Higher ratios resulted in protein precipitation. After incubation with Au-TPPMS and centrifugation supernatant was passed through a 0.1 μm PVDF centrifugal filter (Millipore) followed by size-exclusion chromatography.
2. Higher ratios resulted in protein precipitation. After incubation with Au-TPPMS and centrifugation supernatant was passed through a 0.1 μm PVDF centrifugal filter (Millipore) followed by size-exclusion chromatography.
Dynamic light scattering
Dynamic Light Scattering (DLS) was carried out at RT using a Zetasizer Nano ZSP instrument (Malvern). 12TRAP12 samples were diluted to 0.5 mg mL−1 in 50 mM Tris, 150 mM NaCl pH 7.9 and briefly centrifuged prior to measurement. The measurements were performed in a quartz cuvette with standard settings used for 50 mM Tris, and 150 mM NaCl pH 7.9 buffer. Experiments were repeated twice independently for each sample. Results are given as volume distributions.Stability of 12TRAP12
Thermal and chemical stabilities of 12TRAP12 were tested using a similar method to that described previously.14 All reagents used for the assays (DTT, TCEP, SDS, Triton X-100, Gdn-HCl and urea) were reconstituted in 50 mM Tris, 50 mM NaCl pH 7.9 and mixed with 12TRAP12 samples at RT for overnight incubation. Thermal stability assessment was performed by heating samples at various temperatures for 10 min. Following the incubations, samples were subjected to native PAGE analysis. The stability assessment was repeated twice, each giving uniform results.Native PAGE
Native PAGE was carried out using 3–12% native Bis-Tris gels (Life Technologies). Protein (1 μg) was mixed with native PAGE sample buffer containing 50 mM Bis-Tris, pH 7.2, 10% w/v glycerol, 0.004% w/v bromophenol blue. Electrophoresis was run at 150 V at RT in running buffer containing 50 mM Bis-Tris, pH 6.8, 50 mM Tricine. Unstained NativeMark (Life Technologies) was used as a protein standard. Protein bands were visualized by Instant BlueTM protein stain (Expedeon).Dark blue native PAGE
Dark Blue Native PAGE was performed similarly as Native PAGE with differences as follows. Cathode running buffer contained 50 mM Bis-Tris, pH 6.8, 50 mM Tricine and 0.02% w/v Coomassie Brilliant Blue G-250. After the electrophoresis, the gel was rinsed with MQ water and immersed in fix solution (40% methanol, 10% acetic acid), then heated in microwave for 45 s with maximum power and shaken for 15 min. at RT. After discarding fix solution gel was immersed in destain solution (8% acetic acid), heated in microwave for 45 s with maximum power and shaken at RT until desired background was reached. Further staining was not necessary.Negative stain transmission electron microscopy (TEM)
Samples for negative stain TEM were diluted in 50 mM Tris, 50 mM NaCl, pH 7.9 to a final concentration of approximately 0.05 mg mL−1 and centrifuged for 10 min. at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 × g to remove any precipitate. The sample (2 μl) was placed on previously glow-discharged carbon-coated copper grids (STEM Co.). Excess solution was removed by careful blotting with paper. Samples were further incubated with 3% phosphotungstic acid pH = 8.0 (2 μl) and visualized using a JEOL JEM-1230 electron microscope operated at 80 kV. All TEM measurements were repeated at least twice independently. Acquired images were analyzed using Image J software.
000 × g to remove any precipitate. The sample (2 μl) was placed on previously glow-discharged carbon-coated copper grids (STEM Co.). Excess solution was removed by careful blotting with paper. Samples were further incubated with 3% phosphotungstic acid pH = 8.0 (2 μl) and visualized using a JEOL JEM-1230 electron microscope operated at 80 kV. All TEM measurements were repeated at least twice independently. Acquired images were analyzed using Image J software.
Right/low angle light scattering
Right/Low Angle Light Scattering (RALS/LALS) measurements were performed using an Omnisec Reveal (Malvern) system and Superose 6 Increase 10/300 GL column (GE Healthcare) at 0.5 mL min−1 flow rate on an ÄKTA Purifier FPLC. 100 μg of either 12TRAP12 or 500 μg of 12TRAP(wt) in 50 mM Tris, 150 mM NaCl, pH 7.9 were subjected to the column and run through the RALS/LALS detection system coupled with refractive index (RI) measurement. The average particle molecular mass was calculated using Omnisec Reveal software with a dn/dc value of 0.185 mL g−1 and protein concentration estimated by observed RI. The system was calibrated using 500 μg of thyroglobulin (669 kDa) as a reference on the same column.Structure determination using Cryo-EM
Cryo-EM of 12TRAP12 was carried out as follows: 4 mL of the cage sample at ∼1 mg mL−1 were plunge frozen in liquid ethane using a FEI Vitrobot (blot force = 0, blot time = 4 s, wait time = 0 s, drain time = 0 s). Micrographs were collected using a TitanKrios cryo-microscope with a Falcon III camera at 75k magnification. 7802 micrographs were collected. All micrographs were motion-corrected using MotionCorr219 and CTF estimation was performed using PatchCTF in cryoSPARC (Fig. S4a, ESI†). Particles were picked and extracted using cryoSPARC v2.12.4.20 Firstly they were located using the BlobPicker tool, extracted and classified into 100 2D classes. Best-looking classes (∼40k particles) (Fig. S4c, ESI†) were used to train a Topaz neural network.21,22 Two rounds of training were performed. Each training was followed by particles extraction, and 2D classifications (Fig. S4d and f, ESI†) to select the best-looking classes (Fig. S4e and g, ESI†). Initial 3D reconstruction was made of ∼156k particles and refined in the C1 point group followed by tetrahedral (T) symmetry refinement. After final refinement, due to the relatively low global resolution (7.12 Å) 3D variability analysis (3DVA)23 was performed. Particles from most scattered clusters were discarded and new refinement in both C1 and Td symmetry were undertaken with 7.00 Å final resolution (Fig. S4i, ESI†). As in the previous round, 3DVA showed the flexible nature of the 12mer-TRAP cage (SupplMovie1, ESI†).Cryo-EM of the 11TRAP12 was carried out as follows: 4 mL of the cage sample at ∼1 mg mL−1 were plunged frozen in liquid ethane using FEI Vitrobot (blot force = 0, blot time = 4 s, wait time = 0 s, drain time = 0 s). Micrographs were collected using a TitanKrios cryo-microscope with a Falcon III camera at 75k magnification. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357 micrographs were collected. All micrographs were motion-corrected using MotionCorr219 and CTF estimation was performed using PatchCTF in cryoSPARC (Fig. S5a, ESI†).
357 micrographs were collected. All micrographs were motion-corrected using MotionCorr219 and CTF estimation was performed using PatchCTF in cryoSPARC (Fig. S5a, ESI†).
Particles were picked and extracted using cryoSPARC v2.12.4.20 Firstly, they were located using the BlobPicker tool, extracted and classified into 50 2D classes. Best-looking classes (∼20k particles) (Fig. S5c, ESI†) were used to template pick particles from a subset (1000) of micrographs. Finally, the best particles were used to generate an initial 3D model of 11TRAP12. This model was used to generate 50 back-projected 2D classes used in final template picking (Fig. S5g, ESI†) to select best-looking classes (Fig. S5e and g, ESI†). After another round of reference-free 2D classifications 1.099![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533 particles were selected and 3D classified during ab initio model building. Three obtained classes were evaluated and only one (bearing 406
533 particles were selected and 3D classified during ab initio model building. Three obtained classes were evaluated and only one (bearing 406![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 311 particles) was selected for further steps of refinement. Initial refinement in C1 symmetry gave a good-looking map with an estimated resolution of 6.98 Å (FSC at 0.143 threshold). Final refinement in T (tetrahedral) symmetry resulted in an overall improvement of the map quality and gave a final resolution at the level of 4.68 Å (FSC at 0.143 threshold) (Fig. S5k, ESI†). Both structures were deposited in Electron Microscopy Data Bank under the codes EMD-17195 and EMD-17196 for 11TRAP12 and 12TRAP12 respectively. Data collection statistics are listed in Table S6 (ESI†).
311 particles) was selected for further steps of refinement. Initial refinement in C1 symmetry gave a good-looking map with an estimated resolution of 6.98 Å (FSC at 0.143 threshold). Final refinement in T (tetrahedral) symmetry resulted in an overall improvement of the map quality and gave a final resolution at the level of 4.68 Å (FSC at 0.143 threshold) (Fig. S5k, ESI†). Both structures were deposited in Electron Microscopy Data Bank under the codes EMD-17195 and EMD-17196 for 11TRAP12 and 12TRAP12 respectively. Data collection statistics are listed in Table S6 (ESI†).
Discussion
The discovery that an 11mer protein ring could assemble to form what appeared to be a regular-faced convex polyhedron led to an increased understanding of how real-world proteins can accommodate small deviations to allow them to approximate such a polyhedron. The original TRAP-cage made from 24 copies of the 11mer ring had very small deviations from ideality, reflecting the fact that a hendecagon could almost perfectly be inscribed within each of the 24 pentagonal faces of a pentagonal icositetrahedron. Such an arrangement of rings also allows 10 of the 11 cysteines on the outer rim of the TRAP-cage to form (Au(I)-mediated) coordinate bonds with partner cysteines of neighbouring rings. This minimisation of geometrical error and maximization of bonding likely accounts for the preferred formation of the 24-ring TRAP-cage, and its high stability. The question naturally arises as to what other “almost regular” protein cages could form with sufficiently small distortions such that they could reasonably be viewed as approaching regularity and such that they are likely to form from a physicochemical point of view. The ability to accurately predict the structures of such cages given the starting polygon (e.g., a hendecameric ring) may be useful from a protein design standpoint. We previously developed an algorithm that attempted to carry out such predictions.12 To date, practical probing of the predictive power of the algorithm has been limited to a subset of 11mer TRAP rings. The existence of a 12mer TRAP ring allowed us to test more widely and confirm the usefulness of the algorithm.The cages produced from the 12TRAP have stability profiles resembling those of the geometrically similar 11TRAP12. This is likely due the proteins having to adopt similar deviations from ideality, themselves larger than that seen for the original 11TRAP24 resulting in, for example, a more strained and energetically unfavourable structure (though the cages themselves are still highly stable in general). In the case of 12TRAP12 stability, a notable outlier is the response to surfactant, where high sensitivity is observed. This could be due to the fact that there are a greater number of positively charged residues on the rim of the 12TRAP. This could result in increased binding by the negatively charged head of SDS.
From an applications perspective 12TRAP12 lacks the large holes seen in 11TRAP24, hence may offer a more protective environment for fragile cargoes.
One thing that remains unclear is how dependent the predictive power of the algorithm is on the specificity of the TRAP ring structure and amino acid sequence. The surface features and truncated cone structure of the TRAP ring allow simple connectors between rings to be employed, enabling TRAP rings to be considered as featureless 2-dimensional polygons in the model. While efforts to increase our mathematical understanding of cage geometries have continued to deepen and formalise,13 the limits of this approach, taking into account the three-dimensional reality of constituent proteins and the full extent of potential protein–protein interactions, have yet to be probed.
Data and materials availability
All data needed to evaluate the conclusions in the paper are present in the paper and/or the ESI.† The cryoEM reconstructions are deposited in the Electron Microscopy Data Bank under the codes: EMD-17195 and EMD-17196 for 11TRAP12 and 12TRAP12 respectively.Author contributions
Conceptualization: J. G. H. and A. P. B., experimental design: I. S., A. P. B., A. K., K. M., K. B.-S., A. N., methodology and figure preparation: I. S., A. P. B., A. K., B. M. A. G. P., K. M., K. B.-S., A. N., writing – original draft: I. S., A. P. B., A. K., J. G. H.Conflicts of interest
The authors declare the following competing interests: the authors J. G. H., A. P. B. and I. S. are named on a number of relevant accepted or pending patents that are related to the TRAP-cage system. J. G. H. is also the founder of and holds equity in nCage Therapeutics LLC, which aims to commercialise protein cages for therapeutic applications. I. S. is an employee of nCage Therapeutics. The authors declare that they have no other competing interests.Acknowledgements
I. S., A. P. B., A. K., K. M., A. N., K. B.-S. and J. G. H. were funded by a Polish National Science Centre (NCN,) grant no. 2016/20/W/NZ1/00095 (Symfonia-4). A. P. B., A. N., K. B.-S. and J. G. H. were funded by a Polish National Science Centre (NCN) (Maestro grant no. 2019/34/A/NZ1/00196). I. S. was supported by the Foundation for Polish Science (FNP) within the FNP START 2023 programme. This research was supported in part by PL-Grid Infrastructure. Part of this research took place at SOLARIS National Synchrotron Radiation Centre, using the cryoEM infrastructure. Experiments were performed in collaboration with SOLARIS Staff. Parts of the cryoEM data collection were performed in Astbury Biostructure Laboratory, University of Leeds, UK.References
- P.-S. Huang, S. E. Boyken and D. Baker, Nature, 2016, 537, 320–327 CrossRef CAS PubMed.
- S. L. Lovelock, R. Crawshaw, S. Basler, C. Levy, D. Baker, D. Hilvert and A. P. Green, Nature, 2022, 606, 49–58 CrossRef CAS PubMed.
- A. A. Cohen, N. van Doremalen, A. J. Greaney, H. Andersen, A. Sharma, T. N. Starr, J. R. Keeffe, C. Fan, J. E. Schulz, P. N. P. Gnanapragasam, L. M. Kakutani, A. P. West, G. Saturday, Y. E. Lee, H. Gao, C. A. Jette, M. G. Lewis, T. K. Tan, A. R. Townsend, J. D. Bloom, V. J. Munster and P. J. Bjorkman, Science, 2022, 377, eabq0839 CrossRef CAS PubMed.
- A. C. Walls, B. Fiala, A. Schäfer, S. Wrenn, M. N. Pham, M. Murphy, V. T. Longping, L. Shehata, M. A. O’Connor and C. Chen, Cell, 2020, 183, 1367–1382 CrossRef CAS PubMed.
- J. Marcandalli, B. Fiala, S. Ols, M. Perotti, W. de van der Schueren, J. Snijder, E. Hodge, M. Benhaim, R. Ravichandran and L. Carter, Cell, 2019, 176, 1420–1431 CrossRef CAS PubMed.
- P. S. Arunachalam, Y. Feng, U. Ashraf, M. Hu, A. C. Walls, V. V. Edara, V. I. Zarnitsyna, P. P. Aye, N. Golden, M. C. Miranda, K. W. M. Green, B. M. Threeton, N. J. Maness, B. J. Beddingfield, R. P. Bohm, S. E. Scheuermann, K. Goff, J. Dufour, K. Russell-Lodrigue, E. Kepl, B. Fiala, S. Wrenn, R. Ravichandran, D. Ellis, L. Carter, K. Rogers, L. M. Shirreff, D. E. Ferrell, N. R. Deb Adhikary, J. Fontenot, H. L. Hammond, M. Frieman, A. Grifoni, A. Sette, D. T. O’Hagan, R. Van Der Most, R. Rappuoli, F. Villinger, H. Kleanthous, J. Rappaport, M. S. Suthar, D. Veesler, T. T. Wang, N. P. King and B. Pulendran, Sci. Transl. Med., 2022, 14, eabq4130 CrossRef CAS PubMed.
- F. H. C. Crick and J. D. Watson, Nature, 1956, 177, 473–475 CrossRef CAS PubMed.
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS PubMed.
- R. Twarock and A. Luque, Nat. Commun., 2019, 10, 1–9 CrossRef CAS PubMed.
- F. Madeira, M. Pearce, A. R. N. Tivey, P. Basutkar, J. Lee, O. Edbali, N. Madhusoodanan, A. Kolesnikov and R. Lopez, Nucleic Acids Res., 2022, 50, W276–W279 CrossRef CAS PubMed.
- B. Grünbaum and N. W. Johnson, J. London Math. Soc., 1965, 1, 577–586 CrossRef.
- B. M. A. G. Piette, A. Kowalczyk and J. G. Heddle, Proc. R. Soc. London, Ser. A, 2022, 478, 20210679 Search PubMed.
- B. M. A. G. Piette and Á. Lukács, Symmetry, 2023, 15, 717 CrossRef.
- A. D. Malay, N. Miyazaki, A. Biela, S. Chakraborti, K. Majsterkiewicz, I. Stupka, C. S. Kaplan, A. Kowalczyk, B. M. A. G. Piette, G. K. A. Hochberg, D. Wu, T. P. Wrobel, A. Fineberg, M. S. Kushwah, M. Kelemen, P. Vavpetič, P. Pelicon, P. Kukura, J. L. P. Benesch, K. Iwasaki and J. G. Heddle, Nature, 2019, 569, 438–442 CrossRef CAS PubMed.
- K. Majsterkiewicz, A. P. Biela, S. Maity, M. Sharma, B. M. A. G. Piette, A. Kowalczyk, S. Gaweł, S. Chakraborti, W. H. Roos and J. G. Heddle, Nano Lett., 2022, 22, 3187–3195 CrossRef CAS PubMed.
- M. Sharma, A. Biela, A. Kowalczyk, K. Borzęcka-Solarz, B. Piette, S. Gaweł, J. Bishop, P. Kukura, J. Benesch, M. Imamura, S. Scheuring and J. Heddle, ACS Nanosci. Au, 2022, 2, 404–413 CrossRef CAS PubMed.
- A. D. Malay, J. G. Heddle, S. Tomita, K. Iwasaki, N. Miyazaki, K. Sumitomo, H. Yanagi, I. Yamashita and Y. Uraoka, Nano Lett., 2012, 12, 2056–2059 CrossRef CAS PubMed.
- J. G. Heddle, A. Kowalczyk and B. M. A. G. Piette, Bridges 2019 Conference Proceedings, Tessellations Publishing, Phoenix, Arizona, 2019, pp. 363–366 Search PubMed.
- S. Q. Zheng, E. Palovcak, J. P. Armache, K. A. Verba, Y. Cheng and D. A. Agard, Nat. Methods, 2017, 14, 331–332 CrossRef CAS PubMed.
- A. Punjani, J. L. Rubinstein, D. J. Fleet and M. A. Brubaker, Nat. Methods, 2017, 14, 290–296 CrossRef CAS PubMed.
- T. Bepler, K. Kelley, A. J. Noble and B. Berger, Nat. Commun., 2020, 11, 5208 CrossRef CAS PubMed.
- T. Bepler, A. Morin, M. Rapp, J. Brasch, L. Shapiro, A. J. Noble and B. Berger, Nat. Methods, 2019, 16, 1153–1160 CrossRef CAS PubMed.
- A. Punjani and D. J. Fleet, J. Struct. Biol., 2021, 213, 107702 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tb01659e |
| ‡ Current address: nCage Therapeutics, Krakow, Poland. |
| § Current address: Department of Biosciences, Durham University, Durham, UK. |
| This journal is © The Royal Society of Chemistry 2024 |