Open Access Article
Open Access ArticleControl of the geometry and anisotropy driven by the combination of steric and anion coordination effects in CoII complexes with N6-tripodal ligands: the impact of the size of the ligand on the magnetization relaxation time†
Aritz
Landart
 a,
María Mar
Quesada-Moreno
a,
María Mar
Quesada-Moreno
 b,
María A.
Palacios
b,
María A.
Palacios
 *a,
Yanling
Li
*a,
Yanling
Li
 c,
Mykhaylo
Ozerov
c,
Mykhaylo
Ozerov
 d,
J.
Krzystek
d and
Enrique
Colacio
d,
J.
Krzystek
d and
Enrique
Colacio
 *a
*a
aDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, 18071 Granada, Spain. E-mail: ecolacio@ugr.es
bDepartamento de Química Física y Analítica, Facultad de Ciencias Experimentales, Universidad de Jaén, Campus Las Lagunillas, 23071 Jaén, Spain
cSorbonne Université Institut Parisien de Chimie Moléculaire, CNRS UMR 8232 4 place Jussieu 75252, Paris cedex 5, France
dNational High Magnetic Field Laboratory, Florida State University, Tallahassee, Florida 32310, USA
First published on 24th April 2024
Abstract
Four mononuclear CoII complexes of formula [Co(L)(SCN)2(CH3OH)0.5(H2O)0.5]·1.5H2O·0.75CH3OH (1), [Co(L1)Cl2]·H2O·2CH3CN (2), [Co(L1)(SCN)2]·1.5H2O·CH3OH (3) and [Co(L1)]ClO4·2CH3OH (4) were prepared from the N6-tripodal Schiff base ligands (S)P[N(Me)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)2-Q]3 (L) and (S)P[N(Me)N
C(H)2-Q]3 (L) and (S)P[N(Me)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)1-ISOQ]3 (L1), where Q and ISOQ represent quinolyl and isoquinolyl moieties, respectively. In 1, the L ligand does not coordinate to the CoII ion in a tripodal manner but using a new N,N,S tridentate mode, which is due to the fact that the N6-tripodal coordination promotes a strong steric hindrance between the quinolyl moieties. However, L1 can coordinate to the CoII ions either in a tripodal manner using CoII salts with poorly coordinating anions to give 4 or in a bisbidentate fashion using CoII salt-containing medium to strongly coordinating anions to afford 2 and 3. In the case of L1, there is no steric hindrance between ISOQ moieties after coordination to the CoII ion. The CoII ion exhibits a distorted octahedral geometry for compounds 1–3, with the anions in cis positions for the former and in trans positions for the two latter compounds. Compound 4 shows an intermediate geometry between an octahedral and trigonal prism but closer to the latter one. DC magnetic properties, HFEPR and FIRMS measurements and ab initio calculations demonstrate that distorted octahedral complexes 1–3 exhibit easy-plane magnetic anisotropy (D > 0), whereas compound 4 shows large easy-axis magnetic anisotropy (D < 0). Comparative analysis of the magneto-structural data underlines the important role that is played not only by the coordination geometry but also the electronic effects in determining the anisotropy of the CoII ions. Compounds 2–3 show a field-induced slow relaxation of magnetization. Despite its large easy-axis magnetic anisotropy, compound 4 does not show significant slow relaxation (SMR) above 2 K under zero applied magnetic fields, but its magnetic dilution with ZnII triggers SMR at zero field. Finally, it is worth remarking that compounds 2–4 show smaller relaxation times than the analogous complexes with the tripodal ligand bearing in its arms pyridine instead of isoquinoline moieties, which is most likely due to the increase of the molecular size in the former one.
C(H)1-ISOQ]3 (L1), where Q and ISOQ represent quinolyl and isoquinolyl moieties, respectively. In 1, the L ligand does not coordinate to the CoII ion in a tripodal manner but using a new N,N,S tridentate mode, which is due to the fact that the N6-tripodal coordination promotes a strong steric hindrance between the quinolyl moieties. However, L1 can coordinate to the CoII ions either in a tripodal manner using CoII salts with poorly coordinating anions to give 4 or in a bisbidentate fashion using CoII salt-containing medium to strongly coordinating anions to afford 2 and 3. In the case of L1, there is no steric hindrance between ISOQ moieties after coordination to the CoII ion. The CoII ion exhibits a distorted octahedral geometry for compounds 1–3, with the anions in cis positions for the former and in trans positions for the two latter compounds. Compound 4 shows an intermediate geometry between an octahedral and trigonal prism but closer to the latter one. DC magnetic properties, HFEPR and FIRMS measurements and ab initio calculations demonstrate that distorted octahedral complexes 1–3 exhibit easy-plane magnetic anisotropy (D > 0), whereas compound 4 shows large easy-axis magnetic anisotropy (D < 0). Comparative analysis of the magneto-structural data underlines the important role that is played not only by the coordination geometry but also the electronic effects in determining the anisotropy of the CoII ions. Compounds 2–3 show a field-induced slow relaxation of magnetization. Despite its large easy-axis magnetic anisotropy, compound 4 does not show significant slow relaxation (SMR) above 2 K under zero applied magnetic fields, but its magnetic dilution with ZnII triggers SMR at zero field. Finally, it is worth remarking that compounds 2–4 show smaller relaxation times than the analogous complexes with the tripodal ligand bearing in its arms pyridine instead of isoquinoline moieties, which is most likely due to the increase of the molecular size in the former one.
Introduction
Single-molecule magnets (SMMs) are open-shell metal complexes exhibiting slow relaxation of the magnetization and, as a result, magnetic hysteresis and remnant magnetization when the polarizing field is eliminated below the so-called blocking temperature (TB).1 In addition to these classical properties, SMMs show quantum properties such as quantum tunneling of the magnetization (QTM), quantum coherence and quantum oscillations. This association of classical and quantum properties makes this subclass of materials good candidates for potential technological applications such as high-density data storage, quantum sensing, quantum simulation, and ultimately quantum computing.1,2 The SMMs’ behavior mainly depends on the magnetic anisotropy, which arises from the combined action of spin–orbit coupling (SOC) and ligand field effects. Therefore, it is not surprising that the best SMM properties have been observed for metal complexes containing very anisotropic lanthanide ions, particularly DyIII. It is worth noting that, among these systems, those of mononuclear nature, also called single-ion magnets (SIMs), exhibiting large axial (easy-axis) anisotropy with negligible rhombicity terms, have been shown to be very efficient as SMMs with the Ueff (effective energy barrier for magnetization reversal) and TB as high as 1540 cm−1 and 80 K, respectively.3 These outstanding SIM properties have been achieved because in these mononuclear complexes the magnetic anisotropy can be deliberately regulated by playing with the geometry and electronic nature of the metal ion and the crystal field splitting, which ultimately depends on the electronic and steric effects of the ligands. Among transition metal complexes, some mononuclear linear, tetrahedral and trigonal prismatic CoII-containing complexes with strong easy-axis anisotropy have also shown to be quite efficient SIMs with Ueff and TB up to 450 cm−1 and 5 K, respectively.4 Moreover, some of them are air stable, opening the door toward their incorporation in devices.In this context, we, and others, have recently reported CoII trigonal prismatic complexes with N6-tripodal ligands exhibiting strong easy-axis anisotropy, and in some cases, slow relaxation of the magnetization at zero-field and a pinched at the waist hysteresis loop at 2 K.5 Moreover, experimental and theoretical studies on these compounds established that the easy-axis anisotropy increases linearly as the distortion from TPR-6 to OC-6 decreases with a concomitant increase of the relaxation times.5f,o,p In other words, when the geometry becomes closer to the ideal TPR-6, the SIM properties improve. Moreover, some of the authors have recently shown that the large easy-axis anisotropy of trigonal prismatic CoII ions in a Co3 complex is mandatory, together with the collinearity of the anisotropy axes and magnetic exchange, for observing SMM behaviour at zero field with pinched at the waist hysteresis at 2 K.6
As a continuation of this work, we report here the synthesis, X-ray crystal structure, dc and ac magnetic properties and HFEPR and FIRMS spectroscopic studies of four new CoII complexes with the Schiff base N6-tripodal ligands tris(2-quinolylhydrazonyl)phosphorylsulfide, (S)P[N(Me)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)(2-Q)]3 (L) and tris(1-isoquinolyl hydrazonyl)phosphorylsulfide, (S)P[N(Me)N
C(H)(2-Q)]3 (L) and tris(1-isoquinolyl hydrazonyl)phosphorylsulfide, (S)P[N(Me)N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H)(1-ISOQ)]3 (L1) (see Scheme 1) of formula [Co(L)(SCN)2(CH3OH)0.5(H2O)0.5]·1.5H2O·0.75CH3OH (1), [Co(L1)Cl2]·H2O·2CH3CN (2), [Co(L1)(SCN)2]·1.5H2O·CH3OH (3) and [Co(L1)]ClO4·2CH3OH (4).
C(H)(1-ISOQ)]3 (L1) (see Scheme 1) of formula [Co(L)(SCN)2(CH3OH)0.5(H2O)0.5]·1.5H2O·0.75CH3OH (1), [Co(L1)Cl2]·H2O·2CH3CN (2), [Co(L1)(SCN)2]·1.5H2O·CH3OH (3) and [Co(L1)]ClO4·2CH3OH (4).
The aim of this study is threefold: (i) to analyze how the use of bulky bicyclic aromatic moieties such as quinolyl and isoquinolyl modify the geometry of the CoN6 coordination sphere and, therefore, the magnitude of the magnetic anisotropy regarding previously reported analogous trigonal prismatic CoII complexes; we expect that the presence of bulky groups leads to a more distorted trigonal prismatic geometry and, then, to a decrease in the easy-axis magnetic anisotropy and to worse SIM properties; (ii) to study how the coordination in axial positions of the CoII ion of two π-donor ligands (chloride or κ-N-thiocyanato), giving rise to a distorted octahedral CoN4X2 (Cl− or SCN−) coordination sphere, modifies the magnitude of the magnetic anisotropy compared with previously reported analogous complexes, and (iii) to analyze how the magnetic relaxation dynamics is affected when the size of the molecule increases.
Experimental
Synthetic procedures
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C(H)(2-Q)]3 (L).
Tris(methylhidrazido)phosphorylsulfide (0.45 g, 2.25 mmol) and 2-quinolinecarboxaldehyde (1.06 g, 6.75 mmol) were dissolved in 40 mL of methanol. Afterwards, a few drops of acetic acid were added, and the mixture was refluxed for 21 hours and stirred at room temperature for 24 hours more. Then, the mixture was evaporated to dryness and the resulting yellow oil was recrystallised in chloroform. The solid formed was filtered off and dried in a vacuum. Yield: 47%. Anal. Calc. for C33H30N9PS: C, 64.38; H, 4.91; N, 20.47: S, 5.21. Found: C, 63.97; H, 4.49; N, 20.68; S, 5.35. IR (cm−1): 3100–2800, ν(CH); 1600–1400, ν(C
C(H)(2-Q)]3 (L).
Tris(methylhidrazido)phosphorylsulfide (0.45 g, 2.25 mmol) and 2-quinolinecarboxaldehyde (1.06 g, 6.75 mmol) were dissolved in 40 mL of methanol. Afterwards, a few drops of acetic acid were added, and the mixture was refluxed for 21 hours and stirred at room temperature for 24 hours more. Then, the mixture was evaporated to dryness and the resulting yellow oil was recrystallised in chloroform. The solid formed was filtered off and dried in a vacuum. Yield: 47%. Anal. Calc. for C33H30N9PS: C, 64.38; H, 4.91; N, 20.47: S, 5.21. Found: C, 63.97; H, 4.49; N, 20.68; S, 5.35. IR (cm−1): 3100–2800, ν(CH); 1600–1400, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 950 ν(P
N) and 950 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S). 1H NMR (CDCl3, ppm): 8.05 (d, Hql), 8.0 (s, Himine), 7.78 (d, Hql), 7.7 (m, Hql), 7.6 (dd, Hql), 7.45 (m, Hql), 3.5 (s, Hmethyl).
S). 1H NMR (CDCl3, ppm): 8.05 (d, Hql), 8.0 (s, Himine), 7.78 (d, Hql), 7.7 (m, Hql), 7.6 (dd, Hql), 7.45 (m, Hql), 3.5 (s, Hmethyl).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) C(H)(1-ISOQ)]3 (L1).
In 40 mL of methanol were dissolved tris(methylhidrazido)phosphorylsulfide (0.21 g, 1.06 mmol) and isoquinolinecarboxaldehyde (0.5 g, 3.18 mmol) together with a few drops of acetic acid. The mixture was refluxed for seven hours and then stirred at room temperature for 16 hours more. The precipitated ligand was filtered off and dried in a vacuum. Yield: 31%. Anal. Calc. for C33H30N9PS: C, 64.38; H, 4.91; N, 20.47: S, 5.21. Found: C, 64.17; H, 5.35; N, 20.48; S, 5.26. IR (cm−1): 3000–2800, ν(CH); 1600–1400, ν(C
C(H)(1-ISOQ)]3 (L1).
In 40 mL of methanol were dissolved tris(methylhidrazido)phosphorylsulfide (0.21 g, 1.06 mmol) and isoquinolinecarboxaldehyde (0.5 g, 3.18 mmol) together with a few drops of acetic acid. The mixture was refluxed for seven hours and then stirred at room temperature for 16 hours more. The precipitated ligand was filtered off and dried in a vacuum. Yield: 31%. Anal. Calc. for C33H30N9PS: C, 64.38; H, 4.91; N, 20.47: S, 5.21. Found: C, 64.17; H, 5.35; N, 20.48; S, 5.26. IR (cm−1): 3000–2800, ν(CH); 1600–1400, ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 900 ν(P
N) and 900 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S). 1H NMR (CDCl3, ppm): 9.25 (d, Hiql), 8.5 (d, Hiql), 8.3 (s, Himine), 7.65 (d, Hiql), 7.5 (d, Hiql), 7.4 (m, Hiql), 7.05 (m, Hiql), 3.5 (s, Hmethyl).
S). 1H NMR (CDCl3, ppm): 9.25 (d, Hiql), 8.5 (d, Hiql), 8.3 (s, Himine), 7.65 (d, Hiql), 7.5 (d, Hiql), 7.4 (m, Hiql), 7.05 (m, Hiql), 3.5 (s, Hmethyl).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 950 ν(P
N) and 950 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S). ESI-MS (Da): m/z 732.09, [Co(L)(SCN)]+; m/z 616.18, L+; m/z 369.06, [Co(L1)(CH3OH)2]2+.
S). ESI-MS (Da): m/z 732.09, [Co(L)(SCN)]+; m/z 616.18, L+; m/z 369.06, [Co(L1)(CH3OH)2]2+.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 900 ν(P
N) and 900 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S).
S).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) and 900 ν(P
N) and 900 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S).
S).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1075, ν(Cl–O) and 900 ν(P
N); 1075, ν(Cl–O) and 900 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S). ESI-MS (Da): m/z 773.09, [Co(L1)]2+(ClO4); m/z 337.07, [Co(L1)]2+.
S). ESI-MS (Da): m/z 773.09, [Co(L1)]2+(ClO4); m/z 337.07, [Co(L1)]2+.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and C
C and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N); 1088, ν(Cl–O) and 900 ν(P
N); 1088, ν(Cl–O) and 900 ν(P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S). ESI-MS (Da): m/z 780.07, [Zn(L1)]2+(ClO4); m/z 340.5, [Zn(L1)]2+.
S). ESI-MS (Da): m/z 780.07, [Zn(L1)]2+(ClO4); m/z 340.5, [Zn(L1)]2+.
It is worth noting that all attempts to obtain the diluted version of compounds 1–3 were unsuccessful.
Physical measurements
Elemental analyses were performed on a Fisons-Carlo Erba analyser model EA 1108 and 1H-NMR spectra on a 400 Hz “VARIAN DIRECT DRIVE” spectrometer at the “Centro de Instrumentación Científica” (University of Granada). IR spectra were recorded on a Bruker Tensor 27 spectrophotometer by using ATR detection. The X-ray powder diffraction (XRPD) spectra were registered on a (2θ) Bruker D2-PHASER using CuKα (λ = 1.5418 Å) radiation and LYNXEYE detector, from 5 to 50° (2θ) at a scanning rate of 0.5° 2θ/min (Fig. S1†).Variable-temperature (2–300 K) magnetic susceptibility measurements were carried out on polycrystalline samples under an applied field of 1000 Oe using DynaCool PPMS-9 physical measurement equipment (1, 4′) or a Quantum Design SQUID MPMS XL-5 (4) or XL-7 (2, 3) device. Alternating-current (ac) susceptibility measurements under different applied static fields in the temperature range 2–15 K were performed in PPMS-9 physical measurement equipment in the 50–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz frequency range, using an oscillating field Hac = 10 Oe (2, 3) or Hac = 5 Oe (4′). The ac measurements of complex 4 were recorded using a Quantum Design SQUID MPMS XL-5 device under an oscillating ac field of 4 Oe and ac frequencies in the 1–1500 Hz range. The magnetic susceptibility values were corrected for the diamagnetism of the molecular constituents and sample holder.
000 Hz frequency range, using an oscillating field Hac = 10 Oe (2, 3) or Hac = 5 Oe (4′). The ac measurements of complex 4 were recorded using a Quantum Design SQUID MPMS XL-5 device under an oscillating ac field of 4 Oe and ac frequencies in the 1–1500 Hz range. The magnetic susceptibility values were corrected for the diamagnetism of the molecular constituents and sample holder.
Far-infrared magnetic spectroscopy (FIRMS, also known as frequency-domain THz EPR spectroscopy)8 experiments of compounds 2–4 (no clear magnetic peaks were observed in the spectrum of 1) were performed at the National High Magnetic Field Laboratory using a Bruker Vertex 80v FT-IR spectrometer coupled with a 17 T vertical-bore superconducting magnet in a Voigt configuration (light propagation perpendicular to the external magnetic field). The experimental setup employs broad band terahertz radiation emitted by a mercury arc lamp. The radiation transmitted through the sample was detected by a composite silicon bolometer (Infrared Laboratories) mounted at the end of the quasioptical transmission line. Both the sample and bolometer were cooled by low-pressure helium gas to the temperature of 5 K. The intensity spectra of the microcrystalline powder sample (∼2 mg) bonded by n-eicosane were measured in the spectral region between 14 and 730 cm−1 (0.42–22 THz) with an instrumental resolution of 0.3 cm−1 (9 GHz). To discern the magnetic absorption, the transmission spectrum at each magnetic field was divided by the reference spectrum, which is calculated as the average spectrum for all magnetic fields after removing outlier points at each frequency. Such normalized spectra are only sensitive to tiny transmission changes induced by the magnetic field and exclude a strong nonmagnetic contribution due to vibrational absorptions and an instrumental function. All the data analysis routine was implemented by in-house-written MATLAB code based on the EPR simulation software package EasySpin.9
High-frequency and high-field EPR (HFEPR) spectra of compounds 2–4 were recorded at the National High Magnetic Field Laboratory in a 4.5–10 K temperature range on polycrystalline samples (20–25 mg), using a homodyne spectrometer at the EMR facility associated with a 15/17-T superconducting magnet and a frequency range from 52 to 426 GHz.10 Detection was provided with an InSb hot electron bolometer (QMC Ltd, Cardiff, UK). The magnetic field was modulated at 50 kHz for detection purposes. A Stanford Research Systems SR830 lock-in amplifier converted the modulated signal to dc voltage.
Single-crystal structure determinations
Suitable crystals of 1–4 were mounted on a glass fibre and used for data collection. X-ray diffraction data were collected at 100 K using a Bruker D8 Venture diffractometer (MoKα radiation, λ = 0.71073 Å) fitted with a PHOTON 100 detector. Unit-cell parameters were determined and refined on all the observed reflections using APEX2 software.11 Correction for Lorentz polarization and absorption was applied by the SAINT12 and SADABS13 programs, respectively.The structures were solved using SHELXS (2, 3)14 or SHELXT (1, 4)15 and refined by the full-matrix least-squares method on F2 using the SHELXL-2014/2018![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and OLEX2 programs.17
16 and OLEX2 programs.17
The data collected for compound 1 were of very bad quality. For that reason, a low value of resolution was chosen for data integration as the reflections that appear below this resolution were very weak. In 1, the two quinoline molecules that remain free were generated from the quinoline molecule that is coordinated to the CoII ion. In addition, the uncoordinated quinolines were heavily disordered, and the anisotropic model could not be applied, so the atoms were considered isotropically. One SCN anion was disordered and could be modelled satisfactorily. The oxygen atom coordinated to CoII belongs half time to a water molecule and half time to a methanol molecule. Moreover, in the solvent molecules, the hydrogen atoms bonded to water and methanol molecules could not be reliably positioned and this causes checkCIF alerts concerning the chemical formula. Therefore, all the alerts from the structure of 1 are, mainly, due to the bad quality of the collected data. In compound 3, one of the isoquinoline molecules and the oxygen atom from the methanol and water solvent molecules are disordered, and the disorder model was satisfactory. However, the hydrogen atoms associated with the solvent water molecule could not be directly located from difference Fourier maps. For this reason, the calculated and reported SumFormula differs. In addition, one perchlorate anion of compound 4 is also heavily disordered over two positions. It could be modelled satisfactorily but the oxygen atoms were refined isotropically. In all cases, the hydrogen atom positions were calculated and isotropically refined as riding models to their parent atoms.
A summary of selected data collection and refinement parameters can be found in the ESI (Table S1†) and CCDC 2334787–2334790.†
Computational methodology
Calculations were carried out from the crystallographic structures using the cif files. The electronic structure and magnetic properties have been computed using state-averaged complete active space self-consistent field calculations (SA-CASSCF (7,5)),18 followed by the N-electron valence second-order perturbation theory (NEVPT2) method19 with the def2-TZVPP basis set,20 including the auxiliary basis sets for correlation and Coulomb fitting for all the atoms. All calculations were done with the ORCA 5.0.2 quantum chemistry program package.21 Spin Hamiltonian parameters (D, E and g-tensor) were computed using the effective Hamiltonian S = 3/2. In this case, spin–orbit effects were included using the quasi-degenerate perturbation theory (QDPT).22,23 The employed active space includes seven electrons in five 3d-orbitals of CoII CAS (7,5). We have included all 10 states for the 2S + 1 = 4 (quartet) states arising from the 4F and 4P terms of CoII, and all 40 states for the respective 2S + 1 = 2 (duplet) states arising from the 2P, 2D (twice), 2F, 2G and 2H terms of the CoII ion. ORCA produces two sets of results: CASSCF and NEVPT2. The splitting of d-orbitals due to the ligand field has been computed with the ab initio ligand field theory (AILFT)24 module implemented in the ORCA program package.Results and discussion
The new ligands were obtained by condensation between tris(methylhydrazine)phosphorylsulfide and either 2-quinolinecarboxaldehyde or isoquinoline-1-carbaldehyde in methanol containing some drops of acetic acid for catalyzing the reaction. The ligand L reacts with Co(SCN)2·6H2O in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio and using methanol as solvent, leading to the compound (1). All attempts to obtain other complexes with this ligand using different CoII salts (with coordinating and non-coordinating anions Cl−, Br−, BF4−, ClO4−, NO3−), CoII/L ratios (2/1, 1/1 and 1/2) and solvents (EtOH, CH3CN, MeOH and DMF) were unsuccessful. It is worth noting that in 1 the L ligand does not coordinate to CoII in a tripodal fashion, but as a S,N,N-tridentate ligand, so that only one arm of L coordinates to the CoII ion (see below). The N6-tripodal coordination mode of this ligand could promote a strong steric hindrance between the bulky quinolyl aromatic bicyclic moieties of the three arms of the ligand, because they would be orientated toward the inner part of the complex and placed close to each other. This is the reason why the CoII complexes with the ligand L coordinated in a N6-tripodal fashion and even with only two arms coordinated to the CoII would be unstable. In view of this, we designed L1, which when it coordinates to the CoII either in an N6-tripodal manner or in a bis-bidentate fashion (when only two arms of the ligand are coordinated to the CoII ion) has the isoquinolyl moieties oriented toward the outer part of the complex. Therefore, the steric hindrance significantly diminishes and complexes where the ligand presents these coordination modes could be formed. In fact, the reaction of L1 with different CoII salts led to the formation in a good yield of the crystalline complexes 2–4. It is worth noting that the reaction between L1 and CoII salt-containing medium to strong coordinating anions, such as chloride or thiocyanate, using different CoII/ligand molar ratio and solvents, in no case led to the N6-coordinated cationic complexes [Co(L1)]X2 (X = Cl−, SCN−), but to neutral compounds [Co(L1)X2]. In these latter ones, the ligand shows a bisbidentate coordination mode and the corresponding anions coordinate in trans positions. The formation of the complex [Co(L1)Cl2] (2) seems to indicate that the coordination ion of two chloride anions to the CoII instead of two N-donor atoms belonging to one arm of the L1 ligand is either faster and/or thermodynamically more favorable with the L1 ligand than with other less bulky closely related N6-tripodal ligands.5o,p These latter coordinate to the CoII in an N6-tripodal mode leading to complexes of formula [Co(L′)][CoCl4] (L′ is the N6-tripodal ligand bearing pyridine or imidazole moieties instead of isoquinoline). However, the reaction of Co(ClO4)2 with L1 led to complex 4, where the ligand was able to coordinate the three arms to the CoII ion, due to the poor coordination ability of the perchlorate anion.
1 molar ratio and using methanol as solvent, leading to the compound (1). All attempts to obtain other complexes with this ligand using different CoII salts (with coordinating and non-coordinating anions Cl−, Br−, BF4−, ClO4−, NO3−), CoII/L ratios (2/1, 1/1 and 1/2) and solvents (EtOH, CH3CN, MeOH and DMF) were unsuccessful. It is worth noting that in 1 the L ligand does not coordinate to CoII in a tripodal fashion, but as a S,N,N-tridentate ligand, so that only one arm of L coordinates to the CoII ion (see below). The N6-tripodal coordination mode of this ligand could promote a strong steric hindrance between the bulky quinolyl aromatic bicyclic moieties of the three arms of the ligand, because they would be orientated toward the inner part of the complex and placed close to each other. This is the reason why the CoII complexes with the ligand L coordinated in a N6-tripodal fashion and even with only two arms coordinated to the CoII would be unstable. In view of this, we designed L1, which when it coordinates to the CoII either in an N6-tripodal manner or in a bis-bidentate fashion (when only two arms of the ligand are coordinated to the CoII ion) has the isoquinolyl moieties oriented toward the outer part of the complex. Therefore, the steric hindrance significantly diminishes and complexes where the ligand presents these coordination modes could be formed. In fact, the reaction of L1 with different CoII salts led to the formation in a good yield of the crystalline complexes 2–4. It is worth noting that the reaction between L1 and CoII salt-containing medium to strong coordinating anions, such as chloride or thiocyanate, using different CoII/ligand molar ratio and solvents, in no case led to the N6-coordinated cationic complexes [Co(L1)]X2 (X = Cl−, SCN−), but to neutral compounds [Co(L1)X2]. In these latter ones, the ligand shows a bisbidentate coordination mode and the corresponding anions coordinate in trans positions. The formation of the complex [Co(L1)Cl2] (2) seems to indicate that the coordination ion of two chloride anions to the CoII instead of two N-donor atoms belonging to one arm of the L1 ligand is either faster and/or thermodynamically more favorable with the L1 ligand than with other less bulky closely related N6-tripodal ligands.5o,p These latter coordinate to the CoII in an N6-tripodal mode leading to complexes of formula [Co(L′)][CoCl4] (L′ is the N6-tripodal ligand bearing pyridine or imidazole moieties instead of isoquinoline). However, the reaction of Co(ClO4)2 with L1 led to complex 4, where the ligand was able to coordinate the three arms to the CoII ion, due to the poor coordination ability of the perchlorate anion.
Crystal structures
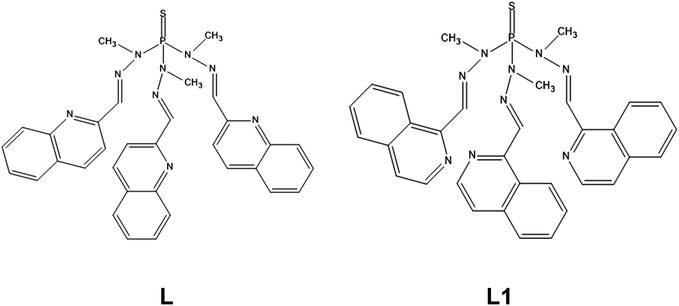
Compound 1 crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . Fig. 1 shows the molecular structure of this complex, which is formed by neutral mononuclear units [Co(L)(SCN)2(MeOH)0.5(H2O)0.5] and three quarters of a methanol and one and a half water molecules of crystallization. Selected bond distances and angles are shown in Table S2.†
. Fig. 1 shows the molecular structure of this complex, which is formed by neutral mononuclear units [Co(L)(SCN)2(MeOH)0.5(H2O)0.5] and three quarters of a methanol and one and a half water molecules of crystallization. Selected bond distances and angles are shown in Table S2.†
Within the mononuclear unit, only one arm of the tripodal L ligand is coordinated to CoII, the other two arms remaining free. The ligand coordinates to the CoII ion in a tridentate chelate coordination mode through the nitrogen atoms of the azomethine group, the quinoline moiety and the sulphur atom of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S group. The nitrogen atoms of two thiocyanate anions are in cis positions and the oxygen atom of a water/methanol molecule completes the distorted octahedral CoN4OS coordination geometry of the CoII ion. It is worth noting that, as far as we know, this is the first time that this coordination mode has been observed for this type of tripodal ligand. Although a complex with a tripodal ligand like L, where the P
S group. The nitrogen atoms of two thiocyanate anions are in cis positions and the oxygen atom of a water/methanol molecule completes the distorted octahedral CoN4OS coordination geometry of the CoII ion. It is worth noting that, as far as we know, this is the first time that this coordination mode has been observed for this type of tripodal ligand. Although a complex with a tripodal ligand like L, where the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S is S-coordinated to an AgI ion, was certainly reported, the ligand does not act as a N,N,S-tridentate ligand with two free arms as in 1, but as a S(NN)2 pentadentate bridging ligand with only a free arm and the sulphur atom acting as bridge between two AgI ions.25
S is S-coordinated to an AgI ion, was certainly reported, the ligand does not act as a N,N,S-tridentate ligand with two free arms as in 1, but as a S(NN)2 pentadentate bridging ligand with only a free arm and the sulphur atom acting as bridge between two AgI ions.25
As previously observed for CoII complexes with this type of tripodal ligand bearing two N-coordinated thiocyanate ligands,5o the Co–NSCN bond distances seem to be shorter than the Co–NL counterparts. Moreover, as expected, the Co–S bond distance appears to be the longest one.
As mentioned above (single-crystal structure determinations), the data collected for 1 were of very bad quality. In consequence, it is not possible to describe properly the intermolecular interactions. However, it seems that there exist weak intermolecular π–π interactions between the quinoline molecules pertaining to the free arms of two different complexes, which lead to a shortest intermolecular Co⋯Co distance of less than 7.5 Å. This distance suggests that the CoII molecules are not well isolated in the crystal lattice.
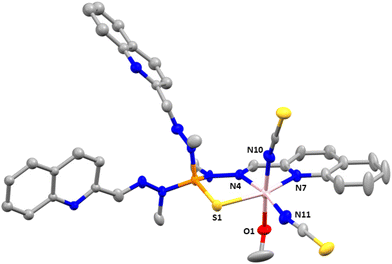
Compounds 2 and 3 crystallize in the monoclinic space group C2/c. The structures consist of neutral mononuclear molecules [Co(L1)Cl2] or [Co(L1)(SCN)2] together with two acetonitrile and one water solvent molecule for 2 and one methanol and one and a half water molecules in the case of 3 (Fig. 2).
In these complexes, the CoII ion is coordinated by two chloride anions (or two thiocyanate ligands for 3) and two arms of the L1 ligand, the third one remaining uncoordinated. In this arrangement, the CoII exhibits a distorted octahedral coordination sphere (CoN4Cl6 for 2 and CoN6 for 3), where the two Cl− anions in 2 (or two nitrogen atoms from two SCN− anions in 3) are in trans positions and two isoquinoline and two imine nitrogen atoms belonging to two of the three arms of the tripodal ligand are in the equatorial plane. Selected bond distances and angles for 2 and 3 are shown in Table S3.†
As can be observed the Co–Cl bond distances in 2 are notably larger than the Co–N ones, whereas the Co–NSCN bond distances, as observed in 1, are the shortest ones in the coordination sphere of 3. With respect to the Co–N bond distances involving donor atoms from the ligand, those belonging to the isoquinoline moiety are slightly smaller than the Co–N bond distances corresponding to the azomethine groups. The shortest intermolecular Co⋯Co distance for 2 is 8.300 Å and for 3 is 8.301 Å.
Finally, there are π–π intermolecular interactions between the coordinated isoquinoline rings with a centroid–centroid distance of 3.900 Å for 2 and 3.693 Å for 3 and between the isoquinoline rings that remain uncoordinated (4.492 Å for 2 and 4.441 Å for 3). Additionally, in 3 there exist hydrogen bond interactions between solvent water molecules (O1 and O3) with a donor–acceptor distance of 2.872 Å and between the oxygen atom pertaining to a water solvent molecule and the nitrogen atom belonging to the isoquinoline ring with a donor–acceptor distance of 2.910 Å.
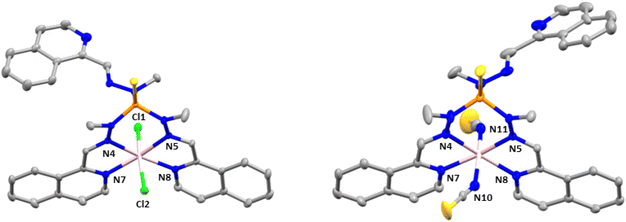
Complex 4 crystallizes in the monoclinic space group P21/n. The structure consists of cationic mononuclear units [Co(L1)]2+ together with two perchlorate anions and two solvent methanol molecules (Fig. 3).
Within the mononuclear unit, the CoII ion presents a CoN6 coordination sphere formed by six nitrogen atoms belonging to the three arms of the ligand that lead to an intermediate geometry between octahedral and trigonal prism, but closer to trigonal prism. Although the Co–N bond distances belonging to the nitrogen atoms of the azomethine group and the nitrogen atoms of the isoquinoline moieties are similar, those involving the isoquinoline nitrogen atoms are slightly larger than the former ones, in opposite direction to that observed in compounds 2 and 3. Moreover, in general, the Co–N distances in compounds 2 and 3 are larger than those in compound 4. The selected bond distances and angles are shown in Table S4.† The shortest intermolecular Co⋯Co distance between molecules is 10.203 Å, indicating that the mononuclear units are well isolated in the structure.
Finally, there are intermolecular hydrogen bond interactions between the methanol molecules and perchlorate anions with distances in the range of 2.782–3.022 Å. In addition, the structure shows π–π interactions between the isoquinolines of neighboring molecules, with a centroid–centroid distance of 3.847 Å.
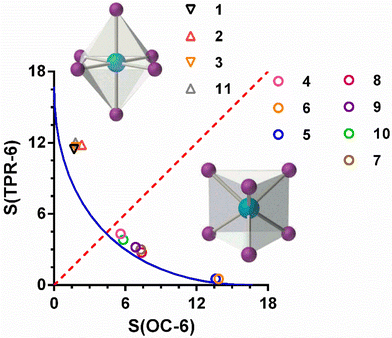
In all the compounds, the coordination geometry adopted by the CoII ion has been evaluated through SHAPE software, which is based on the continuous shape measurements method (CShMs).26a The coordination sphere of the compounds 1–4 is found between the ideal octahedral (OC-6) and trigonal prism (TRP-6) structures (Table S5†).
In the case of complexes 1–3, where the ligand is not coordinated to the CoII ion using its three arms, the S(OC-6) values are found in the 1.5–2.5 range, while the values of S(TPR-6) are found in an 11–12 range. This fact indicates that the coordination geometry of the CoII ion for these three compounds, though axially distorted, is close to octahedral. These values compare well with those calculated for the complex [Co(L3)(SCN)2] 11. In the case of compound 4, in which the three arms of the ligand are coordinated to CoII ion, the values of S(OC-6) and S(TPR-6) are 5.602 and 4.322, respectively, thus indicating that the coordination geometry adopted by the CoII ion is intermediate between an octahedron and a trigonal prism, but closer to the latter one. Moreover, the deviation with respect to the ideal Bailar path for the interconversion between the OC-6 and TPR-6 ideal geometries (Fig. 4) is very small (6.4%). The distortion of the geometry along the OC6 ↔ TPR6 pathway was also calculated using the recently proposed structural parameter (τ6).26b This geometry index is zero for the ideal OC-6 geometry and 1 for the ideal TPR6 shape (see Table S5†). The calculated τ6 values correlates well with the S values extracted with the continuous shape measures, confirming that the coordination environment of compounds 1–3 is close to the OC-6 geometry, whereas compound 4 presents a coordination sphere that is slightly closer to TPR-6 than to OC-6.
Compared with other similar compounds already reported by some of us, in which the tripodal ligand also presents a CoN6 coordination sphere, compound 4 possesses the most intermediate coordination geometry between OC-6 and TPR-6 (Fig. 4). Among these compounds, those containing tripodal ligands with methylimidazole moieties in the arms (L2), [Co(L2)]X2 (X = ClO4−, 5 and BF4−, 6), exhibit coordination spheres very close to the ideal TPR-6 geometry and continuous shape measures S(TPR-6) of 0.533 and 0.486 for 5 and 6, respectively. However, for the compounds containing ligand with pyridine moieties in the arms (L3), [Co(L3)]X2 (X = ClO4−7, BF4−8, ZnCl42−9, CoCl42−10), the CoN6 coordination environment is less distorted than 4 but more than 5 and 6 with S(TPR-6) values of 3.002 and 2.759, 3.196 and 3.839 for 7, 8, 9 and 10, respectively.
Magnetic properties
The magnetic properties of polycrystalline samples of complexes 1–4 were collected in the 2–300 K temperature range under an applied magnetic field of 1000 Oe. They are given in the form χMT vs. T (χM being the molar magnetic susceptibility) in Fig. 5. The χMT values at room temperature for 1–4 of 2.72, 2.80, 2.72 and 2.87 cm3 mol−1 K, respectively, are much higher than the spin-only value (1.875 cm3 mol−1 K) for one isolated isotropic CoII ion with g = 2 and S = 3/2, which points to an unquenched orbital angular momentum of the CoII ions. As the temperature is lowered, the χMT product decreases first slightly from room temperature to about 100 K and then in a sharper manner to reach minimum values at 2 K of 1.66, 1.60, 1.64 and 2.14 cm3 mol−1 K for 1–4, respectively. This behavior is mainly due to the depopulation of the Kramers doublets arising from the spin–orbit coupling (SOC) effects, which ultimately are responsible for the magnetic anisotropy.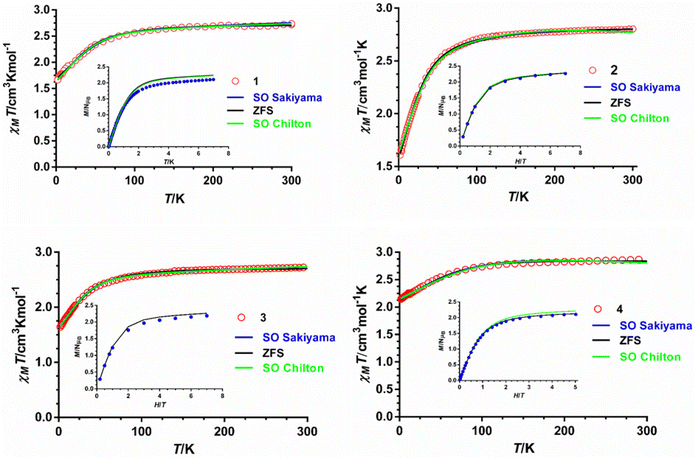 | ||
| Fig. 5 Temperature dependence of χMT (red circles) and field dependence of the magnetization at 2 K (inset, blue circles). Solid lines represent the best fit to eqn (1) (black line), (2) (green line) and (3) (blue line) with the parameters indicated in Table 1. | ||
The field dependence of the magnetization for 1–4 in the 2–7 K temperature range and magnetic fields ranging from 0 to 7 T are given in the insets of Fig. 5. The magnetization values at 2 K and under the maximum applied field of 7 T (5 T in the case of 4) of 2.10, 2.2, 2.18 and 2.10 Nβ for 1–4, respectively, are far away from the theoretical saturation value of 3Nβ expected for an isolated CoII ion with g = 2 and S = 3/2, thus confirming the existence of significant magnetic anisotropy in these complexes. The M vs. H and M vs. H/T isotherms for compounds 1–4 are shown in Fig. S2–S5.† The latter show only a slight dependence on the temperature for complexes 1–3, whereas for 4 the curves virtually superimpose in a single manner, thus suggesting that the energy separation between the ground and first excited Kramers doublets could be very large for these compounds, particularly for complex 4.
From the results of the theoretical ab initio calculations for 1–4 (see below) and using the criterion recently proposed by Boca et al.,27 for quantitatively evaluating the rightness of the spin Hamiltonian theory (hereafter named zero field splitting Hamiltonian, ZFS, eqn (1)) in octahedral and axially distorted octahedral high spin CoII complexes, we can conclude that the application of the ZFS model for analyzing the local magnetic anisotropy of the CoII ions would be appropriate for complexes 1–3. Nevertheless, the limitations of the phenomenological approach based on the ZFS Hamiltonian and the low accuracy of the magnetic measurements for determining the E and |E/D| parameters prevent extracting very reliable ZFS parameters for complexes 1–3, particularly the sign of D and the magnitude of E. Therefore, the D values extracted from the dc magnetic measurements should be considered with caution and, in any case, supported by other techniques.
On the other hand, the use of the ZFS Hamiltonian in the case of 4, which exhibits a trigonal prismatic geometry and first order spin–orbit coupling, cannot be justified. In view of this, a Hamiltonian that explicitly considers this fact, like the Griffith–Figgis Hamiltonian (GF),28 would be, in principle, more appropriate than the ZFS approach. The GF model exploits the T–P isomorphism that takes into consideration that the real orbital angular momentum for the 4T1g ground state in an ideal Oh geometry is equal to the orbital angular momentum of the 4P free ion term multiplied by −3/2 and, therefore, the 4T1g is considered as having an effective orbital moment Leff = 1. Although the GF model was developed for octahedral or axially distorted octahedral (square bipyramid) complexes, it has been also successfully applied to square-pyramidal distorted complexes.29 In this case, the two lowest crystal-field terms derive from the splitting of the 4T1g term and, therefore, the T–P isomorphism could be applicable. However, for distorted trigonal prismatic complexes, where the lowest crystal-field terms arise from the 4E ground term, this choice is more questionable. It should be noted at this point that, regardless of the inappropriateness of the ZFS model in the case of 4, it has been widely applied for analyzing the magnetic anisotropy in trigonal prismatic CoII complexes, since, as far as we know, there is no specific model for trigonal prismatic CoII complexes accounting for unquenched orbital momentum. In view of the above considerations, the magnetic anisotropy parameters extracted from the ZFS and GF Hamiltonians should be taken with caution, as neither of these two approaches is fully appropriate for analyzing the magnetic data of 4. Finally, although, as indicated above, the ZFS Hamiltonian is appropriate for analyzing the magnetic data of complexes 1–3, we have also evaluated the magnetic data of these complexes, which possess a large contribution of the orbital angular momentum, using the GF model implemented in Chilton's PHI software30a (eqn (2)).
Thus, the magnetic susceptibility and magnetization data for 1–4 were simultaneously fitted with the ZFS, as well as with the GF phenomenological Hamiltonians using the PHI program.
The ZFS Hamiltonian is shown in eqn (1).
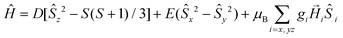 | (1) |
The GF Hamiltonian is as follows:
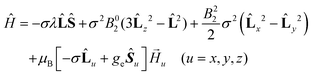 | (2) |
This Hamiltonian operates on the ground 4T1g term of the octahedral high spin CoII ion. The first term describes the interaction between the spin (S = 3/2) and orbital (L = 1) angular momenta through the spin–orbit coupling, where λ represents the spin–orbit coupling constant. The parameter σ represents a combined reduction factor, which comprises the isomorphism coefficient (−3/2) and the orbital-reduction parameter (κ) that considers the covalence effect and the mixing of the 4T1g (4F) and 4T1g (4P) terms (σ varies from −3/2 for a weak ligand field to −1 for a strong ligand field). The second and third terms represent the effect of the axial and rhombic crystal fields (B02 and B22 are the crystal field parameters).
The best fit parameters for compounds 1–4 using the ZFS and GF Hamiltonians are given in Table 1, whereas the corresponding curves are given in Fig. 5. It should be noted that the values extracted for Δaxial with the GF Hamiltonian (eqn (2)) are very similar to those extracted with Sakiyama's software for distorted octahedral high-spin Co(II) complexes with axial symmetry (see Table 1), which uses the related GF Hamiltonian:30b
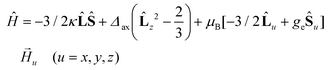 | (3) |
| a ΔE1 = E(KD1) − E(KD2). b 2D* = ΔE1 = [2(D2 + 3E2)1/2]. c g zeff. | ||||
|---|---|---|---|---|
| Complex | 1 | 2 | 3 | 4 |
| Fitting to ZFS model eqn (1) | ||||
| D/cm−1 | 55.0(6) | 34.9(2) | 33.2(3) | −80.9(1) |
| E/cm−1 | 0 (fixed) | 7(1) | 10.18(6) | −0.02(1) |
| g x ,gy | 2.459(3) | 2.245(1) | ||
| g z | 2.28(1) | 2.756(1) | ||
| g iso | 2.437(1) | 2.403(1) | ||
| zJ′ | −0.031(1) | −0.003(1) | ||
| ΔE1/cm−1 | 110.1 | 73.9 | 75.2 | 161.8 |
| Fitting to the GF model eqn (2) | ||||
| σ | −1.5 (fixed) | −1.238(4) | −1.50(1) | −1.29(1) |
| λ/cm−1 | −153(1) | −93.1(4) | −124.6(5) | −150.3(1) |
| B 02/cm−1 | 175(1) | 82.0(8) | 150.3(5) | −334.3(2) |
| B 22/cm−1 | 2.3(9) | 1.9(9) | 8(1) | −2.13(2) |
| Δ axial | 1181.0(1) | 376.6(8) | 1014.5(5) | −1668.9(3) |
| Δ rhombic | 2.6(9) | 1.45(9) | 9(1) | −1.77(2) |
ΔE1/cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
106.1 | 79.6 | 82.1 | 192.9 |
| Fitting to Sakiyama's model eqn (3) | ||||
| λ/cm−1 | −142 | −94 | −120 | −146 |
| κ | 0.93 | 0.83 | 0.97 | 0.86 |
| Δ axial/cm−1 | 911.2 | 398.2 | 920.1 | −1594.6 |
| ΔE 1/cm−1 | 102.1 | 78.4 | 78.9 | 187.5 |
| R | 4.5 × 10−5 | 1.5 × 10−5 | 6.1 × 10−6 | 1.8 × 10−5 |
| HFEPR and FIRMS | ||||
| D/cm−1 | 31.9 | 33.3 | ||
| E/cm−1 | 0 | 8.7 | ||
2D*/cm−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
63.8 | 73.0 | 140–200 | |
| E/D | 0 | 0.26 | ||
| g x ,gy | 2.4 | 2.37 | ||
| g z | 2.0 | 2.10 | 8.4c | |
As can be observed in Table 1, compounds 1–3 show easy-plane magnetic anisotropy (both D and Δax are positive) in line with that expected for pseudo-octahedral CoII high spin mononuclear complexes with nearly octahedral or compressed tetragonal bipyramid geometries (2 and 3 have Dstr values of −1.6 and −7.3, so that the latter geometry is moderately compressed).27 However, compound 4 exhibits a large axial easy-axis magnetic anisotropy, as expected for trigonal prismatic complexes. It should be noted that except for 3, the rest of the compounds exhibit a small rhombic anisotropy.
Finally, it is worth noting that the values of the energy gap between the ground and first excited state (ΔE1) extracted by the three Hamiltonians (Table 1) for each compound are very close. Moreover, these values are slightly higher but compare rather well with those directly extracted by FIRMS.
FIRMS and HFEPR spectroscopy
The zero-field energy gap between the two lowest-energy Kramers doublets (KDs) in an S = 3/2 spin system, as well as the sign and magnitude of the ZFS anisotropy parameters D and E can be in principle extracted from a combination of FIRMS (far-infrared magnetic spectroscopy) and HFEPR (high-frequency and high-field electron paramagnetic spectroscopy). The joint FIRMS and HFEPR maps of turning points as a function of frequency in compounds 2 and 3 (no magnetic transitions could be observed in the spectra of 1) are shown in Fig. 6. The heat maps represent the FIRMS data while the circles are the HFEPR turning points in the same compounds as seen in Fig. S6.†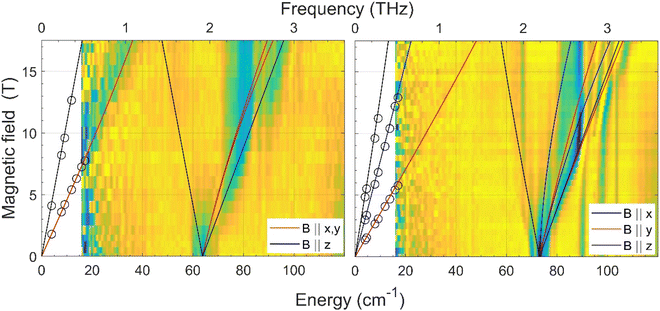 | ||
| Fig. 6 Experimental (magnetic field vs. energy) heat maps of the FIRMS response for complexes 2 (left) and 3 (right). The blue and yellow regions represent resonance absorptions sensitive and insensitive to the field, respectively. The white regions are below the FIRMS sensitivity threshold. The circles represent turning points in the HFEPR spectra. The lines are simulations of those turning points as a function of frequency using the spin Hamiltonian parameters as in Table 1. The meaning of each colour is explained in the labels. | ||
From the analysis of the peaks in the normalized FIRMS transmission spectra of compounds 2 and 3 we obtained the following 2D* values (energy gap between the ground and first excited KD in an S = 3/2 system): 63.8 cm−1 for 2 and 73 cm−1 for 3. These values were then used for analyzing and simulating the HFEPR spectra of these compounds (Fig. S6†), using a powder pattern typical of an S = 3/2 spin state. Compound 2 produced HFEPR spectra that are significantly distorted, partly by dispersion and by a non-ideal powder distribution, but clearly show that its zfs tensor is axial. The g-values obtained by fitting the frequency/field map of the turning points are given in Table 1. Compound 3, on the other hand, displayed better-quality spectra that showed a pronounced rhombicity. As usual for an S = 3/2 spin system, it is not possible to differentiate the rhombicity of the zfs tensor and the g-tensor as being responsible.5o We thus neglected the rhombicity of the latter, assuming it is axial, and were thus able to estimate the E-value on top of the g-values (see Table 1). It is worth mentioning that it was not possible to simulate the EPR spectra using negative D values. The D values extracted by means of the combined FIRMS/HFEPR methodology for complexes 2 and 3 are very close to those extracted from magnetic data.
For compound 4, the situation is qualitatively different than for 3 and 4 in terms of magneto-spectroscopic results. The FIRMS heat map of 4 is presented in Fig. S7.† Although there are several zero-field absorption peaks in the frequency range of 130–230 cm−1, none of them can be positively identified as corresponding to the energy gap between the two lowest KDs. The most likely zf magnetic resonance is the strongest one at 210 cm−1 but we prefer to estimate the 2D* value as lying between 130 and 230 cm−1.
The HFEPR spectra of 4 (Fig. S8†) are also very different to those of 2 and 3 and show a single, extremely weak resonance at any frequency positioned at geff ∼8.4. Such a resonance can only be attributed to the parallel turning point (B||z) of the intra-Kramers transition from MS |−3/2〉 to |+3/2〉 within the ±3/2 manifold. It appears in S = 3/2 complexes with large negative D values (easy-axis anisotropy) and very small but non-negligible E/D values as has been previously observed in CoII complexes with a trigonal prismatic coordination sphere, like 4, and large easy-axis anisotropy, and shows similar HFEPR spectra with gzeff values in the 7–9 range.31 The perpendicular turning points of the same transition (B||x, y) would occur well outside the field range and therefore were not observed. The transition from Ms = |−3/2〉 to |+3/2〉 is forbidden, because it corresponds to ΔMs = ±3 (only transitions with ΔMs = ±1 are allowed), but can be observed because the selection rule is relaxed in the presence of the E-term in the spin Hamiltonian, which mixes the |±3/2〉 and |±1/2〉 Kramers doublets. The larger the E, the more allowed the |−3/2〉 to |+3/2〉 transition becomes. In the case of 4, the exceeding weakness of the observed resonance indicates that E is very small with an estimated E/D ratio of less than 0.03. Therefore, in view of the above considerations it is reasonable to assume that 4 must exhibit very large easy-axis anisotropy with a very small E/D value. This assumption is in good agreement with the spin Hamiltonian parameters (D and E) obtained from the fitting of the magnetic data using the ZFS model (Table 1), the FIRMS results (the estimated 2D* value is very large, between 130 and 230 cm−1), the theoretical calculations (see below) and the spin Hamiltonian parameters found for other CoII complexes with very large easy-axis anisotropy.32,5o,p The fact that the 2D* value extracted from theoretical calculations is somewhat larger than the higher end of the values determined from FIRMS supports this latter value for D*.
Theoretical calculations
We have carried out ab initio multiconfigurational calculations on the experimental X-ray crystal geometries of complexes 1–4 (xyz coordinates for all computed structures are given in Table S6†), using the ORCA 5.0.2 program package,20 thus obtaining the energy of the spin-free states (Table S7†) and the energy of the KDs generated by the spin–orbit (SO) coupling (Table S8†). This latter interaction was computed by using the quasi-degenerate perturbation theory (QDPT). The calculated D and E values using the ZFS model and first excitation energies before and after including spin–orbit effects for CASSCF and CASSCF + NEVPT2 are given in Table 2. The orientation of the of the D-tensor components are given in Fig. S9.† It can be observed in this table that the computed D and E values for 1, 2 and 4 are close to those extracted from magnetic data and FIRMS/HFEPR analysis. Nevertheless, the theoretical values are, as usual, larger than those extracted using experimental techniques, which is due to limitations inherent in the calculation methods and the approach based on the ZFS Hamiltonian.| Compound | Method | D (cm−1) | E/D | E (cm−1) | δE 1 (cm−1) | ΔE1 (cm−1) | g 1, g2, g3 |
|---|---|---|---|---|---|---|---|
| 1 | CASSCF | +98.262 | 0.119672 | 11.759 | 446.0 | 200.70 | 1.89, 2.61, 2.87 |
| CASSCF/NEVPT2 | +87.094 | 0.094115 | 8.197 | 615.3 | 176.49 | 1.93, 2.60, 2.79 | |
| 2 | CASSCF | +42.738 | 0.095614 | 4.086 | 1263.0 | 86.64 | 2.12, 2.48, 2.56 |
| CASSCF/NEVPT2 | +31.796 | 0.179360 | 5.703 | 1658.0 | 66.59 | 2.10, 2.37, 2.46 | |
| 3 | CASSCF | +50.136 | 0.289202 | +14.499 | 1104.3 | 112.15 | 2.06, 2.39, 2.69 |
| CASSCF/NEVPT2 | −39.776 | 0.273560 | −10.881 | 1471.9 | 88.03 | 2.06, 2.30, 2.56 | |
| 4 | CASSCF | −123.640 | 0.066395 | −8.209 | 158.6 | 248.91 | 1.68, 1.76, 3.30 |
| CASSCF/NEVPT2 | −121.420 | 0.052864 | −6.419 | 217.2 | 243.86 | 1.74, 1.82, 3.26 |
In the case of 3, CASSCF and CASSCF/NEVPT2 afford D values of the same order of magnitude but of opposite sign. These contradictory results are usually observed for mononuclear Co(II) compounds with E/D parameters that are close to 1/3, so that they do not show easy-axis or easy-plane but triaxial anisotropy and the sign of D cannot be unequivocally determined from theoretical calculations based on the ZFS Hamiltonian.5o Therefore, in compounds where the sign of D cannot conclusively be obtained from theoretical and magnetic studies, like in 3, the use of other experimental techniques is mandatory. In this regard, as indicated elsewhere, the HFEPR spectra of 3 (see Fig. S6†) unquestionably demonstrate that D > 0 and so the easy-plane anisotropy of the ground state. It is worth noting at this point that, as far as we know, with only one exception, all the CoII complexes with a compressed octahedral CoN6 coordination sphere bearing two thiocyanate anions coordinated in trans positions show, like 3, D > 0.5o,33
The splitting of the d-orbitals for complexes 1–4 was calculated using the ab initio ligand field theory (AILFT) method implemented in ORCA.34 The computed energy diagrams for these compounds are given in Fig. S10–S13,† whereas the composition of the one-electron states appears in Table S9.† Calculations results indicate that complexes 1–3 and complex 4 show the splitting of the d orbitals expected for pseudooctahedral and distorted trigonal prismatic complexes, respectively. The splitting for compounds 1 and 2 is close to 8800 cm−1, whereas those for compounds 3 and 4 are 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 405 and 9590 cm−1, respectively. The former complexes, which are distorted octahedral, apart from the N-acceptor groups belonging to the ligand, possess π-donor ligands (Cl− and S) that reduce the magnitude of the ligand-field splitting. However, compounds 3 and 4 possess either π-N-acceptor groups pertaining to the tripodal ligand (aromatic and imine nitrogen atoms) and weak acceptor NCS− anions for the former or only π-N-acceptor groups belonging to the tripodal ligand for the latter, which favour an increase of the splitting of the d orbitals with regard to 1 and 2. The fact that the splitting of 3 is larger than that of 4 can be justified because the energy span of the d orbitals in OC-6 complexes is larger than that in the TPR-6 counterparts (10 Dq vs. 20/3 Dq).35
405 and 9590 cm−1, respectively. The former complexes, which are distorted octahedral, apart from the N-acceptor groups belonging to the ligand, possess π-donor ligands (Cl− and S) that reduce the magnitude of the ligand-field splitting. However, compounds 3 and 4 possess either π-N-acceptor groups pertaining to the tripodal ligand (aromatic and imine nitrogen atoms) and weak acceptor NCS− anions for the former or only π-N-acceptor groups belonging to the tripodal ligand for the latter, which favour an increase of the splitting of the d orbitals with regard to 1 and 2. The fact that the splitting of 3 is larger than that of 4 can be justified because the energy span of the d orbitals in OC-6 complexes is larger than that in the TPR-6 counterparts (10 Dq vs. 20/3 Dq).35
The splitting of compounds 1–3, which is typical of distorted octahedral complexes, shows two highly destabilized singly occupied d orbitals (dx2−y2 and dz2 arising from the eg system in ideal OC-6 complexes) and three closer energy low-lying d orbitals (dxz, dyz, dxy arising from the t2g systems in OC-6 symmetry). It is worth noting that the highly destabilized orbitals are linear combinations of dx2−y2 and dz2 (except for 3, where they can be considered as pure orbitals), whereas the low-lying orbitals are linear combinations of two orbitals of the dxz, dyz, dxy set. In the case of 4, as expected for a distorted trigonal prismatic geometry, the lowest-lying d orbital is doubly occupied and practically pure dz2. At higher energy, but relatively close to the lowest-lying dz2 (at 1278 and 1529 cm−1), are found one doubly and one singly occupied orbital, which are essentially a linear combination of both dxy and dx2−y2 orbitals with either dxz or dyz orbitals, respectively. Finally, at much higher energy (8926 and 9590 cm−1) are located two singly occupied orbitals, which are largely a linear combination of the dxz and dyz orbitals with either dxy or dx2−y2 orbitals, respectively.
For complexes 1–3, the two first excited quartet states (see Table S7†) are much lower in energy than the other excited ones. In this regard, the second excited states show energies up to approximately 2300 cm−1, whereas the other excited states are located at energies higher than 5500 cm−1. Therefore, the two low-lying quartet excited states must possess the major contribution to D, because their contributions to this parameter are inversely proportional to their relative energy regarding the ground quartet state. The results of the CASSF/NEVPT2 calculations agree with this hypothesis. In the case of 3, the CASSF/NEVPT2 calculations led to a wrong sign of D due to the triaxial anisotropy of the ground state (see above). Therefore, the contributions of the excited quartet states to D for 3 have not been included in Table S10.† In the case of 4, only the first excited state is close to the ground one, as the second excited state is above 4000 cm−1. Therefore, the contribution to D essentially arises from the first excited state (see Table S10†).
Let us at this point undertake a comparative analysis of the D parameters experimentally and theoretically obtained for complexes 1–4 and those published for similar complexes. First, it is important to remark that, when tripodal ligands coordinate in N,N,S-tridentate or bis (N,N-bidentate) forms to the CoII ion, pseudooctahedral Co(II) complexes were obtained, all of them exhibiting positive D values and easy-plane magnetic anisotropy. Specifically, complex 2 and other similar CoIIN4Cl2 pseudo-octahedral complexes have been shown to possess easy-plane magnetic anisotropy with D values in the 27–68 cm−1 range (except for 2, in all cases D was extracted from magnetic data and theoretical calculations).33,36 Moreover, theoretical calculations carried out on the complex [Co(py)4Cl2],33a by changing the axial and transverse ligand fields and keeping the other structural parameters constant, allowed the establishment of the following magneto-structural correlation: for dax/deq ratios <1.02, negative D values are expected, whereas dax/deq ratios >1.06 should lead to positive D values. In fact, the CoIIN4Cl2 complexes for which the D parameter has been experimentally determined from the magnetic data exhibit dax/deq ratios in the 1.07–1.13 range and all of them, as indicated above, show easy-plane magnetic anisotropy. It is worth mentioning that complex 2 and [Co(py)4Cl2] have very close dax/deq ratios (1.13 and 1.12, respectively); however, their respective D values extracted from magnetic data are rather separated (34.9 vs. 68.2 cm−1, respectively). This fact points out that, besides the axial to equatorial bond length ratio, other structural and electronic factors could also affect the magnitude of the D value. Among the former, one could consider the larger deviations in the coordination sphere of 2 of the cis bond angles from 90° (they are found in the 76–114° and 87–93° ranges for 2 and [Co(py)4Cl2], respectively), as well as the smaller trans Cl–Co–Cl bond angle (168.6 vs. 177.4°, respectively).
Regarding complex 3 and its structurally similar CoIIN6 pseudo-octahedral complexes bearing two thiocyanate ligands in trans positions, all of them exhibit dax/deq ratios (dax and deq are the average axial and equatorial bond distances, respectively) within the 0.94–0.97 range and D values in the 30–70 cm−1 range (most part of them extracted from magnetic data).32 Theoretical calculations on this type of compressed bipyramidal complex suggest that to achieve negative D values significantly smaller dax/deq ratios are required.37 It should be mentioned that complex 3 and its analogs having pyridyl instead of isoquinolyl moieties in the three arms of the ligand present very close D values (33.3 vs. 36.33 cm−1) as expected for their very similar structural parameters in the coordination sphere. Finally, it is worth noting that despite the different dax/deq ratios for 2 and 3 (1.13 and 0.97, respectively), they show similar D values, thus indicating that the electronic effects must also play an important role in determining D.
Concerning compound 4, some of us have shown that there exists a magneto-structural correlation between the continuous shape measures and the experimentally extracted D values for trigonal prismatic CoII complexes with a tripodal ligand analogous to L but having a pyridyl moiety instead of an isoquinolyl moiety in each of its arms.5o This correlation indicates that the negative D values linearly decrease in absolute value with the increase of the distortion from TPR-6 to OC-6 along the TPR-6 ↔ OC6 deformation pathway. Using this linear correlation and the S(TPR-6) value for 4 of 4.322, the calculated D value would be much smaller than that found from magnetic data, FIRMS/HFEPR and theoretical calculations. This result suggests that, even though the S(TPR-6) is an essential factor in determining the sign and magnitude of D, other structural factors (compression and truncation of the trigonal prismatic geometry) and the electronic effects of the donor atoms of the ligand should also influence the final value of D.
Dynamic magnetic properties
The dynamics of the magnetization for complexes 1–4 was analysed by carrying out temperature and frequency dependence studies of the ac magnetic susceptibility under an alternating field of either 5 Oe or 10 Oe on polycrystalline samples of the compounds. The aim of this analysis is to disclose if these compounds show slow magnetization relaxation and, if so, to perform a comparative study of their dynamic magnetic properties with those previously reported for closely structurally related CoII complexes. Unfortunately, complexes 1–3 do not show out-of-phase signals (χ′′M) above 2 K at zero applied dc field. This result is not surprising because for CoII Kramers ions with easy-plane anisotropy, the electronuclear spin states arising from the hyperfine interactions between the electronic and nuclear spins have negligible magnetic moments under zero magnetic field and, consequently, they do not show slow magnetic relaxation. Therefore, to observe the potentially slow relaxation of the magnetization in this type of complexes it would be mandatory to apply a magnetic field.38 In addition, calculations with the SINGLE-ANISO code implemented in the ORCA 5.0.2 program package (ESI†) show that QTM in the ground state cannot be ruled out for 1–3, because the matrix element for the QTM transition is significantly larger than 0.1, which is assumed as the minimum value needed for an efficient relaxation mechanism (Fig. S14–S17†).39Compound 4, under a zero applied magnetic field, shows χ′′M signals below 10 K, but without reaching maxima even at the highest used frequency of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz (Fig. S18†). This behaviour could be due to QTM promoted by the existence of transverse anisotropy (theoretical calculations show that compound 4 has a slight but non-negligible transverse magnetic anisotropy, see Table 2), weak dipolar interactions and hyperfine interactions with the CoII nuclear spin (I = 7/2). In fact, SINGLE-ANISO calculations support the existence of QTM, because the matrix element for the QTM transition is 0.12 (Fig. S17†). Moreover, the relatively significant distortion of the molecules of 4 from TPR-6 to OC-6 geometry favours the appearance of significant QTM. In view of the above considerations, one realizes why QTM is generally hard to quench enough so as to detect slow relaxation under zero-field.
000 Hz (Fig. S18†). This behaviour could be due to QTM promoted by the existence of transverse anisotropy (theoretical calculations show that compound 4 has a slight but non-negligible transverse magnetic anisotropy, see Table 2), weak dipolar interactions and hyperfine interactions with the CoII nuclear spin (I = 7/2). In fact, SINGLE-ANISO calculations support the existence of QTM, because the matrix element for the QTM transition is 0.12 (Fig. S17†). Moreover, the relatively significant distortion of the molecules of 4 from TPR-6 to OC-6 geometry favours the appearance of significant QTM. In view of the above considerations, one realizes why QTM is generally hard to quench enough so as to detect slow relaxation under zero-field.
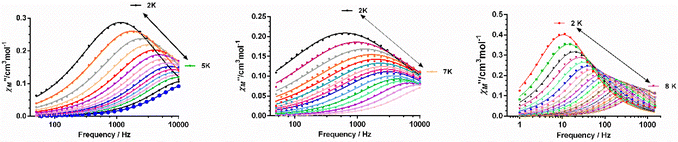
To eliminate fully or partly the QTM in complexes 1–4, ac measurements in the presence of small dc fields were performed. For complex 1 no χ′′M signals were observed at the tested magnetic fields in the 0–3000 Oe range, whereas 2–4 show frequency and temperature dependence of the out-of-phase signals under an applied magnetic field and, therefore, slow relaxation of the magnetization (Fig. S19–S21†). Using the data corresponding to the field and frequency dependence of χ′′M at 2 K for 2 and 3 and 6 K for 4, the optimal field for the ac measurements were determined for each of the compounds. In the case of 2 and 3, the relaxation times could not be accurately extracted from the fitting of the frequency dependence of the χ′′M signals to the generalized Debye model, because the maxima appear beyond the frequency limit of our apparatus. Therefore, the field giving rise to the maximum intensity of the χ′′M signals was the choice. For 4, the field dependence of the relaxation time in form of τ−1vs. H (in tesla units) is given in Fig. S21† (right panel). As expected, the magnetic relaxation slows down up to 0.15 T (this optimal field agrees well with that at which the intensity of the χ′′M signals is maximal) due to the progressive quenching of the QTM. For Hdc > 0.15 T, τ−1 slightly increases as the field increases, due to a small contribution, if one exists, of a direct relaxation process, which would be strongly field dependent. A full set of temperature- and frequency-dependent ac susceptibility measurements were then carried out at the corresponding optimal fields for 2–4 below 15 K (Fig. 7, respectively).
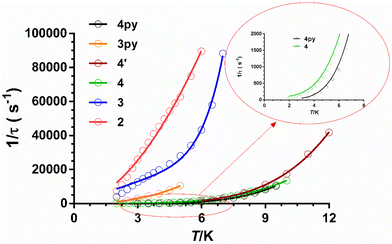
As can be seen in these figures, the three compounds show a clear frequency dependence of the χ′′M signals at different temperatures, thus pointing out the existence of slow magnetic relaxation. From these data and using the generalized Debye model, the temperature dependence of the relaxation time was extracted for 2–4, which is given in Fig. 8.
The τ−1vs. T is generally described by the following equation:
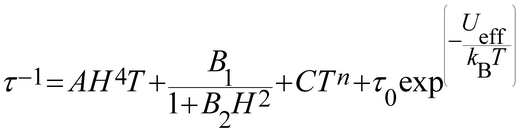 | (4) |
| Compound | U eff (K) | τ 0 (s) | C (s−1 K−n) | n | QTM/s | A (s−1 T−4 K−1) |
|---|---|---|---|---|---|---|
| 2 | 6.88(9) | 3.95(8) × 10−6 | 2866 (330), H = 0.12 T | 1.94(8) | — | — |
| 3 | 24(3) K | 3.(3) × 10−7 | 0.03 (4), H = 0.12 T | 7.4(7) | — | 4290(260) |
| 4 | 30.2(4) | 4(1) × 10−6 | 1.6 (2), H = 0.15 T | 3.93(5) | 0.013 | — |
| 4′ | 43(1) | 6.7(3) × 10−7 | 0.4 (1), H = 0 T | 4.6(1) | — | — |
It is worth mentioning that some mononuclear CoII complexes, even though they have large easy-axis magnetic anisotropy in the ground state, do not present slow magnetic relaxation and SIM behaviour at zero field. This behaviour is likely due to intermolecular interactions that promote fast QTM. Nevertheless, in these systems, the slow magnetic relaxation could be activated by magnetic dilution of the pristine compound, because this process could quench the intermolecular magnetic interactions.42,5o In light of this, we decided to explore if 4′ (the diluted version of 4) would present dilution-triggered slow magnetic relaxation. Compound 4′ presents a Co/Zn = 1/10 ratio, which was supported by dc magnetic measurements. Although the powder X-ray diffractogram is silent, the IR and mass spectra (ESI-MS) point out that 4′ is pure and potentially amorphous, yet equivalent to 4. Temperature- and frequency-dependence ac magnetic measurements under zero field of 4′ (Fig. S27†) display χ′′M signals with maxima in the 6 K (330 Hz)–12 K (6800 Hz) range, typical of slow magnetization relaxation. Therefore, compound 4′ exhibits dilution-induced slow-magnetic relaxation at zero applied field (“hidden SIM” behaviour). The temperature dependence of relaxation times for 4′ (Fig. 8) was analysed with an equation that only considers the existence of the Raman process (under zero magnetic field the direct product should be negligible and the typical tail due to QTM does not appear in the low-temperature region). Moreover, for comparative purposes, the phenomenological Ueff values were extracted from the fitting of the linear high-temperature region of the Arrhenius plots. As expected, the Ueff value is quite lower than the 2D* value determined from magnetic, theoretical calculations and FIRMS. The parameters extracted from these two fittings are given in Table 3.
From the magnetic relaxation parameters gathered in Table 3 and Fig. 8, we can highlight the following facts: (i) in spite of the fact that compound 3 and its analogue containing pyridine instead of isoquinoline moieties, 3Py (compound 11 in Fig. 4), present very similar SHAPE parameters and D values; however, the former relaxes considerably faster than the latter. (ii) Although the D values for 4 and 4py (compound 7 in Fig. 4) extracted from FIRMS are very similar, the former relaxes faster than 4py. In this case, the slightly larger distortion from the ideal TPR-6 geometry for 4 compared with 4py might lead to a lower axiality of the ground and, therefore, to contributing in some extent to the decrease of the relaxation time for the former. (iii) Compound 4 at the optimal field relaxes more slowly than 4′ at the zero field, pointing out once again that the effect of the applied dc field for quenching QTM is larger than that coming from the magnetic dilution. Points (i) and (ii) suggest that the change of the pyridine moiety by the isoquinoline one in the tripodal ligand is essentially responsible for the faster magnetization relaxation observed for 3 and 4 with respect to their closely related 3y and 4py counterparts, respectively. Several recent exciting papers have theoretically clarified the crucial role played by the molecular and lattice vibrations coupled with the electronic spins in the magnetic relaxation of SMMs.43 Some of them specifically dealing with CoII SIMs have revealed that low-energy phonons (the most populated at the low experimental temperatures) can couple with the spin inducing spin-relaxation at low temperatures through anharmonic Orbach and/or Raman mechanisms, which restricts the spin lifetime.43a,h,j Therefore, to build efficient SMMs, static magnetism (controlling the crystal field to increase the single-ion anisotropy and quenching of QTM by strong magnetic coupling between magnetic centres or magnetic dilution) and spin-phonon dynamics (engineering of molecular vibrations) have to be parallel tuned. In connection with this, it was found that the spin dynamics of some linear FeII SIMs was accelerated upon increasing their molecular size, even though they possessed a similar computed energy gap between the ground and first excited states.44 This result highlights the impact of the molecular dimensions on the magnetic relaxation dynamics, which can be explained by the increase of the delocalization of the vibrational modes in the low-energy vibrational spectra when the molecular dimensions increase, thus ultimately favouring the coupling of the spin and the low-energy phonons. The above considerations support that the acceleration of the magnetic relaxation in compounds 3 and 4 regarding 3py and 4y is most likely due to the increase of the molecular size due to the replacement of the pyridine moiety by the bulkier isoquinoline one.
Conclusions
The ongoing results demonstrate that using the tripodal ligand prepared by the condensation of S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) P(NHCH3-NH2)3 and 2-quinolinecarboxaldehyde, a mononuclear distorted octahedral CoII complex with a CoN4SO coordination sphere is obtained, where the ligand is forced, due to the steric hindrance between the quinoline moieties belonging to the three arms, to adopt a N,N,S-tridentate coordination mode instead of the expected N6-trisbidentate tripodal one. However, when a non-sterically hindered tripodal ligand bearing isoquinolyl substituents is used, depending on the coordination ability of the anion, mononuclear complexes are obtained where the ligand acts with either bisbidentate or trisbidentate coordination modes. Thus, utilizing good coordinating anions, such as SCN− or Cl−, tetragonally distorted CoIIN4X2 complexes (X = Cl− or NCS−) are obtained where the anions are in trans positions in the CoII coordination sphere, whereas the four nitrogen atoms of the bisbidentate ligand occupy the equatorial positions. However, using poor coordinating perchlorate anions, the ligand can coordinate to the CoII ion in a N6-trisbidentate tripodal coordination mode, giving rise to a distorted trigonal prismatic CoN6 coordination sphere.
P(NHCH3-NH2)3 and 2-quinolinecarboxaldehyde, a mononuclear distorted octahedral CoII complex with a CoN4SO coordination sphere is obtained, where the ligand is forced, due to the steric hindrance between the quinoline moieties belonging to the three arms, to adopt a N,N,S-tridentate coordination mode instead of the expected N6-trisbidentate tripodal one. However, when a non-sterically hindered tripodal ligand bearing isoquinolyl substituents is used, depending on the coordination ability of the anion, mononuclear complexes are obtained where the ligand acts with either bisbidentate or trisbidentate coordination modes. Thus, utilizing good coordinating anions, such as SCN− or Cl−, tetragonally distorted CoIIN4X2 complexes (X = Cl− or NCS−) are obtained where the anions are in trans positions in the CoII coordination sphere, whereas the four nitrogen atoms of the bisbidentate ligand occupy the equatorial positions. However, using poor coordinating perchlorate anions, the ligand can coordinate to the CoII ion in a N6-trisbidentate tripodal coordination mode, giving rise to a distorted trigonal prismatic CoN6 coordination sphere.
Magnetic measurements, theoretical calculations, FIRMS and EPR show that the distorted octahedral complexes exhibit positive axial anisotropy parameters (D > 0), which are larger for 1 (from magnetic measurements and theoretical calculations) than for 2 and 3. This behaviour is not unexpected as most of this type of complex exhibit D > 0 values. For complexes 2 and 3 the comparative analysis of their magneto-structural data with those found for other similar complexes allows the conclusion that besides the axial to equatorial bond length ratio, other structural and electronic factors must also affect the magnitude of the D value. In contrast to the distorted octahedral complexes, the distorted trigonal prismatic complex 4 shows, as expected, a large easy-axis magnetic anisotropy (D < 0). When the D value for 4 is compared with those of closely related trigonal prismatic CoII complexes, one realizes that even though the distortion from the ideal TPR-6 geometry is an essential factor in determining the sign and magnitude of D, other structural factors (compression and truncation of the trigonal prismatic geometry) and the electronic effects of the donor atoms of the ligand should also influence the final value of D.
Theoretical calculations carried out on compounds 1–4 support that QTM precludes the observation of slow relaxation at zero-field in these compounds. However, compounds 2–4 exhibit field-induced slow relaxation and the temperature dependence of the relaxation time for these compounds can be fitted to a Raman mechanism for the former, Raman and direct ones for the second and Raman, direct and QTM mechanisms for the latter. In all cases, above 3–4 K the Raman is the dominant process. It is of interest that slow relaxation can be observed at zero field for compound 4 after magnetic dilution with ZnII, which quenches the QTM promoted by the intermolecular dipolar interactions. This behaviour is not unexpected in view of its large easy-axis magnetic anisotropy.
Finally, interestingly enough, the magnetic relaxations of 3 and 4 are comparatively faster than those of the analogous compounds bearing pyridine as a substituent in their arms, which appears to be most likely due to the increase of the molecular size due to the replacement of the pyridine moiety by the bulkier isoquinoline one.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
Financial support from the Ministerio de Ciencia e Innovación (project PID2022-138090NB-C21 funded by MCIN/AEI/10.13039/501100011033/FEDER,UE), Junta de Andalucía (FQM-195 and project I+D+i P20_00692), and the University of Granada are grateful acknowledged. The authors acknowledge the Centro de Servicios de Informática y Redes de Comunicaciones (CSIRC) for computational time and facilities. M. M. Q. M. thanks Junta de Andalucía for a postdoctoral fellowship (DOC_01282) and Ministerio de Ciencia e Innovación for a Ramón y Cajal contract (the publication is part of the grant RYC2021-034288-I, funded by MCIN/AEI/10.13039/501100011033 and by the European Union “NextGenerationEU”/PRTR”). Part of this work was performed at the NHMFL, which is funded by the National Science Foundation (cooperative agreement DMR 2128556) and the State of Florida. The authors are grateful to Dr M. Quirós from University of Granada for his help in the crystal structures resolution.References
- (a) D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268 CrossRef CAS PubMed; (b) D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, Oxford, 2006 CrossRef; (c) J. Bartolomé, F. Luis and J. F. Fernández, Molecular magnets: physics and applications, Springer-Verlag, Berlin-Heidelberg, 2014 CrossRef; (d) G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135 RSC; (e) Y.-S. Ming, S. D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381 CrossRef PubMed; (f) A. Day, P. Kalita and V. V. Chandrasekhar, ACS Omega, 2018, 2108(20), 942 Search PubMed; (g) M. Fen and M.-L. Tong, Chem. – Eur. J., 2018, 24, 7574 CrossRef PubMed; (h) A. Sarkar, S. Dey and G. Rajaraman, Chem. – Eur. J., 2020, 26, 14036 CrossRef CAS PubMed; (i) A. Zabala-Lekuona, M. Seco and E. Colacio, Coord. Chem. Rev., 2021, 441, 213984 CrossRef CAS; (j) J. Juráková and I. Šalitroš, Monatsh. Chem., 2022, 153, 1001 CrossRef PubMed; (k) N. F. Chilton, Annu. Rev. Mater. Res., 2022, 52, 79 CrossRef CAS; (l) P. K. Sahu, R. Kharel, S. Shome, S. Goswami and S. Konar, Coord. Chem. Rev., 2023, 475, 2148714 Search PubMed.
- E. Moreno-Pineda and W. Wernsdorfer, Nat. Rev. Phys., 2021, 3, 645 CrossRef CAS.
- (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed; (b) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed; (c) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- (a) X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. D. Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, J. Am. Chem. Soc., 2017, 139, 373 CrossRef CAS PubMed; (b) P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, 7319 CrossRef PubMed.
- (a) S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, J. Am. Chem. Soc., 2013, 135, 7010 CrossRef PubMed; (b) A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. J. Novikov, Phys. Chem. Lett., 2016, 7, 4111 CrossRef CAS PubMed; (c) Y. Y. Zhu, Y. Q. Zhang, T. T. Yin, C. Gao, B. W. Wang and S. Gao, Inorg. Chem., 2015, 54, 5475 CrossRef CAS PubMed; (d) Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802 RSC; (e) T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Chem. Commun., 2017, 53, 4211 RSC; (f) Y. Peng, T. Bodenstein, K. Fink, V. Mereacre, C. E. Anson and A. K. Powell, Phys. Chem. Chem. Phys., 2016, 18, 30135 RSC; (g) B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Y. Zhang, Inorg. Chem., 2018, 57, 14047 CrossRef CAS PubMed; (h) V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792 CrossRef CAS PubMed; (i) A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, ChemPhysChem, 2019, 20, 1001 CrossRef CAS PubMed; (j) C. Villa-Pérez, I. Oyarzabal, G. A. Echeverría, G. C. Valencia-Uribe, J. M. Seco and D. B. Soria, Eur. J. Inorg. Chem., 2016, 4835 CrossRef; (k) C. M. Klug, T. J. Ozumerzifon, I. Bhowmick, B. N. Livesay, A. K. Rappé and M. P. Shores, Dalton Trans., 2019, 48, 9117 RSC; (l) A. A. Pavlov, S. A. Savkina, A. S. Belov, Y. V. Nelyubina, N. N. Efimov, Y. Z. Voloshin and V. V. Novikov, Inorg. Chem., 2017, 56, 6943 CrossRef CAS PubMed; (m) A. S. Belov, Y. Z. Voloshin, A. A. Pavlov, Y. V. Nelyubina, S. A. Belova, Y. V. Zubavichus, V. V. Avdeeva, N. N. Efimov, E. A. Malinina, K. Y. Zhizhin and N. T. Kuznetsov, Inorg. Chem., 2020, 59, 5845 CrossRef CAS PubMed; (n) M. R. Saber, M. K. Singh and K. R. Dunbar, Chem. Commun., 2020, 56, 8492 RSC; (o) A. Landart-Gereka, M. M. Quesada-Moreno, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek, M. A. Palacios and E. Colacio, Inorg. Chem. Front., 2022, 9, 2810 RSC; (p) A. Landart-Gereka, M. M. Quesada-Moreno, M. A. Palacios, I. F. Díaz-Ortega, H. Nojiri, M. Ozerov, J. Krzystek and E. Colacio, Chem. Commun., 2023, 59, 952 RSC.
- A. Zabala-Lekuona, A. Landart-Gereka, M. M. Quesada-Moreno, A. J. Mota, I. F. Díaz-Ortega, H. Nojiri, J. Krzystek, J. M. Seco and E. Colacio, Inorg. Chem., 2023, 62(49), 20030 CrossRef CAS PubMed.
- M. W. Löble, M. Casimiro, D. T. Thielemann, P. Oña-Burgos, I. Fernandez, P. W. Roesky and F. Breher, Chem. – Eur. J., 2012, 18, 5325 CrossRef PubMed.
- J. Nehrkorn, J. Telser, K. Holldack, S. Stoll and A. Schnegg, J. Phys. Chem. B, 2015, 119, 13816 CrossRef CAS PubMed.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42 CrossRef CAS PubMed.
- A. K. Hassan, L. A. Pardi, J. Krzystek, A. Sienkiewicz, P. Goy, M. Rohrer and L. C. Brunel, J. Magn. Reson., 2000, 142, 300–312 CrossRef CAS PubMed.
- APEX2, Bruker AXS, Madison, WI, 2010 Search PubMed.
- SAINT, Version 8.30a, Bruker AXS, Madison, WI, 2013 Search PubMed.
- G. M. Sheldrick, SADABS, Version 2004/1, Bruker AXS, Madison, WI, 2008 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, A. K. Howard and H. Pushman, J. Appl. Crystallogr., 2009, 42, 339 CrossRef CAS.
- P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297 CrossRef CAS; (b) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC; (b) A. Schaefer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef CAS; (c) A. Schaefer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- (a) D. Ganyushin and F. Neese, J. Chem. Phys., 2013, 138, 104113 CrossRef PubMed; (b) D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed; (c) R. Maurice, R. Bastardis, C. D. Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977 CrossRef CAS PubMed; (d) F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- T. Nakajima, Chem. Rev., 2012, 112, 385 CrossRef CAS PubMed.
- J. Jung, M. Atanasov and F. Neese, Inorg. Chem., 2017, 56, 8802 CrossRef CAS PubMed.
- V. Chandrasekhar, M. D. Pandey, K. Gopal and R. Azhakar, Dalton Trans., 2011, 40, 7873 RSC.
- (a) M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE, v2.1, Universitat de Barcelona, Barcelona, Spain, 2013 Search PubMed; (b) J. Moncol , Czech Chem. Soc. Symp. Ser., 2023, 21, 147.
- R. Boca, C. Rajnák and J. Titis, Magnetochemistry, 2023, 9, 100 CrossRef CAS.
- (a) B. N. Figgis and M. A. Hitchman, Ligand Field Theory and its Applications, Wiley-VCH, New York, USA, 2000 Search PubMed; (b) F. Lloret, M. Julve, J. Cano, R. Ruiz-Gracía and E. Pardo, Inorg. Chim. Acta, 2008, 316, 3432 CrossRef.
- (a) J. Juráková, J. D. Midlíková, J. Hrubý, A. Kliuikov, V. T. Santana, J. Pavlik, J. Moncol, E. Čižmár, M. Orlita, I. Mohelský, P. Neugebauer, D. Gentili, M. Cavallini and I. Šalitroš, Inorg. Chem. Front., 2022, 9, 1179 RSC; (b) N. Malinová, J. Juráková, B. Brachňaková, J. D. Midlíková, E. Čižmár, V. N. Santana, R. Herchel, M. Orlita, I. Mohelský, J. Moncol, P. Neugebauer and I. Šalitroš, Cryst. Growth Des., 2023, 23(4), 2430 CrossRef.
- (a) N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164 CrossRef CAS PubMed; (b) H. Sakiyama, J. Chem. Software, 2001, 7(4), 171 CrossRef CAS.
- (a) S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537–9548 CrossRef CAS PubMed; (b) J. R. Pilbrow, J. Magn. Reson., 1978, 31, 479–490 CAS.
- (a) H.-H. Cui, Y.-Q. Zhang, X.-T. Chen, Z. Wang and Z.-L. Xue, Dalton Trans., 2019, 48, 10743–10752 RSC; (b) P. Cucos, F. Tuna, L. Sorace, I. Matei, C. Maxim, S. Shova, R. Gheorghe, A. Caneschi, M. Hillebrand and M. Andruh, Inorg. Chem., 2014, 53, 7738–7747 CrossRef CAS PubMed.
- (a) Y.-F. Deng, M. K. Singh, D. Gan, T. Xiao, Y. Wang, S. Liu, Z. Wang, Z. Ouyang, Y.-Z. Zhang and K. R. Dunbar, Inorg. Chem., 2020, 59, 7622 CrossRef CAS PubMed; (b) P. Zoufalý, A. Kliuikov, E. Čižmár, I. Císařová and R. Herchel, Eur. J. Inorg. Chem., 2021, 1190 CrossRef; (c) J. Vallejo, F. R. Fortea-Pérez, E. Pardo, S. Benmansour, I. Castro, J. Krzystek, D. Armentano and J. Cano, Chem. Sci., 2016, 7, 2286 RSC; (d) Y. Y. Zhu, M. S. Zhu, T. T. Yin, Y. S. Meng, Z. Q. Wu, Y. Q. Zhang and S. Gao, Inorg. Chem., 2015, 54, 3716 CrossRef CAS PubMed; (e) G. Brunet, D. A. Safin, J. Jover, E. Ruiz and M. Murugesu, J. Mater. Chem. C, 2017, 5, 835 RSC.
- E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermüller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Inorg. Chem., 2017, 56, 3102 CrossRef CAS PubMed.
- J. C. Knight, S. Alvarez, A. J. Amoroso, P. G. Edwards and N. Singha, Dalton Trans., 2010, 39, 3870 RSC.
- L. Shi, F.-X. Shen, D. Shao, Y.-Q. Zhang and X.-Y. Wang, CrystEngComm, 2019, 21, 3176 RSC.
- S. Tripathi, S. Vaidya, N. Ahmed, E. A. Klahn, H. Cao, L. Spillecke, C. Koo, S. Spachmann, R. Klingeler, G. Rajaraman, J. Overgaard and M. Shanmugam, Cell Rep. Phys. Sci., 2021, 2, 100404 CrossRef CAS.
- S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Nat. Commun., 2014, 5, 4300 CrossRef PubMed.
- S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Coord. Chem. Rev., 2015, 289–290(1), 379 CrossRef.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Dover, 1970 Search PubMed.
- (a) A. Singh and K. N. Shrivastava, Phys. Status Solidi B, 1979, 95, 273 CrossRef CAS; (b) K. N. Shirivastava, Phys. Status Solidi B, 1983, 117, 437 CrossRef.
- (a) J. Li, Y. Han, F. Cao, R.-M. Wei, Y.-Q. Zhang and Y. Song, Dalton Trans., 2016, 45, 9279 RSC; (b) R. Mitsuhashi, S. Hosoya, T. Suzuki, Y. Sunatsuki, H. Sakiyama and M. Mikuriya, RSC Adv., 2020, 10, 43472 RSC; (c) L. Rigamonti, N. Bridonneau, G. Poneti, L. Tesi, L. Sorace, D. Pinkowicz, J. Jover, E. Ruiz, R. Sessoli and A. Cornia, Chem. – Eur. J., 2018, 24, 8857 CrossRef CAS PubMed; (d) S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Inorg. Chem., 2016, 55, 9537 CrossRef CAS PubMed.
- (a) A. Lunghi and S. Sanvito, J. Chem. Phys., 2020, 153, 174113 CrossRef CAS PubMed; (b) A. Lunghi and S. Sanvito, Sci. Adv., 2019, 5, eaax7163 CrossRef CAS PubMed; (c) A. Albino, S. Benci, M. Atzori, L. Chelazzi, S. Ciattini, A. Taschin, P. Bartolini, A. Lunghi, R. Righini and R. Torre, J. Phys. Chem. C, 2021, 125, 22100 CrossRef CAS PubMed; (d) Z. Hu, A. Ullah, H. Prima-Garcia, S.-H. Chin, Y. Wang, J. Aragó, Z. Shi, A. Gaita-Ariño and E. Coronado, Chem. – Eur. J., 2021, 27, 13242 CrossRef CAS PubMed; (e) M. Briganti, F. Santanni, L. Tesi, F. Totti, R. Sessoli and A. Lunghi, J. Am. Chem. Soc., 2021, 143, 13633 CrossRef CAS PubMed; (f) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125 RSC; (g) F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 580 RSC; (h) D. H. Moseley, S. E. Stavretis, K. Thirunavukkuarasu, M. Ozerov, Y. Cheng, L. L. Daemen, J. Ludwig, Z. Lu, D. Smirnov, C. M. Brown, A. Pandey, A. J. Ramirez-Cuesta, A. C. Lamb, M. Atanasov, E. Bill, F. Neese and Z. L. Xue, Nat. Commun., 2018, 9, 2572 CrossRef PubMed; (i) F. S. Santana, M. Perfetti, M. Briganti, F. Sacco, G. Poneti, E. Ravera, J. F. Soares and R. Sessoli, Chem. Sci., 2022, 13, 5860 RSC; (j) S. Nain, M. Kumara and Md. E. Ali, Phys. Chem. Chem. Phys., 2023, 25, 14848 RSC; (k) A. Castro-Alvarez, Y. Gil, L. Llanos and D. Aravena, Inorg. Chem. Front., 2020, 7, 2478 RSC.
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2334787–2334790. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4dt00622d |
| This journal is © The Royal Society of Chemistry 2024 |